Chance-Constrained Based Voltage Control Framework to Deal with Model Uncertainties in MV Distribution Systems

Abstract

In this paper, a chance-constrained (CC) framework is developed to manage the voltage control problem of medium-voltage (MV) distribution systems subject to model uncertainty. Such epistemic uncertainties are inherent in distribution system analyses given that an exact model of the network components is not available. In this context, relying on the simplified deterministic models can lead to insufficient control decisions. The CC-based voltage control framework is proposed to tackle this issue while being able to control the desired protection level against model uncertainties. The voltage control task disregarding the model uncertainties is firstly formulated as a linear optimization problem. Then, model uncertainty impacts on the above linear optimization problem are evaluated. This analysis defines that the voltage control problem subject to model uncertainties should be modelled with a joint CC formulation. The latter is accordingly relaxed to individual CC optimizations using the proposed methods. The performance of proposed CC voltage control methods is finally tested in comparison with that of the robust optimization. Simulation results confirm the accuracy of confidence level expected from the proposed CC voltage control formulations. The proposed technique allows the system operators to tune the confidence level parameter such that a tradeoff between operation costs and conservatism level is attained.

1. Introduction

Distribution networks have been traditionally designed to meet the maximum load demand while respecting the imposed reliability and cost-effectiveness objectives. They are not prepared to host the distributed generation (DG) units, which boost the short-circuit power, create bidirectional power flows, and induce voltage rise issues [1].

In order to manage voltage constraints of modern distribution systems (also known as active distribution networks), various approaches have been investigated in the literature. The most common voltage control methods are based on using the on-load tap changer mechanism of the substation transformer [2,3,4,5] as well as the control of DG active and reactive powers [2,3,4,5,6,7,8,9,10]. Application of other control measures such as energy storage devices has been also investigated [11]. It is generally known that each of the above voltage control methods has its own advantages and drawbacks, and there is no perfect (single) voltage regulation method. In this regard, the focus has been directed towards coordinated voltage control algorithms based on centralized [2,3,4,5,6,7,8,9,10], decentralized [11,12,13], and distributed techniques, e.g., [14].

Despite differences of the existing voltage control methods in the literature, they have one common feature as they assume that a perfect and up-to-date network model is available. Distribution network models (and parameters) are, however, subject to inaccuracies and uncertainties arisen from the lack of sufficient measurements and presence of complex interdependencies among the network components. The model uncertainty thus is inherent in the distribution system analyses. The model uncertainty, however, differs from the uncertainty in the network working point originating from the intermittent DG powers. Although voltage control studies in the presence of the latter category (uncertainty linked to intermittent renewable generations) are quite rich in the literature, e.g., [15,16,17,18], the research on the voltage control in distribution systems subject to model uncertainty is scarce.

The model uncertainty is usually neglected in the voltage control process by assuming that the load demands are independent of the voltage, e.g., [1,3,4,5,6,7,8,9,10,11], by supposing that the system lines can be modelled with the series impedances, e.g., [1,2,8,9,11,12], that would remain unchanged over the time [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21], by disregarding the internal resistance of the substation transformer, e.g., [1,2,8,9,10,11], etc. In reality, power consumption of loads depends on the voltage, shunt admittances of lines must be taken into consideration, line resistances vary in function of the conductor temperature, and internal resistance of substation transformer has important impact on the node voltages [19].

Relying on the simplified deterministic network models can mislead the calculations and leads to solutions which do not completely remove the voltage violations, as shown in [19]. In order to address this issue, attempts have been made to develop voltage control methods that consider more exact models, for instance by incorporating the voltage dependency of loads [20] or shunt admittances of lines [21]. This strategy would not be effective since those models (and their parameters) are still subject to inaccuracies and uncertainties given that the exact parameters of the network model are not quantifiable, while the latter strategy, e.g., [20,21], increases the formulation complexity and computational burden of the developed control tools.

In addition, to deal with the model uncertainties, voltage control techniques based on the robust optimization have been developed in [22,23]. However, the solution of the robust optimization is known to be conservative. Alternatively, a data-driven voltage control method based on deep reinforcement learning has been proposed in [24,25] to cope with the uncertainties related to both network model and network working point, but the obtained solutions generally contain the same level of conservatism.

In order to cover the above gap in managing the uncertainties while avoiding insufficient or conservative solutions, in the current paper, a novel chance-constrained based voltage control framework is developed to deal with the model uncertainties inherent in the voltage control process. The salient feature of the proposed CC voltage control technique is that it defines a control decision which remains immunized against the uncertainty realization according to a predefined confidence level (or risk factor). This brings us an opportunity to tune the desired confidence level such that a compromise between the voltage management costs and conservatism degree can be achieved.

In view of the above discussion, the main contribution of this paper lies in the proposed formulation of the CC optimization for the voltage control task, which has the following features.

• It preserves the linearity of the original voltage control problem.
• It effectively addresses the complex coupling uncertainties present in the voltage control problem.
• It leads to accurate voltage corrections as expected from the imposed confidence level, which allows us to efficiently cope with the considered uncertainty sources.

The remainder of this paper is structured as follows. Section 2 formulates the voltage control task as a linear optimization problem, and studies impacts of model uncertainties on that problem. Section 3 introduces the concept of CC optimization, and Section 4 describes the proposed CC voltage control framework to deal with the model uncertainty. The studied test distribution system and considered sources of model uncertainty are presented in Section 5. Numerical simulations are conducted in Section 6 in order to evaluate the performance of proposed CC voltage control framework in comparison with the response obtained from the robust optimization formulation. Section 7 discusses further the obtained simulation results, and the paper conclusions are finally given in the Section 8.

2. Voltage Control Problem in MV Distribution System

2.1. A Linear Deterministic Formulation

Let consider the generic linear optimization formulation below where the decision variables $\mathrm{x}$ are defined such that the objective function (1) is minimized subject to the problem constraints (2) to (4). ${\mathrm{C}}^{\mathrm{T}}$ is the transpose vector of coefficients of linear objective function, $A_{eq}$ and $\mathrm{A}$ denote the linear equality and inequality matrices, respectively. The equality and inequality constraints are limited to $b_{eq}$ and $\mathbf{b}$ vectors, respectively. The upper and lower bounds on the control variables are defined by ${\mathbf{u}}_{\mathbf{b}}$ and ${\mathbf{l}}_{\mathbf{b}}$, respectively.

$$\mathrm{Min}: {\mathbf{C}}^{\mathbf{T}}\mathbf{x}$$

(1)

$$\mathbf{Ax}\le \mathbf{b}$$

(2)

$$A_{eq}\mathbf{x}=b_{eq}$$

(3)

$${\mathbf{l}}_{\mathbf{b}}\le \mathbf{x}\le {\mathbf{u}}_{\mathbf{b}}$$

(4)

The voltage control problem aims to remove the voltage violations in the studied system through an optimal exploitation of the available control measures. The voltage control task can be formulated as a linear optimization problem relying on the sensitivity analysis, e.g., [1,2,4,5,7,8,26,27]. The latter provides us with the impacts of control variable changes on the controlled parameters (i.e., the node voltages). Having this information from the sensitivity analysis allows us to neglect the AC power flow balance equations and eventually keeps the optimization problem linear. The sensitivity-based voltage control formulation can be seen as a linearized equivalent of the optimal power flow problem (e.g., [3,6]) that can be solved in almost real time. It constitutes a convex optimization problem (having linear objective function and constraints) that will guarantee the optimality of solutions obtained by the implemented voltage control algorithm. The linear sensitivity-based voltage control problem can be modelled as the following optimization formulation where the active and reactive powers of DGs as well as the transformer tap position act as the employed voltage control methods:

$$\mathrm{Min}: OF={{\displaystyle \sum }}_{x=1}^{\left|G\right|}\left(C_Q\mathsf{\Delta }{Q}_{DGx}+C_P\mathsf{\Delta }{P}_{DGx}\right)+C_{TR}\mathsf{\Delta }Ta{p}_{TR}$$

(5)

$${\displaystyle \sum }_{x=1}^{\left|G\right|}\left(\frac{\partial V_u}{\partial Q_{DGx}}\mathsf{\Delta }{Q}_{DGx}+\frac{\partial V_u}{\partial P_{DGx}}\mathsf{\Delta }{P}_{DGx}\right)+\frac{\partial V_u}{\partial V_{Tap}}\mathsf{\Delta }Ta{p}_{TR}\le \mathsf{\Delta }{V}_u^{req} \forall u,u\in U$$

(6)

$$0\le \mathsf{\Delta }{P}_{DGx}\le \left|P_{DGx}\right| \forall x, x\in G$$

(7)

$$\mathsf{\Delta }{Q}_{DGx}^{min}\le \mathsf{\Delta }{Q}_{DGx}\le \mathsf{\Delta }{Q}_{DGx}^{max} \forall x, x\in G$$

(8)

$$\mathsf{\Delta }Ta{p}_{TR}^{min}\le \mathsf{\Delta }Ta{p}_{TR}\le \mathsf{\Delta }Ta{p}_{TR}^{max}$$

(9)

where $\mathsf{\Delta }{P}_{DGx}$ and $\mathsf{\Delta }{Q}_{DGx}$ are the active and reactive power changes of DG x. $C_P$ and $C_Q$ give the weighting coefficients for the active and reactive power changes of DGs. $\mathsf{\Delta }Ta{p}_{TR}$ and $C_{TR}$ denote the transformer tap changes and its corresponding weighting coefficient, respectively. $G$ and $U$ are the sets including DG units and the buses with voltage violations, respectively. $\frac{\partial V_u}{\partial Q_{DGx}}$, $\frac{\partial V_u}{\partial P_{DGx}}$, and $\frac{\partial V_u}{\partial V_{Tap}}$ are voltage sensitivity coefficients of bus u with respect to the control variables.

The objective function ($OF$) of the voltage control task is given by (5), where the weighting coefficient of each voltage control measure defines the priority of its exploitation. These coefficients can represent the activation cost of each control measure. The inequality constraint (6) considers that the decision variable changes should return the violated voltages within the predefined voltage limits. Therefore, the right-hand side (RHS) of (6) gives the required voltage variations at the nodes with the voltage violations in order to manage the voltage constraints. The physical upper and lower limits on the control variable changes are taken into account using (7)–(9). Accordingly, $P_{DGx}$ gives the available active power of DG x to be curtailed. Also, $\mathsf{\Delta }{Q}_{DGx}^{max}$ and $\mathsf{\Delta }{Q}_{DGx}^{min}$ stand for maximum and minimum possible reactive power changes of DG x while respecting its capability curve. Finally, $\mathsf{\Delta }Ta{p}_{TR}^{max}$ and $\mathsf{\Delta }Ta{p}_{TR}^{min}$ define the possible upward and downward movements of the transformer tap changer, respectively. The voltage sensitivity data needed in (6) are obtained as follows.

• The voltage sensitivity with respect to nodal power changes: it is extracted from the inverse Jacobian matrix in the Newton-Raphson load flow (NRLF) study as explained in [19].
• The voltage sensitivity with respect to (substation) transformer tap changes: it is obtained using the perturb-and-observe method. In the latter, two consecutive load flow studies are performed, subject to one step change in the transformer tap position [2]. The voltage variation at the observed node subject to the step change applied to the perturbation node (the transformer tap position) is evaluated to derive the sensitivity of voltage at the observed node with respect to the transformer tap changer action.

2.2. Model Uncertainty Impacts

Model uncertainty is inherent in the voltage control task since an exact and up-to-date model of the distribution system is not generally at our disposal. In practice, the characteristics of network components (i.e., lines, loads and transformers) are subject to complex and dynamic dependencies, which are difficult to model. Therefore, inaccuracies and uncertainties arise from the assumptions and simplifications adopted during the network component modeling process. For instance, the distribution network analyses are generally carried out considering a fixed value of line resistances obtained at a given conductor temperature (e.g., 20 °C) while in reality, the line resistances vary with the conductor temperature changes [22,23]. Similarly, other types of model uncertainties are neglected in the network analysis when the loads are considered as voltage-independent, the resistance of substation transformer is disregarded, power factors of loads are assumed at a predefined value, etc. These sources of uncertainties have all impacts on the node voltages with various degrees, as studied in [19].

Concerning the linear voltage control formulation presented in (5)–(9), the model uncertainties will affect both left-hand side (LHS) and RHS of inequality constraint (6). Indeed, the model uncertainties will change the voltage sensitivity coefficients as well as the node voltages that respectively define the LHS and RHS of (6). The inequality constraint (6) incorporating model uncertainties is thus reformulated as:

$${\displaystyle \sum }_{x=1}^{\left|G\right|}\left(\frac{{\widetilde{\partial V}}_u}{\partial Q_{DGx}}\mathsf{\Delta }{Q}_{DGx}+\frac{{\widetilde{\partial V}}_u}{\partial P_{DGx}}\mathsf{\Delta }{P}_{DGx}\right)+\frac{{\widetilde{\partial V}}_u}{\partial V_{Tap}}\mathsf{\Delta }Ta{p}_{TR}\le {\widetilde{\mathsf{\Delta }V}}_u^{req} \forall u,u\in U$$

(10)

where $\tilde{y}$ indicates that $y$ is a random variable.

3. Chance-Constrained Optimization

Within the topic of optimization under uncertainty, the chance-constrained formulation proposes to immunize the constraints subject to uncertainty with a confidence level (probability), which allows us to manage the desired robustness level in regard to uncertainty. In other words, the obtained solution of the CC optimization satisfies the constraints subject to uncertainty with at least a given level of probability for all possible realizations of the uncertain parameters present in the respective constraints. Mathematically, the CC counterpart of (2), which is now subject to uncertainty, is expressed as [28,29]:

$$\mathrm{P}\left({\displaystyle \sum }_{j=1}^n{\tilde{a}}_{ij}{x}_j\le {\tilde{b}}_i\right)\ge 1-{ϵ}_i i=1, 2, \dots , m$$

(11)

where P means probability and $1-{ϵ}_i$ gives the confidence level defined for the constraint i (${ϵ}_i$ is the risk factor associated with constraint i). The constraint (11) constitutes a particular form of the CC optimization called in the literature the individual CC. In contrast, when all the constraints in (11), i.e., $i=1, 2, \dots , m$, are required to be simultaneously satisfied with a unique confidence level (i.e., when the RHS of (11) equals to $1-ϵ$), we have another sort of CC optimization, known as the joint CC [28,29]. Generally, the joint CC problems are more complex to formulate and solve due to the presence of more uncertain parameters and the existing coupling among them. In specific cases of the CC optimization, namely, when we deal with the additive uncertainty in the LHS [30,31] or when we have individual CC with RHS uncertainty, the linearity of initial deterministic constraint can be preserved. However, when the uncertainty in the LHS is proportional [30,31,32] or in case with the joint uncertainty, the CC formulation will constitute a nonlinear optimization. In the former case with the proportional uncertainty, the nonlinear problem can be recast as a second-order conic optimization that guarantees the optimality of the solution if we assume a Gaussian distribution of the uncertainty. In the latter case having joint CC, data-driven approaches have been proposed in the literature to deal with the complex coupling of uncertainties [28,29]. Reference [33] also proposes to relax and decompose the joint CC problem to the simplified individual CC.

4. Proposed Chance-Constrained Based Voltage Control Framework

In this section, the CC counterpart of the linear voltage control problem (5)–(9) is derived. To this end, some initial simplifications and assumptions are adopted. The impact of these assumptions will be evaluated through the numerical analyses carried out in Section 6. The proposed CC voltage control framework consists of three parts as described below.

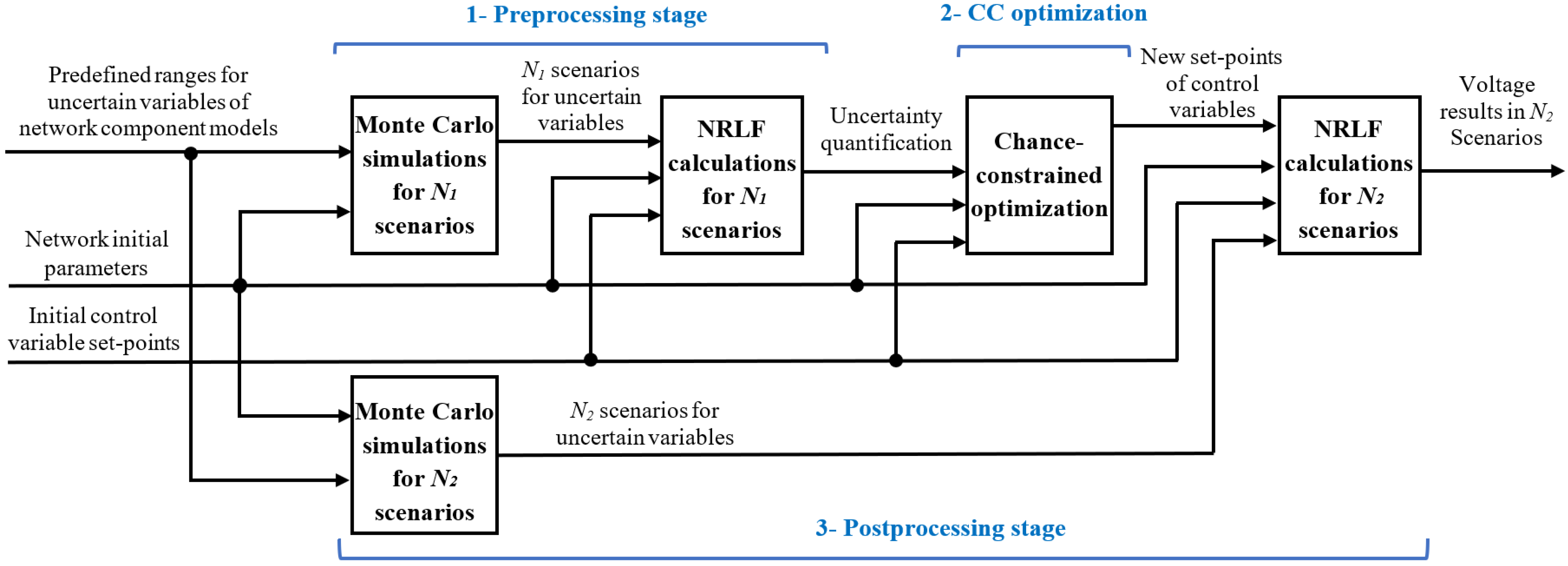
4.1. Preprocessing Stage (Uncertainty Quantification)

In the generic CC formulation, a random variable representing the considered uncertainty is defined according to a distribution function. In our voltage control problem, the uncertainty sources reside in the load, line, and substation transformer models (as explained in Section 5.2). These mentioned uncertainties have impacts on the LHS and RHS of (6), i.e., the voltage sensitivity coefficients and the required voltage modifications, respectively. However, their impacts are not a priory known. To quantify the uncertainty impacts on (6), we need a preprocessing step that first generates N₁ scenarios for uncertain parameters of network component models, and then evaluates those scenarios with load flow calculations. Doing so allows us to establish the CC voltage control formulation. Figure 1 presents the proposed framework to perform the CC voltage control task, and to validate the obtained results.

4.2. Formulating the Chance-Constrained Voltage Control Task

As mentioned before, model uncertainties have impacts on the RHS and LHS of (6). However, it is expected that these impacts are significantly higher on the RHS of (6) compared to the LHS. Indeed, the LHS of (6) includes the voltage sensitivity coefficients that give a linearized relationship between small changes in control variables and node voltages. Contrarily, the RHS of (6) is calculated based on the final node voltages according to a given network working point considering whole amounts of nodal load and generation powers. For the sake of simplicity and aiming at preserving the linearity of the original voltage control problem, we assume that the impact of model uncertainty on the LHS of (6) is negligible. It should be noted that we neglect the model uncertainty impacts on the voltage sensitivity coefficients for a given network operating point. If the latter changes, the voltage sensitivity coefficients are accordingly updated in the preprocessing stage of the proposed CC voltage control framework, while they are again considered to be independent of the model uncertainties, in the rest of voltage control procedure. The relevance of this approximation is evaluated in Section 6.

Disregarding the LHS uncertainties of (6) reduces the final CC voltage control problem to a category having uncertainty only in the RHS, which is mathematically more straightforward to formulate. The CC voltage control problem subject to the RHS uncertainty can be still of the individual or joint type. The respective formulation of mentioned CC categories is detailed below.

In case of the individual CC with the RHS uncertainty, constraint (11) can be simplified as:

$$\mathrm{P}\left({\displaystyle \sum }_{j=1}^n{a}_{ij}{x}_j\le {\tilde{b}}_i\right)\ge 1-{ϵ}_i i=1, 2, \dots , m$$

(12)

The above constraint indicates that the random parameter ${\tilde{b}}_i$ must attain a value greater than or equal to ${\displaystyle \sum }_{j=1}^n{a}_{ij}{x}_j$ with a probability at least equal to $1-{ϵ}_i$ for $i=1, 2, \dots , m$. Mathematically, this is equivalent to impose that the survival function of random variable evaluated at the LHS must be greater than or equal to the confidence level. The survival function is the complement of the cumulative distribution function (CDF) denoted $\Phi$. In other words, the survival function is equivalent to $1-\Phi$. Constraint (12) can be accordingly rewritten as follows [28].

$$1-{\Phi }_{{\tilde{b}}_i}\left({\displaystyle \sum }_{j=1}^n{a}_{ij}{x}_j\le {\tilde{b}}_i\right)\ge 1-{ϵ}_i i=1, 2, \dots , m$$

(13)

The above constraint can be simplified to [28]:

$${\displaystyle \sum }_{j=1}^n{a}_{ij}{x}_j\le {\Phi }_{{\tilde{b}}_i}^{-1}\left({ϵ}_i\right) i=1, 2, \dots , m$$

(14)

where ${\Phi }^{-1}$ stands for the inverse CDF or the quantile function. The constraint (14) is applied to the presented voltage control problem in Section 2.1. The resulting CC equivalent of constraint (6) (in the deterministic voltage control problem) is given below.

$${\displaystyle \sum }_{x=1}^{\left|G\right|}\left(\frac{\partial V_u}{\partial Q_{DGx}}\mathsf{\Delta }{Q}_{DGx}+\frac{\partial V_u}{\partial P_{DGx}}\mathsf{\Delta }{P}_{DGx}\right)+\frac{\partial V_u}{\partial V_{Tap}}\mathsf{\Delta }Ta{p}_{TR}\le {\Phi }_{{\widetilde{\mathsf{\Delta }V}}_u}^{-1}\left({ϵ}_u\right) \forall u,u\in U$$

(15)

The RHS of (15) is known from the analysis carried out in the preprocessing stage. ${\Phi }_{{\widetilde{\mathsf{\Delta }V}}_u}^{-1}\left({ϵ}_u\right)$ gives us the required voltage modification to remove the voltage violation at bus u corresponding to the $ϵ$th quantile of the vector of uncertain voltages at bus u. The constraint (15) leads to a joint CC formulation when it is aimed to immunize all the nodes having voltage violations ($\forall u,u\in U$) with a unique risk value $ϵ$. Given the complex coupling of uncertainties in the joint CC voltage control problem, the individual CC formulation is preferred that can guarantee the linearity of the voltage control problem. In this regard, to convert the joint CC voltage control problem to an individual type, two methods are suggested as follows.

• CC-Method I: It considers only the bus with the biggest voltage violation in the system as the CC. In this case, we are interested in finding a solution, which is immunized with a probability at least equal to $1-ϵ$ against ${\Phi }_{\mathsf{\Delta }V}^{-1}\left(ϵ\right)$ at the bus with the biggest voltage violation.
• CC-Method II: It replaces the unique risk factor of joint CC (${ϵ}^{JCC}$) with a more conservative bound given below according to Bonferroni’s inequality [28,29]. As a result, the initial joint CC can be converted to an approximated individual CC with a reduced risk factor equal to ${ϵ}_i^{ICC}$.

$${ϵ}^{JCC}\le {{\displaystyle \sum }}^{ }{ϵ}_i^{ICC}, i=1, 2, \dots , m$$

(16)

In the CC-Method II, we assume that (16) is applied to the bus with the biggest voltage violation at each feeder of the system (to limit the number of individual CC). We evaluate the performance of the abovementioned methods in the context of the voltage control problem subject to model uncertainty in Section 6.

Overall, the CC voltage control tool has the same objective function and bounds on the control variables as those of the deterministic voltage control approach given by (5) and (7)–(9). The difference of deterministic and CC voltage control methods resides in their voltage constraints. While in the former, the model uncertainty is neglected in (6), the latter considers it via (15). In other words, the resultant individual CC of the (initial joint CC) voltage control problem derived according to CC-Method I and CC-Method II replaces (6) to construct the proposed CC voltage control tool.

4.3. Postprocessing Stage (Result Validation)

The abovementioned CC-based voltage control formulation determines the new set-points of control variables such that the desired level of robustness against model uncertainty can be achieved. In order to verify the latter, complementary analyses are conducted on the obtained set-points of control variables. To this end, Monte Carlo (MC) simulations are performed to generate N₂ scenarios for uncertain parameters of the network component models. Load flow studies are then carried out on each of the N₂ scenarios considering the new set-points of control variables obtained by the CC-based voltage control and other network data. The obtained nodal voltages in N₂ scenarios will be finally analyzed to validate the robustness level of the CC solution in N₂ realizations of uncertainties associated with the network component models.

In the preprocessing stage (prior to formulating the CC voltage control problem), when selecting the needed number of scenarios (i.e., N₁) for capturing uncertainties and defining their impacts, the requirement regarding the execution time of the voltage control task must be considered. Such a limit does not exist when N₂ scenarios are generated to verify the CC results since the corrective decisions have been already taken. Thus, N₂ can be much bigger than N₁ so that the CC voltage control results can be tested for complementary scenarios that are not necessarily included among N₁ scenarios of the preprocessing stage. It should be noted that the defined variation ranges for uncertain parameters of network component models are identical in both preprocessing and postprocessing stages.

5. Studied Distribution System

5.1. Original Studied Distribution System Having Deterministic Models and Parameters

The performance of the proposed CC voltage control framework is evaluated on the so-called “HVUG” test case of the United Kingdom generic distribution system (UKGDS) shown in Figure 2. It is an 11 kV distribution network with underground cables, which includes 77 buses and 8 radial feeders. It feeds 75 load buses (starting from node 3 to node 77) and hosts 22 DG units. The nominal active and reactive powers of loads equal 24.27 MW and 4.85 Mvar, respectively. The DG units are identical, having the rated powers of 3.5 MW. Node 1 is the slack bus connected to the primary side of the substation transformer. Node 2 is connected to the secondary side of the transformer where the transformer tap changer is installed. The substation transformer is represented by a pure reactance equal to 12.5% pu in the transformer base power (80 MVA). The DG capability curves are extracted from [1]. The system loads are voltage independent, distribution lines (cables) are represented by their series longitude impedances, and active powers of DGs are modelled with a negative load.

5.2. Adapted Network Model to Incorporate Considered Sources of Uncertainties

In the original 77-bus UKGDS shown in Figure 2, network components are represented with their simplified deterministic models. Particularly, the system loads are supposed to be voltage-independent, power factors of loads are assumed to be precisely known, internal resistance of substation transformer is disregarded, shunt admittances of cable lines are neglected, and cable resistances are not expected to be affected by the conductor temperature variations. However, these assumptions do not necessarily hold in reality.

Given that the exact and up-to-date (values of) parameters of network component models are not quantifiable, we represent them as random variables that can vary within the predefined intervals according to a defined normal distribution function (more information can be found in [19]).

In this study, our random variables to incorporate the model uncertainty impacts into the voltage control problem are line resistances, shunt admittances of lines, load voltage dependency exponents (see [34]), load power factors, and internal resistance of substation transformer.

6. Simulation Results

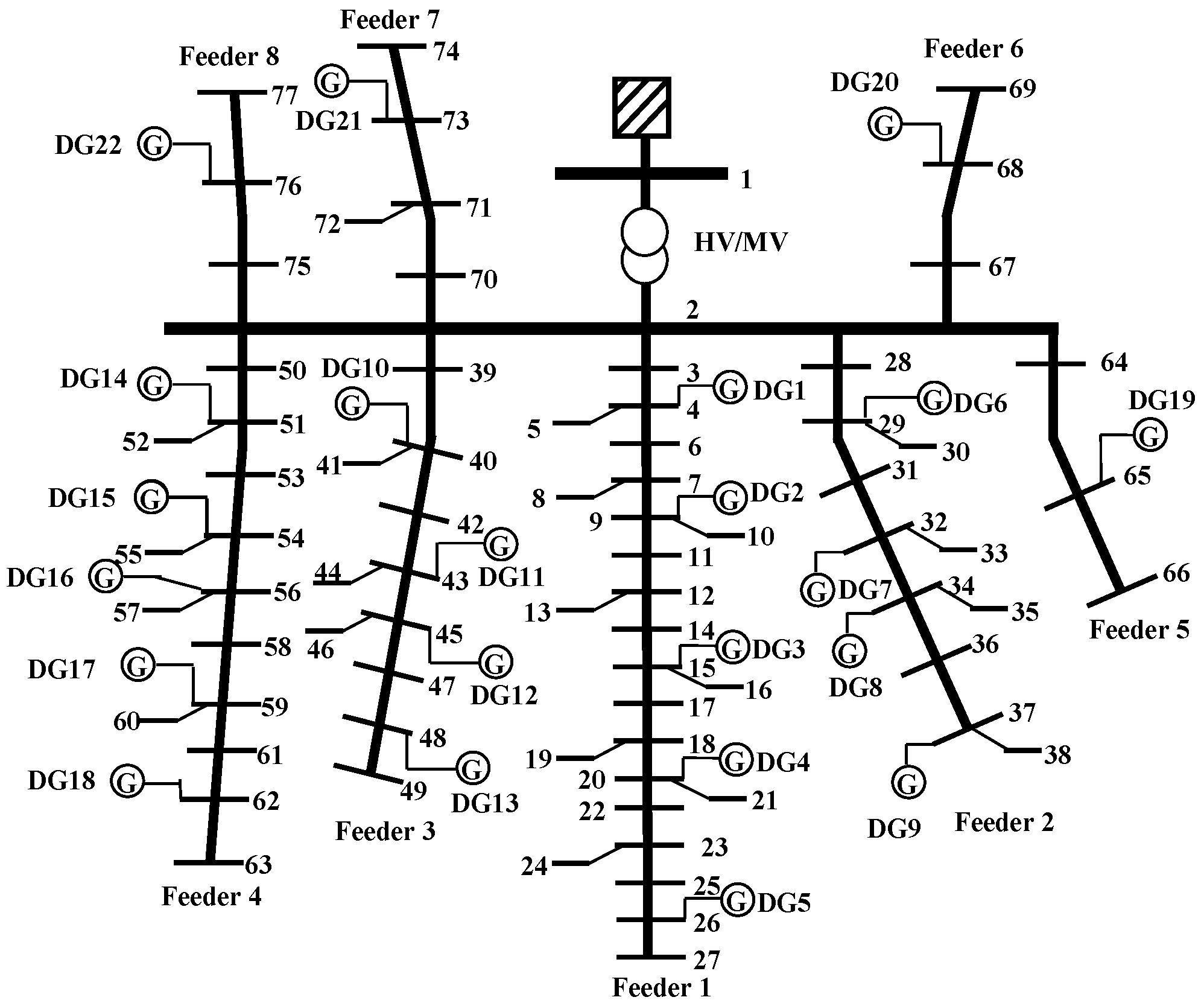
The proposed CC voltage control framework presented in Section 4 is implemented in the MATLAB environment. The performance of the CC voltage control tool is tested on the UKGDS shown in Figure 2 considering an operating point leading to the voltage rise issues. In the studied working point, it is assumed that the load demands are low (=10% of their nominal values) while the DG active powers are at 90% of their rated values. The selected network operating point constitutes the most difficult voltage management task having the highest possible voltage violations. By validating the performance of the proposed voltage control algorithm on the selected working point, it can be expected that the proposed algorithm would be able to manage other network operating points, having naturally smaller voltage violations.

In order to comply with the constraint regarding the calculation time of the voltage control task, in the preprocessing stage (prior to forming the CC optimization), 500 in-sample scenarios (N₁ = 500) are generated by the MC simulations. However, to validate the decisions taken by the CC voltage control tool, the number of out-of-sample scenarios is increased to 5000 (N₂ = 5000).

In the voltage control procedure, it is supposed that the transformer tap changer action has the smallest weighting coefficient compared to other control variables that is equal to 1 (C_TR = 1) while DG reactive power changes are weighted by a factor which is 50% bigger than the tap changer one (i.e., C_Q = 1.5). Also, active power curtailment of DGs is assigned to a coefficient, which is 100% bigger than that of the tap changer (i.e., C_P = 2). The (upper) permitted voltage limit is set to 1.03 pu.

6.1. Model Uncertainty Impacts on Node Voltages

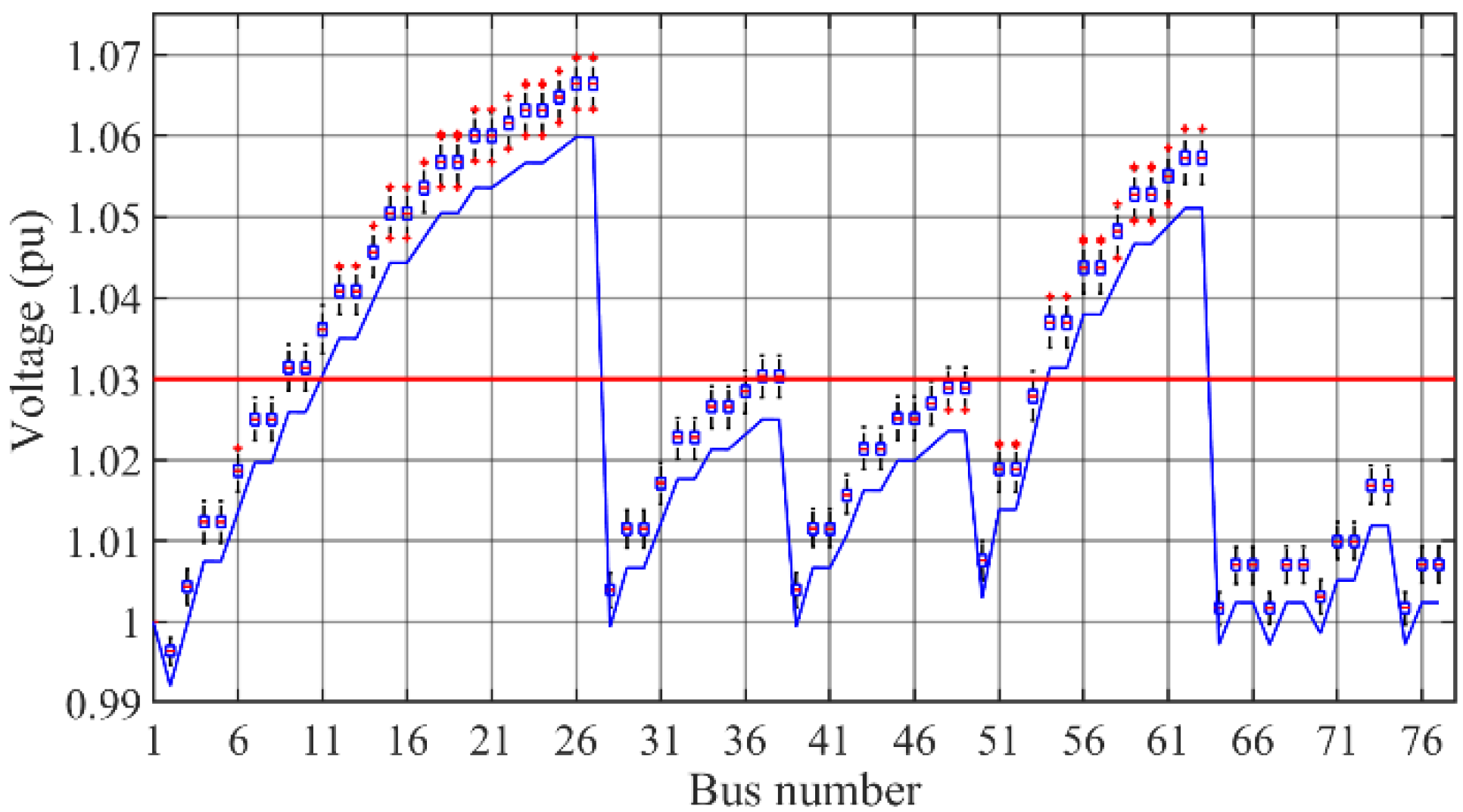
In the first step of our analysis, we are interested to quantify and visualize the impacts of considered sources of model uncertainty on the nodal voltages. To this end, we illustrate in Figure 3, the boxplots of nodal voltages obtained in the preprocessing stage of the CC framework (presented in Figure 1) considering N₁ generated scenarios. Besides, to evaluate the possible nodal voltage variations due to model uncertainty impacts with respect to the case neglecting those effects, we present on the same graph in Figure 3 the node voltages obtained by the deterministic (simplified) network model (which disregards the model uncertainties) with the solid blue line.

As it can be seen in Figure 3, due to model uncertainty impacts, node voltages can have considerable deviations from their own initial values obtained by the deterministic simplified models (shown with the solid blue line). Precisely, these deviations can reach up to 0.01 pu at bus 26, which contains the biggest voltage violation of the studied system. Clearly, the voltage control algorithm relying on the deterministic simplified models (neglecting the model uncertainty impacts) cannot manage the voltages found within the presented boxplots. This motivates the utilization of the voltage control tool that incorporates the model uncertainty impacts while taking the control decisions.

6.2. Performance Analysis of the Chance-Constrained Voltage Control Framework

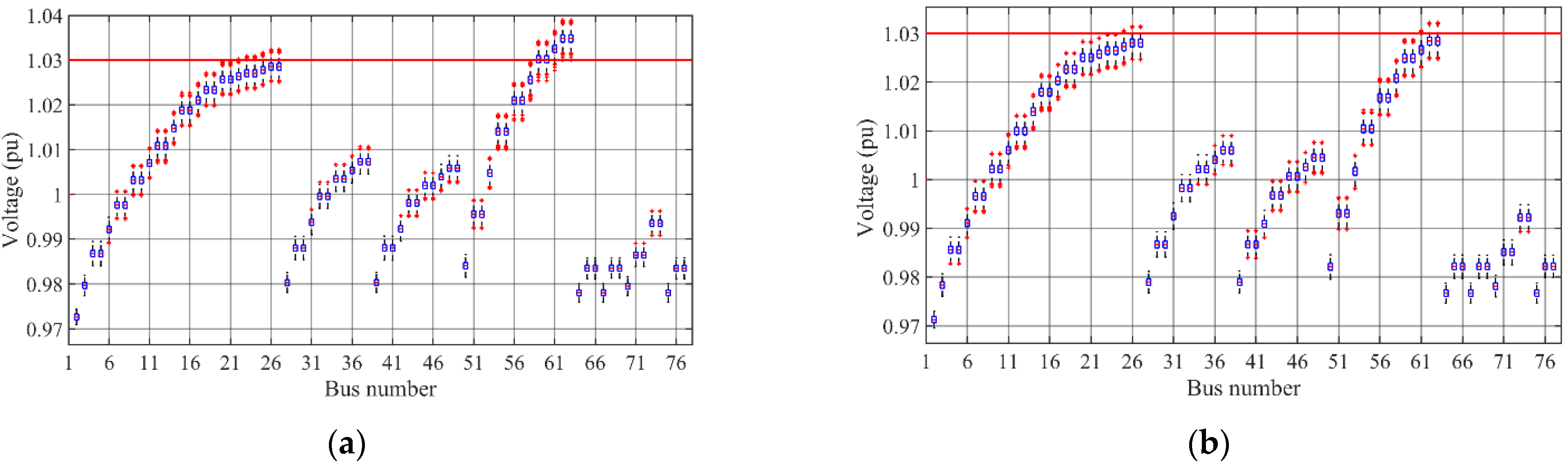
In the second part of this section, we evaluate here the performance of the proposed CC formulation to manage the initial voltages subject to uncertainty (as shown in Figure 3). Both proposed methods leading to the individual CC formulation (namely, (i) relying on the biggest voltage violation of the system and (ii) based on (16)) are tested here. In the former case, the voltage at bus 26 having the biggest initial voltage violation of the system is modeled as CC. In the latter case, buses 26 and 62 having the biggest voltage violations of their own feeders are considered with CC. Figure 4 shows the boxplots of nodal voltages obtained in the postprocessing stage of the CC voltage control framework. The desired confidence level is set to 90% (i.e., $ϵ=0.1$).

In Figure 4a, one can observe that boxplots of voltages corresponding to buses located at the end of feeder 4 (i.e., buses 62 and 63) are placed outside the permitted voltage range. This means that for every possible realization of uncertainty, there will be a voltage violation at those buses, which is not desirable. It is explained by the fact that in Figure 4a (corresponding to CC-Method I), the bus with the biggest violation is only considered with CC (i.e., bus 26). Thus, the possible voltage violations in other feeders are not taken into account. Such a problem does not exist in Figure 4b, where the biggest voltage violation of each feeder is incorporated into the CC voltage control problem according to (16). 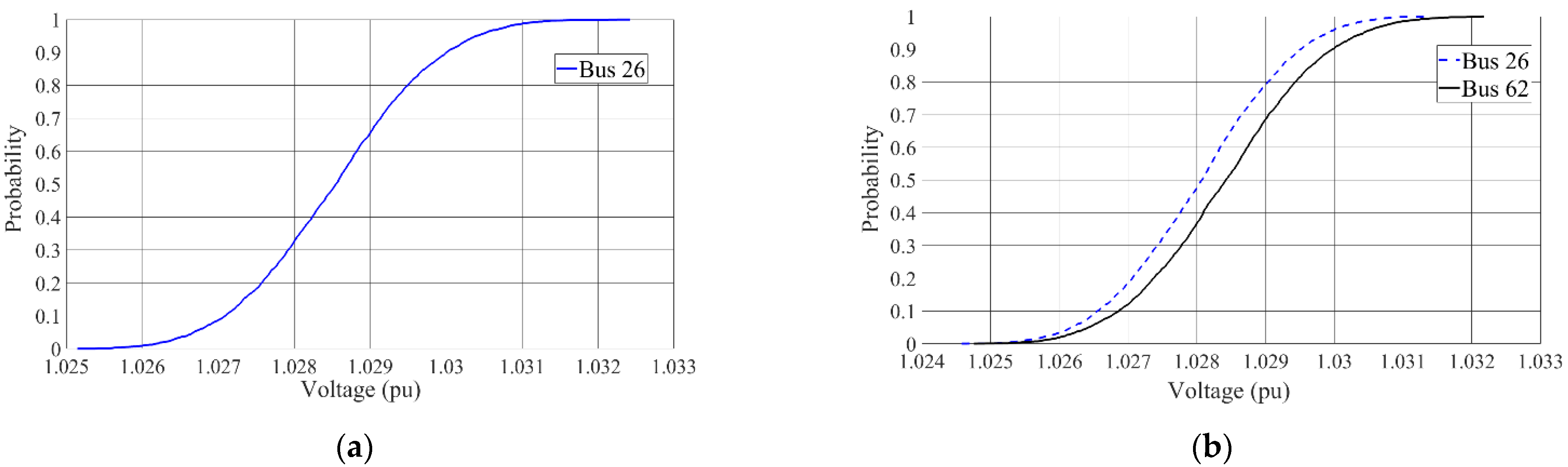In order to have a more exact evaluation, Figure 5 presents the CDF of corrected voltages corresponding to the boxplots shown in Figure 4 for buses 26 and 62.

In Figure 5a, it is seen that the 90th quantile of the voltage at bus 26 (corresponding to the node represented with CC) is exactly equal to 1.03 (i.e., the permitted voltage limit). It reveals that the imposed in-sample CC condition to have the confidence level equal to at least 90% at bus 26 is satisfied with a very high accuracy in the out-of-sample evaluation of voltage at bus 26 in the N₂ scenarios of postprocessing stage. This finding also validates the adopted assumption regarding the fact that the impact of model uncertainty on the LHS of (6) is negligible. Indeed, the implemented CC optimization does not consider the uncertainty in the LHS of (6) and its results are quite accurate.

In Figure 5b, showing the results of CC-Method II where buses 26 and 62 are modelled with CC, it is found that the confidence level of 90% imposed by the CC formulation is respected at those buses, too, but with slightly reduced accuracy at bus 26 compared to the former CC formulation (i.e., Method I).

Table 1. Control decisions taken by the proposed CC voltage control framework with $ϵ=0.1$.

	CC-Method I	CC-Method II
ΔQDGx (Mvar)	ΔQDG5 = 2.31	ΔQDG5 = 2.215
	ΔQDG4 = 0.0744	ΔQDG18 = 0.998
ΔPDGx (Mvar)	NA	NA
ΔTapTR	−4	−4
OF	7.576	8.819

presents the demanded contributions of DG powers and necessary transformer tap movements to manage voltage violations using both above CC methods. In Table 1 and hereafter, NA indicates that a specific control action is not applied. In addition, DGs with the power changes are only indicated in the table and for the rest of DGs (which are not mentioned), power changes are zero.

In Table 1, we can see that within both studied CC methods, the tap changer of the substation transformer needs to move (decrease) its position by 4 steps since it has the smallest weighting coefficient (cost). In CC-Method I, the reactive powers of DGs connected to feeder 1 are also changed since the voltage violation at bus 26 is only considered and those DGs have the highest impacts on the voltage at bus 26. In contrast, using CC-Method II, DGs located in feeders 1 and 4 are both employed to manage the CC voltage of buses 26 and 62. It is clearly observed that the CC-Method II requires more control efforts to manage the voltage control problem as it considers the voltage of bus 62, as well. In addition, the approximation and conservatism inherent in (16) can contribute to the increase in objective function of the CC-Method II with respect to that of the CC-Method I. The latter contribution (linked to (16)) is, however, of less importance than the former (relating to considering extra nodes in the CC voltage control problem).

6.3. Comparative Analysis of Chance-Constrained and Robust Voltage Control Approaches

In the last part of this section, we compare the performance of the proposed CC voltage control with that of the robust voltage algorithm (RVCA) developed in [23] in terms of the conservatism degree of their solutions. Similarly to the proposed CC voltage control framework of this work, the RVCA of [23] relies on the preprocessing stage for uncertainty quantification, and it employs the sensitivity analysis to linearize the relationships between control variables and node voltages. For the sake of comparison of results, the considered network, models and parameters, initial working point, sensitivity analysis methods, bounds on random parameters, initial conditions, etc., are assumed identical in both CC voltage control tool and RVCA.

Table 2. Control decisions taken by the proposed CC framework and the RVCA.

	DVCA	CC-Method I $\mathit{ϵ}=0.2$	CC-Method II $\mathit{ϵ}=0.2$	CC-Method I $\mathit{ϵ}=0.05$	CC-Method II $\mathit{ϵ}=0.05$	RVCA
ΔQDGx (Mvar)	ΔQDG5 = 1.363	ΔQDG5 = 2.301	ΔQDG5 = 2.165	ΔQDG5 = 2.31	ΔQDG5 = 2.241	ΔQDG5 = 2.31
			ΔQDG18 = 0.942	ΔQDG4 = 0.098	ΔQDG18 = 1.034	ΔQDG18 = 1.194
ΔPDGx (Mvar)	NA	NA	NA	NA	NA	NA
ΔTapTR	−4	−4	−4	−4	−4	−4
OF	6.044	7.451	8.661	7.612	8.913	9.361

presents the control variable changes defined by the presented CC voltage control methods for the risk factors equal to 0.2 and 0.05 as well as the RVCA results, which are immunized against the worst realization of uncertainty. In addition, Table 2 gives the corrective control decisions taken when the model uncertainty impacts are neglected by the so-called deterministic voltage control algorithm (DVCA) presented in (5)–(9).

In Table 2, one can observe that the smallest objective function corresponds to the DVCA (=6.044) that disregards the model uncertainty impacts by considering the nominal parameters of network component models. From the voltage results shown in Figure 3, it is, however, known that the response of such a voltage control strategy would not be sufficient to completely remove the voltage violations subject to model uncertainty.

Considering the results obtained by the proposed CC formulations, in Table 2, it is seen that the CC-Method I (only modeling the node with the worst voltage violation as the CC) leads to smaller objective functions compared to those of the CC-Method II. This finding is in line with the results given in the Table 1. Indeed, in order to provide the protection against voltage violations in other nodes (feeders) of the system according to (16), the CC-Method II requires more control resources that result in a higher objective function. In addition, in Table 2, it is noticed that by decreasing the risk factor ($ϵ$), the objective function of the CC voltage control tool increases to provide the required protection against the uncertainty realization. For instance, using the CC-Method II, the risk factors of 0.2, 0.1, and 0.05 respectively lead to the objective functions equal to 8.661, 8.819, and 8.913. In order to verify the accuracy of corrected voltage results by the proposed CC voltage control techniques,

Table 3. Out-of-sample analysis of node voltages corresponding to the imposed confidence level obtained by the proposed CC methods.

	CC-Method I $\mathit{ϵ}=0.2$	CC-Method II $\mathit{ϵ}=0.2$	CC-Method I $\mathit{ϵ}=0.05$	CC-Method II $\mathit{ϵ}=0.05$
${\Phi }_{V_{26}}^{-1}\left(ϵ\right)$ (pu)	1.0299	1.02942	1.02993	1.02927
${\Phi }_{V_{62}}^{-1}\left(ϵ\right)$ (pu)	1.03594	1.02994	1.03679	1.02996

gives the out-of-sample (corrected) voltage values corresponding to the imposed confidence level at buses 26 and 62. The latter buses contain the biggest voltage violations of feeders 1 and 4, respectively.

In Table 3, we can observe that using the CC-Method I, the imposed confidence level relating to the voltage magnitude at bus 26 (i.e., the bus with the biggest voltage violation of the system) is satisfied with a high accuracy. Indeed, the corrected voltage magnitude at bus 26 corresponding to the imposed confidence level (${\Phi }_{V_{26}}^{-1}\left(ϵ\right)$) is quite close to the permitted voltage limit (=1.03 pu). However, it is seen that the control actions taken by the CC-Method I cannot manage the voltage rise at bus 62 since the latter bus is not integrated into this CC voltage control formulation. In contrast, the CC-Method II provides the voltage results that are slightly more conservative (arisen from approximation inherent in (16)) but it can handle the voltage violations of both buses 26 and 62 located in feeders 1 and 4, respectively, as can be seen in Table 3. It should be noted that in Table 3, the closer the out-of-sample (corrected) voltage results are to the permitted 1.03 pu voltage limit, the more exact the employed CC formulation is.

Finally, by taking into account the RVCA results given in Table 2 (having the objective function equal to 9.361), it is revealed that the proposed CC voltage control formulations allow us to adjust the robustness level of the voltage control problem through modifying the risk factor ($ϵ$).

7. Discussion

The simulations carried out in the previous section confirm that the proposed CC voltage control framework can effectively deal with the model uncertainty inherent in the distribution systems. It enables us to adjust the desired confidence level according to which we aim to immunize the voltage control solution subject to uncertainty realizations. While the solution of the voltage control method relying on deterministic simplified models might be insufficient to completely manage the voltage constraints, and on the other hand, the solution of the robust voltage control technique could appear too conservative, the proposed CC framework allows us to find a compromise between the voltage management costs and the conservatism degree. It should be noted that the desired conservatism degree depends not only on the costs of control decisions, but also on the costs associated with the voltage violations. In other words, the optimal risk factor should be determined in accordance with, on the one hand, the costs of corrective control actions, and on the other hand, the voltage violation costs. The more crucial the voltage violation management is, the more justified the price of robustness to pay will be.

The simulation results reveal that the CC-Method I in which the voltage of the bus with the biggest voltage violation is constrained to a confidence level can accurately satisfy the imposed probability condition at that bus, but it cannot address the voltage violations of buses in other feeders of the system. Consequently, the latter method is rather suited for the MV distribution systems with a single feeder. In contrast, the CC-Method II is less accurate (and more conservative), being based on a reduced risk factor (obtained according to (16)), but it can effectively be applied to the distribution systems with multiple feeders.

In this paper, it is also shown that impacts of considered model uncertainty sources on the LHS of voltage constraint (6) (i.e., the voltage sensitivity coefficients) are negligible. Our numerical tests confirm that while being subject to considered model uncertainty sources of this paper, the standard deviation of all sensitivity coefficients in the LHS of (6) does not exceed 0.001 of its respective expected value, which indicates the minor impact of model uncertainties on the voltage sensitivity coefficients. On the contrary, it is demonstrated in Figure 3 that the model uncertainty can cause considerable deviations in node voltages, and consequently, can change the RHS of (6) with respect to the values obtained by the deterministic network model. These two findings lay the foundation of another important conclusion of this paper, that when the network model is integrated into a voltage control tool to evaluate the initial system state (initial voltages), the model uncertainty can noticeably mislead the voltage control problem analyses, resulting in infeasible or inefficient control decisions. Such a problem inherently applies to a wide range of voltage control techniques developed in the literature [1,3,4,5,6,7,8,9,10,11,12,13,15,16,17,18,19,20,21,22,23,24]. Contrarily, when a voltage control tool receives the initial voltages based on the real voltage measurements (and not from a state estimation interface or a load flow study relying on the simplified network model), the model uncertainty impacts on the voltage control problem would be of a minor importance since the uncertainty in initial node voltages (or uncertainty in the RHS of (6)) is removed thanks to the voltage measurements. In the literature, examples of such a voltage control scheme relying on real measurements, like [2], are scarce.

8. Conclusions

A chance-constrained (CC) framework is developed in this paper to deal with the model uncertainty impacts inherent in the voltage control problem of MV distribution systems. Relying on the linearized formulation of the voltage control problem with the voltage sensitivity analysis, its CC counterpart is derived by incorporating uncertainty impacts into the former formulation. The voltage control problem under model uncertainty, consequently, is formulated as a joint CC optimization with right-hand side (RHS) uncertainty. Aiming at preserving the linearity of the original formulation, two methods are proposed to decompose the complex joint couplings of the RHS uncertainties. The developed CC formulations are finally tested on the 77-bus, 11 kV radial distribution system. The simulation results confirm the accuracy of the confidence level expected from both CC formulations. Furthermore, comparative analysis of the CC-based voltage control framework having different risk factors and the voltage control method based on the robust optimization reveals that the proposed CC framework allows us to adjust the robustness level of solutions to find a compromise between the voltage management costs and the desired conservatism level.

Another main finding of this paper relates to the fact that the model uncertainty impacts are of a great importance when calculating the initial system state (initial voltages), while they have minor effects on the voltage sensitivity coefficients. Consequently, the model uncertainty effects can be neglected if a voltage control scheme works based on the real voltage measurements. Otherwise, defining the system state (initial voltages) based on the simplified deterministic models would mislead the voltage control decisions.