Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids
Abstract
:1. Introduction
1.1. The Purpose, Objectives, and Hypothesis of Research
- It is possible to define minutely requirements and constraints of the charging equipment and individual buses at the aggregate level in such a way that taking them into account in an hourly model allows obtaining the feasible disaggregated charging schedules.
- The hourly charging model can be incorporated into the auction-clearing problem, extending the standard formulation with new bidding parameters adopted for storage-based participants.
1.2. Literature Review
1.3. Contribution
- We formulate new mixed-integer linear programming aggregation models regarding the detailed, minutely characteristics and constraints of the charging equipment and the buses. They determine charging availability expressed as minimum and maximum hourly energy requirements.
- We propose only a few aggregated bids parameters that lead to incorporating linear variables and constraints into the standard auction model. The extended auction model determines aggregated hourly charging plan.
- We formulate the new mixed-integer linear programming disaggregation model linking the auction-based hourly plan and the detailed charging characteristics.
- We demonstrate that the bus fleet can be economically scheduled with an auction-clearing model with suitable bid parameters.
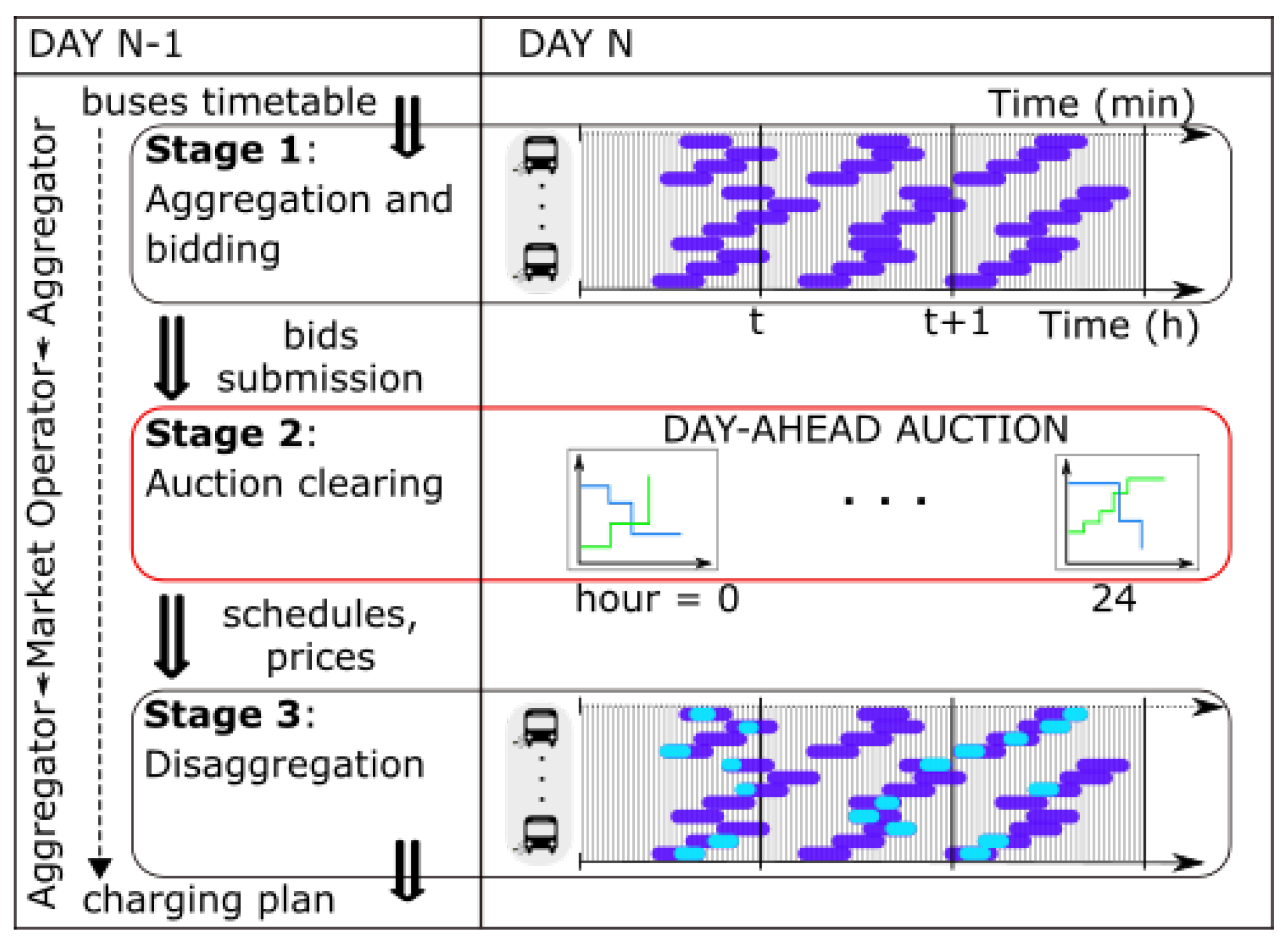
2. Materials and Methods
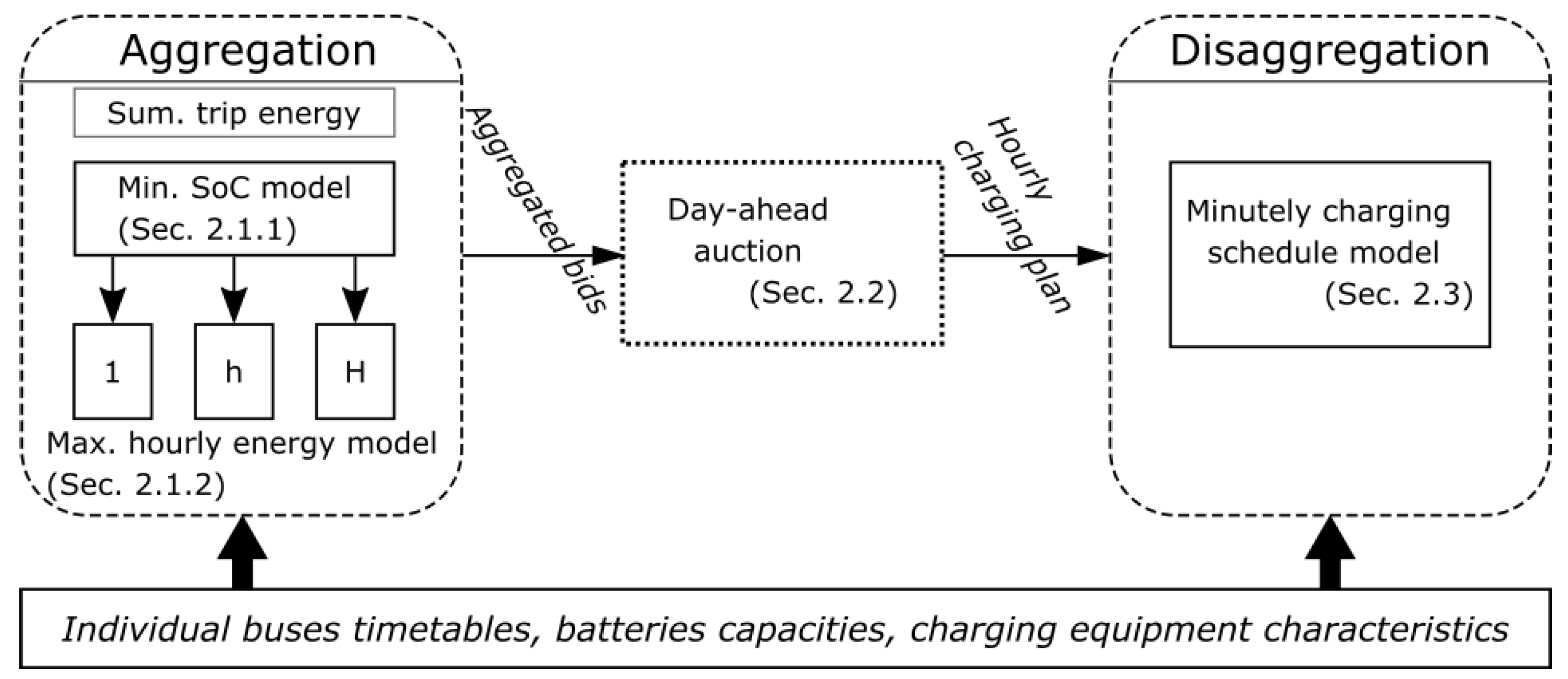
2.1. Aggregation Model
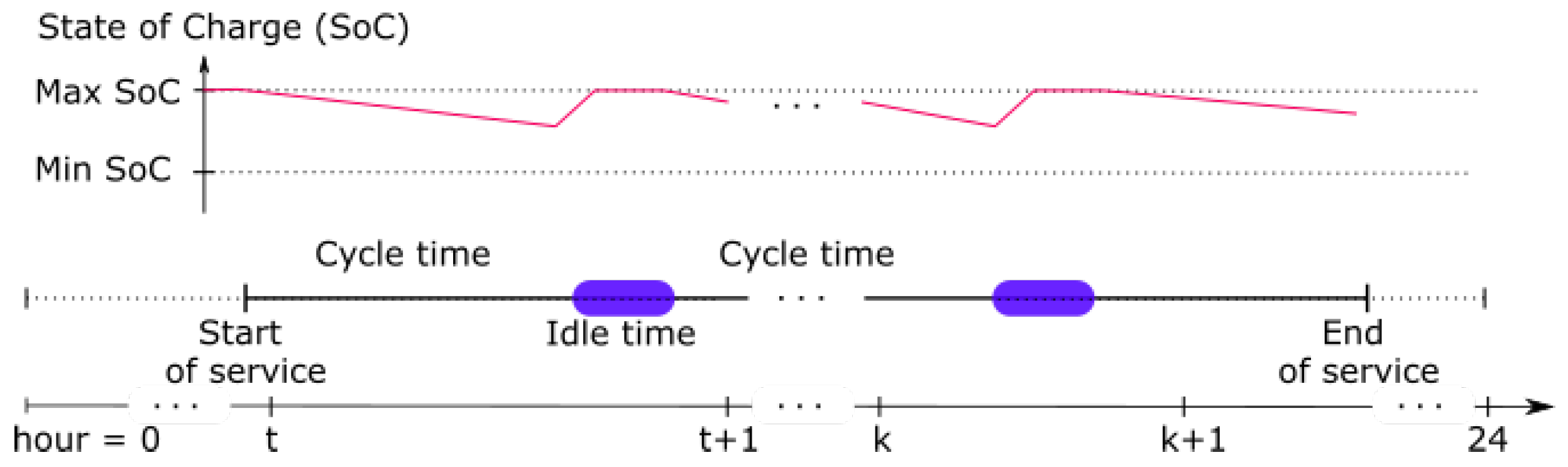
2.1.1. Minimum Hourly SoC Level
2.1.2. Maximum Hourly Energy Requirements
2.2. Auction Model
2.3. Disaggregation Model
2.4. Summary
3. Results
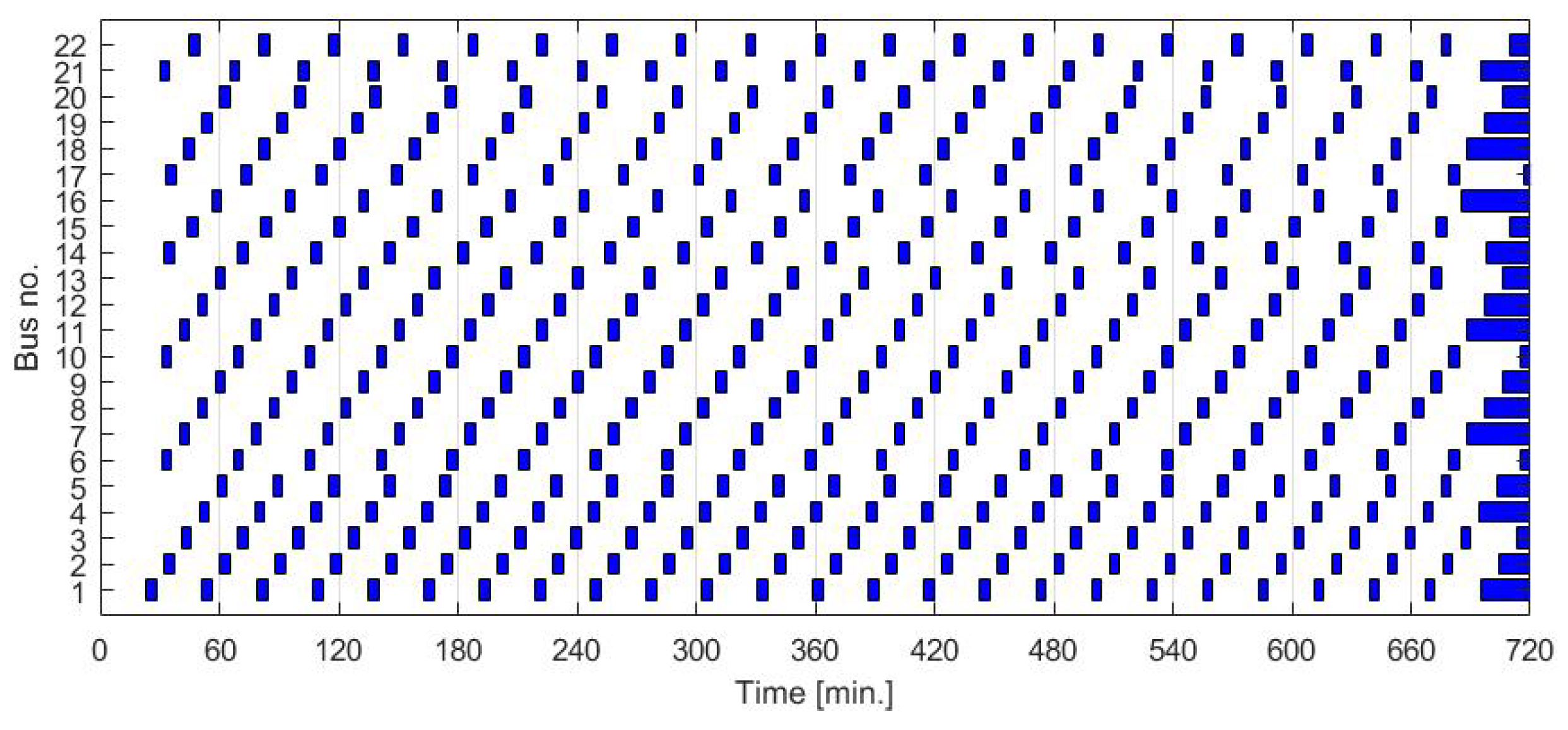
3.1. Data
3.2. Results of the Proposed Approach
3.2.1. Aggregation Results
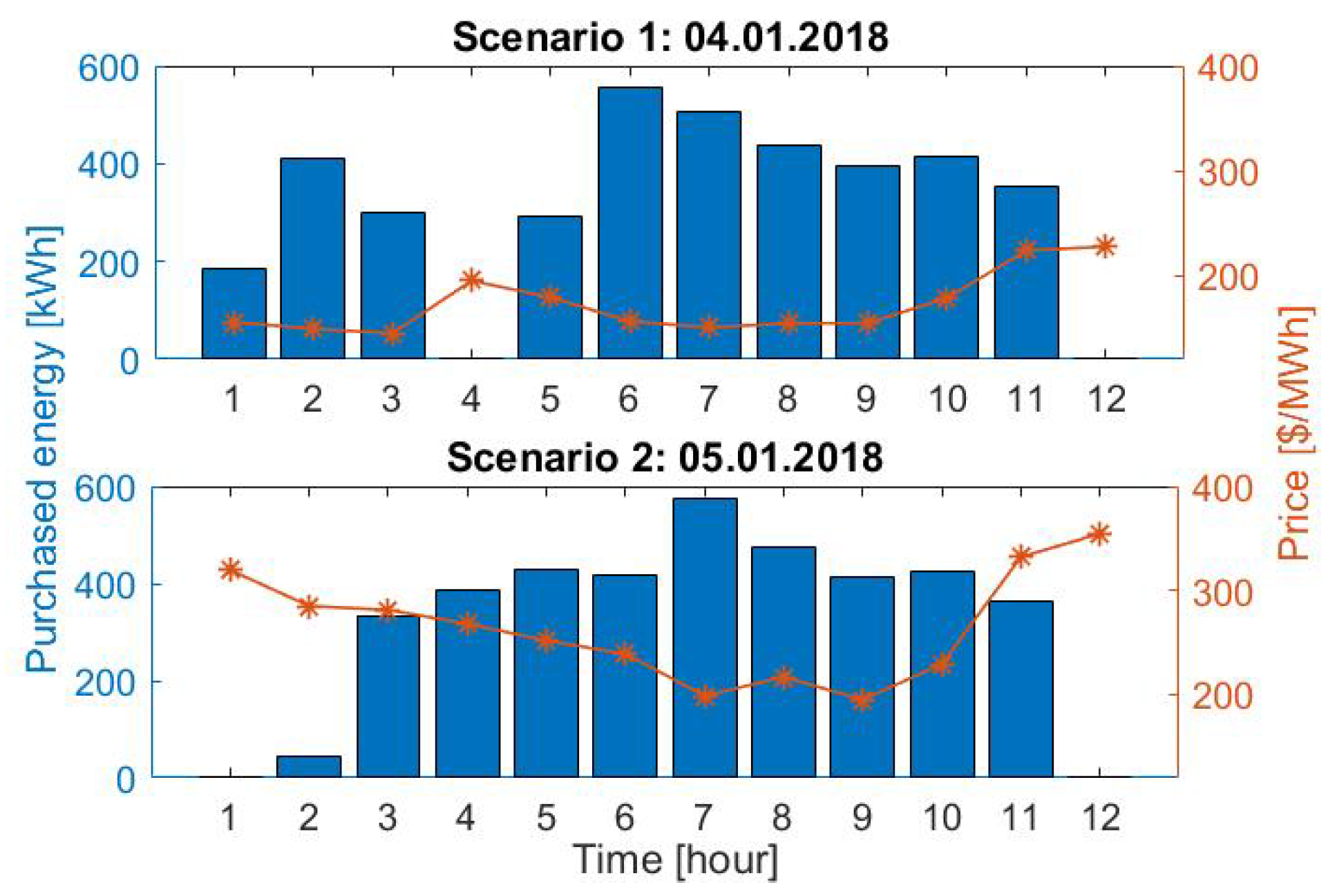
3.2.2. Auction Results
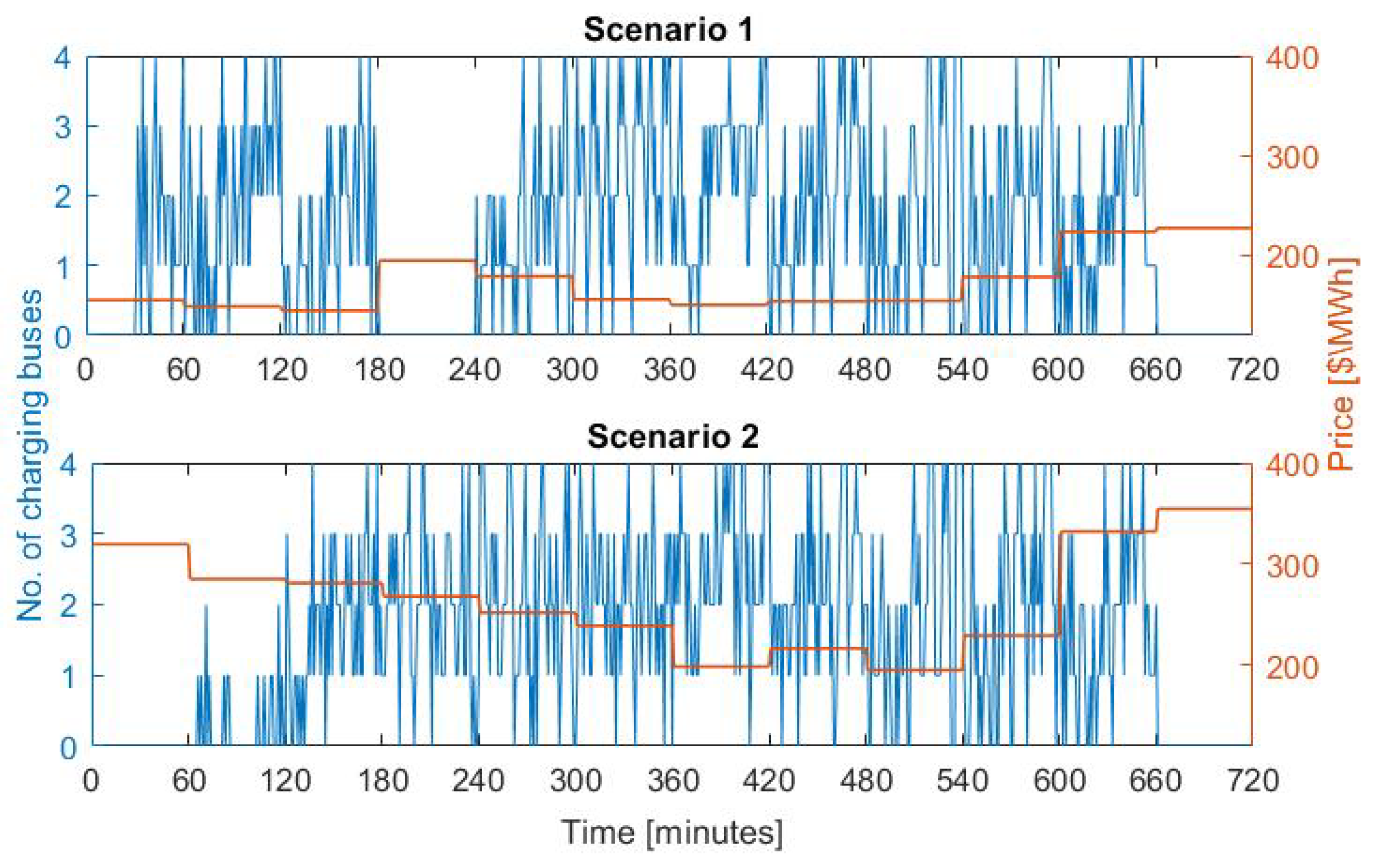
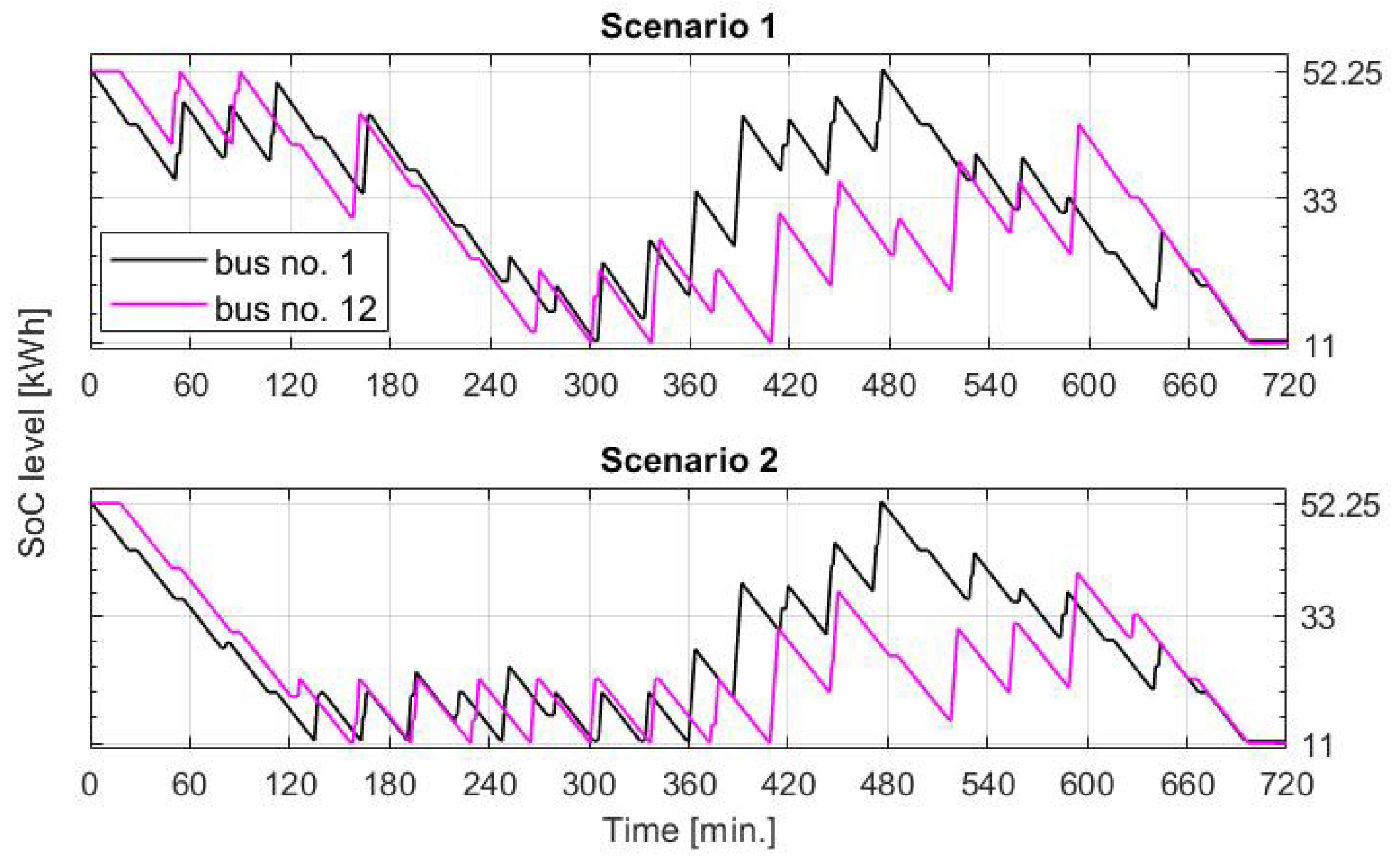
3.2.3. Disaggregation Results
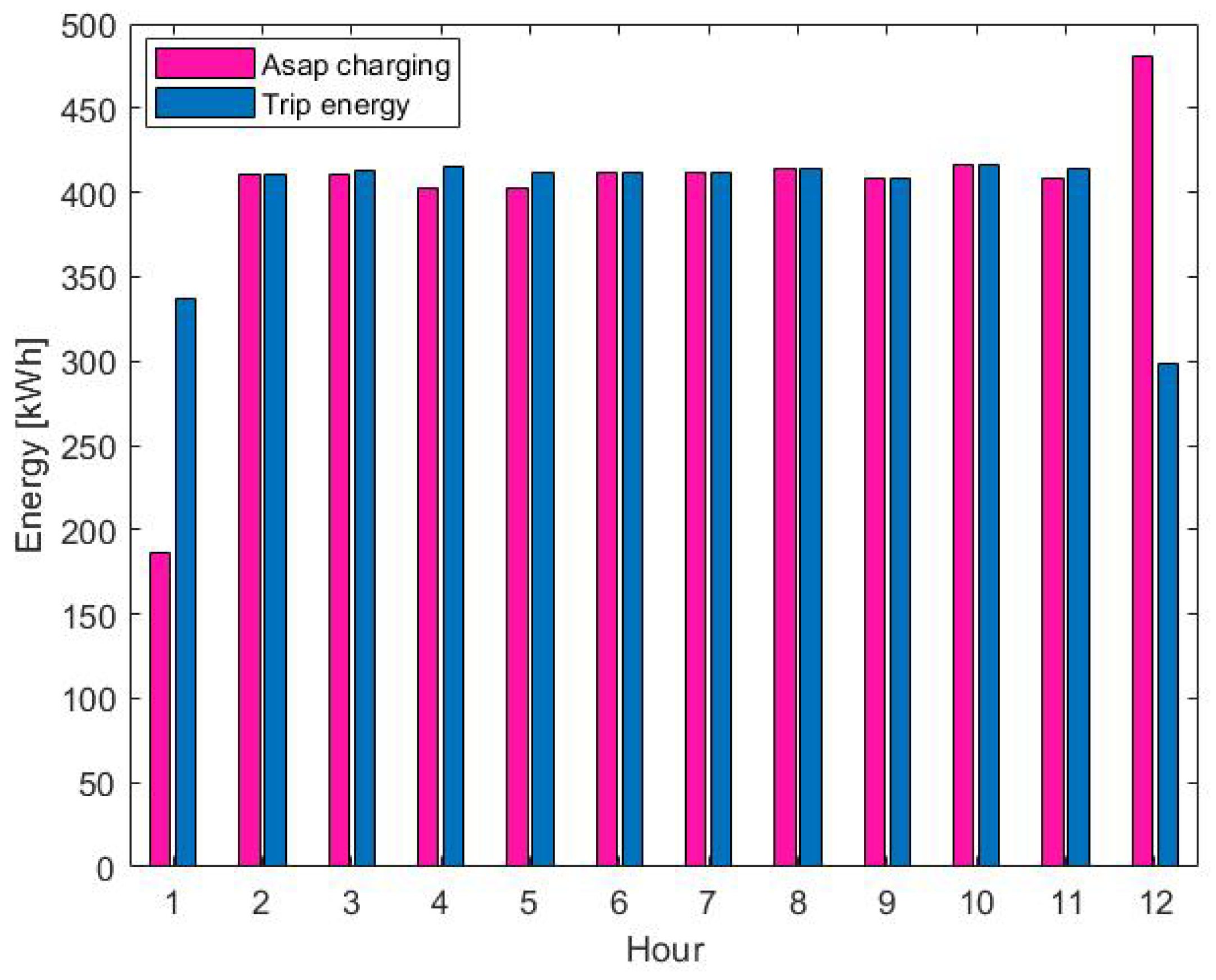
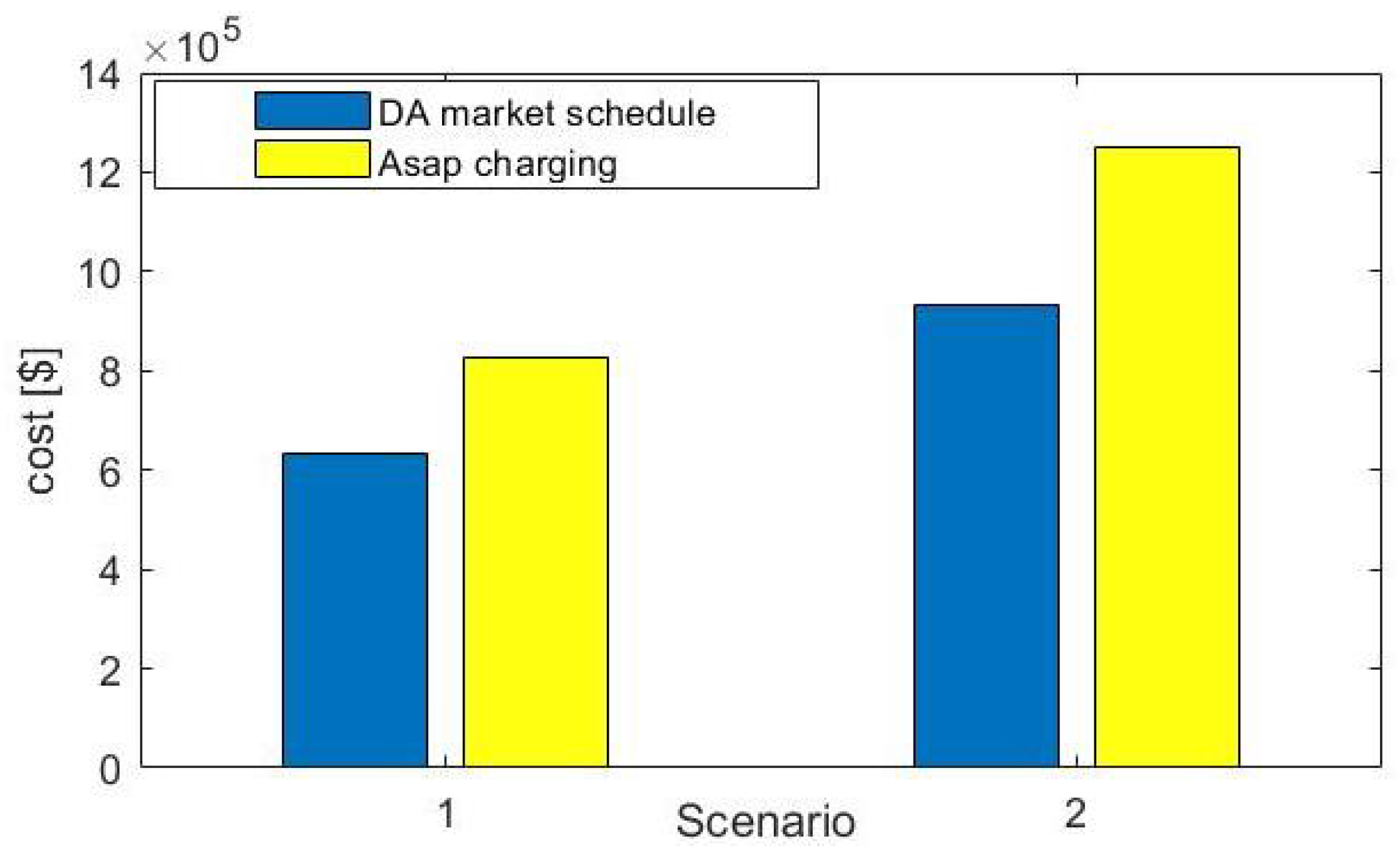
3.3. Cost Savings Analysis
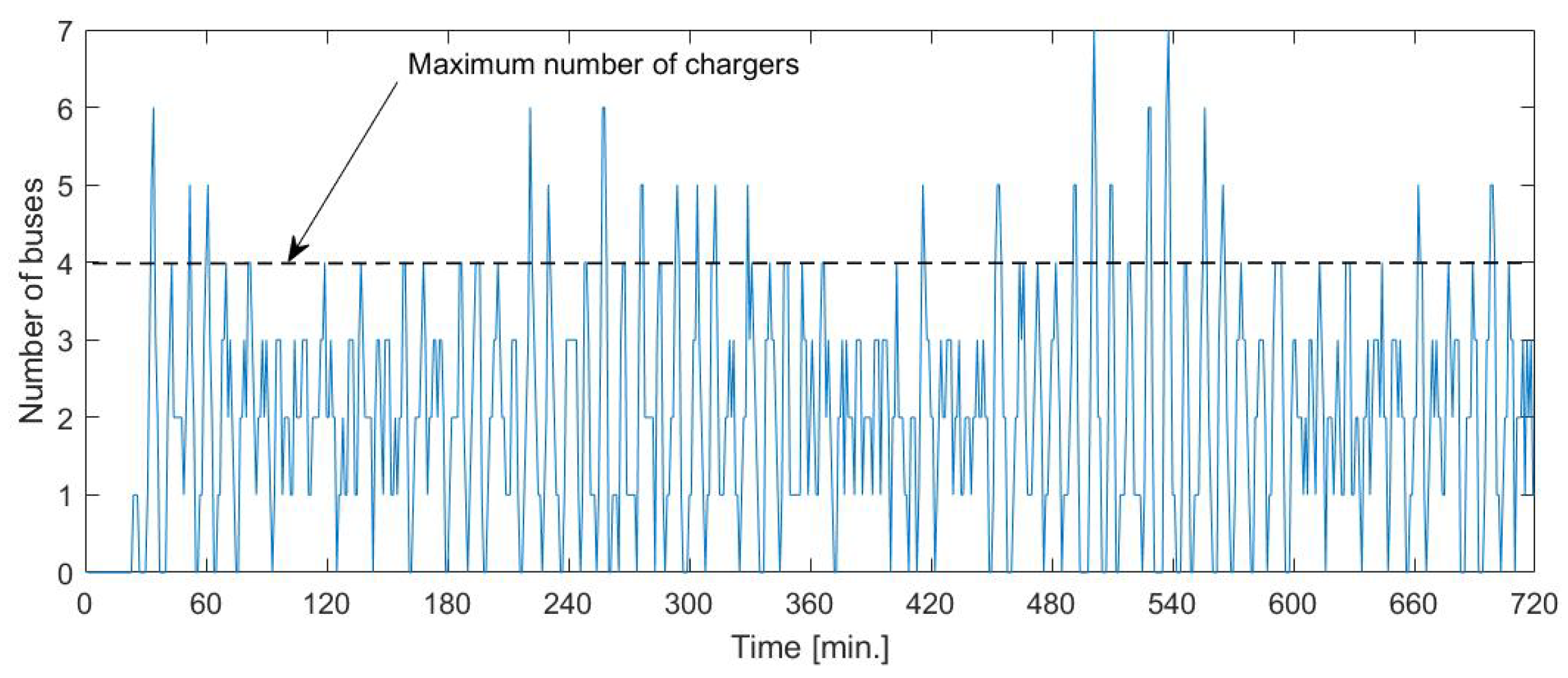
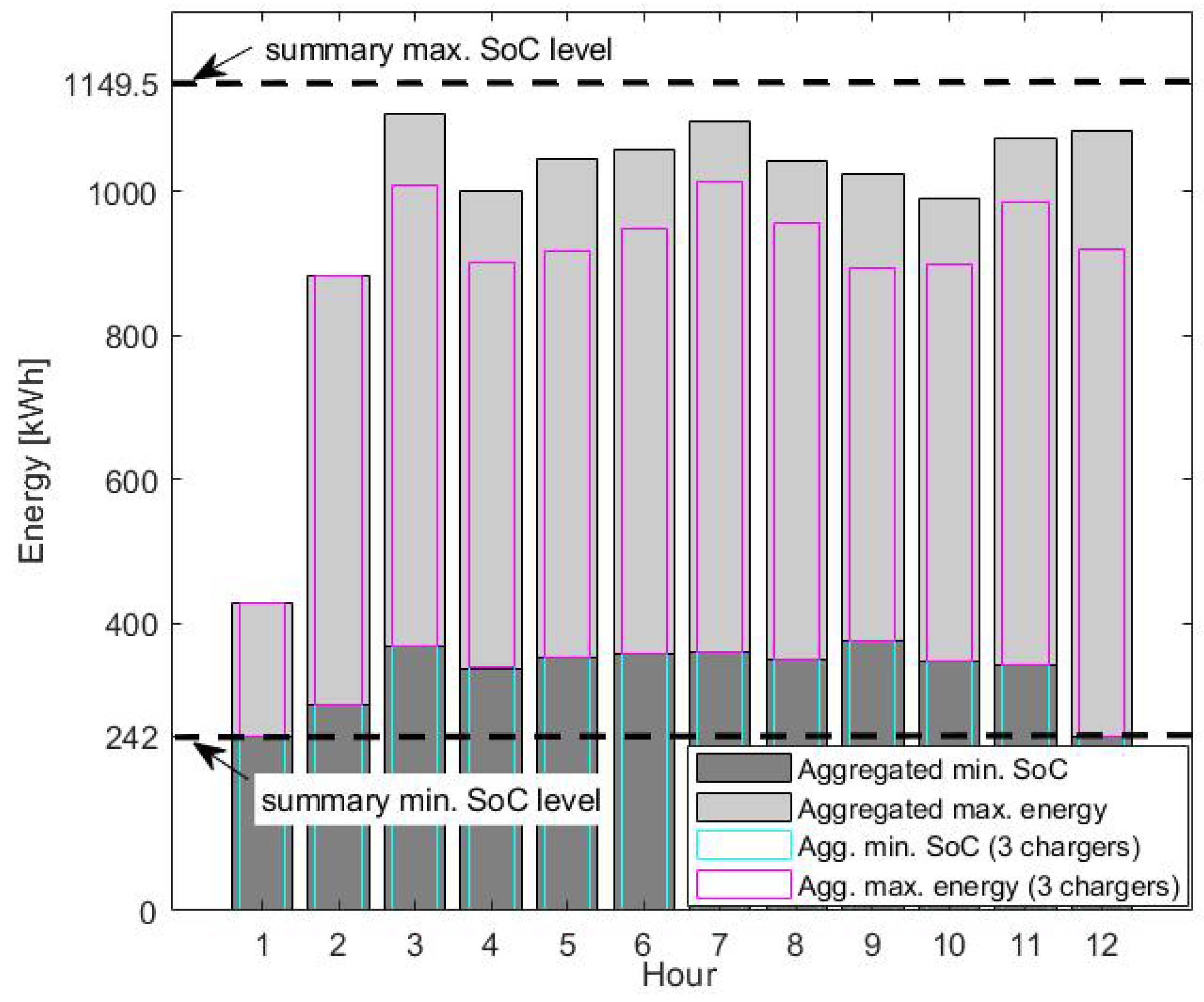
3.4. Sensitivity Analysis of the Number of Chargers
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Indices | |
| b | Index of electric buses |
| h | Index of time periods (hours) |
| t | Index of time periods (minutes) |
| Index of minutes when bus b ends the idle period | |
| Parameters | |
| idle time (in minutes) | |
| 0/1 indicator if bus b is available for charging in minute t | |
| C | Number of chargers |
| c | Maximum unit price for the excess amount of energy set by bus aggregator |
| Per-cycle trip energy demand of bus b | |
| Per-minute trip energy demand of bus b (per-cycle energy use/cycle time) | |
| Maximum battery State of Charge of bus b | |
| Minimum battery State of Charge of bus b | |
| Initial battery State of Charge of bus b | |
| r | Charging rate of a charger |
| Variables used specifically in aggregation/disaggregation model | |
| Charging energy of bus b scheduled in minute t | |
| Binary charging status of bus b in minute t | |
| Battery State of Charge of bus b in minute t | |
| Minimum battery State of Charge of bus b at the end of hour h | |
| Variables in Aggregation model used as Parameters in Auction model | |
| Total energy that must be loaded by buses | |
| Additional energy that can be loaded by buses | |
| Summary hourly trip energy of buses | |
| Aggregated maximum amount of energy that can be loaded in hour h | |
| Aggregated minimum battery State of Charge in hour h | |
| Variables used specifically in auction model | |
| Net supply cost in hour h | |
| Net supply in hour h | |
| Aggregated battery State of Charge in hour h | |
| Auction energy price in hour h derived as the shadow prices to balance constraint () | |
| Variables in Auction model used as Parameters in Disaggregation model | |
| Charging energy scheduled in hour h | |
References
- Pietrzak, O.; Pietrzak, K. The Economic Effects of Electromobility in Sustainable Urban Public Transport. Energies 2021, 14, 878. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, K.; Shen, Z.J.M.; Ye, B.; Miao, L. Multistage large-scale charging station planning for electric buses considering transportation network and power grid. Transp. Res. Part C Emerg. Technol. 2019, 107, 423–443. [Google Scholar] [CrossRef]
- Clairand, J.M.; Guerra-Terán, P.; Serrano-Guerrero, X.; González-Rodríguez, M.; Escrivá-Escrivá, G. Electric Vehicles for Public Transportation in Power Systems: A Review of Methodologies. Energies 2019, 12, 3114. [Google Scholar] [CrossRef] [Green Version]
- Batrancea, I.; Batrancea, L.; Nichita, A.; Gaban, L.; Masca, E.; Morar, I.D.; Fatacean, G.; Moscviciov, A. An econometric approach on production, costs and profit in Romanian coal mining enterprises. Econ. Res. Ekon. Istraživanja 2019, 32, 1019–1036. [Google Scholar] [CrossRef] [Green Version]
- Zoltowska, I. Demand shifting bids in energy auction with non-convexities and transmission constraints. Energy Econ. 2016, 53, 17–27. [Google Scholar] [CrossRef]
- Zoltowska, I.; Lin, J. Availability Bids Enabling Participation of Electric Vehicles in the Wholesale Markets. In Proceedings of the 2019 Electric Vehicles International Conference (EV), Bucharest, Romania, 3–4 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Muratori, M. Impact of uncoordinated plug-in electric vehicle charging on residential power demand. Nat. Energy 2018, 3, 193–201. [Google Scholar] [CrossRef]
- De Filippo, G.; Marano, V.; Sioshansi, R. Simulation of an electric transportation system at The Ohio State University. Appl. Energy 2014, 113, 1686–1691. [Google Scholar] [CrossRef]
- Kontou, E.; Yin, Y.; Ge, Y.E. Cost-effective and ecofriendly plug-in hybrid electric vehicle charging management. Transp. Res. Rec. 2017, 2628, 87–98. [Google Scholar] [CrossRef]
- Moradipari, A.; Tucker, N.; Zhang, T.; Cezar, G.; Alizadeh, M. Mobility-Aware Smart Charging of Electric Bus Fleets. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Chen, H.; Hu, Z.; Xu, Z.; Li, J.; Zhang, H.; Xia, X.; Ning, K.; Peng, M. Coordinated charging strategies for electric bus fast charging stations. In Proceedings of the 2016 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1174–1179. [Google Scholar]
- Chen, H.; Hu, Z.; Zhang, H.; Luo, H. Coordinated charging and discharging strategies for plug-in electric bus fast charging station with energy storage system. IET Gener. Transm. Distrib. 2018, 12, 2019–2028. [Google Scholar] [CrossRef] [Green Version]
- Raab, A.F.; Lauth, E.; Strunz, K.; Göhlich, D. Implementation schemes for electric bus fleets at depots with optimized energy procurements in virtual power plant operations. World Electr. Veh. J. 2019, 10, 5. [Google Scholar] [CrossRef] [Green Version]
- Qin, N.; Gusrialdi, A.; Brooker, R.P.; Ali, T. Numerical analysis of electric bus fast charging strategies for demand charge reduction. Transp. Res. Part A Policy Pract. 2016, 94, 386–396. [Google Scholar] [CrossRef]
- Deng, R.; Liu, Y.; Chen, W.; Liang, H. A Survey on Electric Buses—Energy Storage, Power Management, and Charging Scheduling. IEEE Trans. Intell. Transp. Syst. 2019, 22, 9–22. [Google Scholar] [CrossRef]
- Sioshansi, R.; Denholm, P.; Jenkin, T.; Weiss, J. Estimating the value of electricity storage in PJM: Arbitrage and some welfare effects. Energy Econ. 2009, 31, 269–277. [Google Scholar] [CrossRef]
- Mays, J. Missing incentives for flexibility in wholesale electricity markets. Energy Policy 2021, 149, 112010. [Google Scholar] [CrossRef]
- Federal Energy Regulatory Commission. Electric Storage Participation in Markets Operated by Regional Transmission Organizations and Independent Systems Operators. 2018. Available online: https://elibrary.ferc.gov/eLibrary/docinfo?document_id=14643624 (accessed on 22 June 2021).
- Sakti, A.; Botterud, A.; O’Sullivan, F. Review of wholesale markets and regulations for advanced energy storage services in the United States: Current status and path forward. Energy Policy 2018, 120, 569–579. [Google Scholar] [CrossRef]
- Wang, J.; Kennedy, S.; Kirtley, J. A new wholesale bidding mechanism for enhanced demand response in smart grids. In Proceedings of the 2010 Innovative Smart Grid Technologies (ISGT), Gaithersburg, MD, USA, 19–21 January 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, Y.; Holzer, J.T.; Ferris, M.C. Extending the bidding format to promote demand response. Energy Policy 2015, 86, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Guo, S.; Ren, J.; Zhao, Z.; Ehsan, A.; Zheng, Y. An electric bus power consumption model and optimization of charging scheduling concerning multi-external factors. Energies 2018, 11, 2060. [Google Scholar] [CrossRef] [Green Version]
- Sen, S.; Kothari, D. Optimal thermal generating unit commitment: A review. Int. J. Electr. Power Energy Syst. 1998, 20, 443–451. [Google Scholar] [CrossRef]
- PJM Interconnection, LLC (PJM). PJM Data Viewer: Locational Marginal Pricing. 2020. Available online: https://www.pjm.com/ (accessed on 3 August 2021).

| Bus Line | Cycle Time [min] | Per-Cycle Energy Use [kWh] | Frequency [min] | No. of Buses |
|---|---|---|---|---|
| North Express | 23 | 8.41 | 9 | 5 |
| Loop North | 31 | 10.91 | 9 | 4 |
| Loop South | 31 | 11.08 | 9 | 4 |
| Central Connector | 32 | 12.11 | 12 | 3 |
| East Residential | 33 | 11.62 | 9 | 4 |
| Buckeye Village | 30 | 12.71 | 15 | 2 |
| C | r | ||||||
|---|---|---|---|---|---|---|---|
| 5 min | 4 | 250 kW | 11 kW | 52.25 kW | 52.25 kWh | 3854.98 kWh | 907.5 kWh |
| h | |||
|---|---|---|---|
| 1 | 336.8 | 186.0 | 242.0 |
| 2 | 410.3 | 597.7 | 285.3 |
| 3 | 413.3 | 740.2 | 366.4 |
| 4 | 415.0 | 665.0 | 336.3 |
| 5 | 412.1 | 692.7 | 351.3 |
| 6 | 411.4 | 700.6 | 357.9 |
| 7 | 411.4 | 736.3 | 360.5 |
| 8 | 414.6 | 692.7 | 348.3 |
| 9 | 408.5 | 649.2 | 375.5 |
| 10 | 416.1 | 641.3 | 347.5 |
| 11 | 414.3 | 732.3 | 340.2 |
| 12 | 298.6 | 843.1 | 242.0 |
| h | Scenario 1 | Scenario 2 | ||
|---|---|---|---|---|
| 4 Chargers | 3 Chargers | 4 Chargers | 3 Chargers | |
| 1 | 186.0 | 186.0 | 0.0 | 0.0 |
| 2 | 411.0 | 411.0 | 43.3 | 43.3 |
| 3 | 299.9 | 250.4 | 334.0 | 333.9 |
| 4 | 0.0 | 0.0 | 384.9 | 386.2 |
| 5 | 292.3 | 341.8 | 427.1 | 425.8 |
| 6 | 556.0 | 500.6 | 418.1 | 418.0 |
| 7 | 504.8 | 491.0 | 517.7 | 532.3 |
| 8 | 439.3 | 430.4 | 458.1 | 451.0 |
| 9 | 397.1 | 370.9 | 441.0 | 381.2 |
| 10 | 415.2 | 421.9 | 414.6 | 427.0 |
| 11 | 353.3 | 451.1 | 416.3 | 454.2 |
| 12 | 0.0 | 0.0 | 0.0 | 2.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zoltowska, I.; Lin, J. Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids. Energies 2021, 14, 4727. https://doi.org/10.3390/en14164727
Zoltowska I, Lin J. Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids. Energies. 2021; 14(16):4727. https://doi.org/10.3390/en14164727
Chicago/Turabian StyleZoltowska, Izabela, and Jeremy Lin. 2021. "Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids" Energies 14, no. 16: 4727. https://doi.org/10.3390/en14164727
APA StyleZoltowska, I., & Lin, J. (2021). Optimal Charging Schedule Planning for Electric Buses Using Aggregated Day-Ahead Auction Bids. Energies, 14(16), 4727. https://doi.org/10.3390/en14164727







