Reliability Assessment of Passive Safety Systems for Nuclear Energy Applications: State-of-the-Art and Open Issues

Abstract

Passive systems are fundamental for the safe development of Nuclear Power Plant (NPP) technology. The accurate assessment of their reliability is crucial for their use in the nuclear industry. In this paper, we present a review of the approaches and procedures for the reliability assessment of passive systems. We complete the work by discussing the pending open issues, in particular with respect to the need of novel sensitivity analysis methods, the role of empirical modelling and the integration of passive safety systems assessment in the (static/dynamic) Probabilistic Safety Assessment (PSA) framework.

1. Introduction

Passive systems are in use since the dawning of nuclear power technology. They have, then, received a renewal of interest after the major nuclear accidents in 1979, 1986 and 2011. However, in all, passive systems design has been the focus of a large number of researches and applications that have not led to a common understanding of the benefits and cons of passive safety systems implementation.

On the contrary, a common understanding must be laid down in particular with respect to the reliability of passive systems, for demonstrating their qualification and usefulness for nuclear safety. Specifically, the large uncertainty associated with inadequacies of the design codes used to simulate the complex passive systems physical behavior must be addressed for the reliability assessment, because it may lead to hidden large unreliability.

In comparison to active systems, passive safety systems benefit from less dependence on external energy sources, no need for operator actions to activate them and reduced costs, including easier maintenance. Recognition of those advantages is shared among most stakeholders in the nuclear industry, as demonstrated by the number of nuclear reactor designs that make use of passive safety systems. Yet, it is still necessary to precisely assess and demonstrate the reliability of passive safety systems and the capacity to perform and complete the expected functions. In simple and direct words, passive safety systems may contribute to improving the safety of Nuclear Power Plants (NPPs), provided that their performance-based design and operation are demonstrated by tailored deterministic and reliability assessment methods, approaches and data (e.g., experimental databases) available to industry and regulators [1,2,3,4,5].

With reference to the passive natural circulation of fluid for emergency cooling, the complex set of physical conditions that occurs in the passive safety systems, where no external sources of mechanical energy for the fluid motion are involved, has led the designers of the present-generation reactors to position the main heat sink (i.e., the steam generators for pressurized water reactors and feed-water inlet for boiling water reactors) at a higher elevation with respect to the heat source location (i.e., the core). By so doing, should the forced circulation driven by centrifugal pumps become unavailable, the removal of the decay heat produced by the core is still allowed [6]. For their reliability assessment, mathematical models are typically built [7] to describe the mathematical relationship between the passive system physical parameters influencing the NPP behavior, then translated into detailed mechanistic Thermal-Hydraulic (T–H) computer codes for simulating the effects of various operational transients and accident scenarios on the system [7,8,9,10,11,12,13,14,15].

In practice, characteristics of the system under analysis are only partially captured and, therefore, simulated by the associated T–H code. Moreover, the uncertainties affecting the behavior of passive systems and its modeling are usually much larger than those associated with active systems, challenging the passive systems reliability assessment [16,17,18]. This is due to [1,8,9,10,17,19,20,21,22]: (i) stochastic transitions of intrinsically random phenomena occurring (such as component degradation and failures), and (ii) the lack of experimental results, that mine the completeness of the knowledge about some of that same phenomena [23,24,25]. Such uncertainties translate into uncertainty of the model output uncertainty that, for the sake of a realistic reliability assessment, must be estimated [22,26,27,28].

In this paper, we review the methodological solutions to the T–H passive safety systems reliability assessment. In particular, the approaches for the reliability assessment of nuclear passive systems are described in Section 2: independent failure modes, hardware failure modes, functional failure modes approaches are described in Section 2.1, Section 2.2 and Section 2.3, respectively. In Section 3, the advanced Monte Carlo simulation approaches are introduced. In Section 4, the existing coordinated procedures for reliability evaluation are presented. Open issues, along with the methods proposed in the literature to address these issues, are discussed in Section 5, that include (i) the identification of the most contributing model hypotheses and parameters to the output uncertainty (Section 5.1), (ii) the empirical regression modelling for reducing computational time (Section 5.2), and (iii) the integration of reliability assessment of passive systems into the current Probabilistic Safety Assessment (PSA) (Section 5.3).

2. Approaches for the Reliability Assessment of Passive Systems

In general, the reliability of passive systems depends on:

• systems/components reliability;
• physical phenomena reliability, which accounts for the physical boundary conditions and mechanisms.

This means that, to guarantee a large passive system reliability: well-engineered components (with at least the same reliability as active systems) are to be selected; the physical principles (e.g., gravity and density difference in T–H passive systems) and the effects of surrounding/environments conditions in which they occur and affect the parameters evolution during the accident development (e.g., flow rate and exchanged heat flux in T–H passive systems) are to be fully understood and captured. Both aspects should be considered within a consistent approach to passive system reliability assessment. In what follows, a summary of three different approaches is provided for passive systems performance assessment upon onset of system operation.

2.1. The Independent Failure Modes Approach

The independent failure modes approach entails [16]: (i) identifying the failure modes leading to the unfulfillment of the passive system function, and (ii) evaluating the system failure probability as the probability of failure modes occurrence.

Typically, failure modes are identified from the application of a Failure Modes and Effects Analysis (FMEA) procedure [29].

Conventional probabilistic failure process models commonly used for hardware components (i.e., the exponential distribution, e^−λt, where λ is the failure rate and t is time) are not applicable to model physical processes failures; in this case, each failure is characterized by specific critical physical parameters distributions and a defined failure mode, that implies, for each of these latter, the definition of the probability distributions and failure ranges of the critical physical parameters (for example, for a T–H passive system, these may include non-condensable gas build-up, the undetected leakage, the heat exchange process reduction due to surface oxidation, piping layout, thermal insulation degradation, etc.).

Eventually, to evaluate the probability of the event of failure of the system, Pe_t, the probabilities of the different failure mode events, Pe_i, i = 1,…,n, are combined according to a series logic, assuming mutually non-exclusive independent events [29]:

Pe_t = 1.0 − ((1.0 − Pe₁) ∗ (1.0 − Pe₂) ∗ ... ∗ (1.0 − Pe_n))

(1)

Since this approach assesses the system failure probability assuming that a single failure mode event is sufficient to lose the system function, the resulting value of failure probability of system failure can be conservatively assumed as an upper bound for the unreliability of the system [29].

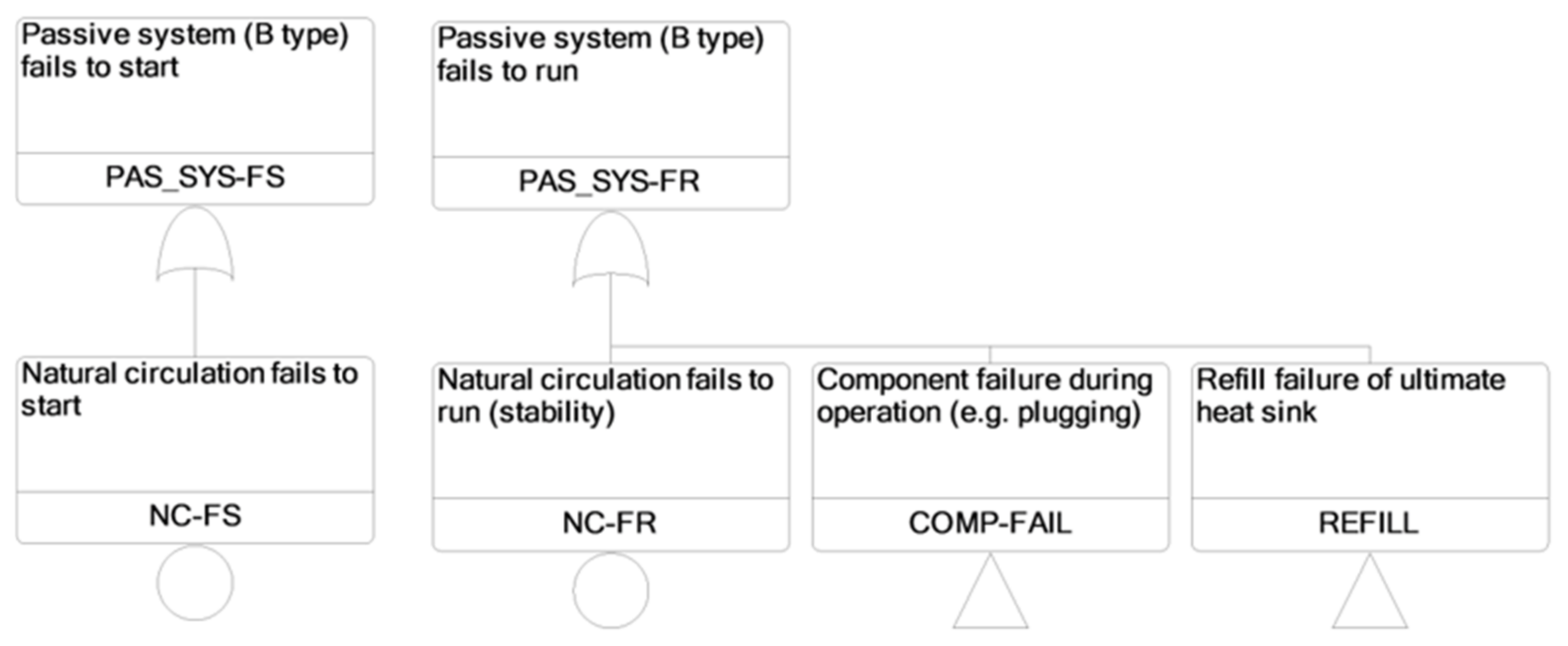
2.2. The Hardware Failure Modes Approach

In the hardware failure modes approach [30], the unreliability of the passive system is obtained by accounting for the probabilities of occurrence of the hardware failures that degrade the physical mechanisms (which the passive system relies upon for its function).

For example, with reference to a typical Isolation Condenser [30], natural circulation failure due to high concentration of non-condensable gas is modelled in terms of the probability of occurrence of vent lines failure to purge the gases [3]; natural circulation failure because of insufficient heat transfer to an external source is assessed through two possible hardware failure modes: (1) insufficient water in the pool and make-up valve malfunctioning, (2) degraded heat transfer conditions due to excessive fouling of the heat exchanger pipes.

Thus, the probabilities of degraded physical mechanisms are expressed in terms of unreliability of the components whose failures degrade the function of the passive system. Some critical aspects of this approach are: (i) lack of completeness of the possible failure modes and corresponding hardware failures), (ii) failures due to unfavourable initial or boundary conditions being neglected, and (iii) fault tree models typically adopted to represent the hardware failure modes may inappropriately replace the complex T–H code behavior and predict interactions among physical phenomena of the system [3].

2.3. The Functional Failure Approach

The functional failure approach is based on the concept of functional failure [31]: in the context of passive systems, this is defined as the probability of failing to achieve a safety function (i.e., the probability of a given safety variable—load—to exceed a safety threshold—capacity). To model uncertainties, probability distributions are assigned, mainly by subjective/engineering judgments, to both the safety threshold (for example, a minimum value of water mass flow required) and safety variable (i.e., the water mass flow circulating through the system).

3. Advanced Monte Carlo Simulation Approach

The functional failure approach (Section 2) relies on the deterministic T–H computer code model (mathematically represented by the nonlinear function f(·)) and the Monte Carlo (MC) propagation of the uncertainties in the code inputs x (i.e., the Probability Density Functions (PDFs) q(x)) to the outputs y = f(x), with respect to which the failure event is defined according to given safety thresholds. The propagation consists in repeating the T–H code computer runs (or simulations) for different sets of the uncertain input values x, sampled from their PDF q(x) [1,2,5,32,33,34,35,36,37,38]. The main strength of MC simulation is that it does not force the analyst to resort to simplifying approximations, since it does not suffer from any T–H model complexity, and is, therefore, expected to provide the most realistic passive system assessment.

On the other hand, it is challenged by the long calculations needed to run the detailed, mechanistic T–H code (one run for each batch of sampled input values) and the computational efforts, increasing with decreasing failure probability [39,40], that, incidentally is particularly small (e.g., less than 10⁻⁴) for functional failure of T–H passive safety systems [5,28].

To reduce the number of T–H code runs and the computational time as much as possible, alternatives to be considered are fast running surrogate regression models (also called response surfaces or metamodels) and advanced Monte Carlo simulation methods [41,42]. Fast-running surrogate regression models mimic the response of the original T–H model code, circumventing the long computing time (as it will be described in Section 5.2: to name a few, polynomial Response Surfaces (RSs) [43], polynomial chaos expansions [44], stochastic collocations [45], Artificial Neural Networks (ANNs) [46,47], Support Vector Machines (SVMs) [48] and kriging [49] (see the following Section 5.2 for details).

Advanced Monte Carlo Simulation allows limiting of the number of code runs, guaranteeing, at the same time, robust estimations [50,51]. The present Section focuses on this latter class of methods.

Among these, Stratified Sampling consists in calculating the probability of each of the non-overlapping subregions (i.e., strata) of the sample space; by randomly sampling a fixed number of outcomes from each stratum (i.e., the stratified samples), the coverage of the sample space is ensured [52,53]. However, the definition of the strata and the calculation of the associated probabilities is a major challenge [53].

Latin Hypercube Sampling (LHS), commonly used in PSA [52,54,55,56,57,58] and reliability assessment problems [59], is a compromise between standard MCS and Stratified Sampling, but it does not overcome enough the performance of standard MCS for small failure probabilities estimation [60], as in the case of passive safety systems reliability assessment.

Subset Simulation (SS) [61,62,63] and Line Sampling (LS) [64,65] have been proposed as advanced MCS methods to tackle the typical multidimensional load-capacity problems of structural reliability assessment: therefore, they can address the problem of the functional failure probability assessment of T–H passive systems [22,47,66].

In the SS approach, the problem is tackled by performing simulations of sequences of (more) frequent events in their conditional probability spaces: finally, the product of the conditional probabilities of such more frequent events is taken as the functional failure probability; Markov Chain Monte Carlo (MCMC) simulations are used to generate the conditional samples [67], which, by sequentially populating the intermediate conditional regions, reach the final functional failure region.

In the LS method, the failure domain of the high-dimensional problem under analysis is explored by means of lines, instead of random points [65]. One-dimensional problems are solved along an “important direction” that optimally points towards the failure domain, in place of the high-dimensional problem [65]. The approach overcomes standard MCS in a wide range of engineering applications [22,39,51,65,68,69,70,71] and allows ideally reducing to zero the variance of the failure probability estimator if the “important direction” is perpendicular to the almost linear boundaries of the failure domain [64].

Finally, the more frequently adopted advanced MCS method is Importance Sampling (IS): in IS, the original PDF q(x) is replaced by an Importance Sampling Density (ISD) g(x) biased towards the MC samples that lead to outputs close to the failure region, in a way to artificially increase the (rare) failure event frequency. To approximate the ideal ISD g*(x) (i.e., the one that would make the standard deviation of the MC estimator result equal to zero) the Adaptive Kernel (AK) [72,73], the Cross-Entropy (CE) [74,75,76], the Variance Minimization (VM) [77] and the Markov Chain Monte Carlo-Importance Sampling (MCMC-IS) [78] methods have been proposed.

Adaptive Metamodel-based Subset Importance Sampling (AM-SIS) is a recently proposed method [79] which combines SS and metamodels (for example, Artificial Neural Networks, ANNs) within an adaptive IS scheme, as follows [78,79]:

• Subset Simulation (SS) is used to create an input batch from the ideal, zero-variance ISD g*(x) relying on an ANN that (i) is adaptively refined in proximity of failure region by means of the samples iteratively produced by SS, and (ii) substitutes the expensive T–H code f(x);
• The g*(x) built at step (1) is used to perform IS and calculate the probability of failure of the T–H passive system.

Notice that the idea of integrating metamodels within efficient MCS schemes has been widely proposed in the literature: see, e.g., [80,81,82,83,84,85,86,87,88].

4. Frameworks for the Reliability Assessment of Passive Systems

A first framework for the reliability assessment of passive systems is the REPAS (Reliability Evaluation of Passive Systems) methodology [3], then continued onto the EU (European Union) project called RMPS (Reliability Methods for Passive Systems) project (https://cordis.europa.eu/project/id/FIKS-CT-2000-00073, accessed on 3 May 2021) [11]. The RMPS methodology is aimed at the: (1) identification and quantification of the sources of uncertainties—combining (often vague and imprecise) expert judgments and the (typically scarce) experimental data available—and determination of the critical parameters, (2) propagation of the uncertainties through thermal–hydraulic (T–) codes and assessment of the passive system unreliability, and (3) introduction of the passive system unreliability in the accident sequences for probabilistic risk analysis. The RMPS methodology has been successfully applied to passive systems providing natural circulation of coolant flow in different types of reactors (BWR, PWR and VVER). A complete example of application concerning the passive residual heat removal system of a CAREM (Central Argentina Reactor de Elementos Modulares) is presented in [89]. Recently, the RMPS methodology has been applied by ANL (Argonne National Laboratory) in studies for the evaluation of the reliability of passive systems designed for GenIV sodium fast reactors: see, for instance, [90].

In the APSRA (Assessment of Passive System ReliAbility) methodology [91], a failure hyper-surface is generated in the space of the critical physical parameters by considering their deviations from the nominal values, after a root-cause analysis is performed to identify the causes of deviation of these parameters, assuming that the deviation of such physical parameters occurs only due to failures of mechanical components. Then, the probability of failure of the passive system is evaluated from the failure probability of these mechanical components. Examples of the APSRA (and its evolution APSRA+) application can be found in [91,92]

The two frameworks, RMPS and APSRA, have certain features in common, as well as distinctive characteristics. To name a few similarities, both methodologies use Best Estimate (BE) codes to estimate the T–H behavior of the passive systems and integrate both probabilistic and deterministic analyses to assess the reliability of the systems; with respect to differences, while the RMPS framework proceeds with the identification and quantification of the parameter uncertainties using probability distributions and propagating their realizations via a T–H code or a response surface, the APSRA methodology assesses the causes of deviation of the parameters from their nominal values.

5. Open Issues

In the following Sections, the open issues regarding the methods and frameworks for the reliability assessment of passive safety systems and for their application are discussed, in particular, with respect to the need of novel sensitivity analysis methods, the role of empirical regression modelling and the integration of passive systems in PSA.

5.1. Sensitivity Analysis Methods

Safety margins are practically verified resorting to T–H codes [41,93]. Recently, these calculations have been performed by BE T–H codes that provide realistic results and avoid over-conservatism [51], and also by the demanding identification and quantification of the uncertainties in the code, which require a large number of simulations [94].

To tackle this challenge, various approaches of Uncertainty Analysis (UA) have been developed, e.g., Code Scaling, Applicability and Uncertainty (CSAU) [95], Automated Statistical Treatment of Uncertainty Method (ASTRUM), Integrated Methodology for Thermal Hydraulics Uncertainty Analysis (IMTHUA) [28]. In all the mentioned approaches, the assumption is that input variables follow statistical distributions: this implies that if N input sets are sampled from these distributions and fed to the BE code, the corresponding N output values can be calculated, propagating the variability of the input variables onto the output. To speed up the computation and substituting the TH code with a simple and faster surrogate, a combination of Order Statistics (OS) [96] and Artificial Neural Networks [97] has been proposed. However, this latter approach does not allow one to completely characterize the PDF of the output variable but only some percentiles [5].

Particularly, SA techniques can be categorized in: Local, Regional and Global [97]. The local approaches provide locally valid information since they analyze the effect on the output of small variations around fixed values of the input parameters. Regional approaches analyze the effects on the output of partial ranges of the inputs distributions. Global approaches analyze the contribution of the entire distribution of the input on the output variability. This makes the global approaches more suitable when models are non-linear and non-monotone, with respect to which, local and regional approaches may fail. The higher capabilities of global approaches are paid by larger computational costs. Examples of global methods are Fourier Amplitude Sensitivity Test (FAST) [52], Response Surface Methodology (RSM) [43] and variance decomposition methods [26].

In this Section, we will illustrate a relatively recent method for global SA, called the distribution-based approach [94]. In practice, the PDF of the output variable is reconstructed, with fewer runs than variance decomposition-based methods, for conducting an SA. Polynomial Chaos Expansion (PCE) methods have been used [44], although the multimodal output variable distribution cannot be modeled by PCE (because, to accurately enough reconstruct the PDF, the order of the expansion and the computational cost become too large) In such cases, Finite Mixture Models (FMMs) [98] can overcome the problem, by naturally “clustering” the T–H code output (e.g., subdividing the inputs leading to output values with large, low, insufficient safety margins) in probabilistic models (i.e., PDFs) composing the mixture. Advantages are (i) the availability the analytical PDF of the model output and (ii) a lower computational cost than classical global SA methods.

To further reduce the computational cost related with the T–H code runs, a framework based on FMMs has been proposed in [94]. The natural clustering made by the FMM on the T–H code output [99] (where one cluster corresponds to one Gaussian model of the mixture) is exploited to develop an ensemble of three SA methods that perform differently depending on the data at hand: input saliency [100], Hellinger distance [101,102] and Kullback–Leibler divergence [101,102]. The advantage offered by the diversity of the methods is the possibility of overcoming possible errors of the individual methods that may occur, due to the limited quantity of data.

The proposed framework applicability to the reliability assessment of passive safety systems is challenging because one must consider the uncertainties affecting the passive systems functional performance [1,16,66,92,103].

In [104], the application of the framework to a Passive Containment Cooling System (PCCS) of an Advanced Pressurized reactor AP1000 during a Loss Of Coolant Accident (LOCA) is shown. The combination of multiple sensitivity rankings is shown to increase the robustness of the results, without any additional T–H code run.

The work in [104] has been extended in [105] by considering three Global SA methods (the Input Saliency (IS), Hellinger Distance (HD), Kullback–Leibler Divergence (KLD)) and Bootstrap [97] that (artificially, but without information bias) increase the amount of data obtained. The framework has been applied to a real case study of a Large Break Loss of Coolant Accident (LBLOCA) in the Zion 1 NPP [106], simulated by the TRACE code.

5.2. Role of Empirical Regression Modelling

To address the computational problem related to the run of the detailed, mechanistic T–H system code, either efficient sampling techniques can be adopted as described in Section 3, or nonparametric order statistics [107] can be employed, especially if only particular statistics (e.g., the 95th percentile) of the outputs of the code are needed [96,108,109], or fast-running, surrogate regression models can be implemented to mimic the long-running T–H model. In general terms, the construction (i.e., training) of such regression models entails using a (reduced) number (e.g., 50–100) input/output patterns of the T–H model code for fitting, by statistical techniques, the response surface of the regression model to the input/output data. Several examples can be found in the literature: in [87,88,110], polynomial Response Surfaces (RSs) are used to calculate the structural failure probability; in [5,34,36], with linear and quadratic polynomial RSs, the reliability analysis of a T–H passive system of an advanced nuclear reactor is performed; Radial Basis Functions (RBFs), Artificial Neural Networks (ANNs) and Support Vector Machines (SVMs) are shown to provide local approximation of the failure domain in structural reliability problems and for the functional failure analysis of a passive safety systems in a Gas-cooled Fast Reactor (GFR), in [48,111,112]; finally, Gaussian meta-models have been used for the sensitivity analysis of inputs driving the radionuclide transport in groundwater as modeled by complex hydrogeological models in [113,114].

5.3. Integration of Passive Systems in PSA

The introduction of passive safety systems in the framework of PSA based on FTs and ETs deserves particular attention. The reason is that the reliability of these systems does not depend only on (mechanical) components failure modes, but also on the occurrence of phenomenological events. This makes the problem nontrivial (see Section 2 and Section 3), because it is difficult to define the status of these systems along an accident sequence only in Boolean terms of ‘success/failure’. An ‘intermediate’ mode of operation of a passive system or, equivalently, a degraded performance of the system (up to the failure point) should be considered, where the passive system might still be capable of providing a functional level sufficient for the mitigation to the accident progression.

5.3.1. Integration of Passive System Reliability into Static PSA

An ET describes—in a logically structured, graphical form—the sequences of events (scenarios) that can possibly originate from an initiating event, depending on the fulfilment (or not) of the functional requirements of the safety (and operational) systems involved in the accident scenario. For each of these systems, an FT displays in graphical/logic form all the combinations of the so-called basic events that cause the failure of the system, by connecting the events through logic gates. The basic events represent the fundamental failure modes of the system and can be assessed by different reliability models and data.

With respect to active safety systems working in conventional, currently operating nuclear facilities, the following two fundamental failure modes are usually considered:

• Start-up failure: for standby active equipment (e.g., pumps, fans), the failure probability of start-up should be assessed, while for valves, the failure probability of opening and/or closing should be modelled.
• Failure during operation: the failure probability during operation of active components (e.g., pumps) should be quantified and modelled in the PSA. To this purpose, the most commonly applied reliability models employ the failure rate and the expected mission time (or functional time) of the component. For components with relatively short mission time (1–2 h), this kind of malfunction is usually modelled within the start-up failure framework.

With respect to passive systems, the applicability of the FT method depends on the passivity level (A, B, C and D), as defined by the IAEA [115].

Type ‘B’ passive systems do not contain any moving mechanical parts and the start-up of the system is triggered by passive phenomena (with the exclusion of valve utilization): in this case, the start-up failure probability of the system is determined only based on the probability that the passive physical phenomenon occurs or not (e.g., that natural circulation develops in the cooling circuit). Failure during operation is, instead, determined by the physical stability of the passive phenomenon (e.g., long-term stability of the natural circulation), which is mainly influenced by the initial and the boundary conditions. It is worth mentioning that, as pointed out before, modelling start-up failure and failure during operation needs the consideration of different physical phenomena, because alterations in boundary conditions during accident mitigation can result in the degradation of the driving forces even after a successful start-up.

When passive systems are concerned, other failure modes are to be considered, such as mechanical equipment failures (e.g., heat exchanger plugging, rupture or leak, etc.), which can also lead to failure during operation [2] and alter the physical stability, and human errors, which can influence the long-term operation of a passive system. In some cases (for example, [89]), these failure modes are considered in a separate FT.

As an example of a type ‘B’ passive system, let us consider a passive residual heat removal system [2] where the heat is transferred into a pool that must be refilled to ensure the fulfillment of the safety function in the long run. The resulting FT for the start-up and during-operation failure modes is shown in Figure 1: the failure probability of the ‘phenomenological’ basic events (i.e., ‘natural circulation fails to start’ NC-FS and ‘natural circulation fails to run’ NC-FR) should be derived from the reliability assessment of the physical phenomenon, while the failure probabilities of the mechanical parts (i.e., ‘component failure during operation’ COMP-FAIL and ‘refill failure of ultimate sink’ REFILL) are the result of classical FMEA or HAZOP methods.

Types ‘C’ and ‘D’ passive systems may contain moving mechanical parts (e.g., check valves in case of type ‘C’ and motor-operated valves in case of type ‘D’), in order to trigger the operation of the system. In this case, the system start-up failure is determined by both the malfunction of the active (or mechanical) component and the probability of the physical phenomenon development, while the failure during operation is determined by the stability of the physical phenomena, the reliability of mechanical parts and the possible failure of the refill procedure (if considered), similarly to type ‘B’ passive systems. Moreover, for type ‘D’ passive systems, the failures of electric power supply and Instrumentation and Control (I & C) systems have to be considered along with the active component failure during start-up.

Typical FTs for start-up failure and failure during operation for type ‘C’ and ‘D’ passive systems are shown in Figure 2.

As usual in traditional PSA, the FTs have to be linked to the ETs, where the passive system success/failure is considered among the ETs header events [116]. In general terms, the call in operation of a passive system results from the malfunction of an active system: therefore, the header representing passive systems is typically preceded by headers of active systems.

Integration can be done by, alternatively:

• Separate headers for start-up failures and failures during operation;
• One header representing both types of failure.

The ETs representing these two alternatives are presented in Figure 3, left and right, respectively.

In the former case, the FTs presented in Figure 1 and Figure 2 are placed behind the two distinct headers (‘Passive System Successfully Starts’ and ‘Passive System Successfully Continues Operation’), whereas in the latter case, the two FTs are linked together into an ‘OR’ gate and placed behind the single header ‘Passive System Successfully Starts and Continues Operation’.

In most cases, the two ET construction approaches result in the same minimal cut-set lists; however, the first approach should be cautiously applied for scenarios where more than one redundant train is available, and the operation of a single train can fulfill the required safety function. In this particular case, some relevant minimal cut-sets are left out from the results. For illustration purposes, consider a passive system with two redundant trains. The top gate of the FT for the start-up failure is an ‘AND’ gate, which links the start-up failures of the two redundant trains. The FT for the failure during operation also has the same structure. As a result, the passive system fails only if both trains fail to start or both trains fail to run, neglecting the minimal cut set ‘one train fails to start and the other train fails to run’. Therefore, in this case (when there are 100% redundant trains), the second option is preferable.

5.3.2. Integration of Passive Systems into Dynamic PSA

In the PSA practice, accident scenarios, though dynamic in nature, are usually analyzed with the ‘static’ ETs and FTs, as discussed in the previous Section 5.3.1.

The current ‘static’ PSA framework is limited when: (i) handling the actual events timing, which ultimately influences the evolution of the scenarios; and (ii) modelling the interactions between the hardware components (i.e., failure rates) and the process variables (temperatures, mass flows, pressures, etc.) [66,104,105,117,118]. In practice, with respect to (i), different orders of the same success and failure events (and/or different timing of these events occurrence) along an accident scenario typically lead to different outcomes; with respect to (ii), the event/scenarios occurrence probabilities are affected by process variables values (temperatures, mass flows, pressures, etc.). This highlights another limitation of the ‘static’ PSA framework, which can only handle Boolean representations of system states (i.e., success or failure), neglecting any intermediate (partial operation) states, which, conversely, is fundamental when concerned with the passive system operation.

In fact, because of its specific features, defining the status of a passive system simply in terms of ‘success’ or ‘failure’, is limited, since ‘intermediate’ modes of operation or equivalently degraded performance states (up to the failure point) are possible and may (still) guarantee some (even limited) operation. This operation could be sufficient to recover a failed system (e.g., through redundancy configuration) and, ultimately, a severe accident.

In complex situations where several (multi-state) safety systems are involved and where human behavior still plays a relevant role, advanced solutions have been proposed and already used for dynamic PSA, like Continuous Event Trees (CETs) [119,120], Dynamic Event Trees (DETs) [121], Discrete DETs (DDETs) [122], Monte Carlo DETs (MCDETs) [123] and Repairable DETs (RDETs) [124], because they provide more realistic frameworks than static FTs and ETs, since they capture the interaction between the process parameters and the passive system states within the dynamical evolution of the accident. The most evident difference between DETs and static ETs is that while ETs are constructed by expert analysts that draw their branches based on success/failure criteria set by the analysts, in DETs, these are spooned by a software that embeds the (deterministic) models simulating the plant dynamics and the (stochastic) models of components failure. Naturally, the DET generates a number of scenarios much larger than that of the classical static FT/ET approaches, so that the a posteriori retrieval of information can become quite burdensome and complex [125,126,127]. Another challenge is related to the relevant effort in terms of computational time required for generating a large number of time-dependent accident scenarios by means of Monte Carlo techniques that are typically employed to deeply and thoroughly explore the entire system state-space, and to cover in principle all the possible combinations of events over long periods of time. This, for thermal hydraulic passive systems, is even more relevant, since during the accident progression their reliability strongly depends (more than other safety systems) upon time and the state/parameter evolution of the system. Therefore, also in this case, resorting to metamodels can help [128], accomplishing the evaluation process of T–H passive systems in a consistent manner.

The goal of dynamic PSA is, therefore, to account for the interaction of the process dynamics and the stochastic nature/behavior of the system at various stages and embed the state/parameter evaluation by deterministic thermal hydraulic codes within a DET generation [129]. The framework should be able to estimate the physical variations of all the system parameters/variables and the frequency of the accident sequences, while taking into proper account the dynamic effects. If the (mechanical) components failure probabilities (e.g., the failure probability per-demand of a valve) are known, then they can be combined with the probability distributions of estimated parameters/variables, in order to predict the probabilistic evolution of each scenario.

In [130], the T–H passive system behavior is represented as a non-stationary stochastic process, where natural circulation is modelled in terms of time-variant performance parameters (e.g., thermal power and mass flow rate) assumed as stochastic variables. In that work, which can be considered as a preliminary attempt to address the dynamic aspect in the context of passive system reliability, the statistics of such stochastic variables (e.g., mean values and standard deviations) change in time, so that the corresponding random variables assume different values in different realizations (i.e., each realization is different).

6. Conclusions, Recommendations and Additional Issues

In this paper, we have laid down a common understanding of the state-of-the-art and open issues with respect to the reliability assessment of passive safety systems for their adoption in nuclear installations. Indeed, such safety systems rely on intrinsic physical phenomena, which makes the assessment of their performance quite challenging to carry out with respect to traditional (active) systems. This is due to the typical scarcity of data in a sufficiently wide range of operational conditions, which introduces relevant (aleatory and epistemic) uncertainties into the analysis. These issues could have a negative impact on the public acceptance of next generation nuclear reactors, which instead—thanks to use of passive systems—should be safer than the current ones. Thus, structured and sound frameworks and techniques must be sought, developed and demonstrated for a robust quantification of the reliability/failure probability of nuclear passive safety systems.

With respect to T–H passive systems, a review of the available approaches and frameworks for the quantification of the reliability of nuclear passive safety systems has been presented, followed by a critical discussion of the pending open issues.

It has turned out that the massive use of expert judgement and subjective assumptions combined with often scarce data requires the propagation of the corresponding uncertainties by simulating numerous times the system behavior under different operating conditions. In this light, the most realistic assessment of the passive system is provided by the functional failure-based approach, thanks to MCS, which is flexible and is not negatively affected by any model complexity: therefore, it does not require any simplifying assumption. On the other hand, often prohibitive computational efforts are required, because a large number of MC-sampled model evaluations must be often carried out for an accurate and precise assessment of the frequently small (e.g., lower than 10⁻⁴) functional failure probability: actually, each evaluation requires the call of a long-running mechanistic code (several hours, per run). Thus, we must resort to advanced methods to tackle the issues associated with the analysis.

As open issues, we focused, in particular, on the role of empirical regression modelling, the need of advanced sensitivity analysis methods and the integration of passive systems in the (static/dynamic) PSA framework. In this regard, we can provide general conclusions and recommendations for those practitioners who tackle the issue of passive systems reliability assessment:

• If the estimation of the passive system functional failure probability is of interest, we suggest combining metamodels with efficient MCS techniques, for example, by constructing and adaptively refining the metamodel by means of samples generated by the advanced MCS method in proximity of the system functional failure region [78,79,80,81,82,83,84,85,86]. An example is represented by the Adaptive Metamodel-based Subset Importance Sampling (AM-SIS) method, recently proposed by some of the authors, which intelligently combines Subset Simulation (SS), Importance Sampling (IS) and iteratively trained Artificial Neural Networks (ANNs) [78,79].
• If thorough uncertainty propagations (e.g., the determination of the PDFs, CDFs, percentiles of the code outputs) and SA are of interest to the analyst, a combination of Finite Mixture Models (FMMs) and ensembles of global SA measures are suggested, as proposed by some of the authors in [94,98].

Finally, it is worth mentioning that, to foster these methods’ acceptance in the nuclear research community and to consequently promote the public acceptance of future reactor designs involving passive safety systems, other (open) issues should be addressed, such as:

• The methods proposed rely on the assessment of the uncertainty (both aleatory and epistemic) in the quantitative description provided by models of the phenomena pertaining to the functions of the passive systems. This requires a systematic, sound and rigorous Inverse Uncertainty Quantification (IUQ) approaches to find a characterization of the input parameters uncertainty that is consistent with the experimental data, while limiting the associated computational burden. Approaches have been already proposed in the open literature, but not yet in the field of passive system reliability assessment [131,132,133,134,135,136].
• If we resort to empirical metamodels for estimating passive systems failure probabilities and carrying out uncertainty and SA, the following problems should be considered:
  • the regression error should be carefully quantified (and possibly controlled) throughout the process, in order to reduce its impact on the entire reliability assessment [81];
  • the higher the input dimensionality (e.g., in the presence of time series data), the higher the size of the training dataset should be to obtain metamodel accuracy. Rigorous (linear or nonlinear) approaches to reduce the input dimensionality (e.g., Principal Component Analysis, PCA, or Stacked Sparse Autoencoders) should be sought, with increased metamodel performances [137];
  • the quality of metamodel training can be negatively affected by noisy data. Data filtering, carried out on the model code predictions, may impact on the metamodel predictive performance [138].
• The introduction of passive safety systems in the framework of PSA deserves particular attention, in particular, when accident scenarios are generated in a dynamic fashion. The reasons are the following:
  • it is difficult to define the state of passive systems along an accident sequence only in the classical binary terms of ‘success/failure’; rather, ‘intermediate’ modes of operation or degraded performances states should be considered, where the passive system might still be capable of providing a functional level sufficient for the mitigation of the accident progression;
  • the amount of accident scenarios to be handled is consistently larger than that associated with the traditional static fault/event tree techniques. Thus, the “a posteriori” retrieval of information can be quite burdensome and difficult. In this view, artificial intelligence techniques could be embraced to address the problem [125,126,127];
  • the thorough exploration of the dynamic state-space of the passive safety system is impracticable by standard (sampling) methods: advanced exploration schemes should be sought to intelligently drive the search towards ‘interesting’ scenarios (e.g., extreme unexpected events), while reducing the computational effort [139,140].