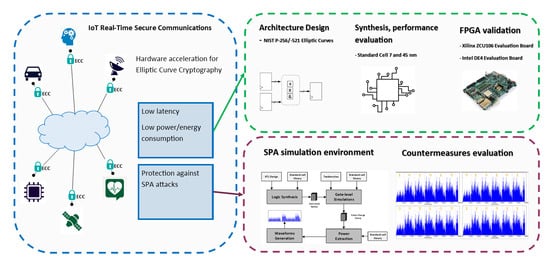
Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications
Abstract
:1. Introduction
- Architectural design of a configurable (at synthesis level) ECC crypto-processor for NIST P-256 and/or NIST P-521 elliptic curves, developed in the framework of the European Processor Initiative together with other cryptographic hardware accelerators (AES, RNG [27,28], SHA [29]). The proposed architecture supports the most used cryptographic schemes based on ECC such as ECDSA, ECDH, ECIES and ECMQV. The design is resistant to timing and SPA attacks and uses a constant-version of Shamir’s trick for Double Point Multiplication, and Fermat’s Little Theorem to execute modular inversion.
- A simulated environment to extract and evaluate the power consumption of the circuit, which allowed the evaluation of the proposed countermeasure against SPA. The proposed simulated approach does not require any dedicated equipment to acquire power samples and can be adopted in the early design phase to help designers find effective architectural and algorithmic solutions against Power attacks.
- Synthesis on the open source 45 nm NANDGATE45 [30] library and 7 nm TSMC silicon technology (the first contribution available to the best of authors’ knowledge) with a complete analysis of the performance in terms of complexity, throughput and power consumption.
- Verification and characterization in terms of resources utilization and throughput on a Xilinx ZCU106 development board equipped with Zynq UltraScale+ xczu7ev-ffvc1156-2-e MPSoC.
2. Related Works
3. Preliminaries on ECC
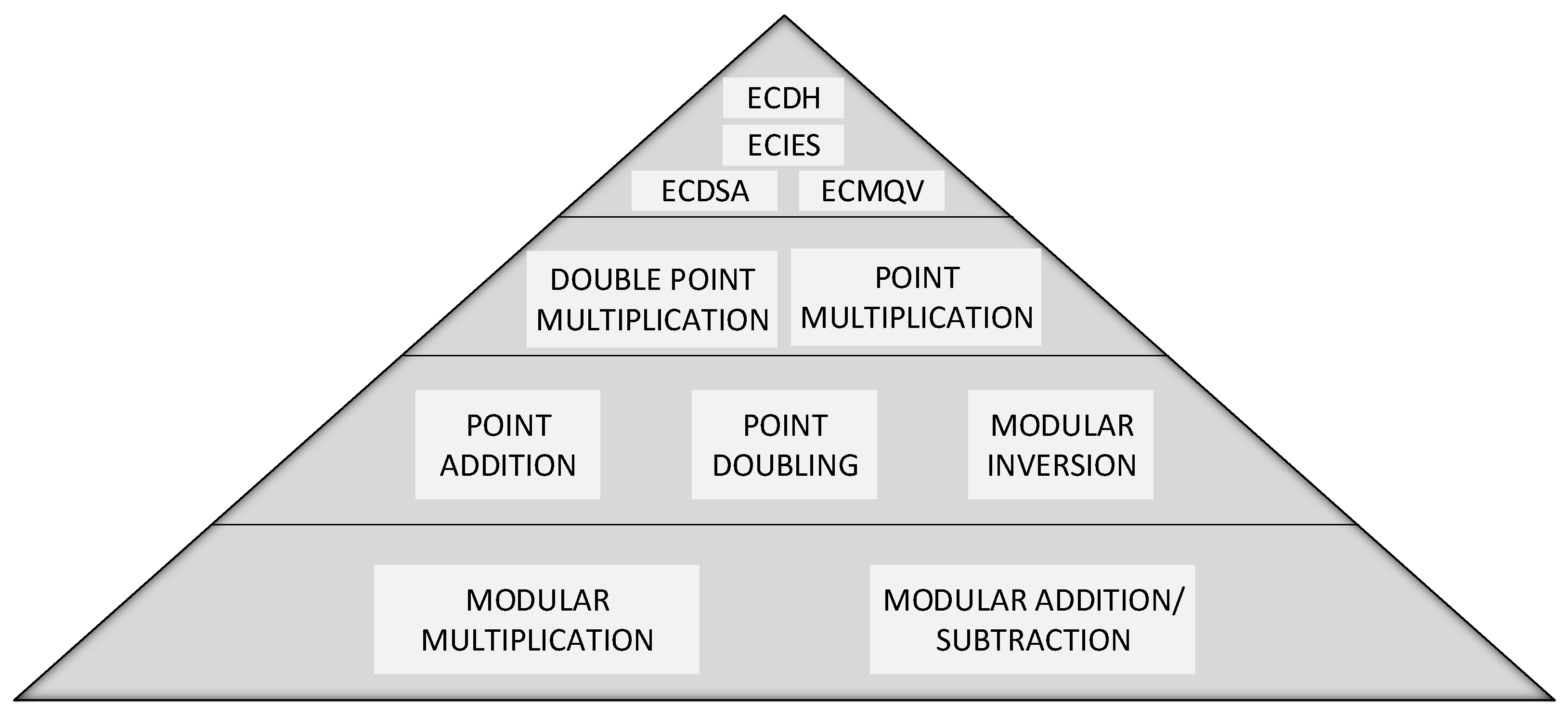
3.1. Elliptic Curve Cryptography
- Point Addition (PA): where
- Point Doubling (PD): wherewhere and are two points on the elliptic curve. It should be noted that all the arithmetic operations (additions, subtractions, multiplications and divisions) described above are on the prime field . PA and PD operations over such group are used to construct many elliptic curve crypto-systems, and a typical hierarchical structure of an ECC crypto-system is reported in Figure 1. At the top level there are protocols such as ECDSA, ECIES, ECDH and ECMQV. In the lower layer there are PM and DPM that will be discussed in Section 3.2; the next layer comprises the basic operations on the ECC points: PA and PD. They require the underlying level that consists of finite field arithmetic operations on such as modular addition, subtraction and multiplication. In our hierarchical structure we placed modular inversion at the same level of PA and PD because we implemented it using Fermat’s Little theorem that exploits the operations at the lowest layer.
3.2. Point Multiplication and SPA
| Algorithm 1 Double-and-Add Right-to-Left. |
Input: Output: 1: 2: 3: for to do 4: if then 5: 6: end if 7: 8: end for 9: return Q |
| Algorithm 2 Double-and-Add-Always Right-to-Left. |
Input: Output: 1: 2: 3: for to do 4: if then 5: 6: else 7: 8: end if 9: 10: end for 11: return Q |
| Algorithm 3 Modified Double-and-Add-Always Right-to-Left. |
Input: Output: 1: one_flag , 2: if then 3: , one_flag 4: end if 5: for to do 6: if then 7: if one_flag then 8: 9: else 10: , 11: end if 12: else 13: if one_flag then 14: 15: else 16: 17: end if 18: end if 19: 20: end for 21: return Q |
| Algorithm 4 Constant Time Version of Shamir’s Trick. |
Input: Output: 1: 2: 3: for to do 4: 5: if and then 6: 7: else if and then 8: 9: else if and then 10: 11: else 12: 13: end if 14: end for 15: return Q |
3.3. Coordinates Representation
4. Proposed Hardware Architecture
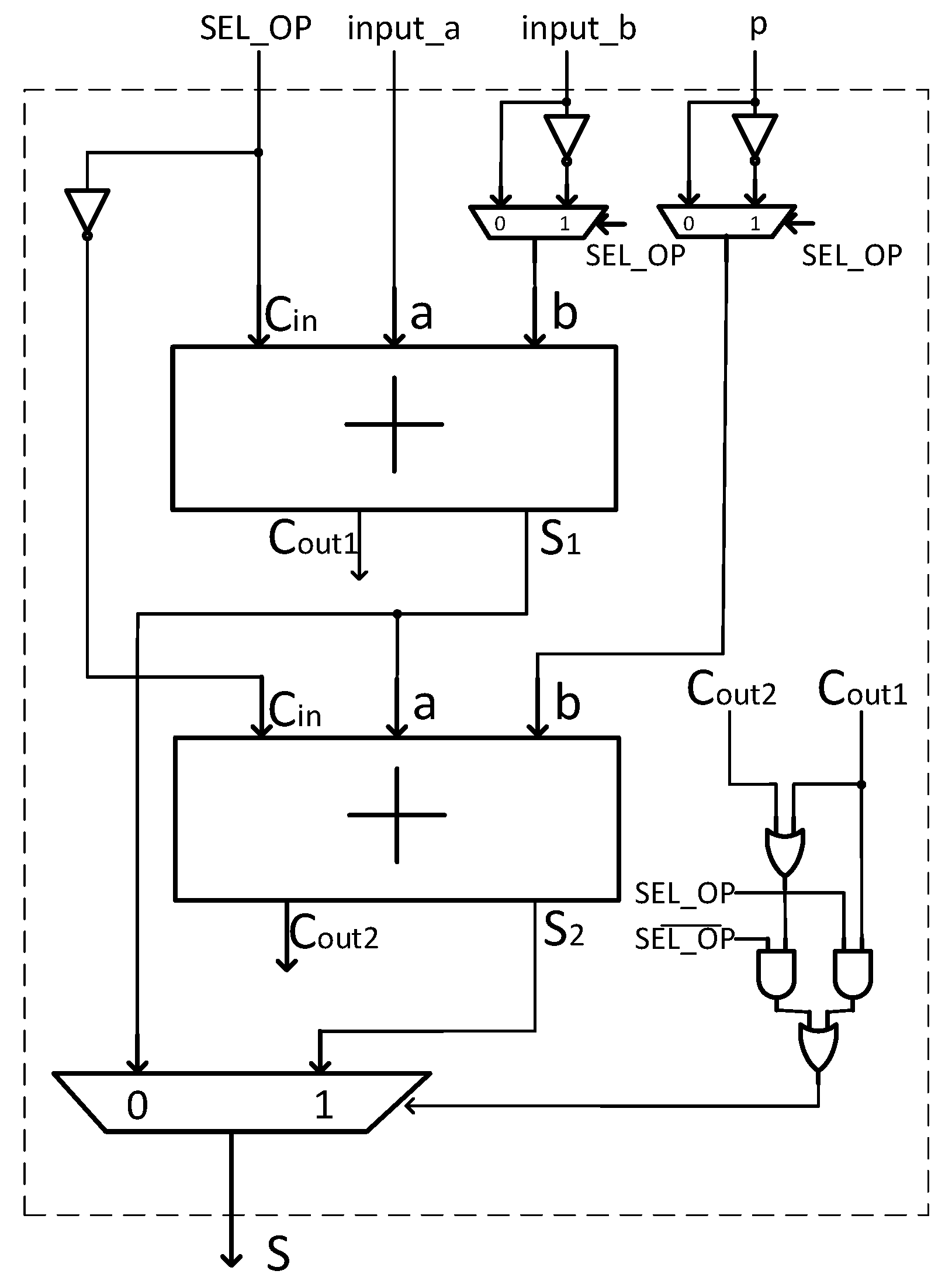
4.1. Modular Addition and Subtraction
| Algorithm 5 Modular Addition/Subtraction. |
Input: , p and Output: 1: if then 2: 3: 4: if then 5: 6: else 7: 8: end if 9: else 10: 11: 12: if then 13: 14: else 15: 16: end if 17: end if 18: return S |
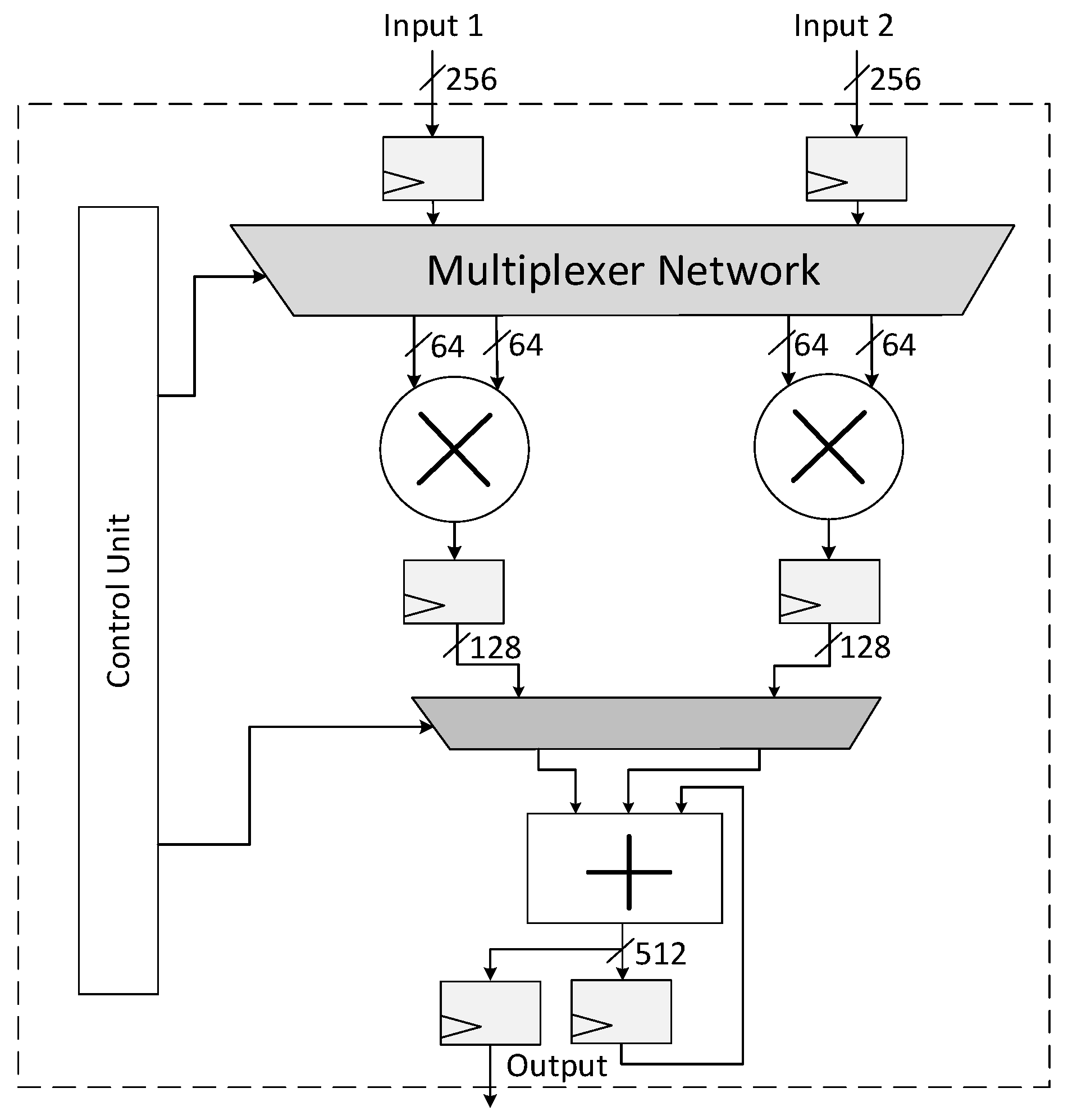
4.2. Modular Multiplication
| Algorithm 6 Fast Modular Reduction for NIST P-256. |
Input: Output: 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: return |
| Algorithm 7 Fast Modular Reduction for NIST P-521. |
Input: Output: 1: return |
| Algorithm 8 Schoolbook-Based Multiplication Algorithm. |
Input: 256-bit integers such that: , . Output: × B 1: × ; × ; 2: × ; × ; 3: × ; × ; 4: × ; × ; 5: × ; × ; 6: × ; × ; 7: × ; × ; 8: × ; × ; 9: 10: return C |
4.3. PA, PD and Modular Inversion
| Algorithm 9 Right-to-left Square-and-Multiply for Modular Exponentation. |
Input: Output: 1: 2: for i from 0 to do 3: if then 4: 5: else 6: 7: end if 8: 9: end for 10: return r1 |
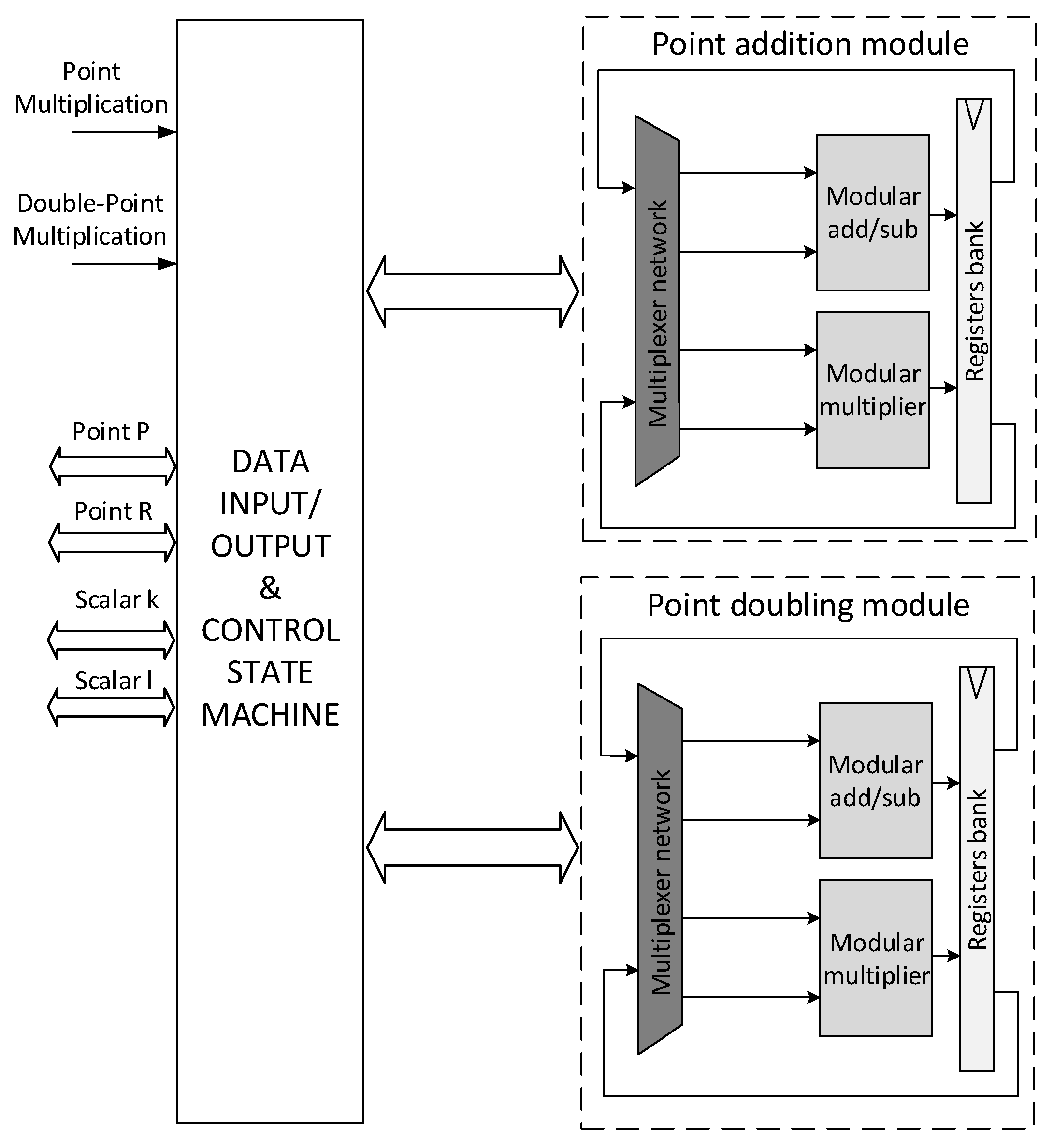
4.4. Overall Architecture
4.5. FPGA Verification
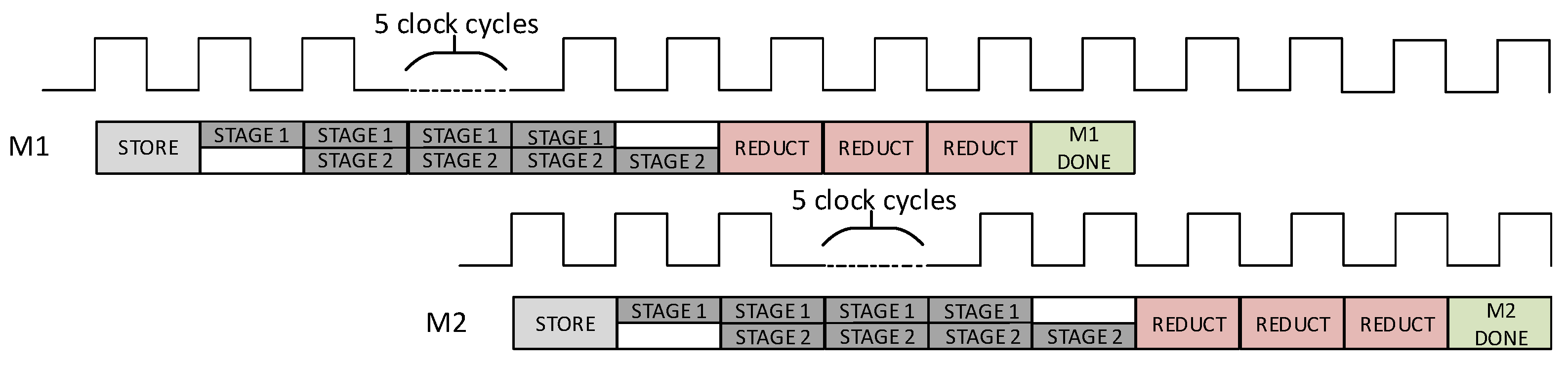
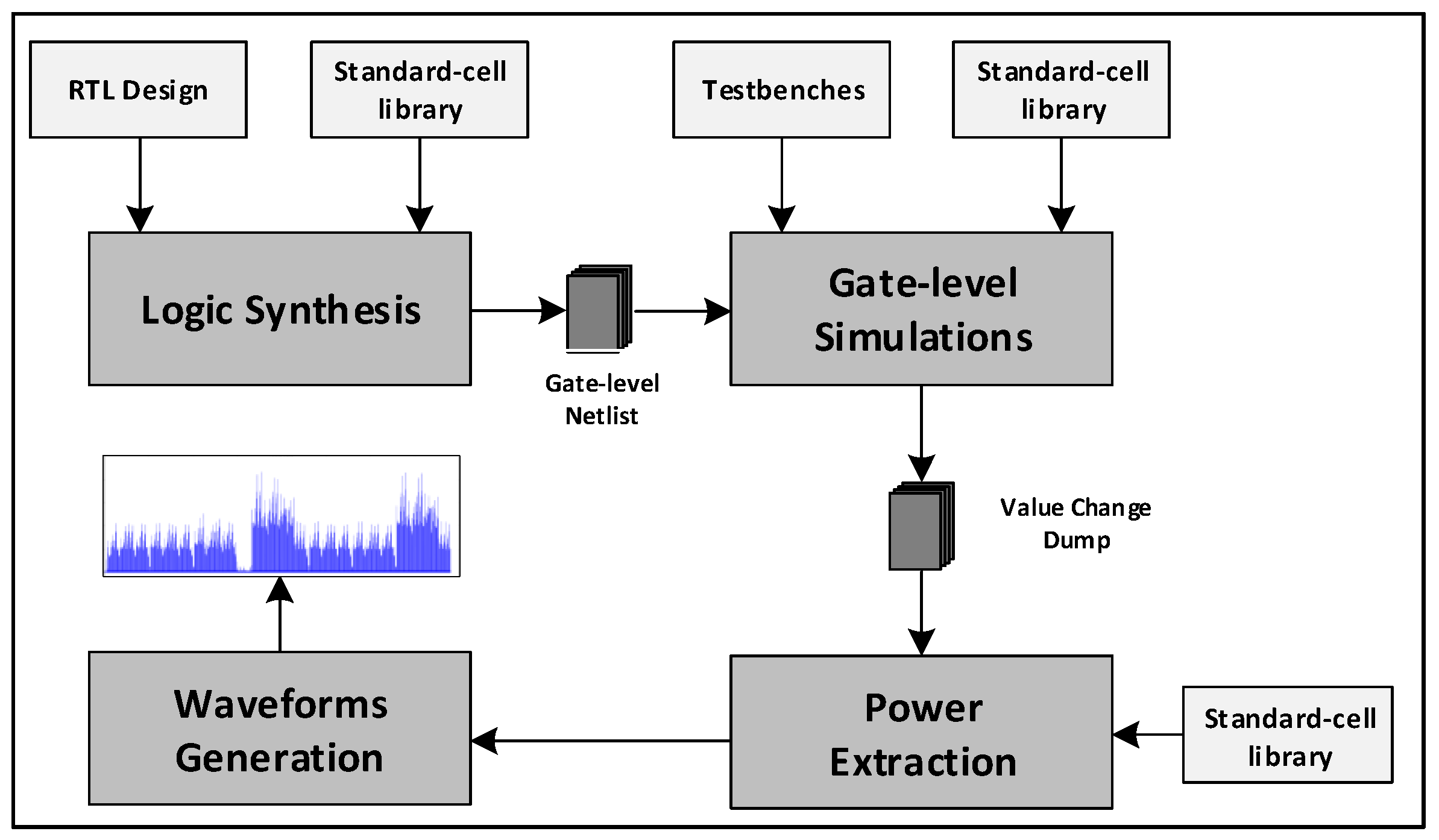
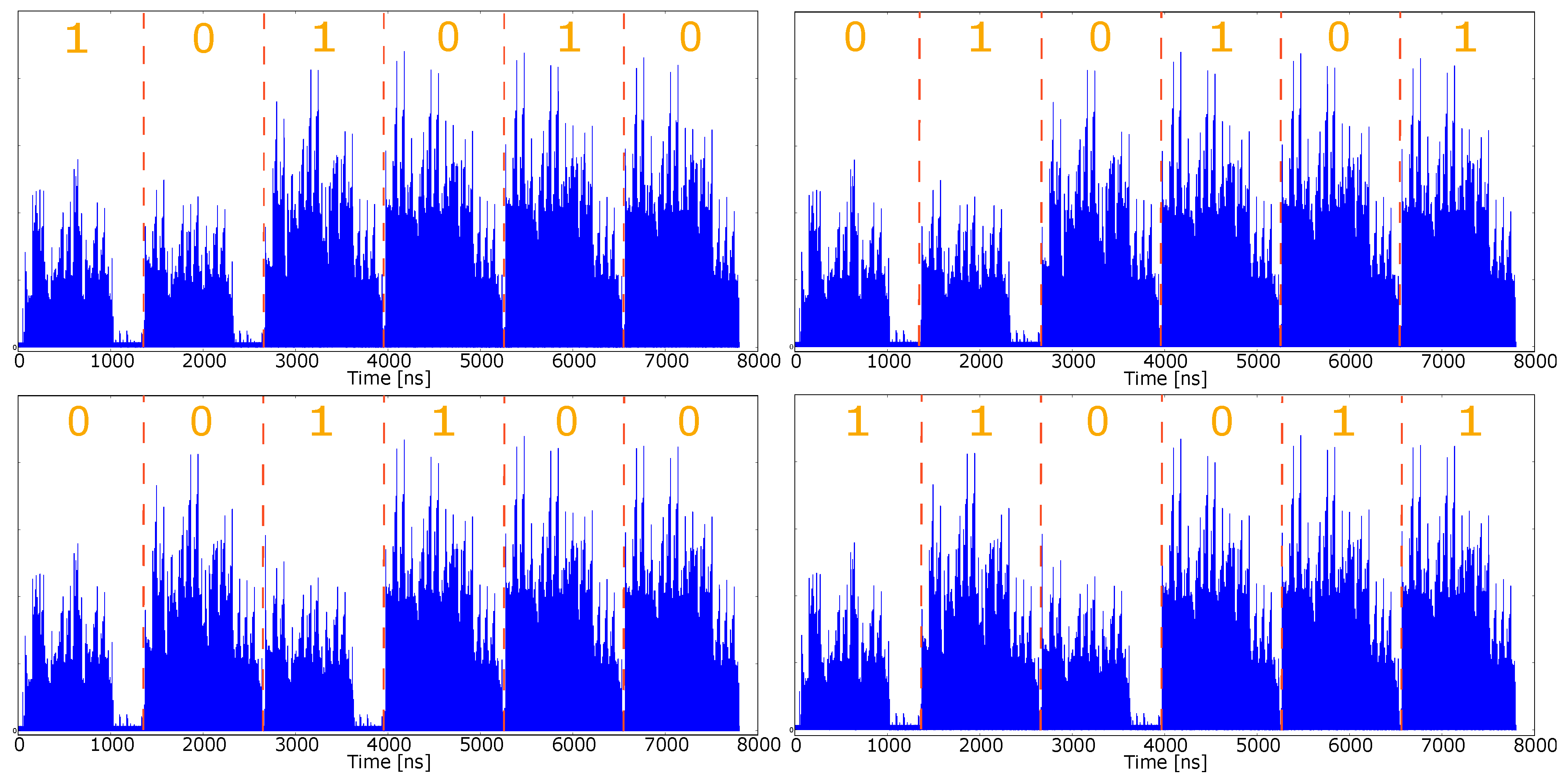
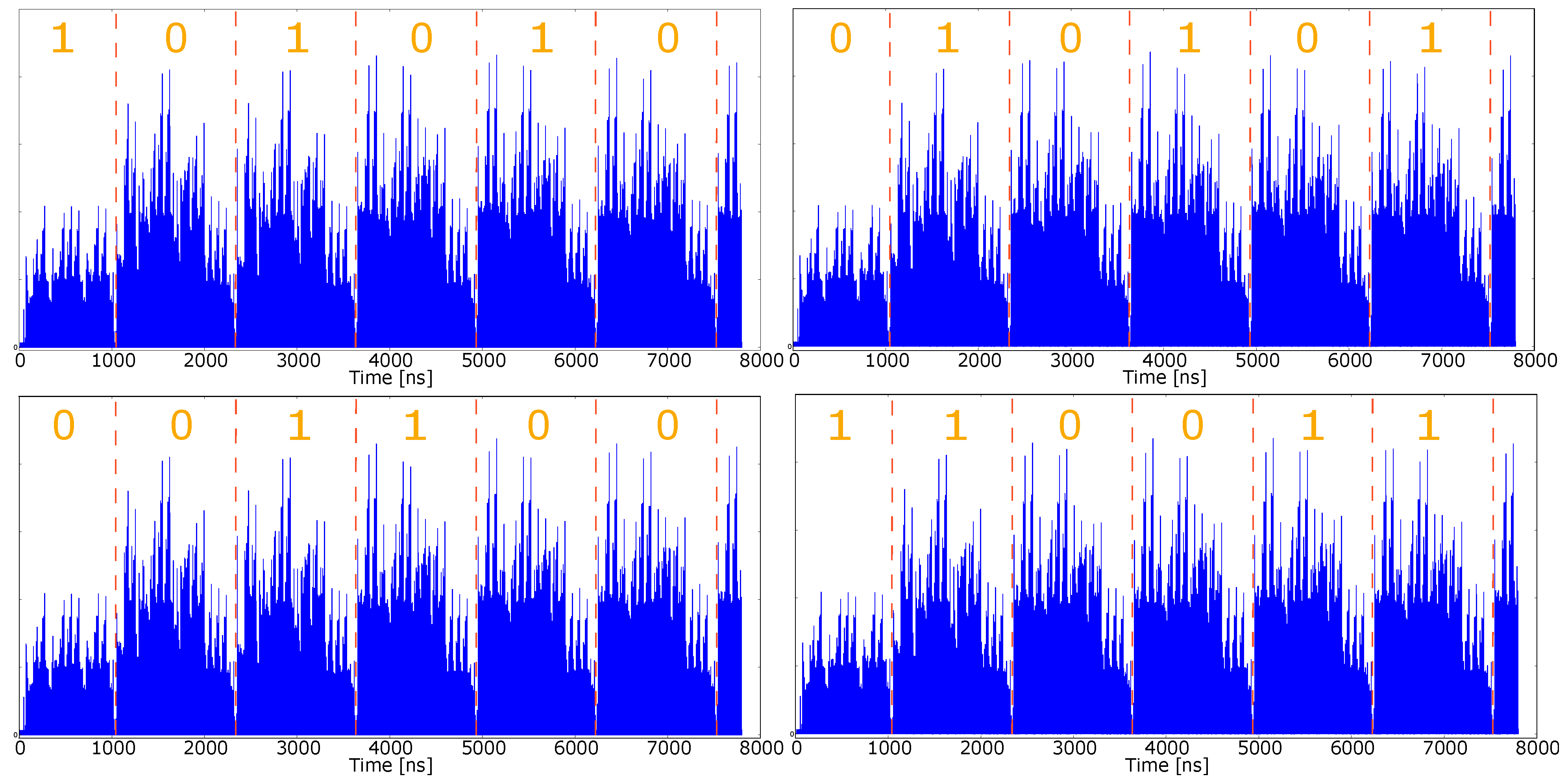
4.6. SPA Assessment through Simulated Approach
5. Results and Comparison
Discussion and Comparison
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Stallings, W. Symmetric Ciphers. In Cryptography and Network Security: Principles and Practice, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Lenstra, A.K.; Verheul, E.R. Selecting cryptographic key sizes. J. Cryptol. 2001, 14, 255–293. [Google Scholar] [CrossRef] [Green Version]
- Miller, V.S. Use of elliptic curves in cryptography. In Proceedings of the Conference on the Theory and Application of Cryptographic Techniques, Linz, Austria, 9–11 April 1985; Springer: Berlin/Heidelberg, Germany, 1985; pp. 417–426. [Google Scholar]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Group, I.W. IEEE 1363-2000: Standard Specifications for Public Key Cryptography; IEEE Standard: New York, NY, USA, 2000; Volume 10017. [Google Scholar]
- NIST. FIPS 186-4—Digital Signature Standard (DSS); Information Technology Laboratory, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- ANSI. X9.62: Public key cryptography for the financial services industry. In The Elliptic Curve Digital Signature Algorithm (ECDSA); American National Standards Institute: Washington, DC, USA, 2005. [Google Scholar]
- Standards for Efficient Cryptography SEC 1, SEC 2: Elliptic Curve Cryptography; Certicom Research: Mississauga, ON, Canada, 2009; Available online: https://www.secg.org (accessed on 10 May 2021).
- Fips, P. 186-2. Digital Signature Standard (dss); National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 2000; Volume 20, p. 13.
- Rescorla, E. The Transport Layer Security (TLS) Protocol Version 1.3, RFC, Volume 8446. 2018. Available online: https://www.rfc-editor.org/info/rfc8446 (accessed on 10 May 2021).
- Burgin, K.; Peck, M. Suite B Profile for Internet Protocol Security (IPsec); Technical Report, RFC 6380. 2011. Available online: https://www.rfc-editor.org/rfc/rfc6380.html (accessed on 7 June 2021).
- Group, I.W. IEEE Standard for Wireless Access in Vehicular Environments-Security Services for Applications and Management Messages; IEEE Std 1609.2-2016; IEEE: New York, NY, USA, 2016; pp. 1–240. [Google Scholar]
- ETSI Technical Specification. ETSI TS 103 097 v1. Intelligent Transport Systems (ITS); Security; Security Header and Certificate Formats, Standard, TC ITS. 2013. Available online: https://www.etsi.org/deliver/etsi_ts/103000_103099/103097/01.04.01_60/ts_103097v010401p.pdf (accessed on 17 April 2021).
- Naveed Aman, M.; Taneja, S.; Sikdar, B.; Chua, K.C.; Alioto, M. Token-Based Security for the Internet of Things With Dynamic Energy-Quality Tradeoff. IEEE Internet Things J. 2019, 6, 2843–2859. [Google Scholar] [CrossRef]
- AlMajed, H.; AlMogren, A. A Secure and Efficient ECC-Based Scheme for Edge Computing and Internet of Things. Sensors 2020, 20, 6158. [Google Scholar] [CrossRef] [PubMed]
- Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Fanucci, L.; Saponara, S.; Patrice, H. Crypto accelerators for power-efficient and realtime on-chip implementation of secure algorithms. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019. [Google Scholar]
- Ledwaba, L.P.; Hancke, G.P.; Venter, H.S.; Isaac, S.J. Performance costs of software cryptography in securing new-generation Internet of energy endpoint devices. IEEE Access 2018, 6, 9303–9323. [Google Scholar] [CrossRef]
- Verri Lucca, A.; Mariano Sborz, G.A.; Leithardt, V.R.Q.; Beko, M.; Albenes Zeferino, C.; Parreira, W.D. A Review of Techniques for Implementing Elliptic Curve Point Multiplication on Hardware. J. Sens. Actuator Netw. 2021, 10, 3. [Google Scholar] [CrossRef]
- Hossain, M.S.; Kong, Y.; Saeedi, E.; Vayalil, N.C. High-performance elliptic curve cryptography processor over NIST prime fields. IET Comput. Digit. Tech. 2016, 11, 33–42. [Google Scholar] [CrossRef]
- Awaludin, A.M.; Larasati, H.T.; Kim, H. High-Speed and Unified ECC Processor for Generic Weierstrass Curves over GF(p) on FPGA. Sensors 2021, 21, 1451. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zheng, X.; Zhang, S.; Cai, S.; Xiong, X. A Low Hardware Consumption Elliptic Curve Cryptographic Architecture over GF(p) in Embedded Application. Electronics 2018, 7, 104. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Lei, B.; Zhang, Y.; Lei, S. A Novel and High-Performance Modular Square Scheme for Elliptic Curve Cryptography Over GF (p). IEEE Trans. Circuits Syst. II Express Briefs 2018, 66, 647–651. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, D.; Guan, Z.; Wang, Z. A High Speed VLSI Implementation of 256-bit Scalar Point Multiplier for ECC over GF (p). In Proceedings of the 2018 IEEE International Conference on Intelligence and Safety for Robotics (ISR), Shenyang, China, 24–27 August 2018; pp. 184–191. [Google Scholar]
- Hankerson, D.; Menezes, A.J.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- European Processor Initiative (EPI). Available online: https://www.european-processor-initiative.eu (accessed on 10 May 2021).
- Nannipieri, P.; Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Belli, J.; Fanucci, L.; Saponara, S. True Random Number Generator Based on Fibonacci-Galois Ring Oscillators for FPGA. Appl. Sci. 2021, 11, 3330. [Google Scholar] [CrossRef]
- Baldanzi, L.; Crocetti, L.; Falaschi, F.; Bertolucci, M.; Belli, J.; Fanucci, L.; Saponara, S. Cryptographically Secure Pseudo-Random Number Generator IP-Core Based on SHA2 Algorithm. Sensors 2020, 20, 1869. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nannipieri, P.; Bertolucci, M.; Baldanzi, L.; Crocetti, L.; Di Matteo, S.; Falaschi, F.; Fanucci, L.; Saponara, S. SHA2 and SHA-3 Accelerator Design in a 7 nm Technology Within the European Processor Initiative. Microprocess. Microsyst. 2021. [Google Scholar] [CrossRef]
- Silvaco PDK 45 nm Open Cell Library. Available online: https://si2.org/open-cell-library (accessed on 30 July 2021).
- Liu, Z.; Liu, D.; Zou, X. An efficient and flexible hardware implementation of the dual-field elliptic curve cryptographic processor. IEEE Trans. Ind. Electron. 2016, 64, 2353–2362. [Google Scholar] [CrossRef]
- Chung, S.C.; Lee, J.W.; Chang, H.C.; Lee, C.Y. A high-performance elliptic curve cryptographic processor over GF (p) with SPA resistance. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems, Seoul, Korea, 20–23 May 2012; pp. 1456–1459. [Google Scholar]
- Chen, G.; Bai, G.; Chen, H. A High-Performance Elliptic Curve Cryptographic Processor for General Curves Over GF (p) Based on a Systolic Arithmetic Unit. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 412–416. [Google Scholar] [CrossRef]
- Brier, E.; Joye, M. Weierstraß elliptic curves and side-channel attacks. In Proceedings of the International Workshop on Public Key Cryptography, Paris, France, 12–14 February 2002; pp. 335–345. [Google Scholar]
- Pontie, S.; Maistri, P.; Leveugle, R. Dummy operations in scalar multiplication over elliptic curves: A tradeoff between security and performance. Microprocess. Microsyst. 2016, 47, 23–36. [Google Scholar] [CrossRef]
- Hall, T.A.; Keller, S.S. Elliptic Curve Digital Signature Algorithm (ECDSA) Validation System (ECDSA2VS); NIST Information Technology Laboratory: Gaithersburg, MD, USA, 2014.
- Synopsys Design Compiler. Available online: https://www.synopsys.com/support/training/rtl-synthesis/design-compiler-rtl-synthesis.html (accessed on 22 June 2021).
- QuestaSim. Available online: https://eda.sw.siemens.com/en-US/ic/questa/simulation/advanced-simulator/ (accessed on 22 June 2021).
- PrimeTime. Available online: https://www.synopsys.com/implementation-and-signoff/signoff/primetime.html (accessed on 22 June 2021).
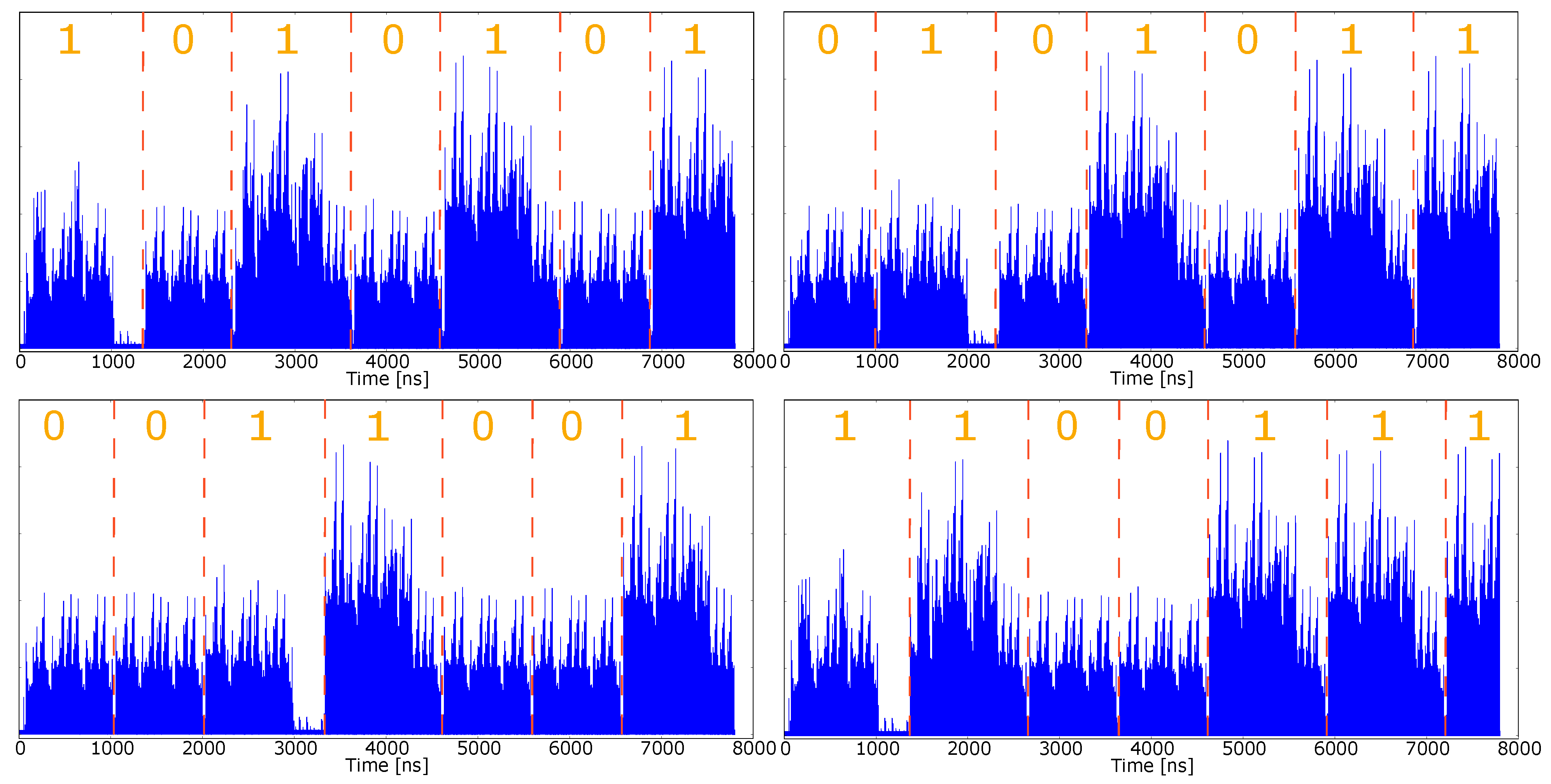
| Affine | Standard Projectives | Jacobian Projectives | |
|---|---|---|---|
| PA | 3M + 1I | 14M | 16M |
| PD | 4M + 1I | 10M | 8M |
| c.c. P-256 | c.c. P-521 | Modular Multiplication | Modular Add/Sub |
|---|---|---|---|
| 0–12 | 0–34 | ||
| 8–20 | 32–66 | ||
| 16–28 | 64–98 | ||
| 24–36 | 96–130 | ||
| 37–49 | 131–165 | ||
| 45–57 | 163–197 | ||
| 53–65 | 195–229 | ||
| 61–73 | 227–261 | ||
| 69–81 | 259–293 | ||
| 82–94 | 294–328 | ||
| 90–102 | 326–360 | ||
| 98–110 | 358–392 | ||
| 106–118 | 390–424 | ||
| 114–126 | 422–456 | ||
| 127 | 457 |
| c.c. P-256 | c.c. P-521 | Modular Multiplication | Modular Add/Sub |
|---|---|---|---|
| 0–12 | 0–34 | , | |
| 8–20 | 32–66 | ||
| 16–28 | 64–98 | ||
| 24–36 | 96–130 | ||
| 37–49 | 131–165 | ||
| 45–57 | 163–197 | ||
| 53–65 | 195–229 | ||
| 61–73 | 227–261 | ||
| 69–81 | 259–293 | ||
| 82–94 | 294–328 | ||
| 95 | 329 |
| Configuration | Process. [nm] | Gate Counts [kGE] | Kcycles | Freq. [MHz] | T [μs] |
|---|---|---|---|---|---|
| P-256 only | 45 | 281 | 36.390 | 400 | 90.975 |
| P-521 only | 45 | 407 | 254.456 | 375 | 686.54 |
| P-256/-521 | 45 | 447 | 36.390/257.456 | 375 | 97.04/686.54 |
| P-256 only | 7 | 279 | 36.390 | 1820 | 19.99 |
| P-521 only | 7 | 405 | 257.456 | 1650 | 156.03 |
| P-256/-521 | 7 | 445 | 36.39/257.456 | 1650 | 22.05/156.03 |
| Config. | CLBs | DSPs | Freq. [MHz] | T [μs] |
|---|---|---|---|---|
| P-256 only | 3444 | 64 | 150 | 242 |
| P-521 only | 5689 | 64 | 120 | 2145 |
| P-256/-521 | 6575 | 64 | 110 | 330/2340 |
| Ref. | Process. [nm] | Gate Counts [kGE] | Primes | Kcycles | Freq. [MHz] | T [μs] | AT | SPA Assessment |
|---|---|---|---|---|---|---|---|---|
| Our | 45 | 281 | P-256 | 36.390 | 400 | 90.97 | 1 | Simulated approach |
| [31] | 55 | 187 | Dual-Field | – | 316 | 1450 | 8.68 | Power extraction |
| [24] | 65 | 3500 | P-256 | 2.35 | 188 | 12.5 | 1.18 | – |
| [20] | 65 | 447 | P-256 | 397.3 | 546.5 | 730 | 8.84 | – |
| [32] | 90 | 540 | 256-bit | 22.3 | 185 | 120 | 1.27 | Theoretical |
| [33] | 130 | 122 | 256-bit | 340 | 556 | 1010 | 1.67 | – |
| [23] | 130 | 77.1 | 256-bit | – | 200 | 860 | 0.9 | – |
| [22] | 130 | 57.05 | 256-bit | 610 | 150 | 4070 | 3.14 | Theoretical |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Matteo, S.; Baldanzi, L.; Crocetti, L.; Nannipieri, P.; Fanucci, L.; Saponara, S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies 2021, 14, 4676. https://doi.org/10.3390/en14154676
Di Matteo S, Baldanzi L, Crocetti L, Nannipieri P, Fanucci L, Saponara S. Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies. 2021; 14(15):4676. https://doi.org/10.3390/en14154676
Chicago/Turabian StyleDi Matteo, Stefano, Luca Baldanzi, Luca Crocetti, Pietro Nannipieri, Luca Fanucci, and Sergio Saponara. 2021. "Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications" Energies 14, no. 15: 4676. https://doi.org/10.3390/en14154676
APA StyleDi Matteo, S., Baldanzi, L., Crocetti, L., Nannipieri, P., Fanucci, L., & Saponara, S. (2021). Secure Elliptic Curve Crypto-Processor for Real-Time IoT Applications. Energies, 14(15), 4676. https://doi.org/10.3390/en14154676