Operating Cost Reduction in Distribution Networks Based on the Optimal Phase-Swapping including the Costs of the Working Groups and Energy Losses
Abstract
:1. Introduction
- The use of an improved sine cosine algorithm (ISCA) to solve the phase-balancing problem; the algorithm was modified by changing the number of points in the codification that can change in each iterative cycle. This was achieved by using an adaptive rule as a function of the maximum number of nodes of the network.
- Hybridization of the ISCA (master stage) with the triangular-based three-phase power flow method (slave stage), which can solve power flow problems in asymmetric networks with loads with Y- and -connections.
- Evaluation of the phase-balancing plan by modifying the objective function to account for the annual costs of the energy losses (including daily active and reactive power curves) and the costs of the working groups that travel along the feeder to implement the optimization plan.
2. General Optimization Model
2.1. Objective Function
2.2. Set of Constraints
2.3. General Model Interpretation
3. Solution Methodology
3.1. Master Stage: Improved Sine Cosine Algorithm
| Algorithm 1: Generation of the descending individual. |
 |
- If the maximum number of iterations is reached, then is reported as the optimal solution.
- If the objective function of the best solution does not improve during iterations, is reported as the optimal solution.
3.2. Slave Stage: Triangular-Based Power Flow Method
| Algorithm 2: General pseudo-code for triangular-based three-phase power flow with loads with - and Y-connections. |
 |
3.3. General Algorithm for the Proposed Master–Slave Optimizer
| Algorithm 3: Master–slave optimization algorithm based on the ISCA and the triangular-based power flow method for phase balancing. |
 |
4. Test Feeders
4.1. 15-Bus Test Feeder
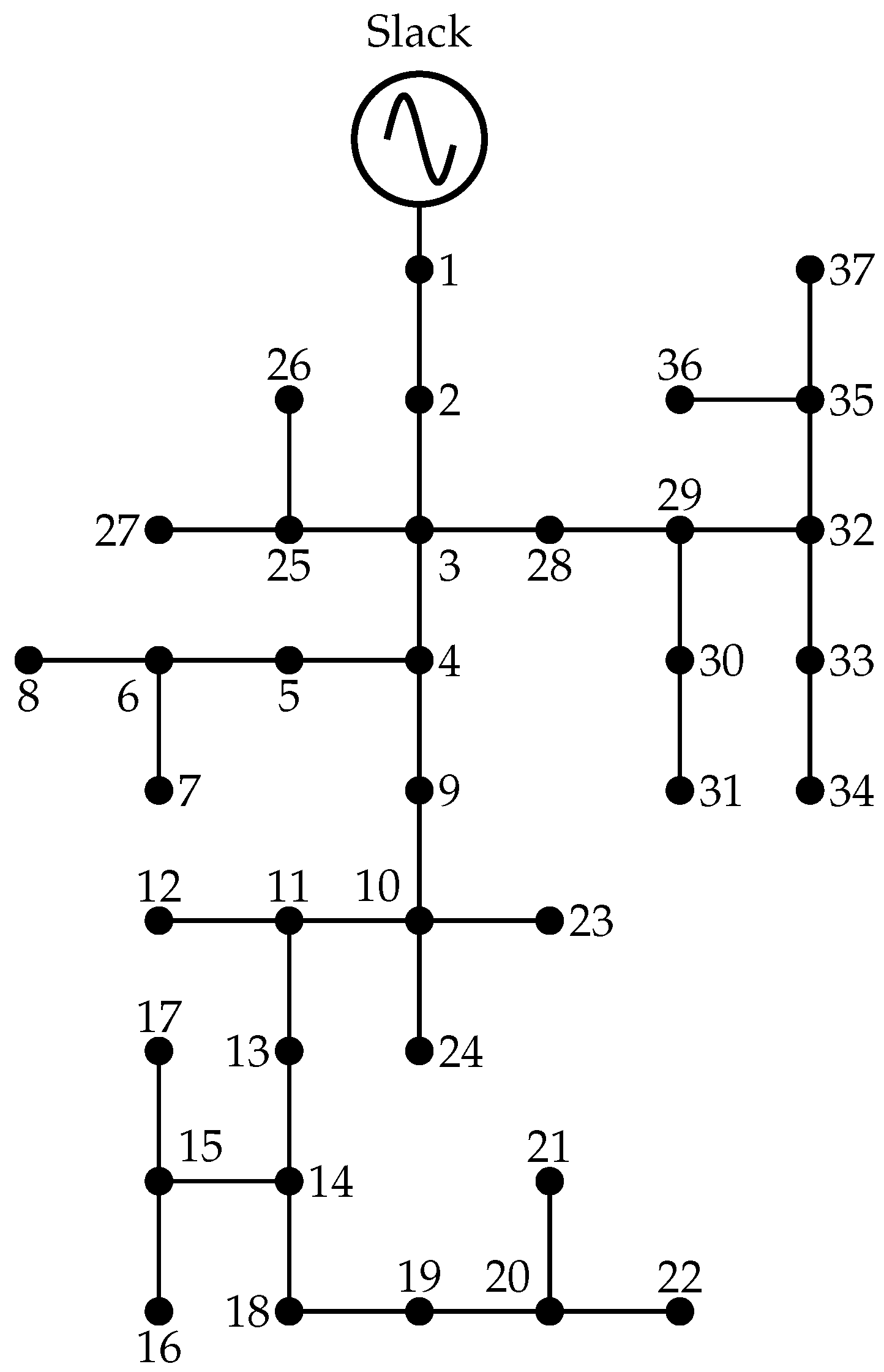
4.2. IEEE 37-Bus Test Feeder
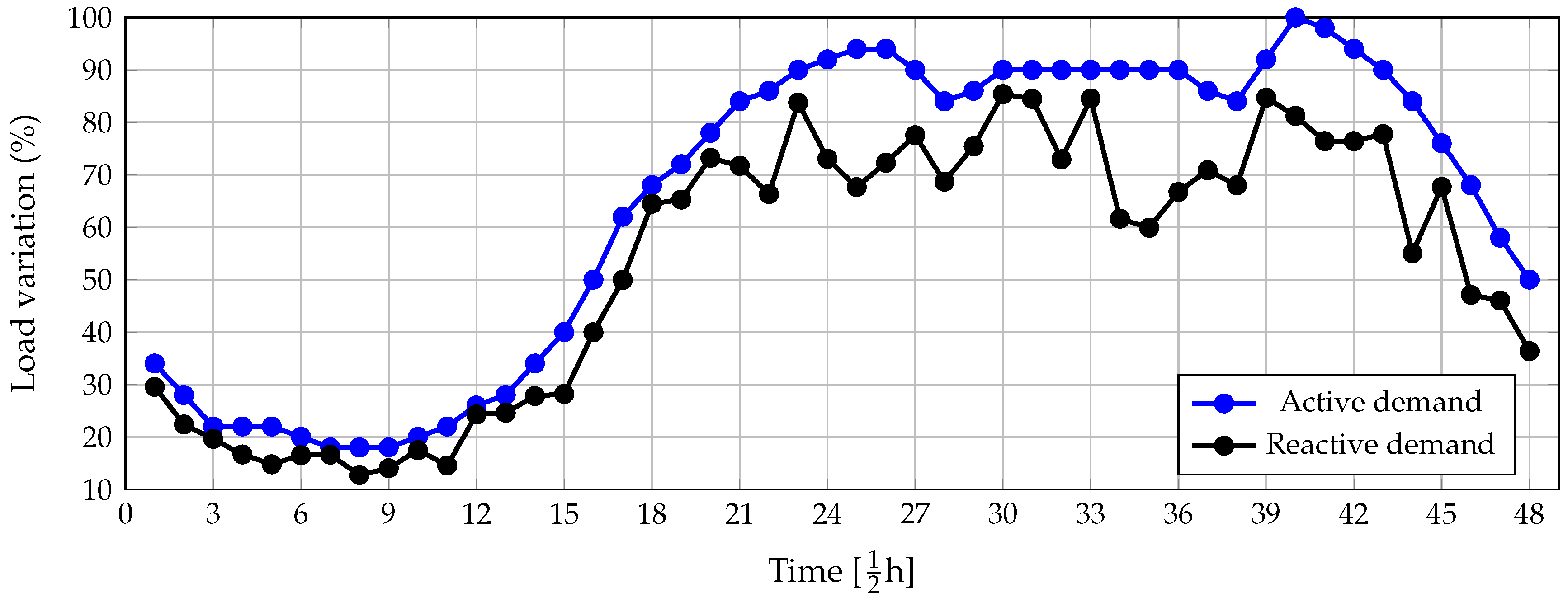
4.3. Behavior of the Demand in a Typical Working Day in Colombia
5. Numerical Analysis
5.1. Parametrization of the Optimization Algorithms
- ✓
- All the optimization methods required at least 50 or more individuals in the population to achieve an adequate objective function performance; the lowest minimum population size was 50, for the proposed ISCA, and the largest minimum population size was 95, for the BHO.
- ✓
- The minimum power losses were obtained by the proposed ISCA, with a value of kW, followed by the CBGA with a value of kW; however, the reliability of the ISCA was better since it had the lowest standard deviation of all the methods compared ( kW), followed by the CBGA as the second-best method with a standard deviation of about kW.
- ✓
- The ISCA presented a small variation between the extreme solutions, with a difference between the minimum and maximum values of kW; the largest difference was obtained with the BHO, with a value of kW. Note that the small difference between the minimum and maximum values in conjunction with the low standard deviation confirms that the ISCA obtained all the solutions inside of a small hypersphere, with the main advantage that most of the solutions obtained near to the optimal are better than the best results of the comparative methods. As an example, see the mean value of the ISCA in comparison with the minimum values of the BHO and the classical SCA.
5.2. Analysis of Annual Operating Costs
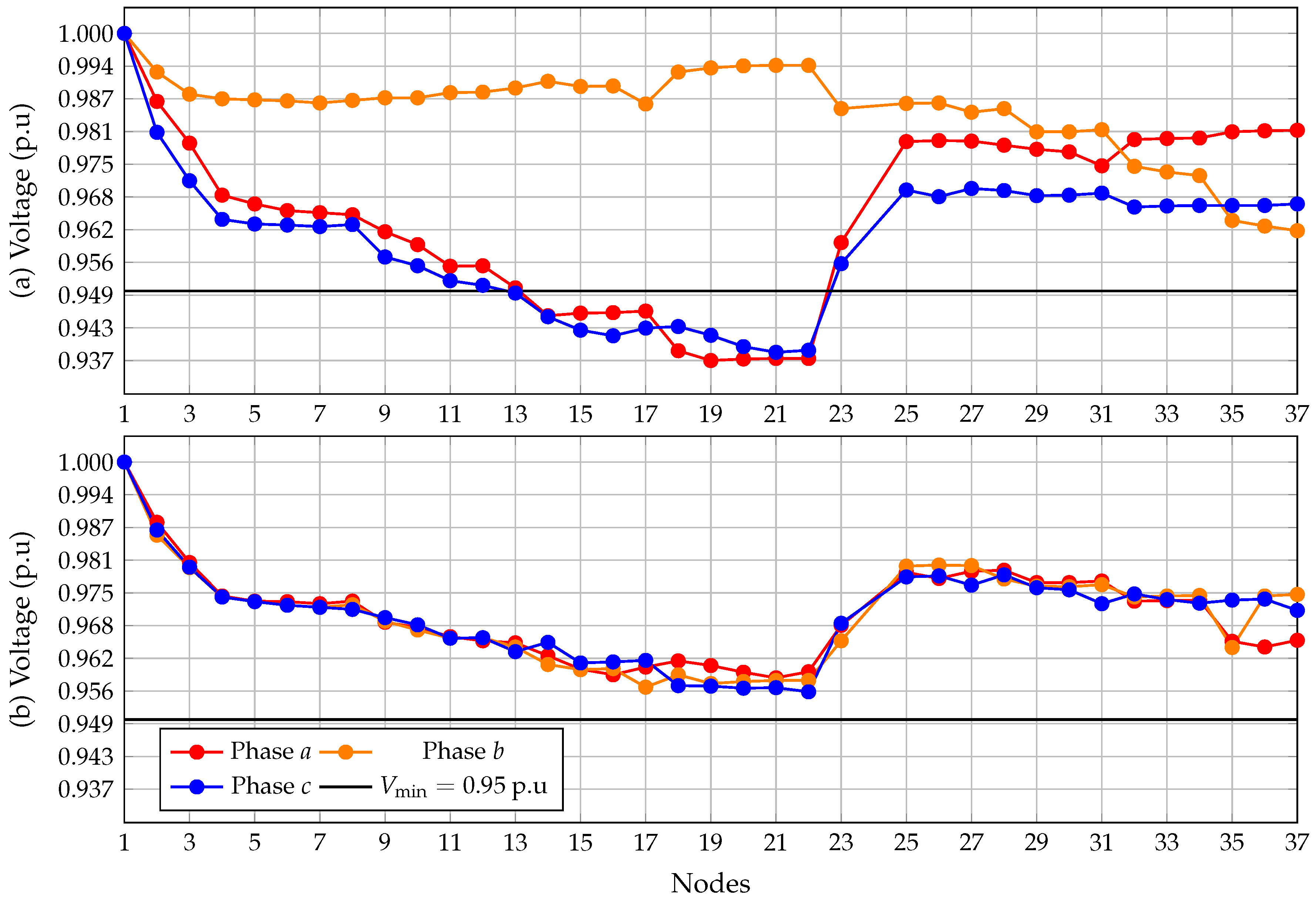
5.3. Complementary Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, L.; Chang, Y.; Liu, M.; Feng, H.; Wu, Q. Typical medium voltage distribution system topologies in China: A review and a comparison of reliability. In Proceedings of the 2014 International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Durham, UK, 7 July 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Temiz, A.; Almalki, A.M.; Kahraman, Ö.; Alshahrani, S.S.; Sönmez, E.B.; Almutairi, S.S.; Nadar, A.; Smiai, M.S.; Alabduljabbar, A.A. Investigation of MV Distribution Networks with High-Penetration Distributed PVs: Study for an Urban Area. Energy Procedia 2017, 141, 517–524. [Google Scholar] [CrossRef]
- Zamani, A.; Sidhu, T.; Yazdani, A. A strategy for protection coordination in radial distribution networks with distributed generators. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Zhu, J.; Bilbro, G.; Chow, M.Y. Phase balancing using simulated annealing. IEEE Trans. Power Syst. 1999, 14, 1508–1513. [Google Scholar] [CrossRef] [Green Version]
- Cortés-Caicedo, B.; Avellaneda-Gómez, L.S.; Montoya, O.D.; Alvarado-Barrios, L.; Chamorro, H.R. Application of the Vortex Search Algorithm to the Phase-Balancing Problem in Distribution Systems. Energies 2021, 14, 1282. [Google Scholar] [CrossRef]
- Riaño, F.E.; Cruz, J.F.; Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L. Reduction of Losses and Operating Costs in Distribution Networks Using a Genetic Algorithm and Mathematical Optimization. Electronics 2021, 10, 419. [Google Scholar] [CrossRef]
- Soma, G.G. Optimal Sizing and Placement of Capacitor Banks in Distribution Networks Using a Genetic Algorithm. Electricity 2021, 2, 187–204. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Rajagopalan, A.; Grisales-Noreña, L.F.; Hernández, J.C. Optimal Selection and Location of Fixed-Step Capacitor Banks in Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Energies 2020, 13, 4914. [Google Scholar] [CrossRef]
- Lueken, C.; Carvalho, P.M.; Apt, J. Distribution grid reconfiguration reduces power losses and helps integrate renewables. Energy Policy 2012, 48, 260–273. [Google Scholar] [CrossRef]
- Vai, V.; Suk, S.; Lorm, R.; Chhlonh, C.; Eng, S.; Bun, L. Optimal Reconfiguration in Distribution Systems with Distributed Generations Based on Modified Sequential Switch Opening and Exchange. Appl. Sci. 2021, 11, 2146. [Google Scholar] [CrossRef]
- Granada-Echeverri, M.; Gallego-Rendón, R.A.; López-Lezama, J.M. Optimal Phase Balancing Planning for Loss Reduction in Distribution Systems using a Specialized Genetic Algorithm. Ingeniería Cienc. 2012, 8, 121–140. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.Y.; Chen, C.S.; Lin, C.H.; Kang, M.S.; Chuang, H.J.; Huang, C.W. Three-phase balancing of distribution feeders using immune algorithm. IET Gener. Transm. Distrib. 2008, 2, 383. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Efficient Operative Cost Reduction in Distribution Grids Considering the Optimal Placement and Sizing of D-STATCOMs Using a Discrete-Continuous VSA. Appl. Sci. 2021, 11, 2175. [Google Scholar] [CrossRef]
- Kong, W.; Ma, K.; Fang, L.; Wei, R.; Li, F. Cost-Benefit Analysis of Phase Balancing Solution for Data-Scarce LV Networks by Cluster-Wise Gaussian Process Regression. IEEE Trans. Power Syst. 2020, 35, 3170–3180. [Google Scholar] [CrossRef]
- Han, X.; Wang, H.; Liang, D. Master-slave game optimization method of smart energy systems considering the uncertainty of renewable energy. Int. J. Energy Res. 2020, 45, 642–660. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Grisales-Noreña, L.F.; Hincapié, R.A.; Granada, M. Improved Genetic Algorithm for Phase-Balancing in Three-Phase Distribution Networks: A Master-Slave Optimization Approach. Computation 2021, 9, 67. [Google Scholar] [CrossRef]
- Fei, C.-G.; Wang, R. Using Phase Swapping to Solve Load Phase Balancing by ADSCHNN in LV Distribution Network. Int. J. Control Autom. 2014, 7, 1–14. [Google Scholar] [CrossRef]
- Siti, M.; Jimoh, A.; Nicolae, D. Phase load balancing in the secondary distribution network using fuzzy logic. In Proceedings of the AFRICON 2007, Windhoek, Namibia, 26–28 September 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Sathiskumar, M.; kumar, A.N.; Lakshminarasimman, L.; Thiruvenkadam, S. A self adaptive hybrid differential evolution algorithm for phase balancing of unbalanced distribution system. Int. J. Electr. Power Energy Syst. 2012, 42, 91–97. [Google Scholar] [CrossRef]
- Hooshmand, R.A.; Soltani, S. Fuzzy Optimal Phase Balancing of Radial and Meshed Distribution Networks Using BF-PSO Algorithm. IEEE Trans. Power Syst. 2012, 27, 47–57. [Google Scholar] [CrossRef]
- Hooshmand, R.; Soltani, S. Simultaneous optimization of phase balancing and reconfiguration in distribution networks using BF–NM algorithm. Int. J. Electr. Power Energy Syst. 2012, 41, 76–86. [Google Scholar] [CrossRef]
- Garces, A.; Gil-González, W.; Montoya, O.D.; Chamorro, H.R.; Alvarado-Barrios, L. A Mixed-Integer Quadratic Formulation of the Phase-Balancing Problem in Residential Microgrids. Appl. Sci. 2021, 11, 1972. [Google Scholar] [CrossRef]
- Montoya, O.D.; Arias-Londoño, A.; Grisales-Noreña, L.F.; Barrios, J.Á.; Chamorro, H.R. Optimal Demand Reconfiguration in Three-Phase Distribution Grids Using an MI-Convex Model. Symmetry 2021, 13, 1124. [Google Scholar] [CrossRef]
- Khodr, H.; Zerpa, I.; de Jesu’s, P.D.O.; Matos, M. Optimal Phase Balancing in Distribution System Using Mixed-Integer Linear Programming. In Proceedings of the 2006 IEEE/PES Transmission & Distribution Conference and Exposition: Latin America, Caracas, Venezuela, 15–18 August 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Turgut, M.S.; Turgut, O.E.; Afan, H.A.; El-Shafie, A. A novel Master–Slave optimization algorithm for generating an optimal release policy in case of reservoir operation. J. Hydrol. 2019, 577, 123959. [Google Scholar] [CrossRef]
- Yang, B.; Chen, Y.; Zhao, Z.; Han, Q. A Master-Slave Particle Swarm Optimization Algorithm for Solving Constrained Optimization Problems. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; IEEE: Piscataway, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Jesus, P.D.O.D.; Alvarez, M.; Yusta, J. Distribution power flow method based on a real quasi-symmetric matrix. Electr. Power Syst. Res. 2013, 95, 148–159. [Google Scholar] [CrossRef]
- Montoya, O.D.; Giraldo, J.S.; Grisales-Noreña, L.F.; Chamorro, H.R.; Alvarado-Barrios, L. Accurate and Efficient Derivative-Free Three-Phase Power Flow Method for Unbalanced Distribution Networks. Computation 2021, 9, 61. [Google Scholar] [CrossRef]
- Naumov, I.V.; Karamov, D.N.; Tretyakov, A.N.; Yakupova, M.A.; Fedorinova, E.S. Asymmetric power consumption in rural electric networks. In Proceedings of the IOP Conference Series: Earth and Environmental Science 2021, Kuala Lumpur, Malaysia, 16 April 2021; Volume 677, p. 032088. [Google Scholar] [CrossRef]
- Hu, R.; Li, Q.; Qiu, F. Ensemble Learning Based Convex Approximation of Three-Phase Power Flow. IEEE Trans. Power Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Shen, T.; Li, Y.; Xiang, J. A Graph-Based Power Flow Method for Balanced Distribution Systems. Energies 2018, 11, 511. [Google Scholar] [CrossRef] [Green Version]
- Marini, A.; Mortazavi, S.; Piegari, L.; Ghazizadeh, M.S. An efficient graph-based power flow algorithm for electrical distribution systems with a comprehensive modeling of distributed generations. Electr. Power Syst. Res. 2019, 170, 229–243. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2020, 10, 26. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Herrera-Briñez, M.C.; Montoya, O.D.; Alvarado-Barrios, L.; Chamorro, H.R. The Equivalence between Successive Approximations and Matricial Load Flow Formulations. Appl. Sci. 2021, 11, 2905. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.; Orozco-Henao, C.; Serra, F. Economic Dispatch of BESS and Renewable Generators in DC Microgrids Using Voltage-Dependent Load Models. Energies 2019, 12, 4494. [Google Scholar] [CrossRef] [Green Version]
- Attia, A.F.; Sehiemy, R.A.E.; Hasanien, H.M. Optimal power flow solution in power systems using a novel Sine-Cosine algorithm. Int. J. Electr. Power Energy Syst. 2018, 99, 331–343. [Google Scholar] [CrossRef]
- Hasan, Z.; El-Hawary, M.E. Optimal Power Flow by Black Hole Optimization Algorithm. In Proceedings of the 2014 IEEE Electrical Power and Energy Conference, Calgary, AB, Canada, 12–14 November 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]




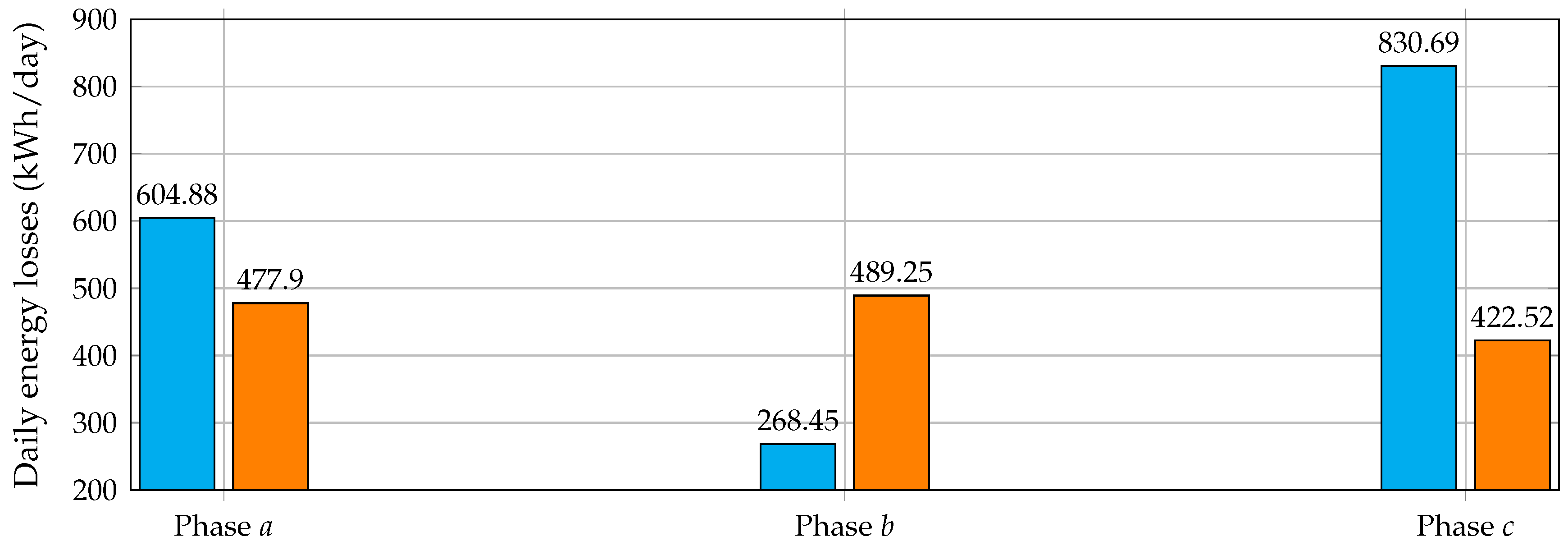
| Optimization Method | Objective Function | Year | Reference |
|---|---|---|---|
| Simulated annealing algorithm | Power losses minimization | 1999 | [4] |
| Mixed-integer linear programming | Optimal current balancing | 2006 | [24] |
| Fuzzy logic approach | Power losses minimization | 2007 | [18] |
| Immune optimization algorithm | Power losses minimization | 2008 | [12] |
| Differential evolution algorithm | Power losses minimization | 2012 | [19] |
| Particle swarm optimization | Power losses minimization | 2012 | [20] |
| Bacterial foraging algorithm | Power losses minimization | 2012 | [21] |
| Chu and Beasley genetic algorithms | Power losses minimization | 2012, 2020, 2021 | [5,11,16] |
| Artificial neural networks | Power losses minimization | 2014 | [17] |
| Discrete vortex search algorithm | Power losses minimization | 2020 | [5] |
| Mixed-integer conic reformulation | Expected energy losses | 2021 | [22] |
| Mixed-integer convex approximation | Average unbalance level | 2021 | [23] |
| Connection Type | Phases | Sequence | Binary Variable |
|---|---|---|---|
| 1 | ABC | ||
| 2 | CAB | No change | |
| 3 | BCA | ||
| 4 | ACB | ||
| 5 | BAC | Change | |
| 6 | CBA |
| Line | Node i | Node j | Cond. | Length (ft) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 603 | 0 | 0 | 725 | 300 | 1100 | 600 |
| 2 | 2 | 3 | 2 | 776 | 480 | 220 | 720 | 600 | 1040 | 558 |
| 3 | 3 | 4 | 3 | 825 | 2250 | 1610 | 0 | 0 | 0 | 0 |
| 4 | 4 | 5 | 3 | 1182 | 700 | 225 | 0 | 0 | 996 | 765 |
| 5 | 5 | 6 | 4 | 350 | 0 | 0 | 820 | 700 | 1220 | 1050 |
| 6 | 2 | 7 | 5 | 691 | 2500 | 1200 | 0 | 0 | 0 | 0 |
| 7 | 7 | 8 | 6 | 539 | 0 | 0 | 960 | 540 | 0 | 0 |
| 8 | 8 | 9 | 6 | 225 | 0 | 0 | 0 | 0 | 2035 | 1104 |
| 9 | 9 | 10 | 6 | 1050 | 1519 | 1250 | 1259 | 1200 | 0 | 0 |
| 10 | 3 | 11 | 3 | 837 | 0 | 0 | 259 | 126 | 1486 | 1235 |
| 11 | 11 | 12 | 4 | 414 | 0 | 0 | 0 | 0 | 1924 | 1857 |
| 12 | 12 | 13 | 5 | 925 | 1670 | 486 | 0 | 0 | 726 | 509 |
| 13 | 6 | 14 | 4 | 386 | 0 | 0 | 850 | 752 | 1450 | 1100 |
| 14 | 14 | 15 | 2 | 401 | 486 | 235 | 887 | 722 | 0 | 0 |
| Conductor | Impedance Matrix (mi) | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| Line | Node i | Node j | Cond. | Length (ft) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 1 | 1850 | 140 | 70 | 140 | 70 | 350 | 175 |
| 2 | 2 | 3 | 2 | 960 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 24 | 4 | 400 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 3 | 27 | 3 | 360 | 0 | 0 | 0 | 0 | 85 | 40 |
| 5 | 3 | 4 | 2 | 1320 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 4 | 5 | 4 | 240 | 0 | 0 | 0 | 0 | 42 | 21 |
| 7 | 4 | 9 | 3 | 600 | 0 | 0 | 0 | 0 | 85 | 40 |
| 8 | 5 | 6 | 3 | 280 | 42 | 21 | 0 | 0 | 0 | 0 |
| 9 | 6 | 7 | 4 | 200 | 42 | 21 | 42 | 21 | 42 | 21 |
| 10 | 6 | 8 | 4 | 280 | 42 | 21 | 0 | 0 | 0 | 0 |
| 11 | 9 | 10 | 3 | 200 | 0 | 0 | 0 | 0 | 0 | 0 |
| 12 | 10 | 23 | 3 | 600 | 0 | 0 | 85 | 40 | 0 | 0 |
| 13 | 10 | 11 | 3 | 320 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 11 | 13 | 3 | 320 | 85 | 40 | 0 | 0 | 0 | 0 |
| 15 | 11 | 12 | 4 | 320 | 0 | 0 | 0 | 0 | 42 | 21 |
| 16 | 13 | 14 | 3 | 560 | 0 | 0 | 0 | 0 | 42 | 21 |
| 17 | 14 | 18 | 3 | 640 | 140 | 70 | 0 | 0 | 0 | 0 |
| 18 | 14 | 15 | 4 | 520 | 0 | 0 | 0 | 0 | 0 | 0 |
| 19 | 15 | 16 | 4 | 200 | 0 | 0 | 0 | 0 | 85 | 40 |
| 20 | 15 | 17 | 4 | 1280 | 0 | 0 | 42 | 21 | 0 | 0 |
| 21 | 18 | 19 | 3 | 400 | 126 | 62 | 0 | 0 | 0 | 0 |
| 22 | 19 | 20 | 3 | 400 | 0 | 0 | 0 | 0 | 0 | 0 |
| 23 | 20 | 22 | 3 | 400 | 0 | 0 | 0 | 0 | 42 | 21 |
| 24 | 20 | 21 | 4 | 200 | 0 | 0 | 0 | 0 | 85 | 40 |
| 25 | 24 | 26 | 4 | 320 | 8 | 4 | 85 | 40 | 0 | 0 |
| 26 | 24 | 25 | 4 | 240 | 0 | 0 | 0 | 0 | 85 | 40 |
| 27 | 27 | 28 | 3 | 520 | 0 | 0 | 0 | 0 | 0 | 0 |
| 28 | 28 | 29 | 4 | 80 | 17 | 8 | 21 | 10 | 0 | 0 |
| 29 | 28 | 31 | 3 | 800 | 0 | 0 | 0 | 0 | 85 | 40 |
| 30 | 29 | 30 | 4 | 520 | 85 | 40 | 0 | 0 | 0 | 0 |
| 31 | 31 | 34 | 4 | 920 | 0 | 0 | 0 | 0 | 0 | 0 |
| 32 | 31 | 32 | 3 | 600 | 0 | 0 | 0 | 0 | 0 | 0 |
| 33 | 32 | 33 | 4 | 280 | 0 | 0 | 42 | 21 | 0 | 0 |
| 34 | 34 | 36 | 4 | 760 | 0 | 0 | 42 | 21 | 0 | 0 |
| 35 | 34 | 35 | 4 | 120 | 0 | 0 | 140 | 70 | 21 | 10 |
| Conductor | Impedance Matrix (mi) | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| Period | Act. (pu) | React. (pu) | Period | Act. (pu) | React. (pu) |
|---|---|---|---|---|---|
| 1 | 0.1700 | 0.1477 | 25 | 0.4700 | 0.3382 |
| 2 | 0.1400 | 0.1119 | 26 | 0.4700 | 0.3614 |
| 3 | 0.1100 | 0.0982 | 27 | 0.4500 | 0.3877 |
| 4 | 0.1100 | 0.0833 | 28 | 0.4200 | 0.3434 |
| 5 | 0.1100 | 0.0739 | 29 | 0.4300 | 0.3771 |
| 6 | 0.1000 | 0.0827 | 30 | 0.4500 | 0.4269 |
| 7 | 0.0900 | 0.0831 | 31 | 0.4500 | 0.4224 |
| 8 | 0.0900 | 0.0637 | 32 | 0.4500 | 0.3647 |
| 9 | 0.0900 | 0.0702 | 33 | 0.4500 | 0.4226 |
| 10 | 0.1000 | 0.0875 | 34 | 0.4500 | 0.3081 |
| 11 | 0.1100 | 0.0728 | 35 | 0.4500 | 0.2994 |
| 12 | 0.1300 | 0.1214 | 36 | 0.4500 | 0.3336 |
| 13 | 0.1400 | 0.1231 | 37 | 0.4300 | 0.3543 |
| 14 | 0.1700 | 0.1390 | 38 | 0.4200 | 0.3399 |
| 15 | 0.2000 | 0.1410 | 39 | 0.4600 | 0.4234 |
| 16 | 0.2500 | 0.1998 | 40 | 0.5000 | 0.4061 |
| 17 | 0.3100 | 0.2497 | 41 | 0.4900 | 0.3820 |
| 18 | 0.3400 | 0.3224 | 42 | 0.4700 | 0.3820 |
| 19 | 0.3600 | 0.3263 | 43 | 0.4500 | 0.3887 |
| 20 | 0.3900 | 0.3661 | 44 | 0.4200 | 0.2751 |
| 21 | 0.4200 | 0.3585 | 45 | 0.3800 | 0.3383 |
| 22 | 0.4300 | 0.3316 | 46 | 0.3400 | 0.2355 |
| 23 | 0.4500 | 0.4187 | 47 | 0.2900 | 0.2301 |
| 24 | 0.4600 | 0.3652 | 48 | 0.2500 | 0.1818 |
| Method | Minimum (kW) | Maximum (kW) | Mean (kW) | Standard Deviation (kW) | Optimal Pop. Size |
|---|---|---|---|---|---|
| CBGA | 109.2218 | 109.9080 | 109.5488 | 0.2075 | 75 |
| BHO | 109.5715 | 113.0922 | 110.7364 | 0.8377 | 95 |
| SCA | 109.5148 | 110.4816 | 109.9611 | 0.2492 | 85 |
| VSA | 109.2855 | 110.1828 | 109.6100 | 0.2485 | 80 |
| ISCA | 109.1980 | 109.6896 | 109.2952 | 0.1144 | 50 |
| Method | Solution | Losses (kW) | Reduction (%) |
|---|---|---|---|
| Benchmark case | 134.2472 | 0.00 | |
| CBGA | 109.2218 | 18.64 | |
| BHO | 109.5715 | 18.38 | |
| SCA | 109.5148 | 18.42 | |
| VSA | 109.2855 | 18.59 | |
| ISCA | 109.1980 | 18.66 |
| Sol. No. | Solution | (USD) | (USD), |
|---|---|---|---|
| Ben. case | 43,226.9376 | 0 | |
| Sol. 1 | 37,452.5749 | 2200 | |
| Sol. 2 | 37,482.4629 | 2100 | |
| Sol. 3 | 37,519.4476 | 2200 | |
| Sol. 4 | 37,533.5646 | 2100 | |
| Sol. 5 | 37,553.2596 | 2100 |
| Benchmark Case | Solution 1 | ||||
|---|---|---|---|---|---|
| Phase | Unb. Active (%) | Unb. Reactive (%) | Phase | Unb. Active (%) | Unb. Reactive (%) |
| a | 11.2332 | 10.8243 | a | 6.8376 | 7.3272 |
| b | 21.9780 | 21.5654 | b | 14.8962 | 15.1540 |
| c | 33.2112 | 32.3897 | c | 8.0586 | 7.8268 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Alarcon-Villamil, J.A.; Hernández, J.C. Operating Cost Reduction in Distribution Networks Based on the Optimal Phase-Swapping including the Costs of the Working Groups and Energy Losses. Energies 2021, 14, 4535. https://doi.org/10.3390/en14154535
Montoya OD, Alarcon-Villamil JA, Hernández JC. Operating Cost Reduction in Distribution Networks Based on the Optimal Phase-Swapping including the Costs of the Working Groups and Energy Losses. Energies. 2021; 14(15):4535. https://doi.org/10.3390/en14154535
Chicago/Turabian StyleMontoya, Oscar Danilo, Jorge Alexander Alarcon-Villamil, and Jesus C. Hernández. 2021. "Operating Cost Reduction in Distribution Networks Based on the Optimal Phase-Swapping including the Costs of the Working Groups and Energy Losses" Energies 14, no. 15: 4535. https://doi.org/10.3390/en14154535
APA StyleMontoya, O. D., Alarcon-Villamil, J. A., & Hernández, J. C. (2021). Operating Cost Reduction in Distribution Networks Based on the Optimal Phase-Swapping including the Costs of the Working Groups and Energy Losses. Energies, 14(15), 4535. https://doi.org/10.3390/en14154535








