Numerical Simulation on Cooling Effect of Working Face under Radiation Cooling Mode in Deep Well
Abstract
:1. Introduction
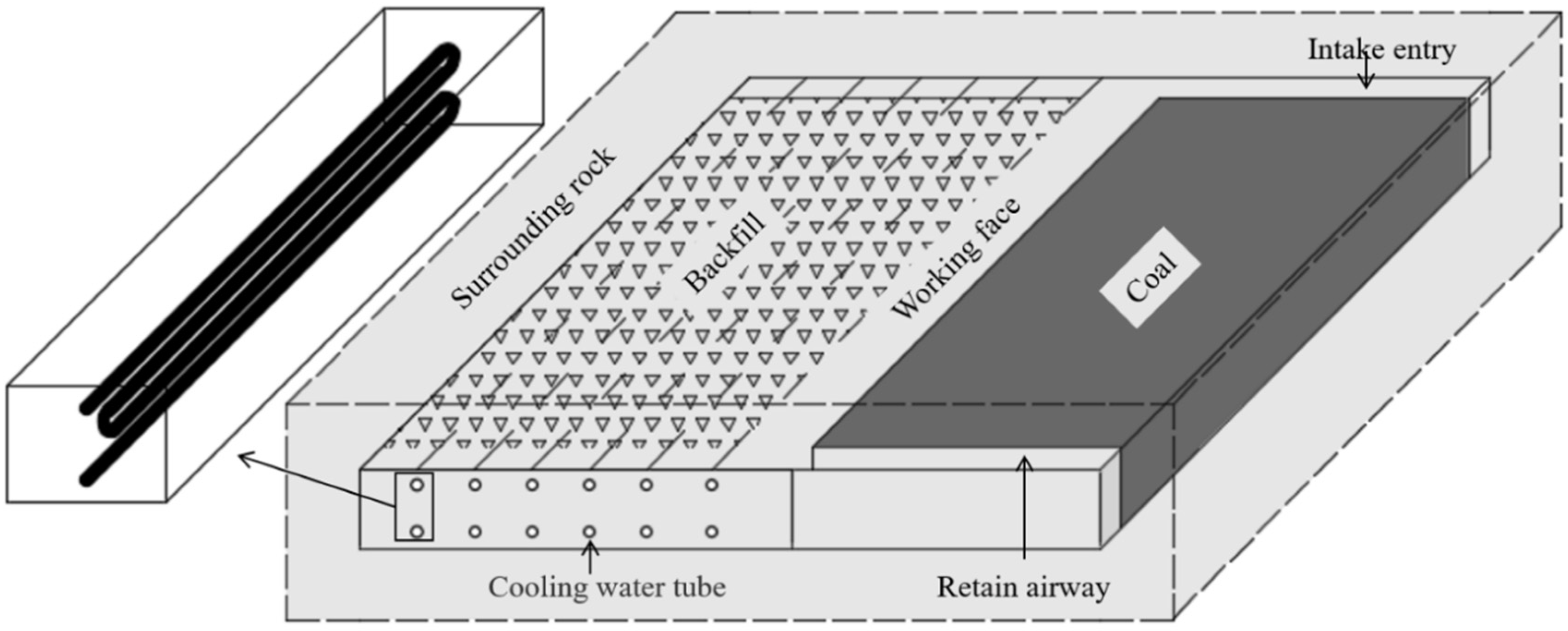
2. Model Establishment
2.1. Basic Assumptions
- (I)
- The temperature of other adjacent surfaces except the cold wall adjacent to the airflow is the original ground temperature at the mining depth;
- (II)
- The original ground temperature at the mining depth remains unchanged and heat is released uniformly along the working face;
- (III)
- The cold wall temperature remains unchanged and the cold is released uniformly along the working face;
- (IV)
- After the goaf is backfilled, the heat brought by air leakage to the working face is not considered, and the internal heat source of the working face is also not considered;
- (V)
- The moisture exchange among the airflow and cold wall, coal wall, surrounding rock, etc., is ignored.
2.2. Mathematical Model
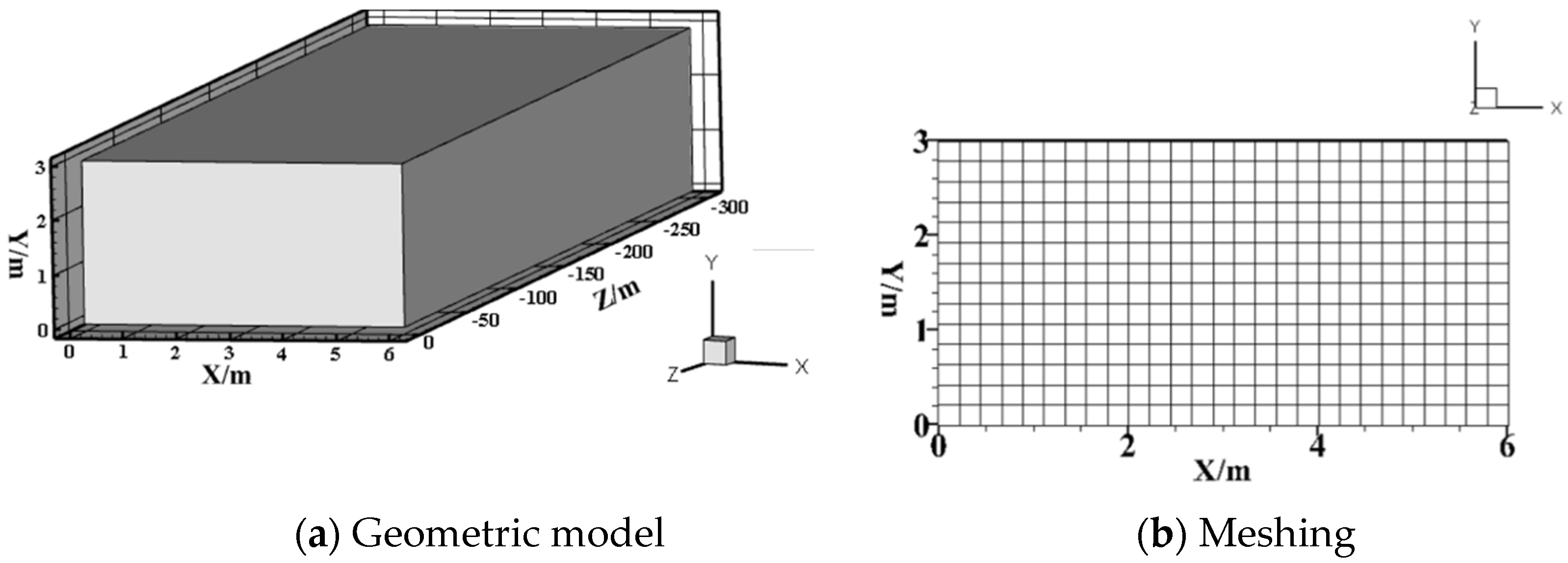
2.3. Geometric Model and Meshing
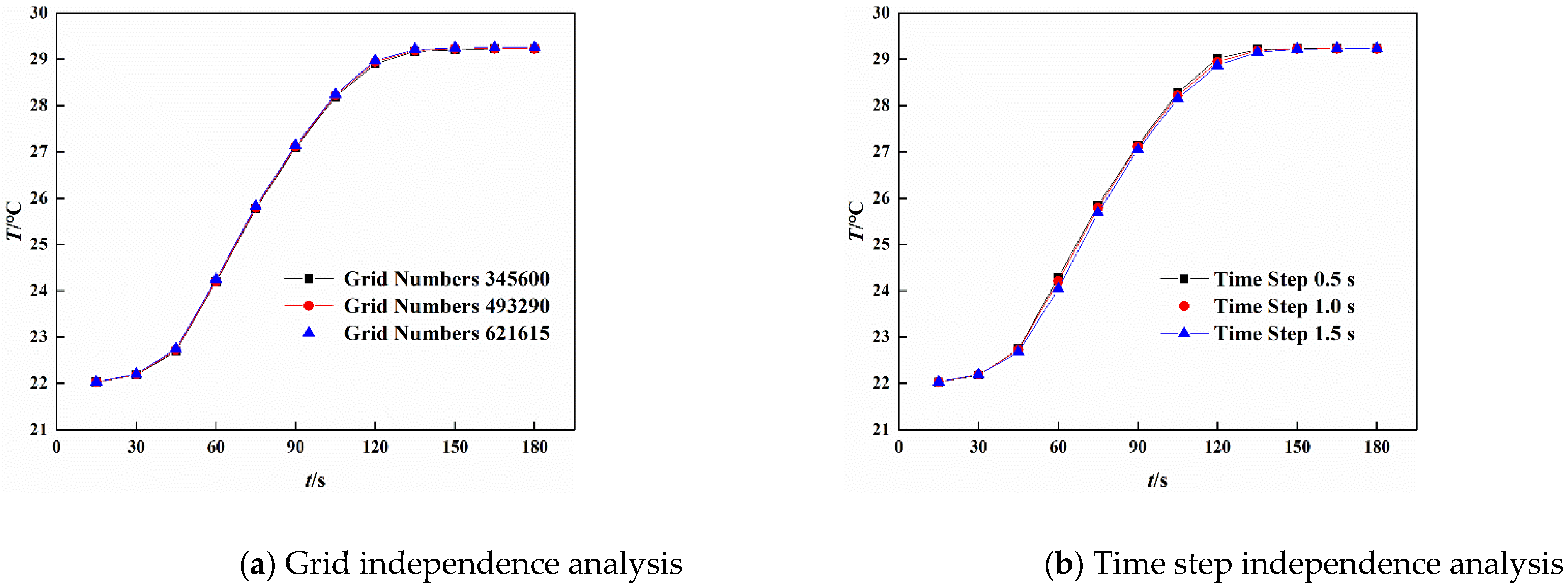
2.4. Independence Analysis
2.5. Fluent Parameters and Solution Settings
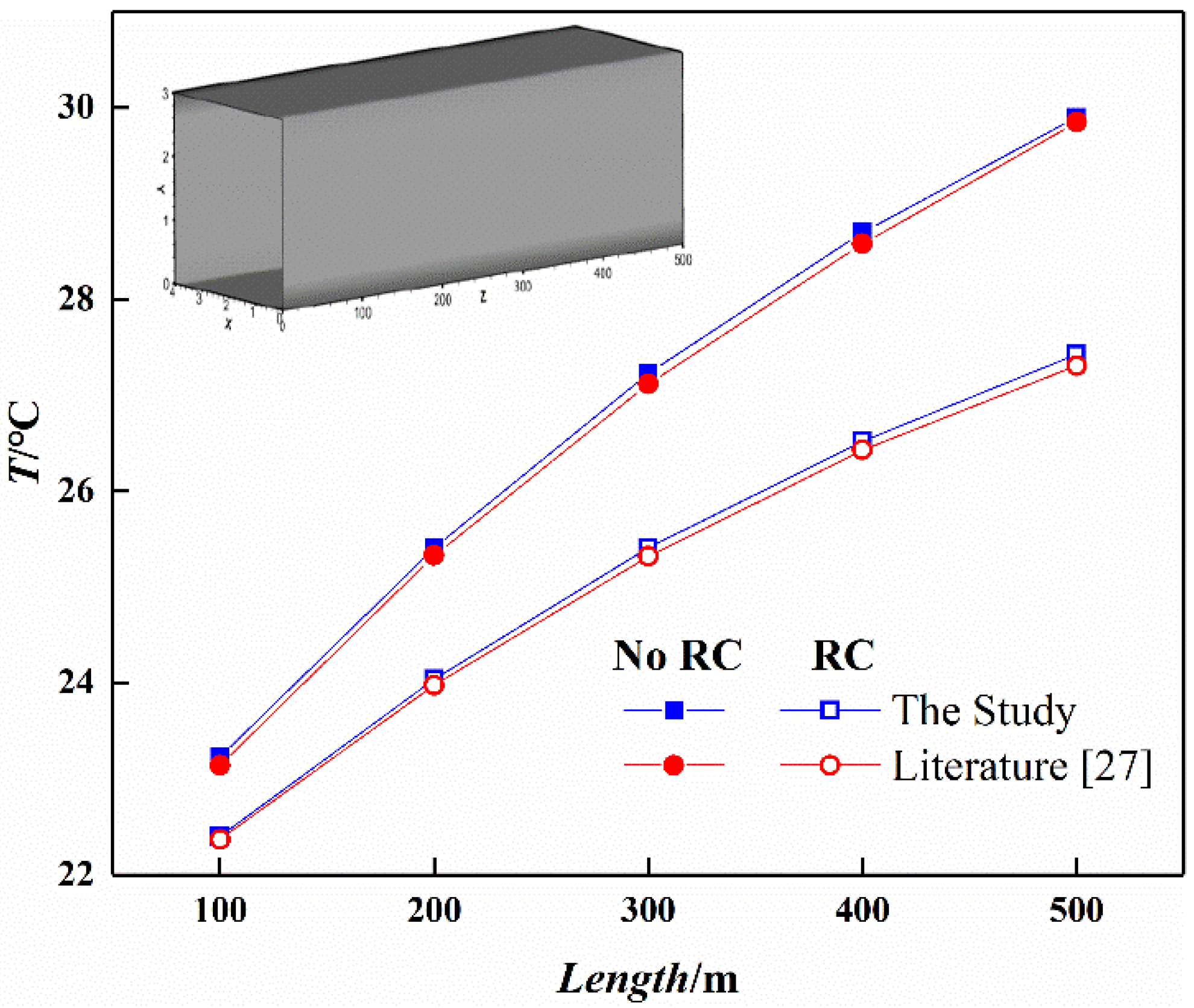
2.6. Model Validation
3. Result and Analysis
3.1. Analysis of Airflow Temperature Variation along the Working Face before and after Cooling
3.2. Analysis of Airflow Temperature Variation at Measuring Points of Working Face before and after Cooling
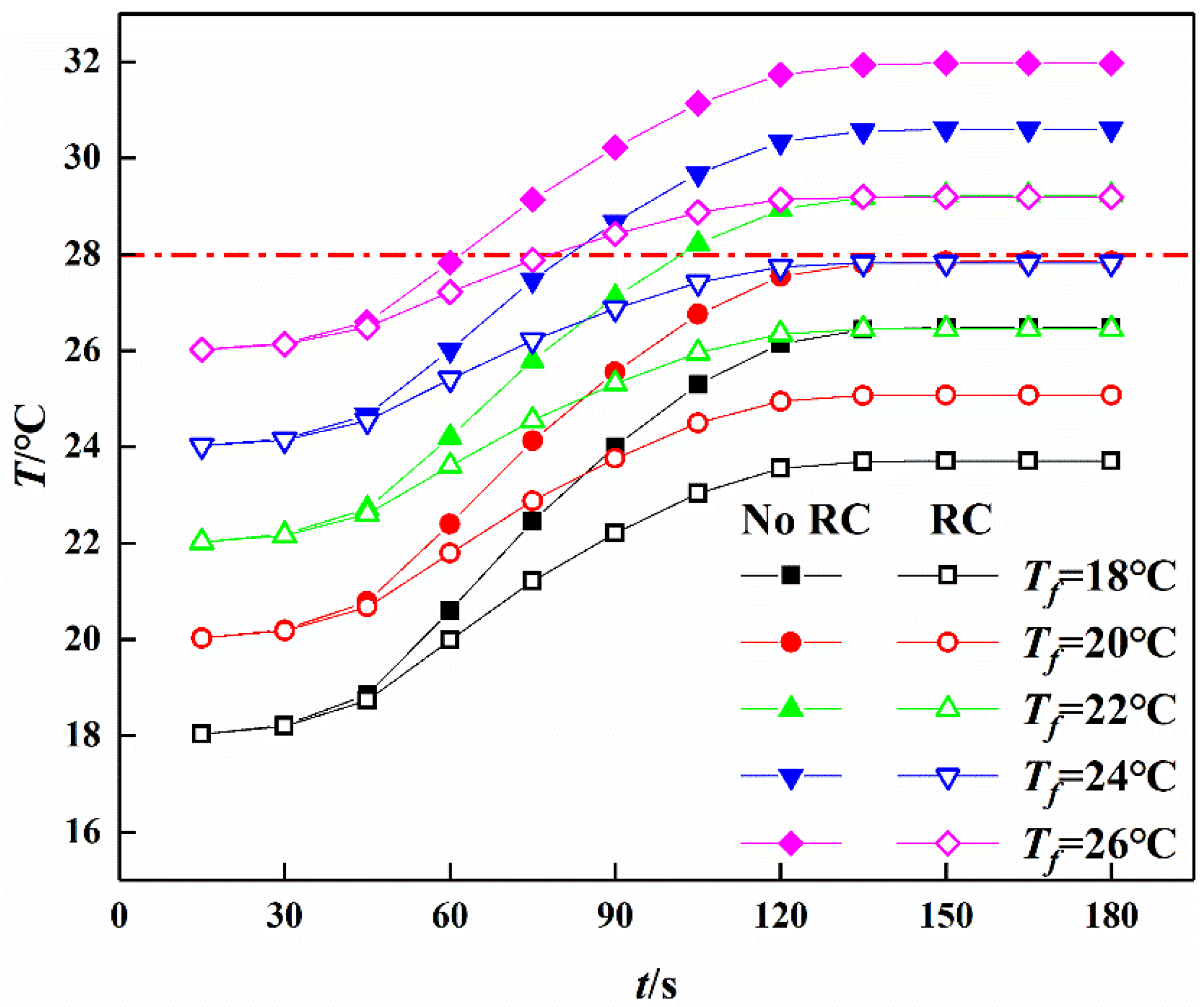
3.3. Effect of Air Supply Temperature on Airflow Temperature
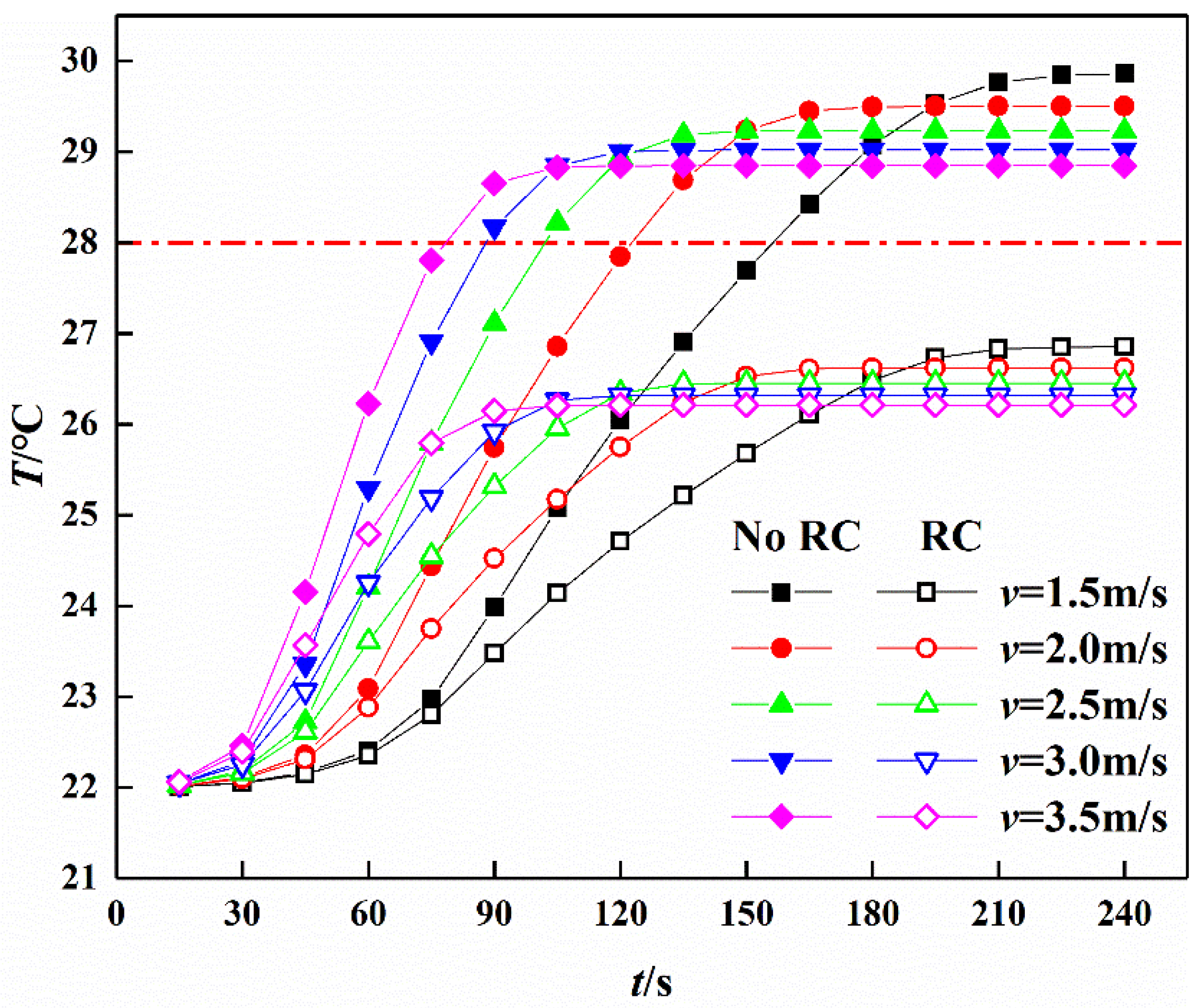
3.4. Effect of Air Supply Velocity on Airflow Temperature
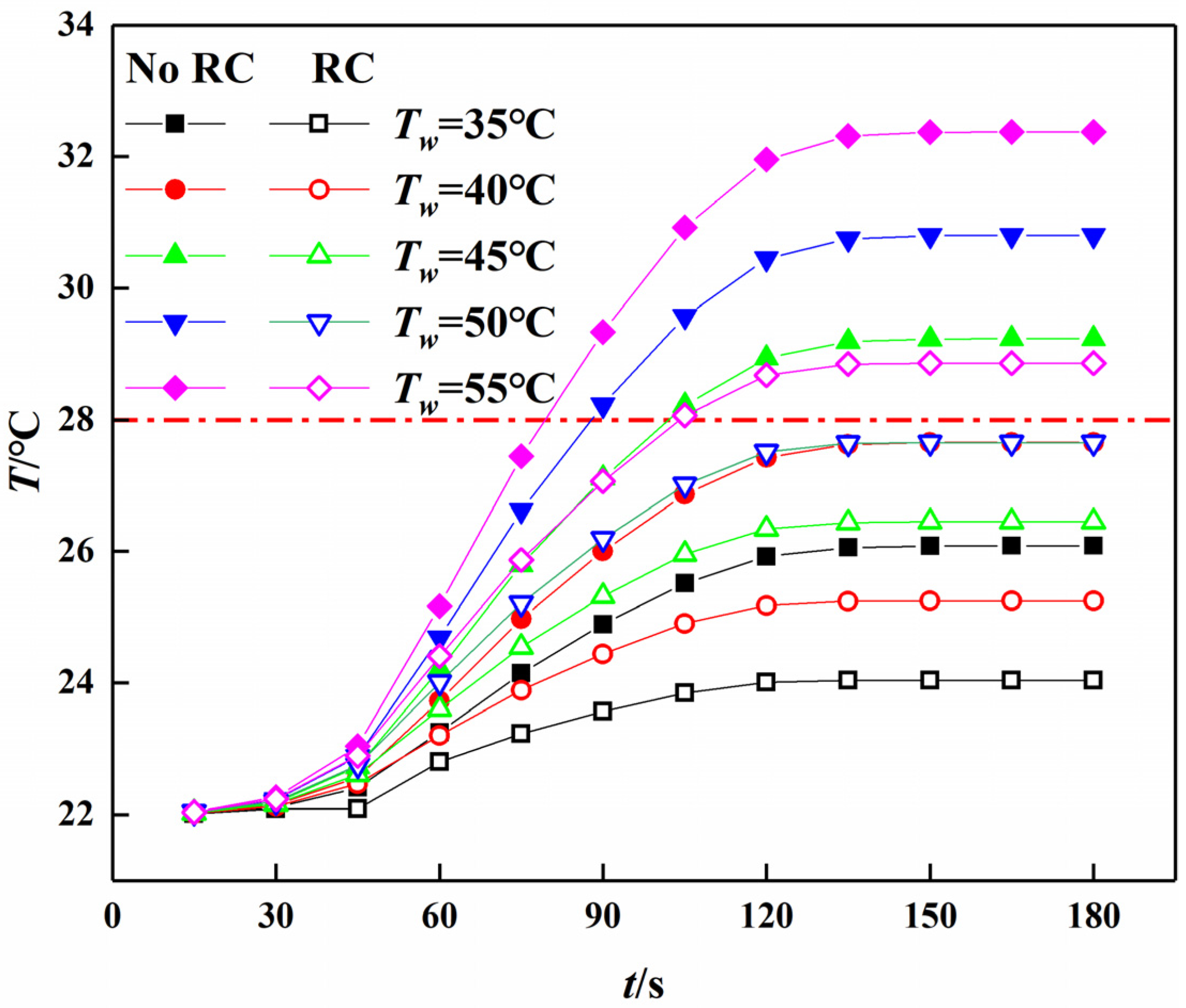
3.5. Effect of Surrounding Wall Temperature on Airflow Temperature
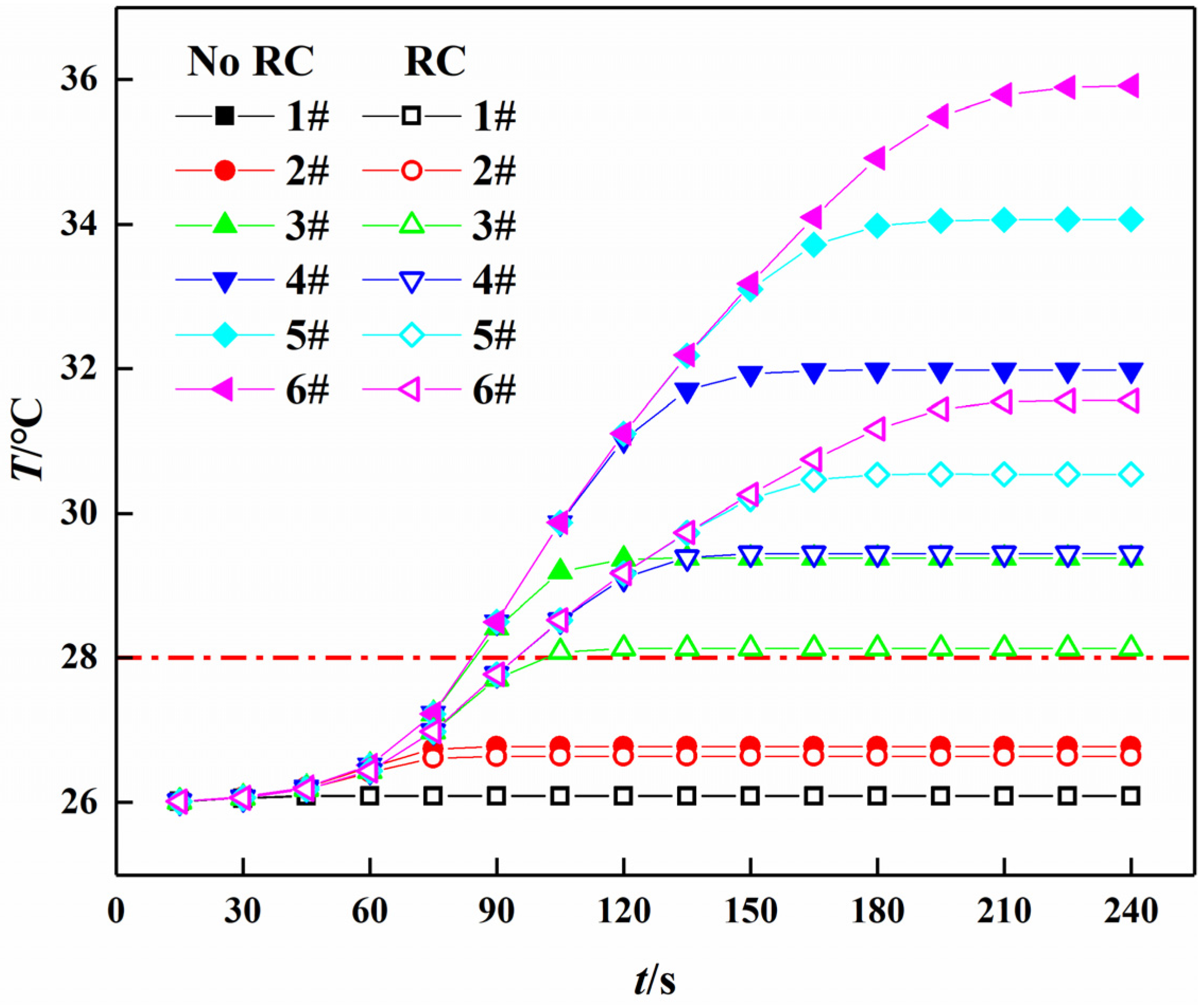
3.6. Airflow Temperature Distribution in Working Face under the Most Unfavorable Condition
4. Conclusions
- (I)
- When cooling measures are not taken, the airflow continuously absorbs heat from the surrounding wall along the working face, and the temperature gradually rises. After cooling by cold wall, the trend of the airflow temperature rising along the working face is slowed down. Compared with before cooling, the temperature increment of Z = 50 m, 100 m, 150 m, 200 m, 250 m and 300 m sections decreases by 0.67 °C, 0.48 °C, 0.40 °C, 0.36 °C, 0.33 °C and 0.29 °C, respectively.
- (II)
- The airflow temperature at measuring points increase with the ventilation time, and the time to reach the stable value is obviously different. The closer to the exit of the working face, the longer the time it takes to reach the stable temperature and the more obvious the cooling effect is. When the air supply temperature is 26 °C, the temperature of the measuring point can reach 31.97 °C without cooling measures, and the temperature of the measuring point is 29.19 °C after adopting cooling measures. Compared with before cooling, the temperature increment is reduced by 2.78 °C.
- (III)
- The higher the air supply velocity, the faster measuring point 3 reaches the maximum temperature, the lower the maximum temperature of the airflow. When the air supply velocity increases from 1.5 m/s to 3.5 m/s, the temperature of measuring point 3 increases to the maximum at 210 s, 165 s, 135 s, 120 s, 90 s respectively. After using cooling measures, the temperature increment decreases to 2.93 °C, 2.84 °C, 2.75 °C, 2.68 °C and 2.50 °C successively.
- (IV)
- When cooling measures are not taken, the airflow temperature of the measuring points increase by 1.57 °C for every 5 °C increase in the surrounding wall temperature after reaching stability. After cooling measures are taken, the surrounding wall temperature is between 35–50 °C, the airflow temperature of measuring point 3 is lower than 28 °C.
- (V)
- When cooling measures are not taken, airflow temperatures of measuring points exceed the limit rapidly, except for the measuring points near the airflow inlet. After cooling measures are taken, the temperature increment of measuring points 1–6 decreases by 0.01 °C, 0.13 °C, 1.25 °C, 2.54 °C, 2.44 °C, 2.51 °C respectively at 240 s.
- (VI)
- In this study, the radiation refrigeration and ventilation combined with operation cooling method not only reduces the temperature of the working face but it also provides a suitable working environment for the staff, realizes the integration of mine cooling and thermal energy utilization, as well as provides a utilization for geothermal resources.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| airflow density (kg/m3) | average temperature of the heating surface (K) | ||
| time (s) | average temperature of the cooling surface (K) | ||
| velocity vector | radiative heat transfer between walls (W·m−2) | ||
| pressure (N) | convective heat transfer between air flow and wall surface (W·m−2) | ||
| viscous stress components | Stephan Boltzmann constant (W·m−2·K−4) | ||
| volumetric forces on elements (N) | comprehensive factor of wall radiation heat transfer | ||
| total energy of the fluid (J) | average airflow temperature (K) | ||
| effective heat transfer parameter | heat transfer coefficient between wall surface and airflow (W·m−2·K−1) | ||
| diffusion flow rate of component j (kg·m −2·s−1) | equivalent diameter of surrounding wall (m) | ||
| heat source term | area (m2) | ||
| average wall temperature of the working face (K) | perimeter (m) |
References
- You, B.; Wu, C.; Li, J.; Liao, H. Physiological responses of people in working faces of deep underground mines. Int. J. Min. Sci. Technol. 2014, 24, 683–688. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Zhao, J.; Ju, M.; De Silva, R.V.S.; Rathnaweera, T.D.; Bandara, A.K.M.S. Opportunities and challenges in deep mining: A brief review. Engineering 2017, 3, 546–551. [Google Scholar] [CrossRef]
- Habibi, A.; Kramer, R.B.; Gillies, A.D.S. Investigating the effects of heat changes in an underground mine. Appl. Therm. Eng. 2015, 90, 1164–1171. [Google Scholar] [CrossRef]
- Wei, H.; Fengtian, Y. The Study of Heat Dissipation Distribution on the Working Face of High-Temperature Mines. In Proceedings of the 2011 International Conference on Electric Technology and Civil Engineering (ICETCE), Lushan, China, 22–24 April 2011; pp. 7039–7043. Available online: http://ieeexplore.ieee.org/document/5774341/ (accessed on 3 March 2021).
- Wei, W.; Deyuan, Y. Analysis on thermal environment and selection od airflow cooling methods in coal mining face. Coal Sci. Technol. 2011, 39, 42–45. [Google Scholar] [CrossRef]
- Yafei, W. Discussion on design temperature of temperature drop in working face of high temperature mine. Coal Eng. 2009, 22–24. [Google Scholar]
- Yang, B.; Jinzhang, J. Heat transfer between surrounding rock and airflow through dry roadway in mine based on FLUENT. J. Liaoning Tech. Univ. (Nat. Sci.) 2015, 34, 1–4. [Google Scholar]
- Zhang, Y.; Guo, D.M.; Han, Q.Y. Research of the best combination of cooling parameters in high temperature work deep stope. Adv. Mater. Res. 2011, 255–260, 3832–3838. [Google Scholar] [CrossRef]
- Gaowei, Y.; Kailei, Y.; Minmin, L.; Dong, H.M. Air flow cooling with precooling air in deep mining roadway. Coal Technol. 2017, 36, 171–173. [Google Scholar]
- Zhang, R.; Wei, D.; Du, C.; Xu, H.; Chang, B.; Zhang, H. Study on the appropriate air volume for ventilation and cooling in horizontal roadway. MINING R.D. 2020, 40, 96–99. [Google Scholar]
- Weijun, L. Rational allocation of ventilation system and machine cooling. Mech. Manag. Dev. 2015, 30, 21–23. [Google Scholar] [CrossRef]
- Feng, X.-P.; Jia, Z.; Liang, H.; Wang, B.; Jiang, X.; Cao, H.; Sun, X. A full air cooling and heating system based on mine water source. Appl. Therm. Eng. 2018, 145, 610–617. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, P. Influence of mine shallow roadway on airflow temperature. Arab. J. Geosci. 2020, 13, 12. [Google Scholar] [CrossRef]
- Zhu, S.; Cheng, J.; Song, W.; Borowski, M.; Zhang, Y.; Yu, B.; Wang, Y.; Qi, C.; Tukkaraja, P.; Hua, G.; et al. Using seasonal temperature difference in underground surrounding rocks to cooling ventilation airflow: A conceptual model and simulation study. Energy Sci. Eng. 2020, 8, 3457–3475. [Google Scholar] [CrossRef] [Green Version]
- Ruichong, Z.; Chengyu, X.; Keping, Z. Study on applicable conditions of high temperature deep well ventilation cooling technology. Gold Sci. Technol. 2019, 27, 888–895. [Google Scholar]
- Miwu, C. Treatment Technology for Heat Damage in Deep Mine. Saf. Coal Mines 2017, 48, 131–134. [Google Scholar]
- Chen, W.; Liang, S.; Liu, J. Proposed split-type vapor compression refrigerator for heat hazard control in deep mines. Appl. Therm. Eng. 2016, 105, 425–435. [Google Scholar] [CrossRef]
- Jing, L.; Shanshan, Z. Determination of a Certain Coal Mining Working Face Wind Cooling Way. Zhongzhou Coal 2016, 30, 32–59. [Google Scholar]
- Yuan, Y.; Zhou, X.; Zhang, X. Numerical and experimental study on the characteristics of radiant ceiling systems. Build. Res. Inf. 2019, 47, 912–927. [Google Scholar] [CrossRef]
- Krajčík, M.; Tomasi, R.; Simone, A.; Olesen, B.W. Thermal comfort and ventilation effectiveness in an office room with radiant floor cooling and displacement ventilation. Sci. Technol. Built Environ. 2016, 22, 317–327. [Google Scholar] [CrossRef] [Green Version]
- Cheng, S.; Chen, Z. Study on indoor comfort of floor radiant cooling and displacement ventilation system in large space. IOP Conf. Ser. Earth Environ. Sci. 2019, 238, 012078. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Chen, Q. Study on dynamic thermal performance and optimization of hybrid systems with capillary mat cooling and displacement ventilation. Int. J. Refrig. 2020, 110, 196–207. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Yuan, X.; Zhu, Y.; Zhang, D. Simulation study on the thermal environment in an office with radiant cooling and displacement ventilation system. Procedia Eng. 2017, 205, 3146–3153. [Google Scholar] [CrossRef]
- Liu, J.; Dalgo, D.A.; Zhu, S.; Li, H.; Zhang, L.; Srebric, J. Performance analysis of a ductless personalized ventilation combined with radiant floor cooling system and displacement ventilation. Build. Simul. 2019, 12, 905–919. [Google Scholar] [CrossRef]
- Jiangong, L.; Xinwang, L.; Tuan, H. Application status and prospect of backfill mining in Chinese coal mines. J. China Soc. 2020, 45, 141–150. [Google Scholar]
- Peng, H. Present situation and development direction of coal mine filling mining technology in China. Inn. Mong. Coal Econ. 2019, 177, 73–76. [Google Scholar]
- State Administration of Work Safety. Coal Mine Safety Rules; China Coal Industry Press: Beijing, China, 2011.
- Zhang, R.-Y. Study of Radiant Floor Cooling and Heating System with Double Layer Phase Change Energy Storage and The thermal Performance. Master’s Thesis, Southeast University, Nanjing, China, 2015. [Google Scholar]
- Lu, N. Study on Thermodynamic Parameters and Cooling Effect of Cold Wall Cooling System. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2019. [Google Scholar]
- Domestic—National Standard—State Administration for Market Regulation CN-GB. Code for Design of Prevention and Elimination of Thermal Disaster in Coal Mines. 2017. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1g6e0p30c0400j60qx7x08g0cj274539&site=xueshu_se (accessed on 3 March 2021).


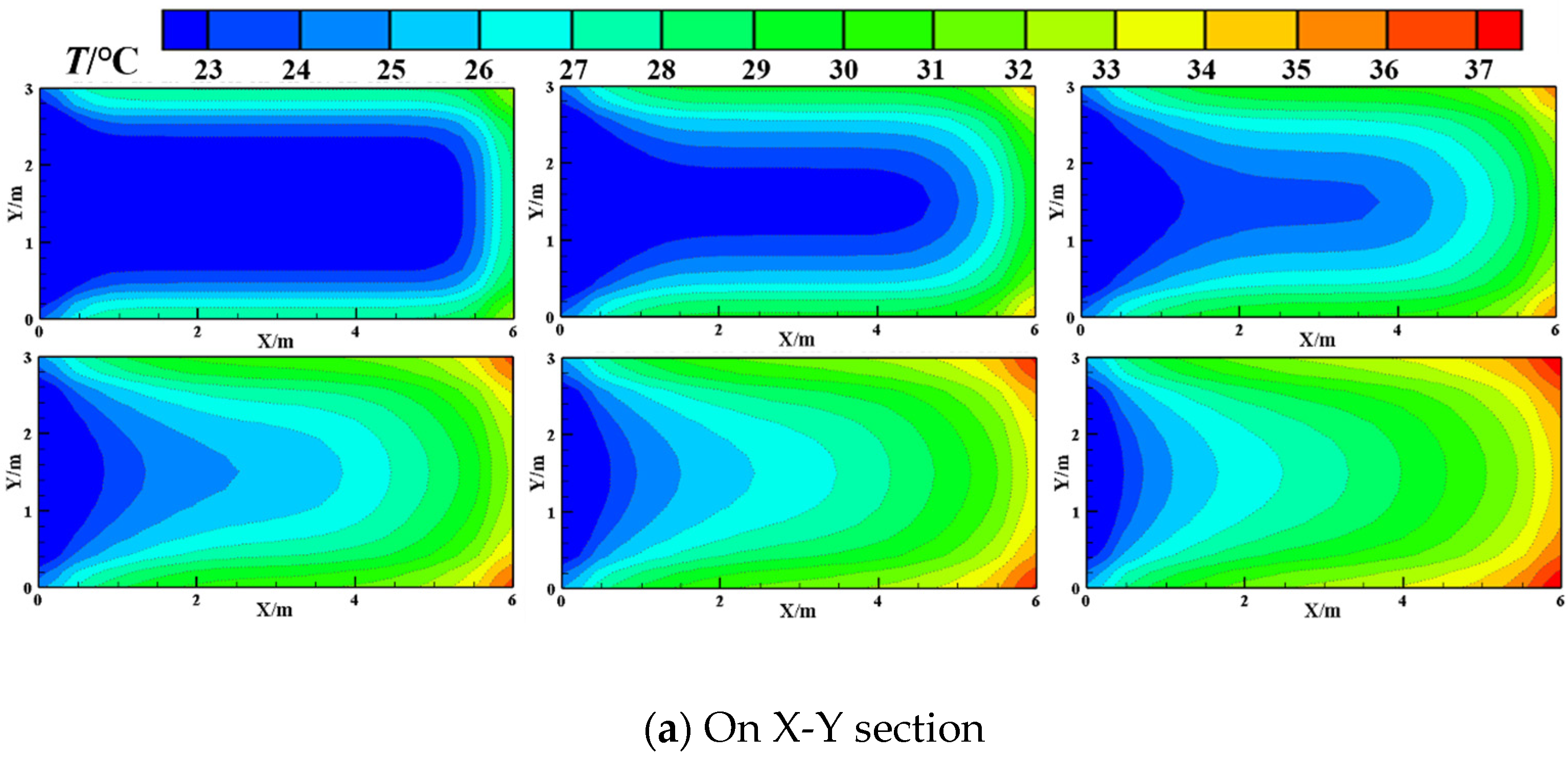
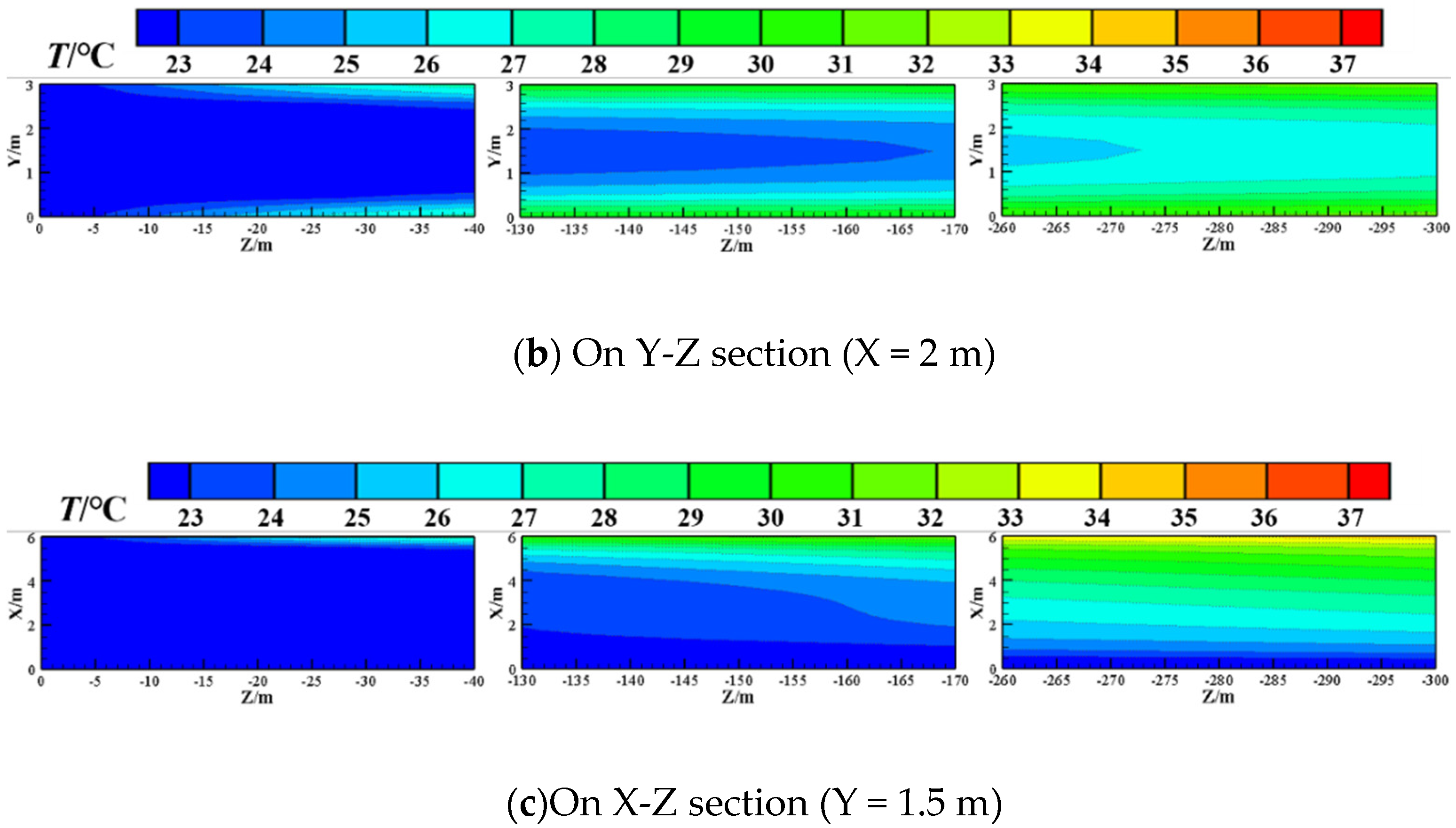
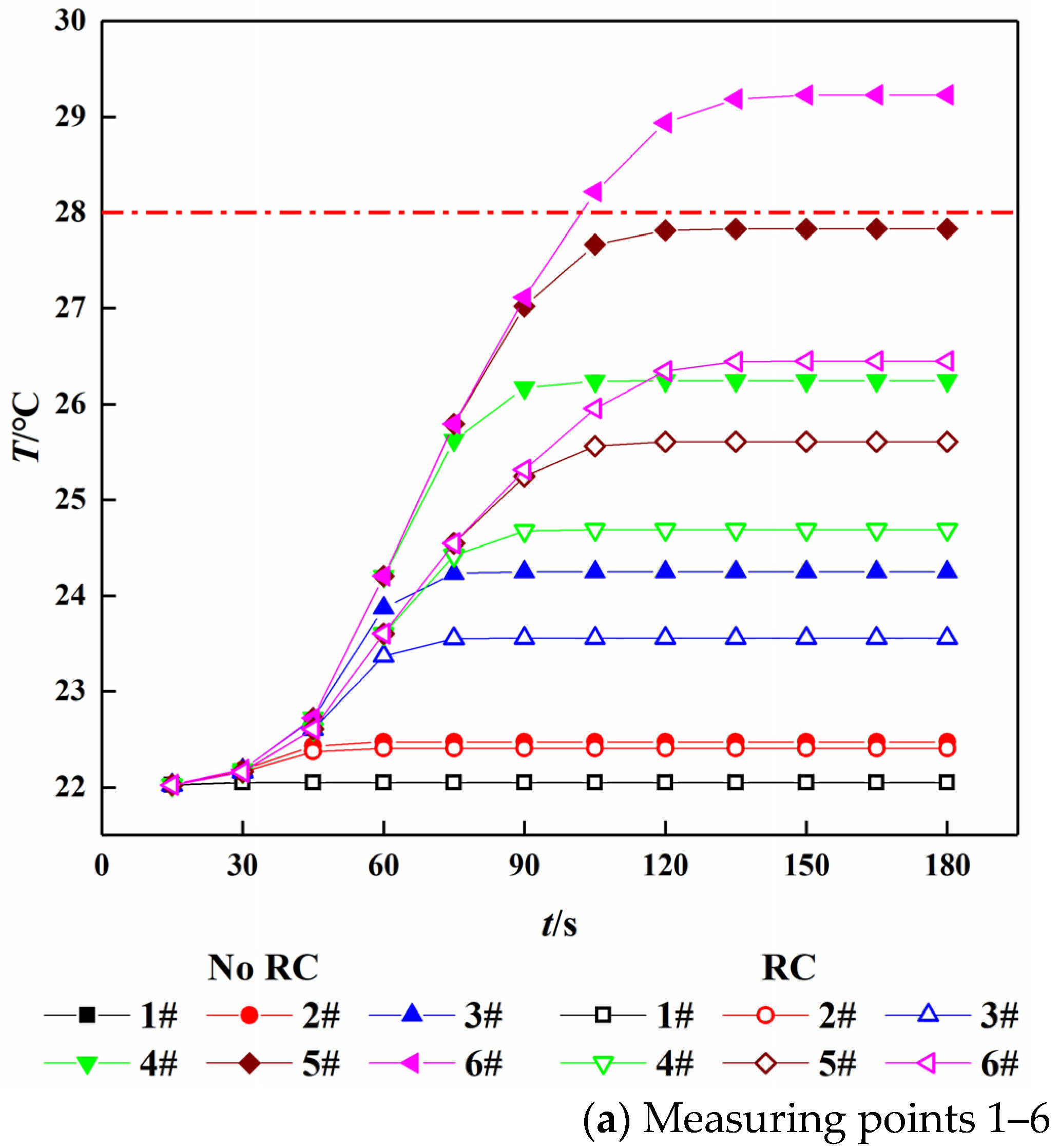
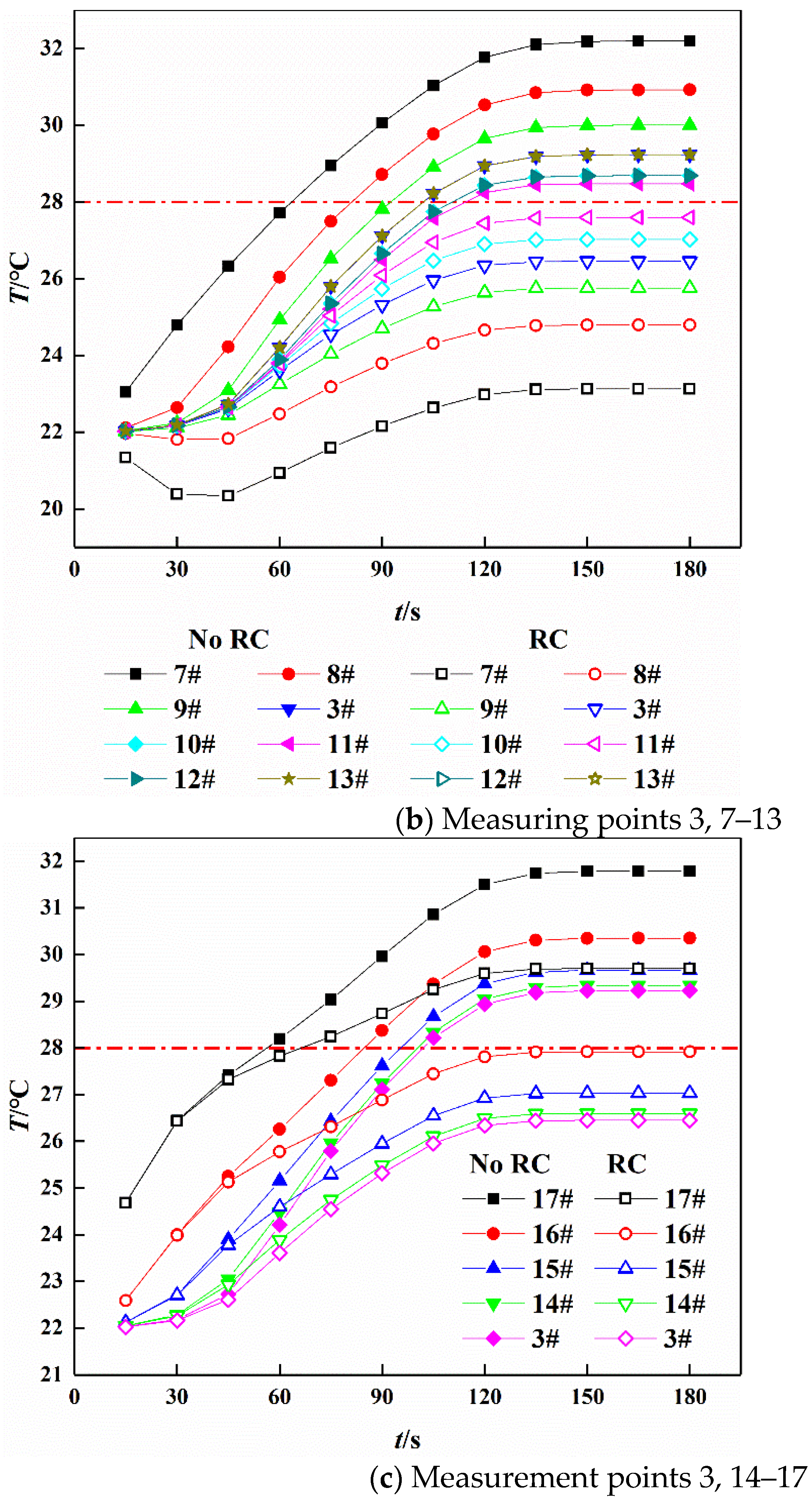
| Z/m | 50 | 100 | 150 | 200 | 250 | 300 | |
|---|---|---|---|---|---|---|---|
| Airflow Temperature/°C | before cooling | 24.41 | 26.19 | 27.71 | 29.11 | 30.42 | 31.62 |
| after cooling | 23.74 | 25.04 | 26.61 | 27.20 | 28.18 | 29.09 | |
| Measuring Point | Temperature/°C | |||
|---|---|---|---|---|
| Before Cooling | After Cooling | |||
| 90 s | 180 s | 90 s | 180 s | |
| 1 | 22.06 | 22.06 | 22.05 | 22.05 |
| 2 | 22.47 | 22.47 | 22.41 | 22.40 |
| 3 | 24.255 | 24.25 | 23.56 | 23.56 |
| 4 | 26.17 | 26.24 | 24.67 | 24.69 |
| 5 | 27.02 | 27.83 | 25.25 | 25.60 |
| 6 | 27.11 | 29.23 | 25.32 | 26.45 |
| 7 | 32.20 | 23.13 | ||
| 8 | 30.92 | 24.79 | ||
| 9 | 30.00 | 25.75 | ||
| 10 | 28.68 | 27.02 | ||
| 11 | 28.48 | 27.60 | ||
| 12 | 28.68 | 28.26 | ||
| 13 | 29.23 | 29.04 | ||
| 14 | 29.34 | 26.60 | ||
| 15 | 29.67 | 27.03 | ||
| 16 | 30.35 | 27.92 | ||
| 17 | 31.79 | 29.70 | ||
| Air Supply Temperatures/°C | 18 | 20 | 22 | 24 | 26 | |
|---|---|---|---|---|---|---|
| Airflow Temperature/°C | Before cooling | 26.49 | 27.86 | 29.23 | 30.60 | 31.97 |
| After cooling | 23.70 | 25.07 | 26.44 | 27.81 | 29.18 | |
| Air supply Velocities/(m/s) | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |
|---|---|---|---|---|---|---|
| Airflow Temperature/°C | Before cooling | 29.76 | 29.45 | 29.19 | 29.00 | 28.65 |
| After cooling | 26.83 | 26.61 | 26.44 | 26.32 | 26.15 | |
| Surrounding Wall Temperatures/°C | 35 | 40 | 45 | 50 | 55 | ||
|---|---|---|---|---|---|---|---|
| Airflow Temperature/°C | Before cooling | 90 s | 24.89 | 26.00 | 27.11 | 28.25 | 29.34 |
| 135 s | 26.09 | 27.66 | 29.23 | 30.80 | 32.37 | ||
| After cooling | 90 s | 23.56 | 24.44 | 25.32 | 26.19 | 27.07 | |
| 135 s | 24.04 | 25.24 | 26.45 | 27.66 | 28.86 | ||
| Measuring Point | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Airflow Temperature/°C | Before cooling | 26.09 | 26.77 | 29.38 | 31.98 | 32.98 | 34.06 |
| After cooling | 26.08 | 26.64 | 28.13 | 29.44 | 30.54 | 31.55 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Bu, B.; Liu, L.; Cao, T.; Ke, Y.; Du, Q. Numerical Simulation on Cooling Effect of Working Face under Radiation Cooling Mode in Deep Well. Energies 2021, 14, 4428. https://doi.org/10.3390/en14154428
Zhang X, Bu B, Liu L, Cao T, Ke Y, Du Q. Numerical Simulation on Cooling Effect of Working Face under Radiation Cooling Mode in Deep Well. Energies. 2021; 14(15):4428. https://doi.org/10.3390/en14154428
Chicago/Turabian StyleZhang, Xiaoyan, Baoyun Bu, Lang Liu, Tianrun Cao, Yaping Ke, and Qiangqiang Du. 2021. "Numerical Simulation on Cooling Effect of Working Face under Radiation Cooling Mode in Deep Well" Energies 14, no. 15: 4428. https://doi.org/10.3390/en14154428
APA StyleZhang, X., Bu, B., Liu, L., Cao, T., Ke, Y., & Du, Q. (2021). Numerical Simulation on Cooling Effect of Working Face under Radiation Cooling Mode in Deep Well. Energies, 14(15), 4428. https://doi.org/10.3390/en14154428






