Numerical Investigation on Two-Phase Flow Heat Transfer Performance and Instability with Discrete Heat Sources in Parallel Channels
Abstract
:1. Introduction
2. Study on Heat Transfer Characteristics
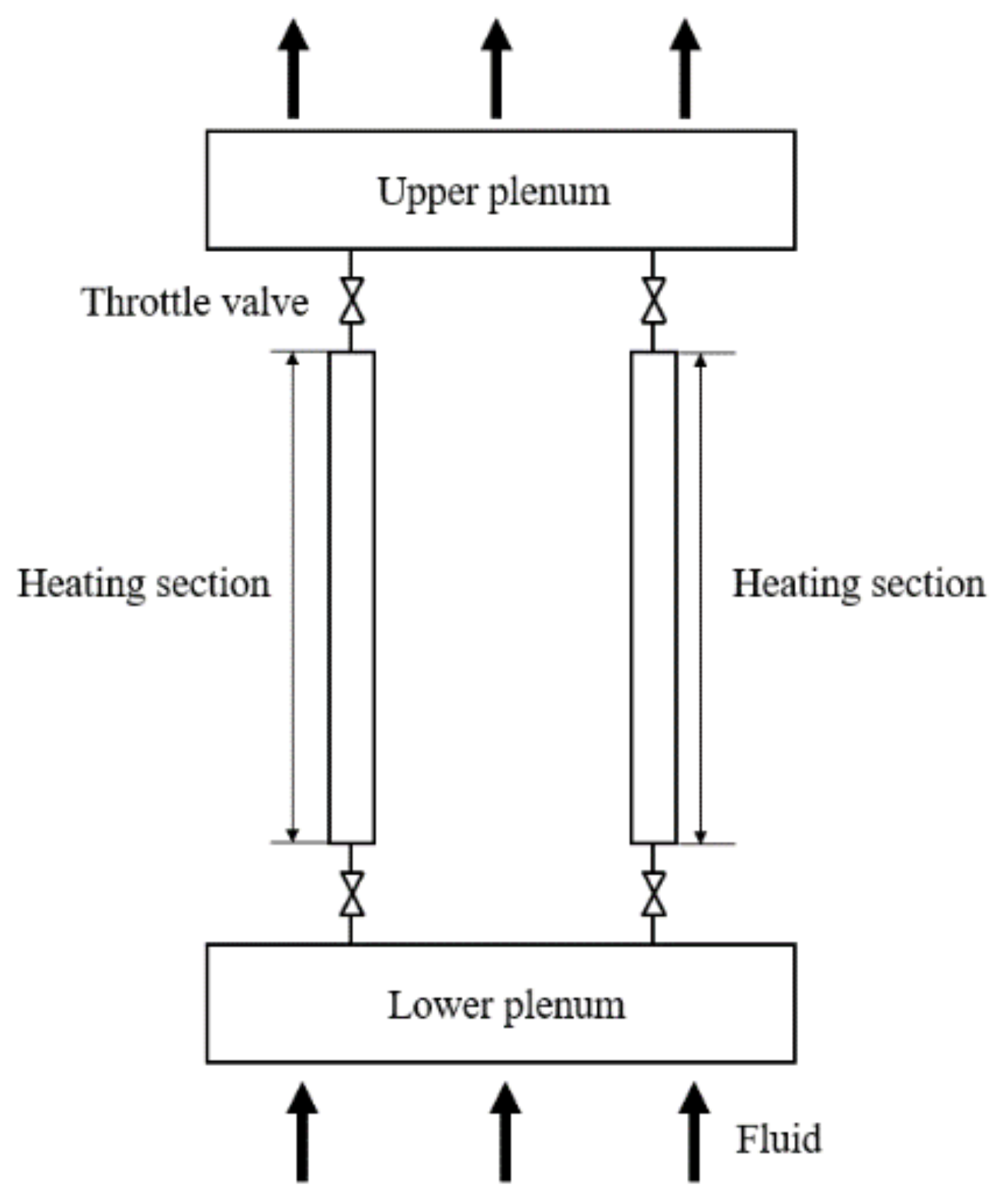
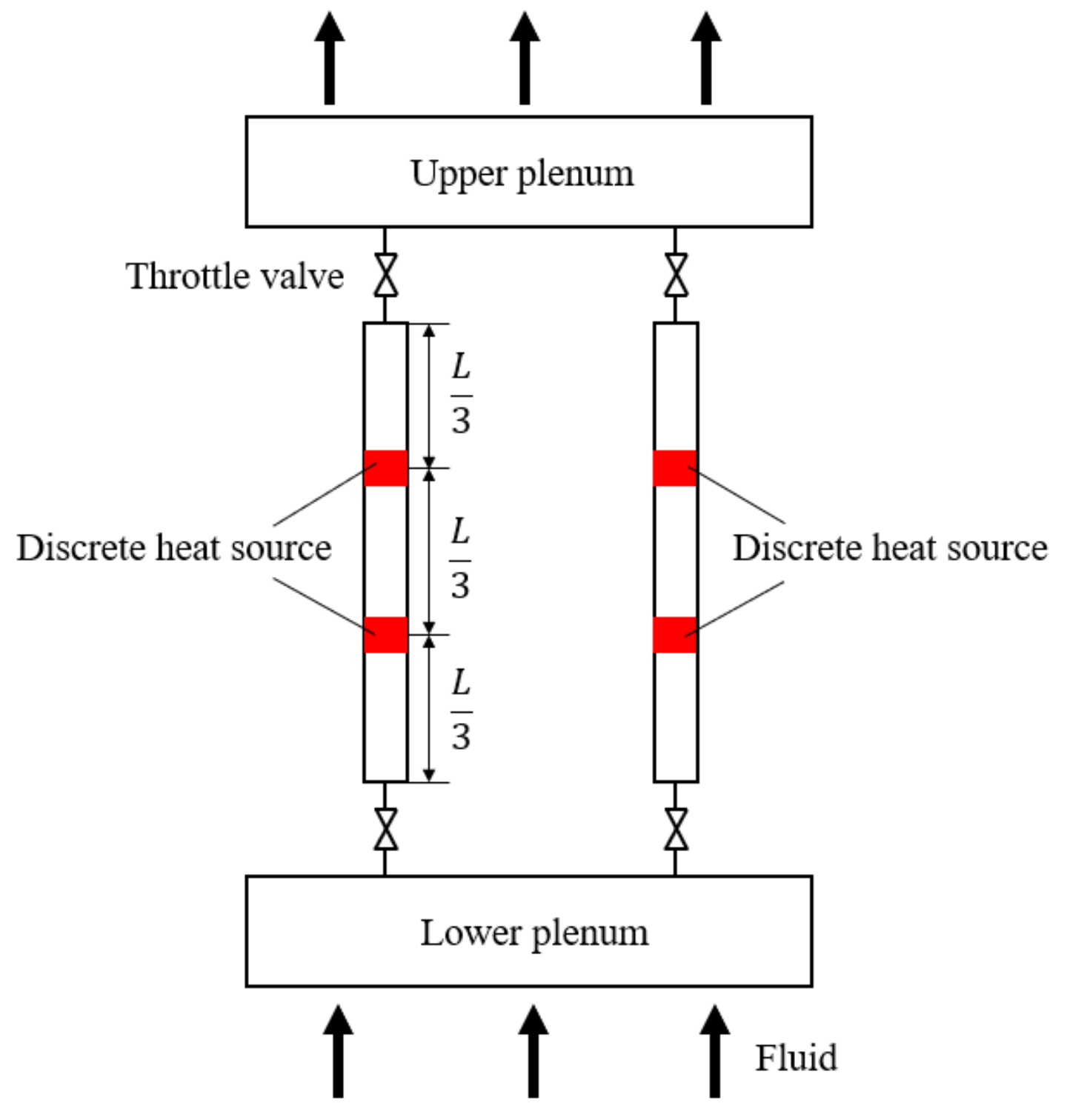
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Governing Equations
2.2.2. Phase Change Model
2.2.3. Solution Methods
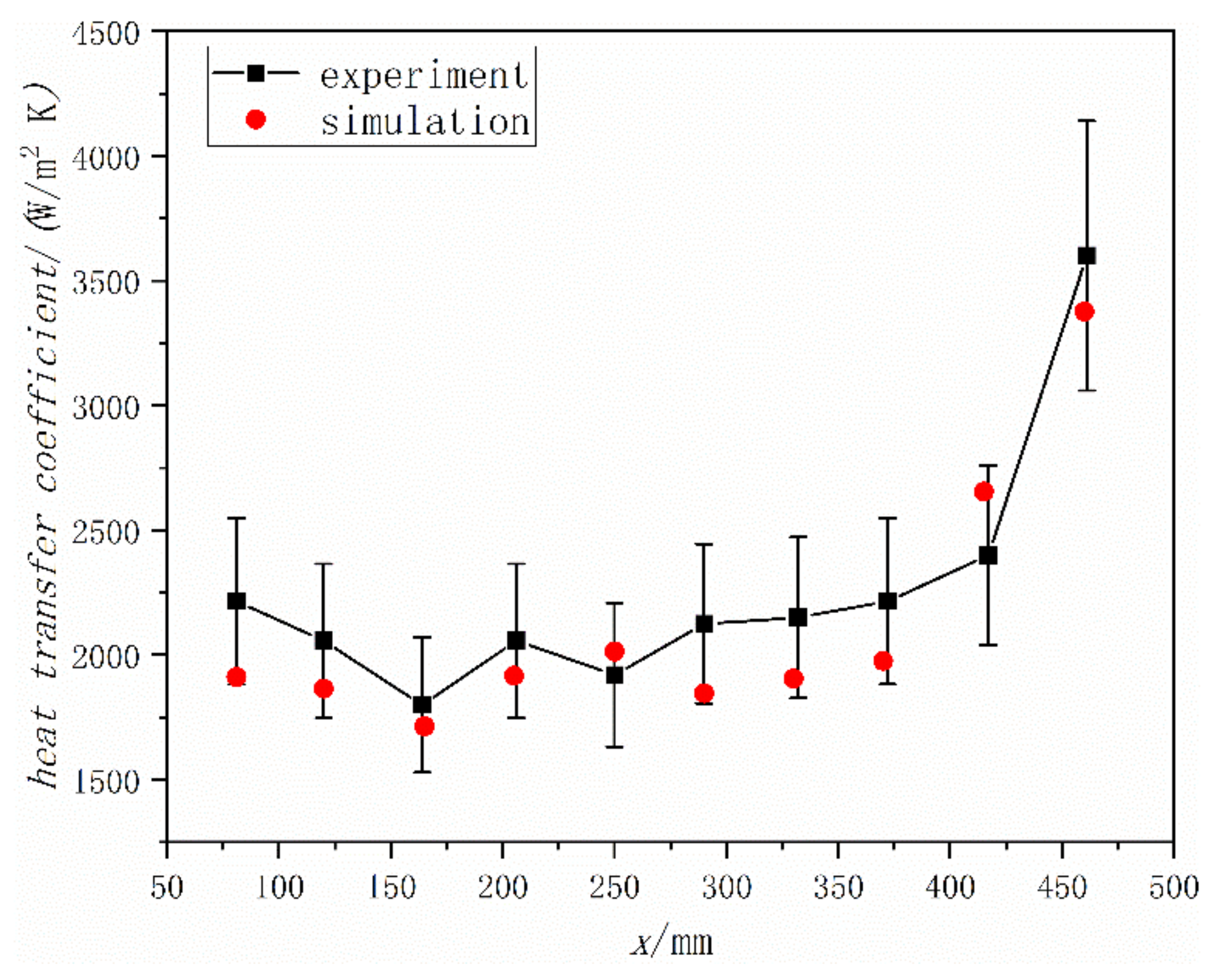
2.3. Validation of the Simulated Method
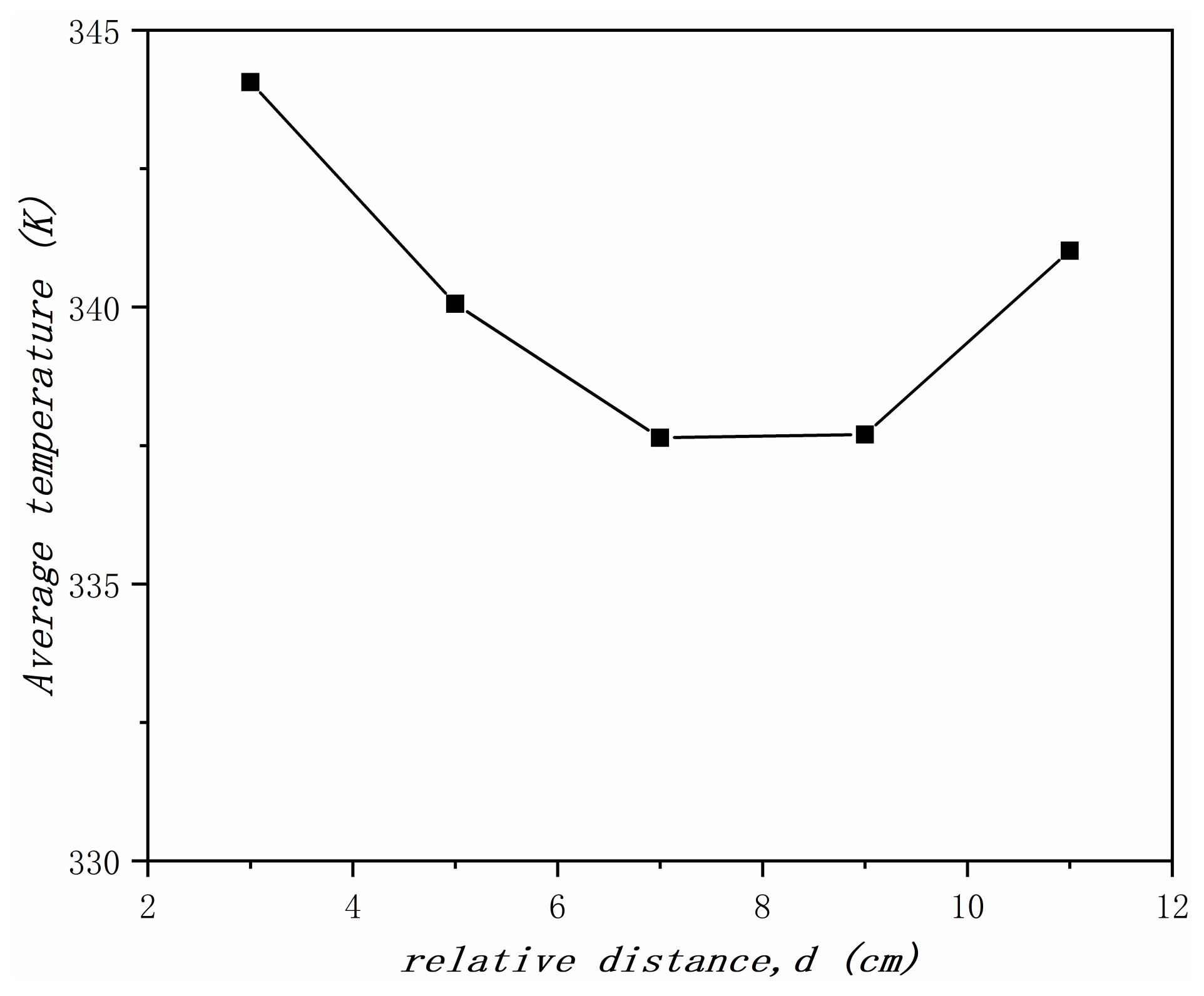
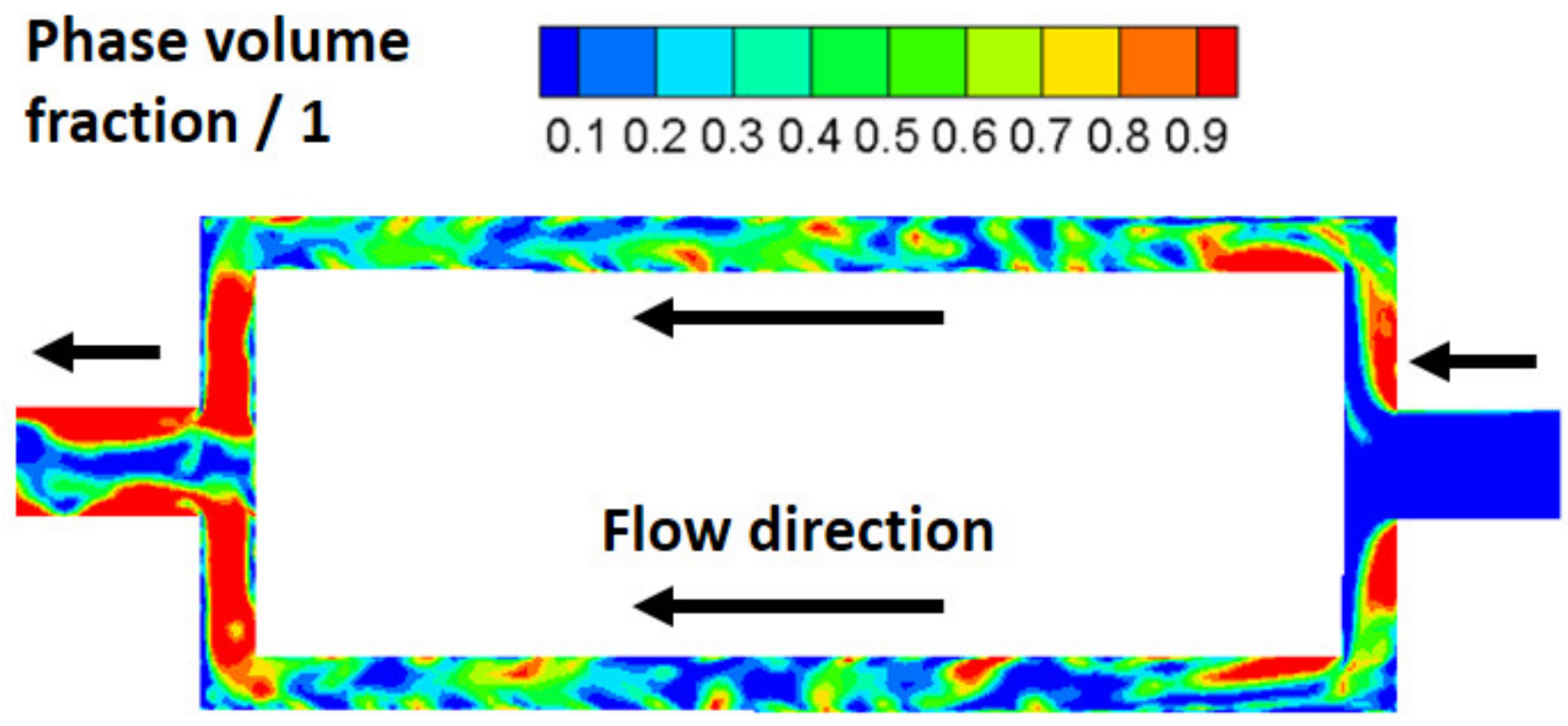
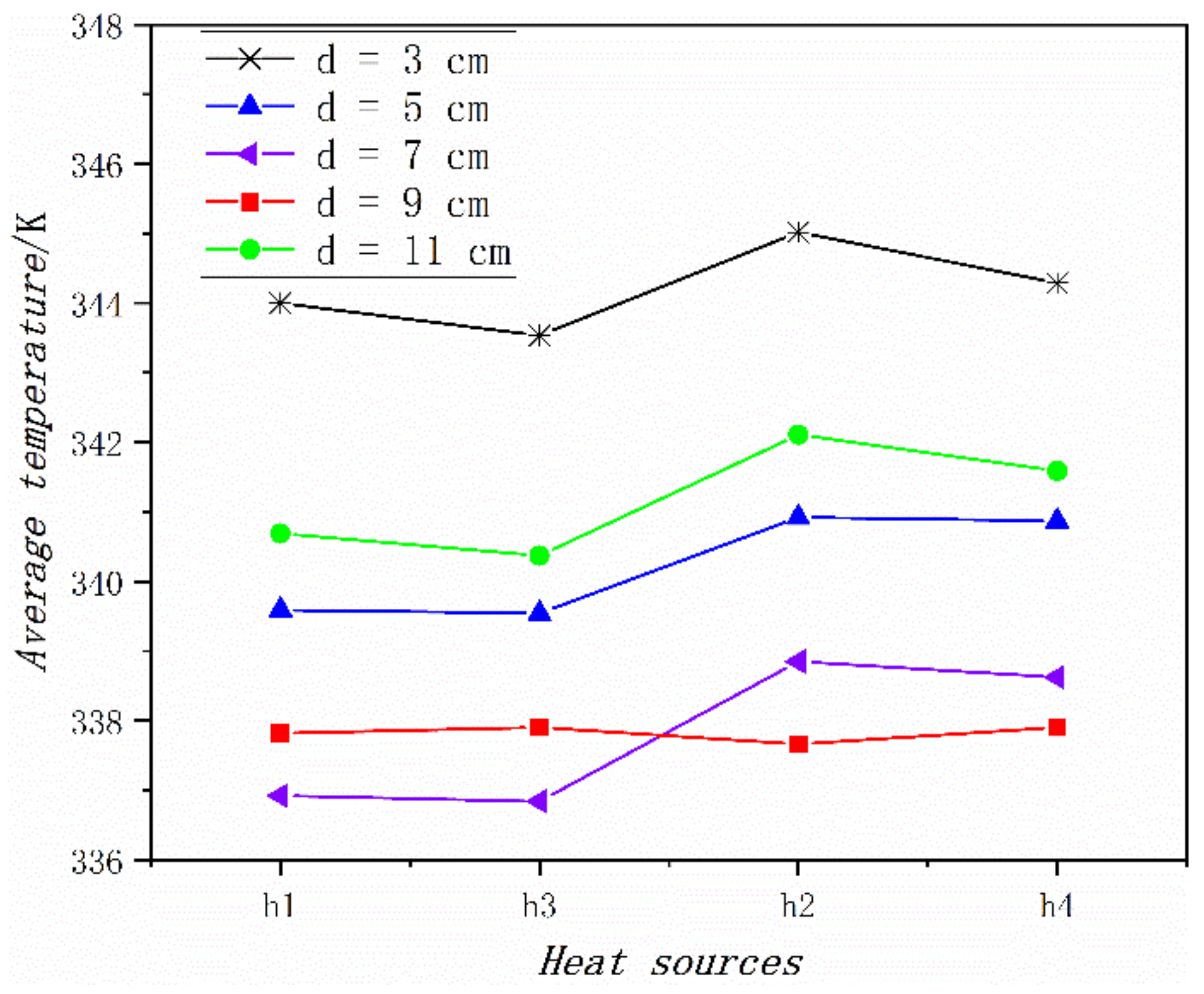
2.4. Results and Discussion
3. Analysis of Flow Instability
3.1. Mathematical Model
- It is simplified to one-dimension, and only the variation of the parameters in the axial direction is considered;
- The entire tube is in thermal equilibrium;
- The fluid at the inlet of the pipeline is always in a state of supercooling;
- Subcooled boiling is not taken into account in the subcooling zone of the pipeline. The simplified physical model is shown in Figure 6.
3.2. Solution Method and Model Validation
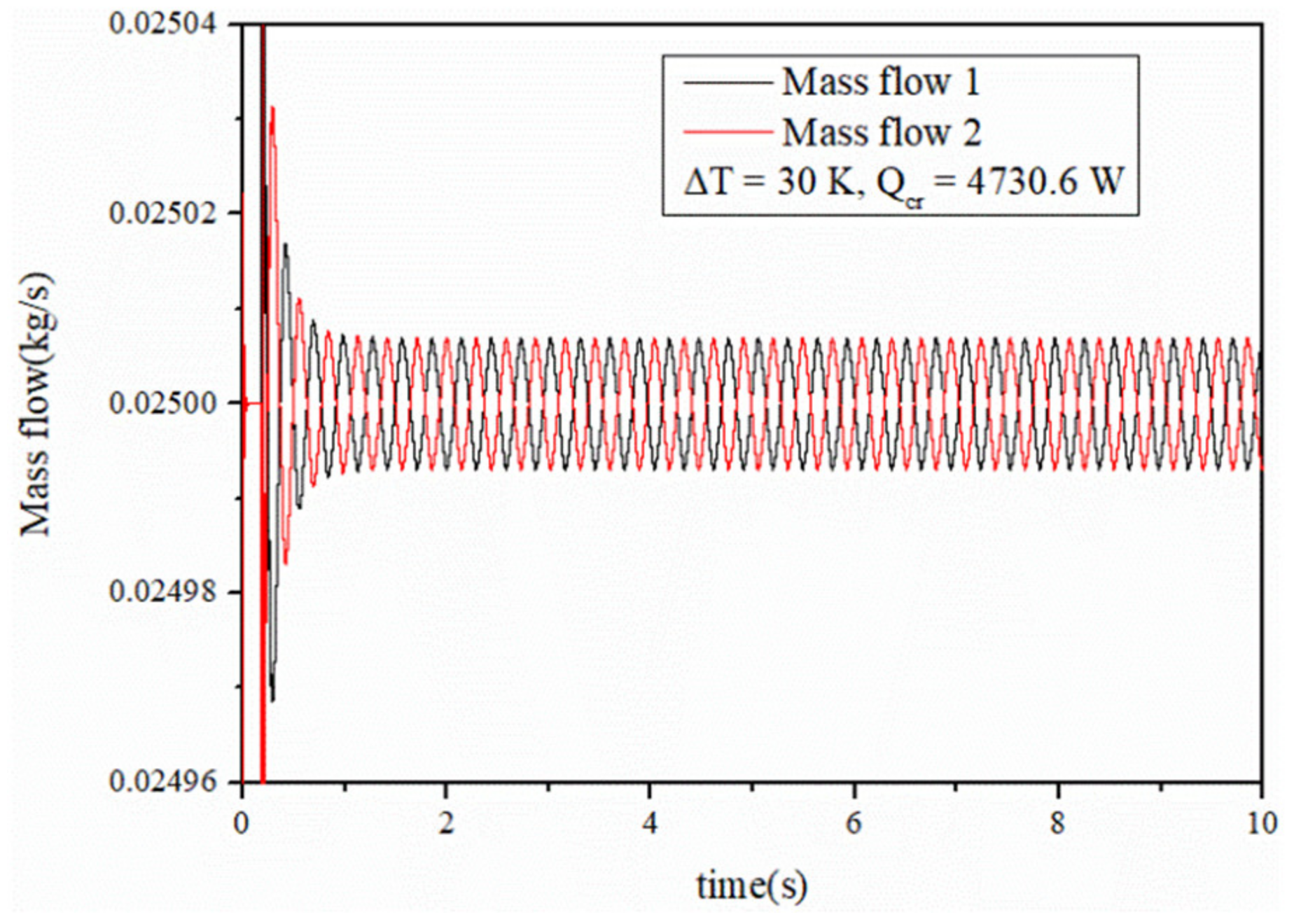
3.3. Result and Discussion
4. Conclusions
- (1)
- The relative positions of discrete heat sources affect the heat transfer effect of two-phase flow, and the heat transfer performance can be improved by reasonably designing the relative position of heat sources.
- (2)
- The closer the distribution of discrete heat sources, the worse the heat transfer effect; for the working condition designed in this paper, the heat transfer effect is best when the distance between the centers of the two discrete heat sources on the same branch channel are within a range of 7–9 cm.
- (3)
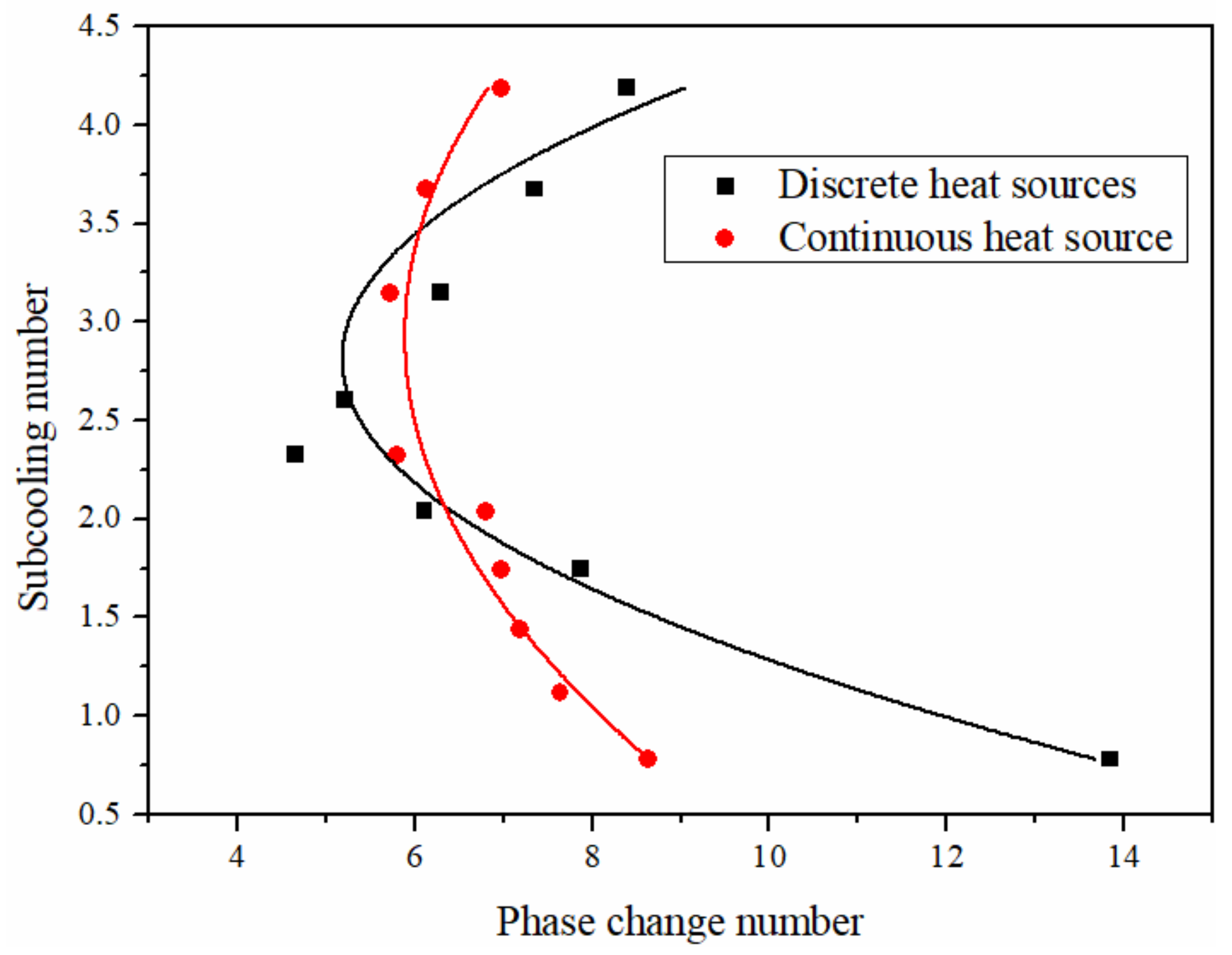
- Compared with the continuous heat source, the discrete heat source with uniform distribution can enhance the flow stability under low and high inlet undercooling.
- (4)
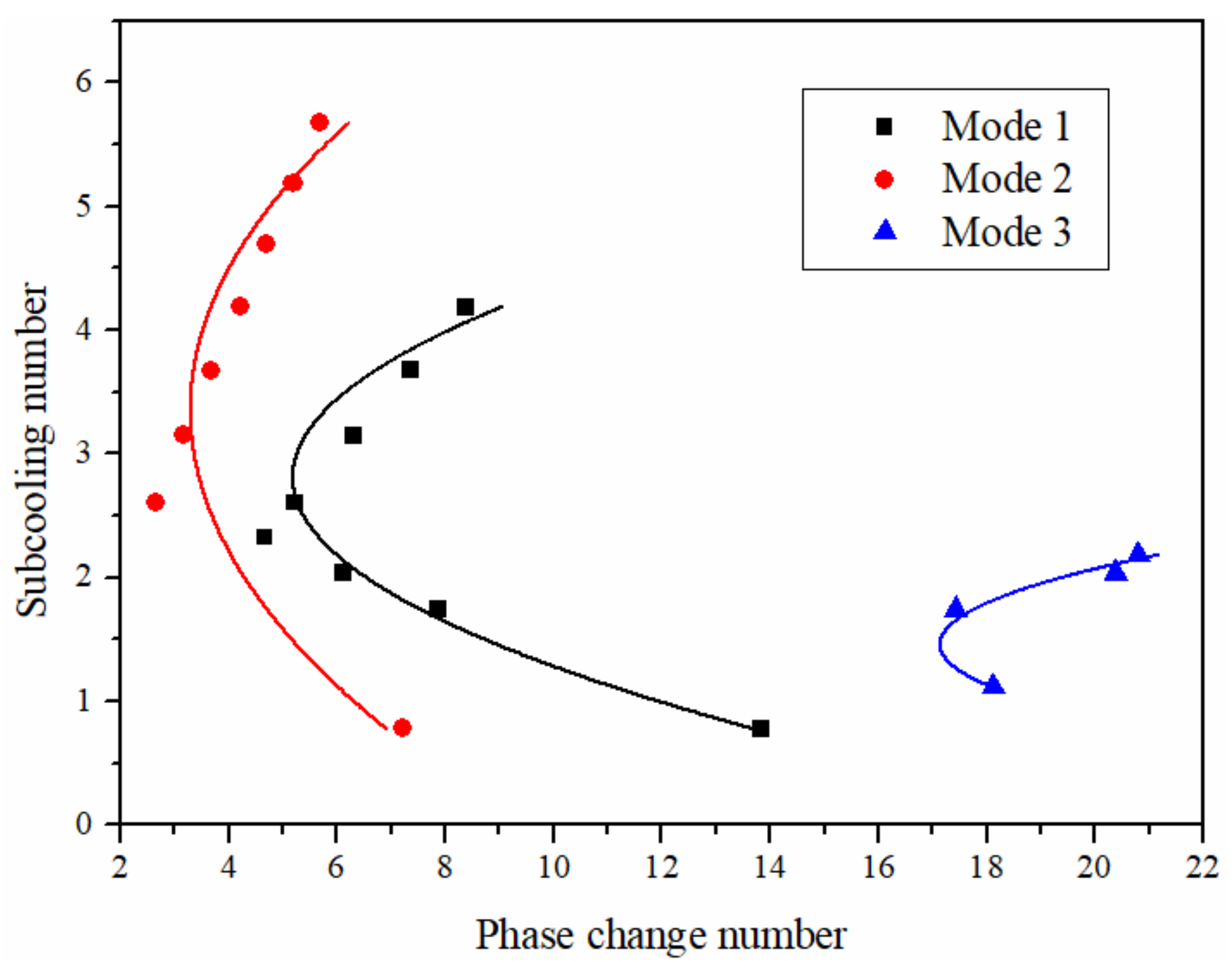
- When the high-power discrete heat source is closer to the flow outlet and the low-power discrete heat source is closer to the flow inlet, the flow stability is improved.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosa, P.; Karayiannis, T.G.; Collins, M.W. Single-phase heat transfer in microchannels: The importance of scaling effects. Appl. Therm. Eng. 2011, 29, 3447–3468. [Google Scholar] [CrossRef] [Green Version]
- Agostini, B.; Fabbri, M.; Park, J.E.; Wojtan, L.; Thome, J.R.; Michel, B. State-of-the-art of high heat flux cooling technologies. Heat Transf. Eng. 2007, 28, 258–281. [Google Scholar] [CrossRef]
- Yen, T.H.; Shoji, M.; Takemura, F.; Suzuki, Y.; Kasagi, N. Visualization of convective boiling heat transfer in single microchannels with different shaped cross-sections. Int. J. Heat Mass Transf. 2006, 49, 3884–3894. [Google Scholar] [CrossRef]
- Deng, D.; Wan, W.; Tang, Y.; Wan, Z.; Liang, D. Experimental investigations on flow boiling performance of reentrant and rectangular microchannels-a comparative study. Int. J. Heat Mass Transf. 2015, 82, 435–446. [Google Scholar] [CrossRef]
- Tran, N.T.; Chyub, M.C. Two-phase pressure drop of refrigerants during flow boiling in small channels: An experimental investigation and correlation development. Int. J. Multiph. Flow 2000, 26, 1739–1754. [Google Scholar] [CrossRef] [Green Version]
- Meng, M.; Yang, Z.; Duan, Y.Y.; Chen, Y. Boiling flow of R141b in vertical and inclined Serpentine Tubes. Int. J. Heat Mass Transf. 2013, 57, 312–320. [Google Scholar] [CrossRef]
- Huang, F.; Zhao, J.; Zhang, Y.; Zhang, H.; Wang, C.; Liu, Z. Numerical analysis on flow pattern and heat transfer characteristics of flow boiling in the mini-channels. Numer. Heat Transf. Part. B Fundam. 2020, 78, 221–247. [Google Scholar] [CrossRef]
- Gorlé, C.; Lee, H.; Houshmand, F.; Asheghi, M.; Goodson, K.; Parida, P.R. Validation study for VOF simulations of boiling in a microchannel. In International Electronic Packaging Technical Conference and Exhibition, Proceedings of the ASME 2015 13th International Conference on Nanochannels, Microchannels, and Minichannels (InterPACK2015), San Francisco, CA, USA, 6–9 July 2015; American Society of Mechanical Engineers: New York, NY, USA, 2015; Volume 56901, p. V003T10A022. [Google Scholar]
- Lorenzini, D.; Joshi, Y. CFD study of flow boiling in silicon microgaps with staggered pin fins for the 3D-stacking of ICs. In Proceedings of the 2016 15th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Las Vegas, NV, USA, 31 May–3 June 2016. [Google Scholar]
- Lee, H.; Agonafer, D.D.; Won, Y.; Houshmand, F.; Gorle, C.; Asheghi, M.; Goodson, K.E. Thermal Modeling of Extreme Heat Flux Microchannel Coolers for GaN-on-SiC Semiconductor Devices. J. Electron. Packag. 2016, 138, 10907. [Google Scholar] [CrossRef] [Green Version]
- Vontas, K.; Andredaki, M.; Georgoulas, A.; Miché, N.; Marengo, M. The effect of surface wettability on flow boiling characteristics within microchannels. Int. J. Heat Mass Transf. 2021, 172, 121133. [Google Scholar] [CrossRef]
- Li, X.; Wei, W.; Wang, R.; Shi, Y. Numerical and experimental investigation of heat transfer on heating surface during subcooled boiling flow of liquid nitrogen. Int. J. Heat Mass Transf. 2009, 52, 1510–1516. [Google Scholar] [CrossRef]
- Soleimani, A.; Sattari, A.; Hanafizadeh, P. Thermal analysis of a microchannel heat sink cooled by two-phase flow boiling of Al2O3 HFE-7100 nanofluid. Therm. Sci. Eng. Prog. 2020, 20, 100693. [Google Scholar] [CrossRef]
- Zhuan, R.; Wang, W. Simulation on nucleate boiling in micro-channel. Int. J. Heat Mass Transf. 2010, 53, 502–512. [Google Scholar] [CrossRef]
- Liu, Q.; Palm, B. Numerical study of bubbles rising and merging during convective boiling in micro-channels. Appl. Therm. Eng. 2016, 99, 1141–1151. [Google Scholar] [CrossRef]
- Yu, J.; Ma, H.; Jiang, Y. A numerical study of heat transfer and pressure drop of hydrocarbon mixture refrigerant during boiling in vertical rectangular minichannel. Appl. Therm. Eng. 2017, 112, 1343–1352. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.F.; Ye, P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Transf. 2008, 51, 1003–1016. [Google Scholar] [CrossRef]
- Hardt, S.; Herbert, S.; Kunkelmann, C.; Mahjoob, S.; Stephan, P. Unidirectional bubble growth in microchannels with asymmetric surface features. Int. J. Heat Mass Transf. 2012, 55, 7056–7062. [Google Scholar] [CrossRef]
- Ma, H.; Cai, W.; Chen, J.; Yao, Y.; Jiang, Y. Numerical investigation on saturated boiling and heat transfer correlations in a vertical rectangular minichannel. Int. J. Therm. Sci. 2016, 102, 285–299. [Google Scholar] [CrossRef]
- Cho, E.S.; Choi, J.W.; Yoon, J.S.; Kim, M.S. Modeling and simulation on the mass flow distribution in microchannel heat sinks with non-uniform heat flux conditions. Int. J. Heat Mass Transf. 2010, 53, 1341–1348. [Google Scholar] [CrossRef]
- Cho, E.S.; Choi, J.W.; Yoon, J.S.; Kim, M.S. Experimental study on microchannel heat sinks considering mass flow distribution with non-uniform heat flux conditions. Int. J. Heat Mass Transf. 2010, 53, 2159–2168. [Google Scholar] [CrossRef]
- Bhowmik, H.; Tso, C.P.; Tou, K.W.; Tan, F.L. Convection heat transfer from discrete heat sources in a liquid cooled rectangular channel. Appl. Therm. Eng. 2005, 25, 2532–2542. [Google Scholar] [CrossRef]
- Kurose, K.; Miyata, K.; Hamamoto, Y.; Mori, H. Flow boiling heat transfer and flow distribution of HFC32 and HFC134a in unequally heated parallel mini-channels. Int. J. Refrig. 2020, 119, 305–315. [Google Scholar] [CrossRef]
- Islam, M.A.; Pal, A.; Thu, K.; Saha, B.B. Study on performance and environmental impact of supermarket refrigeration system in Japan Evergreen. Evergreen 2019, 6, 168–176. [Google Scholar] [CrossRef]
- Kurose, K.; Noboritate, W.; Sakai, S.; Miyata, K.; Hamamoto, Y. An experimental study on flow boiling heat transfer of R410A in parallel two mini-channels heated unequally by high-temperature fluid. Appl. Therm. Eng. 2020, 178, 1359–4311. [Google Scholar] [CrossRef]
- Ghaedamini, H.; Salimpour, M.R.; Mujumdar, A.S. The effect of svelteness on the bifurcation angles role in pressure drop and flow uniformity of tree-shaped microchannels. Appl. Therm. Eng. 2011, 31, 708–716. [Google Scholar] [CrossRef]
- Colombo, M.; Cammi, A.; Papini, D.; Ricotti, M.E. RELAP5/MOD3.3 study on density wave instabilities in single channel and two parallel channels. Prog. Nucl. Energy 2012, 56, 15–23. [Google Scholar]
- Paruya, S.; Maiti, S.; Karmakar, A.; Gupta, P.; Sarkar, J.P. Lumped parameterization of boiling channel—Bifurcations during density wave oscillations. Chem. Eng. Sci. 2012, 74, 310–326. [Google Scholar] [CrossRef]
- Papini, D.; Cammi, A.; Colombo, M.; Ricotti, M.E. Time-domain linear and non-linear studies on density wave oscillations. Chem. Eng. Sci. 2012, 81, 118–139. [Google Scholar] [CrossRef]
- Lu, X.; Wu, Y.; Zhou, L.; Tian, W.; Su, G.; Qiu, S.; Zhang, H. Theoretical investigations on two-phase flow instability in parallel channels under axial non-uniform heating. Ann. Nucl. Energy 2014, 63, 75–82. [Google Scholar] [CrossRef]
- Paul, S.; Singh, S. Linear stability analysis of flow instabilities with a nodalized reduced order model in heated channel. Int. J. Therm. Sci. 2015, 98, 312–331. [Google Scholar] [CrossRef]
- Paul, D.; Singh, S.; Mishra, S. Impact of system pressure on the characteristics of stability boundary for a single-channel flow boiling system. Nonlinear Dyn. 2019, 96, 175–184. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kother, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Lee, W.H. A Pressure Iteration Scheme for Two-phase Flow Modeling. In Multiphase Transport. Fundamentals, Reactor Safety, Applications; Veziroglu, T.N., Ed.; Hemisphere Publishing: Washington, DC, USA, 1980; pp. 407–432. [Google Scholar]
- Lin, S.; Kew, P.A.; Cornwell, K. Two-phase heat transfer to a refrigerant in a 1 mm diameter tube. Int. J. Refrig. 2001, 24, 51–56. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, L.; Bu, S.; Sun, W.; Chen, D.; Pan, L. A study of the heat flux profile effect on parallel channel density wave oscillation in sodium heated heat exchanger. Prog. Nucl. Energy 2019, 112, 135–145. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Shen, Z.M.; Jing, J.G.; Chen, T.K. Experimental study on density wave instability of high pressure vapor-liquid two-phase flow in parallel pipes. J. Eng. Thermophys. 1996, 17, 215–218. [Google Scholar]
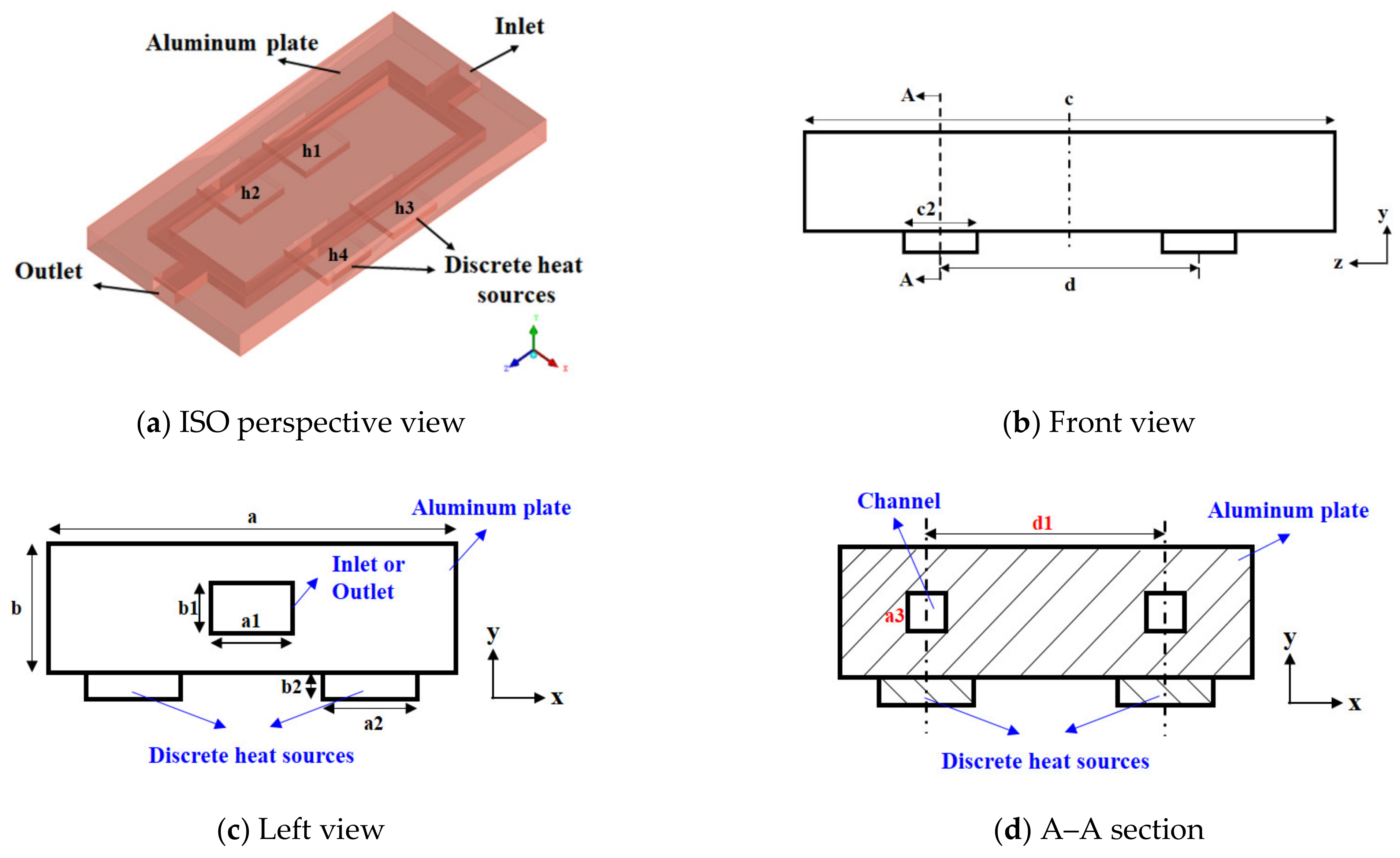


| Parameter | Value |
|---|---|
| Volume of aluminum plate (c × a × b)/cm3 | 14 × 7 × 1 |
| Volume of discrete heat sources (c2 × a2 × b2)/cm3 | 2 × 2 × 0.3 |
| Volume of single continuous heat source/cm3 | 14 × 7 × 0.3 |
| Cross section area of inlet (a1 × b1)/cm2 | 1 × 0.5 |
| Cross section area of outlet (a1 × b1)/cm2 | 1 × 0.5 |
| Cross section area of branch (a3 × a3)/cm2 | 0.5 × 0.5 |
| Axis distance of parallel channel (d1)/cm | 4 |
| Properties | Liquid | Vapor |
|---|---|---|
| Density ρ/(kg/m3) | 1182.2 | 39.025 |
| Viscosity μ/(kg/(m s)) | 0.00018011 | 0.000011965 |
| Coefficient of thermal conductivity k/(W/(m K)) | 0.078424 | 0.014497 |
| Specific heat capacity CP/(J/(kg K)) | 1452.7 | 39.025 |
| Latent heat h/(kJ/kg) | 171.81 | |
| Surface tension /(N/m) | 0.0072429 | |
| Saturation temperature Tsat/K | 304.48 | |
| Case | Grid Number 1 | Average Temperature of 4 Discrete Heat Sources Th/K | |
|---|---|---|---|
| Mesh1 | 361061 | 337.0 | 2.37 × 10−3 |
| Mesh2 | 392049 | 337.8 | 2.07 × 10−3 |
| Mesh3 | 432322 | 338.5 | 5.91 × 10−4 |
| Mesh4 | 545087 | 338.7 | - |
| Parameter | Value |
|---|---|
| Heated length/(mm) | 140 |
| Cross section of channel/(mm2) | 5 × 10 |
| System pressure/(MPa) | 14 |
| Total mass flow/(kg/s) | 0.015 |
| Inlet subcooling/(K) | 10–40 |
| Channel inclination/(°) | 90 |
| Discrete Heat Source | Proportion of Total Heating Power | ||
|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | |
| Source 1 | 0.5 | 0.1 | 0.1 |
| Source 2 | 0.5 | 0.1 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Wang, R.; Yang, P.; Ling, W.; Zeng, M.; Qian, J.; Wang, Q. Numerical Investigation on Two-Phase Flow Heat Transfer Performance and Instability with Discrete Heat Sources in Parallel Channels. Energies 2021, 14, 4408. https://doi.org/10.3390/en14154408
Hu C, Wang R, Yang P, Ling W, Zeng M, Qian J, Wang Q. Numerical Investigation on Two-Phase Flow Heat Transfer Performance and Instability with Discrete Heat Sources in Parallel Channels. Energies. 2021; 14(15):4408. https://doi.org/10.3390/en14154408
Chicago/Turabian StyleHu, Changming, Rui Wang, Ping Yang, Weihao Ling, Min Zeng, Jiyu Qian, and Qiuwang Wang. 2021. "Numerical Investigation on Two-Phase Flow Heat Transfer Performance and Instability with Discrete Heat Sources in Parallel Channels" Energies 14, no. 15: 4408. https://doi.org/10.3390/en14154408
APA StyleHu, C., Wang, R., Yang, P., Ling, W., Zeng, M., Qian, J., & Wang, Q. (2021). Numerical Investigation on Two-Phase Flow Heat Transfer Performance and Instability with Discrete Heat Sources in Parallel Channels. Energies, 14(15), 4408. https://doi.org/10.3390/en14154408








