Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes
Abstract
:1. Introduction
2. Governing Equations for Electrical Resistivity of Cylindrical Samples
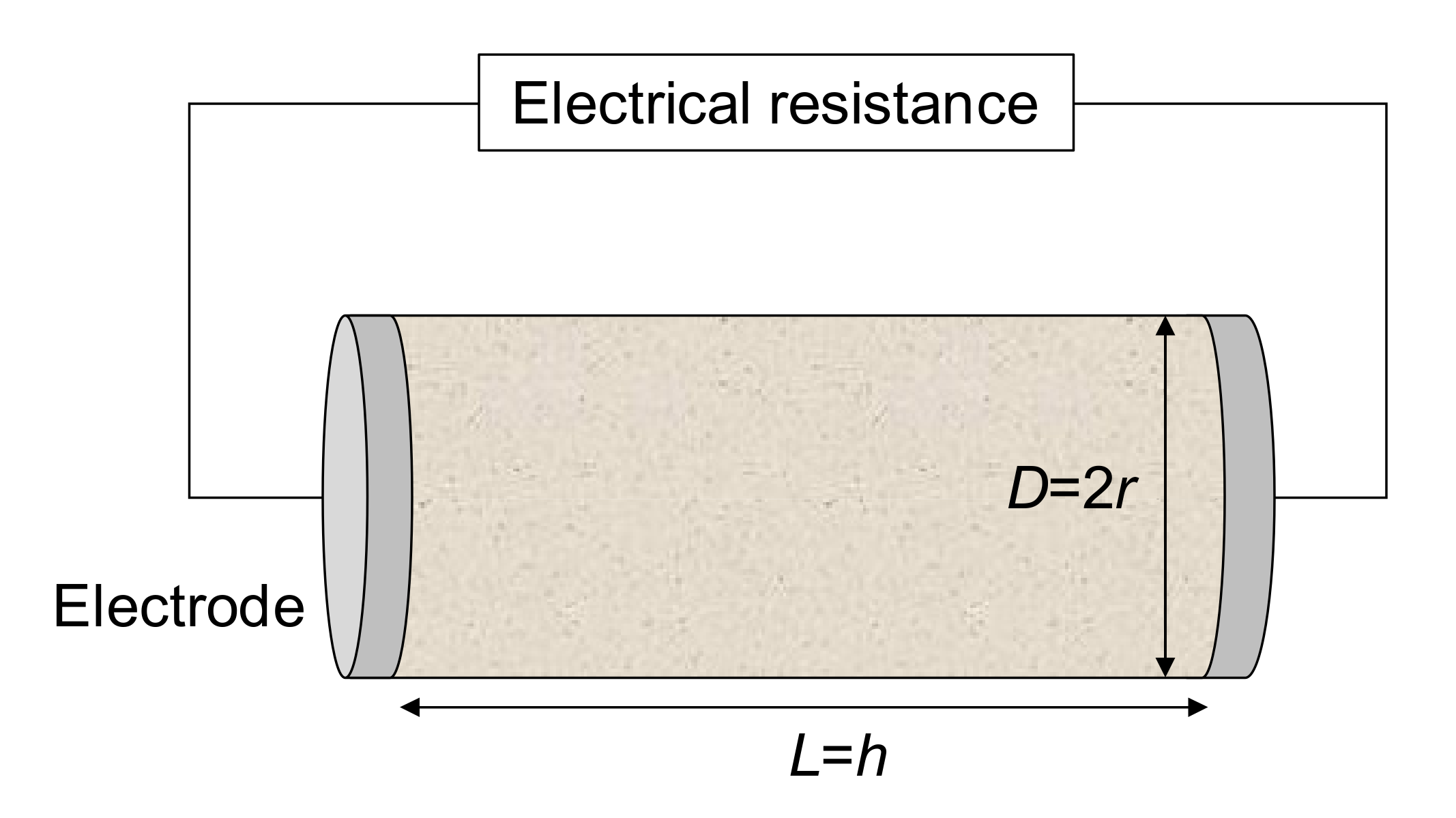
2.1. ASTM Standard for Electrical Resistivity (ASTM G187)
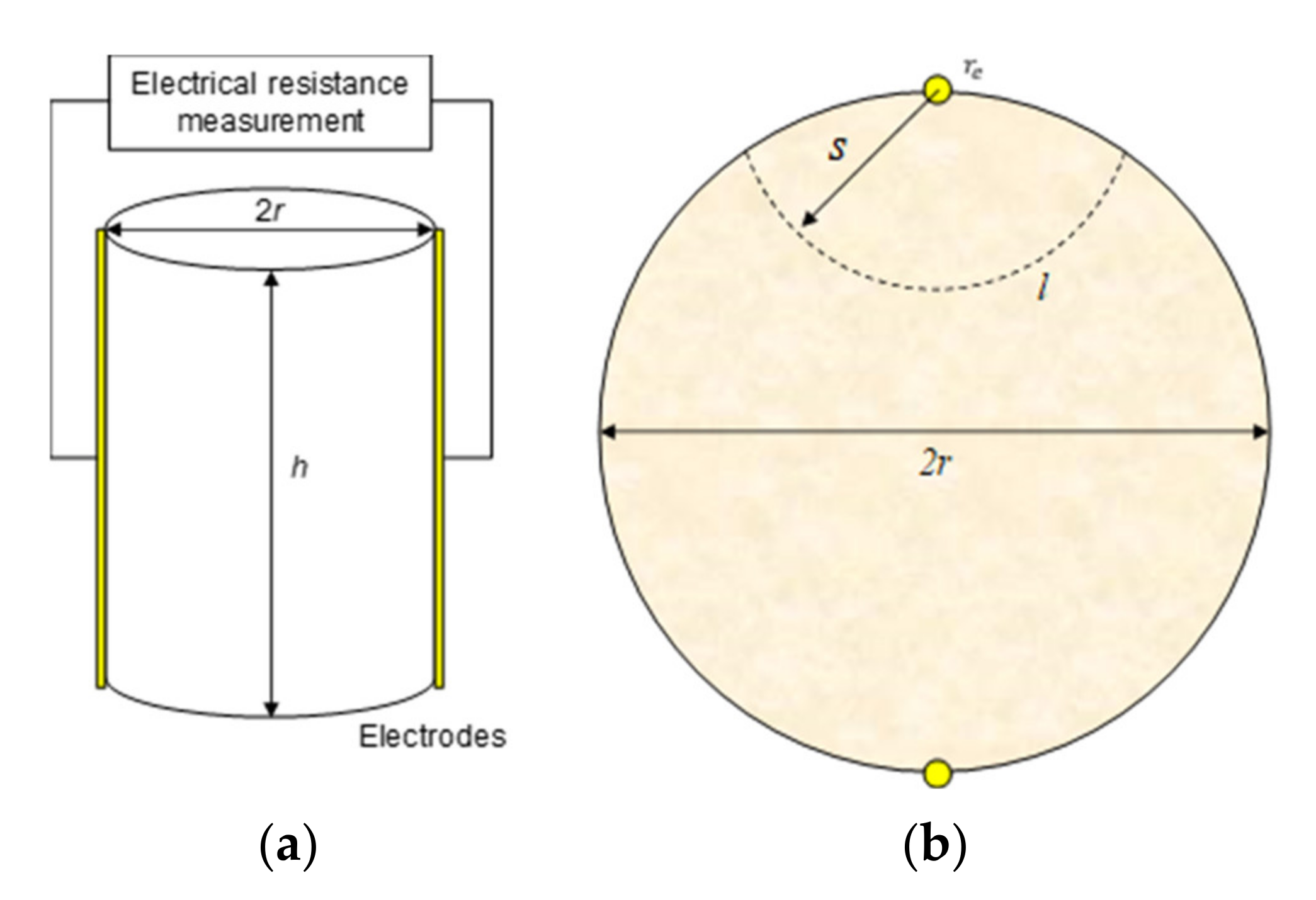
2.2. Electrical Resistivity Measurement with Two Perimeter Electrodes
3. Numerical Simulation
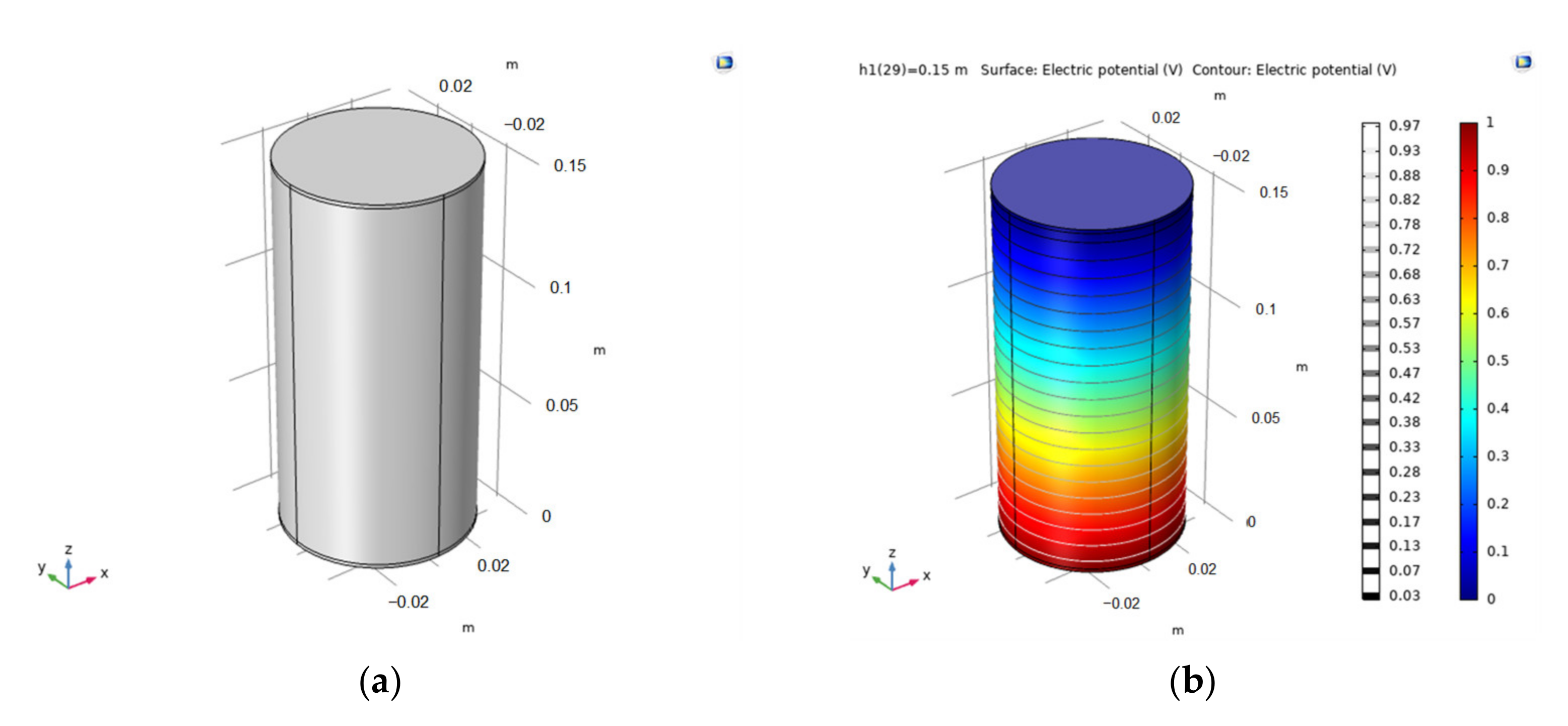
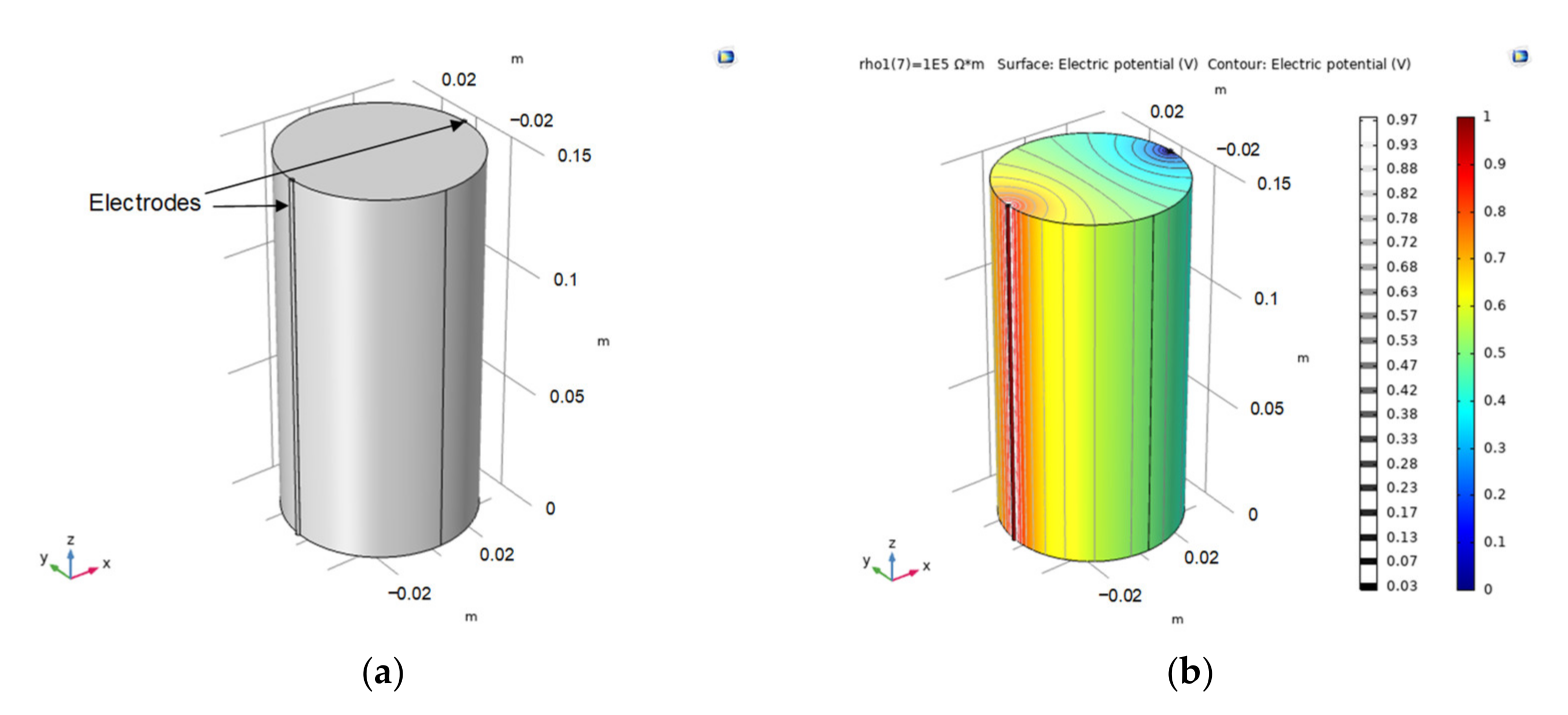
3.1. Simulation Setup
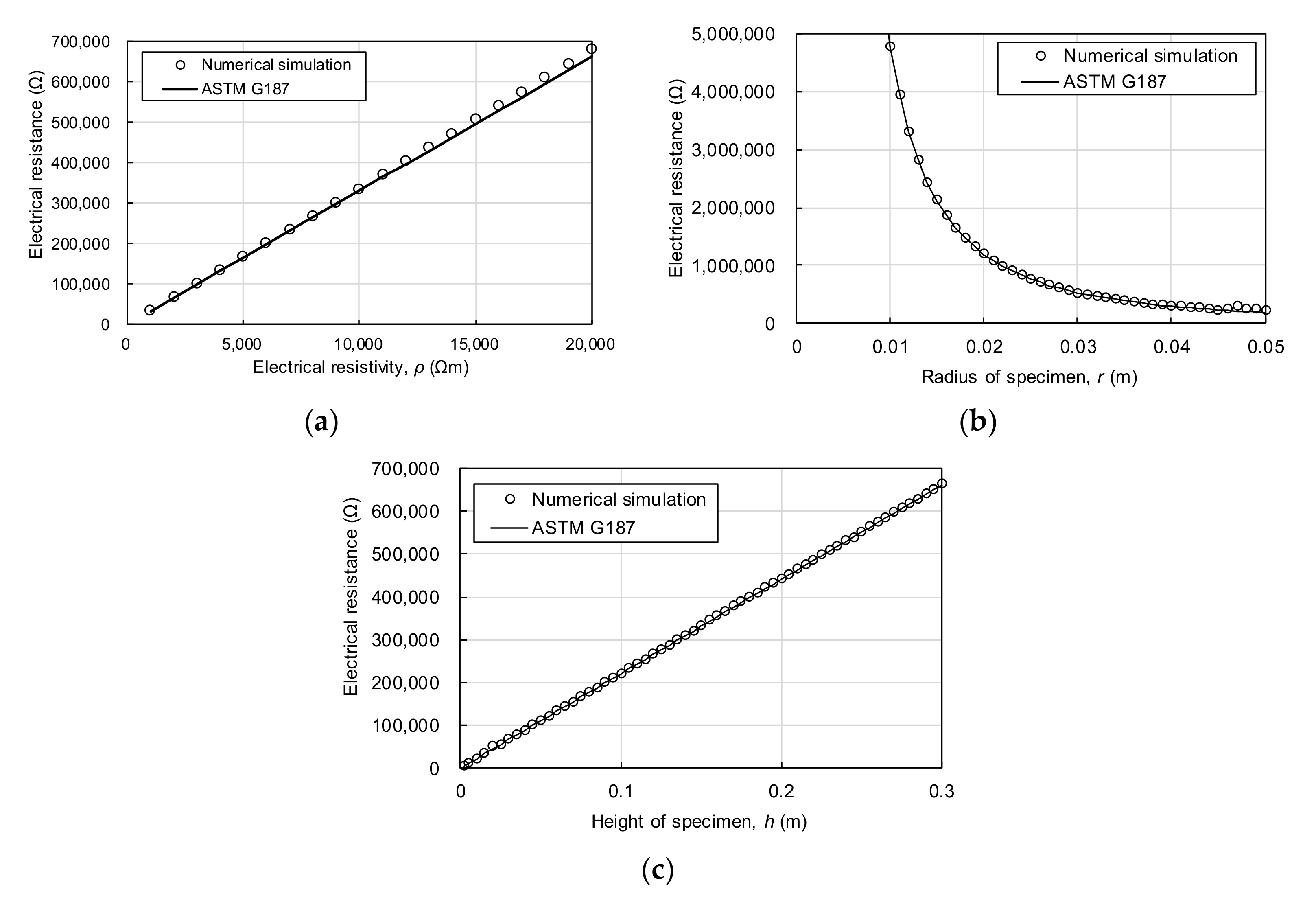
3.2. Verification of the Numerical Simulation Tool with ASTM G187
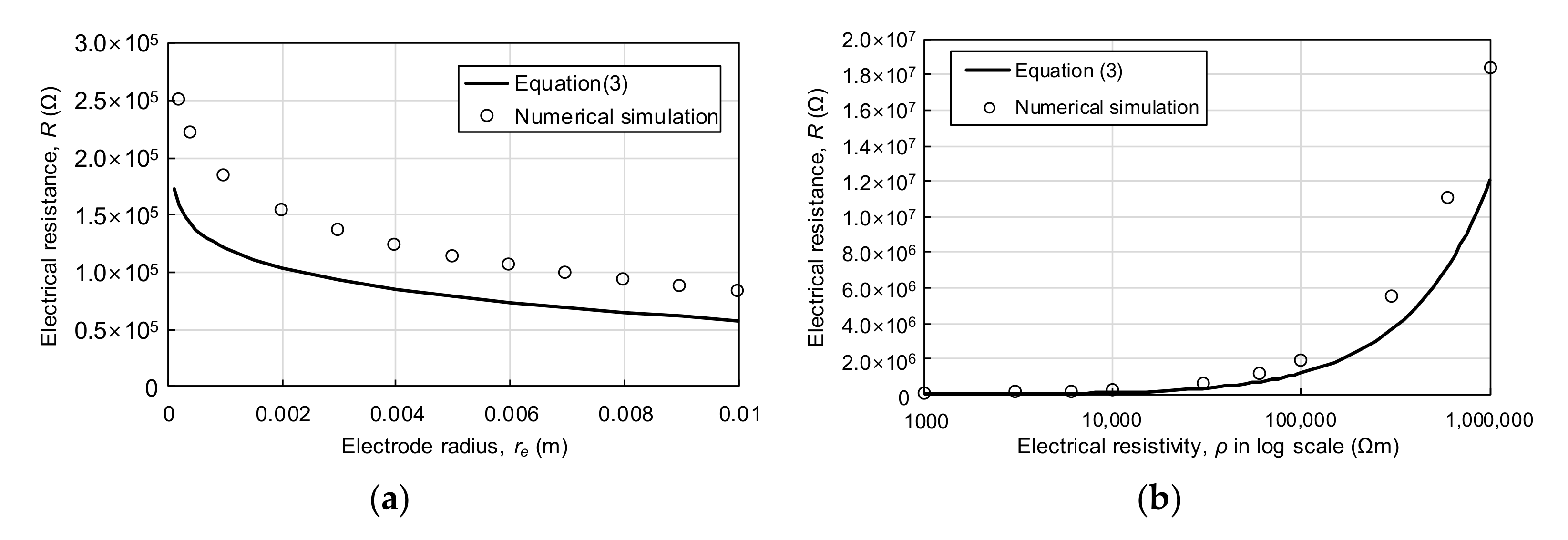
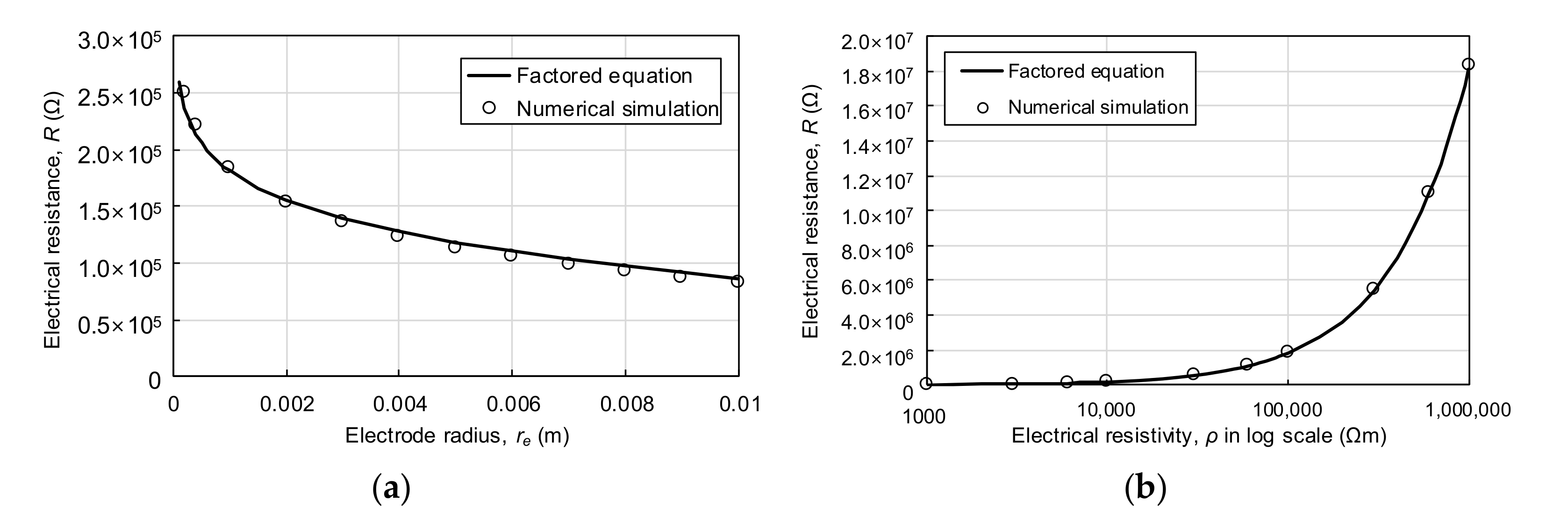
3.3. Verification of the Proposed Method
4. Discussion
4.1. Distortion of the Equipotential Surface
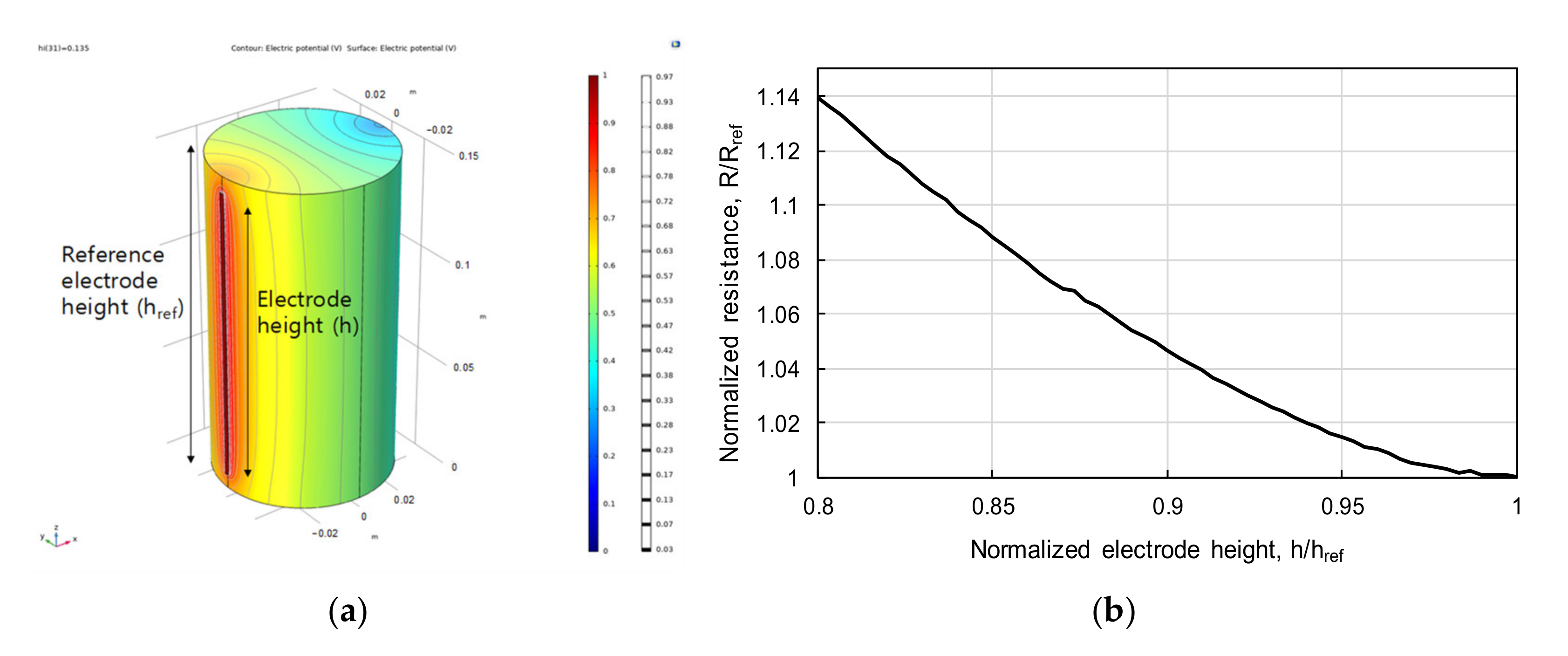
4.2. Effect of Electrode Length
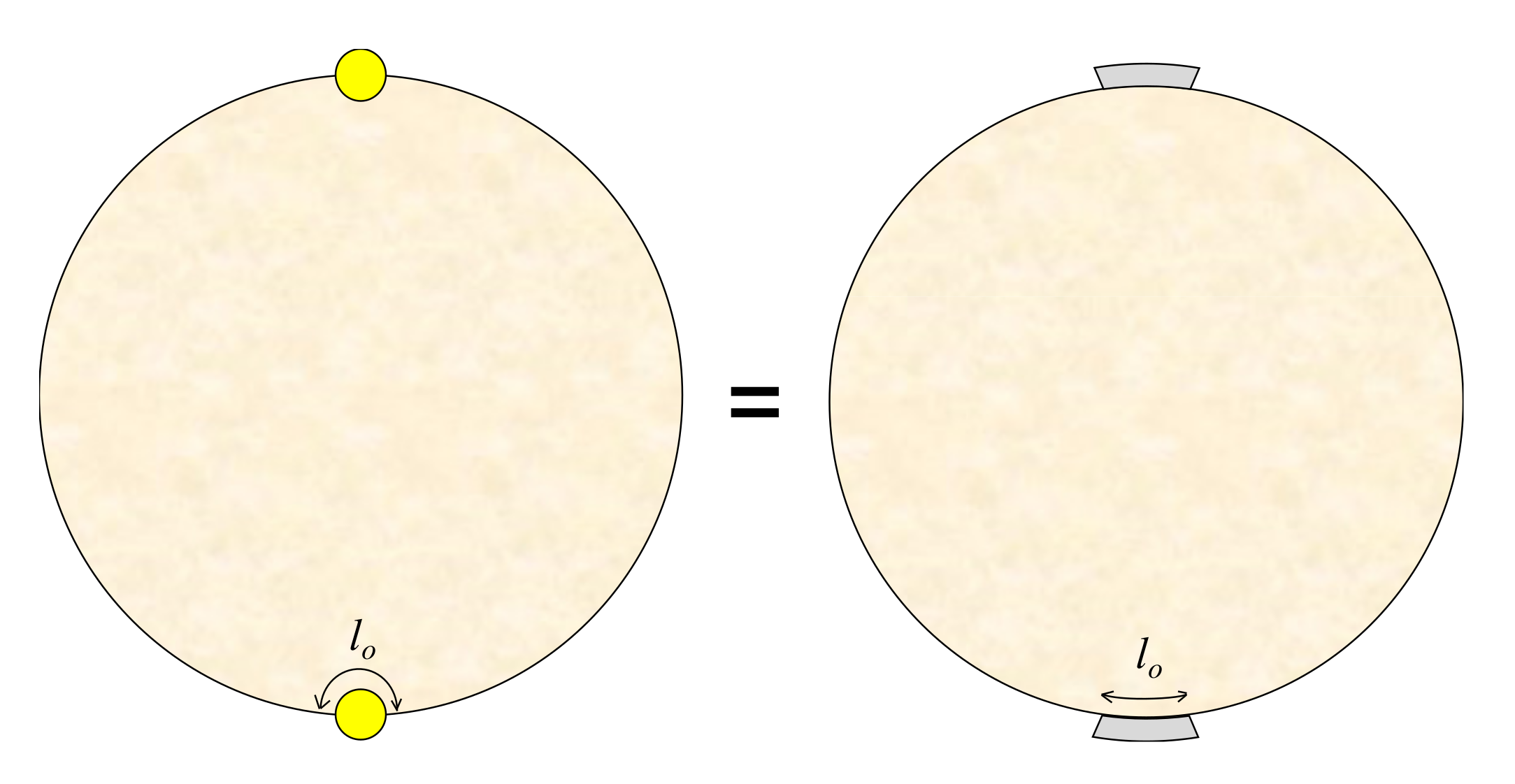
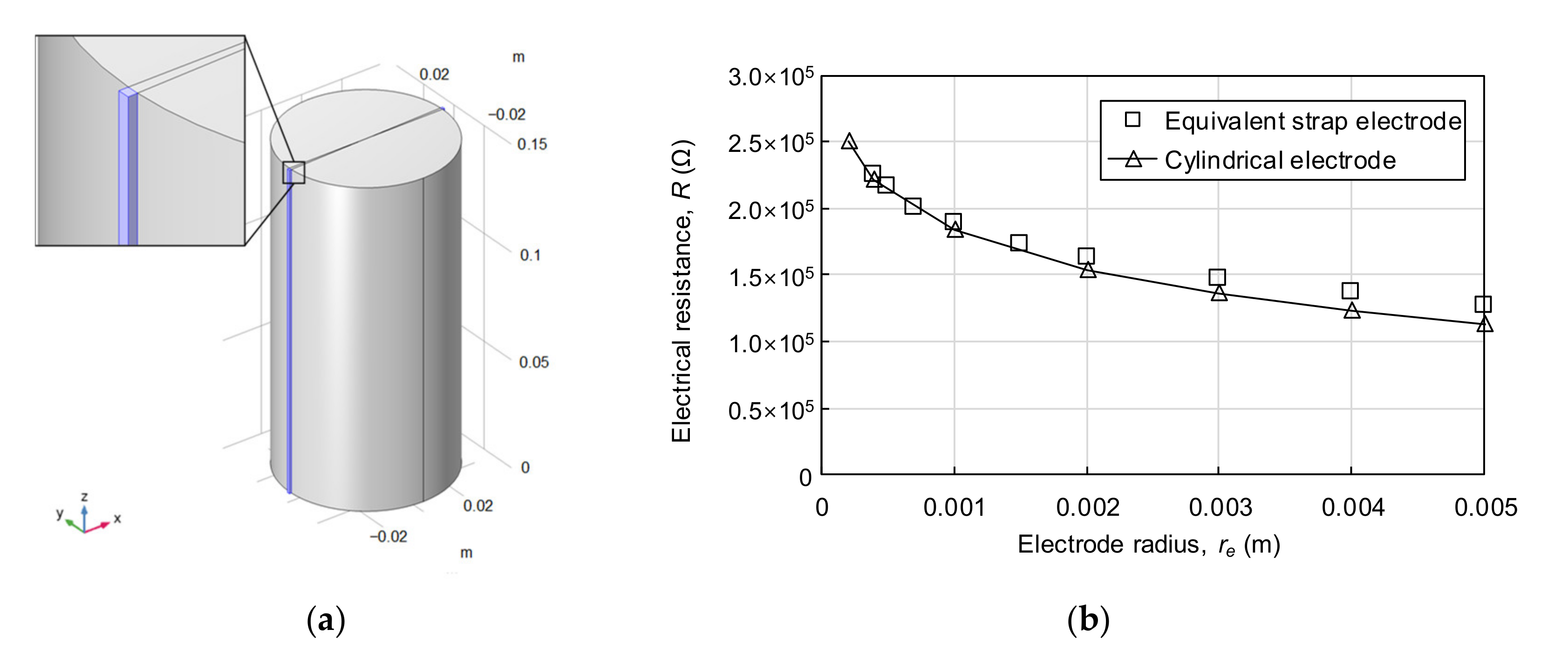
4.3. Equivalent Strap Electrode
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| αp | Geometric factor between the cylindrical electrodes on the sample circumference |
| θ | cos−1(s/2r) |
| ρ | Electrical resistivity of the rock sample |
| h | Height of the sample |
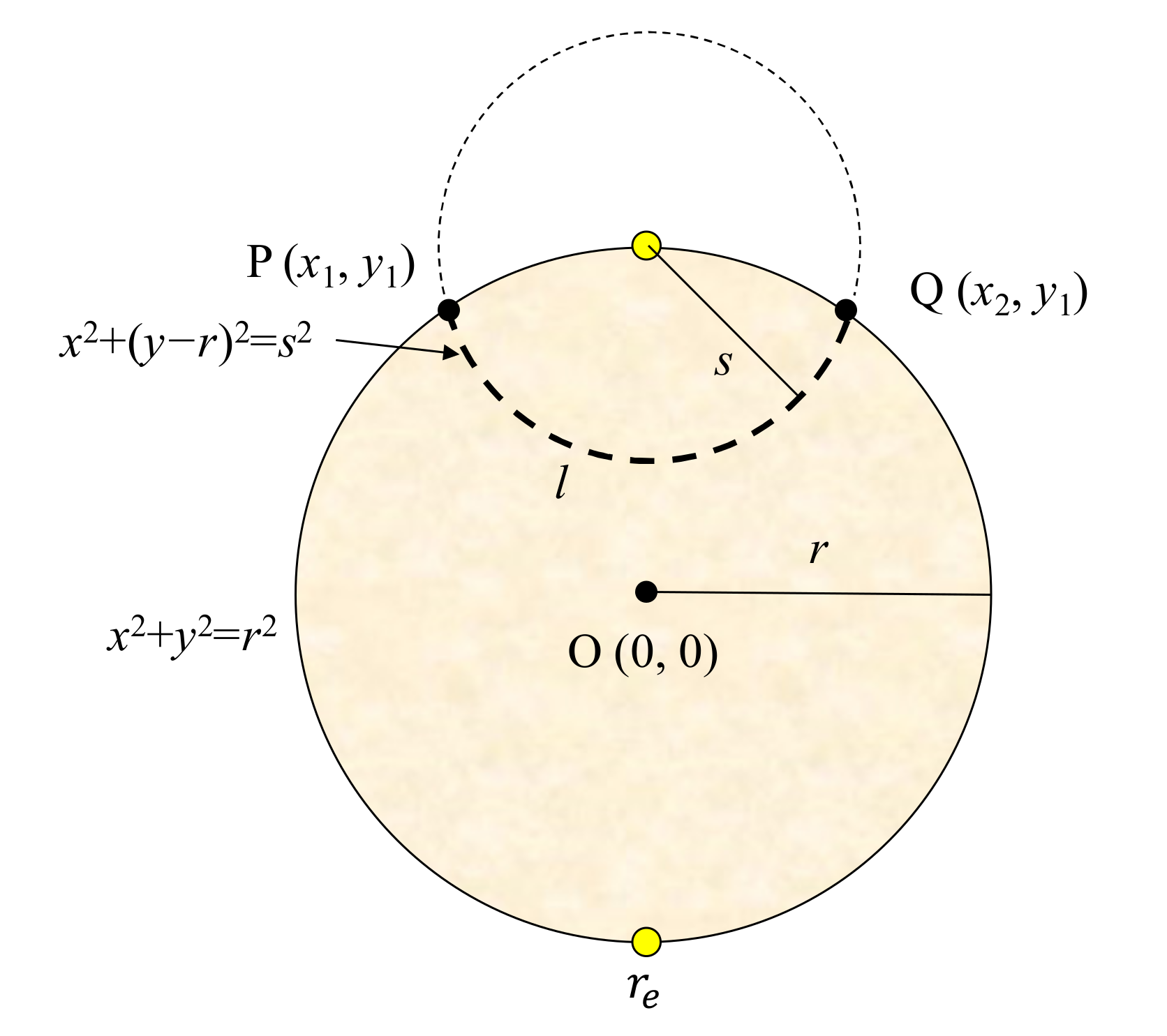
| l | Arc length of the curvature (derived in Appendix A.) |
| r | Radius of the sample |
| re | Radius of the electrodes |
| Rp | Electrical resistance between the cylindrical electrodes on the sample circumference |
| s | Distance from the electrode center to an arbitrary point on the sample circumference |
Appendix A. Derivation of l
References
- Zhou, X.Y.; Sun, D.; Tan, Y.; Zhou, A. Canister spacing in high-level radioactive nuclear waste repository. Ann. Nucl. Energy 2020, 141, 107335. [Google Scholar] [CrossRef]
- Yoon, S.; Jeon, J.S.; Kim, G.Y.; Seong, J.H.; Baik, M.H. Specific heat capacity model for compacted bentonite buffer materials. Ann. Nucl. Energy 2019, 125, 18–25. [Google Scholar] [CrossRef]
- Kim, A.R.; Kim, H.S.; Cho, G.C.; Lee, J. Estimation of model parameters and properties for numerical simulation on geomechanical stability of gas hydrate production in the Ulleung Basin, East Sea, Korea. Quat. Int. 2017, 459, 55–68. [Google Scholar] [CrossRef]
- Davarpanah, A.; Mirshekari, B.; Behbahani, T.J.; Hemmati, M. Integrated production logging tools approach for convenient experimental individual layer permeability measurements in a multi-layered fractured reservoir. J. Pet. Explor. Prod. Technol. 2018, 8, 743–751. [Google Scholar] [CrossRef] [Green Version]
- Brace, W.F.; Walsh, J.B.; Frangos, W.T. Permeability of Granite under High Pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Zhang, M.; Takahashi, M.; Morin, R.H.; Esaki, T. Evaluation and application of the transient-pulse technique for determining the hydraulic properties of low-permeability rocks—Part 1: Theoretical evaluation. Geotech. Test. J. 2000, 23, 83–90. [Google Scholar]
- Glover, P.W.J. A generalized Archie’s law for n phases. Geophysics 2010, 75, E247–E265. [Google Scholar] [CrossRef] [Green Version]
- Byun, Y.H.; Hong, W.T.; Yoon, H.K. Characterization of cementation factor of unconsolidated granular materials through TDR with variable saturated conditions. Materials 2019, 12, 1340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Griffiths, D.H. Application of electrical resistivity measurements for the determination of porosity and permeability in sand-stones. Geoexploration 1976, 14, 207–213. [Google Scholar] [CrossRef]
- Kirkby, A.; Heinson, G.; Krieger, L. Relating permeability and electrical resistivity in fractures using random resistor network models. J. Geophys. Res. Solid Earth 2016, 121, 1546–1564. [Google Scholar] [CrossRef] [Green Version]
- Hong, C.H.; Chong, S.H.; Cho, G.C. Theoretical study on geometries of electrodes in laboratory electrical resistivity measurement. Appl. Sci. 2019, 9, 4167. [Google Scholar] [CrossRef] [Green Version]
- Rekapalli, R.; Sarma, V.S.; Phukon, P. Direct resistivity measurements of core sample using a portable in-situ DC resistivity meter in comparison with HERT data. J. Geol. Soc. India 2015, 86, 211–214. [Google Scholar] [CrossRef]
- Du Plooy, R.; Lopes, S.P.; Villain, G.; Dérobert, X. Development of a multi-ring resistivity cell and multi-electrode resistivity probe for investigation of cover concrete condition. NDT E Int. 2013, 54, 27–36. [Google Scholar] [CrossRef]
- ASTM Standard G187. Standard Test Method for Measurement of Soil Resistivity Using the Two-Electrode Soil Box Method; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- COMSOL Multiphysics® v. 5.5. COMSOL AB, Stockholm, Sweden. Available online: www.comsol.com (accessed on 11 February 2021).
- Clement, R.; Bergeron, M.; Moreau, S. COMSOL Multiphysics modelling for measurement device of electrical resistivity in laboratory test cell. In Proceedings of the 2011 COMSOL Conference, Stuttgart, Germany, 13 October 2011. [Google Scholar]
- Butler, S.L.; Sinha, G. Forward modeling of applied geophysics methods using Comsol and comparison with analytical and laboratory analog models. Comput. Geosci. 2012, 42, 168–176. [Google Scholar] [CrossRef]
- Carmichael, R.S. Practical Handbook of Physical Properties of Rocks and Minerals; CRC Press: Boca Raton, FL, USA, 1988. [Google Scholar]
- Yan, W.; Hong, S.; Chaoshi, R. Optimum design of electrode structure and parameters in electrical impedance tomography. Physiol. Meas. 2006, 27, 291. [Google Scholar] [CrossRef] [PubMed]
- Malmivuo, J.; Plonsey, R. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Bera, T.K.; Chowdhury, A.; Mandai, H.; Kar, K.; Haider, A.; Nagaraju, J. Thin domain wide electrode (TDWE) phantoms for Electrical Impedance Tomography (EIT). In Proceedings of the 2015 Third International Conference on Computer, Communication, Control and Information Technology (C3IT), Hooghly, India, 7–8 February 2015. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-W.; Hong, C.-H.; Kim, J.-S.; Chong, S.-H. Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes. Energies 2021, 14, 4382. https://doi.org/10.3390/en14144382
Kim J-W, Hong C-H, Kim J-S, Chong S-H. Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes. Energies. 2021; 14(14):4382. https://doi.org/10.3390/en14144382
Chicago/Turabian StyleKim, Ji-Won, Chang-Ho Hong, Jin-Seop Kim, and Song-Hun Chong. 2021. "Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes" Energies 14, no. 14: 4382. https://doi.org/10.3390/en14144382
APA StyleKim, J.-W., Hong, C.-H., Kim, J.-S., & Chong, S.-H. (2021). Theoretical and Numerical Study on Electrical Resistivity Measurement of Cylindrical Rock Core Samples Using Perimeter Electrodes. Energies, 14(14), 4382. https://doi.org/10.3390/en14144382





