Effects of Bent Outlet on Characteristics of a Fluidic Oscillator with and without External Flow
Abstract
:1. Introduction
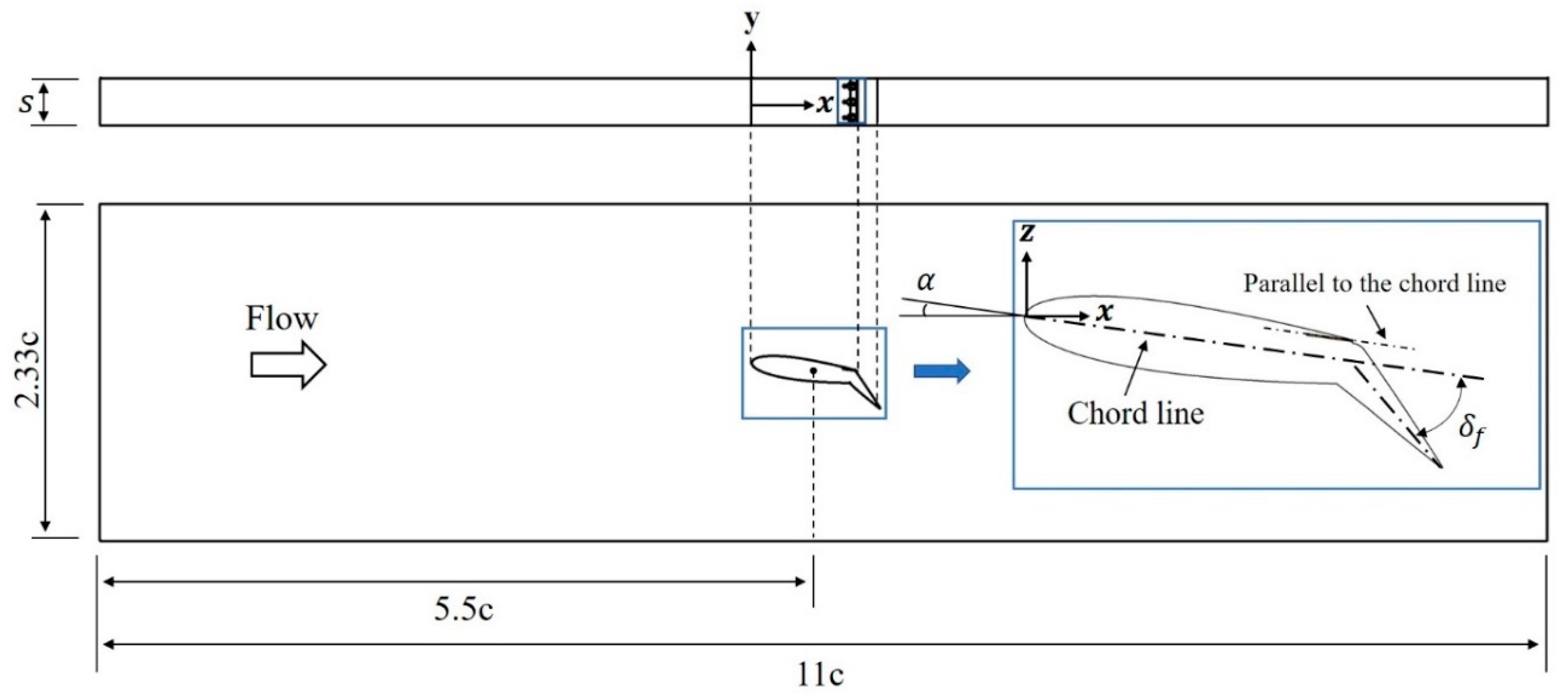
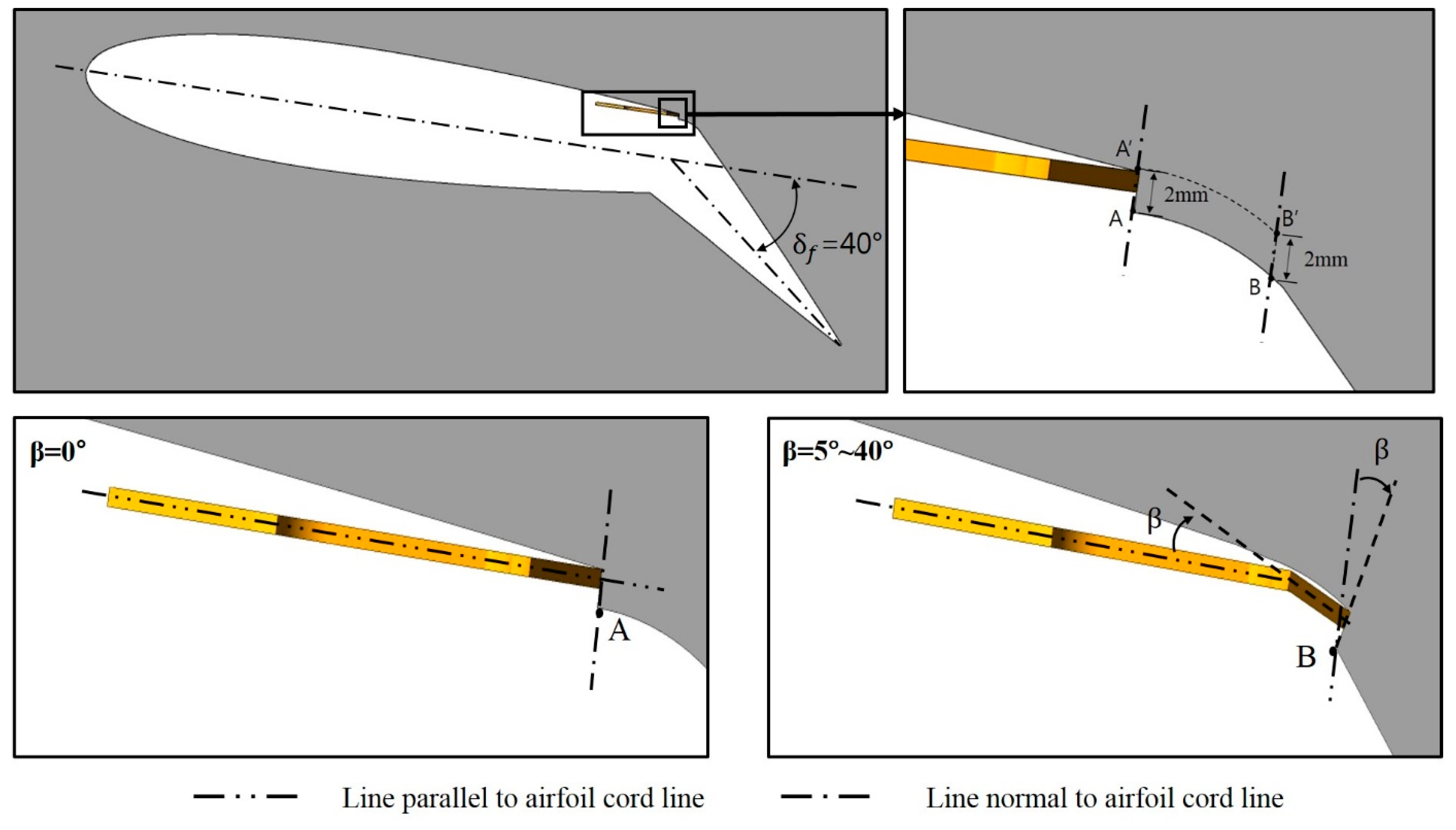
2. Fluidic Oscillator Model and Computational Domain
3. Performance Parameters
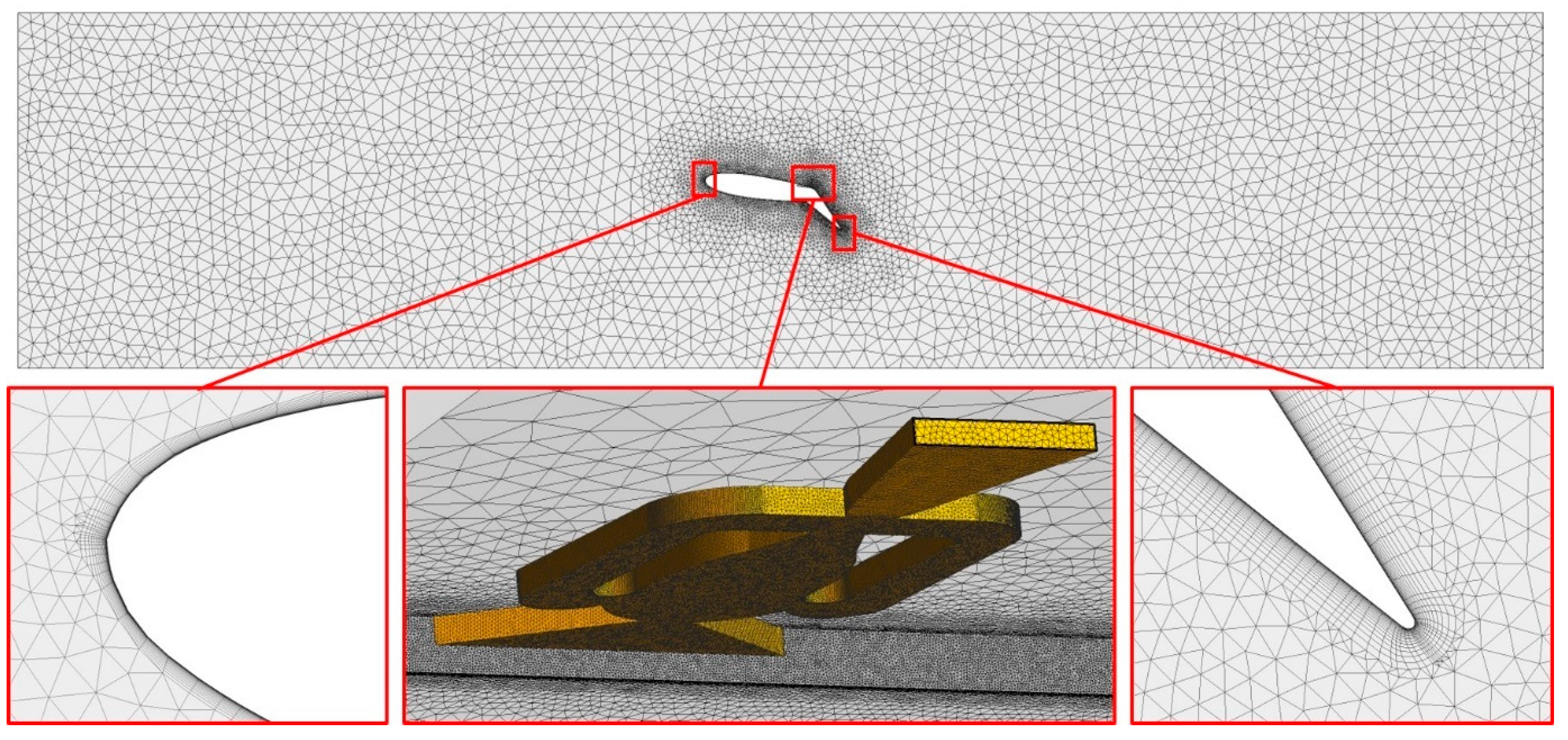
4. Numerical Analysis
5. Results and Discussion
5.1. Grid Conver
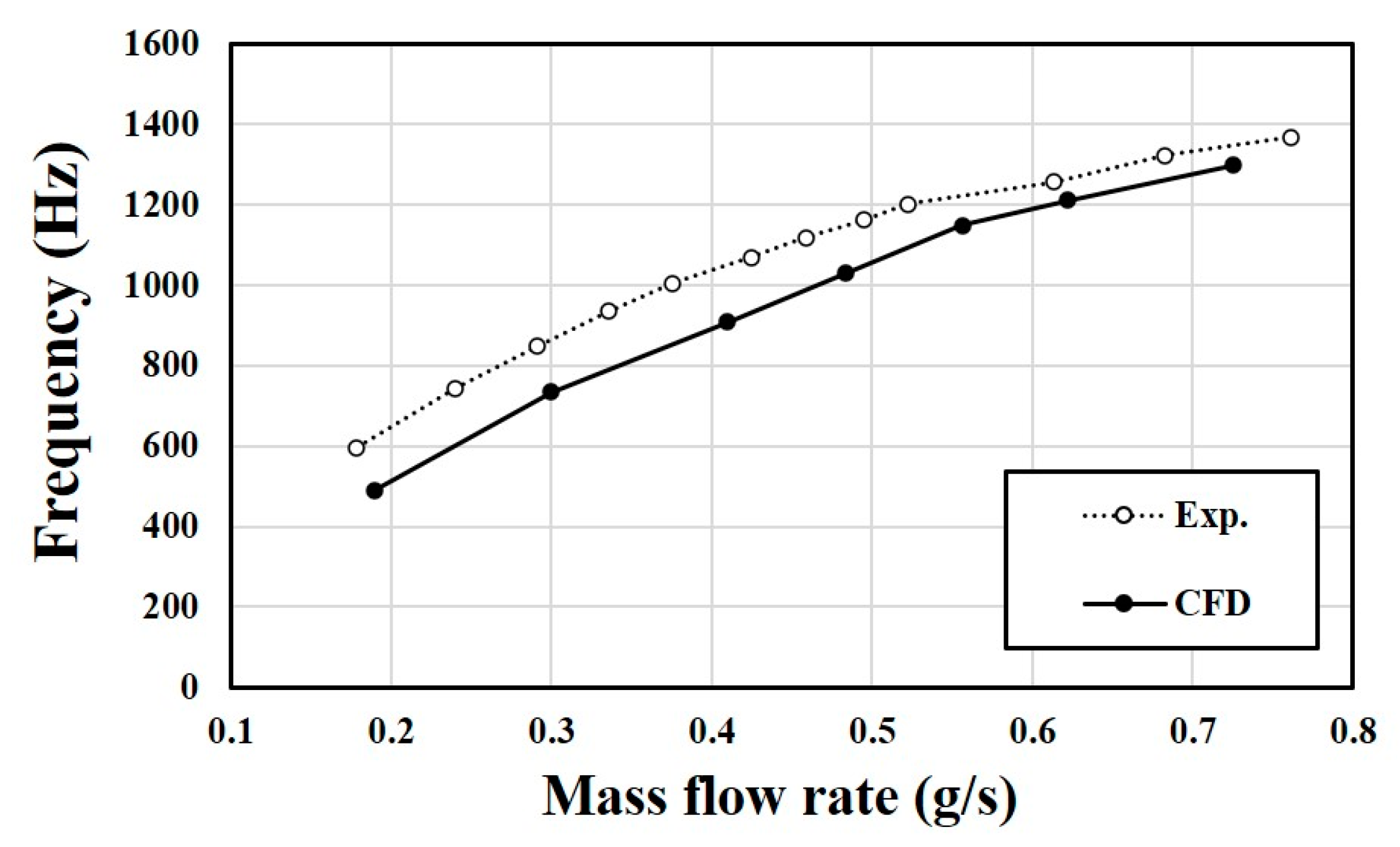
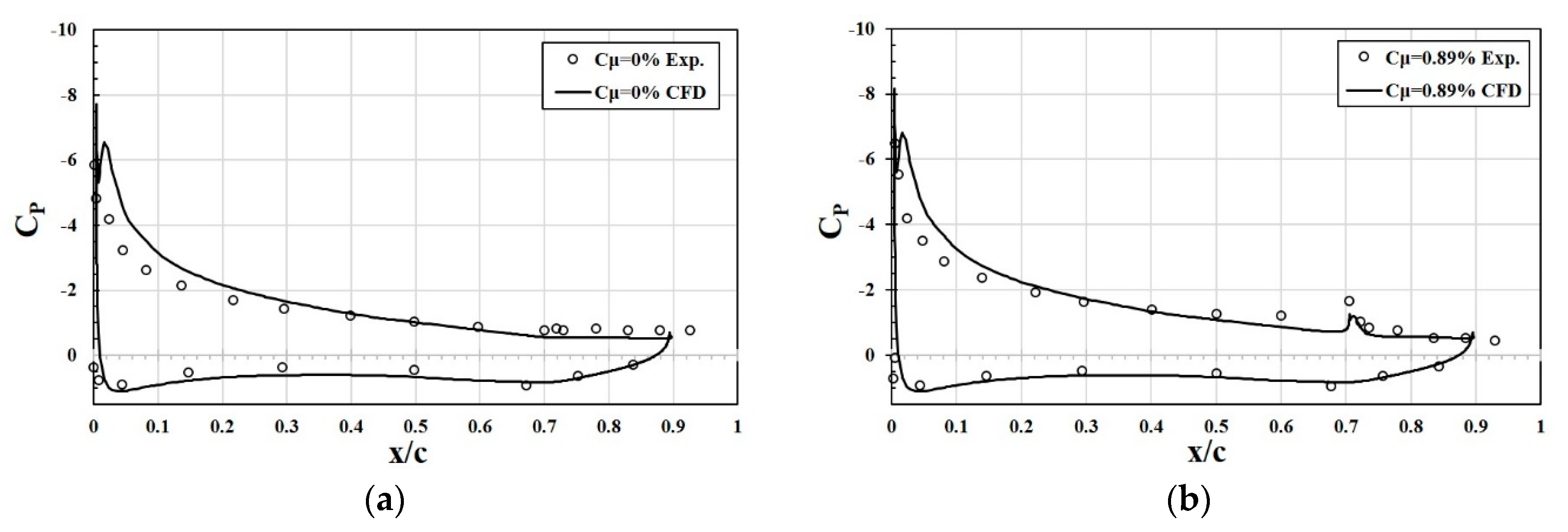
5.2. Validation of Numerical Results
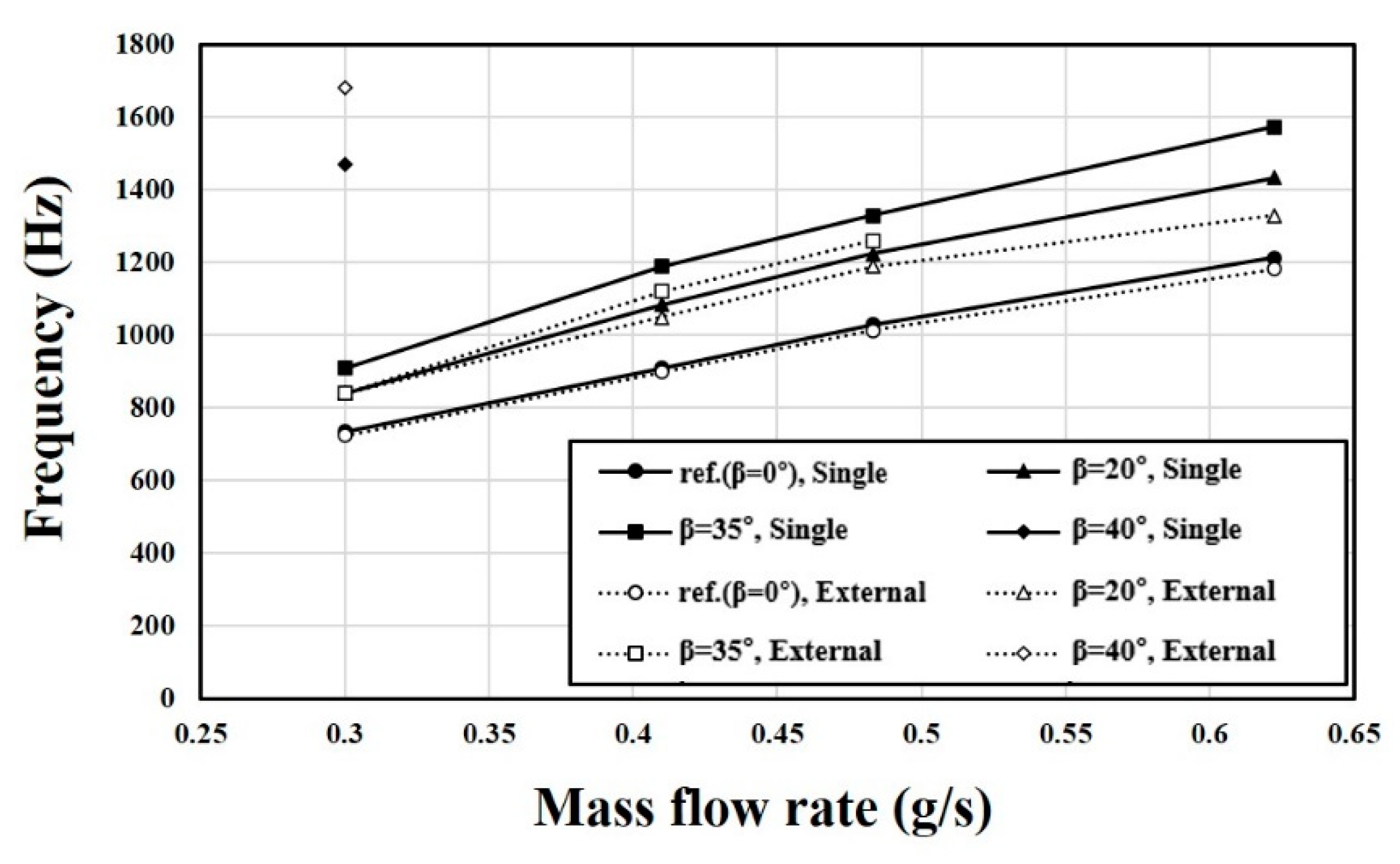
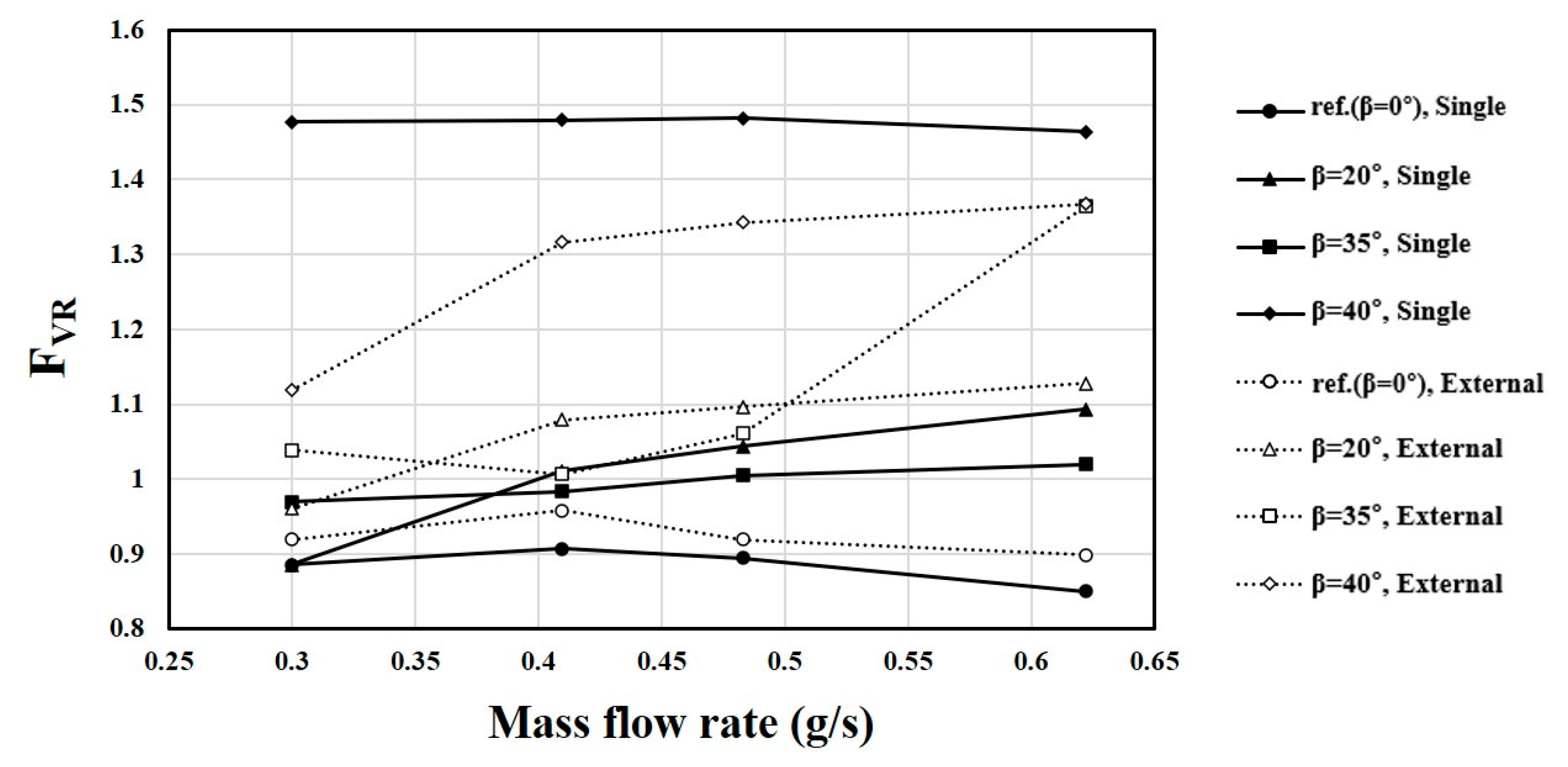
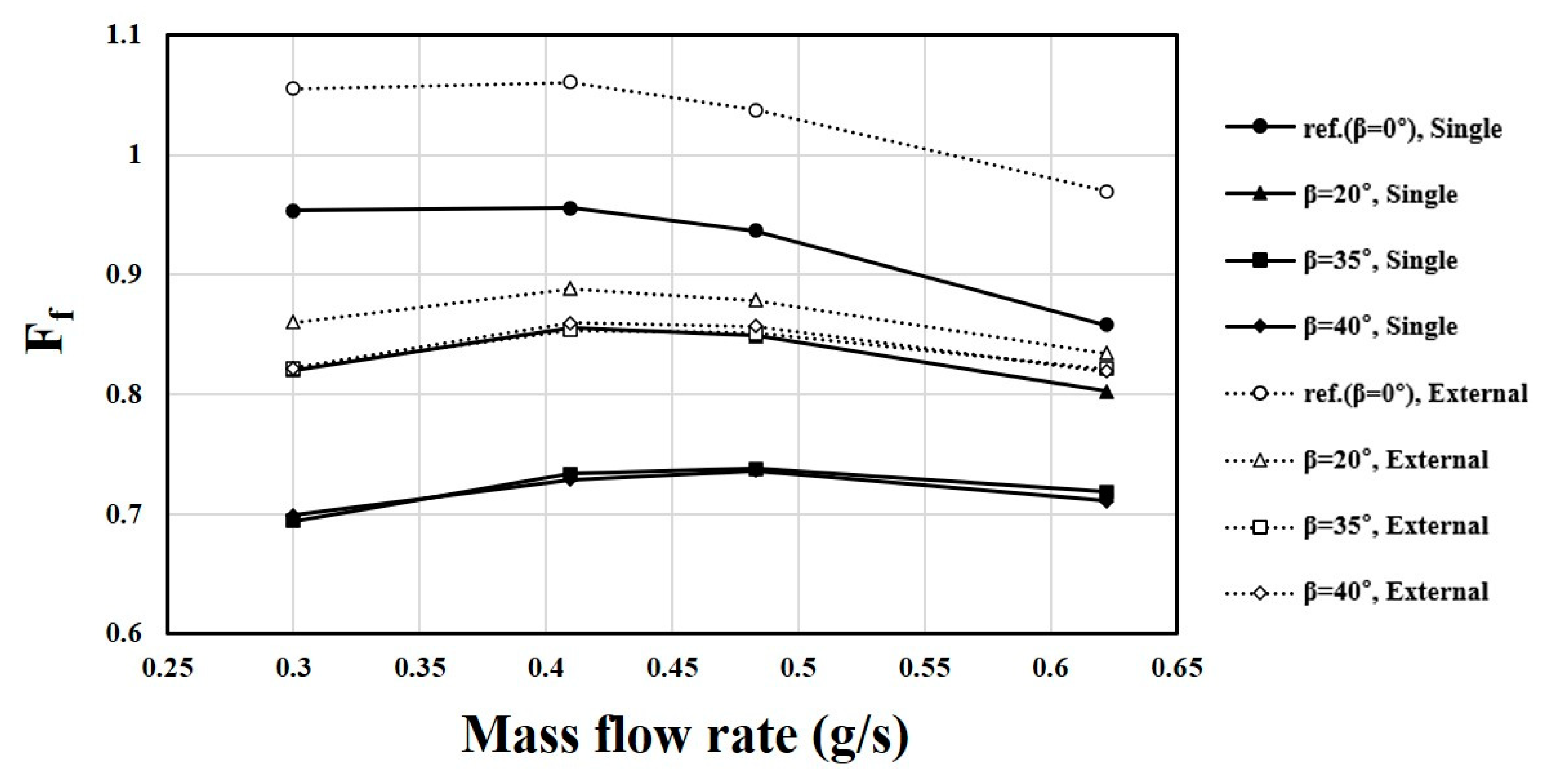
5.3. Single Fluidic Oscillator without External Flow
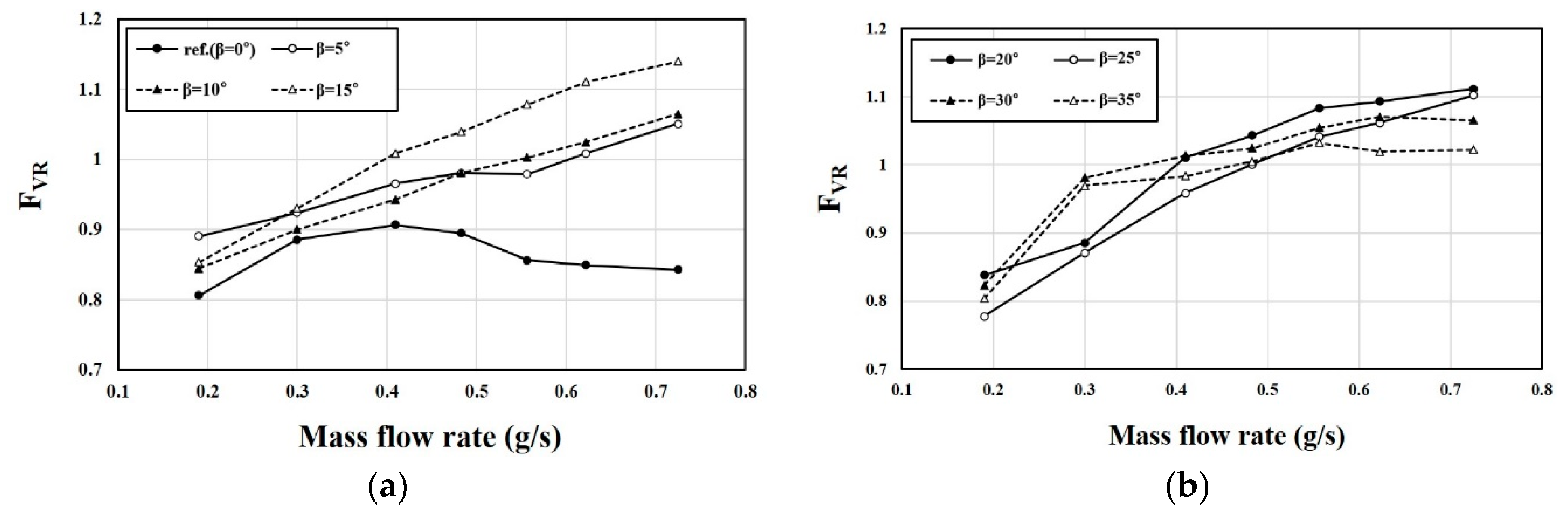
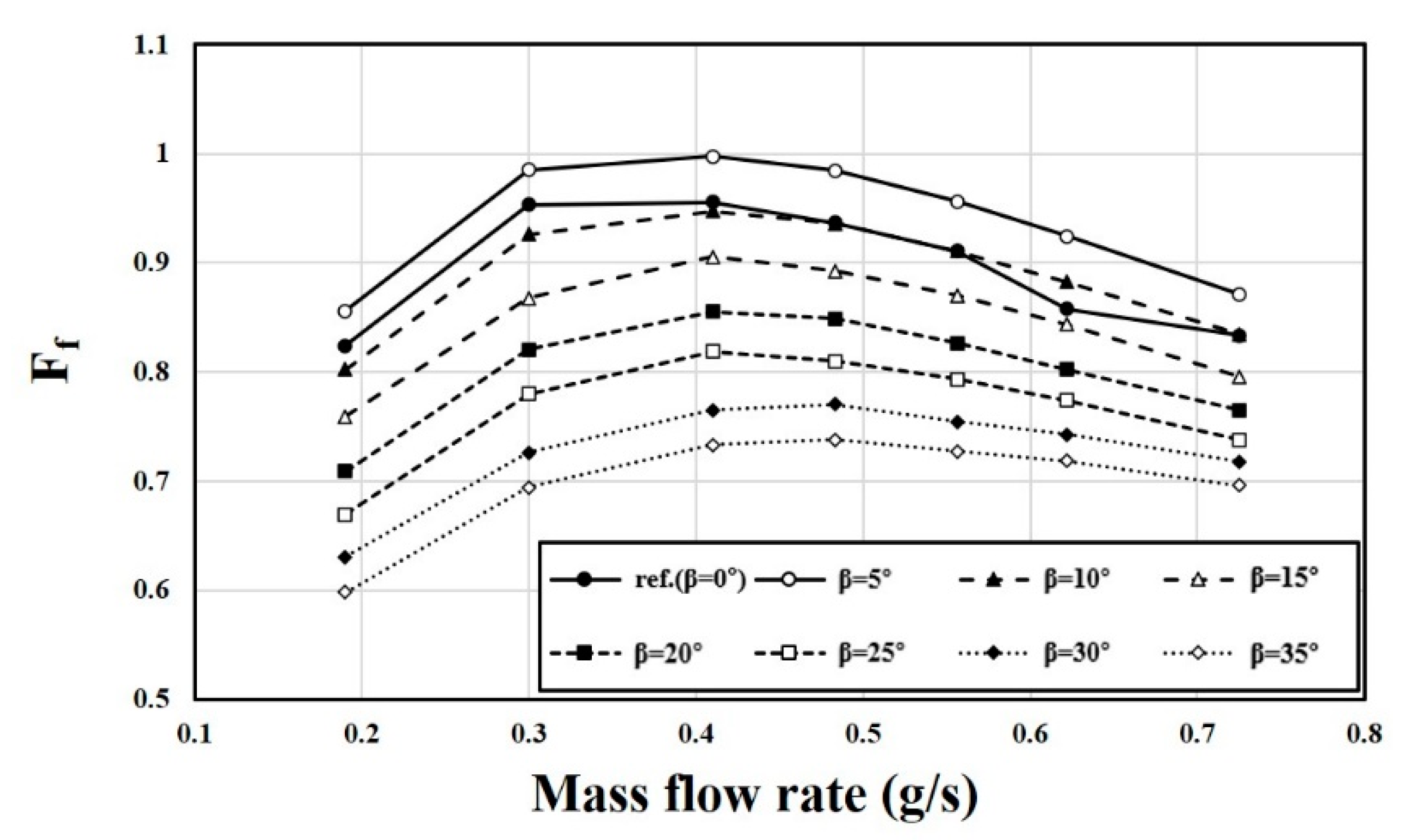
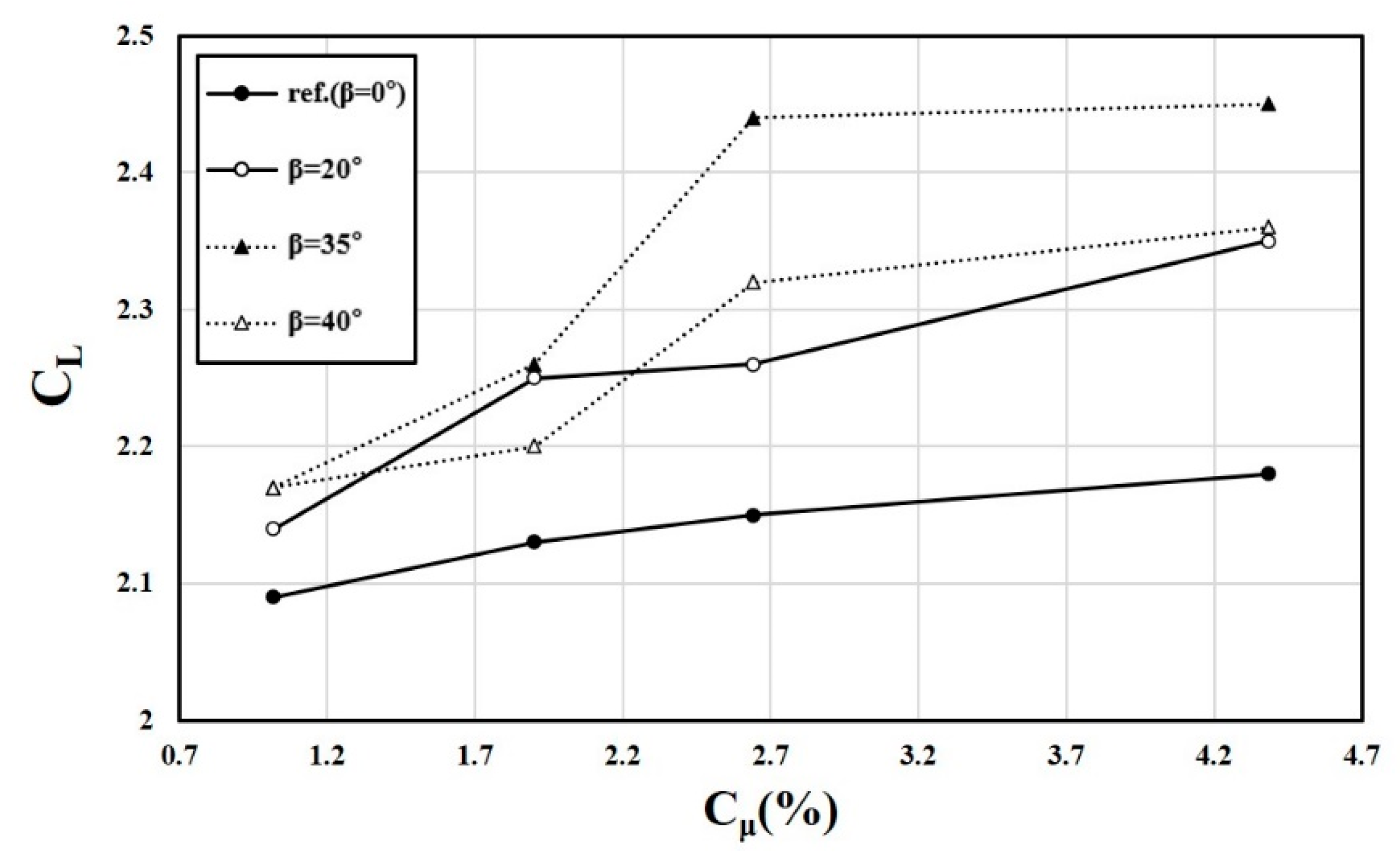
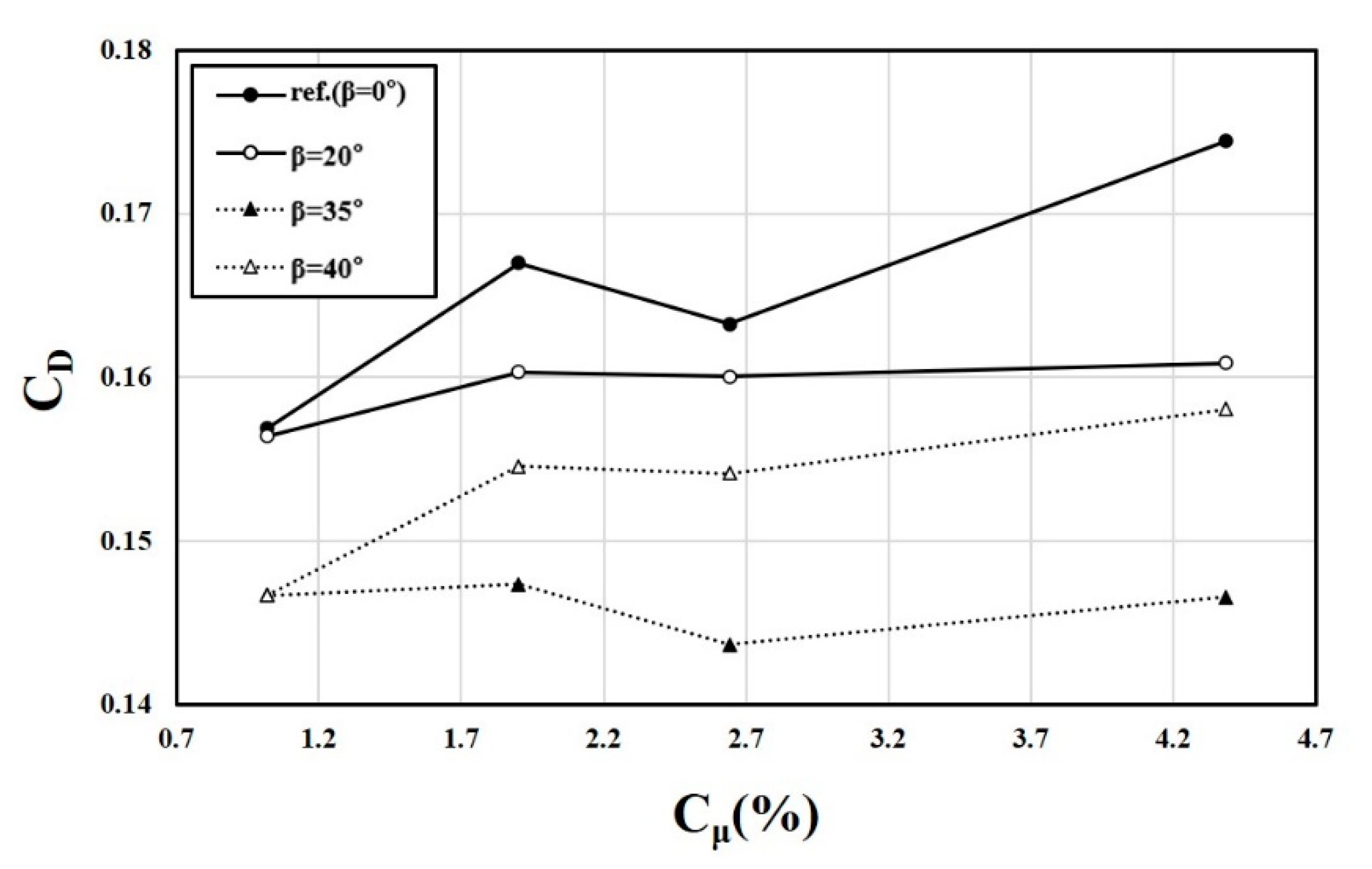
5.4. Effects of External Flow on the Characteristics of the Fluidic Oscillator
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tesar, V.; Zhong, S.; Rasheed, F. New fluidic-oscillator concept for flow-seperation control. AIAA J. 2013, 51, 397–405. [Google Scholar] [CrossRef]
- Gregory, J.; Tomac, M. A review of fluidic oscillator development and application for flow control. AIAA Pap. 2013, 2013–2474. [Google Scholar] [CrossRef]
- Cattafesta, L.N.; Sheplak, M. Actuators for active flow control. Annu. Rev. Fluid Mech. 2011, 43, 247–272. [Google Scholar] [CrossRef] [Green Version]
- Raman, G.; Raghu, S. Cavity resonance suppression using miniature fluidic oscillators. AIAA J. 2004, 42, 2608–2612. [Google Scholar] [CrossRef]
- Hossain, M.A.; Prenter, R.; Lundgreen, R.K.; Ameri, A.; Gregory, J.W.; Bons, J.P. Experimental and Numerical Investigation of Sweeping Jet Film Cooling. ASME J. Turbomach. 2018, 140. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Yu, S.; Zuo, L. Large eddy simulation analysis of the heat transfer enhancement using self-oscillating fluidic oscillators. Int. J. Heat Mass Transf. 2019, 131, 463–471. [Google Scholar] [CrossRef]
- Cerretelli, C.; Wuerz, W.; Gharaibah, E. Unsteady separation control on wind turbine blades using fluidic oscillators. AIAA J. 2010, 48, 1302–1311. [Google Scholar] [CrossRef]
- Feikema, D.; Culley, D. Computational fluid dynamic modeling of a fluidic actuator for flow control. AIAA Aerosp. Sci. Meet. Exhib. 2008, 1–13. [Google Scholar] [CrossRef]
- Seifert, A.; Greenblatt, D.; Wygnanski, I.J. Active separation control: An overview of Reynolds and Mach numbers effects. Aerosp. Sci. Technol. 2004, 8, 569–582. [Google Scholar] [CrossRef]
- Wen, X.; Liu, J.; Li, Z.; Peng, D.; Zhou, W.; Kim, K.C.; Liu, Y. Jet impingement using an adjustable spreading-angle sweeping jet. Aerosp. Sci. Technol. 2020, 105, 105956. [Google Scholar] [CrossRef]
- Al-Battal, N.H.; Cleaver, D.J.; Gursul, I. Unsteady actuation of counter-flowing wall jets for gust load attenuation. Aerosp. Sci. Technol. 2019, 89, 175–191. [Google Scholar] [CrossRef]
- Lei, J.; Zhang, J.; Niu, J. Effect of active oscillation of local surface on the performance of low Reynolds number airfoil. Aerosp. Sci. Technol. 2020, 99, 105774. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, W.; Li, C.; Ding, Q.; Wu, B. Application of flow control strategy of blowing, synthetic and plasma jet actuators in vertical axis wind turbines. Aerosp. Sci. Technol. 2019, 88, 468–480. [Google Scholar] [CrossRef]
- Lee, K.Y.; Chung, H.S.; Cho, D.H.; Sohn, M.H. Flow Separation Control Effects of Blowing Jet on an Airfoil. J. Korean Soc. Aeronaut. Space Sci. 2007, 35, 1059–1066. [Google Scholar] [CrossRef]
- Nagib, H.; Kiedaisch, J.; Reinhard, P.; Demanett, B. Control Techniques for Flows with Large Separated Regions: A New Look at Scailing Parameters. AIAA Pap. 2006, 2006–2857. [Google Scholar] [CrossRef]
- Koklu, M.; Owens, L.R. Flow Separation Control over a Ramp using Sweeping Jet Actuators. In Proceedings of the 7th AIAA Flow Control Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Jones, G.S.; Milholen, W.E.; Chan, D.T.; Melton, L.; Goodliff, S.L.; Cagle, C.M. A Sweeping Jet Application on a High Reynolds Number Semispan Supercritical Wing Configuration. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef] [Green Version]
- Melton, L.P.; Koklu, M.; Andino, M.; Lin, J.C. Active Flow Control via Discrete Sweeping and Steady Jets on a Simple-Hinged Flap. AIAA J. 2018, 56. [Google Scholar] [CrossRef]
- Seele, R.; Graff, E.; Lin, J.; Wygnanski, I. Performance enhancement of a vertical tail model with sweeping jet actuators. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Koklu, M. The Effects of Sweeping Jet Actuator Parameters on Flow Separation Control. AIAA J. 2018, 56, 100–110. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.-H.; Kim, K.-Y. Effects of Installation Conditions of Fluidic Oscillators on Control of Flow Separation. AIAA J. 2019, 57, 5208–5219. [Google Scholar] [CrossRef]
- Kim, S.-H.; Kim, K.-Y. Effects of installation location of fluidic oscillators on aerodynamic performance of an airfoil. Aerosp. Sci. Technol. 2020, 99, 105735. [Google Scholar] [CrossRef]
- Melton, L.P.; Koklu, M. Active Flow Control using Sweeping Jet Actuators on A Semi-Sapn Wing Model. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef] [Green Version]
- Melton, L.P.; Koklu, M.; Andino, M.; Lin, J.C.; Edelman, L. Sweeping Jet Optimization Studies. In Proceedings of the 8th AIAA Flow Control Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef] [Green Version]
- Ostermann, F.; Woszidlo, R.; Nayeri, C.; Paschereit, C.O. Experimental Comparison between the Flow Field of Two Common Fluidic Oscillator Designs. In Proceedings of the 53 rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; Volume 10, p. 6. [Google Scholar] [CrossRef]
- Jeong, H.S.; Kim, K.Y. Shape Optimization of a Feedback-Channel Fluidic Oscillator. Eng. Appl. Comput. Fluid Mech. 2017, 12, 169–181. [Google Scholar] [CrossRef] [Green Version]
- Pandey, R.J.; Kim, K.Y. Numerical Modeling of Internal Flow in A Fluidic Oscillator. J. Mech. Sci. Technol. 2018, 32, 1041–1048. [Google Scholar] [CrossRef]
- Pandey, R.J.; Kim, K.Y. Comparative Analysis of Flow in a Fluidic Oscillator Using Large Eddy Simulation and Unsteady Reynolds-Averaged Navier-Stokes Analysis. Fluid Dyn. Res. 2018, 50, 065515. [Google Scholar] [CrossRef]
- Kim, N.H.; Kim, K.Y. Flow control using fluidic oscillators on an airfoil with a flap. Eng. Appl. Comput. Fluid Mech. 2021, 15, 377–390. [Google Scholar] [CrossRef]
- Melton, L.P. Active Flow Separation Control on a NACA 0015 Wing using Fluidic Actuators. In Proceedings of the 7th AIAA Journal Flow Control Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- ANSYS. ANSYS CFX-Solver Theory Guide-Release 15.0; ANSYS Inc.: Canonsburg, PA, USA, 2014. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Bardina, J.E.; Huang, P.G.; Coakley, T.J. Turbulence Modeling Validation. AIAA Pap. 1997, 1997–2121. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]
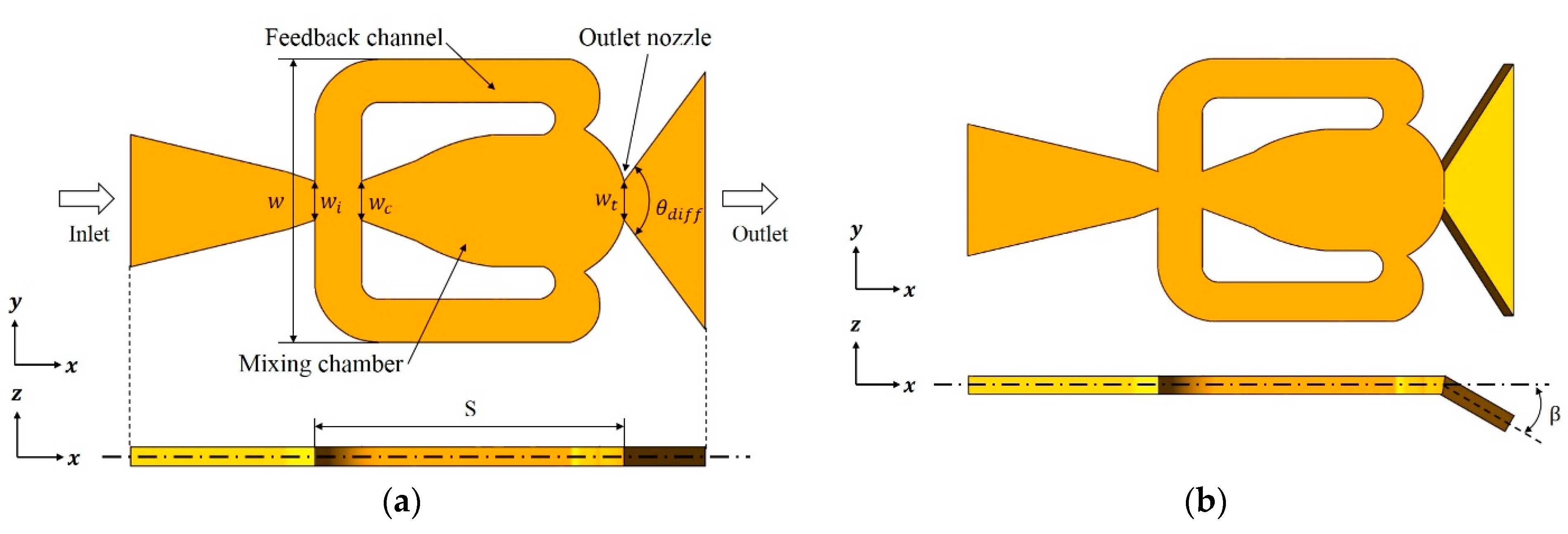



| Parameter | Value |
|---|---|
| Fluidic oscillator width, w (mm) | 14.3 |
| Inlet nozzle width, wi (mm) | 2.0 |
| Inlet chamber width, wc (mm) | 2.03 |
| Outlet throttle width, wt (mm) | 2.0 |
| Fluidic oscillator height, h (mm) | 1.0 |
| Inlet nozzle feedback channel width, (mm) | 2.41 |
| Diffuser angle of outlet nozzle, θdiff (°) | 107 |
| Distance between the inlet of mixing chamber and the throat, S(mm) | 15.6 |
| Parameter | Value | |
|---|---|---|
| Number of cells | N1/N2/N3 | 4.7 × 105/3 × 105/2.1 × 105 |
| Grid refinement factor | r | 1.3 |
| Computed jet frequencies corresponding to N1, N2, and N3 | f1 f2 f3 | 1298.7 1272.4 1176.5 |
| Apparent order | p | 4.93 |
| Extrapolated values | 1308.6 | |
| Approximate relative error | 2.025% | |
| Extrapolated relative error | 0.759% | |
| Grid-convergence index | 0.957% |
| Parameter | Value | |
|---|---|---|
| Number of cells | N1/N2/N3 | 3.8 × 106/3.1 × 106/2.6 × 106 |
| Grid-refinement factor | r | 1.3 |
| Computed lift coefficients (CL) corresponding to N1, N2, and N3 | CL1 CL2 CL3 | 2.135 2.147 2.198 |
| Apparent order | p | 5.51 |
| Extrapolated values | 2.131 | |
| Approximate relative error | 0.562% | |
| Extrapolated relative error | 0.188% | |
| Grid-convergence index | 0.072% |
| Angle of Attack (α) | Lift Coefficient | Relative Error (%) | |
|---|---|---|---|
| Experiment | CFD | ||
| 0 | 1.87 | 1.45 | 28.9 |
| 4 | 2.13 | 1.79 | 18.9 |
| 8 | 2.34 | 2.13 | 9.8 |
| 10 | 2.43 | 2.35 | 3.4 |
| 11 | 2.44 | 2.41 | 1.2 |
| 0.300 | 1.02 |
| 0.410 | 1.90 |
| 0.483 | 2.64 |
| 0.622 | 4.38 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, N.-H.; Kim, K.-Y. Effects of Bent Outlet on Characteristics of a Fluidic Oscillator with and without External Flow. Energies 2021, 14, 4342. https://doi.org/10.3390/en14144342
Kim N-H, Kim K-Y. Effects of Bent Outlet on Characteristics of a Fluidic Oscillator with and without External Flow. Energies. 2021; 14(14):4342. https://doi.org/10.3390/en14144342
Chicago/Turabian StyleKim, Nam-Hun, and Kwang-Yong Kim. 2021. "Effects of Bent Outlet on Characteristics of a Fluidic Oscillator with and without External Flow" Energies 14, no. 14: 4342. https://doi.org/10.3390/en14144342
APA StyleKim, N.-H., & Kim, K.-Y. (2021). Effects of Bent Outlet on Characteristics of a Fluidic Oscillator with and without External Flow. Energies, 14(14), 4342. https://doi.org/10.3390/en14144342







