Energy Dissipation during Surface Interaction of an Underactuated Robot for Planetary Exploration
Abstract
:1. Introduction
- formulation of a valuable method for a limited number of runs and enabling the separation of crucial energy loss factors inside the highly energetic actuator;
- providing valuable data of energy dissipation during surface interaction as a critical factor for decreasing path planning uncertainties for planetary hopping robots;
- demonstration of the performance of the actual prototype of a highly energetic actuator suitable for utilization in a proposed hopping system for exemplary lunar scenarios.
2. Research Outline
2.1. Hopter—The Case Study
- main platform: 6.5 kg;
- actuating legs: 2.5 kg;
- drive springs: 1.0 kg (whilst the mass of the drive springs divides equally between the main platform and actuating legs).
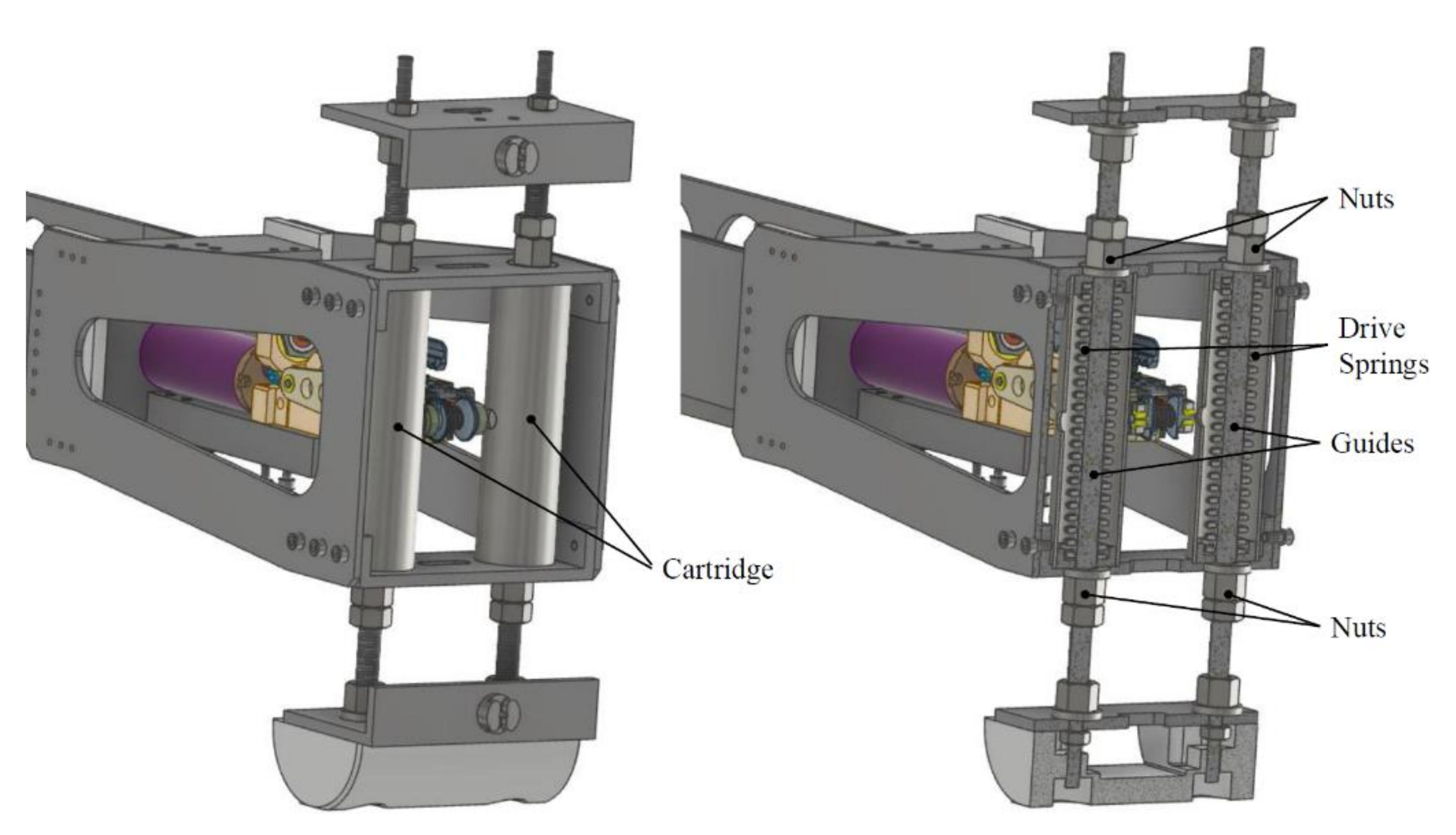
2.2. Design and Prototype of the Actuating Mechanism
- An active system, called the actuator, aims to control loading the potential energy in the suspension and allow it to release at the desired moment. It is described in Section 2.2.1.;
- A passive system of accumulation and releasing mechanical energy called suspension, where energy is accumulated in two compression drive springs in a configuration introduced here as the floating spring design and described in Section 2.2.2.;
- The outer structure of the actuating leg which remains in contact with the surface and protects the interior of the robot (not studied in this research).
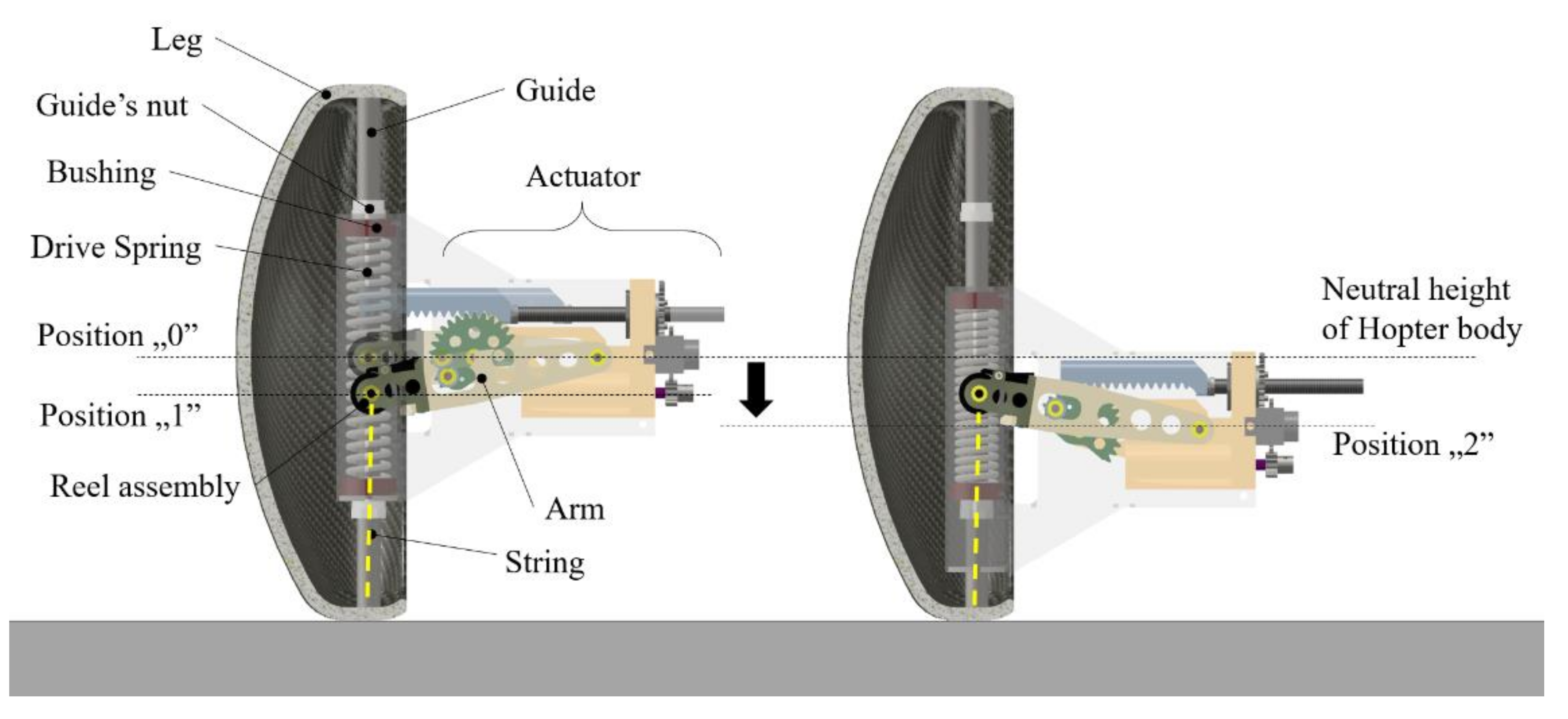
2.2.1. The Operational Sequence of the Actuator
- The arm is actuated through a gear and a ball screw. It is relocated from neutral (horizontal) position “0” downwards to the extreme position “1”. The string is locked in the reel assembly;
- The arm is moved upwards and pulls the leg against the drive springs through the string. Naturally, the legs rest on the ground; therefore, the main platform is being lowered to position “2”;
- Position “2” can be adjusted to tension the drive springs to the desired energy levels. Once it is reached, the reel assembly is ready to release the string, the main platform is accelerated upwards, and performs the jump.
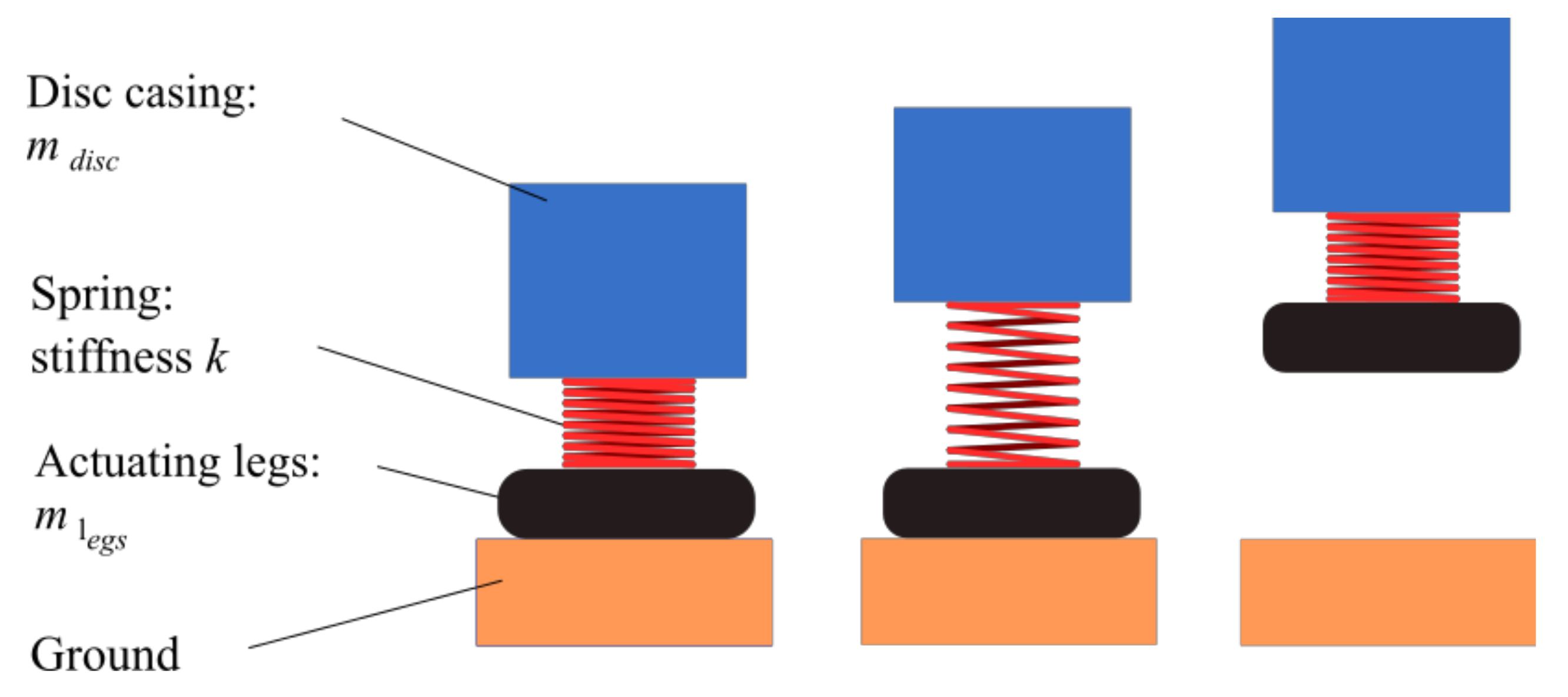
2.2.2. Actuating Leg Suspension with Drive Springs
2.2.3. Definition of Energies Occurring in the Actuating Mechanism and Jumping Process
3. Materials and Methods
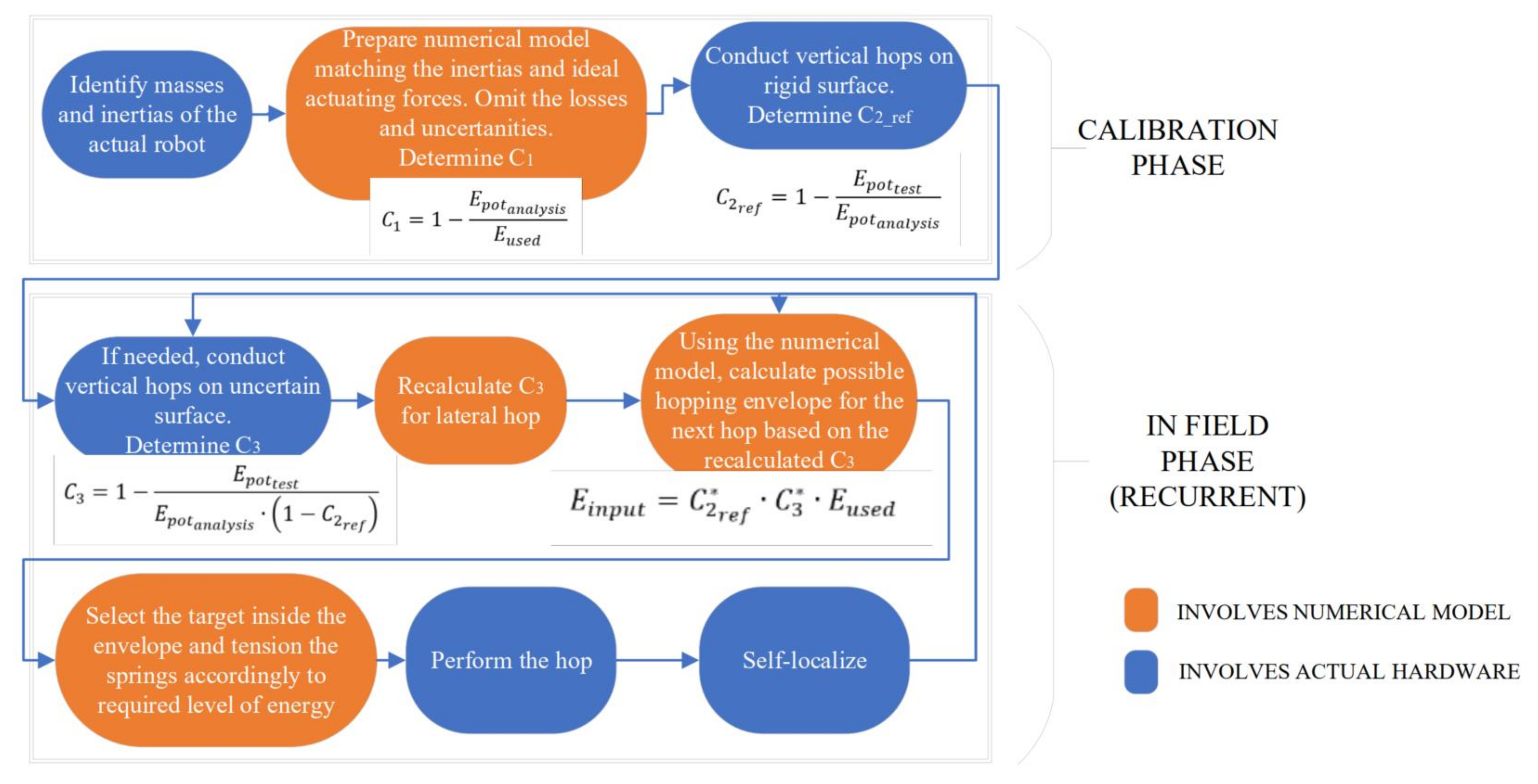
3.1. Objectives and Basic Methodology Description
- demonstrate the system’s functionality on the actual prototype, i.e., symmetrical actuation of the floating spring, actuating mechanism tensioning the actuating leg through a reel assembly and string system;
- validate the multibody analysis and confirm the assumed dynamics of the system;
- identify the percent of energy dissipated or lost in the actuating mechanism;
- identify the percent of energy dissipation in contact with the surface to narrow down the hopping uncertainties;
- eventually, demonstrate how the method translates to errors of the performance predictions of the 1-D system utilizing the identified coefficients as simple scaling factors in the control loop.
- the energy losses due to atmospheric drag are considered negligible. They are part of loss energy Eloss as defined in Table 1 and are not concerned at this level of detail in this research;
- the tests are unidirectional, and the primary focus is on dissipation energy normal to the surface since they become a point of reference to other configurations which may be considered in the future. One set of tests was done for a configuration inclined by 20°, which is helpful to indicate the amount of energy dissipation when lateral forces occur in the vectorization of a 3-D system;
- the energy dissipation of surface interaction is a property of a pair of objects (i.e., surface material and actuating leg); therefore, various shapes and contact areas are studied.
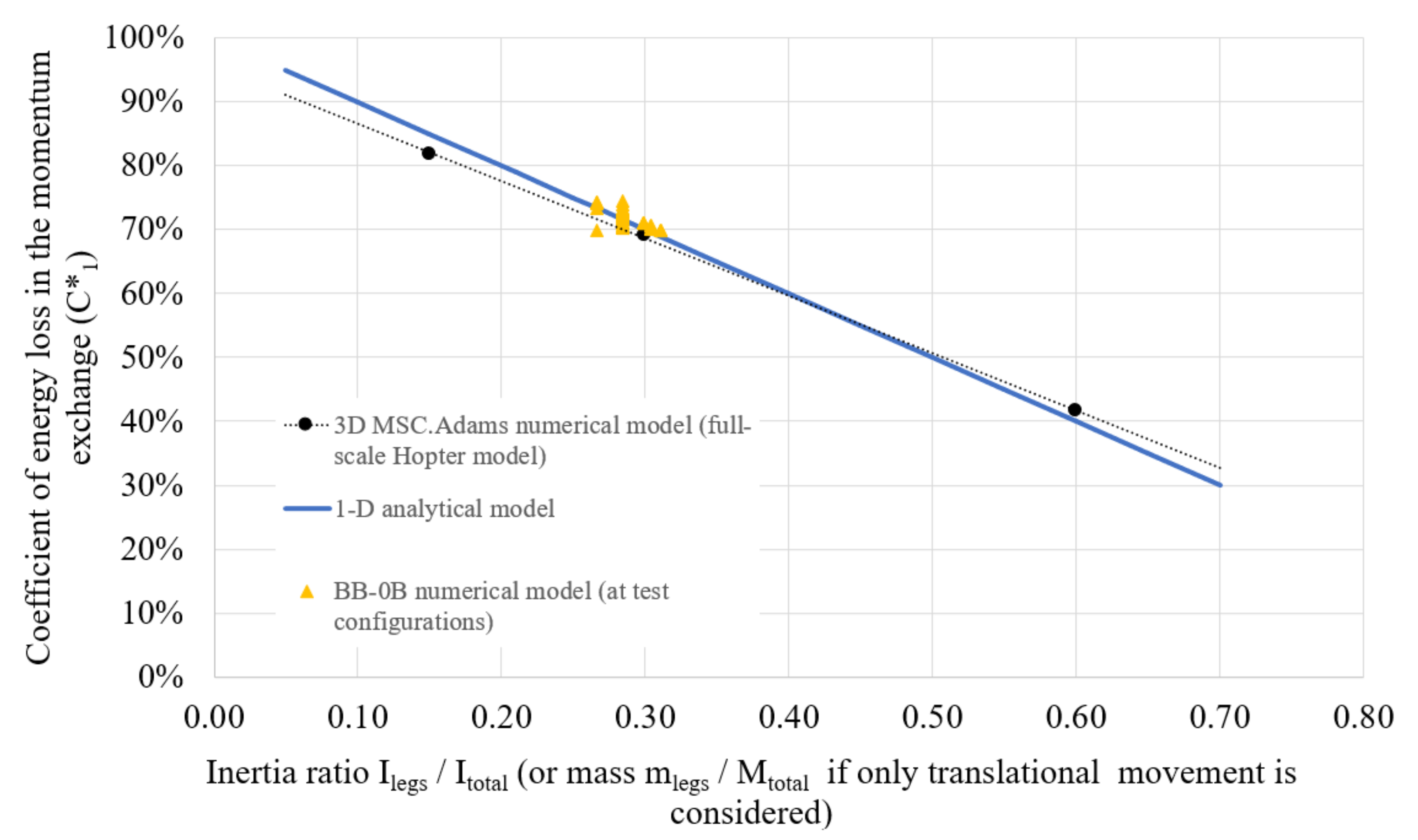
3.2. Cross-Validation of the Reference Models. Definition of Factor C1
3.3. The Theoretical Model of the Energy Losses in the System (Definition of Energy Loss Coefficients)
- Coefficient of energy loss in the momentum exchange (C1, also );
- Coefficient of energy loss in the mechanism’s friction (C2_ref, also ) It will come in handy later that C2_ref can be calculated against all trials (multiple runs) or for specific reference jumps done before jumping on non-solid surfaces. Therefore, we get: C2_ref_avarage or C2_ref_direct. Ideally, C2_ref_avarage and C2_ref_direct should be the same or close to each other, which would prove that the results of this approach are consistent;
- Coefficient of energy dissipation in the surface (C3, also ).
- can be maximized based on the analysis done in Figure 9;
- depends on the friction and design of the mechanism itself;
- depends on two factors: (1) properties of the surface which we can only control by navigating the robot through surfaces characterized by a high coefficient or (2) hypothetically by a design of the actuating leg (e.g., by increasing its surface-to-surface contact, which needs to be confirmed by tests).
- mass distribution of the components of the testbed and its configuration was recorded to match coefficient C1 properly;
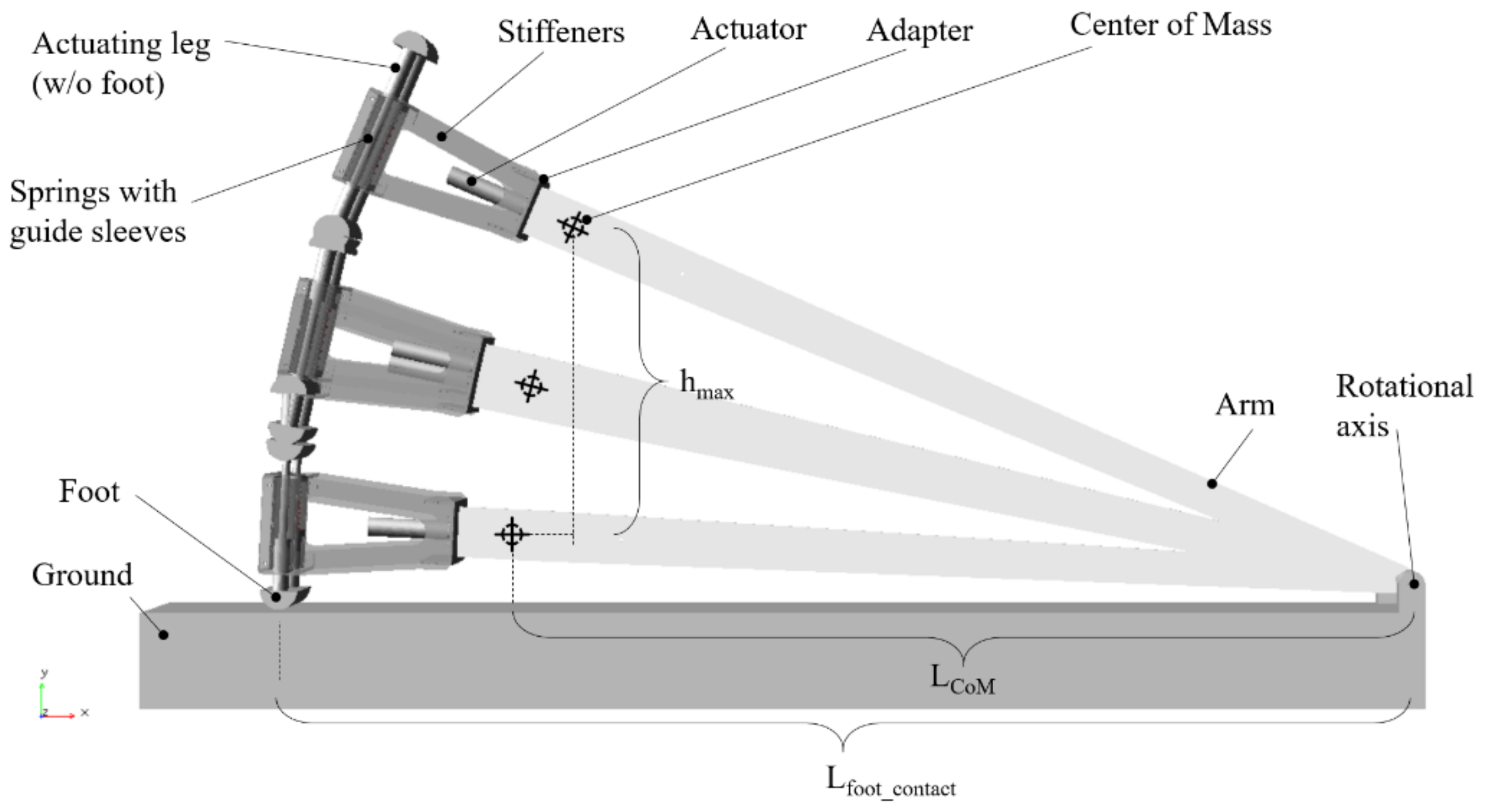
- measured and recorded compression of the springs from actuating mechanism for each test run. The distances were measured with a caliper, directly before the tensioning and then just before the jump; the calculated delta is dimension fused in Figure 7;
- initial compression of the springs from the weight of the system was calculated from a given stiffness constant and measured mass (M) of the device under test (distance fgrav in Figure 7);
- with the above measurements, total accumulated energy in the springs was established (Espr), their force (proper to determine load limits of the mechanism), and eventually the energy devoted to jump itself (Eused);
- height of jump of the center of mass in the numerical model ( and actual tests-bed () were monitored;
- the other parameters and coefficients are linked to Equations (2)–(4) and outlined in Appendix B.
3.4. Description of the BB-0B Test Set-Up and Test Plan
- Prepare the surface;
- Make sure the mechanism is aligned and free to move;
- Measure the initial distance between the foot and the body (initial state of the compression);
- Compress the springs to the desired energy (here in BB-0B, we always used the maximum compression, which allowed them to accumulate up to 24 J);
- Measure the final distance between the foot and the body and calculate the delta fused;
- Turn on a camera placed perpendicular to the actuation plane and point towards the center of mass (CoM) of the test set-up;
- Trigger the electromagnet to disarm the holding mechanism;
- The jump is performed;
- Stop recording and turn off the power supply after the movement is settled back.
- Configuration #0—actuating leg with a barefoot configuration where two steel rods finished with small, rounded nuts are in direct contact with a hard metallic surface. The steel-on-steel pair was chosen to ensure high rigidity between the surface and the actuating leg. Consequently, this one was used in the initial reference jumps to compare the analytical model since the energy dissipation on the rigid surface can be considered negligible.
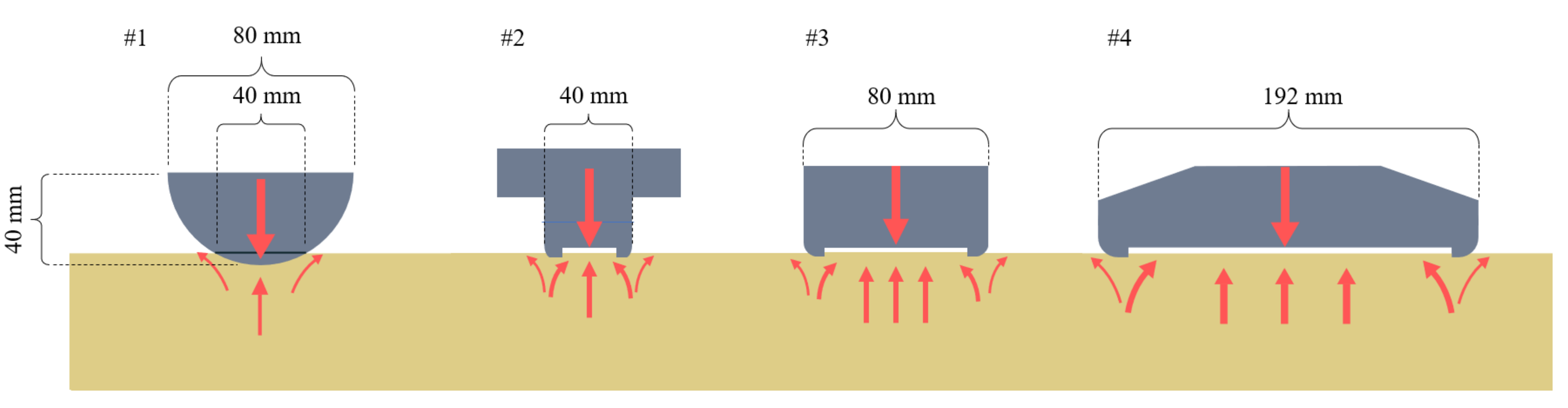
- Configuration #1—actuating leg with a rounded foot in the shape of a half-cylinder 134 mm long and with a radius of 40 mm. The effective contact area with quartz sand was measured to around 54 cm2.
- Configuration #2—actuating leg contact area like in configuration #1 (around 54 cm2), but with a flat footpad instead.
- Configuration #3—actuating leg with a flat surface contact area based on a width equivalent to the diameter of the round foot from configuration #1 (around 107 cm2).
- Configuration #4—actuating leg with a flat foot with a contact area significantly larger (here 4.8 times) than contact area from configuration #1 (around 257 cm2).
- Feet with flat surface contact areas (#2, #3, #4) were used to provide information on the scaling laws of dissipation coefficient against the contact areas;
- Round foot (#1) can be compared with small and medium feet (#2, #3), from which observations can be derived on drag coefficients depending on the shape of the foot;
- Round foot possesses the same contact with a surface regardless of the angle of actuation and therefore is used as a reference foot for comparison of performance between all types of regolith analogs and at tilted test.
- Syar sand, a Martian regolith analog, was selected due to its high cohesion typical for surfaces of Mars, Moon, and smaller celestial bodies;
- Quartz sand, contrary to Syar, the quartz sand is incohesive; selected because it provides a good reference which can be easily reproduced;
- Expanded clay, selected due to its mimic of lightweight and sharp edges;
- Quartz aggregate, selected due to their higher density in contrary to expanded clay.
3.5. Description of the MSC Adams Model for BB-0B
- The friction in the bearing of the main hinge (the rotational axis) was measured and is about 0.012 Nm. Therefore, energy losses are proven negligible at the angles measured during the test (less than 15° of the angular movement).
- The contact between the actuating leg and the surface and between the spring sleeves and the body part is defined with the following parameters: stiffness 105 N/mm and force exponent 2.2. It is considered a relatively rigid contact. The minimal damping factors were introduced only to reduce the numerical uncertainties in the analysis.
- The goal of the analysis is to determine the Ejump_total defined in Figure 7 to feed it in Equation (2), so we are looking for pure energy and assume the losses and dissipations are negligible as described previously in Section 3.3. The top position of the center of mass (hmax) was determined from the analysis and used to calculate the Ejump_total = Epot_analysis.
- In the numerical model, the spring displacement was constant (contrary to the actual model). Therefore, the preload and stiffness coefficient had to be adjusted each time for each run of the analysis to provide the released energy of Eused as described in Section 3.2. A minimal damping factor was added in the spring to eliminate numerical errors and allow the system to settle with time.
4. Results
- Validation of the coefficient C1 (efficiency of the system determined by the mass distribution) and confirmation of the applicability of the analysis model as described in Section 3.2;
- Determination of coefficient C2_ref (average losses of energies in the mechanism—e.g., friction—for reference jumps);
- Determination of coefficient C3 (factor of energy dissipation with the surface);
- Results for a relation between foot-pad geometries and energy dissipation;
- Implications of other observations that may impact the robot’s displacement strategies, i.e., rapid compaction of cohesive material below the hopping robot or probing the surface before taking a large leap;
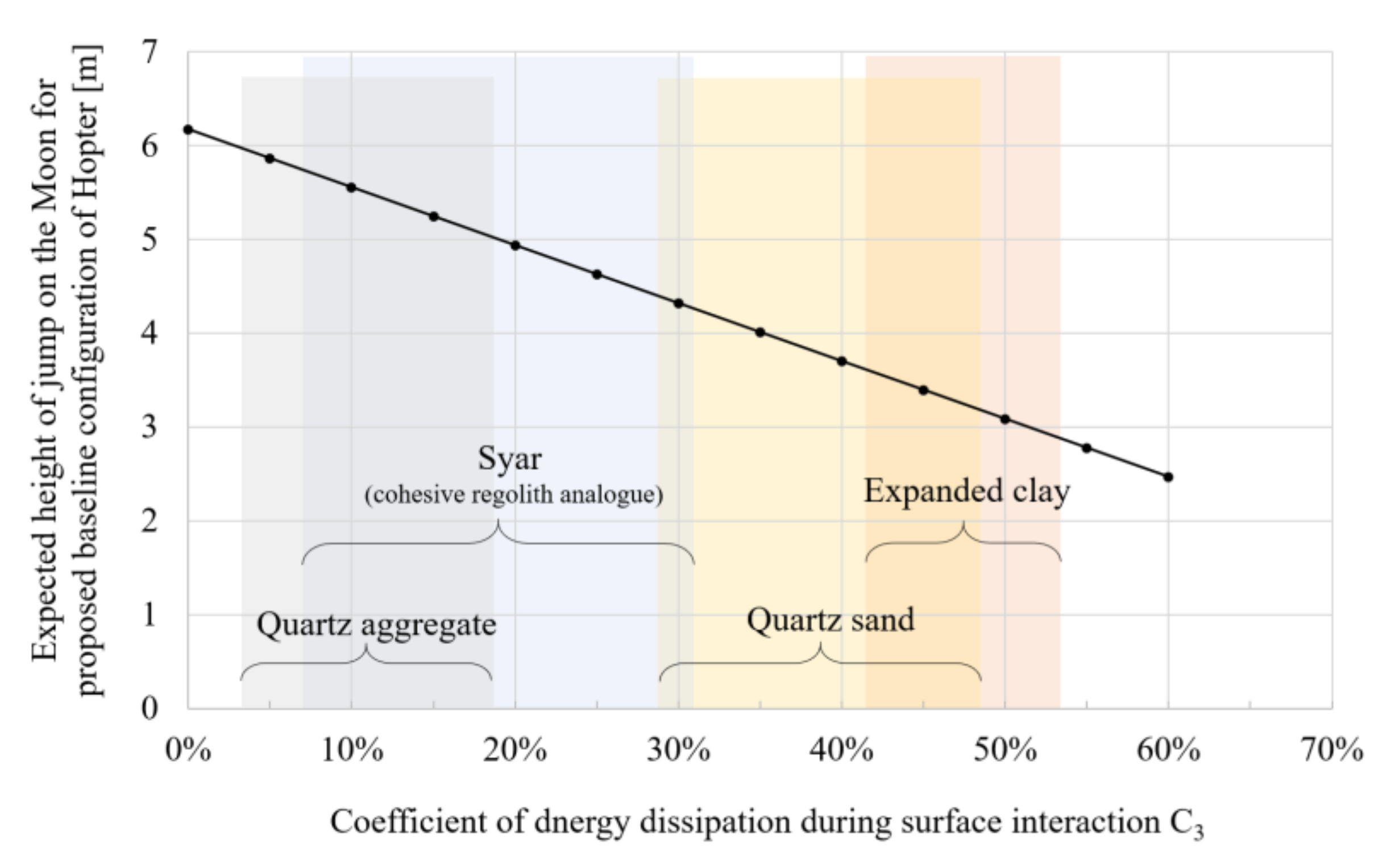
- Projections of maximum height of jump for Hopter case study;
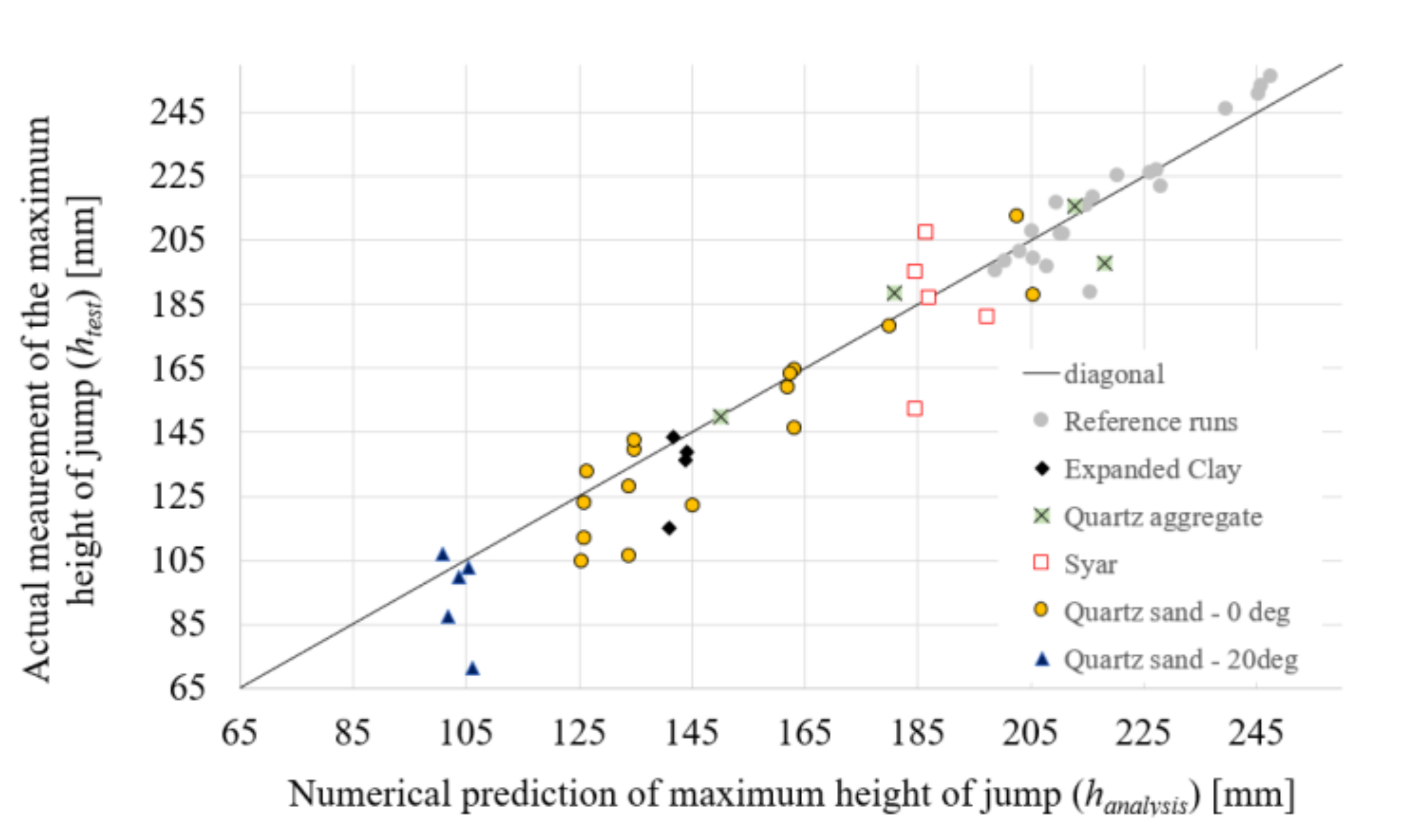
- Results for reverse analysis and mean absolute error calculations as potential feedback for the robot’s trajectory planning.
4.1. Results of C1 (Based on Analysis) and Defining C2_ref for Reference Jumps
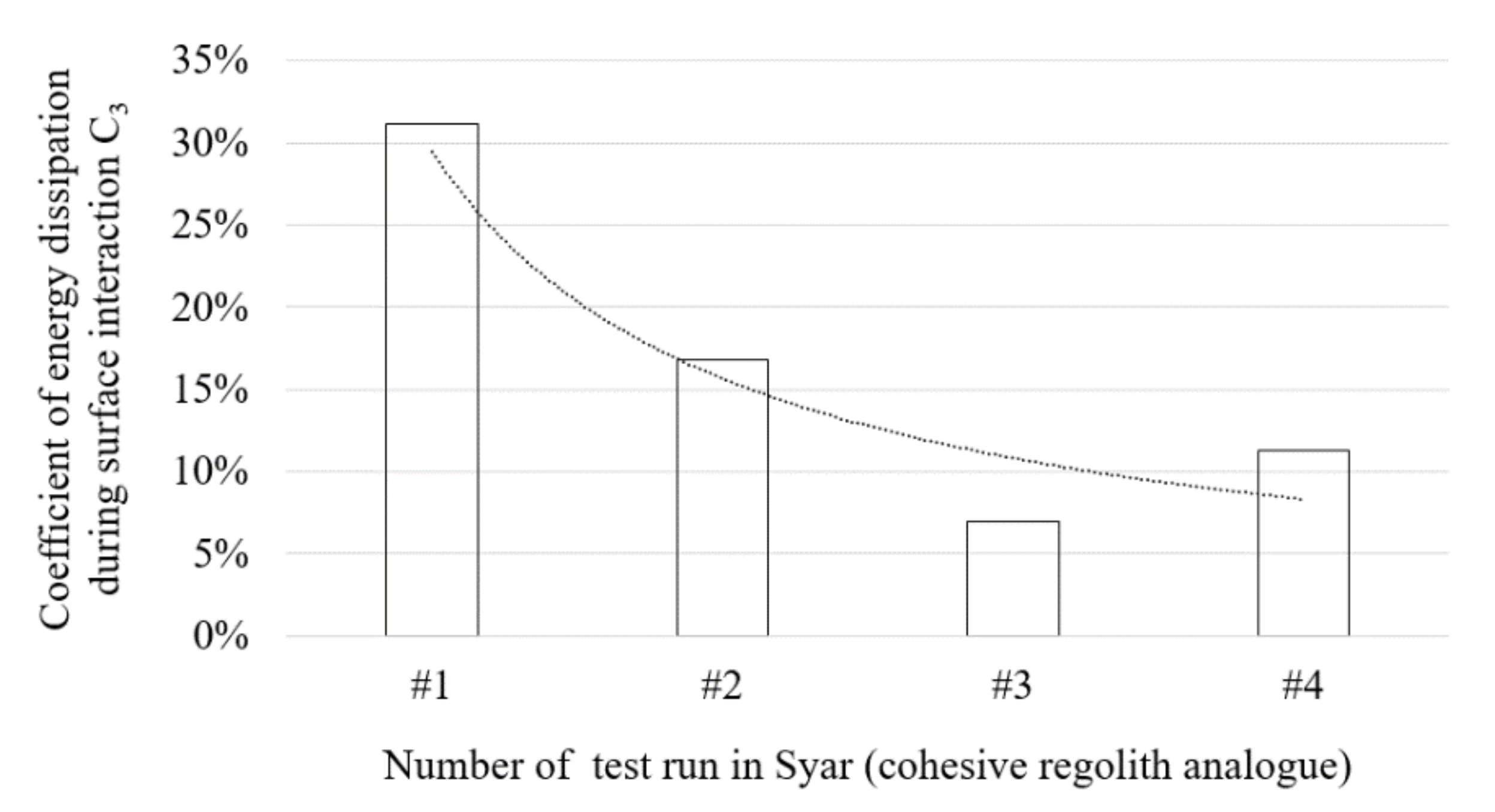
4.2. Results of C3 for Jumps on the Non-Solid Surfaces
4.3. Other Observations
4.4. Results for Reverse Analysis and Projection of the Results to the Hopter Case Study
5. Discussion
5.1. Lessons Learned
- Actuators input energy, controlled by measurement of a deflection of the springs;
- The effective kinetic or potential energy of the hopping system, which can be determined by either measurement of the height of the jump (as done here but may be tricky for planetary application) or time of travel between actuators trigger and the first contact with the ground (i.e., by monitoring internal accelerometer). The latter is sufficient since the physics of projected vertical motion are well known.
5.2. Open Matters and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Simplified Analytical Model for Vertical Hops
- jumping on a rigid surface and no internal losses, then the Ejump_total = Epot;
- the stiffness of the spring is substantial, and therefore Egrav tends to zero, and therefore Espr is equal Eused.
Appendix B. Formulation of Energy Dissipation Coefficients
- (a)
- in MSC Adams multibody analysis, the Esurf and Eloss are considered as close to zero and negligible (the minimal damping factors, not affecting the results, were introduces to the boundary conditions to omit the numerical uncertainties);
- (b)
- for the reference jumps on a solid surface, it is assumed that the Esurf is also negligibly small;
- (c)
- Egrav is known because we know the stiffness of the spring and weight of the system (and hence we do not measure the initial compression of the springs, i.e., fgrav from Figure 7);
- (d)
- Espr and Eused are known because we measure the total compression of springs before and after the spring tensioning procedure (i.e., fused from Figure 7).
- (e)
- the internal sub-systems inside the robot (e.g., batteries, payload, etc.) are considered rigidly fixed, and the inertia of the robot’s platform does not vary with time (i.e., there are no moving masses inside).
Appendix B.1. Coefficient of Energy Loss in the Momentum Exchange (C1)
Appendix B.2. Coefficient of Energy Loss in the Mechanism’s Friction (C2_ref)
Appendix B.3. Coefficient of Energy Dissipation in the Surface (C3)
Appendix B.4. Formulae for the Potential Energy of the Hopping Robot (Epot) and the Maximum Height of the Jump (hmax)
References
- Castillo-Rogez, J.C.; Pavone, M.; Nesnas, I.A.D.; Hoffman, J.A. Expected science return of spatially-extended in-situ exploration at small Solar system bodies. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012. [Google Scholar] [CrossRef]
- Nesnas, I.A.; Matthews, J.B.; Abad-Manterola, P.; Burdick, J.W.; Edlund, J.A.; Morrison, J.C.; Peters, R.D.; Tanner, M.M.; Miyake, R.N.; Solish, B.S.; et al. Axel and DuAxel rovers for the sustainable exploration of extreme terrains. J. Field Robot. 2012, 29, 663–685. [Google Scholar] [CrossRef]
- Nesnas, I.A.; Kerber, L.; Parness, A.; Kornfeld, R.; Sellar, G.; Mcgarey, P.; Brown, T.; Paton, M.; Smith, M.; Johnson, A.; et al. Moon Diver: A Discovery Mission Concept for Understanding the History of Secondary Crusts through the Exploration of a Lunar Mare Pit. In Proceedings of the 2019 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2019. [Google Scholar] [CrossRef]
- Yoshimitsu, T.; Kubota, T. Engineering challenges and results by MINEVRA-II asteroid surface rovers. J. Robot. Soc. Jpn. 2020, 38, 754–761. [Google Scholar] [CrossRef]
- Kemurdzhian, A.; Bogomolov, A.; Brodskii, P.; Gromov, V.; Dolginov, S.; Kirnozov, F.F.; Kozlov, G.V.; Komissarov, V.I.; Ksanfomality, L.V.; Kucherenko, V.I.; et al. Study of Phobos’ Surface with a Movable Robot. In Scientific and Methodological Aspects of the Phobos Study; Space Research Institute: Moscow, Russia, 1986; pp. 357–367. [Google Scholar]
- Reid, R.G.; Roveda, L.; Nesnas, I.A.D.; Pavone, M. Contact Dynamics of Internally-Actuated Platforms for the Exploration of Small Solar System Bodies. In Proceedings of the i-SAIRAS, Montreal, QC, Canada, 17–19 June 2014. [Google Scholar]
- Clark, B.C.; Sunshine, J.M.; A’Hearn, M.F.; Cochran, A.L.; Farnham, T.L.; Harris, W.M.; McCoy, T.J.; Veverka, J. Comet Hopper: A Mission Concept for Exploring the Heterogeneity of Comets. Proceedings of LPI Asteroids, Comets, Meteors, Baltimore, MD, USA, 14–18 July 2008. [Google Scholar]
- Fiorini, P.; Bovo, F.; Bertelli, L.; Munteanu, M.G. Solving the landing problem of hopping robots: The elastic cage design. In Proceedings of the ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA), Noordwijk, The Netherlands, 11–14 November 2008. [Google Scholar]
- Lee, P.; Riedel, J.E.; Jones-Wilson, L.L.; Brandeau, E.J.; O’Farrel, C.; Gallon, J.C.P.R.S. Globetrotter: An airbag hopper for Mars surface and pit/cave exploration. In Proceedings of the LPI Ninth International Conference on Mars, Pasadena, CA, USA, 22–25 July 2019. [Google Scholar]
- Landis, G.A.; Oleson, S.R.; Abel, P.; Bur, M.; Colozza, A.; Faller, B.; Fittje, J.; Gyekenyesi, J.; Hartwig, J.; Jones, R.; et al. Missions to Triton and Pluto using a Hopper Vehicle with In-Situ Refueling. In Proceedings of the 70th International Astronautical Congress (IAC), Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Kalita, H.; Thangavelautham, J. Exploration of extreme environments with current and emerging robot systems. Curr. Robot. Rep. 2020, 1, 94–104. [Google Scholar] [CrossRef]
- Mège, D.; Gurgurewicz, J.; Grygorczuk, J.; Wiśniewski, Ł.; Thornell, G. The Highland Terrain Hopper (HOPTER): Concept and use cases of a new locomotion system for the exploration of low gravity Solar System bodies. Acta Astronaut. 2016, 121, 200–220. [Google Scholar] [CrossRef]
- Byl, K.; Byl, M.; Rutschmann, M.; Satzinger, B.; van Blarigan, L.; Piovan, G.; Cortell, J. Series-elastic actuation prototype for rought terrain hopping. In Proceedings of the IEEE International Conference on Technologies for Practical Robot Applications, Woburn, MA, USA, 23–24 April 2012. [Google Scholar] [CrossRef]
- Batts, Z.; Kim, J.; Yamane, K. Design of a hopping mechanism using a voice coil actuator: Linear elastic actuator in parallel (LEAP). In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar] [CrossRef]
- Bai, L.; Zheng, F.; Chen, X.; Sun, Y.; Hou, J. Design and Experimental Evaluation of a Single-Actuator Continuous Hopping Robot Using the Geared Symmetric Multi-Bar Mechanism. Appl. Sci. 2019, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Ambrose, E.; Csomay-Shanklin, N.; Or, Y.; Ames, A. Design and Comparative Analysis of 1D Hopping Robots. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 4–8 November 2019. [Google Scholar]
- Wilburn, G.; Kalita, H.; Thangavelautham, J. Development and testing of an engineering model of an asteroid hopping robot. In Proceedings of the International Astronautical Congress, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Kalita, H.; Schwartz, S.; Asphaug, E.; Thangavelautham, J. Mobility and Science Operations on an Asteroid Using a Hopping Small Spacecraft on Stilts. 2018. Available online: https://arxiv.org/abs/1801.09482 (accessed on 1 March 2021).
- Oshashi, E.; Ohnishi, K. Hopping height control for hopping robots. Electr. Eng. Jpn. 2006, 155, 650–665. [Google Scholar]
- Kobashi, K.; Bando, A.; Nagaoka, K.; Yoshida, K. Tumbling and Hopping Locomotion Control for a Minor Body Exploration Robot. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar] [CrossRef]
- Cherouvim, N.; Papadopoulos, P. Control of hopping speed and height over unknown rough terrain using a single actuator. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar] [CrossRef]
- Hyon, S.H.; Emura, T.; Mita, T. Dynamics-based control of a one-legged hopping robot. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2003, 217, 83–98. [Google Scholar] [CrossRef]
- Zabihi, M.; Alasty, A. Dynamic stability and control of a novel handspringing robot. Mech. Mach. Theory 2019, 137, 154–171. [Google Scholar] [CrossRef]
- Yesilevskiy, Y.; Gan, Z.; Remy, C.D. Energy-optimal hopping in parallel and series elastic 1D monopods. J. Mech. Robot. 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Kalveram, K.T.; Häufle, D.; Grimmer, S.; Seyfarth, A. Energy management that generates hopping: Comparison of virtual, robotic and human bouncing. In Proceedings of the International Conference on Simulation, Modelling and Programming for Autonomous Robots, Darmstadt, Germany, 15–16 November 2010. [Google Scholar]
- Chen, G.; Tu, J.; Ti, X.; Hu, H. A Single-legged Robot Inspired by the Jumping Mechanism of Click Beetles and Its Hopping Dynamics Analysis. J. Bionic Eng. 2020, 17, 1109–1125. [Google Scholar] [CrossRef]
- Hockman, B.; Reid, R.G.; Nesnas, I.A.D.; Pavone, M. Experimental Methods for Mobility and Surface Operations of Microgravity Robots. In 2016 International Symposium on Experimental Robotics; Springer Proceedings in Advanced, Robotics; Kulić, D., Nakamura, Y., Khatib, O., Venture, G., Eds.; Springer: Cham, Switzerland, 2017; Volume 1. [Google Scholar] [CrossRef]
- Moritz, C.T.; Farley, C.T. Human hoppers compensate for simultaneous changes in surface compression and damping. J. Biomech. 2004, 39, 1030–1038. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, K.; Otsuki, M.; Kubota, T.; Morino, Y. RFT-Based Analysis of Mobility Performance of Hopping Rover on Soft Soil for Planetary Exploration. In Proceedings of the 13th International Symposium on Artificial Intelligence, Robotics and Automation in Space (i-SAIRAS 2016), Beijing, China, 20–22 June 2016. [Google Scholar]
- Sakamoto, K.; Otsuki, M.; Kubota, T.; Morino, Y. Hopping Motion Estimation on Soft Soil by Resistive Force Theory. J. Robot. Mechatron. 2017, 29, 895–901. [Google Scholar] [CrossRef]
- Vasilopoulos, V.; Paraskevas, I.S.; Papadopoulos, E.G. Monopod hopping on compliant terrains. Robot. Auton. Syst. 2018, 102, 13–26. [Google Scholar] [CrossRef]
- Maeda, T.; Kunii, Y.; Yoshikawa, K.; Otsuki, M.; Yoshimitsu, T.; Kubota, T. Design of shoe plate for small hopping rover on loose soil. In Proceedings of the 2018 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2018. [Google Scholar] [CrossRef]
- Roberts, S.; Koditschek, D.E. Mitigating energy loss in a robot hopping on a physically emulated dissipative surface. In Proceedings of the International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Wiśniewski, Ł.; Grygorczuk, J.; Węclewski, P.; Mege, D.; Gurgurewicz, J.; Zielińska, T.; Gritsevich, M.; Peltoniemi, J. Mobility and terrain accessibility analysis for Hopter—An underactuated mobile robot for planetary exploration. In Proceedings of the ESA Workshop on Advanced Space Technologies for Robotics and Automation (ASTRA), Leiden, The Netherlands, 20–22 June 2017. [Google Scholar]
- Wiśniewski, Ł.; Grygorczuk, J.; Mege, D.; Gurgurewicz, J. Design Features of Novel High Energy Impulsive Drive of Underactuated Mobile Robot for Planetary Exploration. In Proceedings of the 17th European Space Mechanisms and Tribology Symposium, Hatfield, UK, 20–22 September 2017. [Google Scholar]
- Marshall, J.P.; Hurley, R.C.; Arthur, D.; Vlahinic, I.; Senatore, C.; Iagnemma, K.; Trease, B.; Andrade, J.E. Failures in sand in reduced gravity environments. J. Mech. Phys. Solids 2018. [Google Scholar] [CrossRef] [Green Version]
- Karapiperis, K.; Marshall, J.P.; Andrade, J.E. Reduced Gravity Effects on the Strength of Granular Matter: DEM Simulations versus Experiments. J. Geotech. Geoenviron. Eng. 2020, 146. [Google Scholar] [CrossRef]
- Maeda, T.; Kunii, Y.; Yoshikawa, K.; Otsuki, M.; Yoshimitsu, T.; Kubota, T. Hopping simulation for small rover using regolith model considering the result of vacuum and small gravity flight experiment. In Proceedings of the i-SAIRAS 2018, Madrid, Spain, 4–6 June 2018. [Google Scholar]
- Hubicki, C.M.; Aguilar, J.J.; Goldman, D.I.; Ames, A. Tractable terrain-aware motion planning on granular media: An impulsive jumping study. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, X.; Yuan, Y. Principled reward shaping for reinforcement learning via lyapunov stability theory. Neurocomputing 2020, 393, 83–90. [Google Scholar] [CrossRef]
- Kusano, Y.; Tsutsumi, K. Hopping height control of an active suspension type leg module based on reinforcement learning and a neural network. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and System, Lausanne, Switzerland, 30 September–4 October 2002. [Google Scholar] [CrossRef]
- Biele, J.; Ulamec, S.; Maibaum, M.; Roll, R.; Witte, L.; Jurado, E.; Muñoz, P.; Arnold, W.; Auster, H.-U.; Casas, C.M.; et al. The landing(s) of Philae and inferences about comet surface mechanical properties. Science 2015, 349, 6247. [Google Scholar] [CrossRef] [PubMed]
- Spohn, T.; Knollenberg, J.; Ball, A.J.; Banaszkiewicz, M.; Benkhoff, J.; Grott, M.; Kührt, E.; Kossacki, K.J.; Marczewski, W.; Pelivan, I.; et al. Thermal and mechanical properties of the near-surface layers of comet 67P/Churyumov-Gerasimenko. Science 2015, 349, 6247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yano, H.; Kubota, T.; Miyamoto, H.; Okada, T.; Scheeres, D.; Takagi, Y.; Yoshida, K.; Abe, M.; Abe, S.; Barnouin, O.; et al. Touchdown of the Hayabusa Spacecraft at the Muses Sea on Itokawa. Science 2006, 312, 1350–1353. [Google Scholar] [CrossRef]
- A’Hearn, M.F.; Belton, M.J.S.; Delamere, W.A.; Kissel, J.; Klaasen, K.P.; McFadden, L.A.; Meech, K.J.; Melosh, H.J.; Schultz, P.H.; Sunshine, J.M.; et al. Deep Impact: Excavating Comet Tempel 1. Science 2005, 310, 5746. [Google Scholar] [CrossRef] [Green Version]
- Wisniewski, L.; Reid, R.G.; Nesnas, I.A.; Chmielewski, A.; Grygorczuk, J. In Situ Measurements of Regolith Properties on Small Solar System Bodies using Spacecraft/Rover Hybrids. In Proceedings of the 69th International Astronautical Congress (IAC), Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Sullivan, R.; Anderson, R.; Biesiadecki, J.; Bond, T.; Stewart, H. Martian Regolith Cohesions and Angles of Internal Friction from Analysis of Mer Wheel Trenches. Proceedings of 38th Lunar and Planetary Science Conference, League City, TX, USA, 12–16 March 2007. [Google Scholar]
- European Cooperation for Space Standarization. ECSS, ECSS-E-HB-11A Technology Readiness Level (TRL) Guidelines; ESA-ESTEC, Requirements & Standards Division: Noordwijk, The Netherlands, 2017. [Google Scholar]




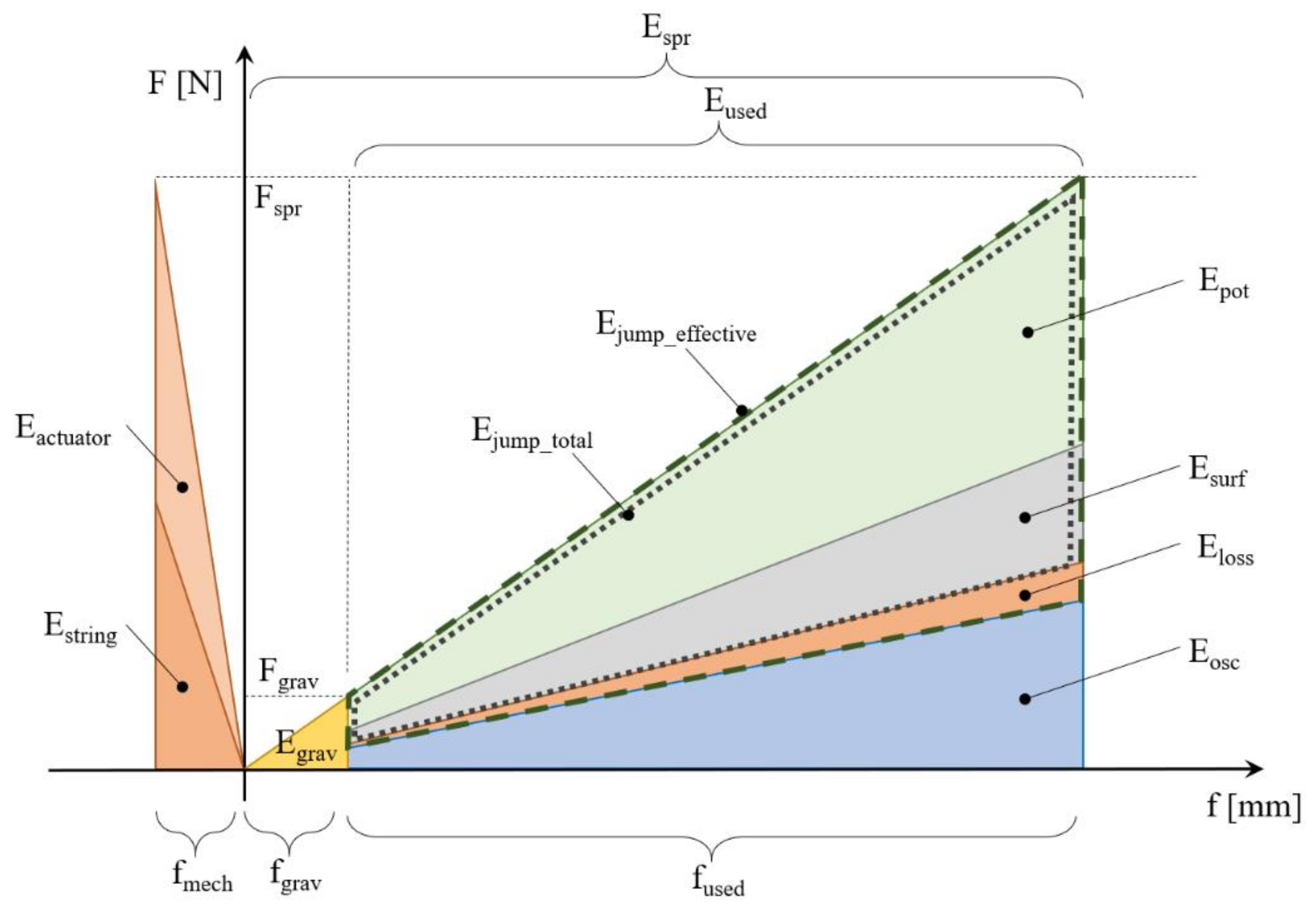









| Symbol | Description | Expected Value at Baseline in Hopter (the Full-Scale Target Model) | Contribution to the Jump |
|---|---|---|---|
| The right side of the plot | |||
| Espr | Total potential energy accumulated in the drive springs | Greater than 50 J to compensate for surface interaction losses, other contributors, and the left-hand side factors | Yes, directly |
| Egrav | Initial potential energy accumulated in the springs resulted from the weight of the hopper resting on the springs. | Becomes insignificant for larger stiffnesses of the drive springs and smaller gravities. Expected <1% of the Espr | Not contributing to the jump directly but reduces the effective Espr to Eused |
| Eosc | The energy lost in the momentum exchange between disc casing and actuating legs | It depends on the mass ratios, as demonstrated in Section 3.2. Expected between 20–40% of the Espr | Yes, it reduces the Ejump_total |
| Eloss | All losses linked to the dynamics of the actuating mechanism during the release of the springs, e.g., the kinetic energy of the reel axis (Ereel kinetic), internal and external friction of the drive springs (Esus) or any other undefined, e.g., atmosphere drag (Eother) | Expected to reduce below 5% of the Espr | Yes, it reduces the Ejump_effective |
| Esurf | The energy dissipated in the contact of the leg with the surface (regolith, soil, etc.) | Depends on the surface material and design of the foot of the actuating leg | Yes, it reduces the Epot |
| Epot | The remaining effective kinetic/potential energy resulting from the jump | In the laboratory conditions can be measured either by the height of the jump (hmax) or the maximum velocity of the robot. The objective is to maximize this energy | Pure jump energy |
| The left side of the plot | |||
| Estring | Potential energy accumulated in the elongation of the string | Ideally should be minimized by proper design | Not contributing to the jump. Only reducing effective compression of springs |
| Eactuator | Potential energy accumulated in the elastic deformation of the actuator when acting against the drive springs through the string | ||
| Type of Material | Description | Average Density [kg/m3] |
|---|---|---|
| Syar | Analogue of Martian regolith, highly cohesive | 2010 |
| Quartz sand | Grain size: 0.5–1.0 mm | 1840 |
| Expanded clay | Grain size: 8–16 mm | 270 |
| Quartz aggregate | Grain size: 8–16 mm | 1700 |
| Component | Config. #0 | Config. #1 | Config. #2 | Config. #3 | Config. #4 | Units |
|---|---|---|---|---|---|---|
| Foot | none | 113.6 | 299.5 | 216.9 | 247.0 | g |
| Actuating leg (without foot) | 1060 | g | ||||
| Springs with guide sleeves | 351.7 | g | ||||
| Stiffeners | 1077.0 | g | ||||
| Actuator | 989.38 | g | ||||
| Adapter | 1283.5 | g | ||||
| Arm | 1938.5 | g | ||||
| Rotational axis | 888.7 | g | ||||
| Actuating leg’s moment of inertia w.r.t. rotational axis (Ileg) | 3.912 | 4.271 | 4.860 | 4.599 | 4.694 | kg m2 |
| Full BB-0B’s moment of ineria w.r.t. rotational axis (Itotal) | 14.679 | 15.039 | 15.628 | 15.366 | 15.462 | kg m2 |
| C1 coefficient (ratio of Ileg/Itotal) | 26.6% | 28.4% | 31.1% | 29.9% | 30.4% | - |
| Configuration | Average C1 | Expected C1 | Coefficient C2 (*) |
|---|---|---|---|
| #0 | 26.8% (25.6–30.2%) (based on 5 runs) | 26.6% | 2.6% (0.0–5.7%) (based on 5 ref runs) |
| #1 | 27.9 % (25.4–29.7%) (based on 35 runs) | 28.4 % | 5.9% (1.1–16.4%) (based on 11 ref runs) |
| #2 | 30.1% (30.07–30.13%) (based on 4 runs) | 31.1% | 7.2% (based on 1 ref run) |
| #3 | 29.0% (28.95–29.03%) (based on 6 runs) | 29.9% | 3.8% (based on 2 ref runs) |
| #4 | 29.6% (29.32–29.92%) (based on 4 runs) | 30.4% | 3.1% (based on 1 ref run) |
| Surface Type | Foot and Testbed Inclination | C3 Average (Range) for C2_ref_direct | C3 Average (Range) for C2_ref_average | No. of Runs | Density [kg/m3] (as in Table 2) |
|---|---|---|---|---|---|
| Syar | Foot: Config 1 (round) Angle: 0° | 18.2% (7.2–31.3%) | 18.1% (7.0–31.2%) | 5 | 2010 |
| Quartz sand | Foot: Config 1 (round) Angle: 0° | 35.9% (29.3–47.2%) | 38.8% (31.7–47.9%) | 6 | 1840 |
| Quartz sand | Foot: Config 1 (round) Angle: 20° | 58.1% (51.0–68.9%) | 57.9% (50.7–68.7%) | 5 | 1840 |
| Quartz sand | Foot: Config 2 (small flat) Angle: 0° | 42.4% (34.7–47.9%) | 43.9% (36.4–49.2%) | 3 | 1840 |
| Quartz sand | Foot: Config 3 (medium flat) Angle: 0° | 26.3% (23.5–32.2%) | 25.6% (22.8–31.5%) | 4 | 1840 |
| Quartz sand | Foot: Config 4 (large flat) Angle: 0° | 15.1% (9.8–21.4%) | 13.6% (8.2–20.0%) | 3 | 1840 |
| Expanded clay | Foot: Config 1 (round) Angle: 0° | 46.0% (41.9–52.9%) | 44.4% (40.2–51.6%) | 4 | 270 |
| Quartz aggregate | Foot: Config 1 (round) Angle: 0° | 11.4% (6.4–19.1%) | 8.8% (3.7–16.8%) | 4 | 1700 |
| Description | No. of Runs | MAE |
|---|---|---|
| Syar @ 0deg | 5 | 8.6% |
| Quartz sand @ 0deg | 16 | 7.1% |
| Quartz sand @ 20deg | 5 | 11.7% |
| Expanded clay @ 0deg | 4 | 7.1% |
| Quartz aggregate @ 0deg | 4 | 3.7% |
| Total | 34 | 7.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wiśniewski, Ł.; Grygorczuk, J.; Zajko, P.; Przerwa, M.; Wasilewski, G.; Gurgurewicz, J.; Mège, D. Energy Dissipation during Surface Interaction of an Underactuated Robot for Planetary Exploration. Energies 2021, 14, 4282. https://doi.org/10.3390/en14144282
Wiśniewski Ł, Grygorczuk J, Zajko P, Przerwa M, Wasilewski G, Gurgurewicz J, Mège D. Energy Dissipation during Surface Interaction of an Underactuated Robot for Planetary Exploration. Energies. 2021; 14(14):4282. https://doi.org/10.3390/en14144282
Chicago/Turabian StyleWiśniewski, Łukasz, Jerzy Grygorczuk, Paweł Zajko, Mateusz Przerwa, Gordon Wasilewski, Joanna Gurgurewicz, and Daniel Mège. 2021. "Energy Dissipation during Surface Interaction of an Underactuated Robot for Planetary Exploration" Energies 14, no. 14: 4282. https://doi.org/10.3390/en14144282
APA StyleWiśniewski, Ł., Grygorczuk, J., Zajko, P., Przerwa, M., Wasilewski, G., Gurgurewicz, J., & Mège, D. (2021). Energy Dissipation during Surface Interaction of an Underactuated Robot for Planetary Exploration. Energies, 14(14), 4282. https://doi.org/10.3390/en14144282






