Validation of Modified Algebraic Model during Transitional Flow in HVAC Duct
Abstract
:1. Introduction
2. Governing Equations
3. Numerical Simulations
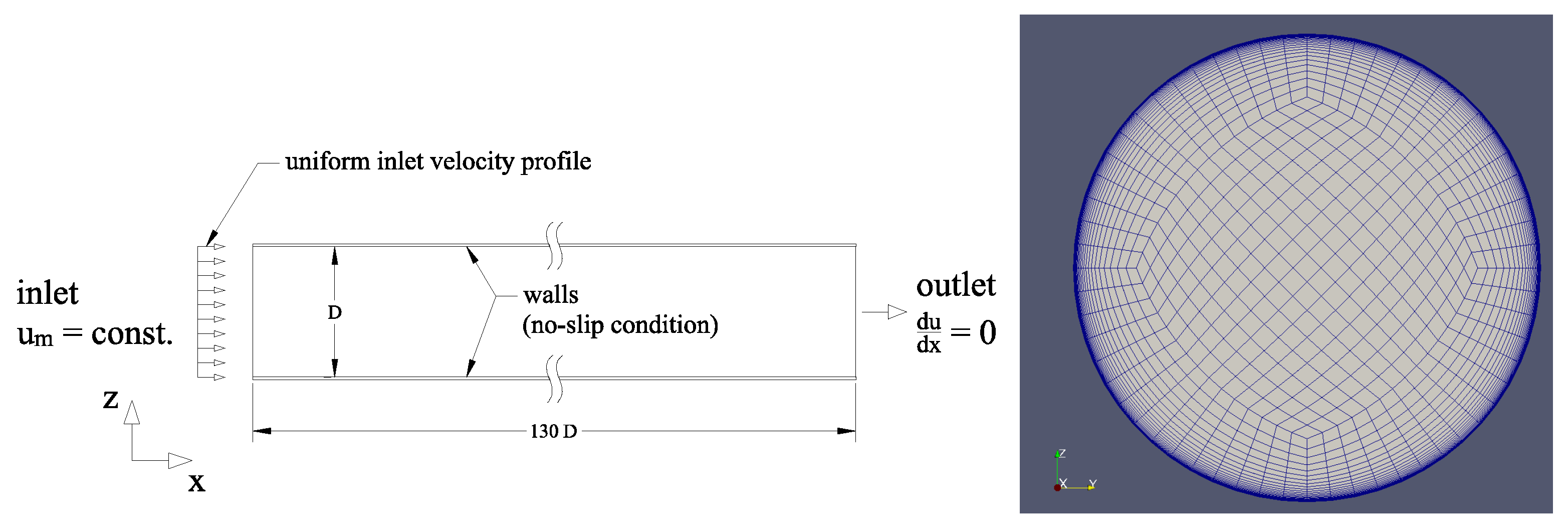
3.1. Mesh
3.2. Boundary Conditions
- inlet k and calculated using inlet turbulence intensity ;
- no slip velocity on walls;
- no wall function for k, and fields;
- constant pressure at the outlet;
- no velocity change at the outlet.
4. Experiment Setup
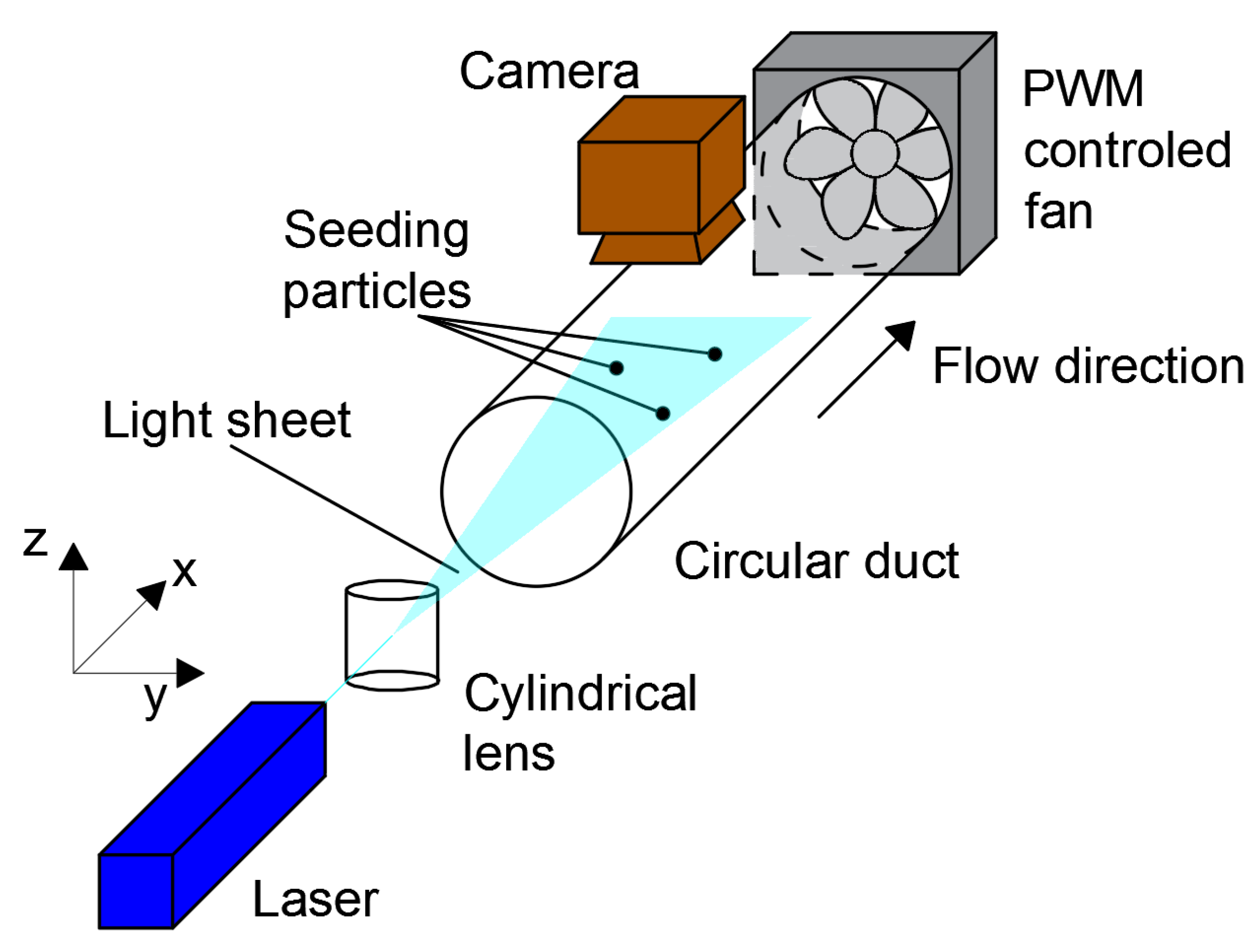
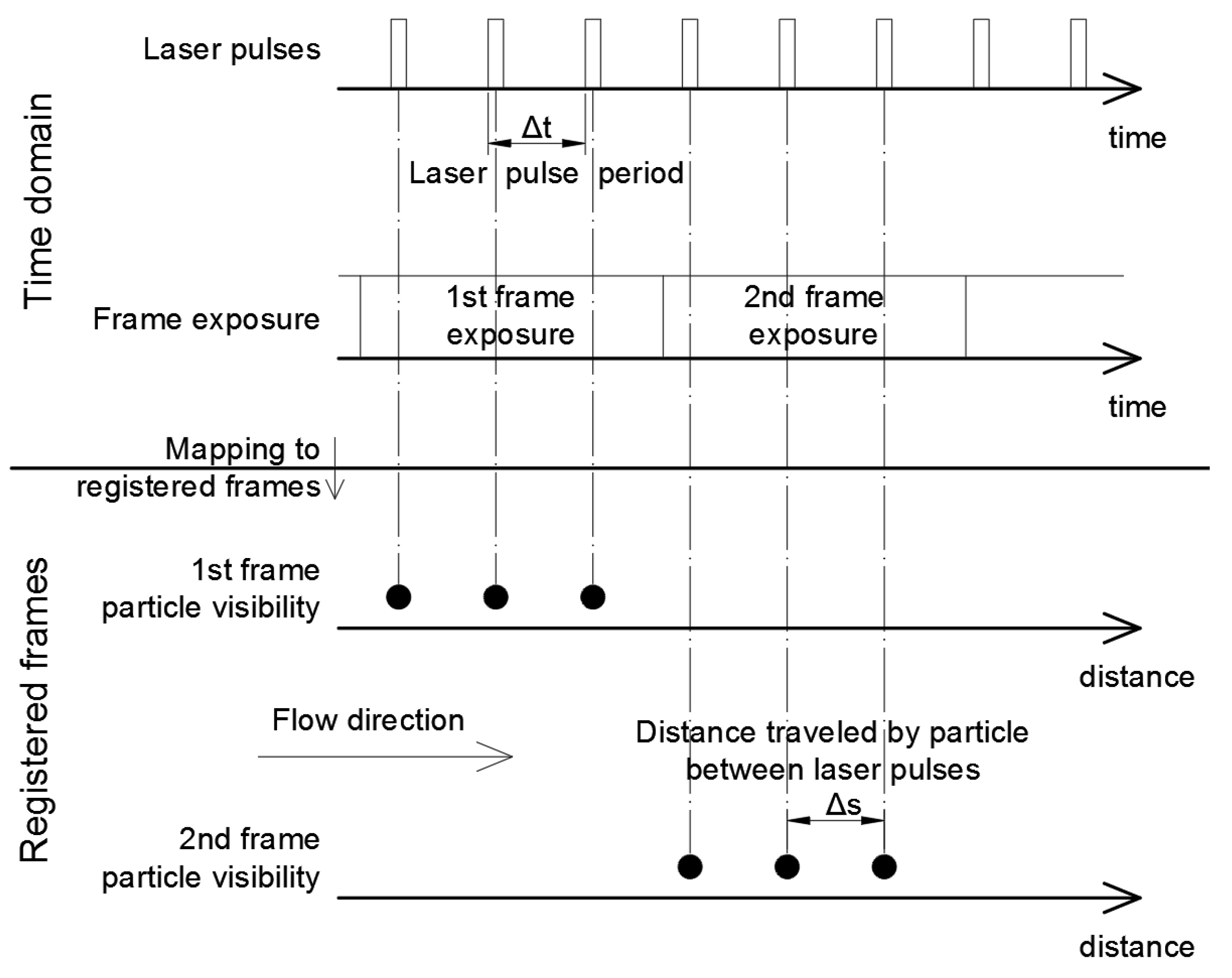
4.1. Measurement Method
4.2. Image Calibration
4.3. Image Processing
4.4. Seeding Particle Type
4.5. Image Analysis and Velocity Profile Calculation
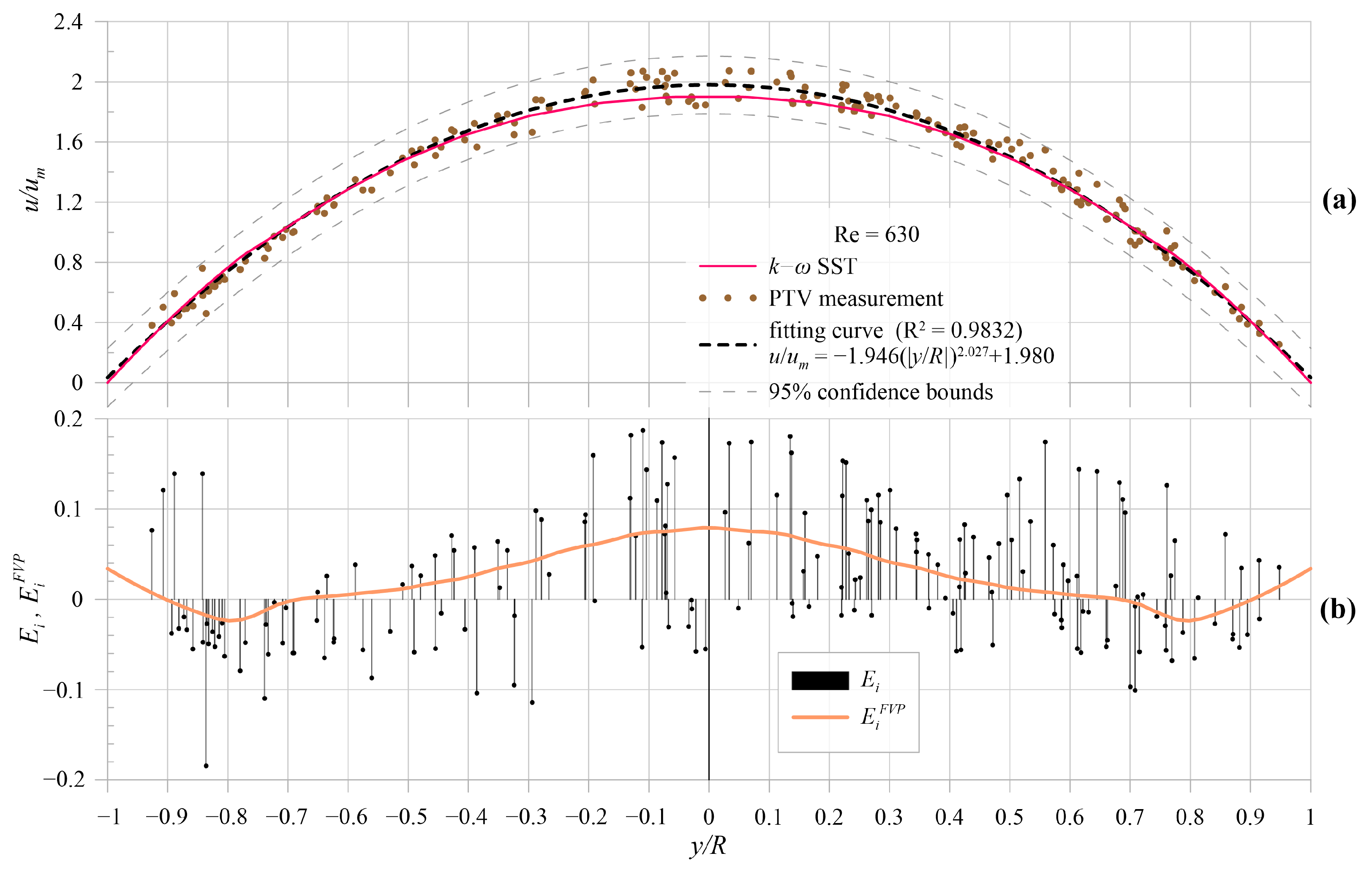
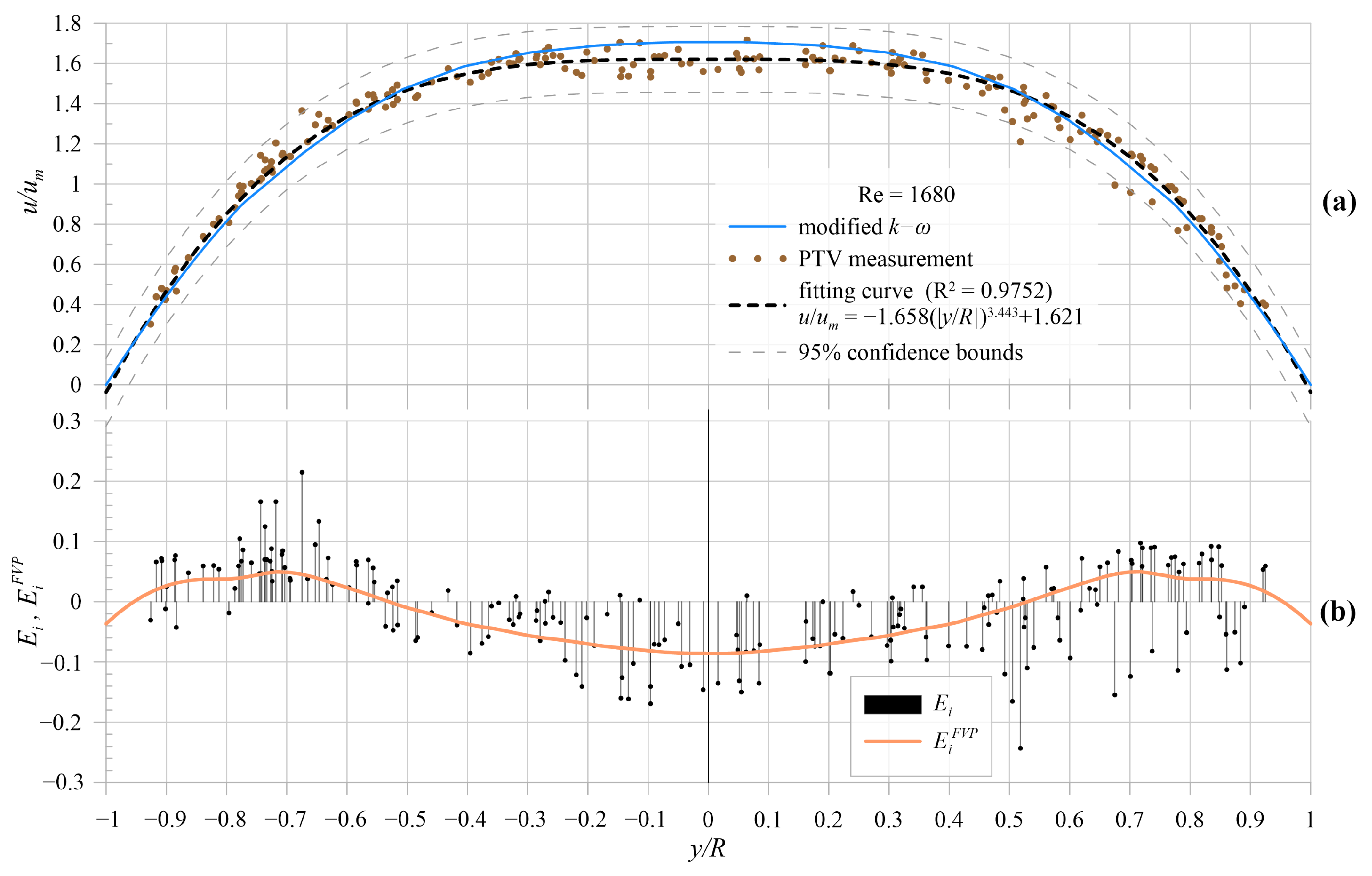
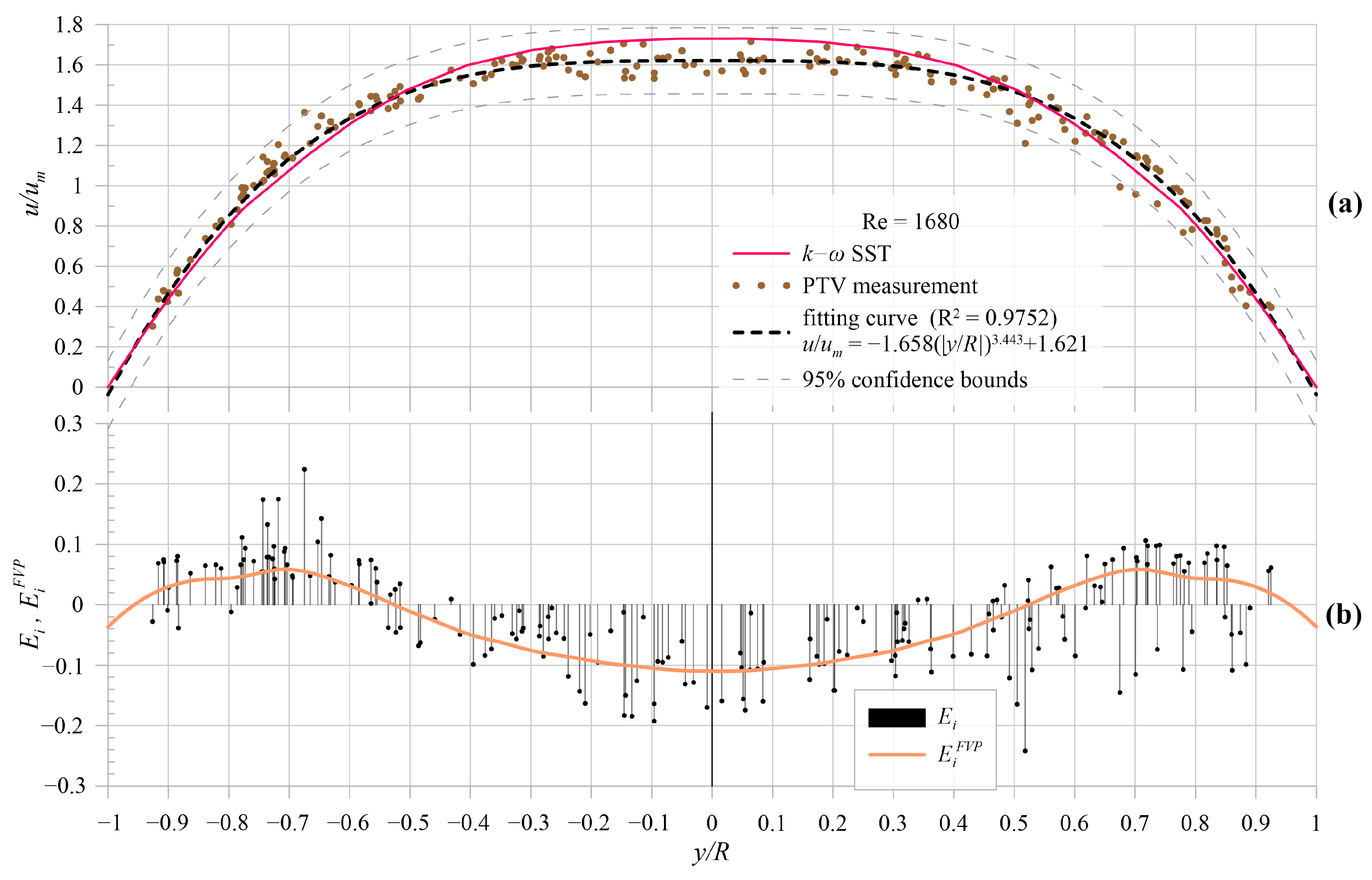
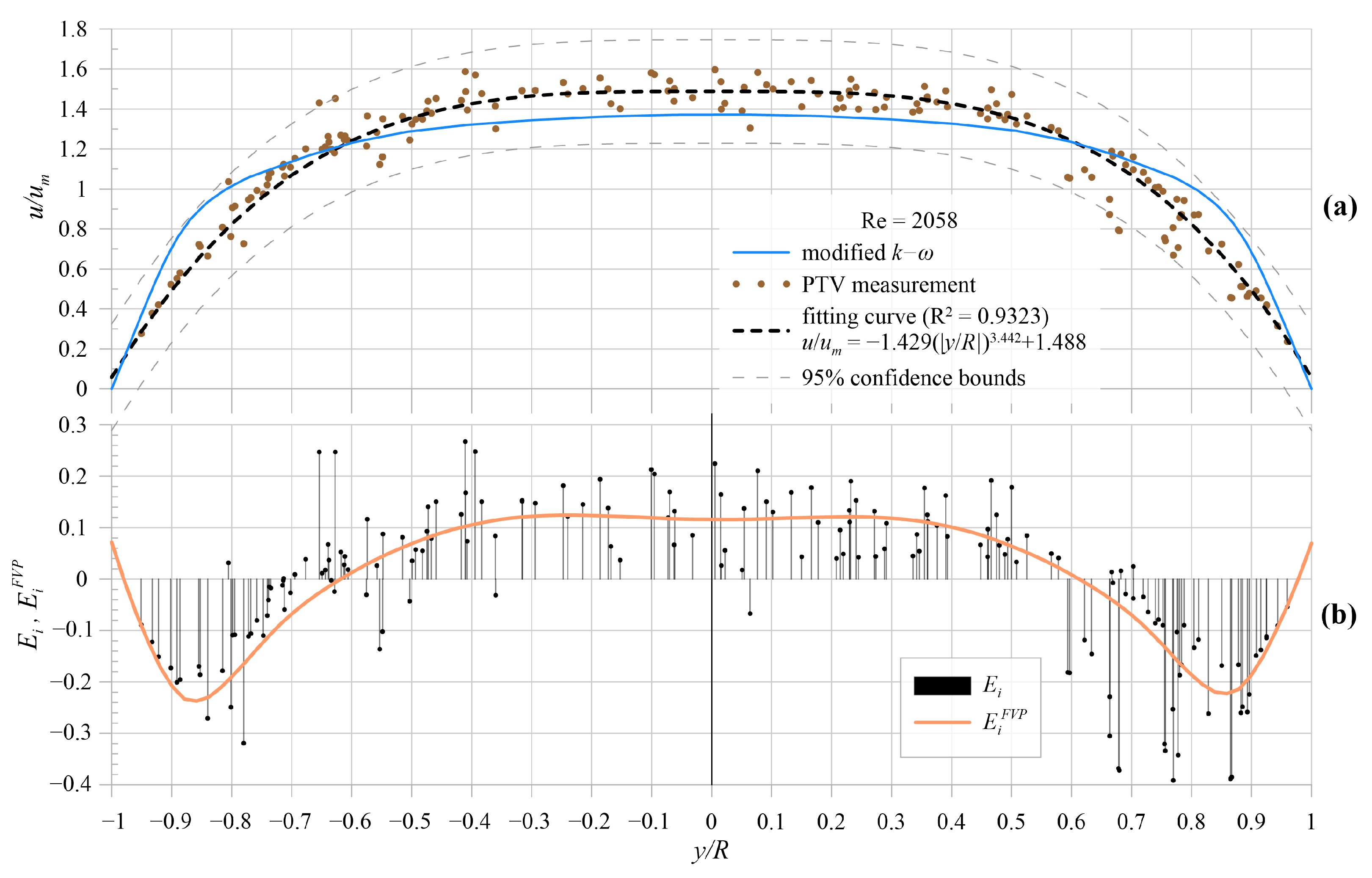
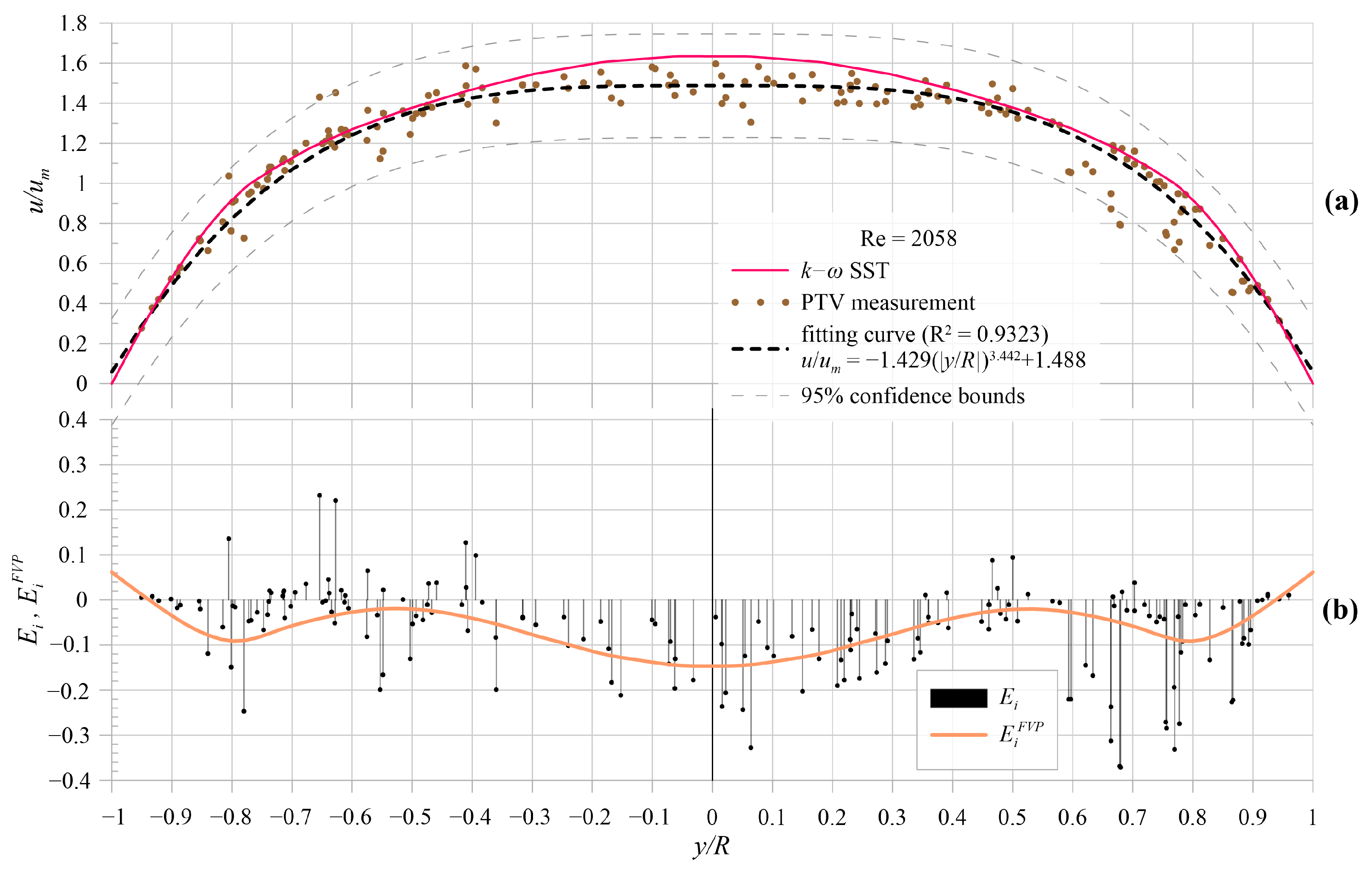
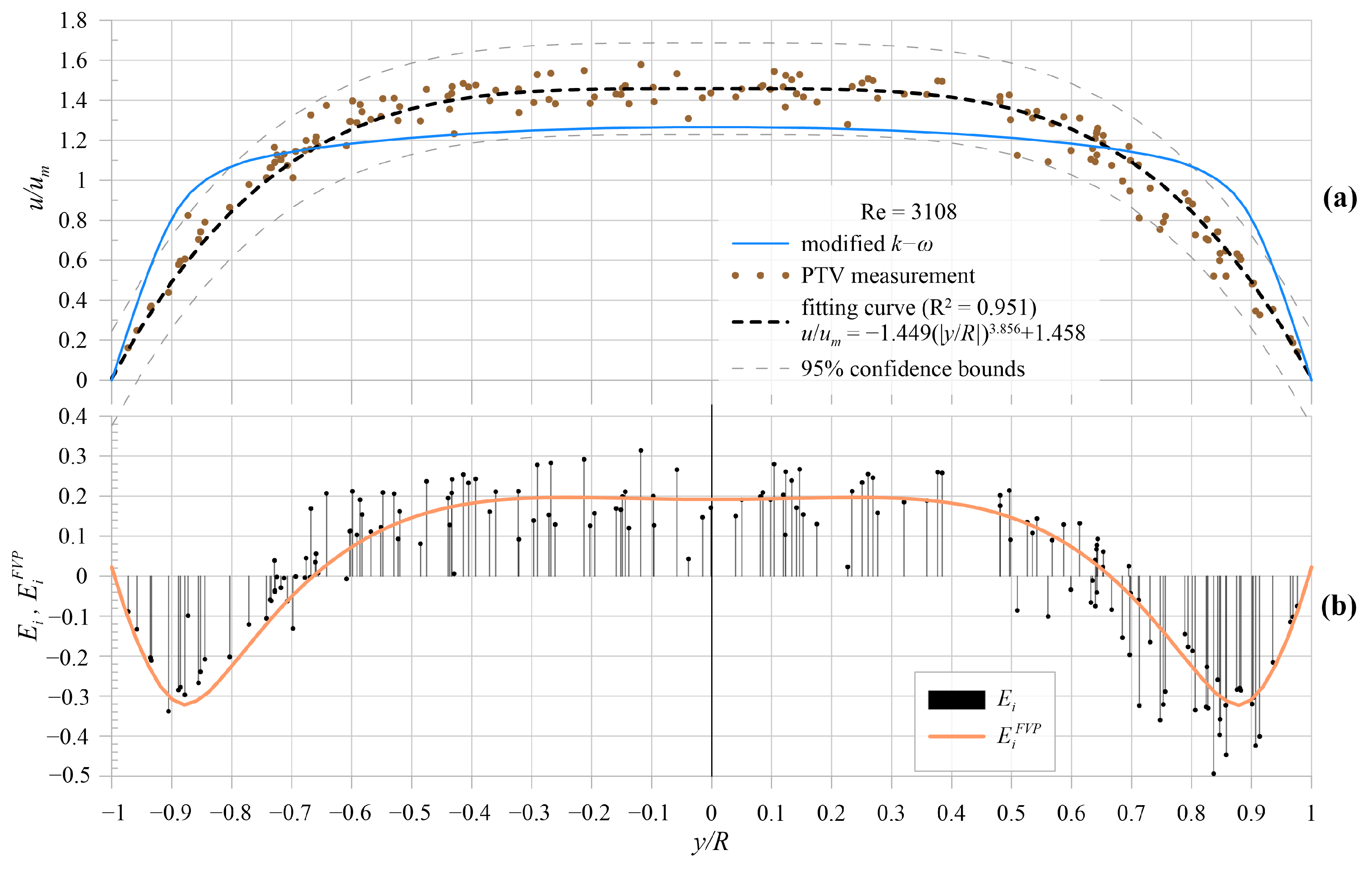
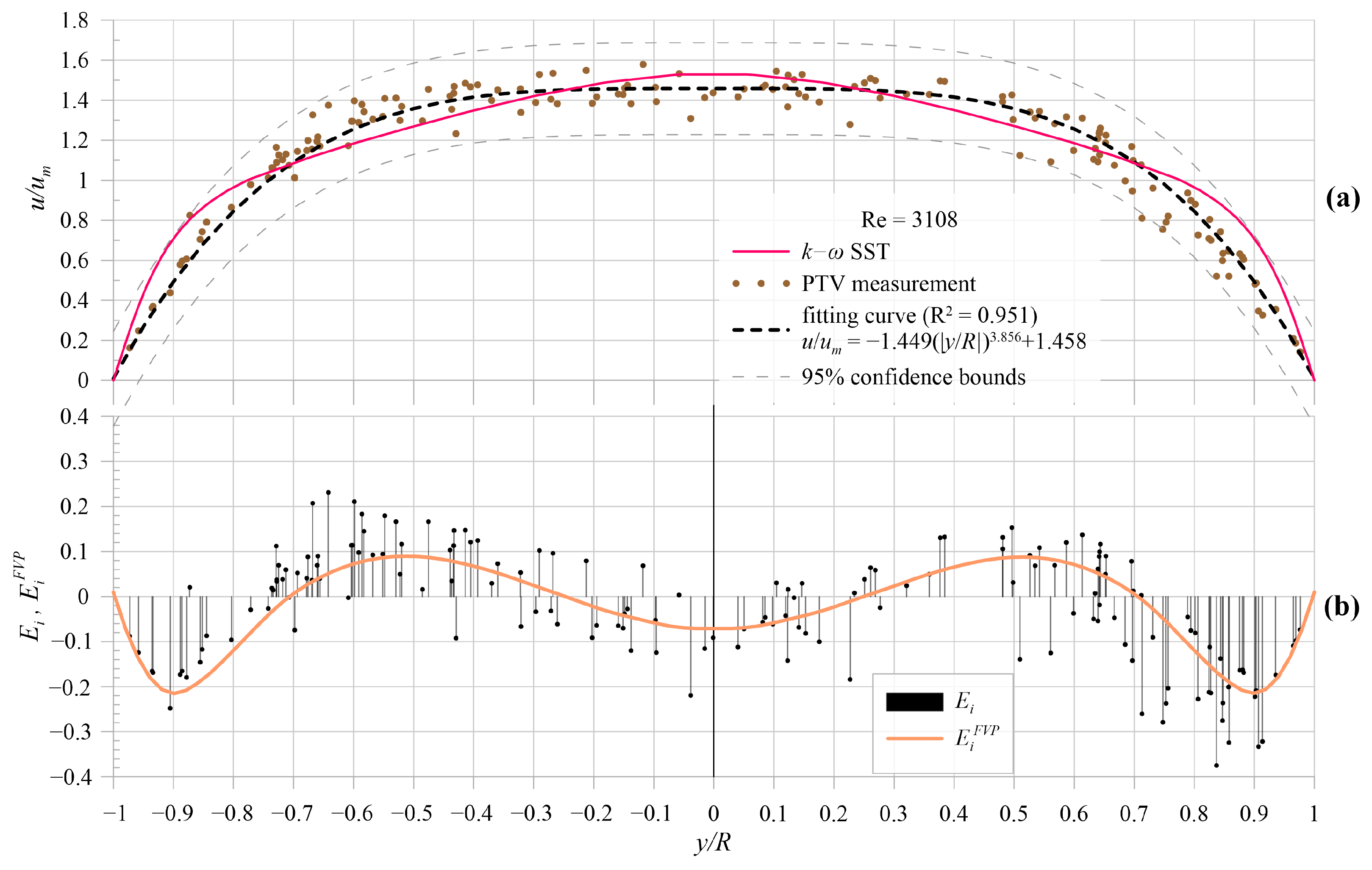
5. Results and Comparison
5.1. Model Results
5.2. Experimental Model Validation
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| k | turbulent kinetic energy [m/s] |
| large-scale turbulent kinetic energy [m/s] | |
| small-scale turbulent kinetic energy [m/s] | |
| Re | Reynolds number [-] |
| components of shear rate tensor [1/s] | |
| turbulence intensity [%] | |
| u | velocity [m/s] |
| mean flow velocity [m/s] | |
| dimensionless wall distance [-] | |
| intermittency factor [-] | |
| fluid kinematic viscosity [m/s] | |
| large-scale turbulent viscosity [m/s] | |
| small-scale turbulent viscosity [m/s] | |
| turbulent viscosity [m/s] | |
| fluid density [kg/m] | |
| shear stress [Pa] | |
| specific dissipation rate [1/s] | |
| CFD | Computational Fluid Dynamics |
| FVP | Fitted Velocity Profile |
| HVAC | Heat, Ventilation, Air Condition |
| PTV | Particle Tracking Velocimetry |
| RMSE | Root Mean Square Error |
References
- Shao, L.; Riffat, S. Accuracy of CFD for predicting pressure losses in HVAC duct fittings. Appl. Energy 1995, 51, 233–248. [Google Scholar] [CrossRef]
- Zhong, W.; Zhang, T.; Tamura, T. CFD Simulation of Convective Heat Transfer on Vernacular Sustainable Architecture: Validation and Application of Methodology. Sustainability 2019, 11, 4231. [Google Scholar] [CrossRef] [Green Version]
- Ren, C.; Cao, S.J. Development and application of linear ventilation and temperature models for indoor environmental prediction and HVAC systems control. Sustain. Cities Soc. 2019, 51, 101673. [Google Scholar] [CrossRef]
- Pichurov, G.; Stankov, P.; Markov, D. Hvac control based on CFD analysis of room airflow. IFAC Proc. Vol. 2006, 39, 213–218. [Google Scholar] [CrossRef]
- Tian, W.; Han, X.; Zuo, W.; Wang, Q.; Fu, Y.; Jin, M. An optimization platform based on coupled indoor environment and HVAC simulation and its application in optimal thermostat placement. Energy Build. 2019, 199, 342–351. [Google Scholar] [CrossRef]
- Adegbenro, A.; Short, M.; Angione, C. An Integrated Approach to Adaptive Control and Supervisory Optimisation of HVAC Control Systems for Demand Response Applications. Energies 2021, 14, 2078. [Google Scholar] [CrossRef]
- Taler, D. Determining velocity and friction factor for turbulent flow in smooth tubes. Int. J. Therm. Sci. 2016, 105, 109–122. [Google Scholar] [CrossRef]
- Abraham, J.; Sparrow, E.; Tong, J. Heat transfer in all pipe flow regimes: Laminar, transitional/intermittent, and turbulent. Int. J. Heat Mass Transf. 2009, 52, 557–563. [Google Scholar] [CrossRef]
- Rup, K.; Duda, P.; Danys, L. Determination of heat transfer coefficients on the surfaces of plastic tubes. Heat Mass Transf. 2002, 39, 89–95. [Google Scholar] [CrossRef]
- Fernando, N.; Narayana, M. Limiting value of Reynolds Averaged Simulation in numerical prediction of flow over NACA4415 airfoil. In Proceedings of the 2016 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 5–6 April 2016. [Google Scholar] [CrossRef]
- Boiko, A.V.; Demyanko, K.V.; Inozemtsev, A.A.; Kirilovskiy, S.V.; Nechepurenko, Y.M.; Paduchev, A.P.; Poplavskaya, T.V. Determination of the laminar-turbulent transition location in numerical simulations of subsonic and transonic flows past a flat plate. Thermophys. Aeromech. 2019, 26, 629–637. [Google Scholar] [CrossRef]
- Kirilovskiy, S.V.; Boiko, A.V.; Demyanko, K.V.; Ivanov, A.V.; Nechepurenko, Y.M.; Poplavskaya, T.V. Numerical simulation of the laminar-turbulent transition on a swept wing in a subsonic flow. J. Phys. Conf. Ser. 2019, 1359, 012070. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Esmaeilpour, M.; Vizinho, R.; Younesi, A.; Pàscoa, J. Assessment of RANS turbulence models for numerical study of laminar-turbulent transition in convection heat transfer. Int. J. Heat Mass Transf. 2017, 115, 1288–1308. [Google Scholar] [CrossRef]
- Vizinho, R.; Páscoa, J.; Silvestre, M. Turbulent transition modeling through mechanical considerations. Appl. Math. Comput. 2015, 269, 308–325. [Google Scholar] [CrossRef]
- Kubacki, S.; Dick, E. An algebraic model for bypass transition in turbomachinery boundary layer flows. Int. J. Heat Fluid Flow 2016, 58, 68–83. [Google Scholar] [CrossRef]
- Nering, K.; Rup, K. An improved algebraic model for bypass transition for calculation of transitional flow in parallel-plate channel. Int. J. Therm. Sci. 2019, 135, 471–477. [Google Scholar] [CrossRef]
- Bernardos, L.; Richez, F.; Gleize, V.; Gerolymos, G.A. Algebraic Nonlocal Transition Modeling of Laminar Separation Bubbles Using k-ω Turbulence Models. AIAA J. 2019, 57, 553–565. [Google Scholar] [CrossRef]
- Wilcox, D. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 2006. [Google Scholar]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Nering, K.; Rup, K. Modified algebraic model of laminar-turbulent transition for internal flows. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1743–1753. [Google Scholar] [CrossRef]
- You, H.; Tinoco, R.O. Quantifying the Response of Grass Carp Larvae to Acoustic Stimuli Using Particle-Tracking Velocimetry. Water 2021, 13, 603. [Google Scholar] [CrossRef]
- Özdemir, O.Ç.; Conahan, J.M.; Müftü, S. Particle Velocimetry, CFD, and the Role of Particle Sphericity in Cold Spray. Coatings 2020, 10, 1254. [Google Scholar] [CrossRef]
- Wang, R.; Duan, R.; Jia, H. Experimental Validation of Falling Liquid Film Models: Velocity Assumption and Velocity Field Comparison. Polymers 2021, 13, 1205. [Google Scholar] [CrossRef]
- Yang, T.; Liu, Z.; Chen, Y.; Yu, Y. Real-Time, Inexpensive, and Portable Measurement of Water Surface Velocity through Smartphone. Water 2020, 12, 3358. [Google Scholar] [CrossRef]
- Ma, J.; Niu, X.; Liu, X.; Wang, Y.; Wen, T.; Zhang, J. Thermal Infrared Imagery Integrated with Terrestrial Laser Scanning and Particle Tracking Velocimetry for Characterization of Landslide Model Failure. Sensors 2019, 20, 219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nering, K.; Rup, K. An improved algebraic model for by-pass transition for calculation of transitional flow in pipe and parallel-plate channels. Therm. Sci. 2019, 23, 1123–1131. [Google Scholar] [CrossRef] [Green Version]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables: Part I — Model Formulation. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar] [CrossRef] [Green Version]
- Langtry, R.B.; Menter, F.R.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A Correlation-Based Transition Model Using Local Variables—Part II: Test Cases and Industrial Applications. J. Turbomach. 2004, 128, 423–434. [Google Scholar] [CrossRef]
- Abraham, J.P.; Sparrow, E.M.; Tong, J.C.K. Breakdown of Laminar Pipe Flow into Transitional Intermittency and Subsequent Attainment of Fully Developed Intermittent or Turbulent Flow. Numer. Heat Transf. Part B Fundam. 2008, 54, 103–115. [Google Scholar] [CrossRef]
- Rabani, M.; Madessa, H.B.; Nord, N. Building Retrofitting through Coupling of Building Energy Simulation-Optimization Tool with CFD and Daylight Programs. Energies 2021, 14, 2180. [Google Scholar] [CrossRef]
- Russo, F.; Basse, N.T. Scaling of turbulence intensity for low-speed flow in smooth pipes. Flow Meas. Instrum. 2016, 52, 101–114. [Google Scholar] [CrossRef]
- Badar, A.; Buchholz, R.; Lou, Y.; Ziegler, F. CFD based analysis of flow distribution in a coaxial vacuum tube solar collector with laminar flow conditions. Int. J. Energy Environ. Eng. 2012, 3, 24. [Google Scholar] [CrossRef] [Green Version]
- García-Guendulain, J.; Riesco-Avila, J.; Elizalde-Blancas, F.; Belman-Flores, J.; Serrano-Arellano, J. Numerical Study on the Effect of Distribution Plates in the Manifolds on the Flow Distribution and Thermal Performance of a Flat Plate Solar Collector. Energies 2018, 11, 1077. [Google Scholar] [CrossRef] [Green Version]
- Langtry, R. Extending the Gamma-Rethetat Correlation based Transition Model for Crossflow Effects (Invited). In Proceedings of the 45th AIAA Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Cierpka, C.; Lütke, B.; Kähler, C.J. Higher order multi-frame particle tracking velocimetry. Exp. Fluids 2013, 54. [Google Scholar] [CrossRef] [Green Version]
- Hadad, T.; Gurka, R. Effects of particle size, concentration and surface coating on turbulent flow properties obtained using PIV/PTV. Exp. Therm. Fluid Sci. 2013, 45, 203–212. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Afzal, N.; Seena, A.; Bushra, A. Power Law Velocity Profile in Fully Developed Turbulent Pipe and Channel Flows. J. Hydraul. Eng. 2007, 133, 1080–1086. [Google Scholar] [CrossRef]




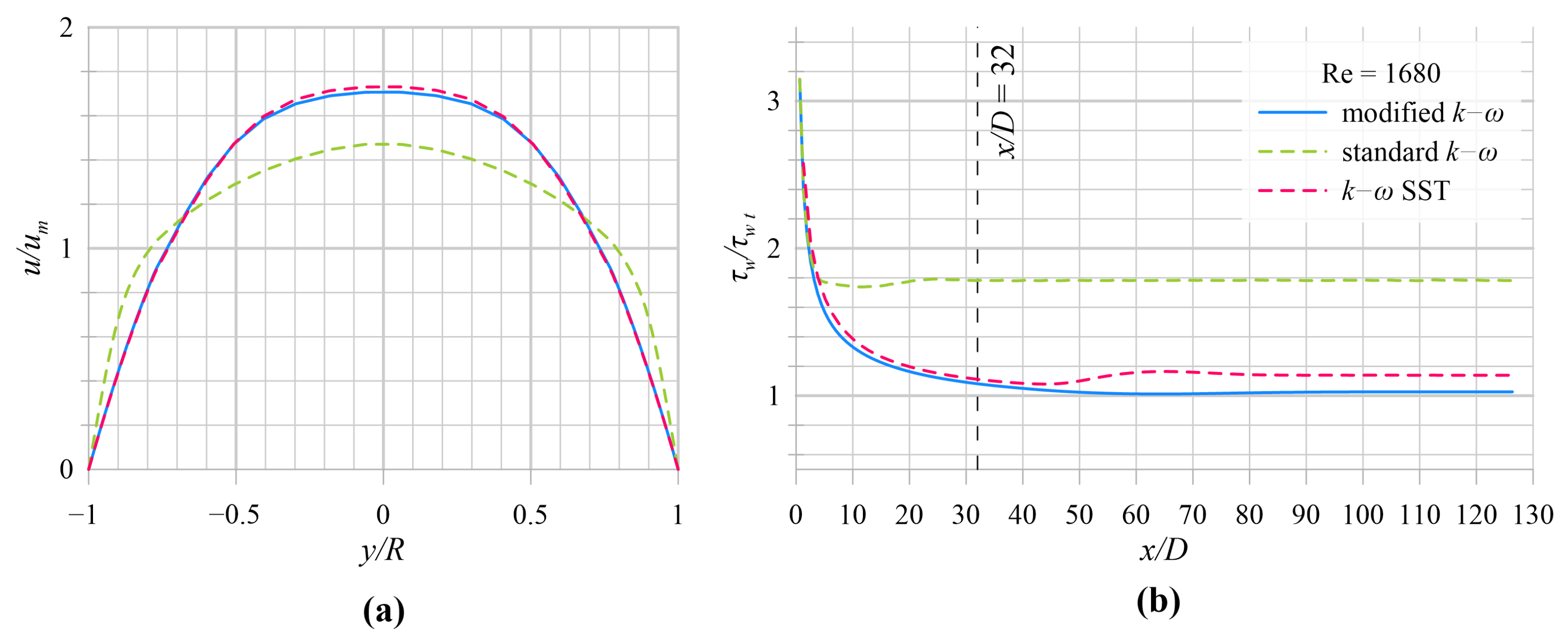
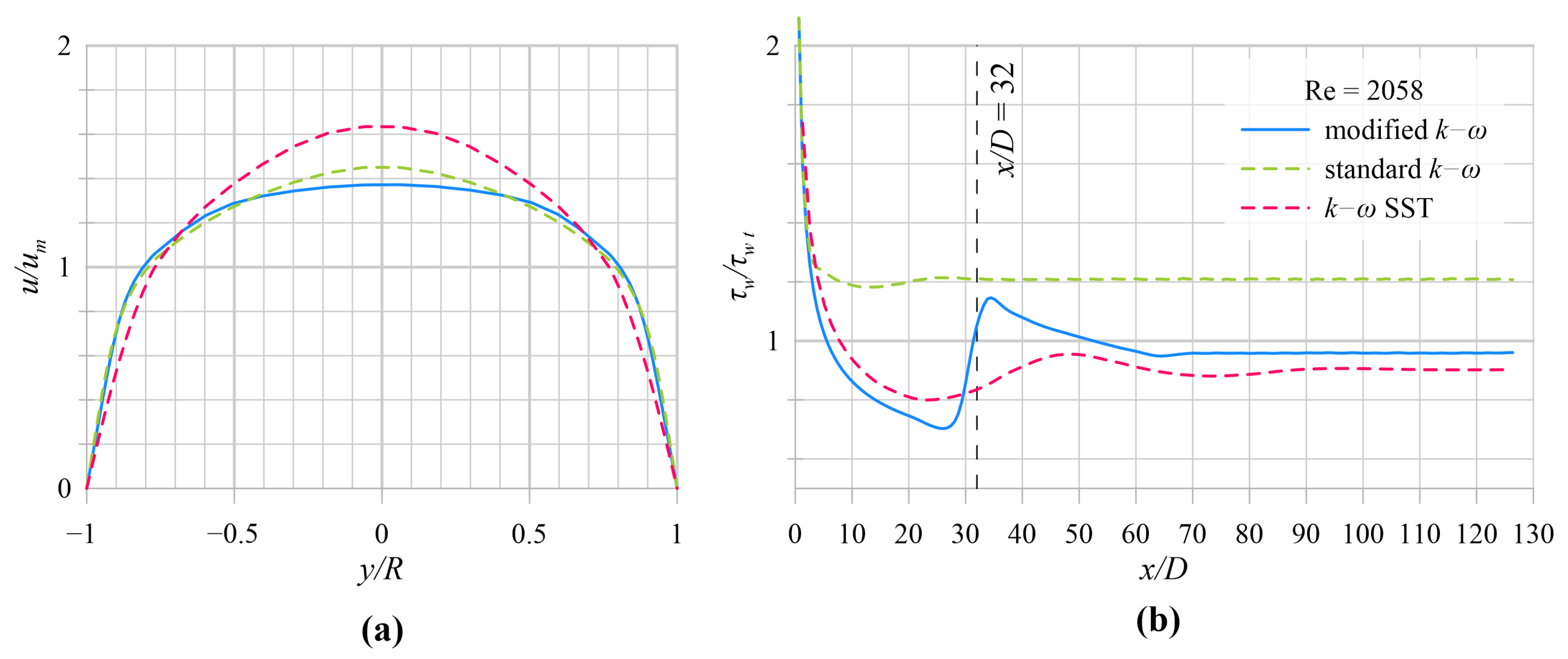
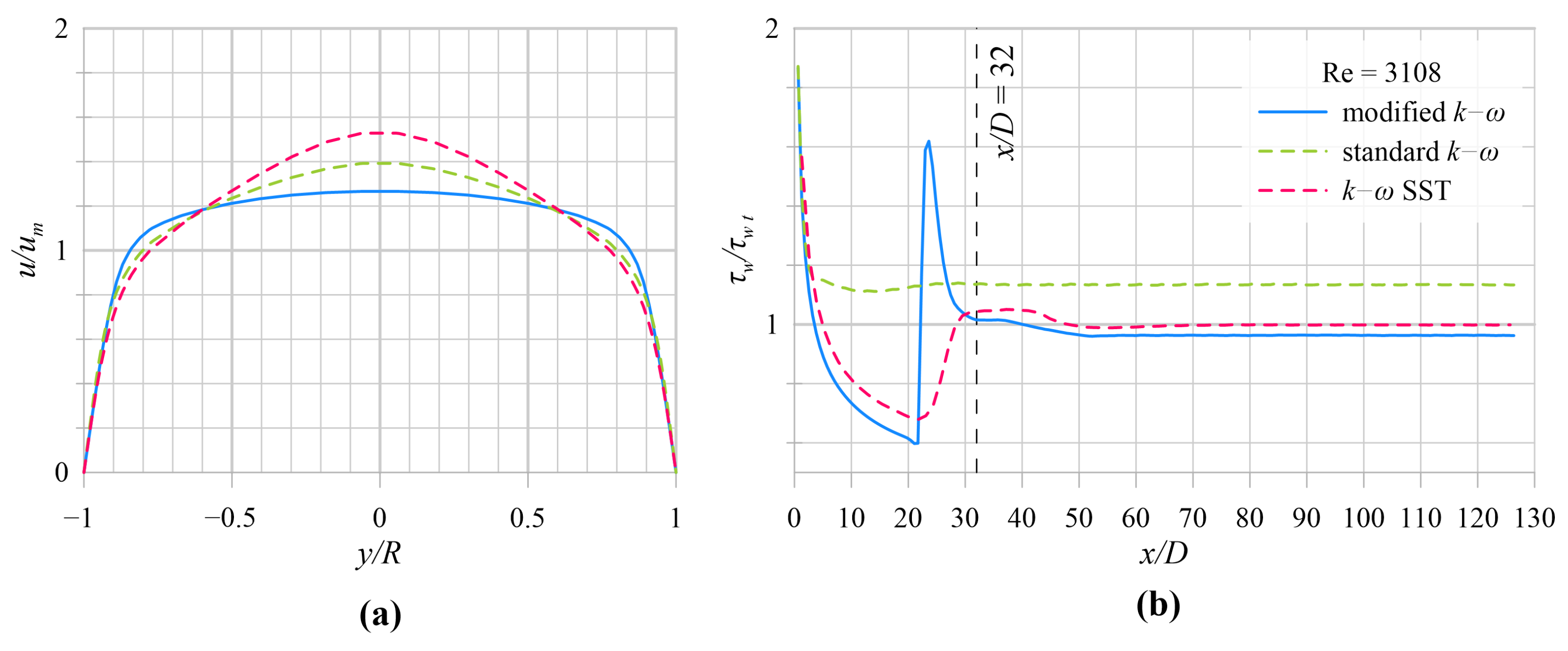
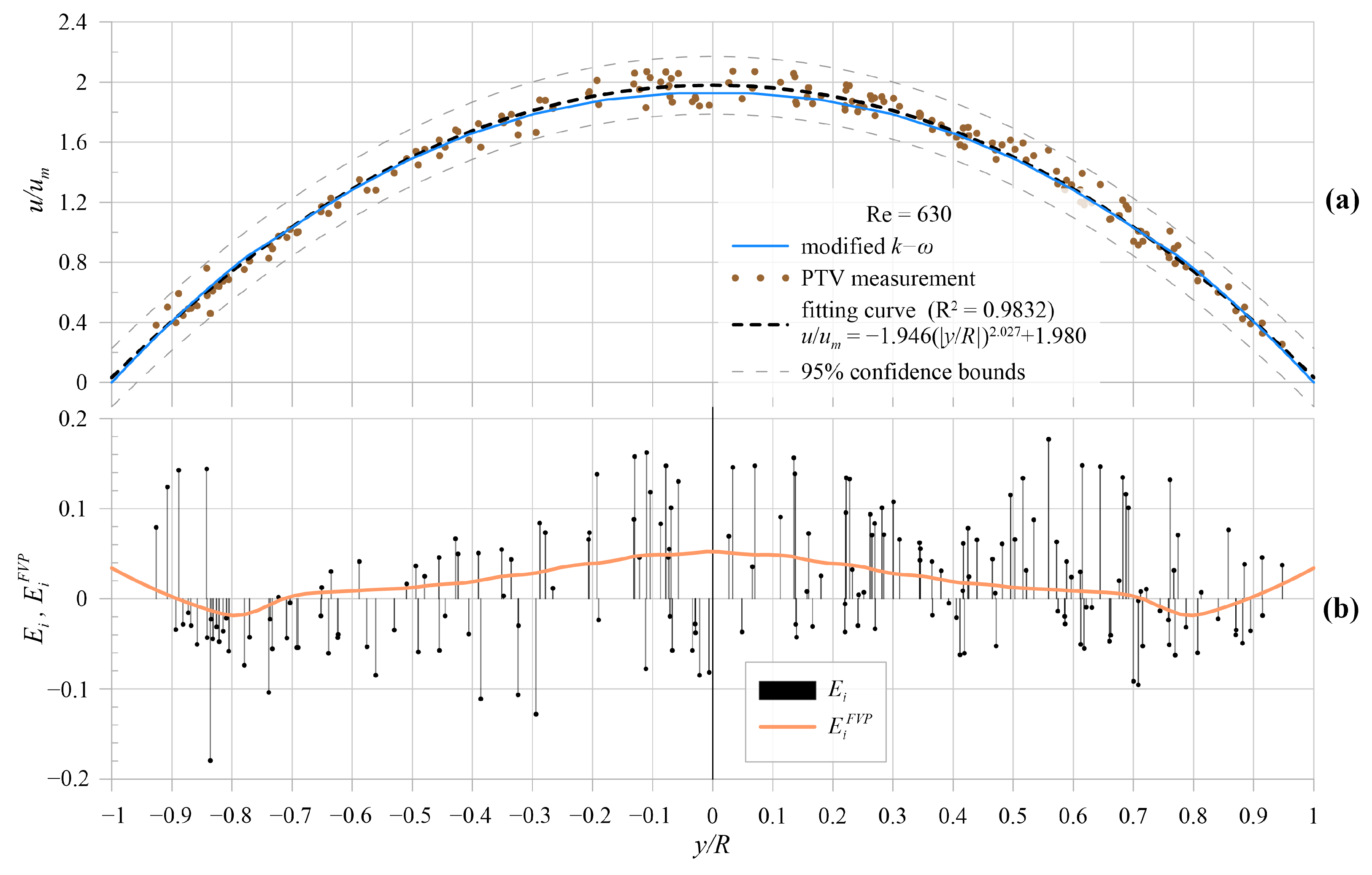
| 15.5 | 10 | 6.8 | 0.875 | 0.3 | 0.55 | 0.09 | 0.52 | 0.5 | 0.6 |
| Mesh No. | Elements | ||||
|---|---|---|---|---|---|
| 1 | 2,340,000 | 0.0002839 | 0.0007702 | 0.00096762 | 0.00294555 |
| 2 | 3,135,000 | 0.0002811 | 0.0007716 | 0.00102617 | 0.00221557 |
| 3 | 4,095,000 | 0.0002799 | 0.0007740 | 0.00131656 | 0.00257593 |
| 4 | 4,788,000 | 0.0002785 | 0.0007780 | 0.00143378 | 0.00283741 |
| 5 | 5,535,000 | 0.0002772 | 0.0007821 | 0.00145272 | 0.00288723 |
| 6 | 6,336,000 | 0.0002772 | 0.0007888 | 0.00147504 | 0.00292444 |
| Mesh No. | Elements | ||||
|---|---|---|---|---|---|
| 1 | 2,340,000 | 0.0002871 | 0.0011365 | 0.00114578 | unstable |
| 2 | 3,135,000 | 0.0002869 | 0.0009390 | 0.00154990 | 0.00315847 |
| 3 | 4,095,000 | 0.0002869 | 0.0009146 | 0.00146410 | 0.00313742 |
| 4 | 4,788,000 | 0.0002873 | 0.0008736 | 0.00138051 | 0.00302111 |
| 5 | 5,535,000 | 0.0002873 | 0.0008679 | 0.00136535 | 0.00299605 |
| 6 | 6,336,000 | 0.0002874 | 0.0008523 | 0.00135157 | 0.00297665 |
| Re | |
|---|---|
| 630 | 0.016 |
| 1680 | 0.026 |
| 2058 | 0.036 |
| 3108 | 0.051 |
| Re | Inlet [%] | |
|---|---|---|
| 1680 | 6.3 | 102.4 |
| 2058 | 6.2 | 104.3 |
| 3108 | 5.9 | 108.4 |
| Range | 0–45 m/s |
| Accuracy | 0–0.5 m/s: cm/s |
| 0.5–1.5 m/s: cm/s | |
| >1.5 m/s: 4% | |
| Response time | 10 ms |
| Resolution | 0.01 m/s |
| Sensing element | platinum wire m |
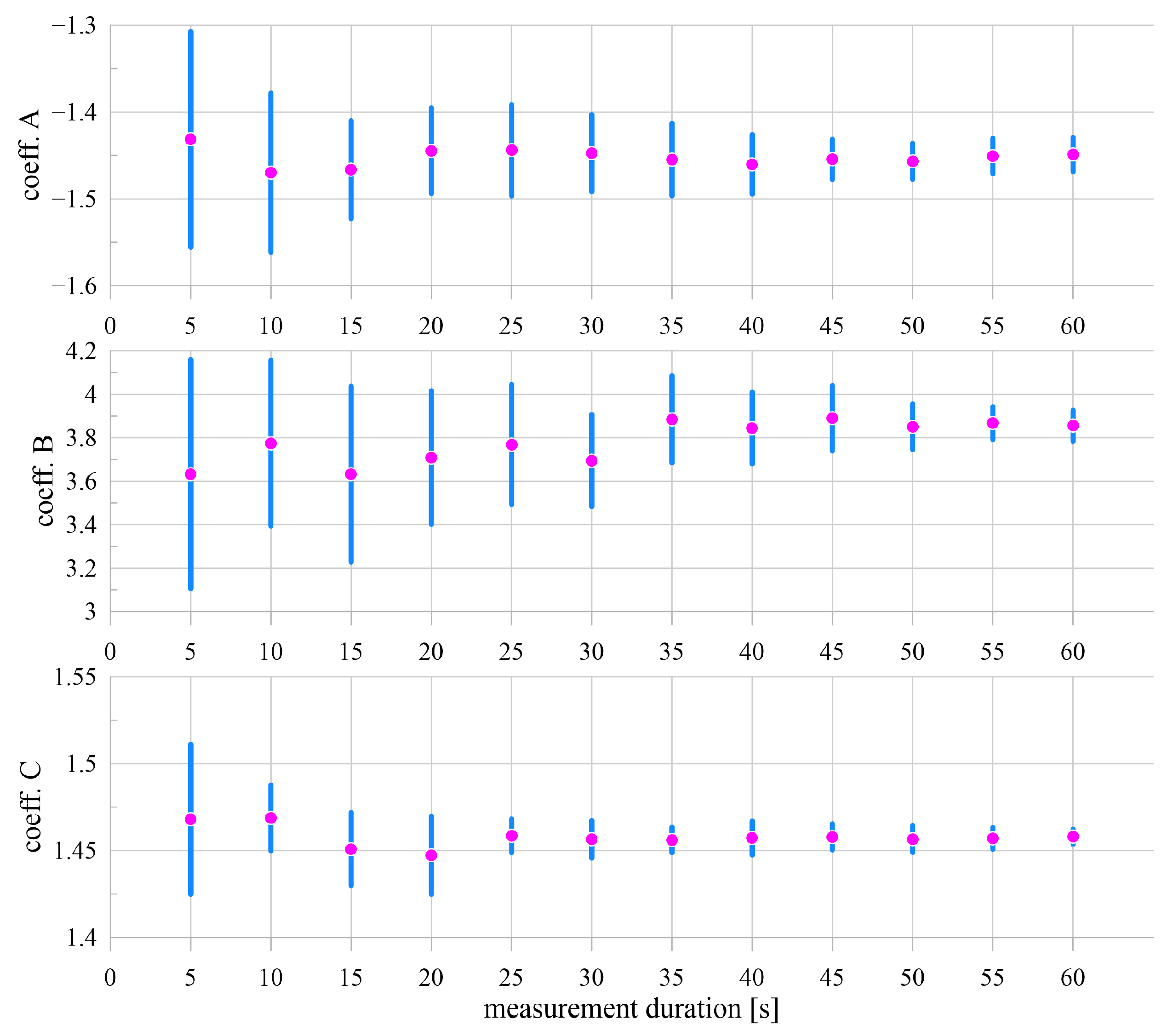
| Minimal Measurement Duration [s] | |||
|---|---|---|---|
| Coefficient of Equation (20) | A | B | C |
| Following average value of coefficient is varying less than 0.5% two times in a row | 45 | 60 | 35 |
| Following standard deviation value is for coefficient is less than 2% of average two times in a row | 45 | 60 | 35 |
| Re | Modified | |
|---|---|---|
| 630 | 0.072 | 0.078 |
| 1680 | 0.076 | 0.086 |
| 2058 | 0.151 | 0.119 |
| 3108 | 0.199 | 0.128 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nering, K.; Nering, K. Validation of Modified Algebraic Model during Transitional Flow in HVAC Duct. Energies 2021, 14, 3975. https://doi.org/10.3390/en14133975
Nering K, Nering K. Validation of Modified Algebraic Model during Transitional Flow in HVAC Duct. Energies. 2021; 14(13):3975. https://doi.org/10.3390/en14133975
Chicago/Turabian StyleNering, Konrad, and Krzysztof Nering. 2021. "Validation of Modified Algebraic Model during Transitional Flow in HVAC Duct" Energies 14, no. 13: 3975. https://doi.org/10.3390/en14133975
APA StyleNering, K., & Nering, K. (2021). Validation of Modified Algebraic Model during Transitional Flow in HVAC Duct. Energies, 14(13), 3975. https://doi.org/10.3390/en14133975






