A Methodology for Robust Load Reduction in Wind Turbine Blades Using Flow Control Devices
Abstract
1. Introduction
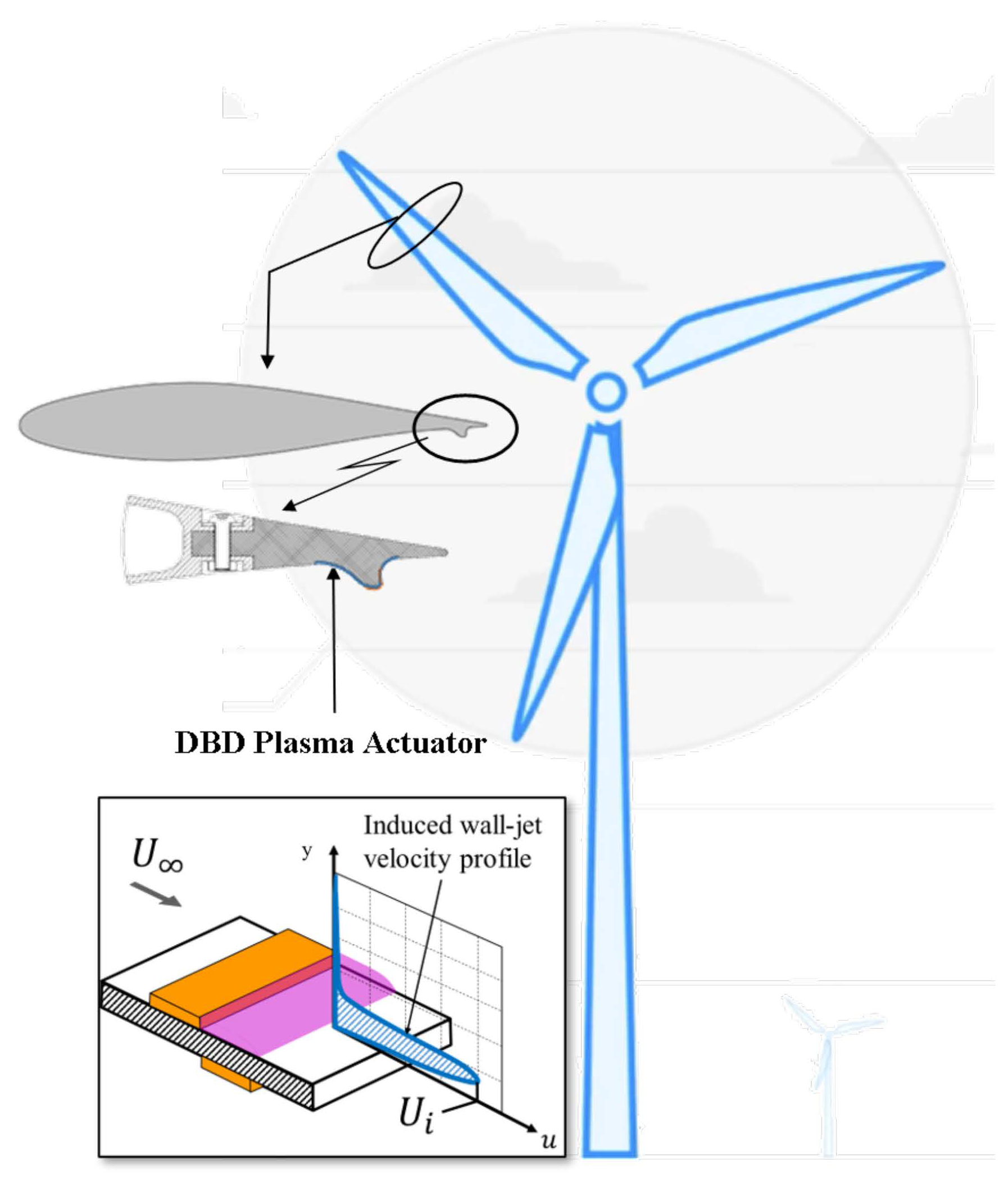
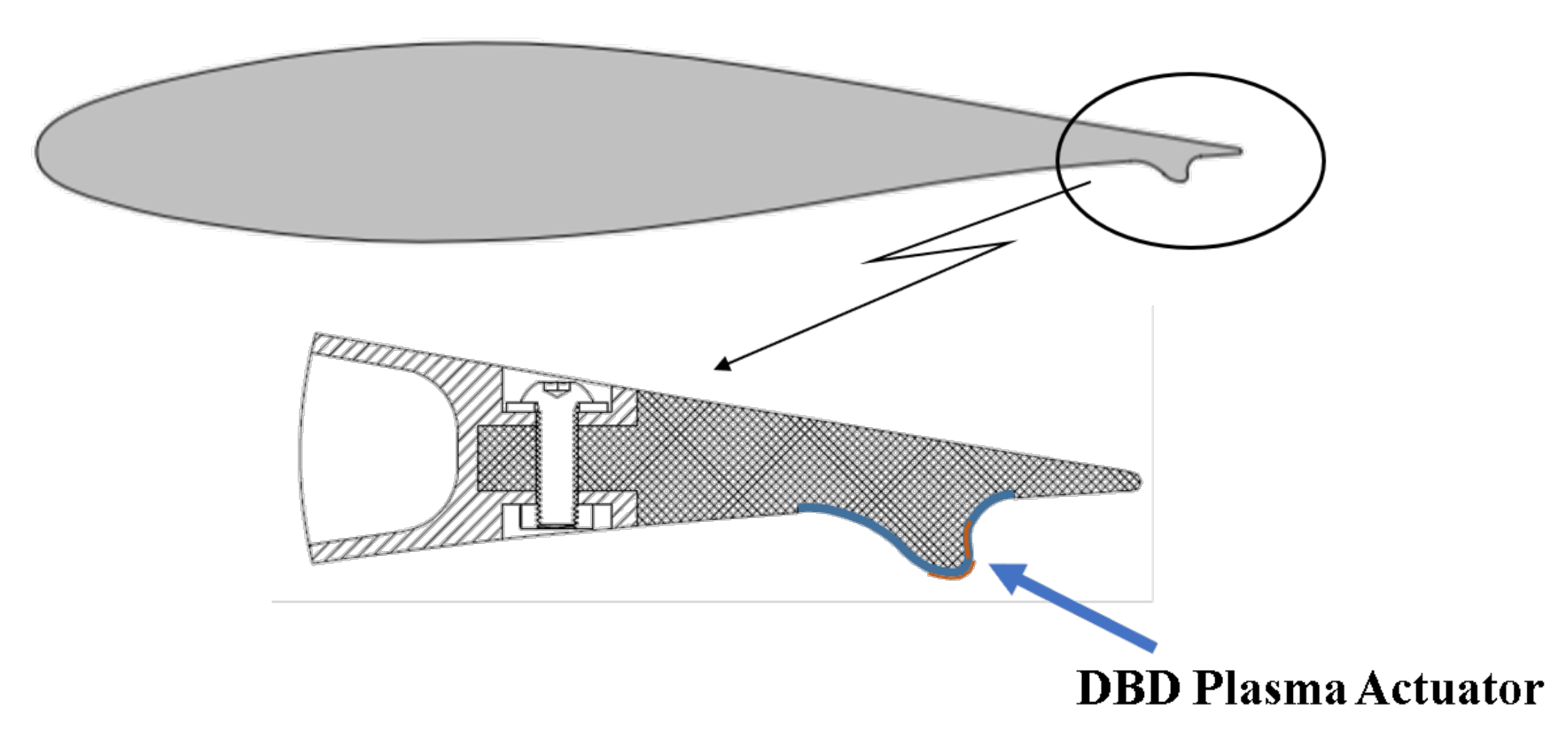
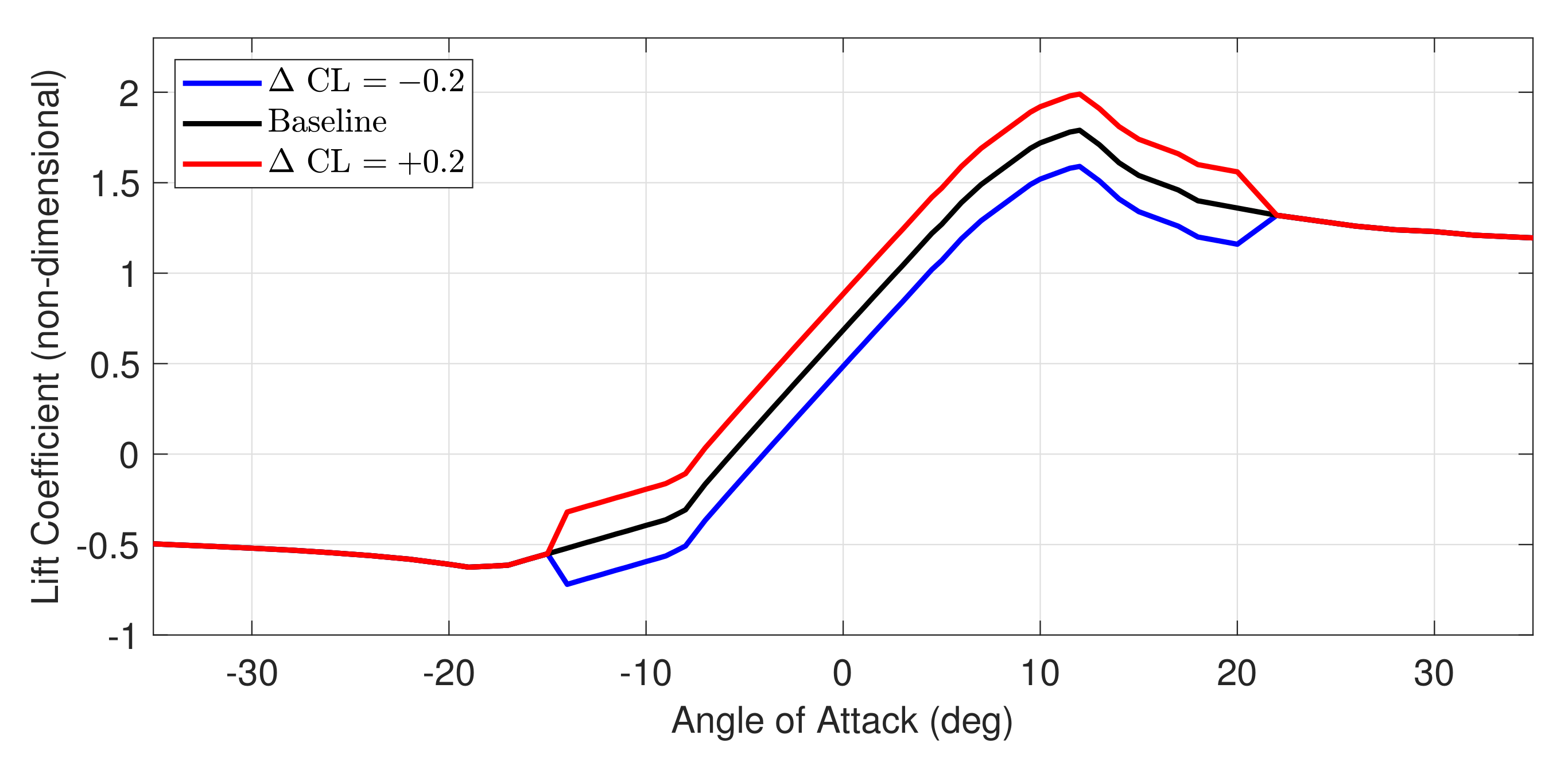
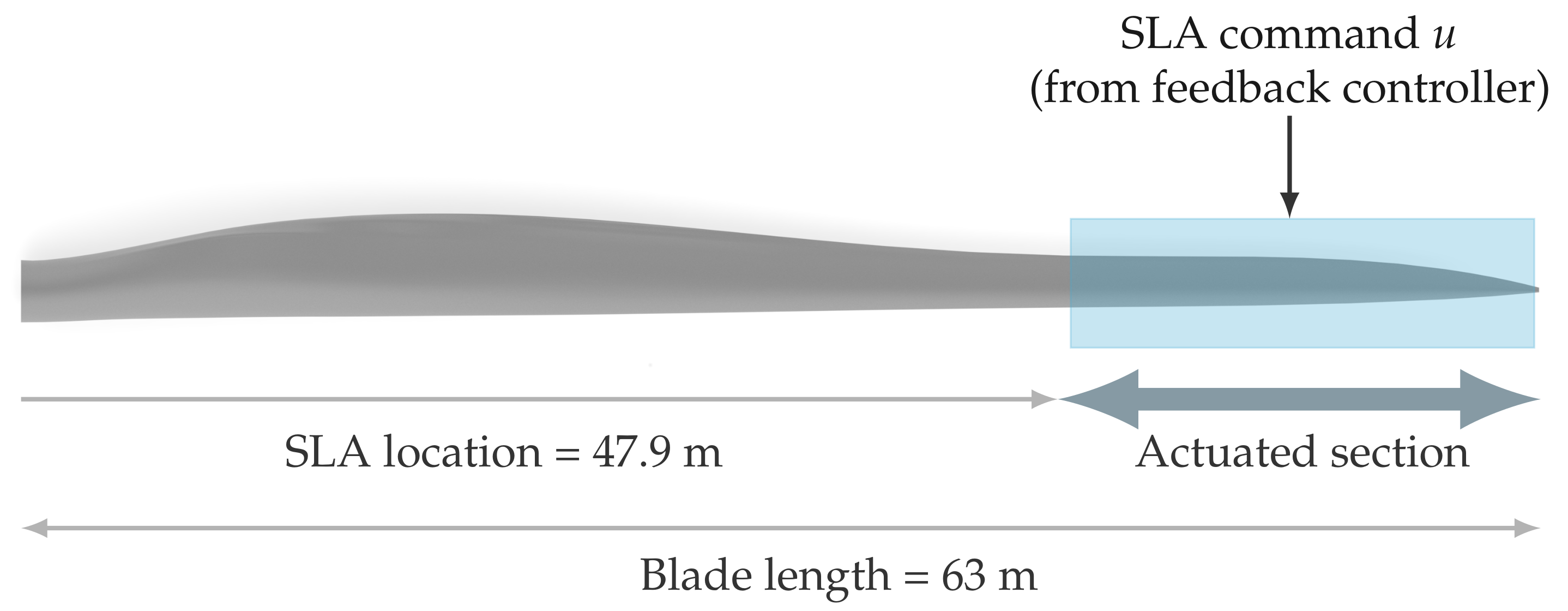
- Modeling the effect of the DBD plasma actuator as a dynamic change in local lift coefficient at the location where the actuator is placed. We refer to this modeling assumption as sectional lift actuation (SLA).
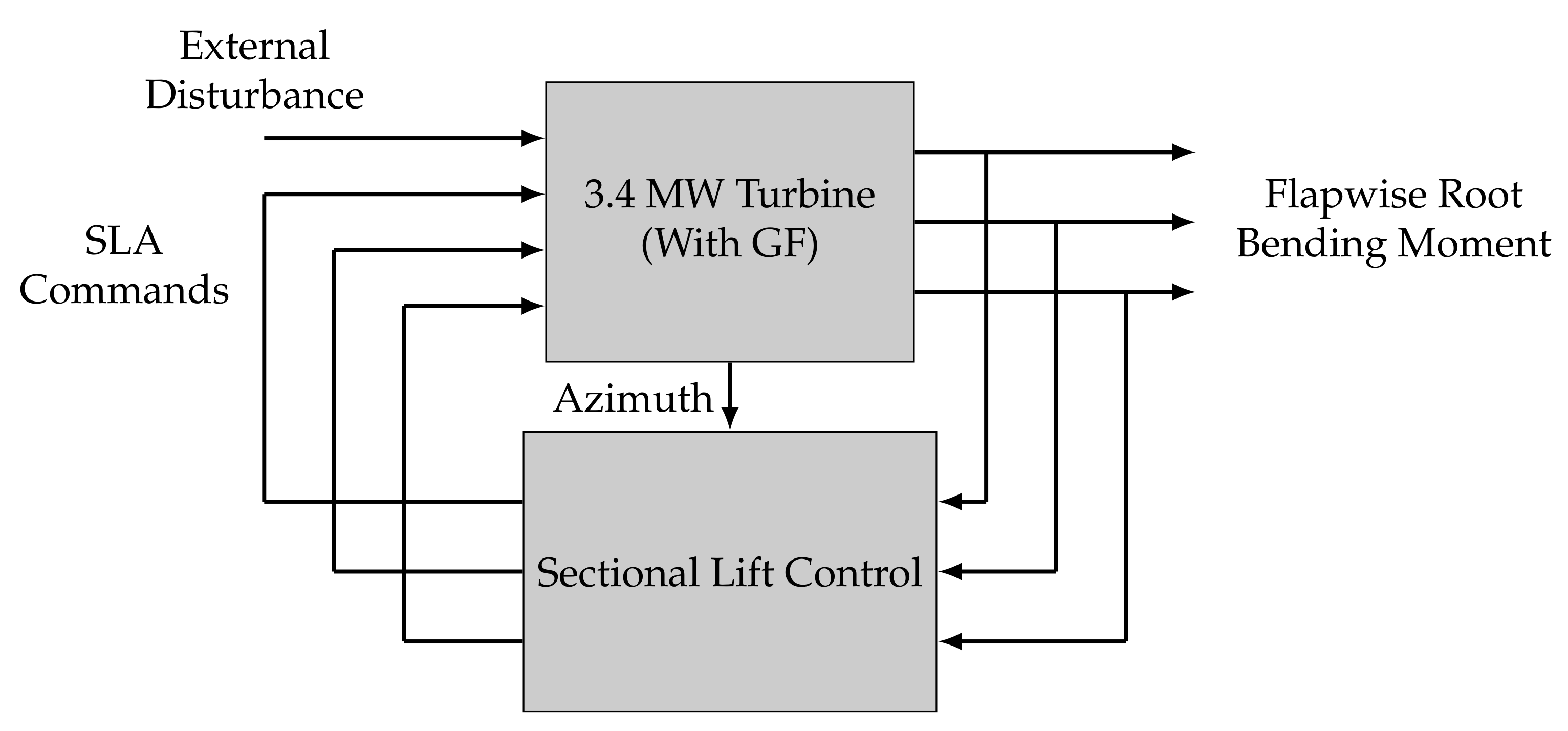
- A control system architecture based on the well-known multi-blade coordinate transformation [6] to reduce dynamic loads of the blade-root flapwise bending moments. This control system, which drives the sectional lift actuators, is coined sectional lift control (SLC).
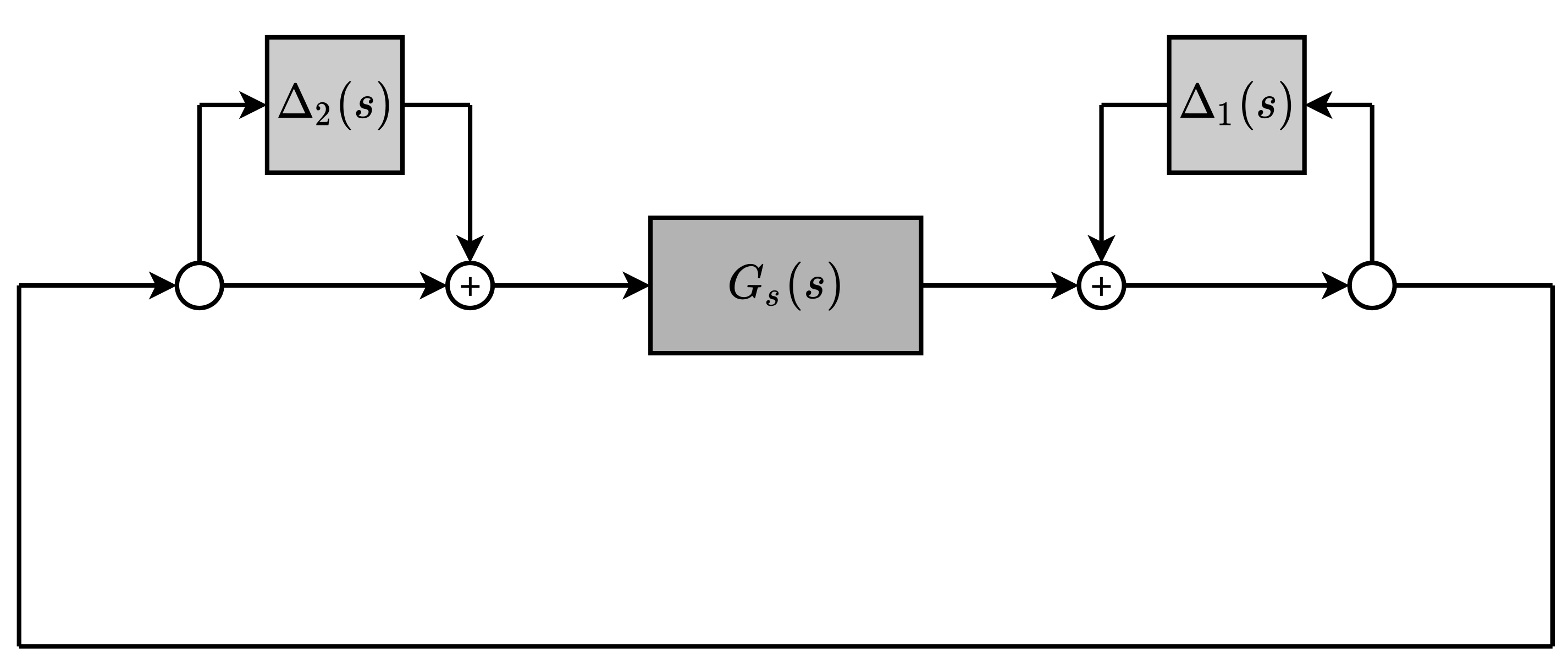
- A feedback control algorithm designed to achieve load reduction and robustness to both (a) parametric uncertainty in the design model and (b) unmodeled dynamics.
2. Turbine Specifications
3. Sectional Lift Actuators
4. Sectional Lift Control
4.1. SLC Design and Evaluation Criteria
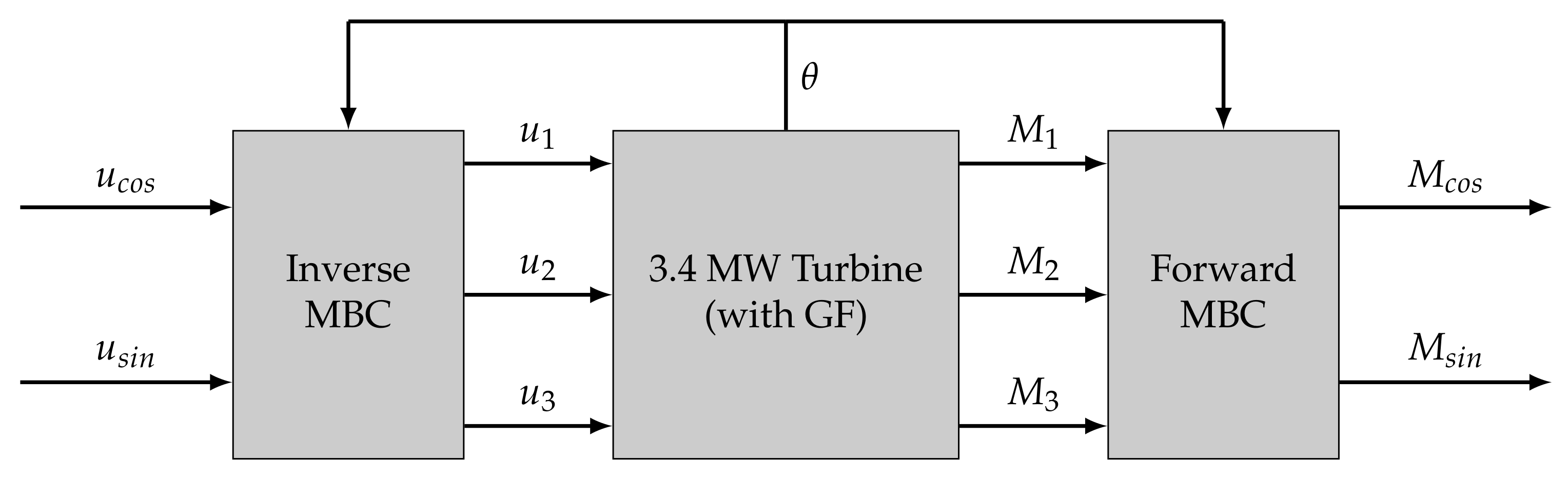
4.2. Multi-Blade Coordinate Transformation
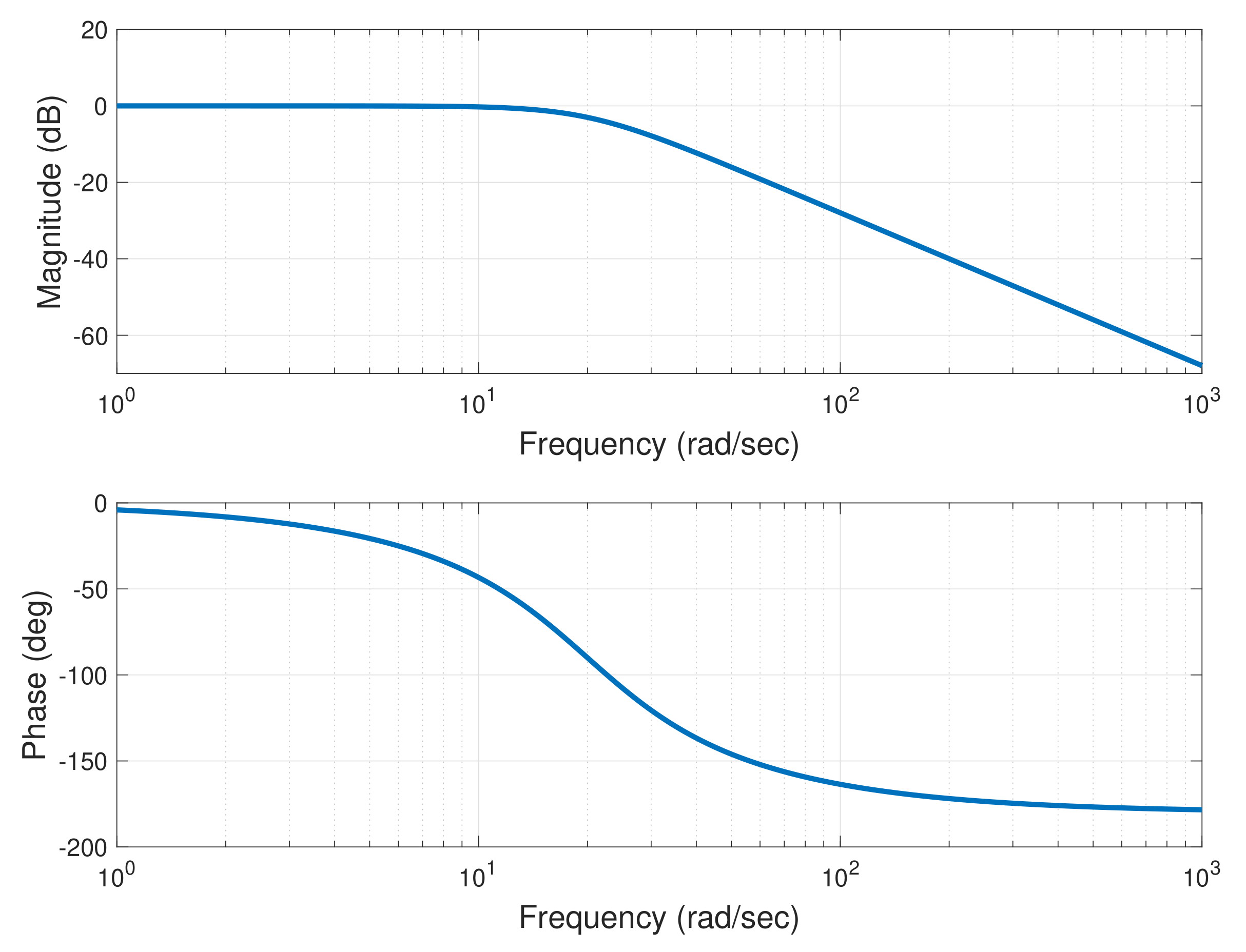
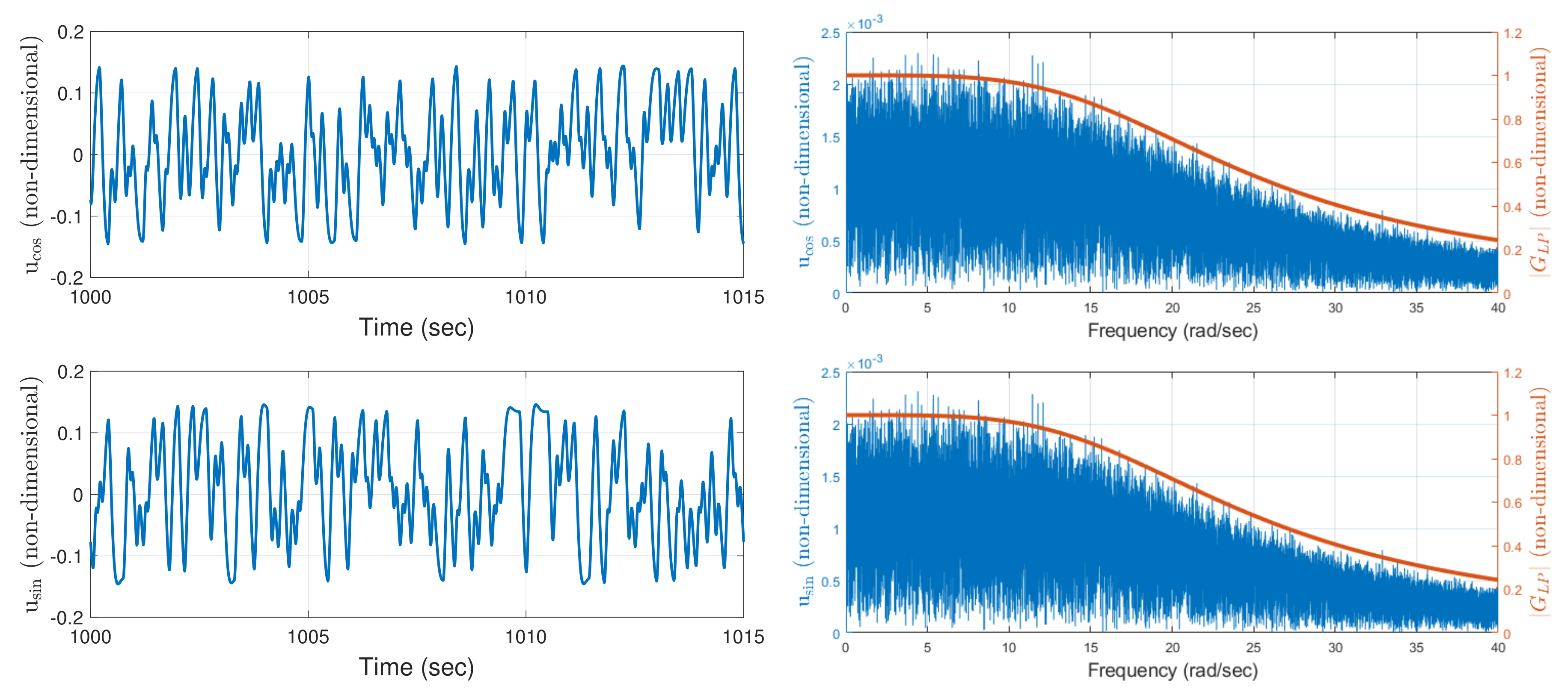
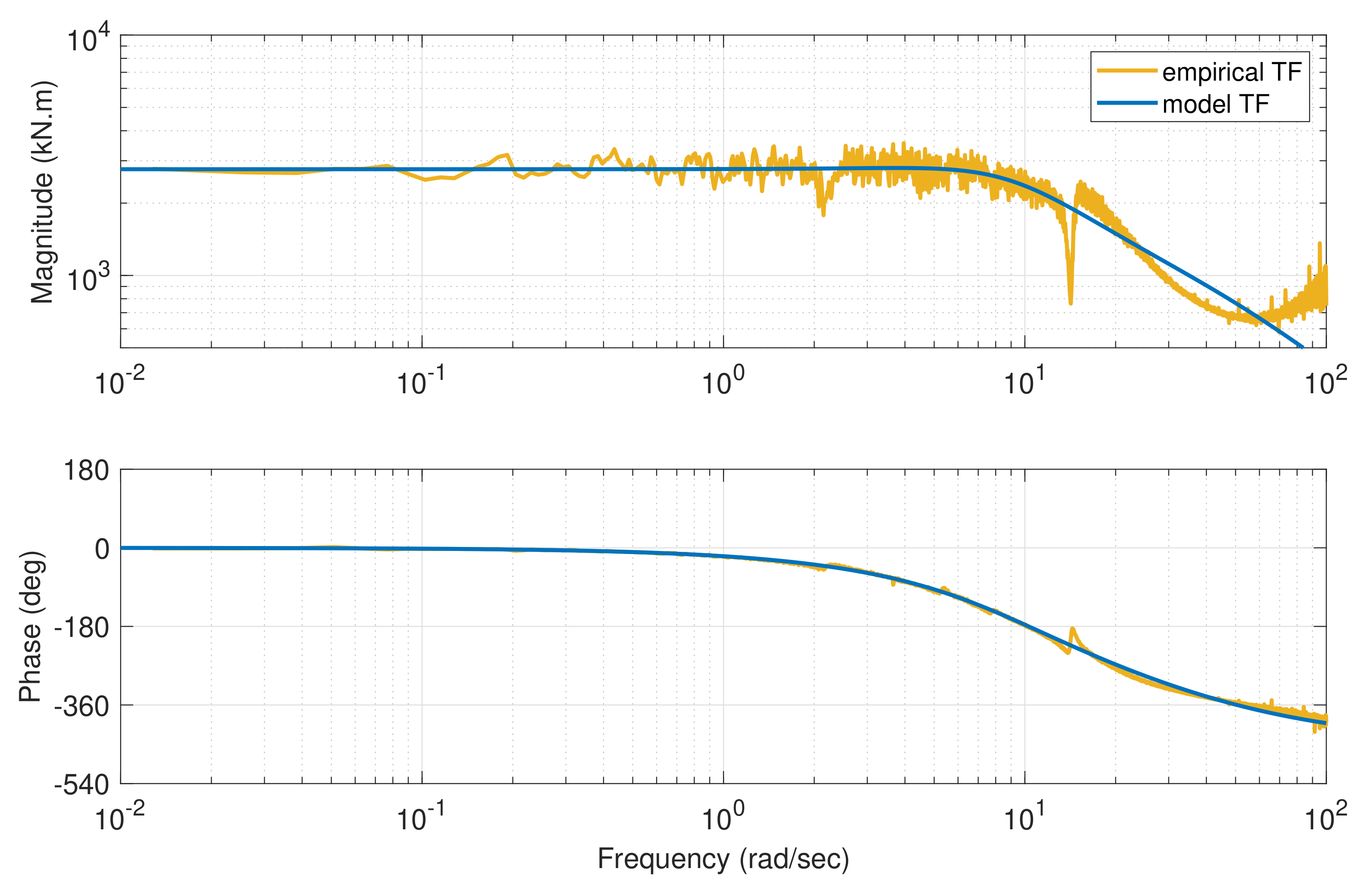
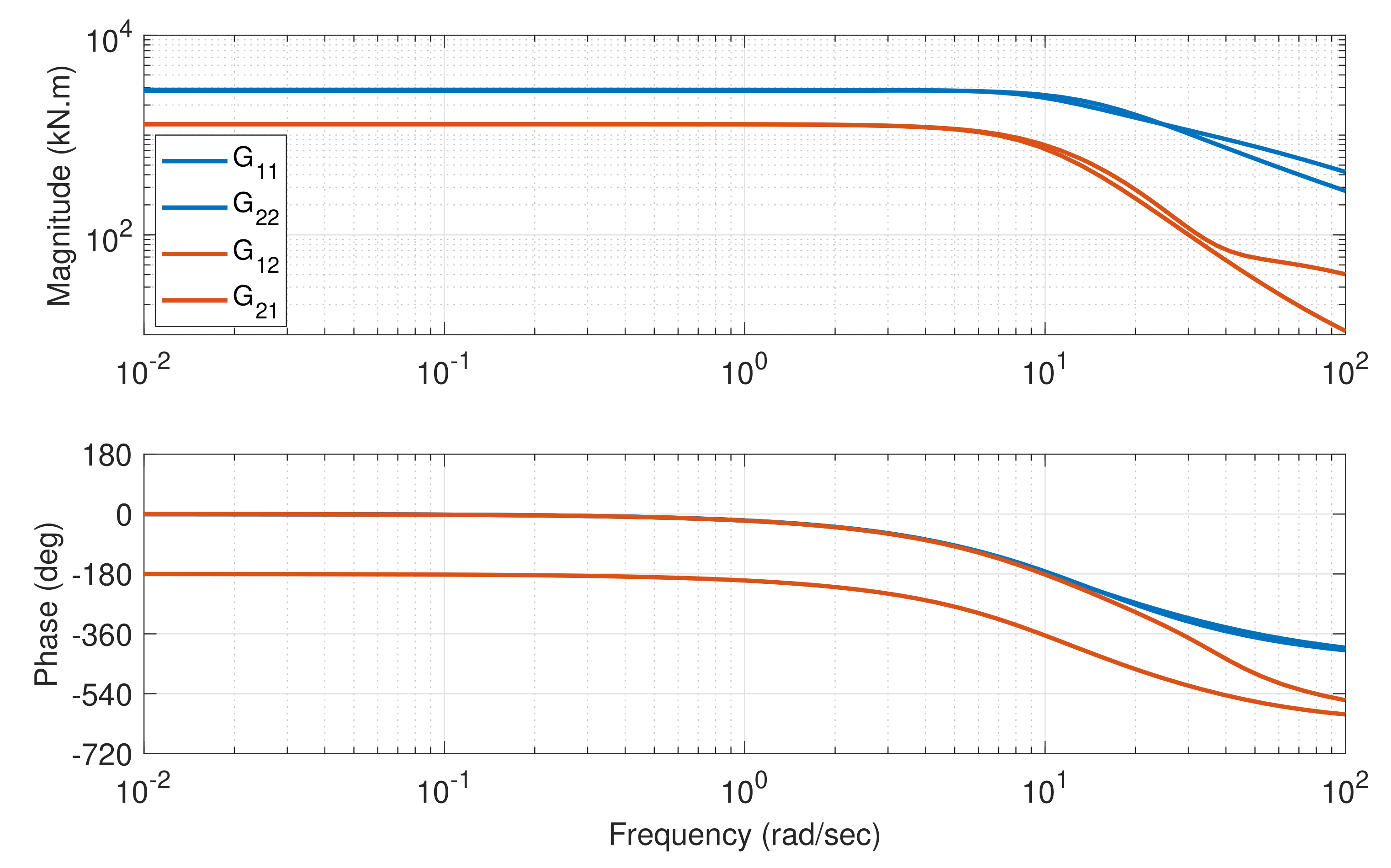
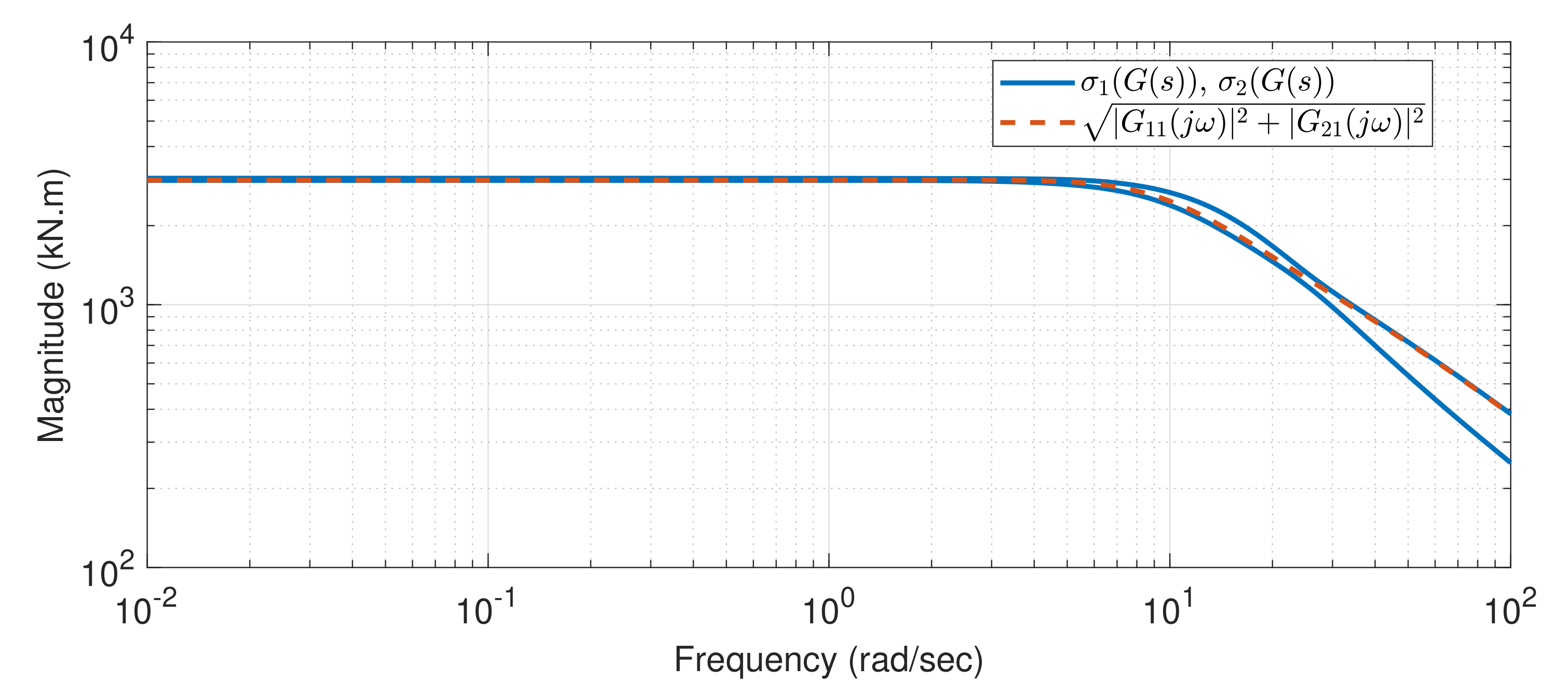
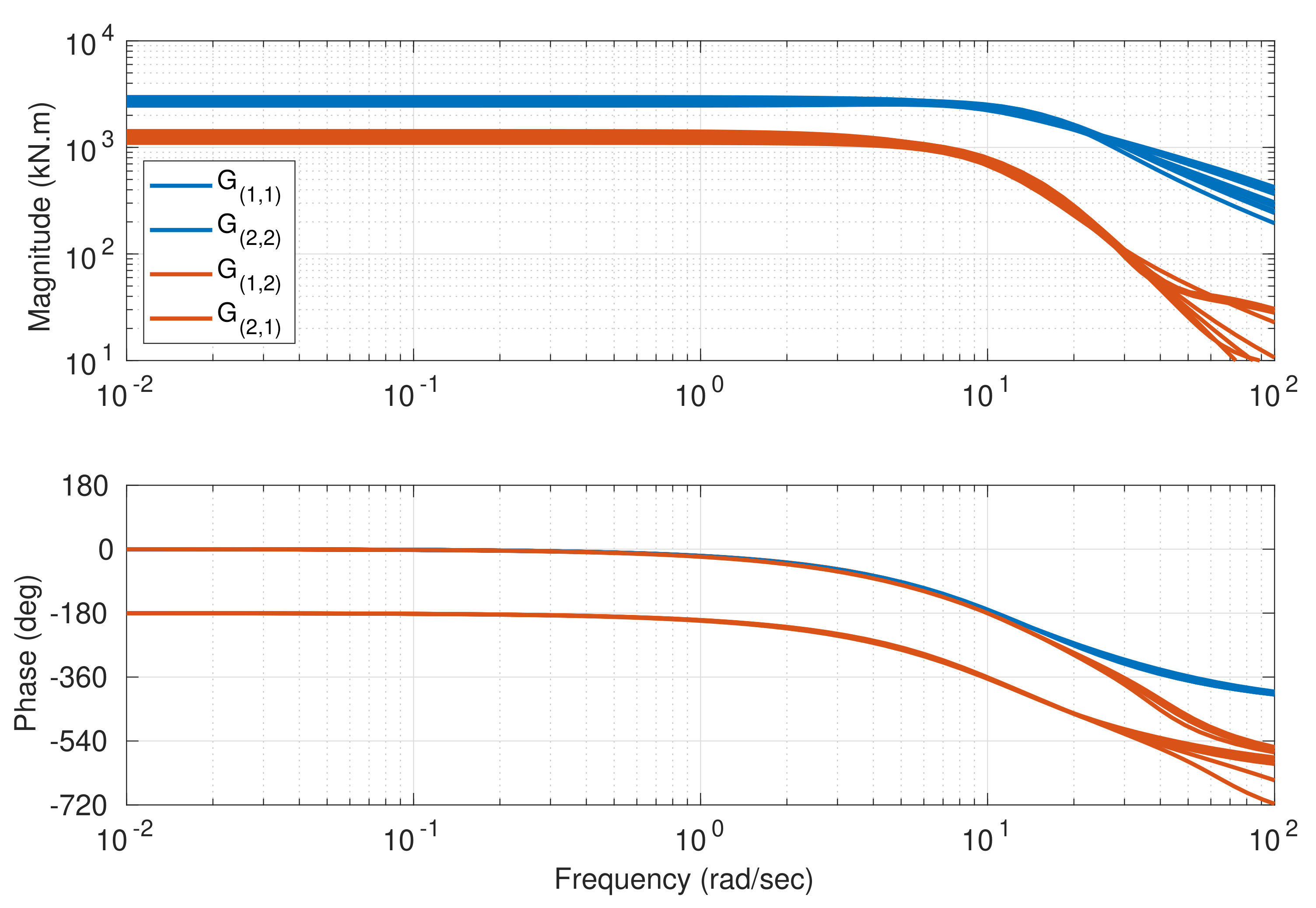
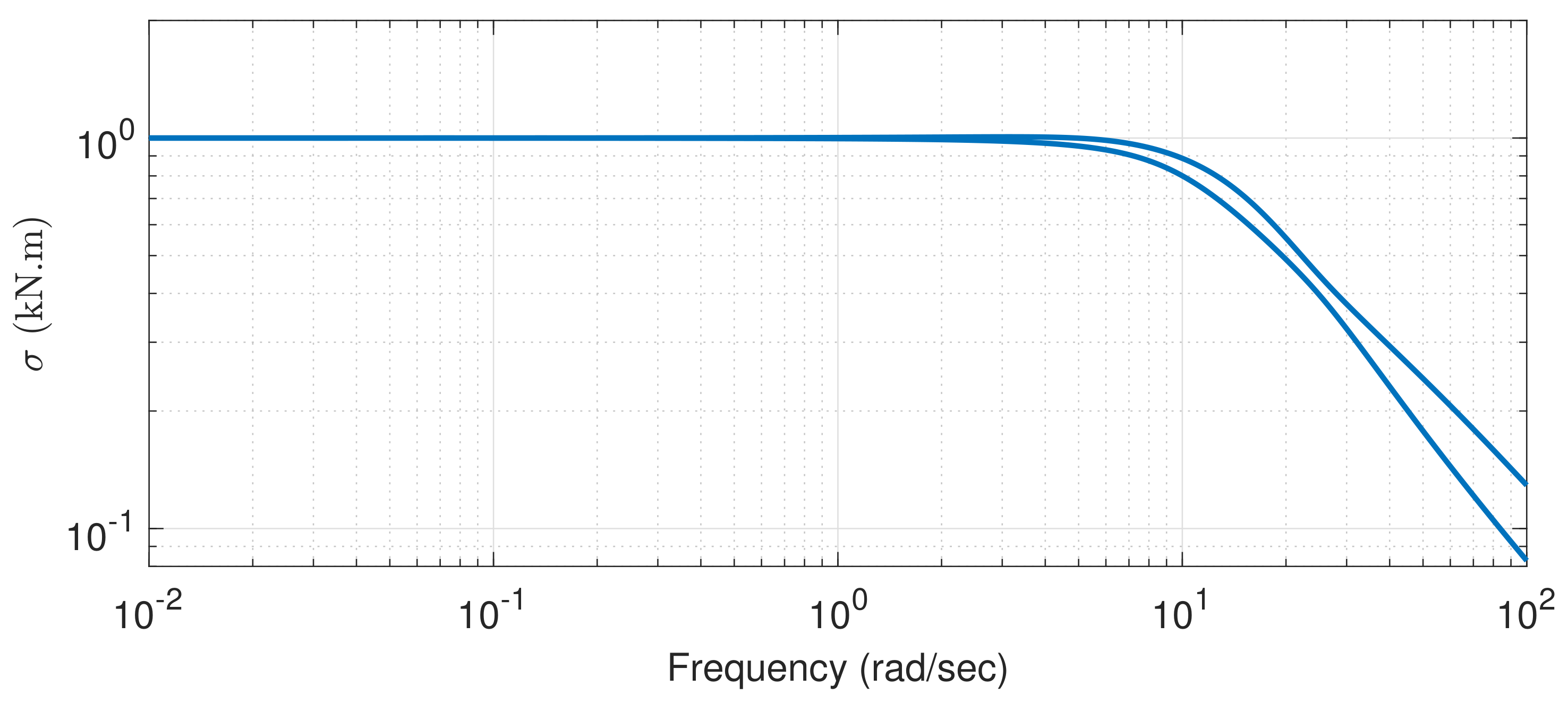
4.3. Design Model via System Identification
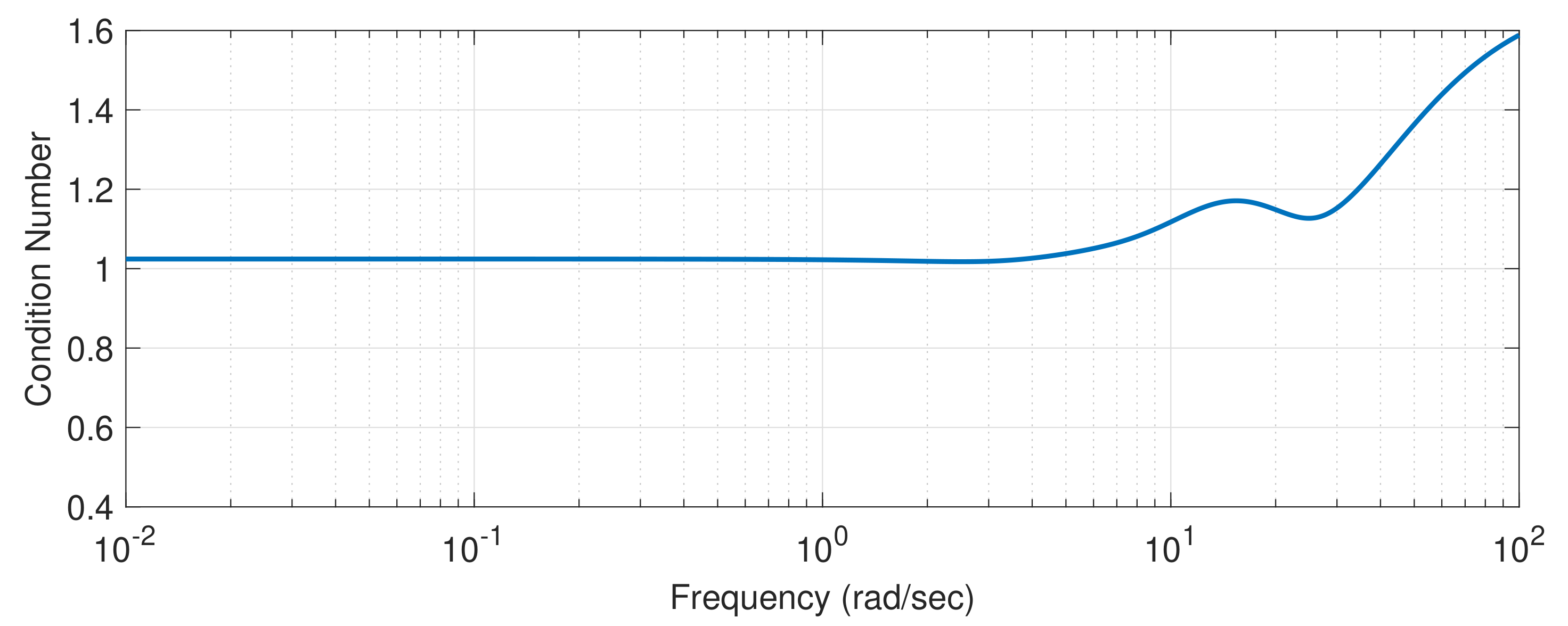
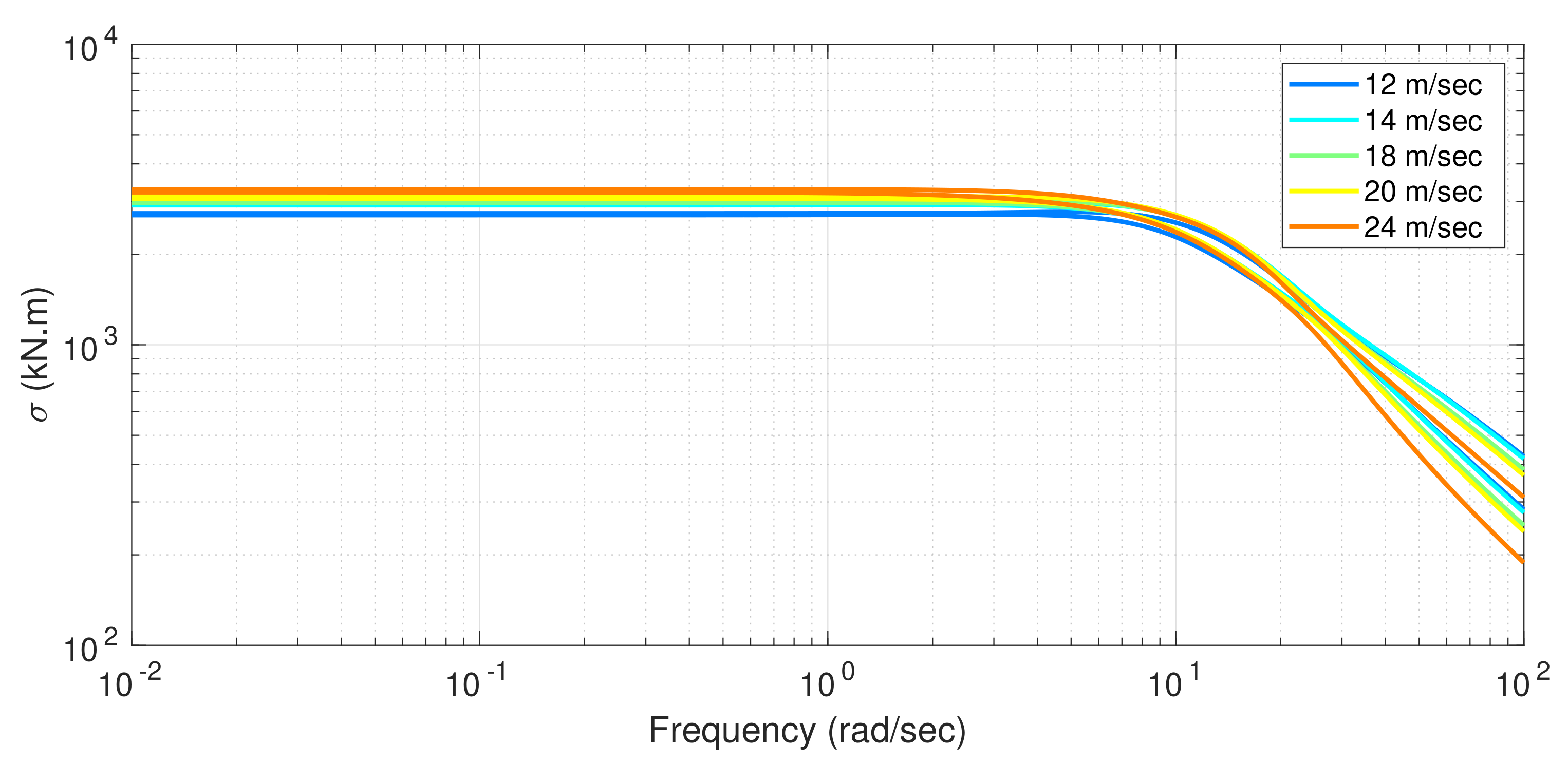
4.4. Variation of Design Model with Wind Speed
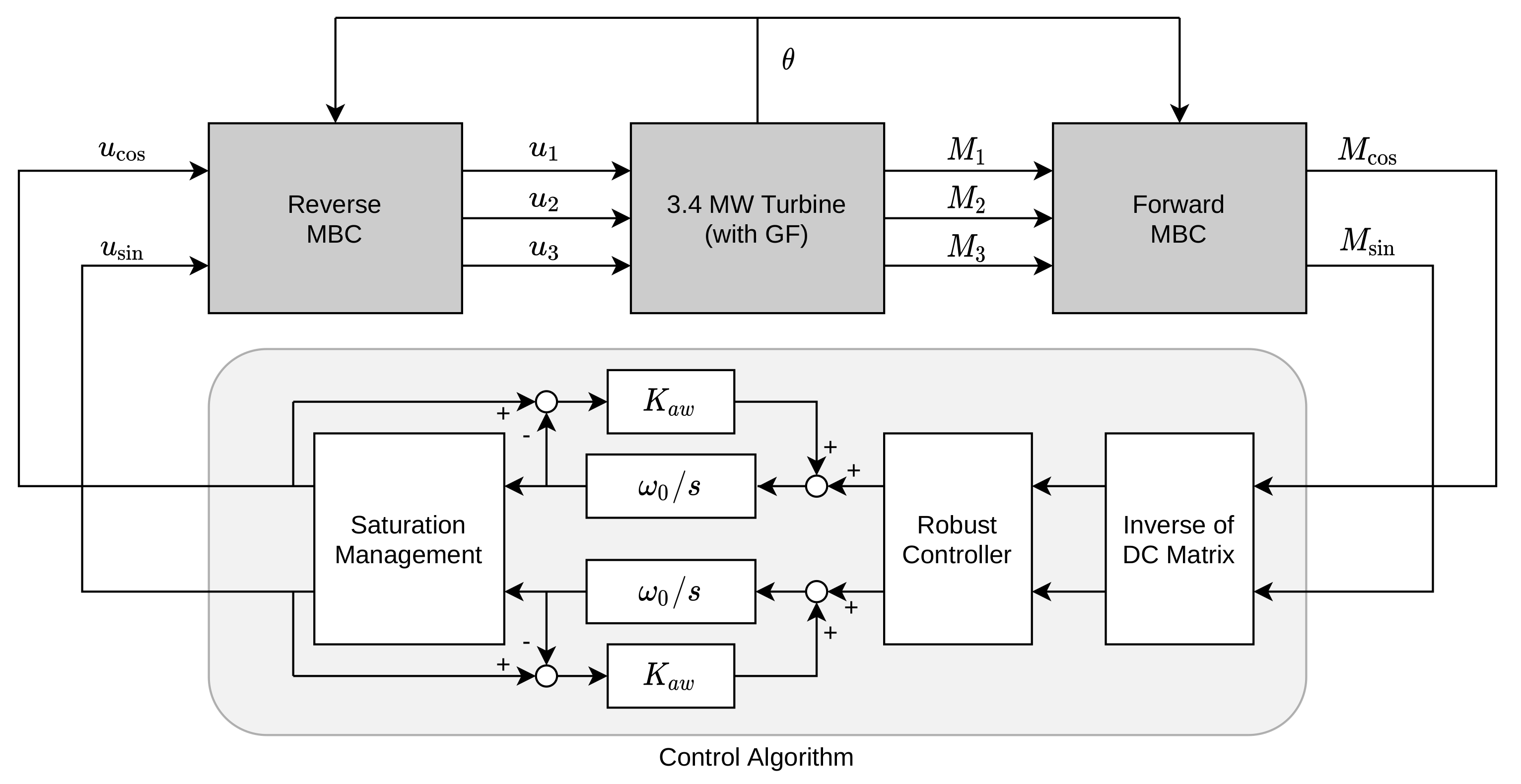
4.5. Sectional Lift Control Architecture
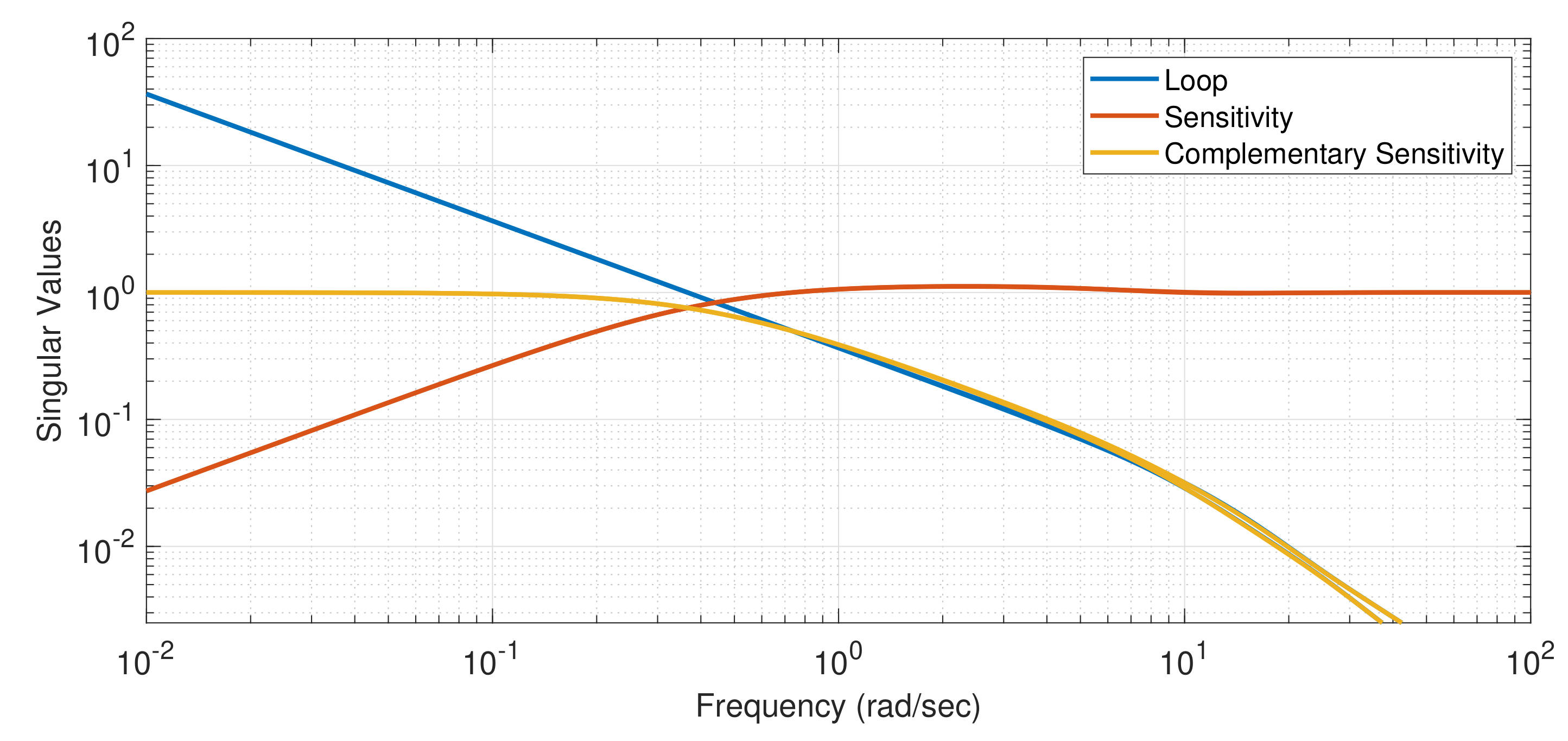
4.6. Synthesis of the Control Algorithm
Saturation Management
5. Loads and Performance Evaluation
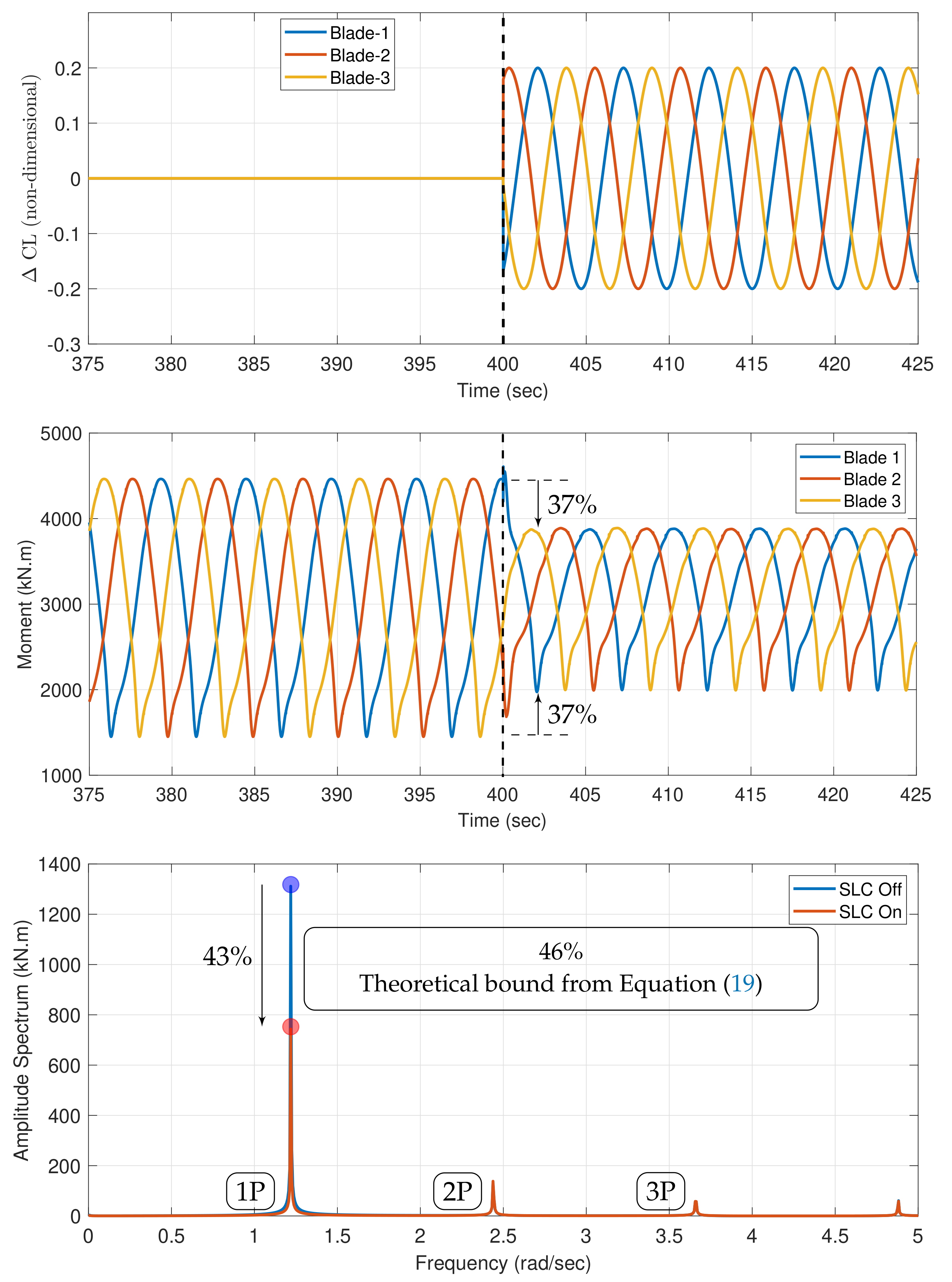
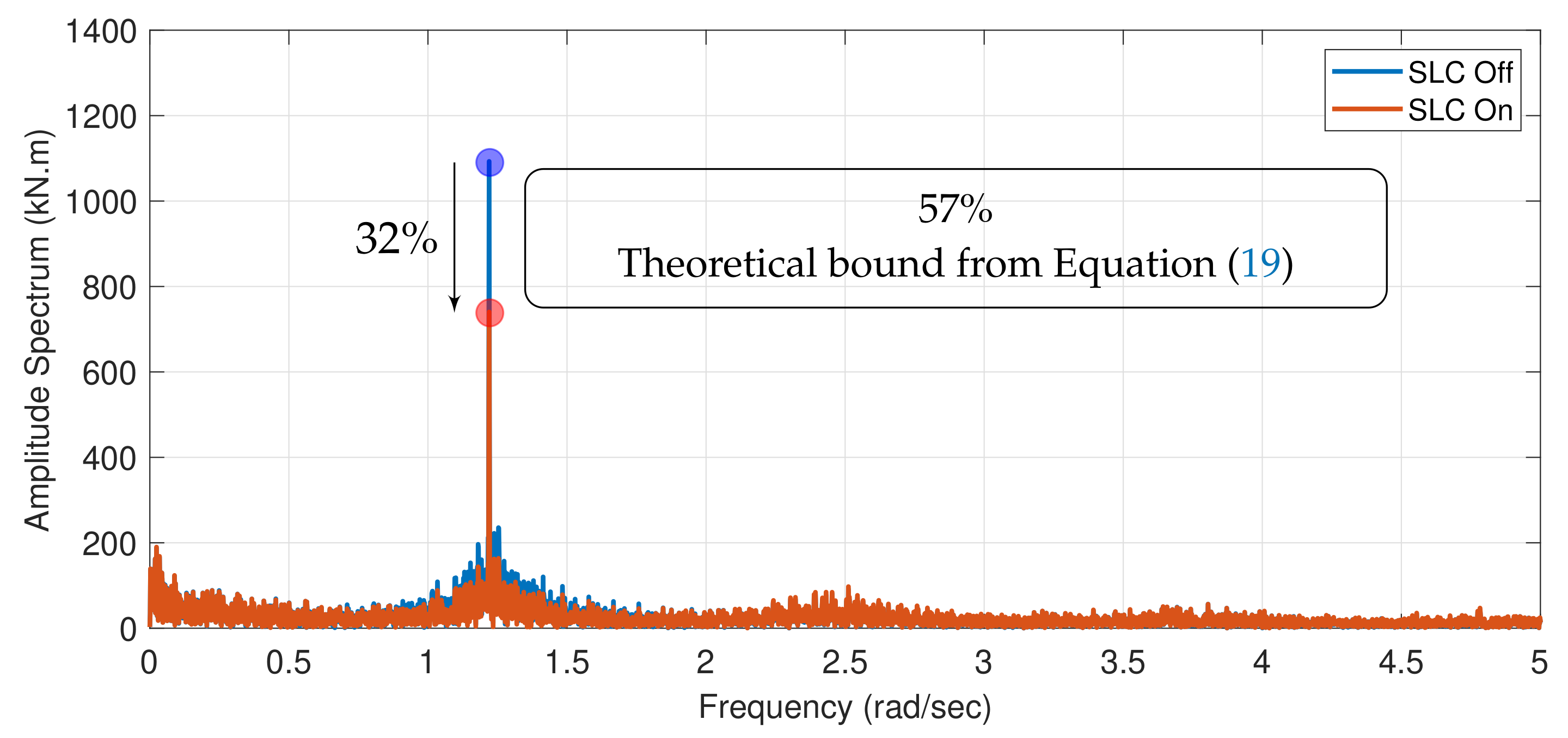
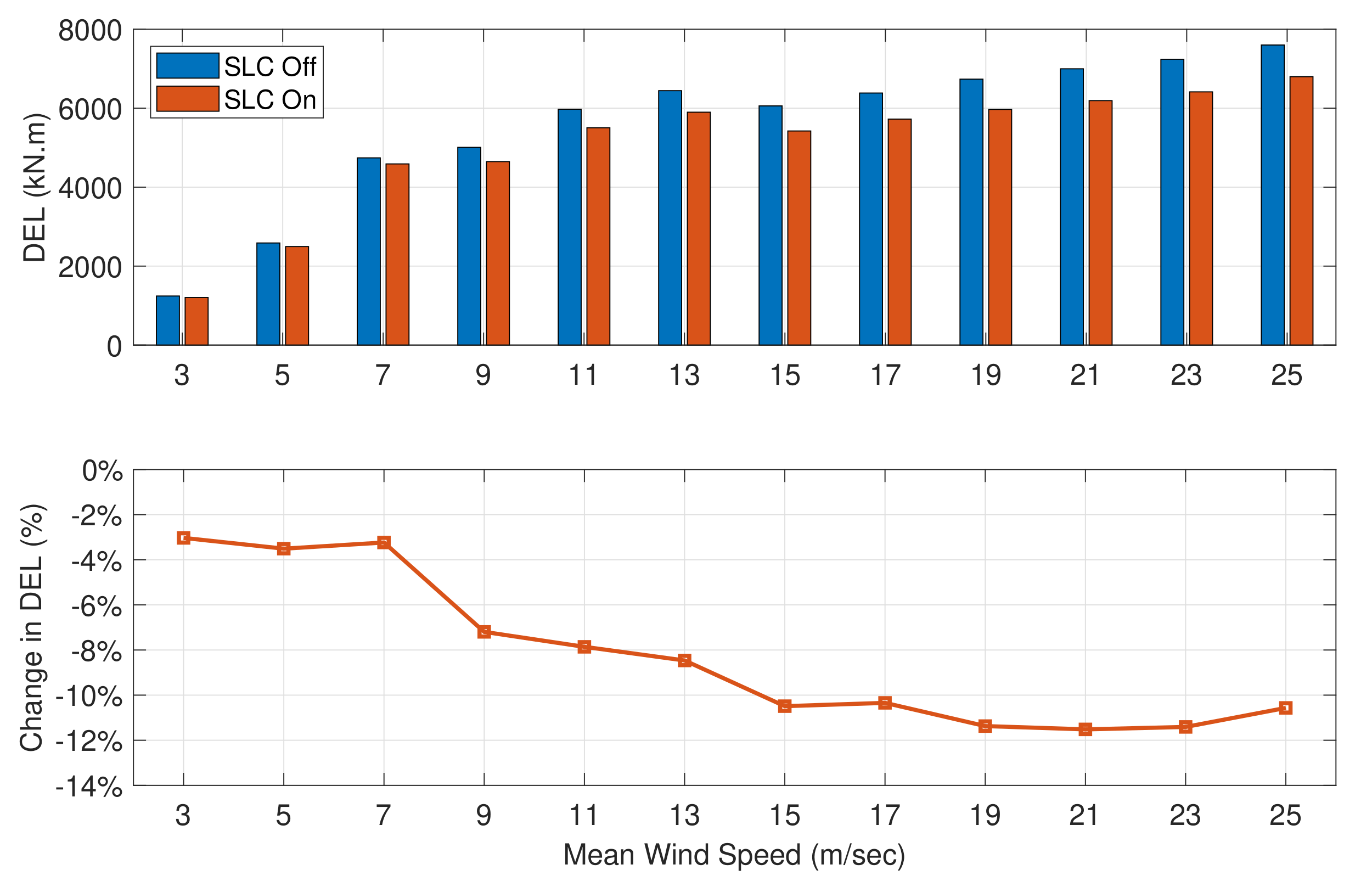
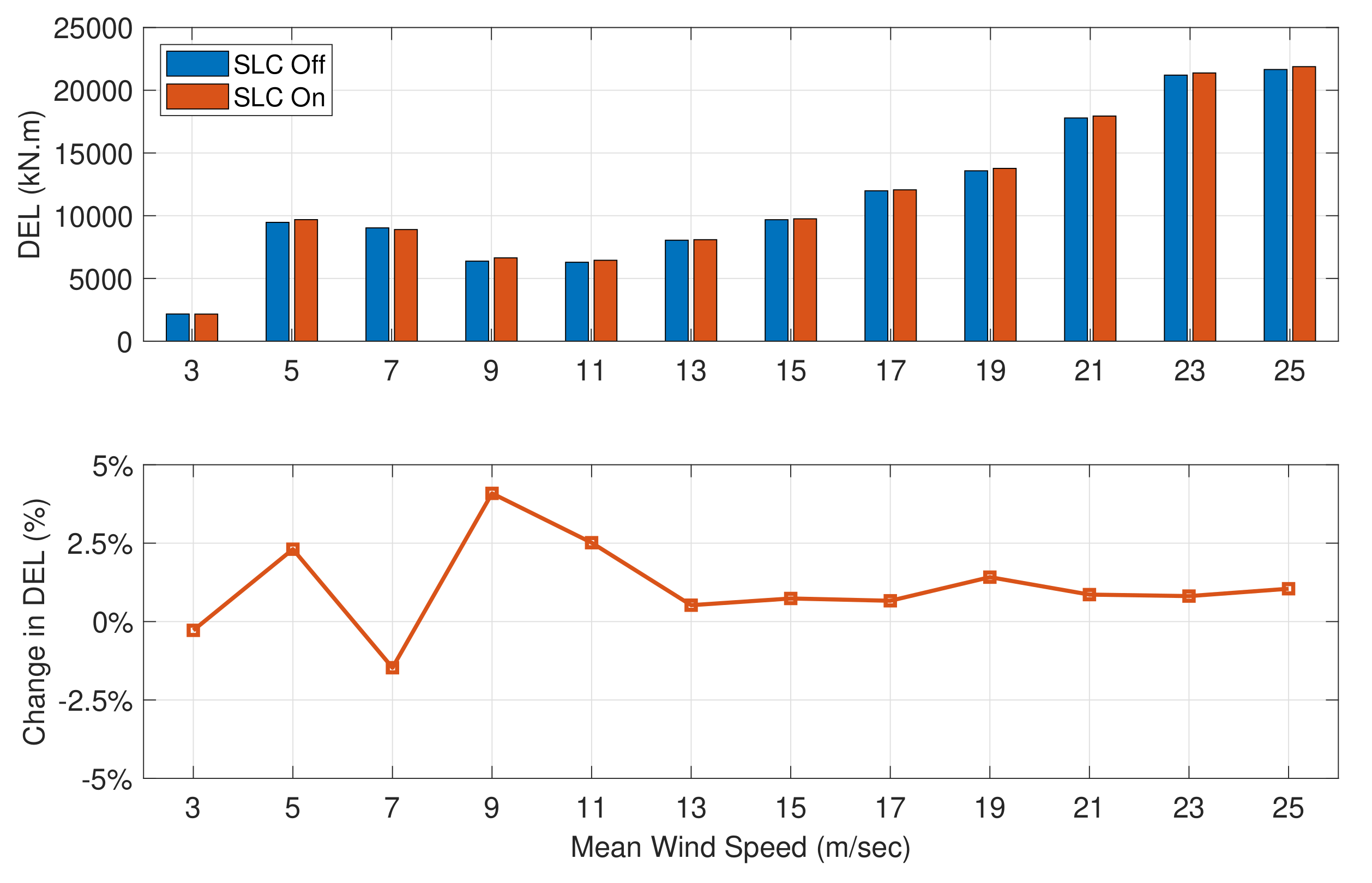
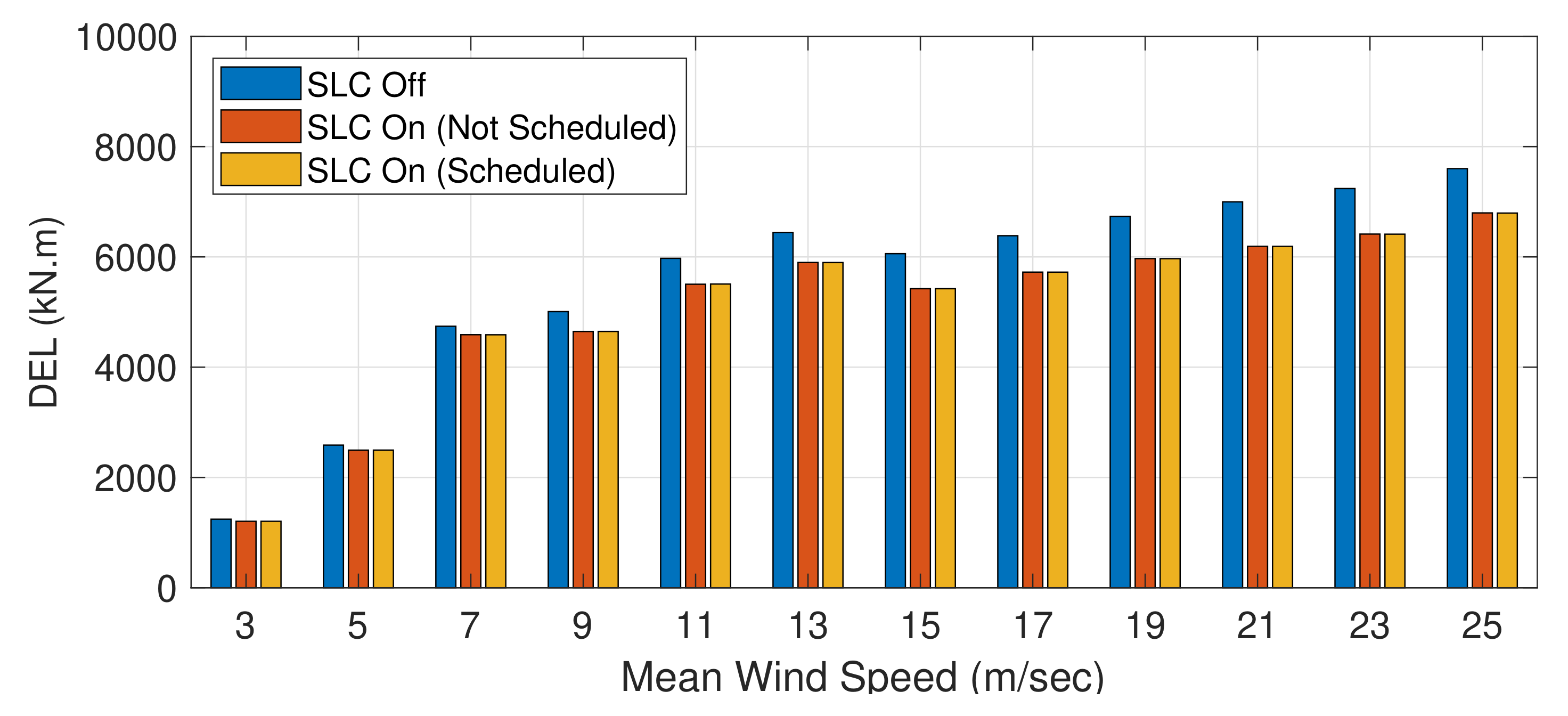
5.1. Primary Load
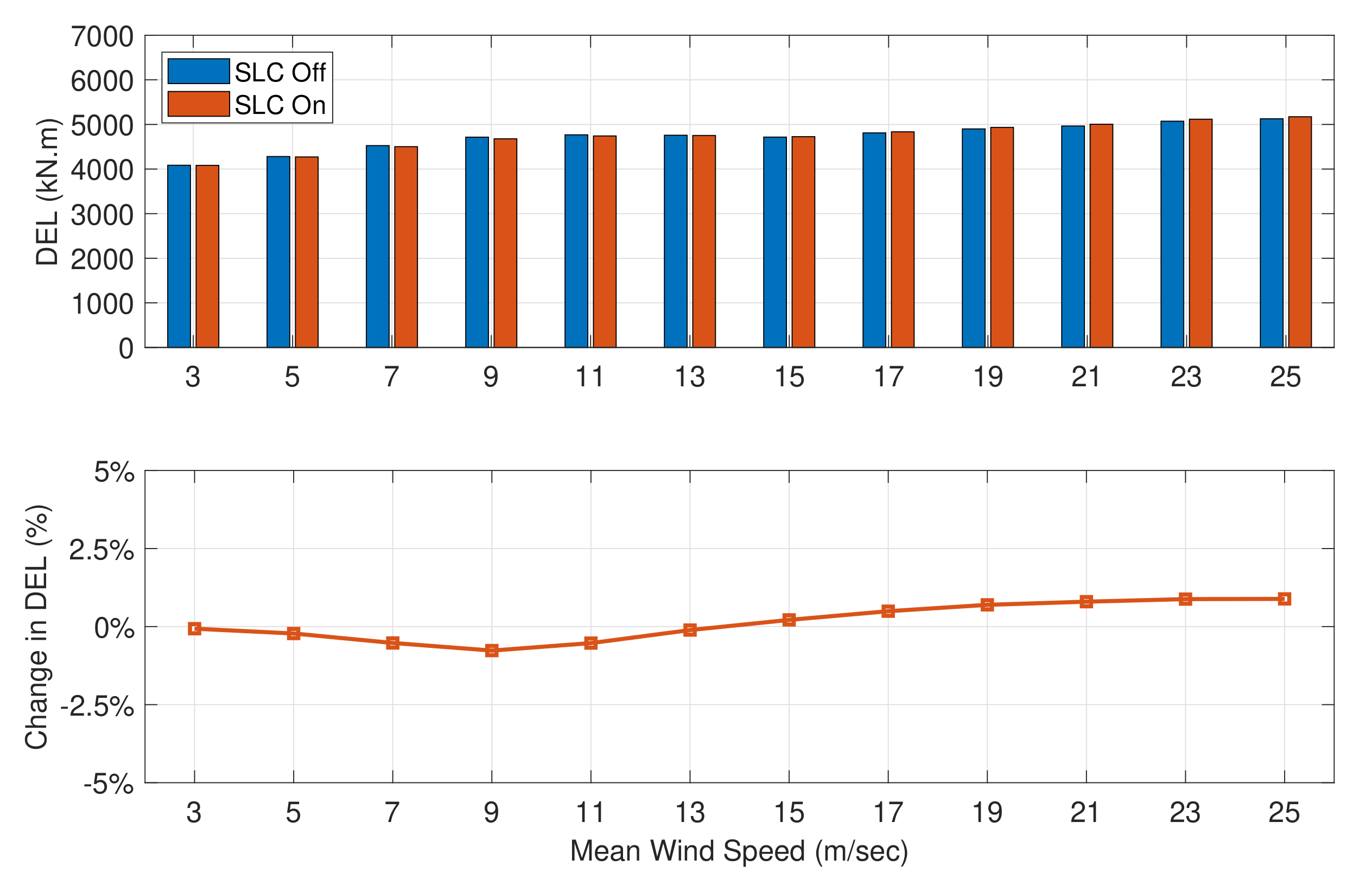
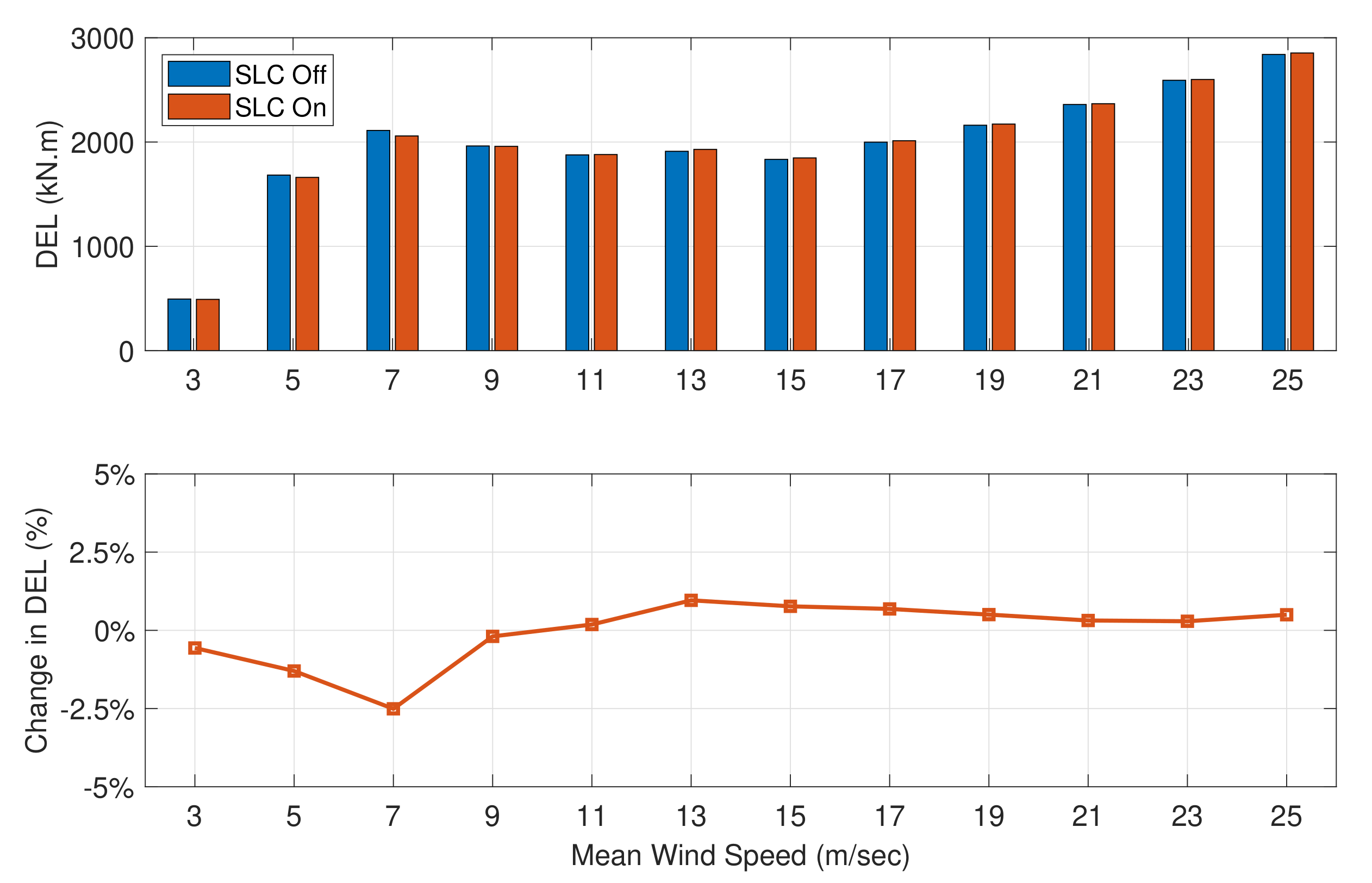
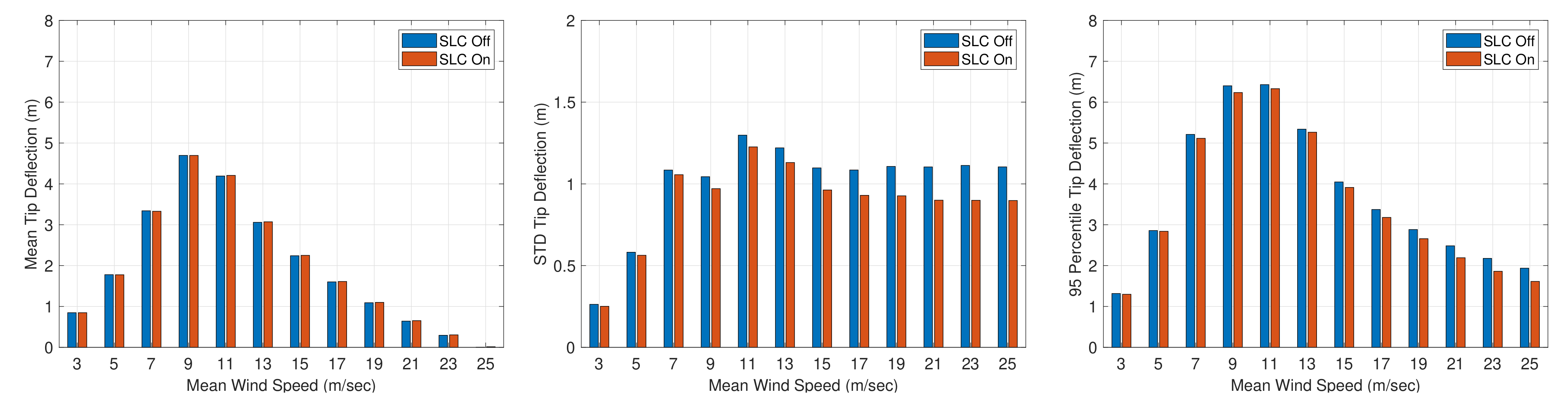
5.2. Secondary Loads
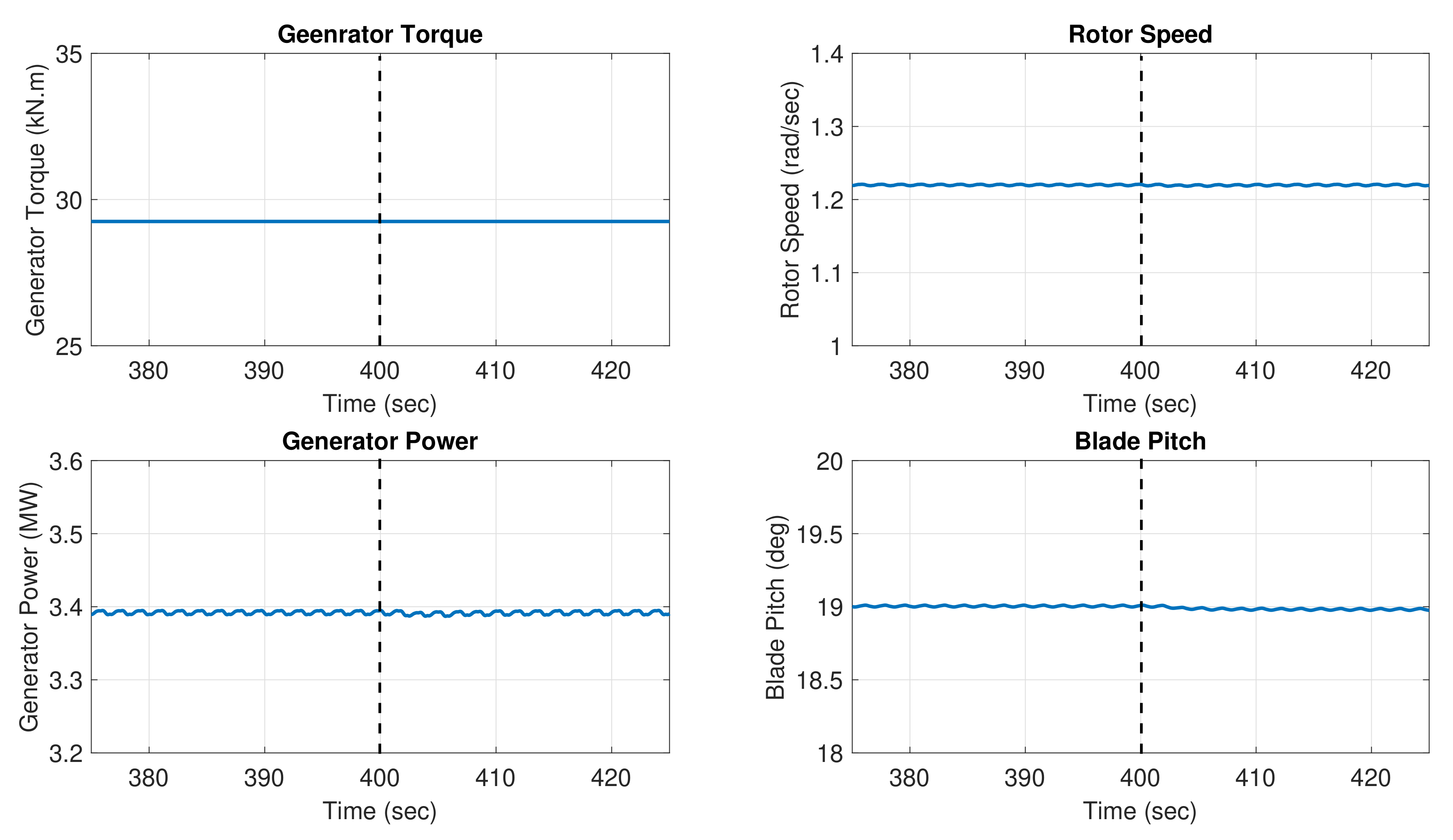
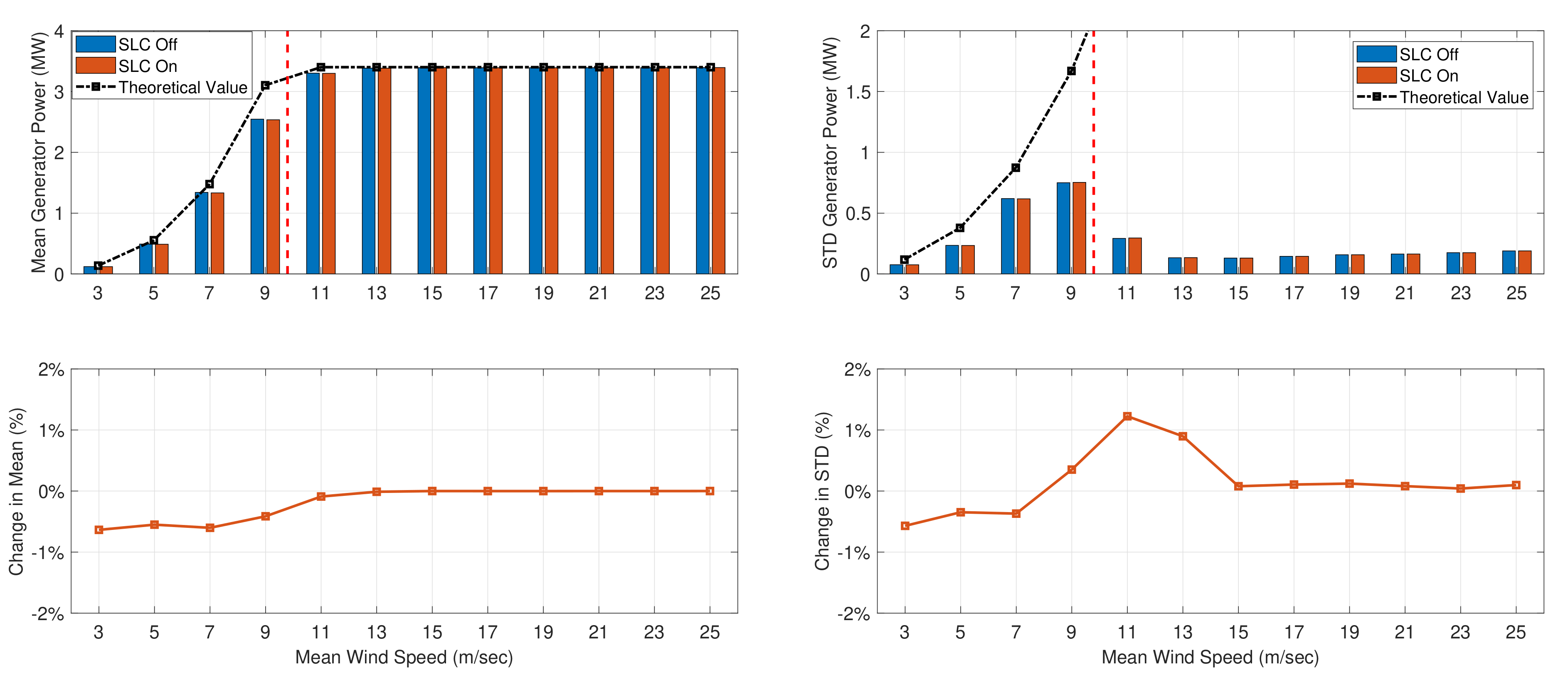
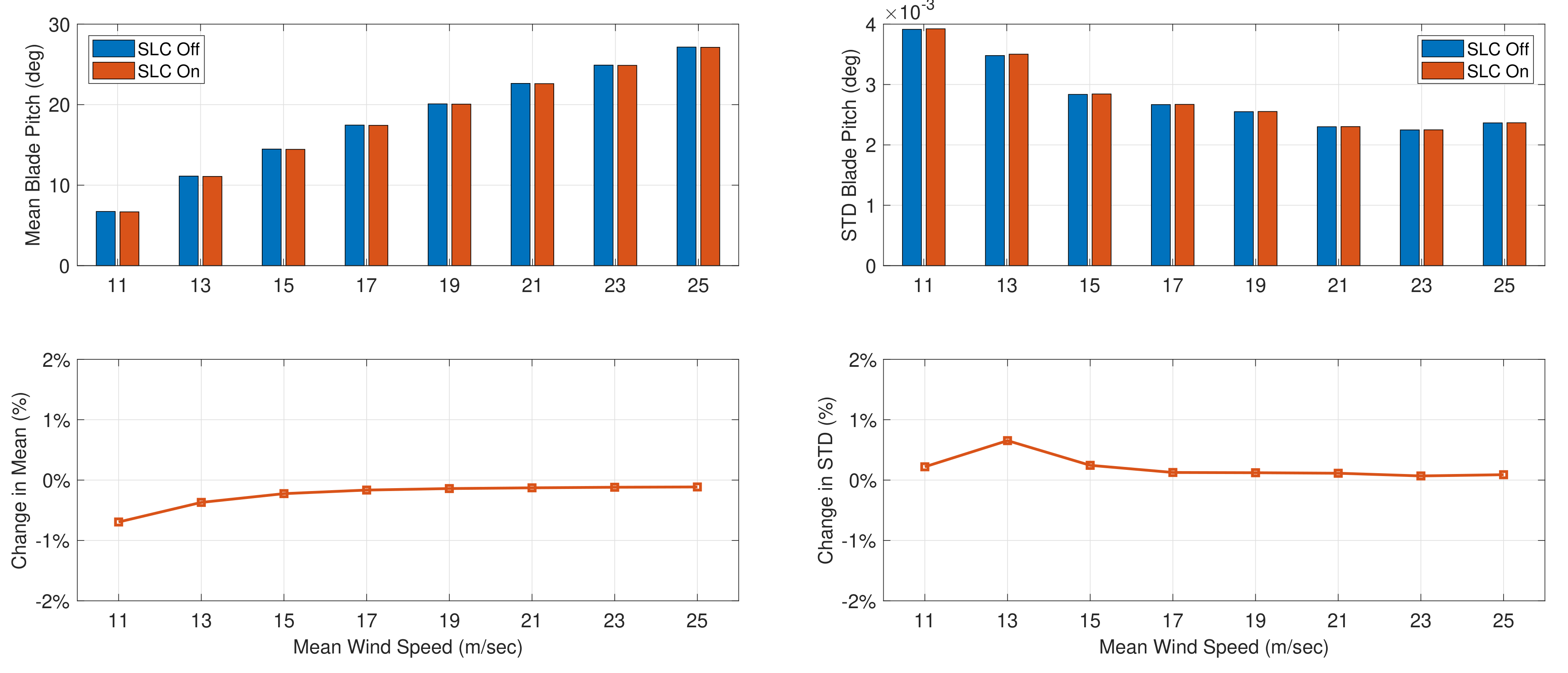
5.3. Turbine Activity
5.4. Scheduling the SLC with Wind Speed
6. Conclusions
- The SLC is model-based and can be designed from simple approximate models (physics-based or data) due to the explicit incorporation of a robust stability margin to both parametric uncertainty and unmodeled dynamics.
- The SLC does not interact with the main turbine controller and reduces the controlled loads in below- and above-rated wind conditions, without adverse impacts on turbine power or blade pitch activity.
- The methodology is directly applicable to an actual wind turbine equipped with DBD plasma actuators (or other flow control devices) by using system identification tools to obtain a model from the actuator signals (voltage for DBD plasma actuators) to the controlled moments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AEP | Annual Energy Production |
| DBD | Dielectric Barrier Discharge |
| DEL | Damage Equivalent Load |
| GF | Gurney Flap |
| IPC | Individual Pitch Control |
| LCOE | Levelized Cost of Energy |
| MBC | Multiblade Coordinate (Transformation) |
| MIMO | Multiple-Input, Multiple-Output |
| NREL | National Renewable Energy Laboratory |
| NRMSE | Normalized Root Mean Square Error |
| PRBS | Pseudo-Random Binary Signal |
| SISO | Single-Input, Single-Output |
| SLC | Sectional Lift Control |
| STD | Standard Deviation |
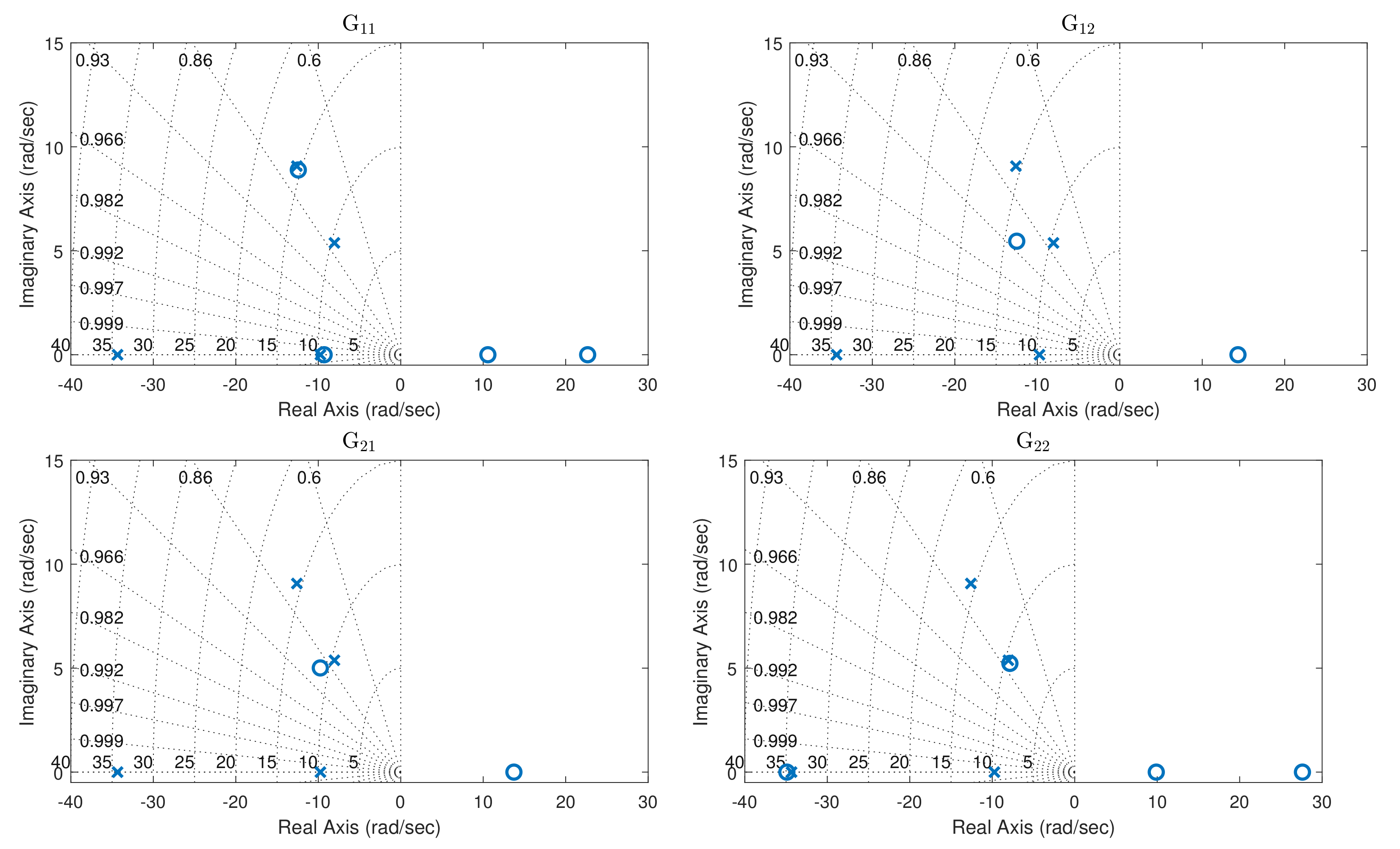
Appendix A. Details of the Identified Model
Appendix B. Proof of Lemma 1
References
- McKenna, R.; vd Leye, P.O.; Fichtner, W. Key challenges and prospects for large wind turbines. Renew. Sustain. Energy Rev. 2016, 53, 1212–1221. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Individual blade pitch control for load reduction. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2003, 6, 119–128. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Further load reductions with individual pitch control. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2005, 8, 481–485. [Google Scholar] [CrossRef]
- Caselitz, P.; Kleinkauf, W.; Krüger, T.; Petschenka, J.; Reichardt, M.; Störzel, K. Reduction of fatigue loads on wind energy converters by advanced control methods. In Proceedings of the European Wind Energy Conference, Dublin Castle, Ireland, 6–9 October 1997; pp. 555–558. [Google Scholar]
- Zhang, Y.; Chen, Z.; Cheng, M. Proportional resonant individual pitch control for mitigation of wind turbines loads. IET Renew. Power Gener. 2013, 7, 191–200. [Google Scholar] [CrossRef]
- Bir, G. Multi-blade coordinate transformation and its application to wind turbine analysis. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 1300. [Google Scholar]
- Liu, C.; Li, Y.; Cooney, J.A.; Fine, N.E.; Rotea, M.A. NREL FAST modeling for blade load control with plasma actuators. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 1644–1649. [Google Scholar]
- Lu, Q.; Bowyer, R.; Jones, B.L. Analysis and design of Coleman transform-based individual pitch controllers for wind-turbine load reduction. Wind Energy 2015, 18, 1451–1468. [Google Scholar] [CrossRef]
- Leithead, W.; Neilson, V.; Dominguez, S. Alleviation of unbalanced rotor loads by single blade controllers. In Proceedings of the European Wind Energy Conference (EWEC), Marseille, France, 16–19 March 2009; pp. 576–615. [Google Scholar]
- Leithead, W.; Neilson, V.; Dominguez, S.; Dutka, A. A novel approach to structural load control using intelligent actuators. In Proceedings of the IEEE 2009 17th Mediterranean Conference on Control and Automation, Thessaloniki, Greece, 24–26 June 2009; pp. 1257–1262. [Google Scholar]
- Lio, W.H.; Jones, B.L.; Lu, Q.; Rossiter, J.A. Fundamental performance similarities between individual pitch control strategies for wind turbines. Int. J. Control 2017, 90, 37–52. [Google Scholar] [CrossRef]
- Selvam, K.; Kanev, S.; van Wingerden, J.W.; van Engelen, T.; Verhaegen, M. Feedback–feedforward individual pitch control for wind turbine load reduction. Int. J. Robust Nonlinear Control. IFAC Affil. J. 2009, 19, 72–91. [Google Scholar] [CrossRef]
- Dunne, F.; Pao, L.Y.; Wright, A.D.; Jonkman, B.; Kelley, N. Adding feedforward blade pitch control to standard feedback controllers for load mitigation in wind turbines. Mechatronics 2011, 21, 682–690. [Google Scholar] [CrossRef]
- Larsen, T.J.; Madsen, H.A.; Thomsen, K. Active load reduction using individual pitch, based on local blade flow measurements. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2005, 8, 67–80. [Google Scholar] [CrossRef]
- Schlipf, D.; Schlipf, D.J.; Kühn, M. Nonlinear model predictive control of wind turbines using LIDAR. Wind Energy 2013, 16, 1107–1129. [Google Scholar] [CrossRef]
- Petrović, V.; Jelavić, M.; Baotić, M. MPC framework for constrained wind turbine individual pitch control. Wind Energy 2021, 24, 54–68. [Google Scholar] [CrossRef]
- Han, Y.; Leithead, W. Combined wind turbine fatigue and ultimate load reduction by individual blade control. J. Phys. Conf. Ser. 2014, 524, 012062. [Google Scholar] [CrossRef]
- Barlas, T.K.; van Kuik, G.A. Review of state of the art in smart rotor control research for wind turbines. Prog. Aerosp. Sci. 2010, 46, 1–27. [Google Scholar] [CrossRef]
- Johnson, S.J.; Baker, J.P.; Van Dam, C.; Berg, D. An overview of active load control techniques for wind turbines with an emphasis on microtabs. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2010, 13, 239–253. [Google Scholar] [CrossRef]
- Andersen, P.B.; Henriksen, L.; Gaunaa, M.; Bak, C.; Buhl, T. Deformable trailing edge flaps for modern megawatt wind turbine controllers using strain gauge sensors. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2010, 13, 193–206. [Google Scholar] [CrossRef]
- Barlas, T.; Van der Veen, G.; Van Kuik, G. Model predictive control for wind turbines with distributed active flaps: Incorporating inflow signals and actuator constraints. Wind Energy 2012, 15, 757–771. [Google Scholar] [CrossRef]
- Lackner, M.A.; van Kuik, G. A comparison of smart rotor control approaches using trailing edge flaps and individual pitch control. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 2010, 13, 117–134. [Google Scholar] [CrossRef]
- Castaignet, D.; Barlas, T.; Buhl, T.; Poulsen, N.K.; Wedel-Heinen, J.J.; Olesen, N.A.; Bak, C.; Kim, T. Full-scale test of trailing edge flaps on a Vestas V27 wind turbine: Active load reduction and system identification. Wind Energy 2014, 17, 549–564. [Google Scholar] [CrossRef]
- Cooney, J.A.; Szlatenyi, C.; Fine, N.E. The development and demonstration of a plasma flow control system on a 20 kW wind turbine. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1302. [Google Scholar]
- Griffith, D.T.; Fine, N.E.; Cooney, J.A.; Rotea, M.A.; Iungo, G.V. Active Aerodynamic Load Control for Improved Wind Turbine Design. J. Phys. Conf. Ser. 2020, 1618, 052079. [Google Scholar] [CrossRef]
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind TCP Task 37: Systems Engineering in Wind Energy-WP2.1 Reference Wind Turbines; National Renewable Energy Lab.: Golden, CO, USA, 2019.
- Chetan, M.; Sadman, S.; Griffith, D.T.; Gupta, A.; Rotea, M. Co-Design of a 3.4 MW Wind Turbine with Integrated Plasma Actuator-based Load Control. Submitt. Wind. Energy 2021, unpublished. [Google Scholar]
- TC88-MT. IEC 61400-3: Wind turbines—Part 1: Design requirements. Int. Electrotech. Comm. Geneva 2005, 64, 1–85. [Google Scholar]
- Documentation, S. Simulation and Model-Based Design. 2020. Available online: https://ww2.mathworks.cn/products/simulink.html (accessed on 12 June 2021).
- Liu, C.; Gupta, A.; Rotea, M. Multi-Sectional Lift Actuation for Wind Turbine Load Alleviation. J. Phys. Conf. Ser. 2020, 1618, 022018. [Google Scholar] [CrossRef]
- Jonkman, J. The new modularization framework for the FAST wind turbine CAE tool. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Dallas, TX, USA, 7–10 January 2013; p. 202. [Google Scholar]
- Burton, T.; Sharpe, D.; Jenkins, N.; Bossanyi, E. Wind Energy Handbook; Wiley: New York, USA, 2001; Volume 2. [Google Scholar]
- Eggers, A., Jr.; Digumarthi, R.; Chaney, K. Wind shear and turbulence effects on rotor fatigue and loads control. J. Sol. Energy Eng. 2003, 125, 402–409. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C. Essentials of Robust Control; Prentice Hall: Upper Saddle River, NJ, USA, 1998; Volume 104. [Google Scholar]
- McFarlane, D.; Glover, K. A loop-shaping design procedure using H∞ synthesis. IEEE Trans. Autom. Control 1992, 37, 759–769. [Google Scholar] [CrossRef]
- Lackner, M.; Rotea, M.; Saheba, R. Active structural control of offshore wind turbines. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; p. 1000. [Google Scholar]
- Lackner, M.A.; Rotea, M.A. Structural control of floating wind turbines. Mechatronics 2011, 21, 704–719. [Google Scholar] [CrossRef]
- Hayman, G. MLife Theory Manual for Version 1.00; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2012; Volume 74, p. 106.
- Hayman, G.; Buhl, M., Jr. Mlife Users Guide for Version 1.00; National Renewable Energy Laboratory: Golden, CO, USA, 2012; Volume 74, p. 112.
- The MathWorks Inc. System Identification Toolbox; The MathWorks Inc.: Natick, MA, USA, 2019. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Ungurán, R.; Petrović, V.; Pao, L.Y.; Kühn, M. Smart rotor control of wind turbines under actuator limitations. In Proceedings of the IEEE 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 3474–3481. [Google Scholar]
- Åström, K.J.; Hägglund, T.; Astrom, K.J. Advanced PID Control; ISA-The Instrumentation, Systems, and Automation Society: Fort Belvoir, VI, USA, 2006; Volume 461. [Google Scholar]
- Jonkman, B. TurbSim User’s Guide v2. 00.00; National Renewable Energy Laboratory: Golden, CO, USA, 2014.

| Properties | Value | Properties | Value |
|---|---|---|---|
| Class and category | IEC Class 3A | Rotor orientation | Upwind |
| Control | Variable speed, variable pitch | Maximum power coefficient | 0.47 |
| Power | MW | Gear ratio | 97 |
| Rotor diameter | 130 m | Hub height | 110 m |
| Cut-in wind speed | 4 m/s | Minimum rotor speed | rpm |
| Rated wind speed | m/s | Rated rotor speed | rpm |
| Cut-out wind speed | 25 m/s | Maximum rotor speed | rpm |
| Evaluation Criteria | Comments |
|---|---|
| Loads and Deflections | |
| Blade-root flapwise bending moments | Primary load |
| Blade-root edgewise bending moments | Secondary load |
| Drive train torsion | Secondary load |
| Tower fore-aft moment | Secondary load |
| Tower side-side moment | Secondary load |
| Blade deflection | Secondary metric |
| Turbine Performance | |
| Power produced | |
| Rotor angular speed | |
| Collective pitch | Above-rated wind conditions |
| Degree of Freedom | Description |
|---|---|
| FlapDOF1 | First flapwise blade mode DOF |
| FlapDOF2 | Second flapwise blade mode DOF |
| EdgeDOF | First edgewise blade mode DOF |
| DrTrDOF | Drivetrain rotational-flexibility DOF |
| GenDOF | Generator DOF |
| TwFADOF1 | First fore-aft tower bending-mode DOF |
| TwFADOF2 | Second fore-aft tower bending-mode DOF |
| TwSSDOF1 | First side-to-side tower bending-mode DOF |
| TwSSDOF2 | Second side-to-side tower bending-mode DOF |
| Model Order | NRMSE |
|---|---|
| 5 | 0.25 |
| 6 | 0.18 |
| 7 | 0.37 |
| 8 | 0.20 |
| Parameter | Value |
|---|---|
| Actuator Limits | −0.2 to +0.2 |
| 100 | |
| (rad/s) | 0.37 |
| DC-gain (kN·m) | |
| Robust Controller | I (Identity Matrix) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, A.; Rotea, M.A.; Chetan, M.; Sakib, M.S.; Griffith, D.T. A Methodology for Robust Load Reduction in Wind Turbine Blades Using Flow Control Devices. Energies 2021, 14, 3500. https://doi.org/10.3390/en14123500
Gupta A, Rotea MA, Chetan M, Sakib MS, Griffith DT. A Methodology for Robust Load Reduction in Wind Turbine Blades Using Flow Control Devices. Energies. 2021; 14(12):3500. https://doi.org/10.3390/en14123500
Chicago/Turabian StyleGupta, Abhineet, Mario A. Rotea, Mayank Chetan, Mohammad S. Sakib, and D. Todd Griffith. 2021. "A Methodology for Robust Load Reduction in Wind Turbine Blades Using Flow Control Devices" Energies 14, no. 12: 3500. https://doi.org/10.3390/en14123500
APA StyleGupta, A., Rotea, M. A., Chetan, M., Sakib, M. S., & Griffith, D. T. (2021). A Methodology for Robust Load Reduction in Wind Turbine Blades Using Flow Control Devices. Energies, 14(12), 3500. https://doi.org/10.3390/en14123500







