Design Study on Customised Piezoelectric Elements for Energy Harvesting in Total Hip Replacements

Abstract

Energy harvesting is a promising approach to power novel instrumented implants that have passive sensory functions or actuators for therapeutic measures. We recently proposed a new piezoelectric concept for energy harvesting in total hip replacements. The mechanical implant safety and the feasibility of power generation were numerically demonstrated. However, the power output for the chosen piezoelectric element was low. Therefore, we investigated in the present study different geometry variants for an increased power output for in vivo applications. Using the same finite element model, we focused on new, customised piezoelectric element geometries to optimally exploit the available space for integration of the energy harvesting system, while maintaining the mechanical safety of the implant. The result of our iterative design study was an increased power output from 29.8 to 729.9 µW. This amount is sufficient for low-power electronics.

1. Introduction

Instrumentation of implants is a promising approach to enhance their functionalities and further improve the clinical outcome. With regard to joint endoprostheses, sensors for monitoring implant-related parameters (e.g., implant loading and daily life activity, implant loosening, etc. [1]) can provide data for clinical decisions and therapeutic actions. These data are also relevant for ongoing implant development. Beyond passive diagnostic functions, active measures are investigated, e.g., electrical stimulation to promote bone growth [2,3,4]. To power sensors and actuators, an adequate energy supply is required. Therefore, energy harvesting is an innovative solution that provides continuous and independent energy for an autonomous instrumented implant without the drawbacks of batteries (limited lifetime, risk of leakage) or external power supply (dependence on external components).

The first concept for an energy harvesting system (EHS) for a load bearing endoprosthetic implant was reported by Platt et al. [5,6]. Piezoelectric multilayer elements were placed in the tibial tray of a total knee replacement (TKR). This system was improved by Almouahed et al. [7,8]. Wilson et al. and Safaei et al. modified the concept by moving the piezoelectric transducers to the polyethylene insert of the TKR [9,10]. Other EHS concepts in TKR were based on electromagnetic or triboelectric transducers [11,12]. With regard to total hip replacements (THR), Morais et al. were the first presenting an EHS [13]. The electromagnetic generator, consisting of coils and a magnet-spring system, was placed in a total hip stem. This concept was extended by Santos et al. to a multisource EHS with an additional rotation movement-based electromagnetic generator in the femoral joint and a vibration-based piezoelectric generator in the implanted femoral head [14]. Since then and to the best of the author’s knowledge, our recently published study is the first work on EHSs in THRs [15]. We presented a piezoelectric-based concept that transduces the mechanical loads from human gait into electrical energy by transmitting the acting force on the THR to a lead zirconate titanate (PZT) multilayer element deforming the element and applying mechanical strain (see Figure 1). The piezoelectric element is encapsulated in an ultra-high molecular weight polyethylene (UHMW-PE) housing which fills a cavity excised from the original metallic total hip stem (see Figure 2, Materials and Methods). The generated energy can be used to power various instrumentations. By linking the generated voltage to the implant loading, the EHS can serve in a first application as a self-powered load sensor.

In our previous work [15], we numerically investigated the implant’s fatigue safety and the feasibility of energy harvesting, however, the numerically approximated power output was quite low for the assumed off-the-shelf piezoelectric element (single configuration 8.1 µW, stacked configuration 31.1 µW). Hence, the aim of the present numerical design study was to investigate changes of the cavity and piezoelectric element to increase the maximum power output, while maintaining the mechanical safety of the implant using finite element analysis (FEA). Therefore, the geometry of the introduced cavity was modified or the geometry of the piezoelectric element was changed to better exploit the space available. For the latter, customised geometries were analysed. To the author’s knowledge this approach is new in piezoelectric energy harvesting for load-bearing orthopaedic implants; in the work of the above-referenced groups on EHS concepts in TKR only standard products have been employed to adopt the geometry (seize, height) or number of piezoelectric elements [8,10].

2. Materials and Methods

The finite element model was based on our previous work and is briefly described below, further details are specified in [15]. Following that, the different regarded geometry variants and the process of our iterative design study for the customised geometries were described.

2.1. Finite Element Model

A femoral geometry from a previous reconstruction on basis of computed tomography (CT) data was used [16,17]. Landmarks, necessary for the virtual implantation and load application were created (e.g., femur axis, neck axis, femoral head centre, epicondyles, femoral notch). A femur coordinate system was defined according to Bergmann et al. [18]. The total hip stem geometry (Exeter V40, size 37.5 mm N°3, Stryker, Howmedica Osteonics Corp, Mahwah, NJ, USA) was generated and reconstructed by 3D-scan. Accordingly, landmarks were created (implant stem axis, implant neck axis and virtual head centre) in SolidWorks 2018 (Dassault Systèmes, VélizyVillacoublay, France). From the implant, a cavity was subtracted and replaced with a UHMW-PE housing to contain the various piezoelectric element geometries. The initial designs of the cavity and piezoelectric element were according to [15]. Then, the implant’s virtual head centre and the femoral head centre were superimposed and the total hip stem axis was aligned with the femoral axis. Around the implant, a bone cement mantle of 3 mm thickness was defined. To complete the virtual implantation, the femoral neck and femoral head were resected and a bone cavity was created to house the implant and the bone cement mantle. Figure 1 shows the virtual implantation and the different components of the modified implant.

The full CAD model was imported into the finite element software ANSYS Workbench V19.2 (Ansys Inc., Canonsburg, PA, USA). According to Heller et al. (based on in vivo measurements [18] and musculo-skeletal modelling [19]), a reduced set of four muscle forces and a hip contact force for normal walking were applied for the instance of maximum total hip contact force, scaled to the body weight of an average patient of 75 kg [20]. Using the physiologically based boundary conditions of Speirs et al. [21], the system was fully constrained allowing the typical bending of a femur [15].

Between the bone and the bone cement mantle, a bonded contact was applied. All other contacts were defined to be frictional (frictional coefficient µ = 0.35 between bone cement mantel and implant [22], µ = 0.15 between UHMW-PE housing and implant [23]; for contact between the UHMW-PE housing and piezoelectric element, respectively, bone cement mantle µ = 0.3 was assumed).

The complex geometries of femur, implant and UHWM-PE housing were meshed with quadratic solid tetrahedral elements while the simpler geometries of the piezoelectric element and the bone cement layer were meshed with quadratic hexahedral elements. The mesh densities for the different components were in accordance with the mesh densities from our sensitivity analysis from [15], based on a mesh independence study. Please note that the single layers of the multilayer piezoelectric element are not individually modelled in contrast to our previous work [15], meaning in this region the element height is reduced. For the larger customised geometries, the very small mesh size would substantially increase the numerical problem size and exceed the computing capacity of our hardware system as pretests showed. Since the simulated open circuit voltage was of no interest in this study, this approach is straightforward. However, we compared both approaches for the off-the-shelf configurations (see below).

All materials were defined linear elastic. The material properties are listed in

Table 1. Material properties of the defined components in the finite element model.

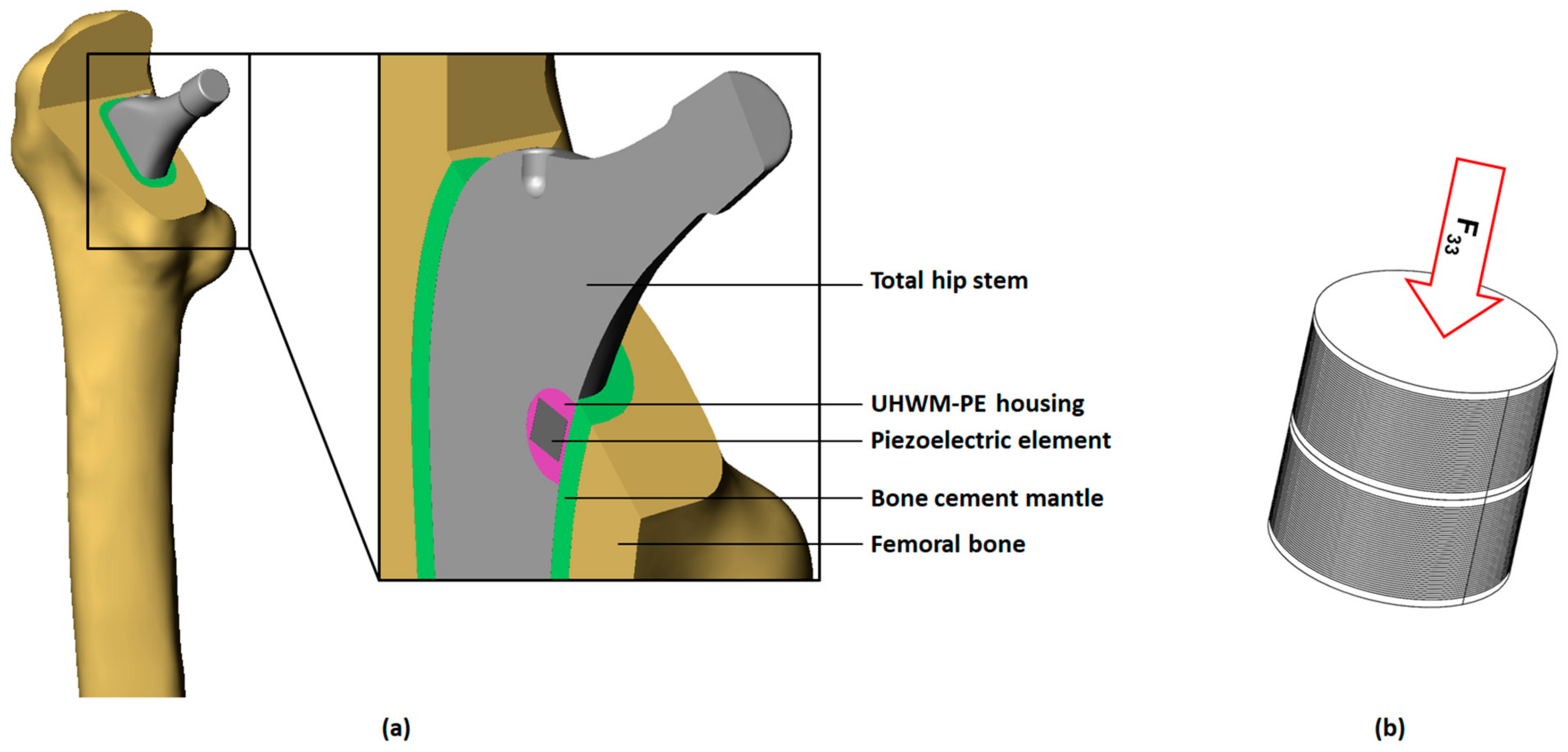
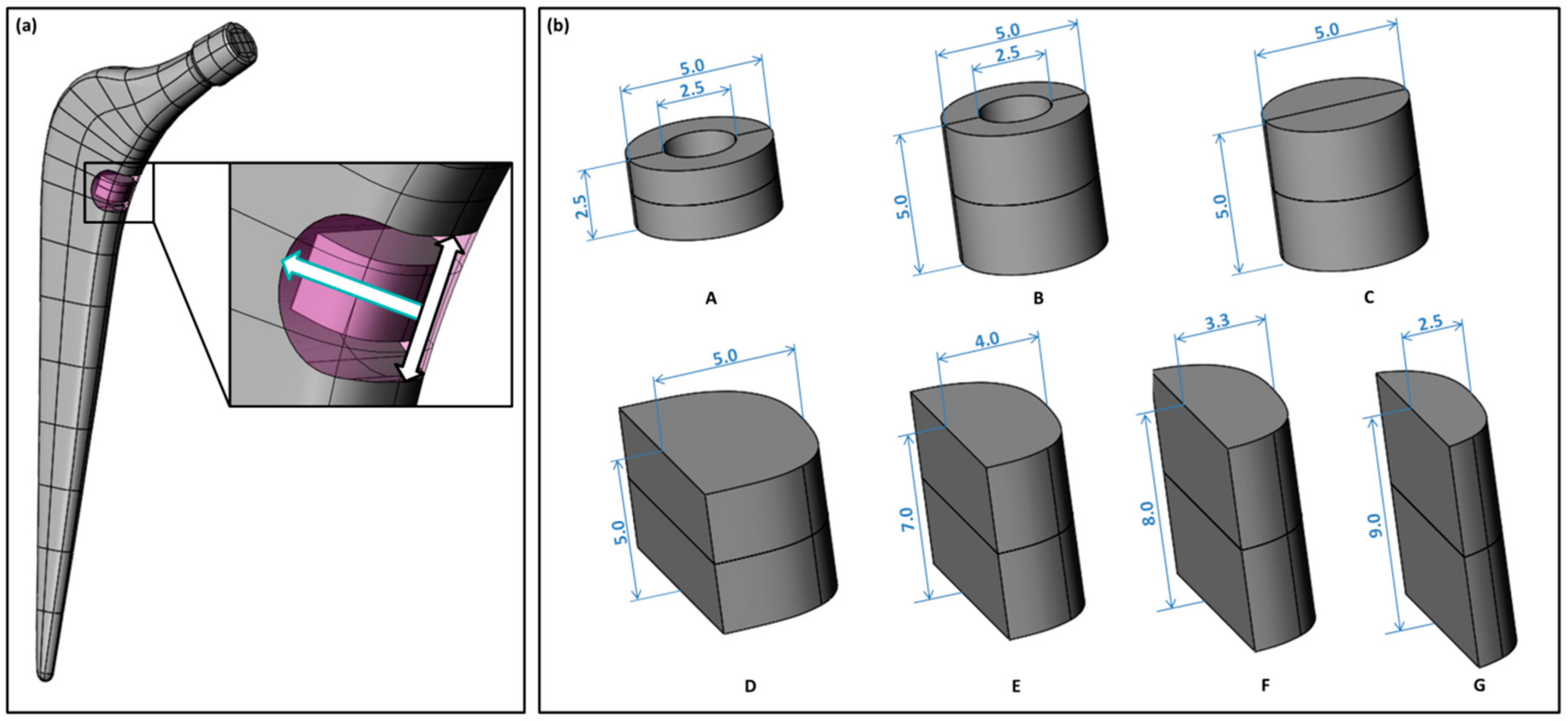
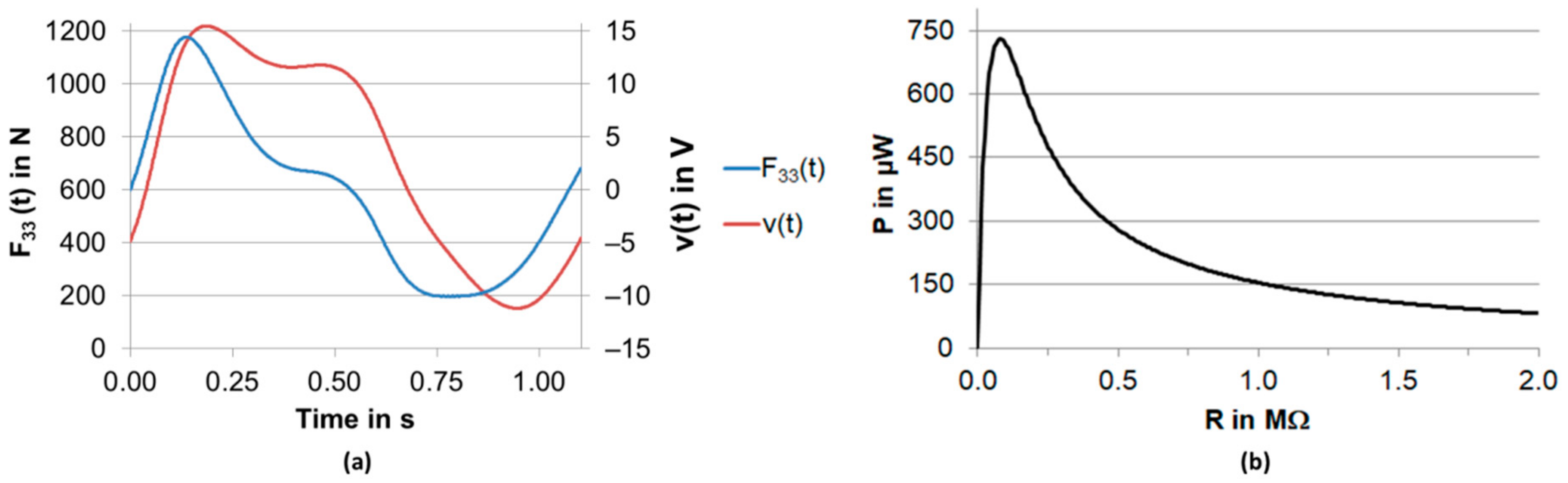
Component	Young’s Modulus (GPa)	Poisson’s Ratio 1 (-)
Metallic implant	195 [26]	0.3
Bone cement mantle	2.3 [27]	0.3
UHMW-PE housing	0.83 [28]	0.46 [28]
PZT piezoelectric element	52.4 [29]	0.35 [29]
Femoral bone	6850 × ρapp1.49 [25], max. value 20 GPa [30,31]	0.3

¹ a Poisson’s ratio of 0.3 was assumed, if no other data was available.

. We accounted for the heterogeneous stiffness distribution of the bone by applying material mapping. Bonemat V3.2 was used to assign different Young’s moduli on basis of the CT data [24]. The density–elasticity relationship of Morgen et al. on basis of the apparent density ρ_app [25] was assumed with a maximum Young’s modulus of 20 GPa, please see [15] for more detail.

The implicit static structural simulations were performed on a high-performance Linux cluster with two Intel^® Xeon^® Gold 6248 CPU processors (2.50 GHz) and 192 GB RAM per node. A sparse direct solver was used.

2.2. Postprocessing

With regard to the mechanical implant safety, we evaluated the von Mises stress in the metallic implant component at the cavity ground (σ_Imp), where a local stress concentration is induced by integration of the EHS. This parameter was considered uncritical when not exceeding 290.9 MPa which was the global stress maximum for the unmodified geometry in the same loading situation, shown in [15]. For the piezoelectric element, the von Mises stress (σ_Piez) was evaluated in the mid plane, since the contact situation leads to local stress singularities at the top and bottom end faces. The limit was defined as 30.0 MPa. This value was specified by the manufacturer as maximum preload for using the element with a constant force [32].

For the approximation of the generated power, we followed the approach of Wilson and Safaei et al., and calculated the generated voltage v(t) on basis of a force profile F₃₃(t) by solving the differential equation for different load resistance R

$$\frac{{\mathrm{n}}_{\mathrm{layer}}{\mathsf{\epsilon }}_{33}^{\mathrm{T}}\mathrm{A}}{\frac{h}{{\mathrm{n}}_{\mathrm{layer}}}}\frac{\mathrm{dv}\left(\mathrm{t}\right)}{\mathrm{dt}}+\frac{\mathrm{v}\left(\mathrm{t}\right)}{\mathrm{R}}{=\mathrm{n}}_{\mathrm{layer}}{\mathrm{d}}_{33}{\dot{\mathrm{F}}}_{33}(\mathrm{t}),$$

(1)

where the first term represents the capacity of the piezoelectric element [9,10]. The piezoelectric element is defined by its base area A, its height h, the number of layers n_layer and the piezoelectric constants ${\mathsf{\epsilon }}_{33}^{\mathrm{T}}$ and d₃₃. In the design study, the base area A of the element was variable, as well as the height h and the resulting number of layers n_layer. The layer thickness was kept constant at h_layer = 0.05 mm as for the off-the-shelf piezoelectric elements specified by the manufacturer. The used input parameters for the piezoelectric element are listed in

Table 2. Parameters defining the piezoelectric element (${\epsilon }_0$ = 8.854E − 12 As/(Vm)).

Parameter	Value
A	Variable
h	Variable, minus passive layers
hlayer	0.05 mm
nlayer	Variable, defined by h and hlayer
${\mathsf{\epsilon }}_{33}^{\mathrm{T}}/{\epsilon }_0$	1751 [29]
d33	3.996E − 10 m/V [29]

. Since the off-the-shelf piezoelectric elements had passive top and bottom layers of around 0.175 mm thickness at a height of 2.5 mm for each single element (i.e., 2.15 mm of active height and 43 layers for a single element and 4.35 mm of active height and 86 layers for the stacked element, respectively) we assumed an according passive proportion for the customised geometries. If necessary, we reduced the active height to obtain an integer number of layers, thereby choosing for a conservative power approximation.

The acting hip contact force for a full gait cycle of the duration T for normal walking of a patient with average weight from Bergmann et al. was scaled to the contact force acting on the piezoelectric elements end faces F₃₃ from the FEA [18]. The resulting load profile F₃₃(t) approximated the force profile on the piezoelectric element, requiring only the simulation of a single load step (Figure 3a exemplary shows the scaled force profile for the final design). The generated power for different load resistance R was calculated by

$$\mathrm{P}=\frac{1}{\mathrm{T}}{{\displaystyle \int }}_0^{\mathrm{T}}\frac{\mathrm{v}2\left(\mathrm{t}\right)}{\mathrm{R}}\mathrm{dt}$$

(2)

The maximum power for the best matching resistance was used as output parameter. All output parameters are summarised in

Table 3. Output parameters.

Symbol	Output Parameter	Limit
σImp	Stress maximum at cavity base (metallic implant component)	290.9 MPa
σPiez	Stress maximum in the piezoelectric element’s mid plane	30.0 MPa
F33	Contact force acting on the piezoelectric element’s end face	n/a
P	Approximated power output	To be maximised

.

2.3. Geometry Variants

Recalculation of previous data: For the customised geometries the individual representation of the multilayer elements would exceed the computational capacity, as mentioned above. For comparison with our previous data and as reference basis for new simulations, we recalculated the off-the-shelf configurations (single and stacked multilayer piezoelectric element, see Figure 2) with the approach described above, neglecting the layers in the simulation, and considering them only for the power calculation.

New geometries: In addition to the off-the-shelf stacked piezoelectric element with a ring base area, we considered a full cylinder stacked multilayer element.

To better use the available space in the cavity, a fully customised piezoelectric element cross-section was generated (see Figure 2). It was ensured that the piezoelectric element is fully encapsulated by the UHMW-PE housing and a minimum wall thickness comparable to the off-the-shelf configurations was maintained. The initial height was chosen to be comparable to the stacked multilayer element (h = 5 mm). The general configuration (material properties, layer thickness, proportion of passive layers to the active height assuming stacks) was unchanged.

Iterative design study: On basis of the initial customised geometry, we conducted a design study to optimise the power output. Starting with the initial cavity design, we successively changed the piezoelectric element’s height to find the geometry providing the maximum power output, but ensuring compliance with the defined critical stress values (Table 3). The larger the piezoelectric element’s height, the shorter its extension towards the cavity needed to be defined to fit in the UHMW-PE housing (see Figure 2b, A to G). The best design point was then used as input for a new cavity geometry where we changed the cavity height or depth (see Figure 2a for the definition). Again, the piezoelectric element’s height was changed to comply with our specified stress values. After five new cavity geometries and over 20 simulated design points, we stopped the study. All design point geometries are presented and listed in Figure A1 and

Table A1. Overview of all designs with customised piezoelectric element geometries.

, Appendix A.

3. Results

Initially, our simplified approach neglecting the single layers was analysed on the basis of the off-the-shelf configurations. The results were compared to identical configurations from previous data from [15]. The difference was < 5% for all output parameters but for the stress in the stacked piezoelectric element (see in

Table 4. Comparison of output data when considering or neglecting the individual layers of the piezoelectric element during FEA.

	Variant	σImp (MPa)	σPiez (MPa)	F33 (N)	P (µW)
Single	Layers	269.4	14.0	141.6	8.1
	No layers	269.6	14.1	140.6	8.0
	Difference (%)	0.08%	0.64%	−0.67%	−1.33%
Stack	Layers	267.2	16.9	196.3	31.1
	No layers	267.6	15.1	192.0	29.8
	Difference (%)	0.14%	−10.71%	−2.20%	−4.36%

). However, the absolute difference of < 2 MPa was acceptably small. All results are summarised in Table 4.

The generated power for the off-the-shelf geometries was highest for the stacked configuration (29.8 µW, factor 3.7 compared to the single element), see

Table 5. Output results of the different geometry variants and the initial and final geometry variants for the iterative design study.

Variant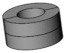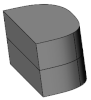
	Single	Stacked	Stacked	Initial Final
	Off-The-Shelf		Full Cylinder	Customised Geometry
σImp (MPa)	269.6	267.6	266.6	256.6	273.4
σPiez (MPa)	14.1	15.1	11.9	16.9	29.7
F33 (N)	140.6	192.0	207.7	536.0	1218.7
P (µW)	8.0	29.8	26.1	77.8	729.9

. The acting contact force F₃₃ was notably larger, and the stress in the piezoelectric element rose compared to the single element. The full cylinder also absorbed more load, however, the stress in the piezoelectric element was smaller and thereby less voltage and power were generated. All the three design variants fulfilled the stress criteria for the metallic implant component and for the piezoelectric element (see Table 5).

The initial customised geometry was of the same height as the stacked circular geometries and showed a 2.6 times higher power output (77.8 µW). By our iterative design study, we could successively find new geometries fulfilling our specified stress limits and presenting higher power output (see Figure A1 and Table A1, Appendix A). We stopped the study after over 20 design points and 5 new cavity geometries. The calculated power for the final design was 729.9 µW (i.e., an increase of nearly factor 25 to the stacked off-the-shelf configuration, see Table 5).

For the final design, the force profile F₃₃(t) is shown in Figure 3a together with the generated voltage profile for the best matching load resistor (R = 0.08 MΩ). The power output for different load resistance is displayed in Figure 3b, with the calculated peak of 729.9 µW.

4. Discussion

The results for the simplified modelling of the piezoelectric element showed that the influence was minimal when individual layers of the piezoelectric element were neglected. This was expected, since apart from that the model and approach were identical. The impact on the metallic component itself can be disregarded. The deviations for the generated power were higher than for the contact force F_33. This has already been shown in our previous work and can be explained by the linear relationship between force and generated voltage which in contrast is contained as squared value in the calculation of the power (see Equation (2)) [15]. The difference for the stress in the piezoelectric element especially for the larger stacked configuration may result from the different height of the finite elements in the very area. The element height was notably smaller when the individual layers were modelled. With respect to the minor absolute deviation, the difference is acceptable and the approach still considered straightforward since the reduction of the model size is necessary to allow the simulation of larger piezoelectric elements of increased height or increased base area. To minimise the mesh density influence for a good comparability of the different design points in the iterative design study, the finite element height for the piezoelectric elements was kept constant for all design points.

As our previous study already showed, a stacked configuration with the same base area led to a higher force transmission, resulting in a higher stress and higher generated power [15]. In contrast, a full cylinder of the same height had no benefit with regard to the power. The slight increased force value did not compensate the increased stiffness by the larger base area, leading to lower deformation and stresses, and thereby lower power output. However, a higher force F₃₃ can be withstood. This can be realised by increasing the height or base area to maximise the force transmission on the piezoelectric element. Therefore, the overall design aspect of the EHS with the mediating function of the UHWM-PE housing allows perfectly matching the piezoelectric elements geometry while maintaining the cavity geometry. This is demonstrated by the initial customised geometry; increasing the base area using the maximum available space for the same height largely raised the generated power but showed a tolerable stress level. The potential of a higher piezoelectric element, pushing the stress to the specified allowed limit, is not even exploited.

The iterative geometry study was a successful approach and highlighted the following aspect: by changing the piezoelectric element’s height, a design point for each generation was found which was below the defined stress levels but had a higher generated power output than the best design from the previous cavity geometry generation. Only for one cavity geometry no valid design point was found. The final power output value of nearly 730 µW shows improvement to the off-the-shelf designs, and improvement by the iterative geometry study, when comparing the final design to the best design of the initial cavity geometry. The voltage and power curves, exemplarily shown for the final design, are in accordance with our previous work [15]. Due to the higher acting force level of F₃₃ and the new configuration of the piezoelectric element, the generated voltage maximum was higher and the best matching resistance was slightly shifted to a lower value.

The calculated generated power is in the range of generated power by EHSs of other work groups: Almouahed et al. increased their output for the optimised design from 1.81 to 3.28 mW [8], Safaei et al. presented a power output of 269.1 µW for their latest design [33] (also raised by a factor > 20 compared to their initial work [34,35]). With regard to EHSs in THRs, Santos et al. calculated a power output of around 55 µW which summed up for all three harvesters [14]. Studies have shown that low power sensory and active functions in implants (e.g., intermitting monitoring and data transmission) need power sources in the range of 100 µW [11,36]. Therefore, the generated power output of our proposed EHS with a customised design can be considered sufficient. We do not expect that further increase by a higher number of additional piezoelectric elements is feasible. In contrast to TKR where much more space is available (in the polyethylene insert or the tibial tray), the area for piezoelectric element placement is much more limited in THR, where the piezoelectric element must be placed in an area which is under compressive load and where the implant cross section is large enough [15]. With our design we have found a good trade-off for a cavity size, which is sufficiently large to integrate a piezoelectric element, but does maintain the mechanical safety of the implant.

A limitation of our study is the calculation of the generated power only for resistive loads. Typical energy harvesting circuitry includes further and more complex components, e.g., rectifiers to convert the alternating current to direct current, voltage regulators and storage devices [37,38]. The efficiency of this electronic circuit determines the amount of energy that is available from the raw harvested energy. For low-frequency piezoelectric transducers, minimum energy loss is a challenging task and circuitry design was discussed already for the first energy harvesting concepts in orthopaedic implants [6,39]. This topic is part of ongoing research, even though commercialised solutions are already available [37,38,40]. In future studies, we will use the piezoelectric EHS as part of a self-powered load sensor. Within this work, we are able to investigate energy harvesting circuitry and efficiency.

With regard to the chosen limits for the evaluation of the mechanical safety, one has to keep in mind that fatigue values are usually determined for test specimens under specific manufacturing and testing conditions. The chosen value for the metallic component was the maximum stress value, taken from a study with the identical loading situation for the unmodified implant geometry [15]. This approach is conservative, since the literature value for the same material, investigated under a stress ratio typical for implants (R = 0.1) at 37 °C tested in Eagle’s medium, is notably higher (470 MPa) [41]. This means that the latter value could also be suited for comparison, allowing higher stress values for the metallic component than in this study; however, the heat treatment or surface finish could differ from the present sample. In our recent research, we showed for our initial design that higher fatigue stress values can be endured [42]. In the absence of fatigue data for multilayer piezoelectric elements used as transducers under the specified loading conditions, we used the manufacturer’s specification for maximum preload as the critical value for the piezoelectric element. Other literature fatigue data of stacked multilayer piezoelectric element actuators with a preload of 20 MPa is available [43]. A different manufacturer with comparable multilayer elements recommends a compressive stress range of up to 80 MPa for unstacked elements [44]. More specific fatigue data, especially for stacked multilayer piezoelectric elements in comparable loading situations and tested as transducer is desirable to exploit the full power generation capacity. The latter highlights the necessity of experimental testing.

In conclusion, this numerical study showed the potential of piezoelectric energy harvesting in THRs with customised geometries. The effort for the new geometries can be outweighed by the highly increased power output in contrast to only relying on standard products. Since manufacturing of customised piezoelectric geometries is many times more expansive than off-the-shelf elements, our work provides the required basis to proceed to experimental investigations. After realising the production of the proposed piezoelectric elements, experimental testing of the power generation and of the fatigue properties of the full system is required. This should also include worst case scenarios, e.g., representing higher loads simulating running, stumbling or implant loosening according to [42]. If the experiments show data allowing for higher loadings, the presented design study could be redone with new limit values. With regard to biocompatibility of the system and the toxicity of lead in PZT ceramics, the UHMW-PE housing already serves as environmental sealing which can be improved by other encapsulation techniques [15], however future studies should also consider lead-free piezoelectric materials [38].