A Comparative Study of Machine Learning-Based Methods for Global Horizontal Irradiance Forecasting
Abstract
1. Introduction
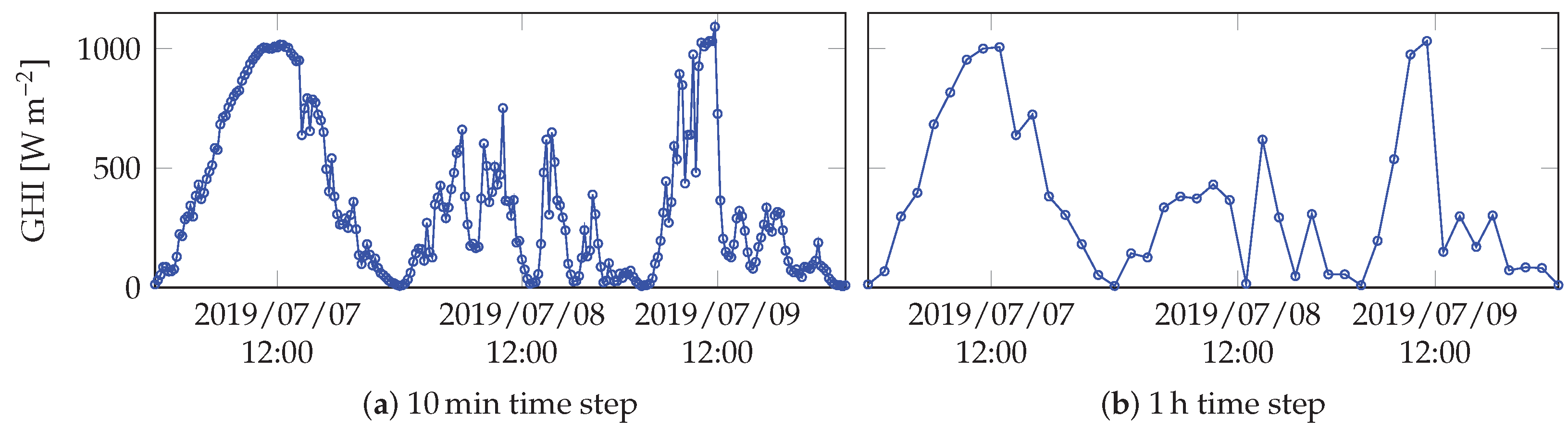
- Most studies use databases having at least a 1-hour time step, which leads to the impossibility of intrahour forecasting and to significant simplification of GHI dynamics, as illustrated in Figure 1.
- Regarding input data: some studies use only endogenous data, while others use additional data, which prevents from making fair comparisons between methods.
- Some authors forecast GHI directly, others the clear-sky index (using clear-sky models as pre- and postprocessing steps) or even PV power generation.
- The models are developed using a two-year GHI database with a 10 time step. As can be seen in Table 1, in previous machine learning studies the time step is usually 1 . However, such a time step leads to significant simplification of GHI dynamics: as can be noticed in Figure 1, GHI data sampled with 10 time step exhibit more fluctuations and are thus more difficult to forecast.
- Contrary to developing a specific model for each forecast horizon, as shown in some studies in the literature [13,28], we made the choice of multi-horizon forecasting models. Developing a specific model for each forecast horizon can be computationally demanding when many horizons are considered and it would be more practical to use a multi-horizon forecasting model when trying to run the algorithms in situ to produce real-time forecasts at various horizons, especially when intrahour forecasts are needed. Therefore, in this paper, the models are developed for multi-step ahead GHI forecasting and once the training phase is over, the models are used to forecast GHI for all horizons.
- Besides, many authors generally choose classical performance criteria (nRMSE, MAE, MBE, MAPE) for their models’ evaluation. In the present paper, two criteria are used in addition to the nRMSE: DMAE, that accounts for temporal distortion error and absolute magnitude error simultaneously; and CWC, that assesses the quality of prediction intervals. These criteria provide more detailed and comprehensive information about the models’ performance, and allow an in-depth analysis of their forecasts.
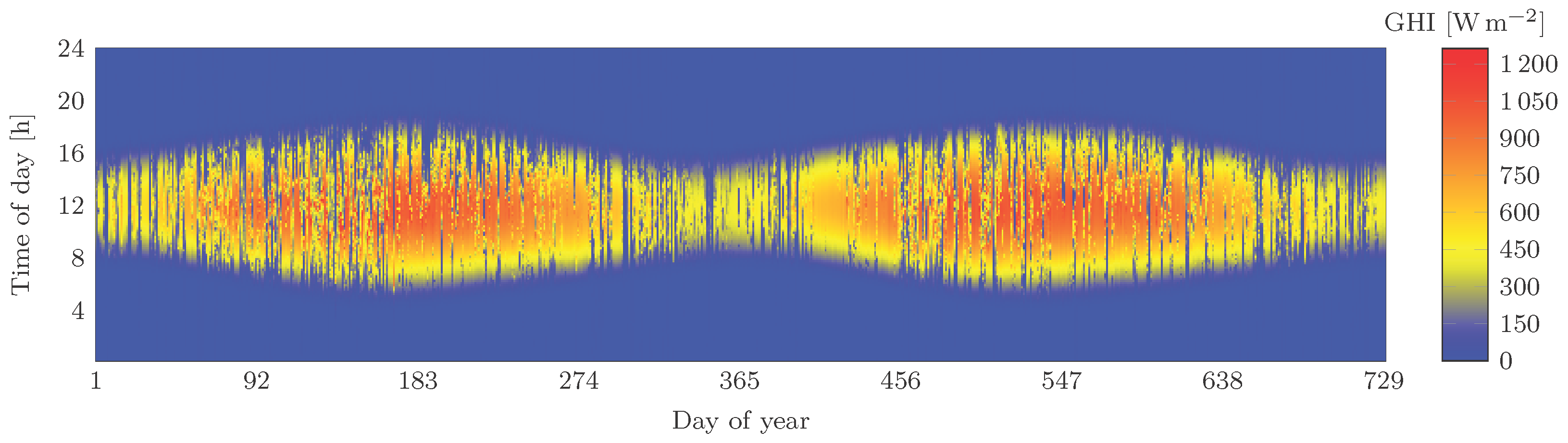
2. Data Description
3. Forecasting Methods Included in the Comparative Study
3.1. Scaled Persistence Model
3.2. Gaussian Processes
3.2.1. Kernels Used in This Study
- The SE-ARD kernel , expressed as a product of squared exponential (SE) kernels over input dimensions each having a different length-scale, is given by:where is the amplitude and are the length-scales which control the function’s variation along each input dimension. This kernel is a covariance function commonly chosen as default in Gaussian processes applications, because it has relatively few and easy-interpretable parameters to estimate. Moreover, it can be seen as an universal kernel, capable of learning any continuous function given enough data, under some conditions that are investigated in [46].
- The RQ-ARD (rational quadratic) kernel is given by:where characterizes the relative weighting of large-scale and small-scale variations. The RQ kernel can be seen as an infinite sum of SE kernels with different characteristic length-scales [38] and models functions that vary smoothly across many length-scales. Analogously, the RQ-ARD kernel, which allows the modelling of functions that exhibit multi-scale variations along each input dimension, can be seen as an infinite sum of SE-ARD kernels.
3.2.2. Gaussian Process Regression
3.2.3. Training a GPR Model
3.3. Support Vector Machines
3.3.1. Support Vector Regression
3.3.2. Least Squares Support Vector Regression
3.4. Artificial Neural Networks
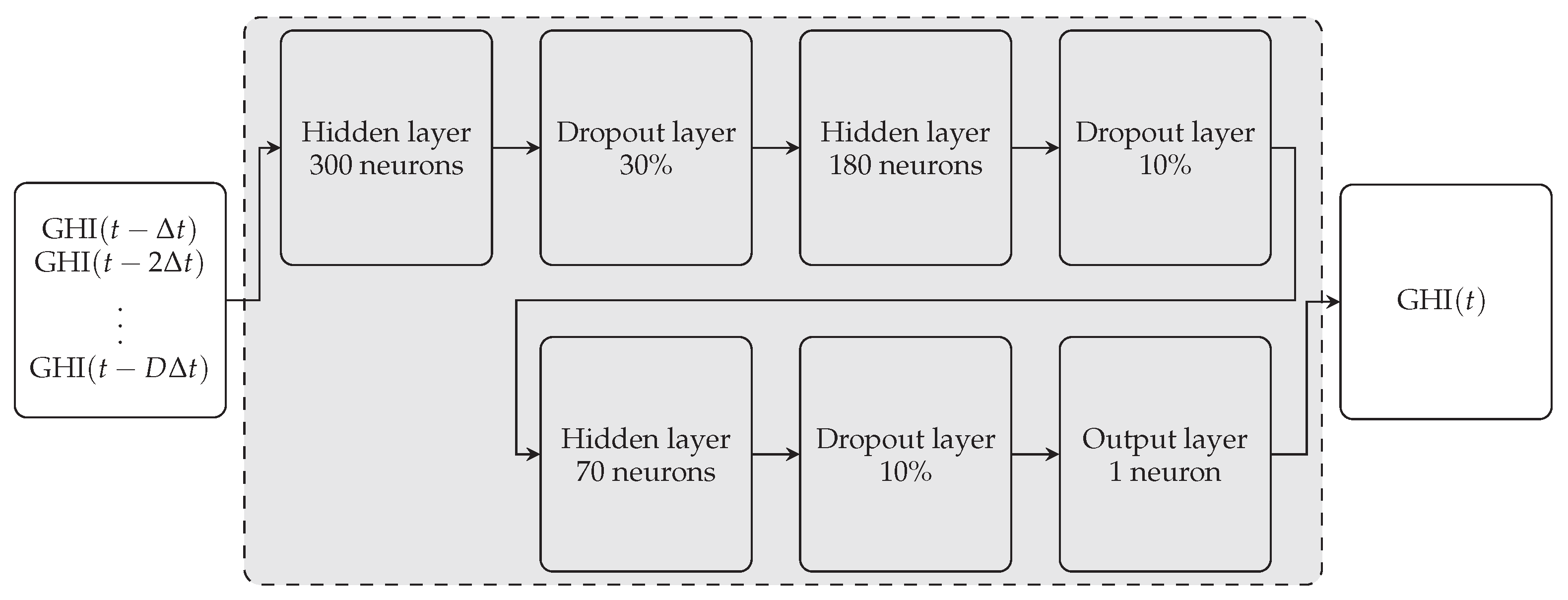
3.4.1. Multilayer Perceptron
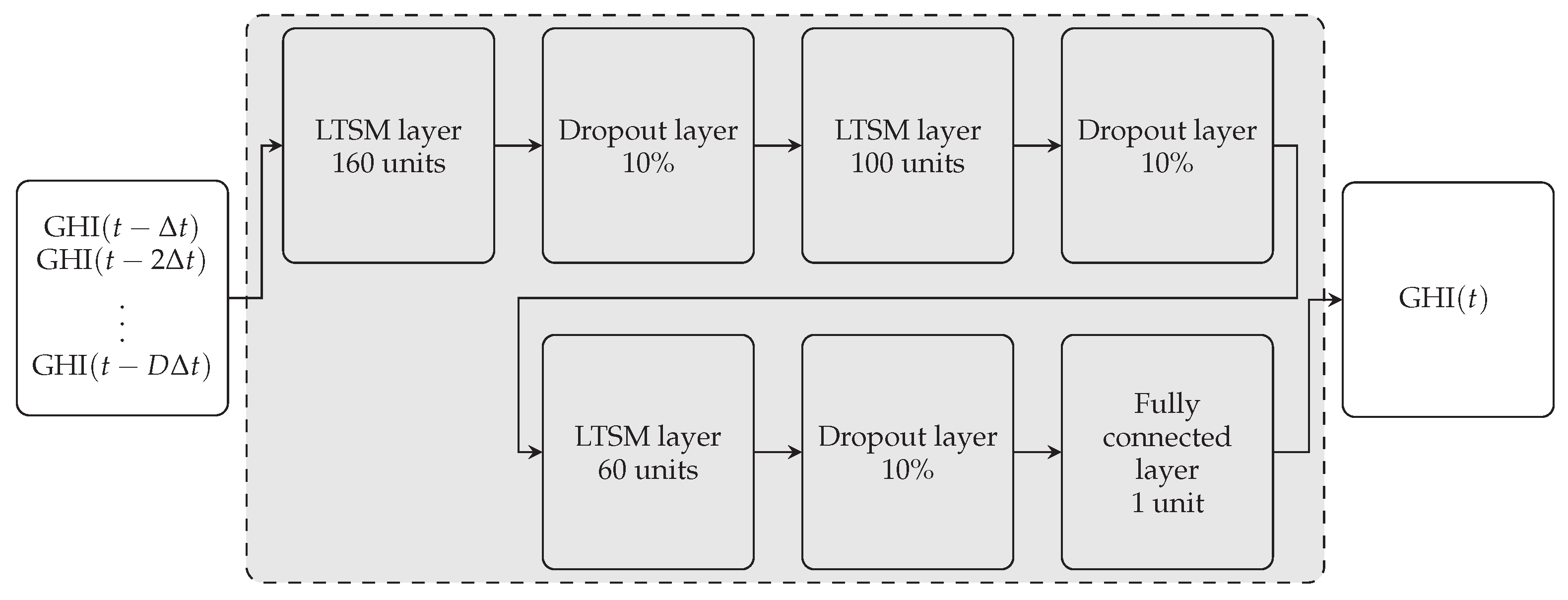
3.4.2. Long Short-Term Memory
3.4.3. Training Algorithm
4. Results
4.1. Performance Criteria
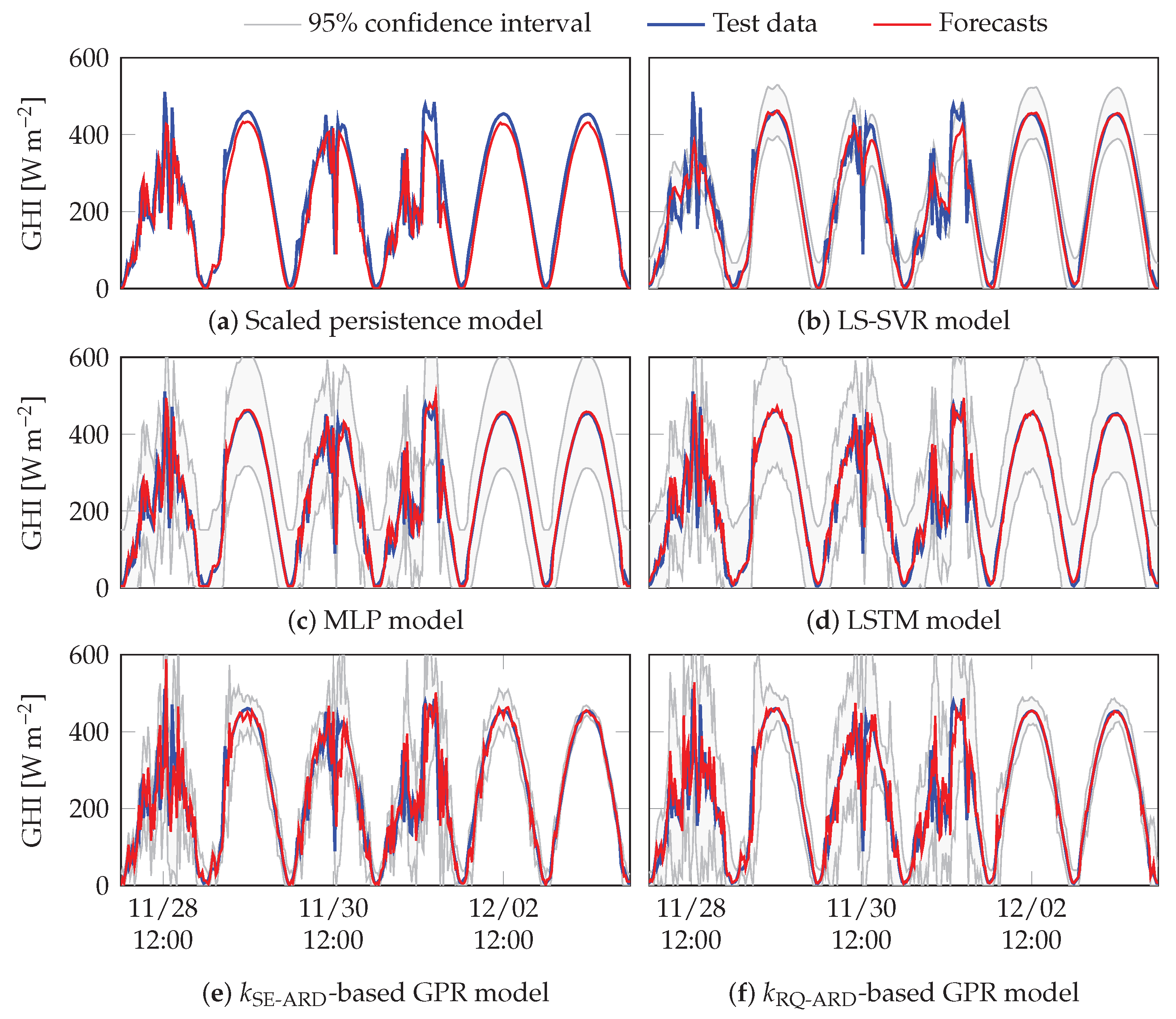
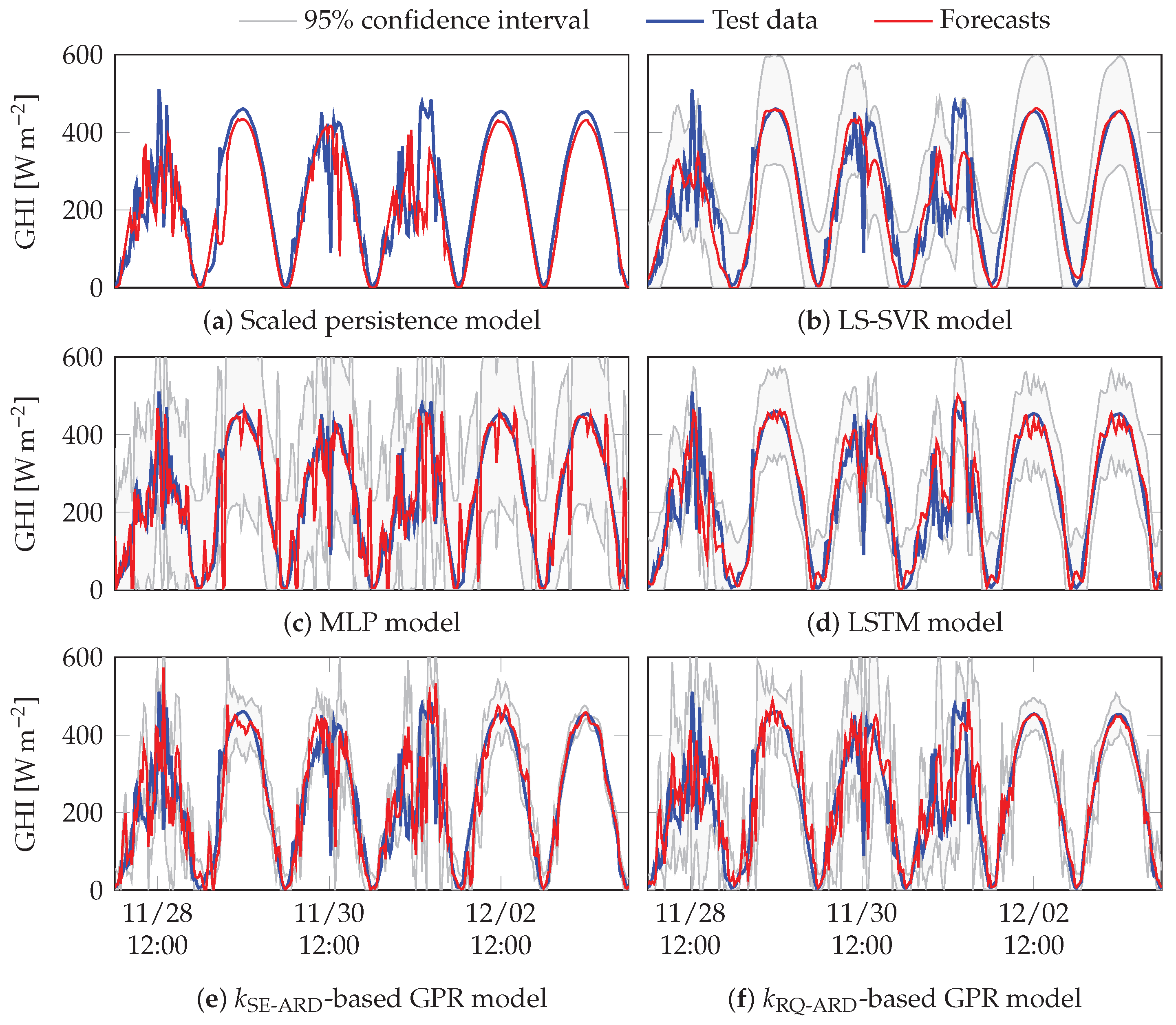
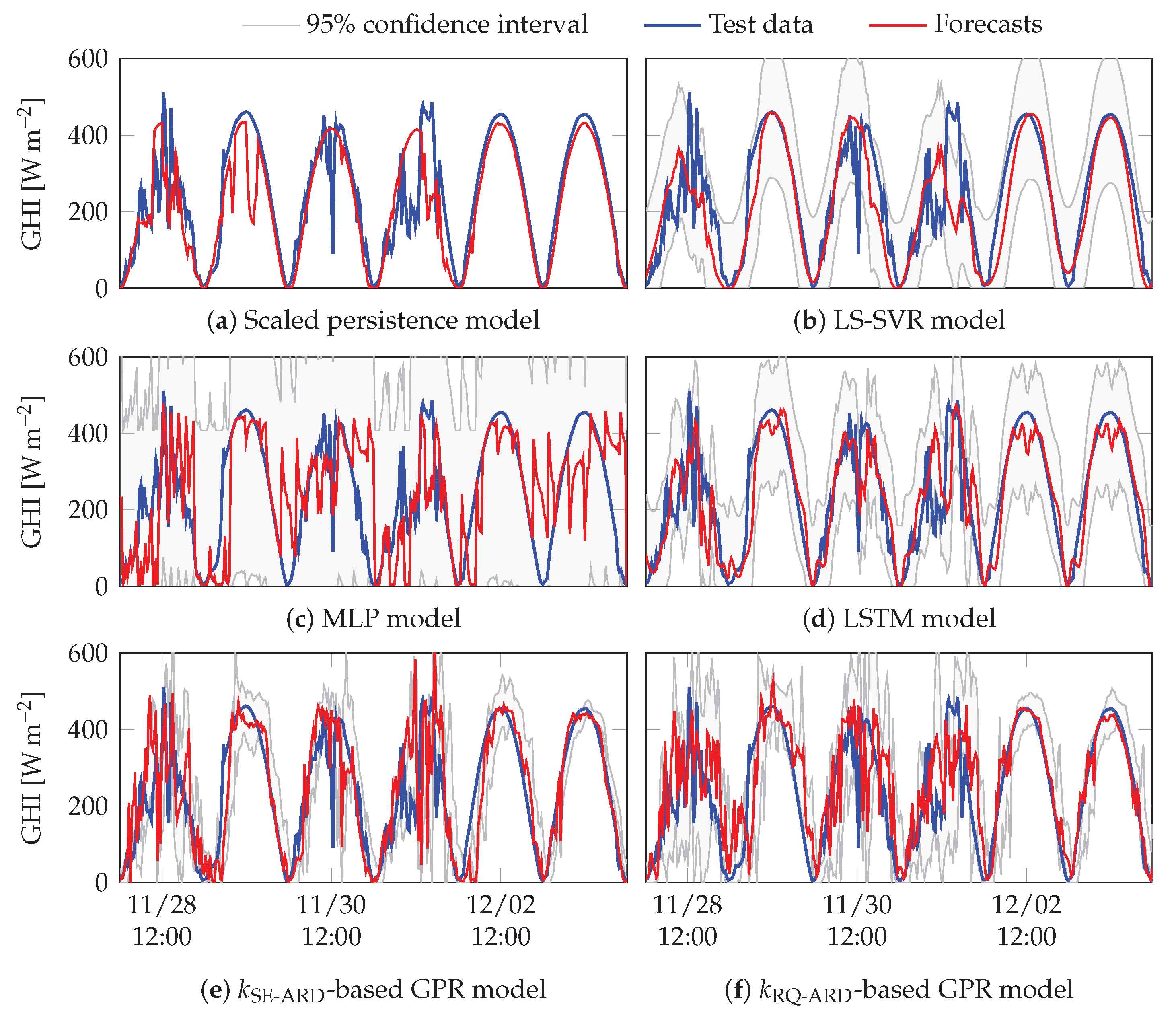
4.2. Forecasting Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Optical air mass |
| ANN | Artificial neural networks |
| AR | Autoregressive model |
| ARD | Automatic relevance determination |
| CNN | Convolutional neural networks |
| CWC | Coverage width-based criterion |
| DMAE | Dynamic mean absolute error |
| DHI | Diffuse horizontal irradiance |
| DNI | Direct normal irradiance |
| GHI | Global horizontal irradiance |
| GP | Gaussian process |
| GPR | Gaussian process regression |
| kNN | k-nearest neighbours |
| LSTM | Long short-term memory |
| (n)MAE | (Normalized) mean absolute error |
| MAPE | Mean absolute prediction error |
| (n)MBE | (Normalized) mean bias error |
| MLP | Multilayer perceptron |
| MSE | Mean squared error |
| NWP | Numerical weather prediction |
| PV | Photovoltaic |
| RBF | Radial basis function |
| ReLU | Rectified linear unit |
| (n)RMSE | (Normalized) root mean square error |
| RQ | Rational quadratic |
| SE | Squared exponential |
| SVM | Support vector machine |
| SVR | Support vector regression |
| (LS-)SVR | (Least-squares) support vector regression |
References
- Eltawil, M.A.; Zhao, Z. Grid-connected photovoltaic power systems: Technical and potential problems—A review. Renew. Sustain. Energy Rev. 2010, 14, 112–129. [Google Scholar] [CrossRef]
- Zahedi, A. A review of drivers, benefits, and challenges in integrating renewable energy sources into electricity grid. Renew. Sustain. Energy Rev. 2011, 15, 4775–4779. [Google Scholar] [CrossRef]
- Olowu, T.O.; Sundararajan, A.; Moghaddami, M.; Sarwat, A.I. Future Challenges and Mitigation Methods for High Photovoltaic Penetration: A Survey. Energies 2018, 11, 1782. [Google Scholar] [CrossRef]
- Nwaigwe, K.N.; Mutabilwa, P.; Dintwa, E. An overview of solar power (PV systems) integration into electricity grids. Mater. Sci. Energy Technol. 2019, 2, 629–633. [Google Scholar] [CrossRef]
- Sinsel, S.R.; Riemke, R.L.; Hoffmann, V.H. Challenges and solution technologies for the integration of variable renewable energy sources—a review. Renew. Energy 2020, 145, 2271–2285. [Google Scholar] [CrossRef]
- Dkhili, N.; Eynard, J.; Thil, S.; Grieu, S. A survey of modelling and smart management tools for power grids with prolific distributed generation. Sustain. Energy Grids Netw. 2020, 21, 100284. [Google Scholar] [CrossRef]
- Manjarres, D.; Alonso, R.; Gil-Lopez, S.; Landa-Torres, I. Solar Energy Forecasting and Optimization System for Efficient Renewable Energy Integration. In Data Analytics for Renewable Energy Integration: Informing the Generation and Distribution of Renewable Energy; Woon, W.L., Aung, Z., Kramer, O., Madnick, S., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–12. [Google Scholar]
- Kroposki, B. Integrating high levels of variable renewable energy into electric power systems. J. Mod. Power Syst. Clean Energy 2017, 5, 831–837. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M.D. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Lorenz, E.; Heinemann, D. Prediction of solar irradiance and photovoltaic power. In Comprehensive Renewable Energy; Sayigh, A., Ed.; Elsevier: Oxford, UK, 2012; pp. 239–292. [Google Scholar] [CrossRef]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Diagne, M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef]
- Lauret, P.; Voyant, C.; Soubdhan, T.; David, M.; Poggi, P. A benchmarking of machine learning techniques for solar radiation forecasting in an insular context. Sol. Energy 2015, 112, 446–457. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; de Pison, F.J.M.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Ahmed, A.; Khalid, M. A review on the selected applications of forecasting models in renewable power systems. Renew. Sustain. Energy Rev. 2019, 100, 9–21. [Google Scholar] [CrossRef]
- Yang, H.; Kurtz, B.; Nguyen, D.; Urquhart, B.; Chow, C.W.; Ghonima, M.; Kleissl, J. Solar irradiance forecasting using a ground-based sky imager developed at UC San Diego. Sol. Energy 2014, 103, 502–524. [Google Scholar] [CrossRef]
- Nou, J.; Chauvin, R.; Eynard, J.; Thil, S.; Grieu, S. Towards the intrahour forecasting of direct normal irradiance using sky-imaging data. Heliyon 2018, 4, e00598. [Google Scholar] [CrossRef]
- Wang, P.; van Westrhenen, R.; Meirink, J.F.; van der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Mathiesen, P.; Collier, C.; Kleissl, J. A high-resolution, cloud-assimilating numerical weather prediction model for solar irradiance forecasting. Sol. Energy 2013, 92, 47–61. [Google Scholar] [CrossRef]
- Gala, Y.; Fernández, A.; Díaz, J.; Dorronsoro, J.R. Hybrid machine learning forecasting of solar radiation values. Neurocomputing 2016, 176, 48–59. [Google Scholar] [CrossRef]
- Hocaoglu, F.O.; Serttas, F. A novel hybrid (Mycielski-Markov) model for hourly solar radiation forecasting. Renew. Energy 2017, 108, 635–643. [Google Scholar] [CrossRef]
- Guermoui, M.; Melgani, F.; Gairaa, K.; Mekhalfi, M.L. A comprehensive review of hybrid models for solar radiation forecasting. J. Clean. Prod. 2020, 258, 120357. [Google Scholar] [CrossRef]
- Chandola, D.; Gupta, H.; Tikkiwal, V.A.; Bohra, M.K. Multi-step ahead forecasting of global solar radiation for arid zones using deep learning. Procedia Comput. Sci. 2020, 167, 626–635. [Google Scholar] [CrossRef]
- Tolba, H.; Dkhili, N.; Nou, J.; Eynard, J.; Thil, S.; Grieu, S. Multi-Horizon Forecasting of Global Horizontal Irradiance Using Online Gaussian Process Regression: A Kernel Study. Energies 2020, 13, 4184. [Google Scholar] [CrossRef]
- Gbémou, S.; Tolba, H.; Thil, S.; Grieu, S. Global horizontal irradiance forecasting using online sparse Gaussian process regression based on quasiperiodic kernels. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/ICPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Inanlouganji, A.; Reddy, A.T.; Katipamula, S. Evaluation of regression and neural network models for solar forecasting over different short-term horizons. Sci. Technol. Built Environ. 2018, 24, 1004–1013. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Sikinioti-Lock, A.; Shah, N. Machine-learning methods for integrated renewable power generation: A comparative study of artificial neural networks, support vector regression, and Gaussian process regression. Renew. Sustain. Energy Rev. 2019, 108, 513–538. [Google Scholar] [CrossRef]
- Nou, J.; Chauvin, R.; Thil, S.; Grieu, S. A new approach to the real-time assessment of the clear-sky direct normal irradiance. Appl. Math. Model. 2016, 40, 7245–7264. [Google Scholar] [CrossRef]
- Sfetsos, A.; Coonick, A.H. Univariate and multivariate forecasting of hourly solar radiation with artificial intelligence techniques. Sol. Energy 2000, 68, 169–178. [Google Scholar] [CrossRef]
- Alzahrani, A.; Shamsi, P.; Dagli, C.; Ferdowsi, M. Solar Irradiance Forecasting Using Deep Neural Networks. Procedia Comput. Sci. 2017, 114, 304–313. [Google Scholar] [CrossRef]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.L. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef]
- Bae, K.Y.; Jang, H.S.; Sung, D.K. Hourly Solar Irradiance Prediction Based on Support Vector Machine and Its Error Analysis. IEEE Trans. Power Syst. 2017, 32, 935–945. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, J. SolarNet: A sky image-based deep convolutional neural network for intra-hour solar forecasting. Sol. Energy 2020, 204, 71–78. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Duvenaud, D.; Lloyd, J.; Grosse, R.; Tenenbaum, J.; Zoubin, G. Structure Discovery in Nonparametric Regression through Compositional Kernel Search. In Proceedings of the 30th International Conference on Machine Learning, 16–21 June 2013; Dasgupta, S., McAllester, D., Eds.; PMLR: Atlanta, GA, USA, 2013; Volume 28, pp. 1166–1174. [Google Scholar]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Suykens, J.A.K.; Van Gestel, T.; De Brabanter, J.; De Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: Singapore, 2002. [Google Scholar] [CrossRef]
- Antonanzas-Torres, F.; Urraca, R.; Polo, J.; Perpiñán-Lamigueiro, O.; Escobar, R. Clear sky solar irradiance models: A review of seventy models. Renew. Sustain. Energy Rev. 2019, 107, 374–387. [Google Scholar] [CrossRef]
- Chauvin, R.; Nou, J.; Eynard, J.; Thil, S.; Grieu, S. A new approach to the real-time assessment and intraday forecasting of clear-sky direct normal irradiance. Sol. Energy 2018, 167, 35–51. [Google Scholar] [CrossRef]
- Ineichen, P.; Perez, R. A new airmass independent formulation for the Linke turbidity coefficient. Sol. Energy 2002, 73, 151–157. [Google Scholar] [CrossRef]
- Kasten, F.; Young, A.T. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 28, 4735–4738. [Google Scholar] [CrossRef] [PubMed]
- Roberts, S.; Osborne, M.; Ebden, M.; Reece, S.; Gibson, N.; Aigrain, S. Gaussian processes for time-series modelling. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20110550. [Google Scholar] [CrossRef]
- Duvenaud, D.K.; Nickisch, H.; Rasmussen, C.E. Additive Gaussian Processes. In Advances in Neural Information Processing Systems 24; Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2011; pp. 226–234. [Google Scholar]
- Micchelli, C.; Xu, Y.; Zhang, H. Universal Kernels. Mathematics 2006, 7, 2651–2667. [Google Scholar]
- MacKay, D.J.C. Introduction to Gaussian processes. In Neural Networks and Machine Learning; Bishop, C.M., Ed.; Springer: Berlin/Heidenberg, Germany, 1998; Chapter 11; pp. 133–165. [Google Scholar]
- Chen, Z.; Wang, B. How priors of initial hyperparameters affect Gaussian process regression models. Neurocomputing 2018, 275, 1702–1710. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Vapnik, V.N.; Golowich, S.E.; Smola, A.J. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. In Advances in Neural Information Processing Systems 9; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 281–287. [Google Scholar]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.J.; Vapnik, V.N. Support Vector Regression Machines. In Advances in Neural Information Processing Systems 9; Mozer, M.C., Jordan, M.I., Petsche, T., Eds.; MIT Press: Cambridge, MA, USA, 1997; pp. 155–161. [Google Scholar]
- Burges, C.J.C. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Lerner, A. Pattern Recognition using Generalized Portrait Method. Autom. Remote Control 1963, 24, 774–780. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Suykens, J.; Horváth, G.; Basu, S.; Micchelli, C.; Vandewalle, J. Advances in Learning Theory: Methods, Models and Applications; IOS Press: Amsterdam, The Netherlands, 2003; Volume 190. [Google Scholar]
- Zhang, G.P. Neural Networks for Time-Series Forecasting. In Handbook of Natural Computing; Rozenberg, G., Bäck, T., Kok, J.N., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 461–477. [Google Scholar] [CrossRef]
- Reddy, K.S.; Ranjan, M. Solar resource estimation using artificial neural networks and comparison with other correlation models. Energy Convers. Manag. 2003, 44, 2519–2530. [Google Scholar] [CrossRef]
- Amrouche, B.; Pivert, X.L. Artificial neural network based daily local forecasting for global solar radiation. Appl. Energy 2014, 130, 333–341. [Google Scholar] [CrossRef]
- Brownlee, J. Deep Learning for Time Series Forecasting: Predict the Future with MLPs, CNNs and LSTMs in Python; Machine Learning Mastery, 2018; Available online: https://machinelearningmastery.com/deep-learning-for-time-series-forecasting/ (accessed on 2 June 2012).
- Siami-Namini, S.; Tavakoli, N.; Siami Namin, A. A Comparison of ARIMA and LSTM in Forecasting Time Series. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2018; pp. 1394–1401. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the 30th International Conference on Machine Learning Research, 16–21 June 2013; Dasgupta, S., McAllester, D., Eds.; PMLR: Atlanta, GA, USA, 2013; Volume 28, pp. 1310–1318. [Google Scholar]
- Hochreiter, S. The Vanishing Gradient Problem during Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Improving neural networks by preventing co-adaptation of feature detectors. Comput. Res. Repos. (CoRR) 2012, arXiv:1207.0580v1. [Google Scholar]
- Frías-Paredes, L.; Mallor, F.; Gastón-Romeo, M.; León, T. Dynamic mean absolute error as new measure for assessing forecasting errors. Energy Convers. Manag. 2018, 162, 176–188. [Google Scholar] [CrossRef]
- Quan, H.; Srinivasan, D.; Khosravi, A. Short-Term Load and Wind Power Forecasting Using Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, A.; Nahavandi, S.; Creighton, D.; Atiya, A.F. Lower Upper Bound Estimation Method for Construction of Neural Network-Based Prediction Intervals. IEEE Trans. Neural Netw. 2011, 22, 337–346. [Google Scholar] [CrossRef] [PubMed]
- De Brabanter, K.; De Brabanter, J.; Suykens, J.A.K.; De Moor, B. Approximate Confidence and Prediction Intervals for Least Squares Support Vector Regression. IEEE Trans. Neural Netw. 2011, 22, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Khosravi, A.; Nahavandi, S.; Creighton, D.C.; Atiya, A.F. Comprehensive Review of Neural Network-Based Prediction Intervals and New Advances. IEEE Trans. Neural Netw. 2011, 22, 1341–1356. [Google Scholar] [CrossRef] [PubMed]
- Pearce, T.; Brintrup, A.; Zaki, M.; Neely, A. High-Quality Prediction Intervals for Deep Learning: A Distribution-Free, Ensembled Approach. In Proceedings of the 35th International Conference on Machine Learning Research, Stockholm Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR Stockholmsmässan: Stockholm, Sweden, 2018; Volume 80, pp. 4075–4084. [Google Scholar]
- Quiñonero-Candela, J.; Rasmussen, C.E. A Unifying View of Sparse Approximate Gaussian Process Regression. J. Mach. Learn. Res. 2005, 6, 1939–1959. [Google Scholar]


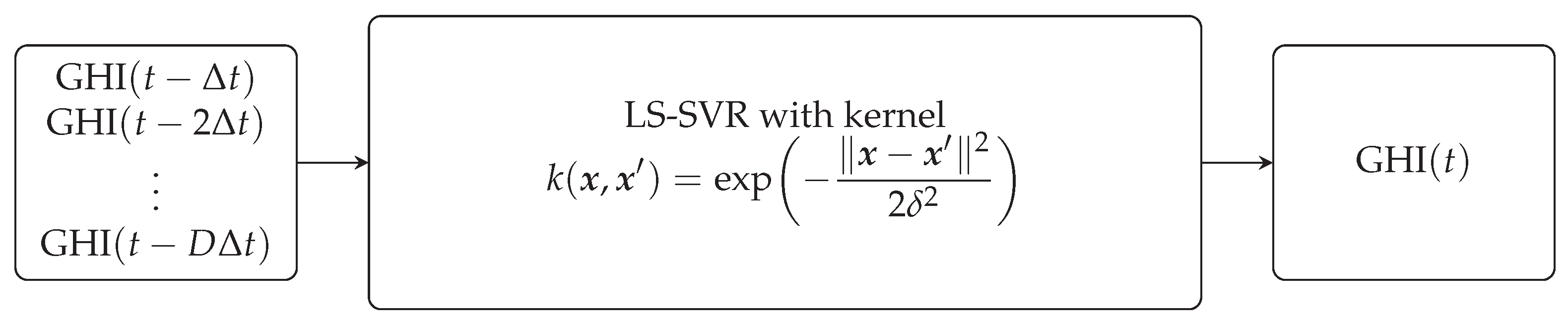
| Authors | Forecast Horizons | Forecasting Methods | Data Time Step | Performance Criteria | Input Variables | Output Variables | Database |
|---|---|---|---|---|---|---|---|
| Sharifzadeh et al. [28] | to | ANN, SVR, GPR | MSE | PV power, temperature, DHI, DNI | PV power | From 1985 to 2014 | |
| Benali et al. [26] | to | Scaled persistence, MLP, Random forest | RMSE, nRMSE, MAE, nMAE | GHI, DNI, DHI | GHI, DNI, DHI | Data covering three years | |
| Chandola et al. [23] | to | LSTM | RMSE, MAPE | DHI, DNI, dew point, temperature, pressure, relative humidity, wind direction, wind speed | GHI | From 2010 to 2014 | |
| Lauret et al. [13] | to | Persistence, scaled persistence, AR, MLP, SVR, GPR | nRMSE, nMAE, nMBE, s-skill score | Clear sky index | Clear sky index | Three sites; for each site, one-year data for training and one-year data for test | |
| Tolba et al. [24] | to | Persistence, GPR | nRMSE | Time | GHI | Two datasets, each covering a period of 45 days; 30 days for training and 15 days for test | |
| Gbémou et al. (present paper) | to | Scaled persistence, MLP, LSTM, LS-SVR, GPR | nRMSE, DMAE, CWC | GHI | GHI | One-year data for training and one-year data for test |
| Forecast Horizon | 10 | 1 | 4 |
|---|---|---|---|
| Scaled persistence | 0.2020 | 0.3435 | 0.4628 |
| LS-SVR | 0.2197 | 0.3305 | 0.4317 |
| LSTM | 0.2016 | 0.3089 | 0.3995 |
| MLP | 0.1985 | 0.3210 | 0.4449 |
| -based GPR | 0.2057 | 0.3140 | 0.4020 |
| -based GPR | 0.2079 | 0.3287 | 0.4285 |
| Forecast Horizon | 10 | 1 | 4 |
|---|---|---|---|
| Scaled persistence | 0.04951 | 0.08201 | 0.13481 |
| LS-SVR | 0.05582 | 0.08463 | 0.14753 |
| LSTM | 0.03317 | 0.05587 | 0.08956 |
| MLP | 0.02948 | 0.07248 | 0.15173 |
| -based GPR | 0.03419 | 0.05677 | 0.08912 |
| -based GPR | 0.04416 | 0.06718 | 0.09816 |
| Forecast Horizon | 10 | 1 | 4 |
|---|---|---|---|
| LS-SVR | 0.5660 | 1.1136 | 9.8391 |
| LSTM | 0.4734 | 0.8283 | 2.1642 |
| MLP | 0.4609 | 0.7031 | 2.2884 |
| -based GPR | 0.4574 | 0.6026 | 2.8651 |
| -based GPR | 0.4966 | 0.7610 | 8.8394 |
| Model | Training Time () | Number of Parameters | Execution Time for One Forecast () |
|---|---|---|---|
| LS-SVR | 133 | 26,457 | 4.12 |
| LSTM | 20 | 127,459 | 0.05 |
| MLP | 10 | 58,635 | 0.02 |
| -based GPR | 209 | 26,457 | 12.59 |
| -based GPR | 200 | 26,457 | 12.59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gbémou, S.; Eynard, J.; Thil, S.; Guillot, E.; Grieu, S. A Comparative Study of Machine Learning-Based Methods for Global Horizontal Irradiance Forecasting. Energies 2021, 14, 3192. https://doi.org/10.3390/en14113192
Gbémou S, Eynard J, Thil S, Guillot E, Grieu S. A Comparative Study of Machine Learning-Based Methods for Global Horizontal Irradiance Forecasting. Energies. 2021; 14(11):3192. https://doi.org/10.3390/en14113192
Chicago/Turabian StyleGbémou, Shab, Julien Eynard, Stéphane Thil, Emmanuel Guillot, and Stéphane Grieu. 2021. "A Comparative Study of Machine Learning-Based Methods for Global Horizontal Irradiance Forecasting" Energies 14, no. 11: 3192. https://doi.org/10.3390/en14113192
APA StyleGbémou, S., Eynard, J., Thil, S., Guillot, E., & Grieu, S. (2021). A Comparative Study of Machine Learning-Based Methods for Global Horizontal Irradiance Forecasting. Energies, 14(11), 3192. https://doi.org/10.3390/en14113192







