Operational Planning of Energy for Non-Interconnected Zones: A Simulation-Optimization Approach and a Case Study to Tackle Energy Poverty in Colombia
Abstract
1. Introduction
2. Problem Context and Mathematical Model
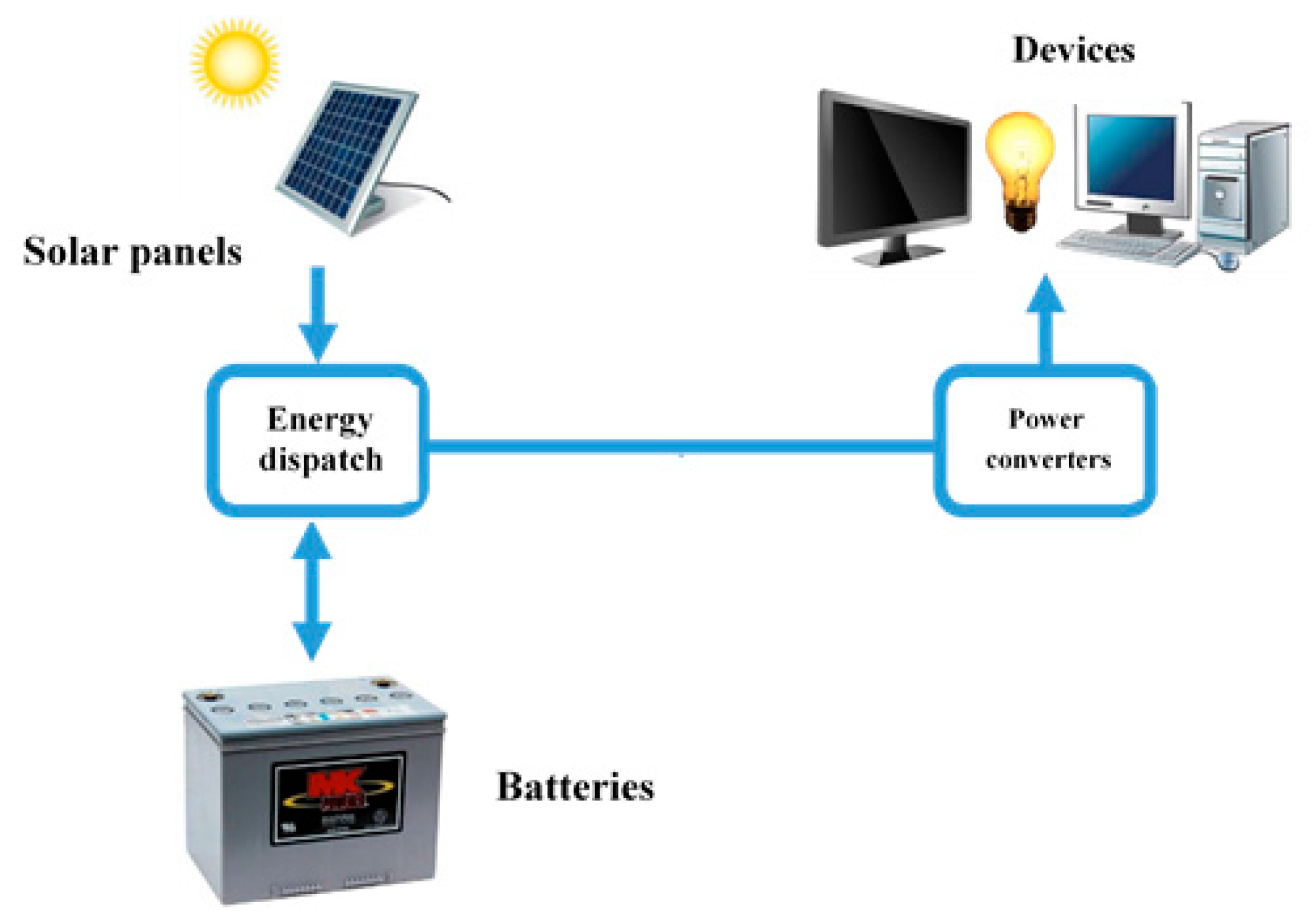
2.1. Problem Context
2.2. Mathematical Model
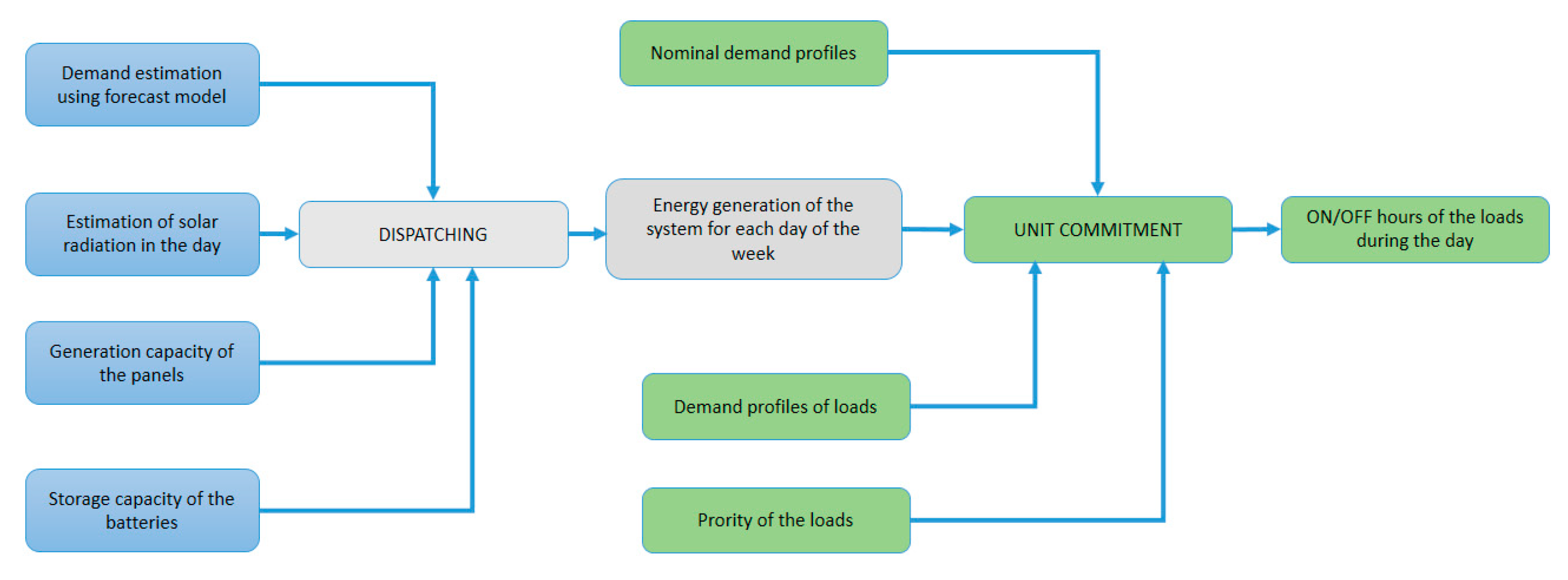
3. Solution Approach
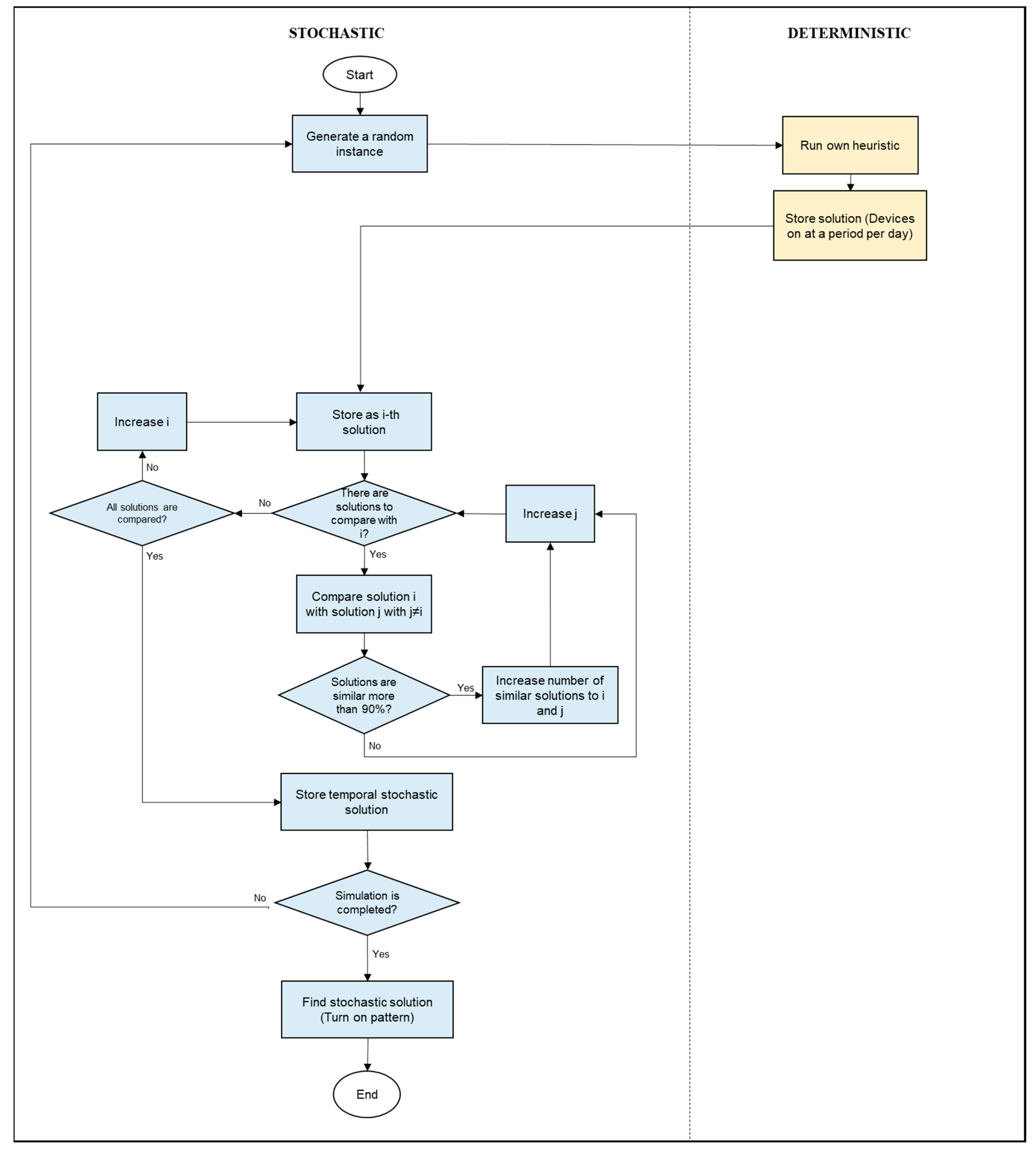
3.1. Solving the Stochastic Problem: A Simulation-Optimization Framework
3.2. Solving the Deterministic Problem: A Heuristic Approach
| Algorithm 1. Dispatching phase. | |||||
| Input: Output: | |||||
| For to | |||||
| For to | |||||
| If , then | |||||
| Assign energy to the batteries Assign the offer sent to the loads as | |||||
| Else | |||||
| Total available energy in the batteries is the energy from the batteries plus the available energy from solar panels Sort descending the demand of each device and store it as For to | |||||
| If demand can be satisfied | |||||
| Increase offer sent to the loads in the demand is the energy from the batteries minus the demand | |||||
| End if | |||||
| End | |||||
| End if | |||||
| End | |||||
| End | |||||
| Algorithm 2. Unit commitment phase. | ||||
| Input:Priority Output: | ||||
| For to | ||||
| For to | ||||
| Sort descending the demand of each device k according to priority. This is For to | ||||
| If demand can be satisfied with | ||||
Decrease offer sent to the leads in the demand | ||||
| Else | ||||
| End if | ||||
| End | ||||
| End | ||||
| End | ||||
4. Computational Experiments
4.1. Heuristic Performance
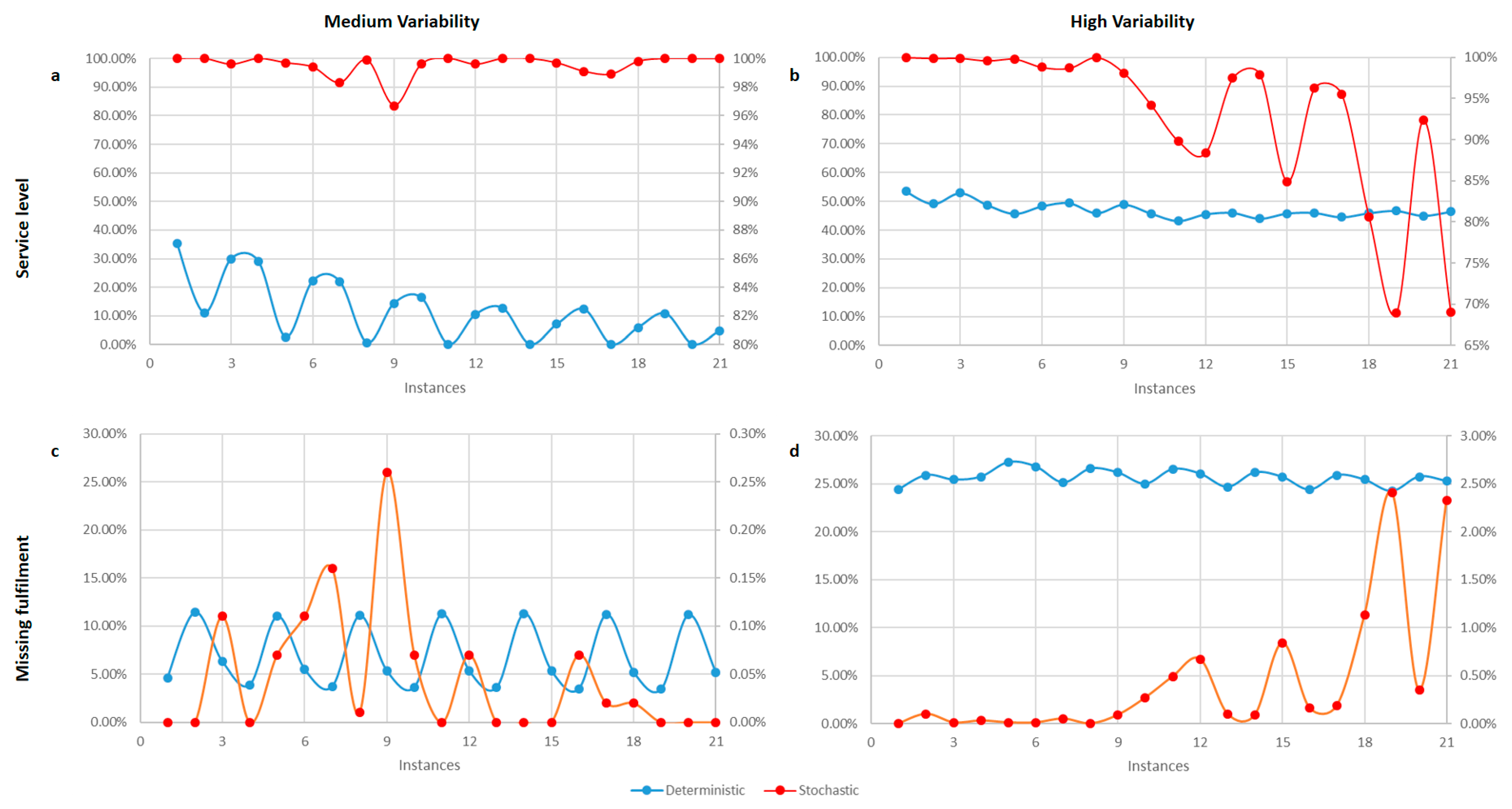
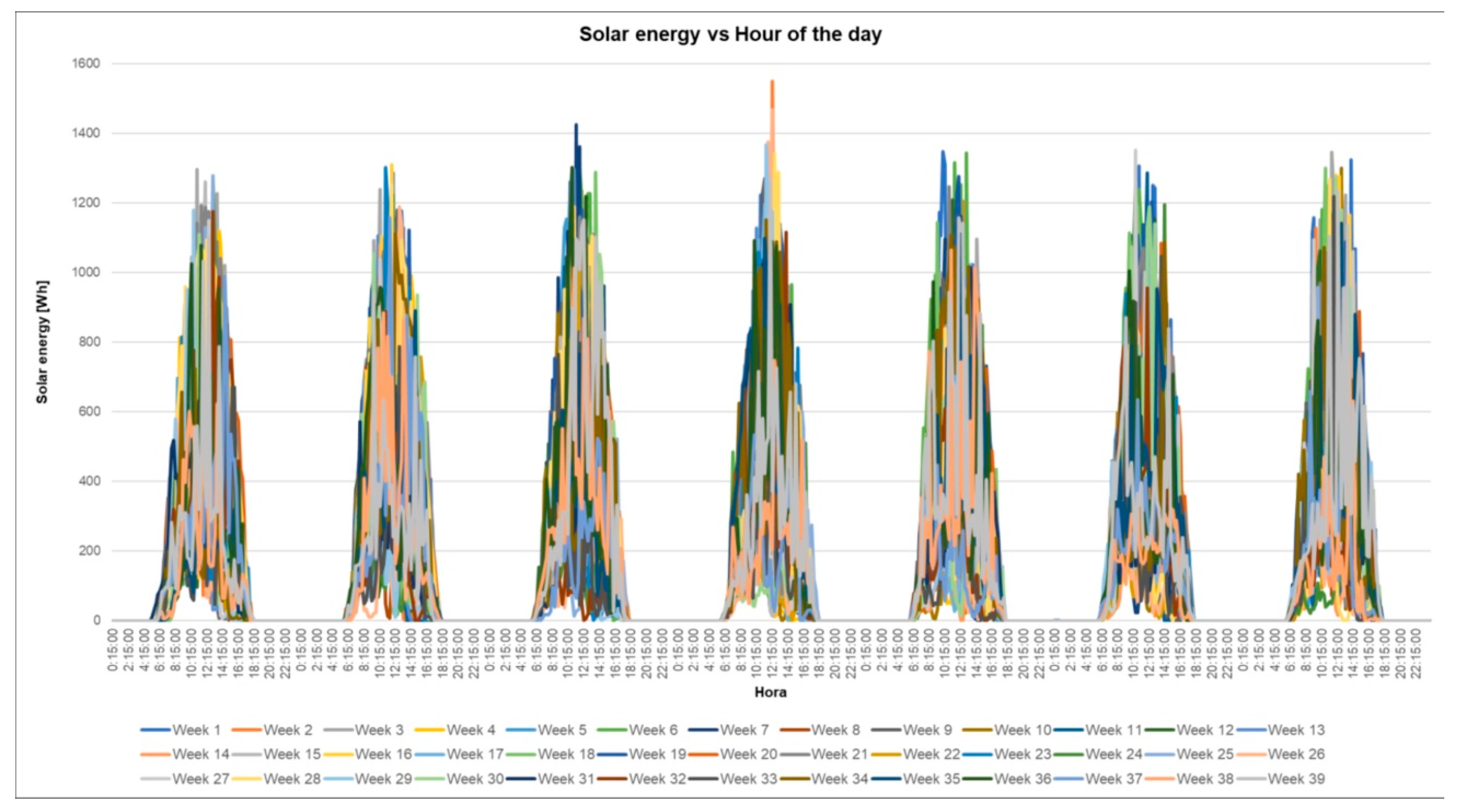
4.2. Including Variability
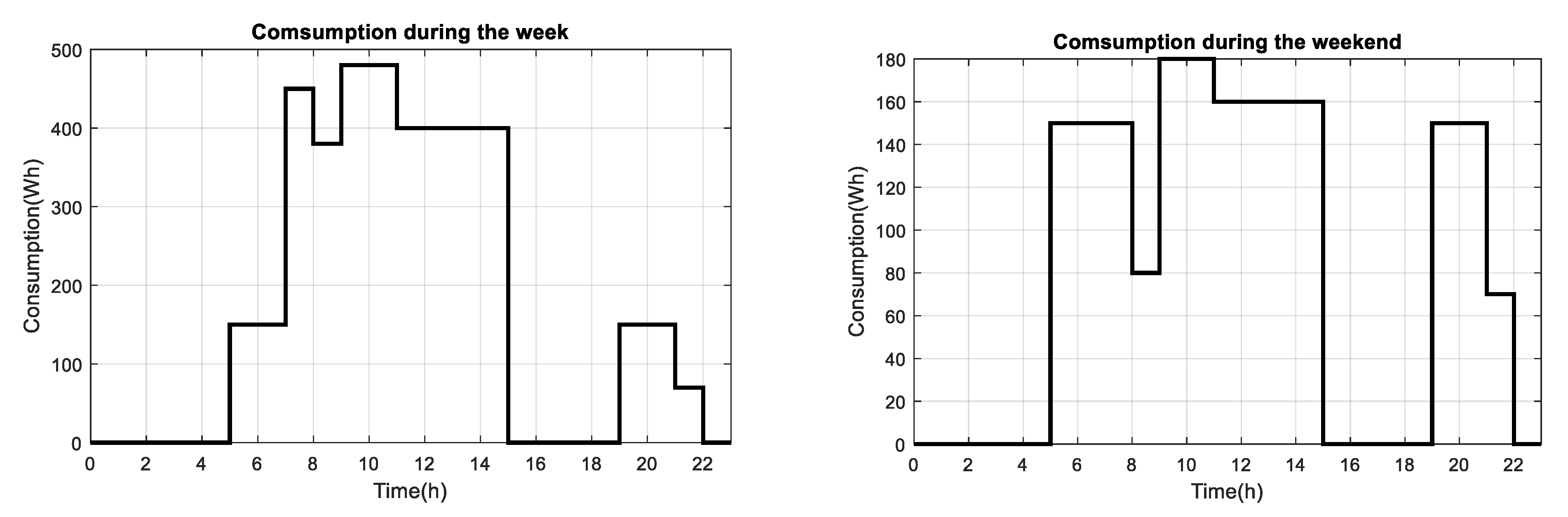
5. Operational Energy Planning at “Volcanes”: A Case Study in Colombia
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Baños, R.; Manzano-Agugliaro, F.; Montoya, F.; Gil, C.; Alcayde, A.; Gómez, J. Optimization methods applied to renewable and sustainable energy: A review. Renew. Sustain. Energy Rev. 2011, 15, 1753–1766. [Google Scholar] [CrossRef]
- Suberu, M.Y.; Mustafa, M.W.; Bashir, N. Energy storage systems for renewable energy power sector integration and mitigation of intermittency. Renew. Sustain. Energy Rev. 2014, 35, 499–514. [Google Scholar] [CrossRef]
- Elmouatamid, A.; Ouladsine, R.; Bakhouya, M.; El Kamoun, N.; Khaidar, M.; Zine-Dine, K. Review of Control and Energy Management Approaches in Micro-Grid Systems. Energies 2020, 14, 168. [Google Scholar] [CrossRef]
- Obeng, G.Y.; Evers, H.-D.; Akuffo, F.; Braimah, I.; Brew-Hammond, A. Solar photovoltaic electrification and rural energy-poverty in Ghana. Energy Sustain. Dev. 2008, 12, 43–54. [Google Scholar] [CrossRef]
- Palit, D. Solar energy programs for rural electrification: Experiences and lessons from South Asia. Energy Sustain. Dev. 2013, 17, 270–279. [Google Scholar] [CrossRef]
- United Nations. Sustainable Development Goals—Goal 7; United Nations: San Francisco, CA, USA, 2016. [Google Scholar]
- Primc, K.; Slabe-Erker, R. Social policy or energy policy? Time to reconsider energy poverty policies. Energy Sustain. Dev. 2020, 55, 32–36. [Google Scholar] [CrossRef]
- Szabó, S.; Bódis, K.; Huld, T.; Moner-Girona, M. Sustainable energy planning: Leapfrogging the energy poverty gap in Africa. Renew. Sustain. Energy Rev. 2013, 28, 500–509. [Google Scholar] [CrossRef]
- Caruso, G.; Colantonio, E.; Gattone, S.A. Relationships between Renewable Energy Consumption, Social Factors, and Health: A Panel Vector Auto Regression Analysis of a Cluster of 12 EU Countries. Sustainability 2020, 12, 2915. [Google Scholar] [CrossRef]
- Zeren, F.; Akkuş, H.T. The relationship between renewable energy consumption and trade openness: New evidence from emerging economies. Renew. Energy 2020, 147, 322–329. [Google Scholar] [CrossRef]
- WHO. WHO Global Conference Recommends Reducing Deaths from Air Pollution by Two-Thirds by 2030; WHO: Geneva, Switzerland, 2018; Available online: https://sdg.iisd.org/news/who-global-conference-recommends-reducing-deaths-from-air-pollution-by-two-thirds-by-2030/ (accessed on 23 April 2021).
- Ellabban, O.; Abu-Rub, H.; Blaabjerg, F. Renewable energy resources: Current status, future prospects and their enabling technology. Renew. Sustain. Energy Rev. 2014, 39, 748–764. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, X.; Shuai, C.; Huang, F.; Zhang, P.; Zhou, M.; Li, R. Evaluation of energy and environmental performances of Solar Photovoltaic-based Targeted Poverty Alleviation Plants in China. Energy Sustain. Dev. 2020, 56, 73–87. [Google Scholar] [CrossRef]
- Motta, O.D.; Aguilar, S.J.; Hurtado, E. A review to regulation and incentives of renewable energies. Revista Fac. de Cienc. Económicas Investig. y Reflexión 2012, 20, 55–67. [Google Scholar]
- Arango, S. Simulation of alternative regulations in the Colombian electricity market. Socio Econ. Plan. Sci. 2007, 41, 305–319. [Google Scholar] [CrossRef]
- Lacey-Barnacle, M.; Robison, R.; Foulds, C. Energy justice in the developing world: A review of theoretical frameworks, key research themes and policy implications. Energy Sustain. Dev. 2020, 55, 122–138. [Google Scholar] [CrossRef]
- XM S.A. E.S.P. Paratec Parámetros Técnicos Del Sim. Available online: http://paratec.xm.com.co/paratec/SitePages/generacion.aspx?q=capacidad (accessed on 14 April 2021).
- Ashok, S. Optimised model for community-based hybrid energy system. Renew. Energy 2007, 32, 1155–1164. [Google Scholar] [CrossRef]
- Pezzini, P.; Gomis-Bellmunt, O.; Sudrià-Andreu, A. Optimization techniques to improve energy efficiency in power systems. Renew. Sustain. Energy Rev. 2011, 15, 2028–2041. [Google Scholar] [CrossRef]
- Cormio, C.; Dicorato, M.; Minoia, A.; Trovato, M. A regional energy planning methodology including renewable energy sources and environmental constraints. Renew. Sustain. Energy Rev. 2003, 7, 99–130. [Google Scholar] [CrossRef]
- Abdul-Salam, Y.; Phimister, E. How effective are heuristic solutions for electricity planning in developing countries. Socio Econ. Plan. Sci. 2016, 55, 14–24. [Google Scholar] [CrossRef]
- Pohekar, S.; Ramachandran, M. Application of multi-criteria decision making to sustainable energy planning—A review. Renew. Sustain. Energy Rev. 2004, 8, 365–381. [Google Scholar] [CrossRef]
- Gasser, P.; Suter, J.; Cinelli, M.; Spada, M.; Burgherr, P.; Hirschberg, S.; Kadziński, M.; Stojadinović, B. Comprehensive resilience assessment of electricity supply security for 140 countries. Ecol. Indic. 2020, 110, 105731. [Google Scholar] [CrossRef]
- Sadollah, A.; Nasir, M.; Geem, Z.W. Sustainability and Optimization: From Conceptual Fundamentals to Applications. Sustainability 2020, 12, 2027. [Google Scholar] [CrossRef]
- Micangeli, A.; Fioriti, D.; Cherubini, P.; Duenas-Martinez, P. Optimal Design of Isolated Mini-Grids with Deterministic Methods: Matching Predictive Operating Strategies with Low Computational Requirements. Energies 2020, 13, 4214. [Google Scholar] [CrossRef]
- Zhou, W.; Lou, C.; Li, Z.; Lu, L.; Yang, H. Current status of research on optimum sizing of stand-alone hybrid solar–wind power generation systems. Appl. Energy 2010, 87, 380–389. [Google Scholar] [CrossRef]
- Khare, A.; Rangnekar, S. A review of particle swarm optimization and its applications in Solar Photovoltaic system. Appl. Soft Comput. 2013, 13, 2997–3006. [Google Scholar] [CrossRef]
- Borowski, P.F. Zonal and Nodal Models of Energy Market in European Union. Energies 2020, 13, 4182. [Google Scholar] [CrossRef]
- Mosavi, A.; Qasem, S.N.; Shokri, M.; Band, S.S.; Mohammadzadeh, A. Fractional-Order Fuzzy Control Approach for Photovoltaic/Battery Systems under Unknown Dynamics, Variable Irradiation and Temperature. Electronics 2020, 9, 1455. [Google Scholar] [CrossRef]
- Basmadjian, R.; De Meer, H. A Heuristics-Based Policy to Reduce the Curtailment of Solar-Power Generation Empowered by Energy-Storage Systems. Electronics 2018, 7, 349. [Google Scholar] [CrossRef]
- Mallor, F.; Azcárate, C.; Blanco, R.; Mateo, P. Operational management of renewable energy systems with storage using an optimisation-based simulation methodology. J. Simul. 2015, 9, 263–278. [Google Scholar] [CrossRef]
- Azcárate, C.; Mallor, F.; Mateo, P. Tactical and operational management of wind energy systems with storage using a probabilistic forecast of the energy resource. Renew. Energy 2017, 102, 445–456. [Google Scholar] [CrossRef]
- Ahmed, D.; Ebeed, M.; Ali, A.; Alghamdi, A.; Kamel, S. Multi-Objective Energy Management of a Micro-Grid Considering Stochastic Nature of Load and Renewable Energy Resources. Electronics 2021, 10, 403. [Google Scholar] [CrossRef]
- Branco, H.; Castro, R.; Lopes, A.S. Battery energy storage systems as a way to integrate renewable energy in small isolated power systems. Energy Sustain. Dev. 2018, 43, 90–99. [Google Scholar] [CrossRef]
- Jeon, C.; Shin, J. Long-term renewable energy technology valuation using system dynamics and Monte Carlo simulation: Photovoltaic technology case. Energy 2014, 66, 447–457. [Google Scholar] [CrossRef]
- Aly, A.; Moner-Girona, M.; Szabó, S.; Pedersen, A.B.; Jensen, S.S. Barriers to Large-scale Solar Power in Tanzania. Energy Sustain. Dev. 2019, 48, 43–58. [Google Scholar] [CrossRef]
- Ezbakhe, F.; Pérez-Foguet, A. Decision analysis for sustainable development: The case of renewable energy planning under uncertainty. Eur. J. Oper. Res. 2021, 291, 601–613. [Google Scholar] [CrossRef]
- Juan, A.A.; Faulin, J.; Grasman, S.E.; Rabe, M.; Figueira, G. A review of simheuristics: Extending metaheuristics to deal with stochastic combinatorial optimization problems. Oper. Res. Perspect. 2015, 2, 62–72. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, J.; Yu, L.; Zhu, J.; Li, Z.; Tang, L. A sustainable water-food-energy plan to confront climatic and socioeconomic changes using simulation-optimization approach. Appl. Energy 2019, 236, 743–759. [Google Scholar] [CrossRef]
- Ferrara, M.; Rolfo, A.; Prunotto, F.; Fabrizio, E. EDeSSOpt—Energy Demand and Supply Simultaneous Optimization for cost-optimized design: Application to a multi-family building. Appl. Energy 2019, 236, 1231–1248. [Google Scholar] [CrossRef]
- Roberts, J.J.; Cassula, A.M.; Silveira, J.L.; Bortoni, E.D.C.; Mendiburu, A.Z. Robust multi-objective optimization of a renewable based hybrid power system. Appl. Energy 2018, 223, 52–68. [Google Scholar] [CrossRef]
- Karaki, S.H.; Chedid, R.B.; Ramadan, R. Probabilistic performance assessment of autonomous solar-wind energy conversion systems. IEEE Trans. Energy Convers. 1999, 14, 766–772. [Google Scholar] [CrossRef]
- Chen, X.; Ankenman, B.; Nelson, B.L. Common random numbers and stochastic kriging. In Proceedings of the 2010 Winter Simulation Conference, Baltimore, MD, USA, 5–8 December 2010; pp. 947–956. [Google Scholar] [CrossRef]
- Figueira, G.; Almada-Lobo, B. Hybrid simulation–optimization methods: A taxonomy and discussion. Simul. Model. Pr. Theory 2014, 46, 118–134. [Google Scholar] [CrossRef]
- Cheng, R.C.H.; Currie, C.S.M. Input modelling for multimodal data. J. Oper. Res. Soc. 2019, 71, 1038–1052. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Radinger, T.; Echazarra, A.; Guerrero, G.; Valenzuela, J.P. OECD Reviews of School Resources: Colombia 2018; OECD Publishing: Paris, France, 2018. [Google Scholar] [CrossRef]

| Type | Effective Capacity (MW) | Percentage of the Effective Capacity |
|---|---|---|
| Cogenerated | 166.40 | 00.95 |
| Wind power | 18.42 | 00.10 |
| Hydraulic energy | 11,944.79 | 68.03 |
| Solar energy | 80,346 | 00.46 |
| Thermal energy | 5346.94 | 30.45 |
| Total Capacity | 17,557.01 | 100.00 |
| Case | Days | Mathematical Model | Heuristic | |||
|---|---|---|---|---|---|---|
| Time (s) | OF | Time (s) | OF | GAP | ||
| 1 | 1 | 40 | 149.4 | 0.52 | 154.5 | 3.4% |
| 2 | 1 | 10 | 162.3 | 0.22 | 166.4 | 2.5% |
| 3 | 1 | 20 | 147.0 | 0.44 | 150.8 | 2.6% |
| 4 | 2 | 15 | 298.1 | 0.78 | 308.9 | 3.6% |
| 5 | 2 | 15 | 324.1 | 0.66 | 332.8 | 2.7% |
| 6 | 2 | 15 | 293.3 | 0.66 | 301.6 | 2.8% |
| 7 | 3 | 280 | 445.1 | 0.91 | 463.4 | 4.1% |
| 8 | 3 | 10 | 486.0 | 0.82 | 499.2 | 2.7% |
| 9 | 3 | 400 | 438.3 | 0.79 | 452.4 | 3.2% |
| 10 | 4 | 300 | 596.5 | 1.2 | 617.9 | 3.6% |
| 11 | 4 | 60 | 644.9 | 1.11 | 665.6 | 3.2% |
| 12 | 4 | 781 | 580.3 | 1.02 | 603.2 | 3.9% |
| 13 | 5 | 21,100 | 738.8 | 1.37 | 772.3 | 4.5% |
| 14 | 5 | 12,143 | 744.1 | 1.31 | 832.0 | 11.8% |
| 15 | 5 | 1.18 | 754.0 | |||
| 16 | 6 | 1622 | 888.3 | 1.54 | 926.8 | 4.3% |
| 17 | 6 | 1724 | 867.0 | 1.49 | 998.4 | 15.2% |
| 18 | 6 | 1.45 | 904.8 | |||
| 19 | 7 | 1.71 | 1081.3 | |||
| 20 | 7 | 1.72 | 1164.8 | |||
| 21 | 7 | 1.61 | 1055.6 | |||
| Loads (k) | Code | Average Hours of Use | Demand per Hour (Wh) | Quantity |
|---|---|---|---|---|
| Exterior bulbs | EX | 4 | 20 | 4 |
| Classroom bulbs | BSC | 4 | 20 | 4 |
| Computers | PC | 8 | 60 | 5 |
| TV | TV | 6 | 100 | 1 |
| Electrical outlet | TA | 6 | 50 | 1 |
| Room bulb | BH | 6 | 20 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acuna, M.; Silva, C.; Tocaruncho, A.; Vargas, D.; Patiño, D.; Barrera, D.; Peña, J. Operational Planning of Energy for Non-Interconnected Zones: A Simulation-Optimization Approach and a Case Study to Tackle Energy Poverty in Colombia. Energies 2021, 14, 2789. https://doi.org/10.3390/en14102789
Acuna M, Silva C, Tocaruncho A, Vargas D, Patiño D, Barrera D, Peña J. Operational Planning of Energy for Non-Interconnected Zones: A Simulation-Optimization Approach and a Case Study to Tackle Energy Poverty in Colombia. Energies. 2021; 14(10):2789. https://doi.org/10.3390/en14102789
Chicago/Turabian StyleAcuna, Maria, Carlos Silva, Andrés Tocaruncho, Diana Vargas, Diego Patiño, David Barrera, and Johan Peña. 2021. "Operational Planning of Energy for Non-Interconnected Zones: A Simulation-Optimization Approach and a Case Study to Tackle Energy Poverty in Colombia" Energies 14, no. 10: 2789. https://doi.org/10.3390/en14102789
APA StyleAcuna, M., Silva, C., Tocaruncho, A., Vargas, D., Patiño, D., Barrera, D., & Peña, J. (2021). Operational Planning of Energy for Non-Interconnected Zones: A Simulation-Optimization Approach and a Case Study to Tackle Energy Poverty in Colombia. Energies, 14(10), 2789. https://doi.org/10.3390/en14102789








