On Multiple-Resonator-based Implementation of IEC/IEEE Standard P-Class Compliant PMUs
Abstract
1. Introduction
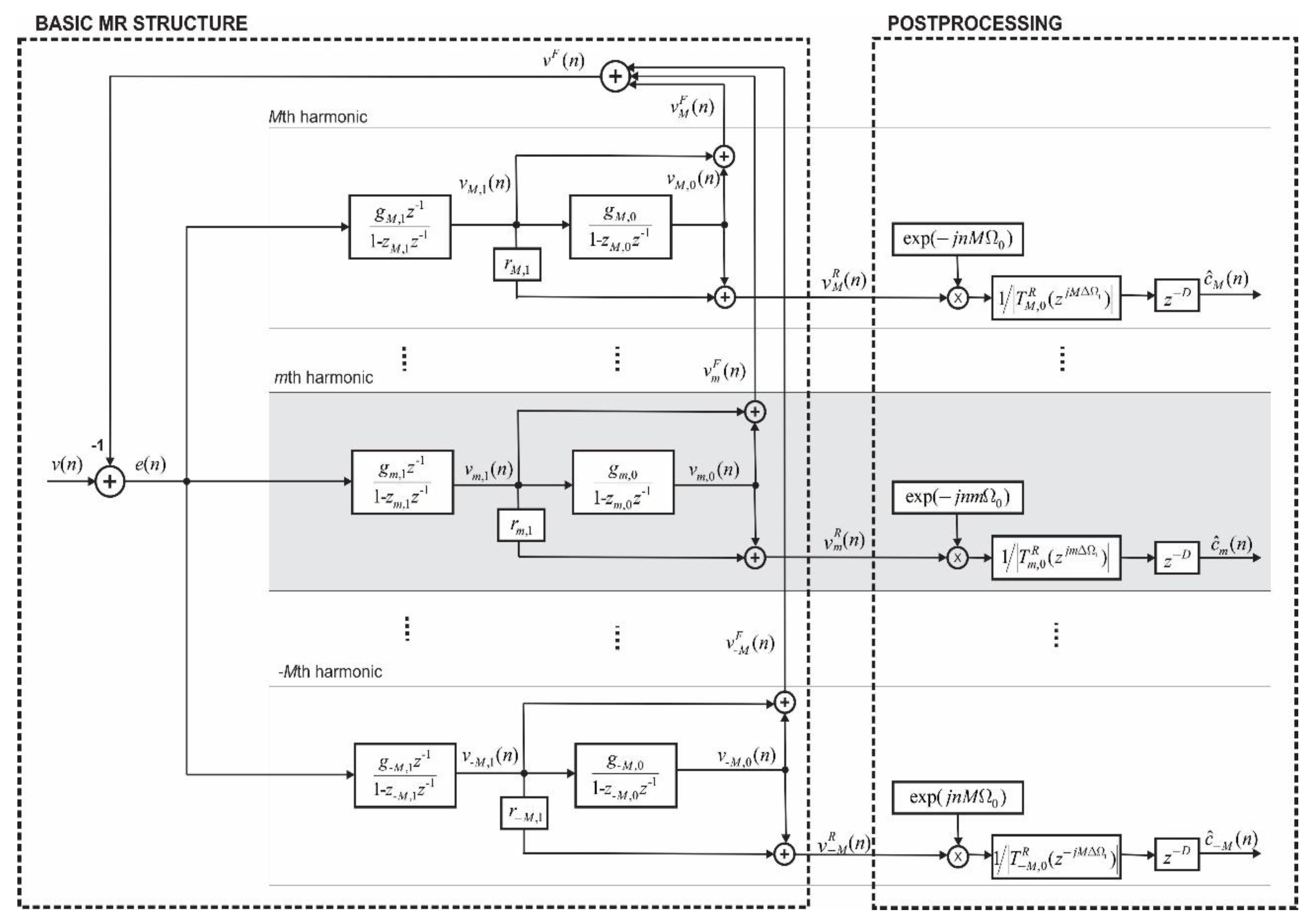
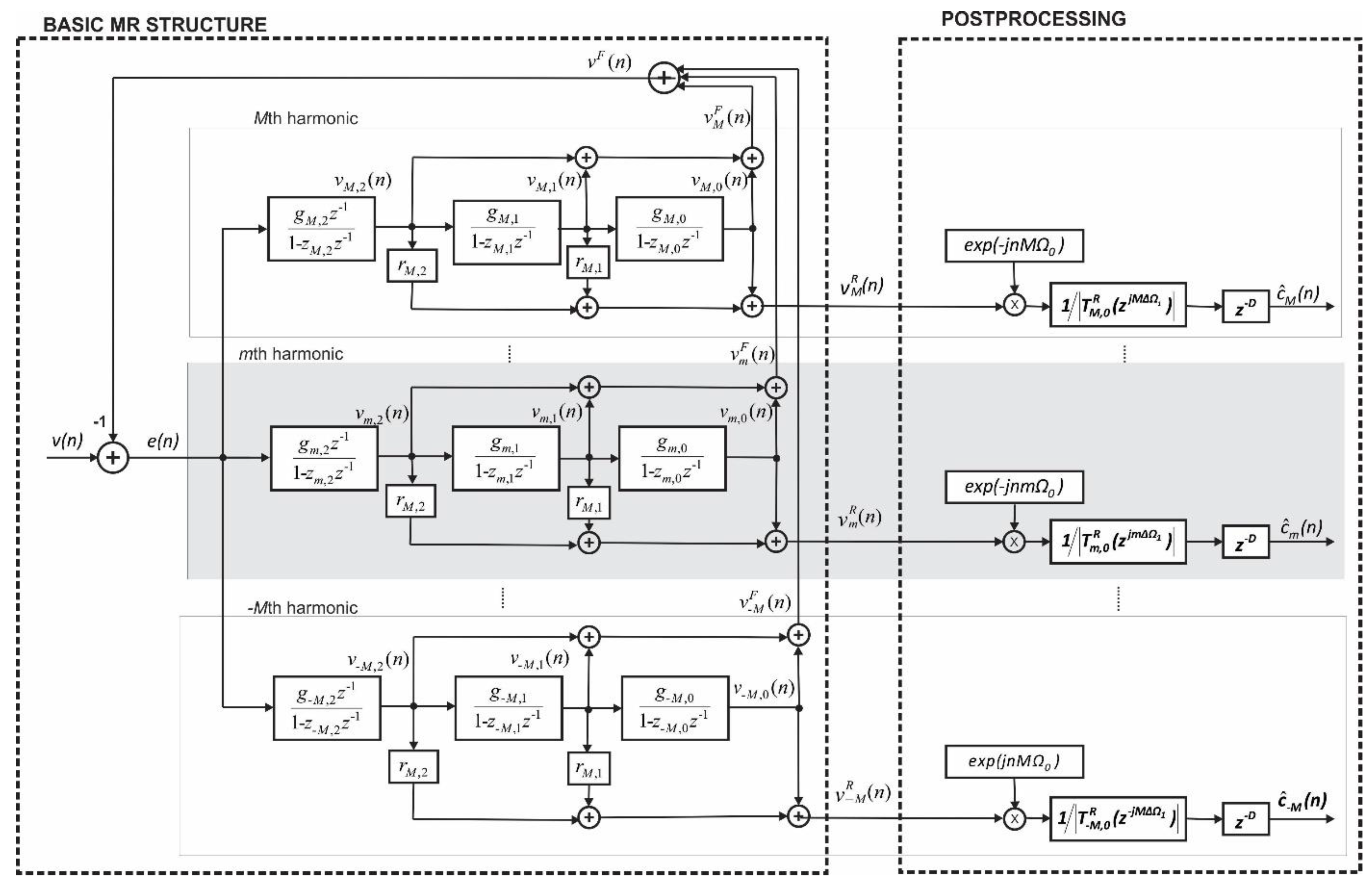
2. MR-Filter Structure
2.1. K = 1. Type (The Second-Order) Harmonic Analyzer
2.2. K = 2. Type (The Third-Order) Harmonic Analyzer
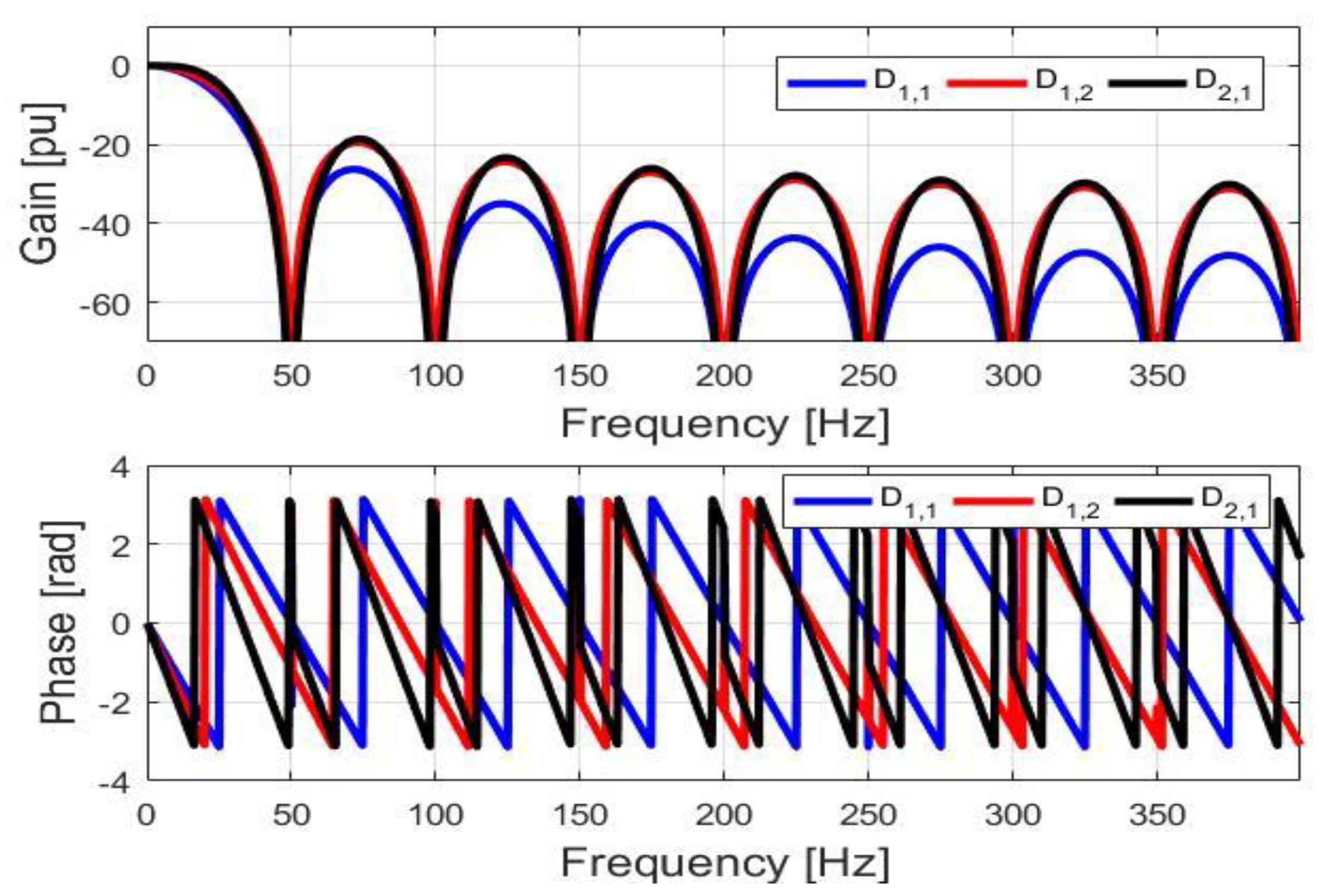
2.3. Frequency Responses of the Selected Characteristic Cases
3. Postprocessing
3.1. Harmonic Phasor Estimation
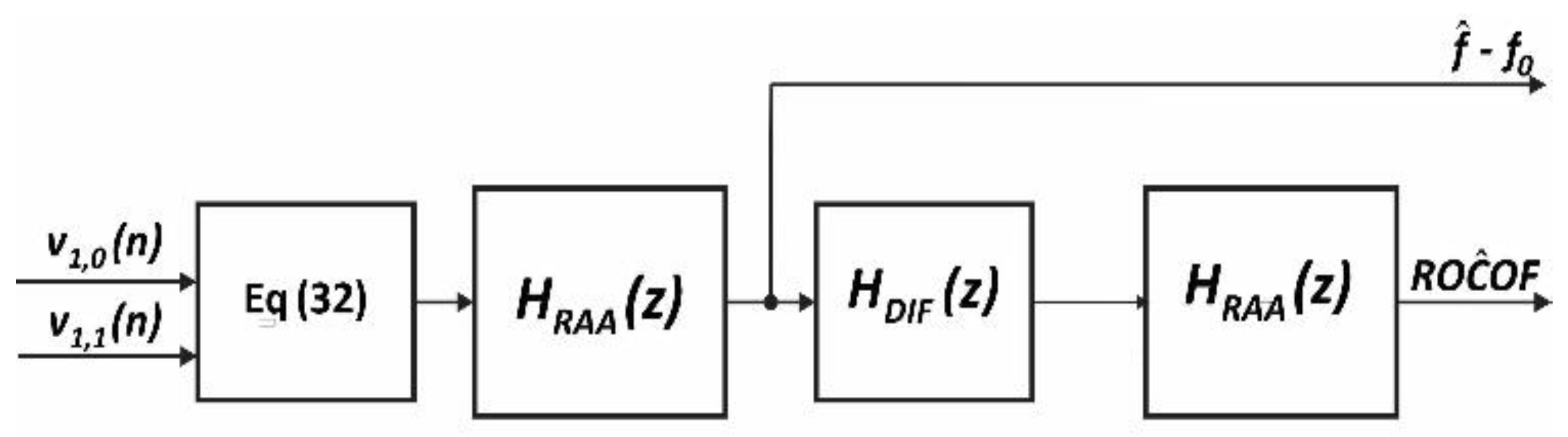
3.2. Frequency and ROCOF Estimation
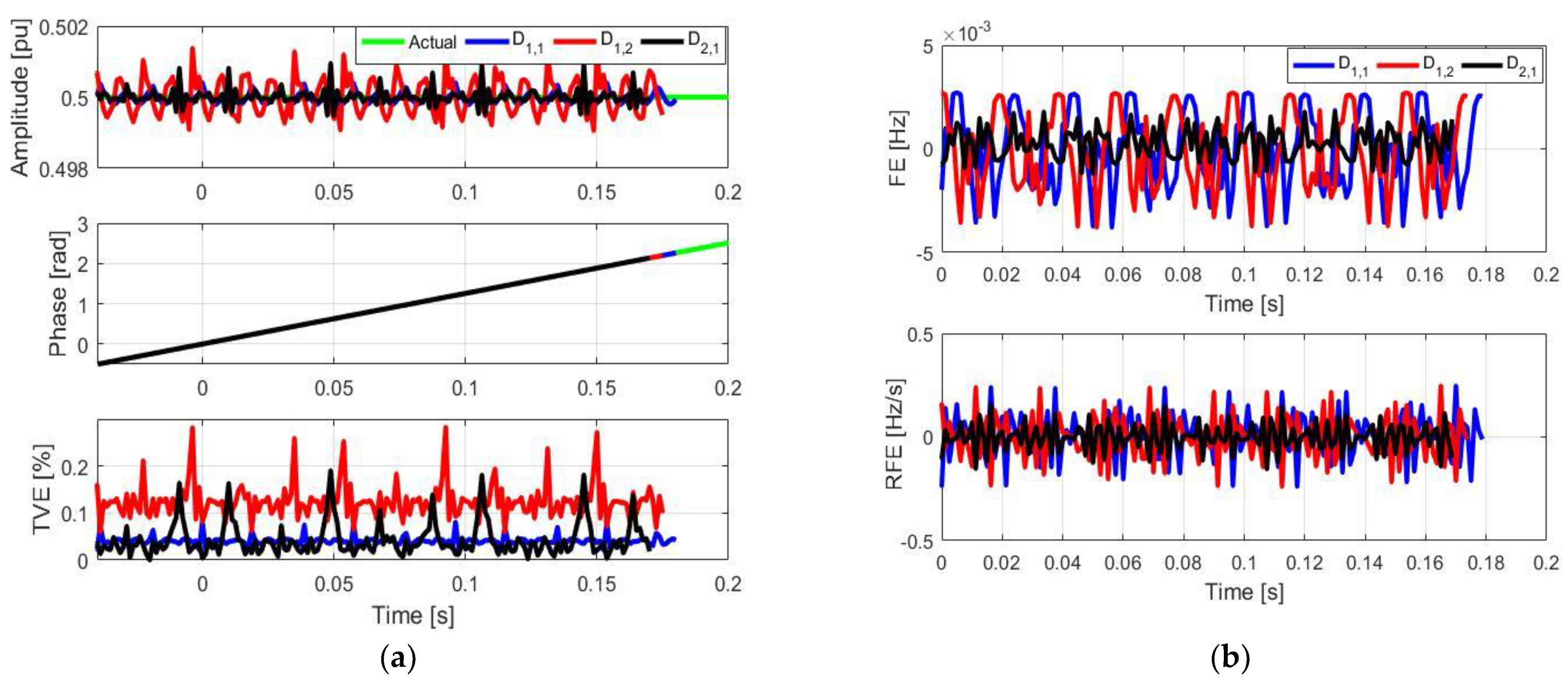
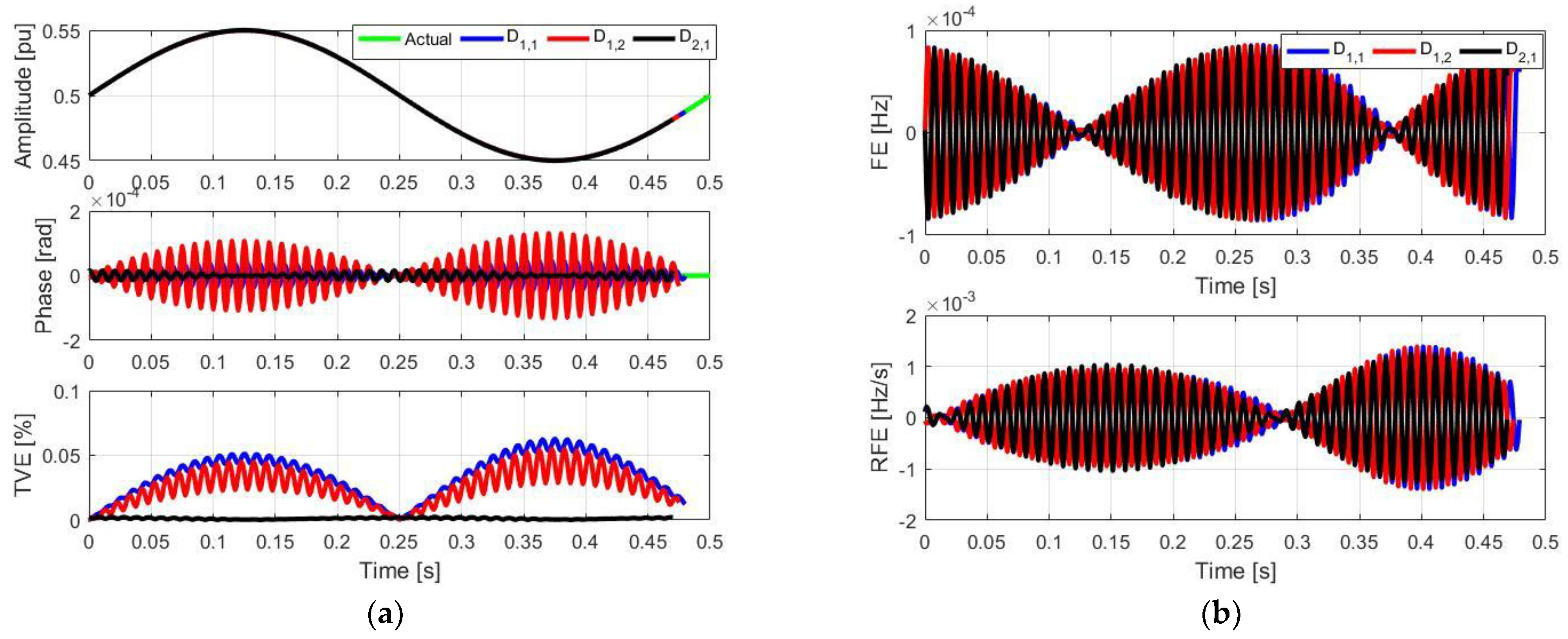
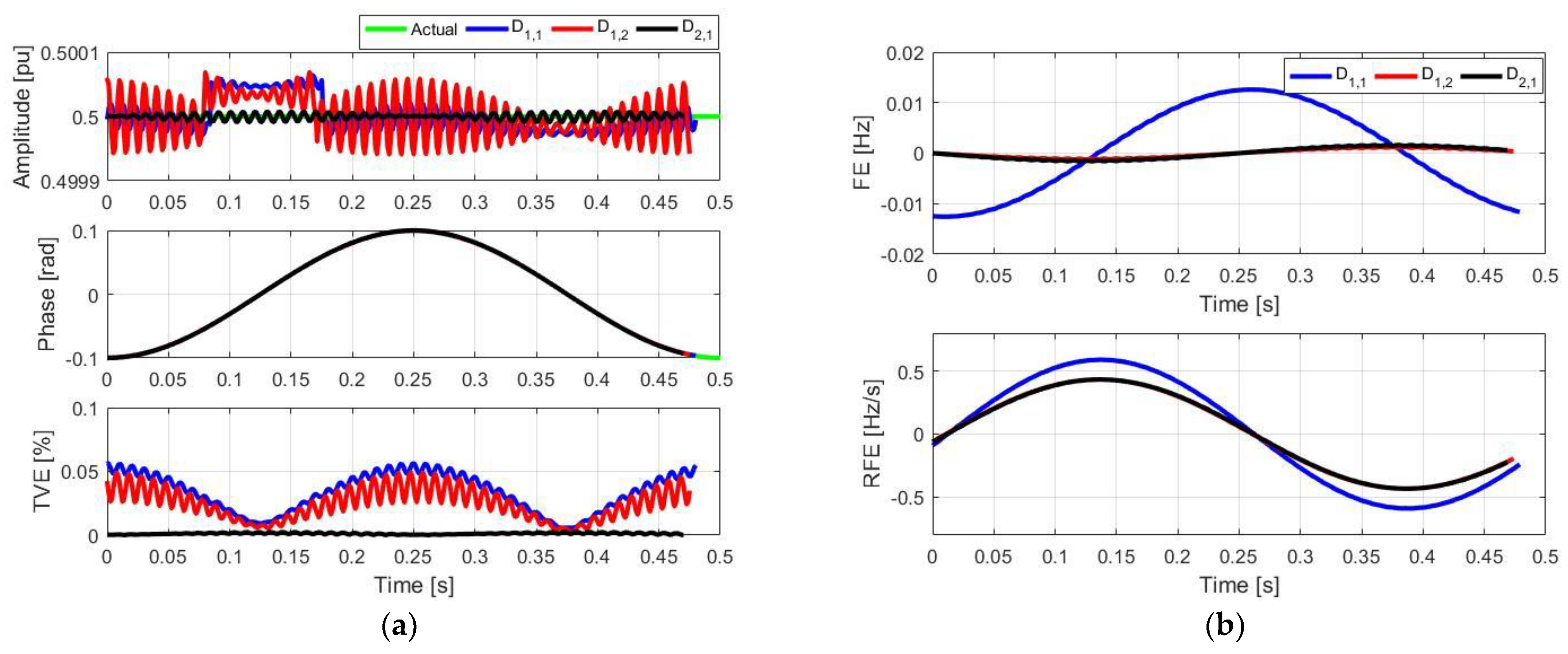
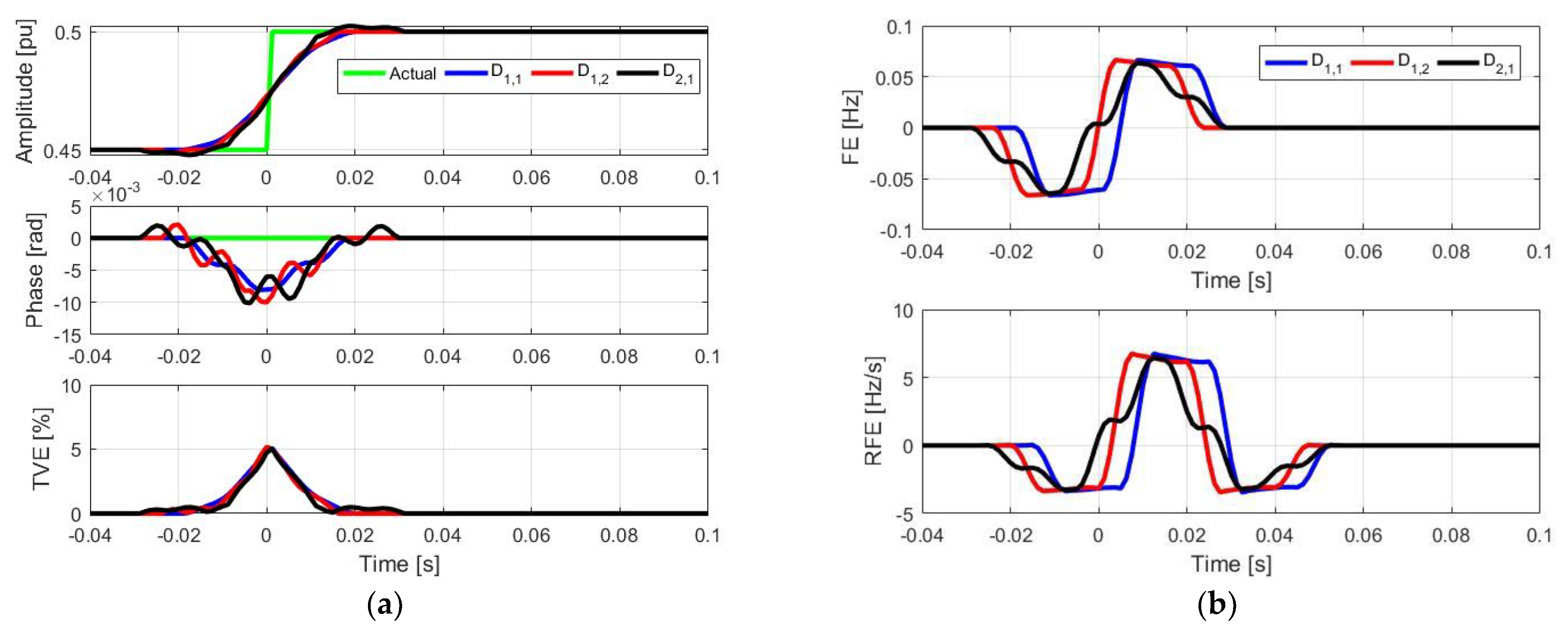
4. Simulation Results
4.1. Steady-State Characteristic
4.2. Amplitude and Phase Modulated Signals
4.3. Amplitude and Phase Step Signals
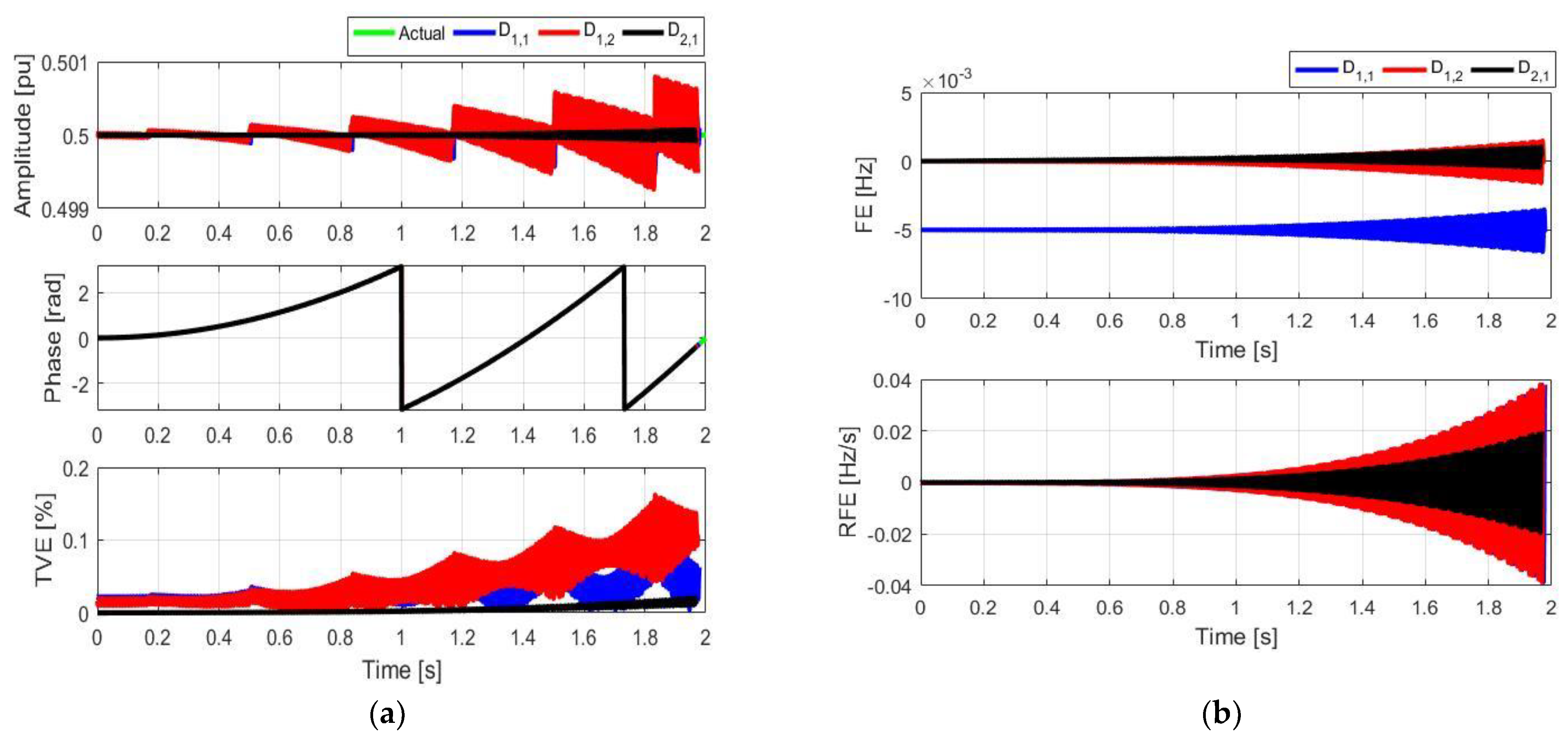
4.4. Frequency Ramp
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
References
- Monti, A.; Muscas, C.; Ponci, F. Phasor Measurement Units and Wide Area Monitoring Systems: From the Sensors to the System; Elsevier Inc.: Amsterdam, The Netherlands, 2016. [Google Scholar] [CrossRef]
- Castello, P.; Ferrari, P.; Flammini, A.; Muscas, C.; Rinaldi, S. A New IED with PMU Functionalities for Electrical Substations. IEEE Trans. Instrum. Meas. 2013, 62, 3209–3217. [Google Scholar] [CrossRef]
- Jain, A.; Samantaray, S.R.; Geoffroy, L.; Kamwa, I. Synchrophasors Data Analytics Framework for Power Grid Control and Dynamic Stability Monitoring. Eng. Technol. Ref. 2016, 1. [Google Scholar] [CrossRef]
- Atalik, T.; Çadirci, I.; Demirci, T.; Ermis, M.; Inan, T.; Kalaycioglu, A.S.; Salor, Ö. Multipurpose Platform for Power System Monitoring and Analysis with Sample Grid Applications. IEEE Trans. Instrum. Meas. 2014, 63, 566–582. [Google Scholar] [CrossRef]
- Laverty, D.M.; Best, R.J.; Brogan, P.; Al Khatib, I.; Vanfretti, L.; Morrow, D.J. The OpenPMU Platform for Open-Source Phasor Measurements. IEEE Trans. Instrum. Meas. 2013, 62, 701–709. [Google Scholar] [CrossRef]
- IEC/IEEE Standard 60255-118-1:2018 Part 118-1: Synchrophasor Measurements for Power Systems; IEEE STD23444; International Electrotechnical Commission: Geneva, Switzerland, 2018; ISBN 978-1-5044-5361-5. [CrossRef]
- IEEE Std C37.118.1-2011, IEEE Standard for Synchrophasor Measurements for Power Systems; IEEE STD97167; IEEE Inc.: New York, NY, USA, 2011; ISBN 978-0-7381-6811-1. [CrossRef]
- IEEE Std C37.118.1a-2014, IEEE Standard for Synchrophasor Measurements for Power Systems—Amendment 1: Modification of Selected Performance Requirements; IEEE STD98573; IEEE Inc.: New York, NY, USA, 2014; ISBN 978-0-7381-8978-9. [CrossRef]
- Martin, K.E.; Goldstein, A.R.; Adamiak, M.G.; Antonova, G.; Begovic, M.; Benmouyal, G.; Brunello, G.; Dickerson, B.; Hu, Y.; Jalali, M.; et al. Synchrophasor Measurements under the IEEE Standard C37.118.1-2011 with Amendment C37.118.1a. IEEE Trans. Power Deliv. 2015, 30, 1514–1522. [Google Scholar] [CrossRef]
- Premerlani, W.; Kasztenny, B.; Adamiak, M. Development and Implementation of a Synchrophasor Estimator Capable of Measurements under Dynamic Conditions. IEEE Trans. Power Deliv. 2007, 23, 109–123. [Google Scholar] [CrossRef]
- Phadke, A.G.; Kasztenny, B. Synchronized Phasor and Frequency Measurement under Transient Conditions. IEEE Trans. Power Deliv. 2008, 24, 89–95. [Google Scholar] [CrossRef]
- Mai, R.K.; He, Z.Y.; Fu, L.; Kirby, B.; Bo, Z.Q. A Dynamic Synchrophasor Estimation Algorithm for Online Application. IEEE Trans. Power Deliv. 2010, 25, 570–578. [Google Scholar] [CrossRef]
- Barchi, G.; MacIi, D.; Petri, D. Synchrophasor Estimators Accuracy: A Comparative Analysis. IEEE Trans. Instrum. Meas. 2013, 62, 963–973. [Google Scholar] [CrossRef]
- Belega, D.; MacIi, D.; Petri, D. Fast Synchrophasor Estimation by Means of Frequency-Domain and Time-Domain Algorithms. IEEE Trans. Instrum. Meas. 2013, 63, 388–401. [Google Scholar] [CrossRef]
- De Carvalho, J.R.; Duque, C.A.; Lima, M.A.A.; Coury, D.V.; Ribeiro, P.F. A Novel DFT-Based Method for Spectral Analysis under Time-Varying Frequency Conditions. Electr. Power Syst. Res. 2014, 108, 74–81. [Google Scholar] [CrossRef]
- Belega, D.; Dallet, D. Multifrequency Signal Analysis by Interpolated DFT Method with Maximum Sidelobe Decay Windows. Measurement 2009, 42, 420–426. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy Analysis of the Multicycle Synchrophasor Estimator Provided by the Interpolated DFT Algorithm. IEEE Trans. Instrum. Meas. 2013, 62, 942–953. [Google Scholar] [CrossRef]
- Romano, P.; Paolone, M. Enhanced Interpolated-DFT for Synchrophasor Estimation in FPGAs: Theory, Implementation, and Validation of a PMU Prototype. IEEE Trans. Instrum. Meas. 2014, 63, 2824–2836. [Google Scholar] [CrossRef]
- Petri, D.; Fontanelli, D.; Macii, D. A Frequency-Domain Algorithm for Dynamic Synchrophasor and Frequency Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 2330–2340. [Google Scholar] [CrossRef]
- Derviskadic, A.; Romano, P.; Paolone, M. Iterative-Interpolated DFT for Synchrophasor Estimation: A Single Algorithm for P-and M-Class Compliant PMUs. IEEE Trans. Instrum. Meas. 2017, 67, 547–558. [Google Scholar] [CrossRef]
- Tosato, P.; Macii, D.; Luiso, M.; Brunelli, D.; Gallo, D.; Landi, C. A Tuned Lightweight Estimation Algorithm for Low-Cost Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2018, 67, 1047–1057. [Google Scholar] [CrossRef]
- Chakir, M.; Kamwa, I.; Le Huy, H. Extended C37.118.1 PMU Algorithms for Joint Tracking of Fundamental and Harmonic Phasors in Stressed Power Systems and Microgrids. IEEE Trans. Power Deliv. 2014, 29, 1465–1480. [Google Scholar] [CrossRef]
- Belega, D.; Petri, D. Accuracy of Synchrophasor Measurements Provided by the Sine-Fit Algorithms. In Proceedings of the 2012 IEEE International Energy Conference and Exhibition, ENERGYCON 2012, Florence, Italy, 9–12 September 2012; pp. 921–926. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, Q.; Wang, F.; Huang, S. Dynamic Harmonic Synchrophasor Estimator Based on Sinc Interpolation Functions. IEEE Trans. Instrum. Meas. 2018, 68, 3054–3065. [Google Scholar] [CrossRef]
- Chen, L.; Zhao, W.; Wang, F.; Huang, S. Harmonic Phasor Estimator for P-Class Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2020, 69, 1556–1565. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; De La O Serna, J.A. Dynamic Harmonic Analysis through Taylor-Fourier Transform. IEEE Trans. Instrum. Meas. 2010, 60, 804–813. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; De La O Serna, J.A. Polynomial Implementation of the Taylor-Fourier Transform for Harmonic Analysis. IEEE Trans. Instrum. Meas. 2014, 63, 2846–2854. [Google Scholar] [CrossRef]
- Petrović, P.; Damljanović, N. Dynamic Phasors Estimation Based on Taylor-Fourier Expansion and Gram Matrix Representation. Math. Probl. Eng. 2018, 2018, 7613814. [Google Scholar] [CrossRef]
- Zecevic, Z.; Krstajic, B. Dynamic Harmonic Phasor Estimation by Adaptive Taylor-Based Bandpass Filter. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- De La O Serna, J.A.; Rodríguez-Maldonado, J. Instantaneous Oscillating Phasor Estimates with TaylorK-Kalman Filters. IEEE Trans. Power Syst. 2011, 26, 2336–2344. [Google Scholar] [CrossRef]
- De La O Serna, J.A.; Rodríguez-Maldonado, J. Taylor-Kalman-Fourier Filters for Instantaneous Oscillating Phasor and Harmonic Estimates. IEEE Trans. Instrum. Meas. 2012, 61, 941–951. [Google Scholar] [CrossRef]
- Liu, J.; Ni, F.; Pegoraro, P.A.; Ponci, F.; Monti, A.; Muscas, C. Fundamental and Harmonie Synchrophasors Estimation Using Modified Taylor-Kaiman Filter. In Proceedings of the 2012 IEEE International Workshop on Applied Measurements for Power Systems, AMPS 2012 Proceedings, Aachen, Germany, 26–28 September 2012; IEEE Inc.: New York, NY, USA, 2012; pp. 30–35. [Google Scholar] [CrossRef]
- Karimi-Ghartemani, M.; Ooi, B.T.; Bakhshai, A. Application of Enhanced Phase-Locked Loop System to the Computation of Synchrophasors. IEEE Trans. Power Deliv. 2010, 26, 22–32. [Google Scholar] [CrossRef]
- McNamara, D.M.; Ziarani, A.K.; Ortmeyer, T.H. A New Technique of Measurement of Nonstationary Harmonics. IEEE Trans. Power Deliv. 2006, 22, 387–395. [Google Scholar] [CrossRef]
- De La O Serna, J.A. Synchrophasor Measurement with Polynomial Phase-Locked-Loop Taylor-Fourier Filters. IEEE Trans. Instrum. Meas. 2015, 64, 328–337. [Google Scholar] [CrossRef]
- Messina, F.; Marchi, P.; Vega, L.R.; Galarza, C.G.; Laiz, H. A Novel Modular Positive-Sequence Synchrophasor Estimation Algorithm for PMUs. IEEE Trans. Instrum. Meas. 2016, 66, 1164–1175. [Google Scholar] [CrossRef]
- de la O Serna, J.A. Dynamic Phasor Estimates for Power System Oscillations. IEEE Trans. Instrum. Meas. 2007, 56, 1648–1657. [Google Scholar] [CrossRef]
- Badrkhani Ajaei, F.; Sanaye-Pasand, M.; Davarpanah, M.; Rezaei-Zare, A.; Iravani, R. Mitigating the Impacts of CCVT Subsidence Transients on the Distance Relay. IEEE Trans. Power Deliv. 2012, 27, 497–505. [Google Scholar] [CrossRef]
- Das, S.; Sidhu, T. A Simple Synchrophasor Estimation Algorithm Considering IEEE Standard C37.118.1-2011 and Protection Requirements. IEEE Trans. Instrum. Meas. 2013, 62, 2704–2715. [Google Scholar] [CrossRef]
- Platas-Garza, M.A.; De La O Serna, J.A. Dynamic Phasor and Frequency Estimates through Maximally Flat Differentiators. IEEE Trans. Instrum. Meas. 2009, 59, 1803–1811. [Google Scholar] [CrossRef]
- Giarnetti, S.; Leccese, F.; Caciotta, M. Non Recursive Multi-Harmonic Least Squares Fitting for Grid Frequency Estimation. Measurement 2015, 66, 229–237. [Google Scholar] [CrossRef]
- Giarnetti, S.; Leccese, F.; Caciotta, M. Non Recursive Nonlinear Least Squares for Periodic Signal Fitting. Measurement 2017, 103, 208–216. [Google Scholar] [CrossRef]
- Ren, J.; Kezunovic, M. An Adaptive Phasor Estimator for Power System Waveforms Containing Transients. IEEE Trans. Power Deliv. 2012, 27, 735–745. [Google Scholar] [CrossRef]
- Marques, C.A.G.; Ribeiro, M.V.; Duque, C.A.; Ribeiro, P.F.; Da Silva, E.A.B. A Controlled Filtering Method for Estimating Harmonics of Off-Nominal Frequencies. IEEE Trans. Smart Grid 2011, 3, 38–49. [Google Scholar] [CrossRef]
- Lin, H.C. Fast Tracking of Time-Varying Power System Frequency and Harmonics Using Iterative-Loop Approaching Algorithm. IEEE Trans. Ind. Electron. 2007, 54, 974–983. [Google Scholar] [CrossRef]
- Terzija, V.V. Improved Recursive Newton-Type Algorithm for Frequency and Spectra Estimation in Power Systems. IEEE Trans. Instrum. Meas. 2003, 52, 1654–1659. [Google Scholar] [CrossRef]
- Terzija, V.V.; Stanojević, V. Two-Stage Improved Recursive Newton-Type Algorithm for Power-Quality Indices Estimation. IEEE Trans. Power Deliv. 2007, 22, 1351–1359. [Google Scholar] [CrossRef]
- Singh, S.K.; Sinha, N.; Goswami, A.K.; Sinha, N. Robust Estimation of Power System Harmonics Using a Hybrid Firefly Based Recursive Least Square Algorithm. Int. J. Electr. Power Energy Syst. 2016, 80, 287–296. [Google Scholar] [CrossRef]
- Sadinezhad, I.; Agelidis, V.G. Real-Time Power System Phasors and Harmonics Estimation Using a New Decoupled Recursive-Least-Squares Technique for DSP Implementation. IEEE Trans. Ind. Electron. 2012, 60, 2295–2308. [Google Scholar] [CrossRef]
- Ray, P.K.; Puhan, P.S.; Panda, G. Real Time Harmonics Estimation of Distorted Power System Signal. Int. J. Electr. Power Energy Syst. 2016, 75, 91–98. [Google Scholar] [CrossRef]
- Yang, J.Z.; Yu, C.S.; Liu, C.W. A New Method for Power Signal Harmonic Analysis. IEEE Trans. Power Deliv. 2005, 20, 1235–1239. [Google Scholar] [CrossRef]
- Sohn, S.W.; Lim, Y.B.; Yun, J.J.; Choi, H.; Bae, H.D. A Filter Bank and a Self-Tuning Adaptive Filter for the Harmonic and Interharmonic Estimation in Power Signals. IEEE Trans. Instrum. Meas. 2011, 61, 64–73. [Google Scholar] [CrossRef]
- Duda, K.; Zielinski, T.P.; Bien, A.; Barczentewicz, S.H. Harmonic Phasor Estimation with Flat-Top FIR Filter. IEEE Trans. Instrum. Meas. 2019, 69, 2039–2047. [Google Scholar] [CrossRef]
- De La O Serna, J.A. Synchrophasor Estimation Using Prony’s Method. IEEE Trans. Instrum. Meas. 2013, 62, 2119–2128. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Tramarin, F. Resolution Enhancement by Compressive Sensing in Power Quality and Phasor Measurement. IEEE Trans. Instrum. Meas. 2014, 63, 2358–2367. [Google Scholar] [CrossRef]
- Bertocco, M.; Frigo, G.; Narduzzi, C.; Muscas, C.; Pegoraro, P.A. Compressive Sensing of a Taylor-Fourier Multifrequency Model for Synchrophasor Estimation. IEEE Trans. Instrum. Meas. 2015, 64, 3274–3283. [Google Scholar] [CrossRef]
- Toscani, S.; Muscas, C. A Space Vector Based Approach for Synchrophasor Measurement. In Proceedings of the Conference Record-IEEE Instrumentation and Measurement Technology Conference, Montevideo, Uruguay, 12–15 May 2014; pp. 257–261. [Google Scholar] [CrossRef]
- Aminifar, F.; Fotuhi-Firuzabad, M.; Safdarian, A.; Davoudi, A.; Shahidehpour, M. Synchrophasor Measurement Technology in Power Systems: Panorama and State-of-the-Art. IEEE Access 2014, 2, 1607–1628. [Google Scholar] [CrossRef]
- Kusljevic, M.D.; Tomic, J.J. Multiple-Resonator-Based Power System Taylor-Fourier Harmonic Analysis. IEEE Trans. Instrum. Meas. 2014, 64, 554–563. [Google Scholar] [CrossRef]
- Kušljević, M.D. Quasi Multiple-Resonator-Based Harmonic Analysis. Measurement 2016, 94, 471–473. [Google Scholar] [CrossRef]
- Kusljevic, M.D.; Tomic, J.J.; Poljak, P.D. Maximally Flat-Frequency-Response Multiple-Resonator-Based Harmonic Analysis. IEEE Trans. Instrum. Meas. 2017, 66, 3387–3398. [Google Scholar] [CrossRef]

| Estimator type | ||
|---|---|---|
| 16 | 0.0000 | |
| 20 | −0.2500 |
| Estimator type | |||
|---|---|---|---|
| 24 | −0.0213 | −0.1250 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kušljević, M.D.; Tomić, J.J.; Poljak, P.D. On Multiple-Resonator-based Implementation of IEC/IEEE Standard P-Class Compliant PMUs. Energies 2021, 14, 198. https://doi.org/10.3390/en14010198
Kušljević MD, Tomić JJ, Poljak PD. On Multiple-Resonator-based Implementation of IEC/IEEE Standard P-Class Compliant PMUs. Energies. 2021; 14(1):198. https://doi.org/10.3390/en14010198
Chicago/Turabian StyleKušljević, Miodrag D., Josif J. Tomić, and Predrag D. Poljak. 2021. "On Multiple-Resonator-based Implementation of IEC/IEEE Standard P-Class Compliant PMUs" Energies 14, no. 1: 198. https://doi.org/10.3390/en14010198
APA StyleKušljević, M. D., Tomić, J. J., & Poljak, P. D. (2021). On Multiple-Resonator-based Implementation of IEC/IEEE Standard P-Class Compliant PMUs. Energies, 14(1), 198. https://doi.org/10.3390/en14010198






