Virtual Visualization of Generator Operation Condition through Generator Capability Curve
Abstract
1. Introduction
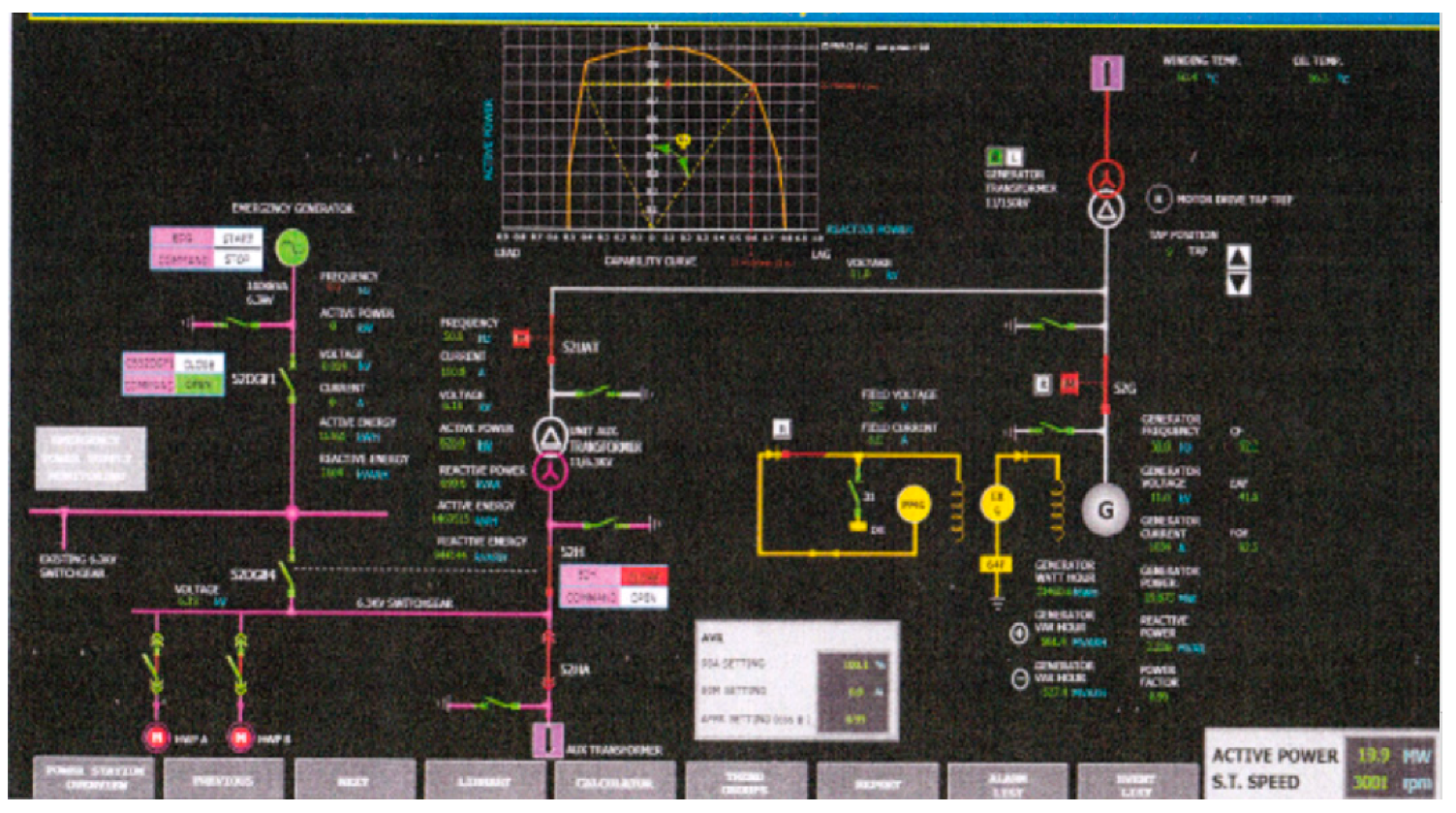
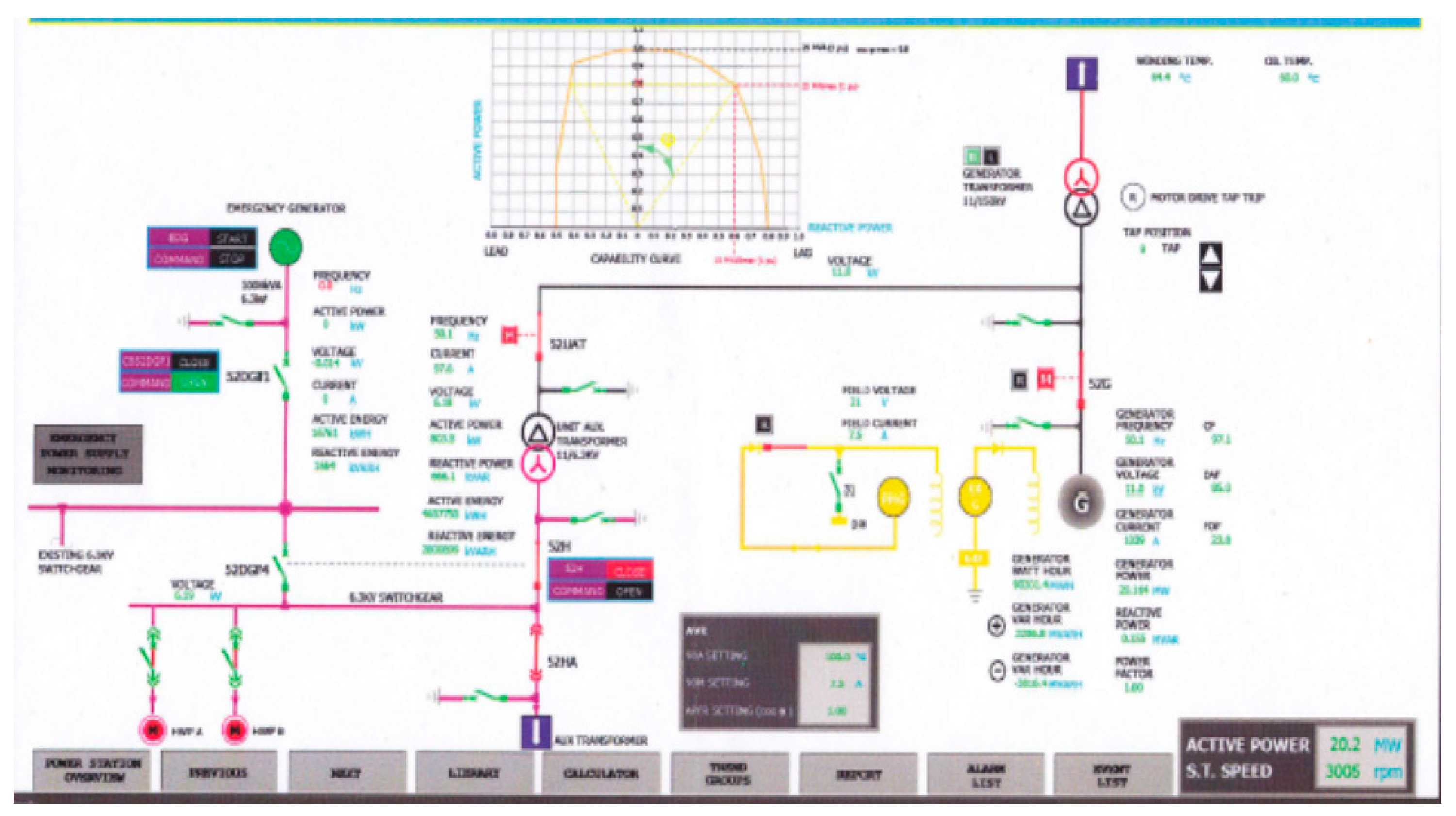
- Developing a virtual visualization of a capability curve simulation to visualize the generator operation conditions. The visualization of GCC is used to monitor the working point of the generator.
- The simulation of the generator capability curve visualization is able to show the various possibilities that occur in the operation of a generator as they happen in reality.
2. Generator Capability Curve
2.1. Devolopment of Generator Capability Curves
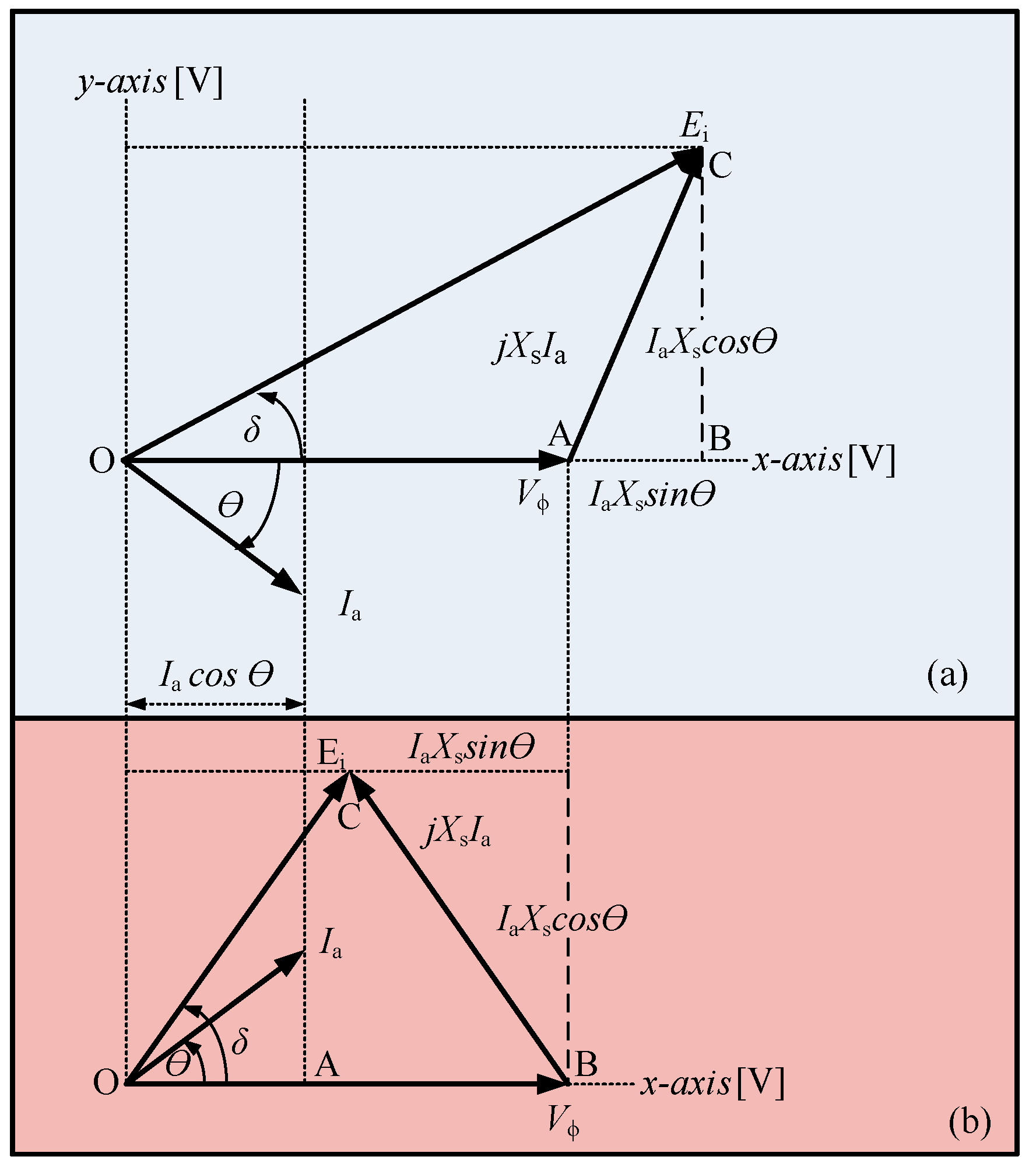
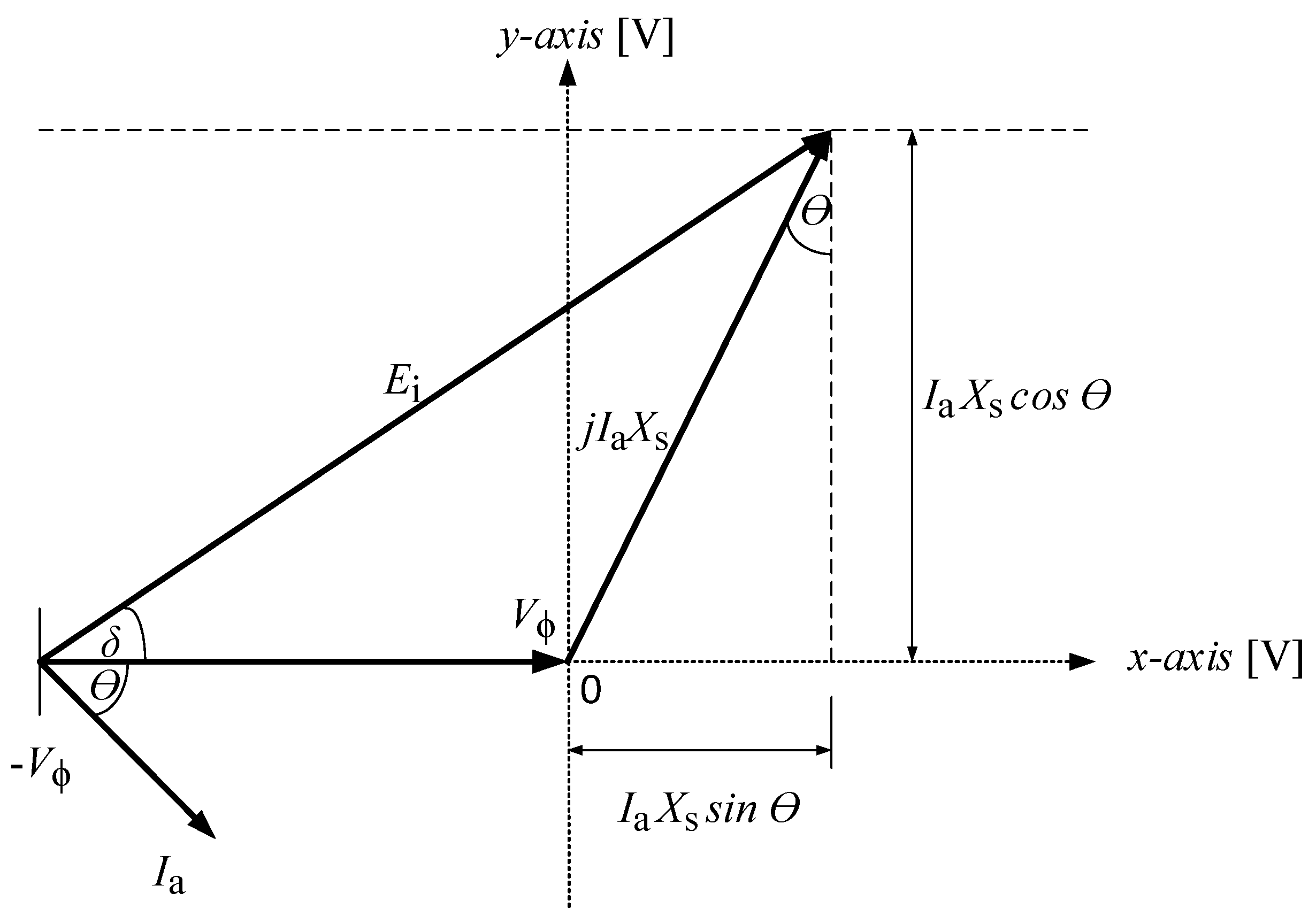
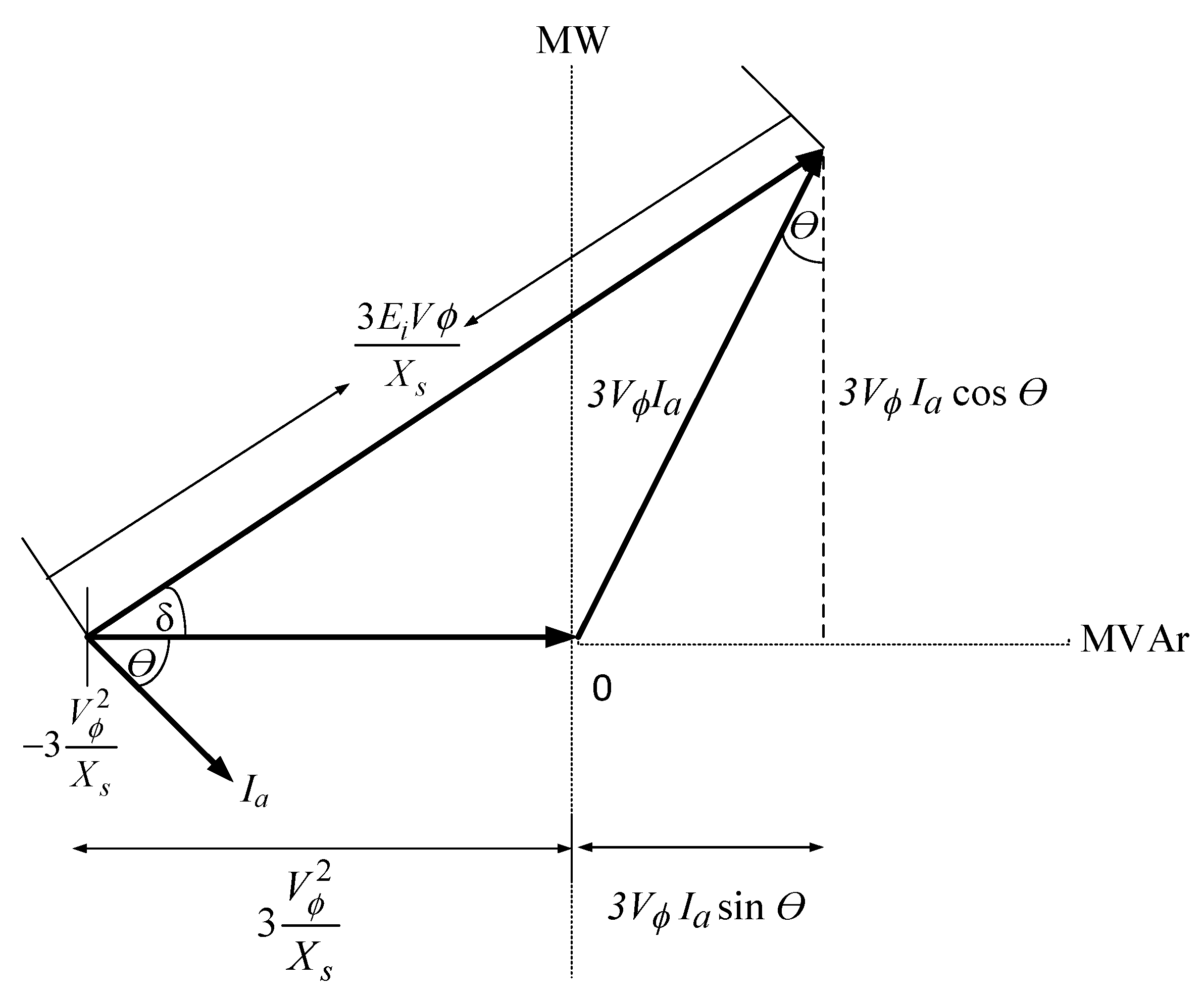
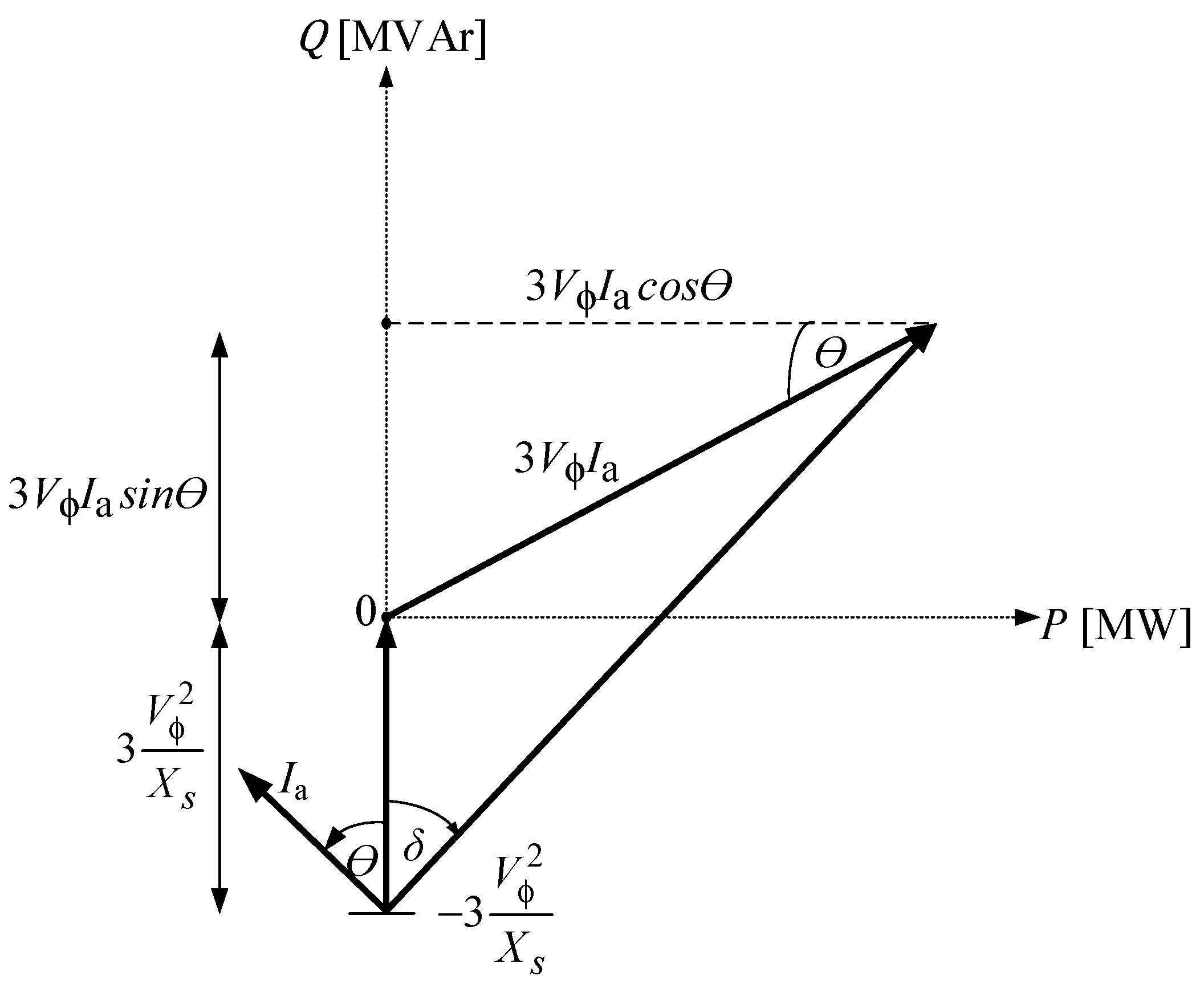
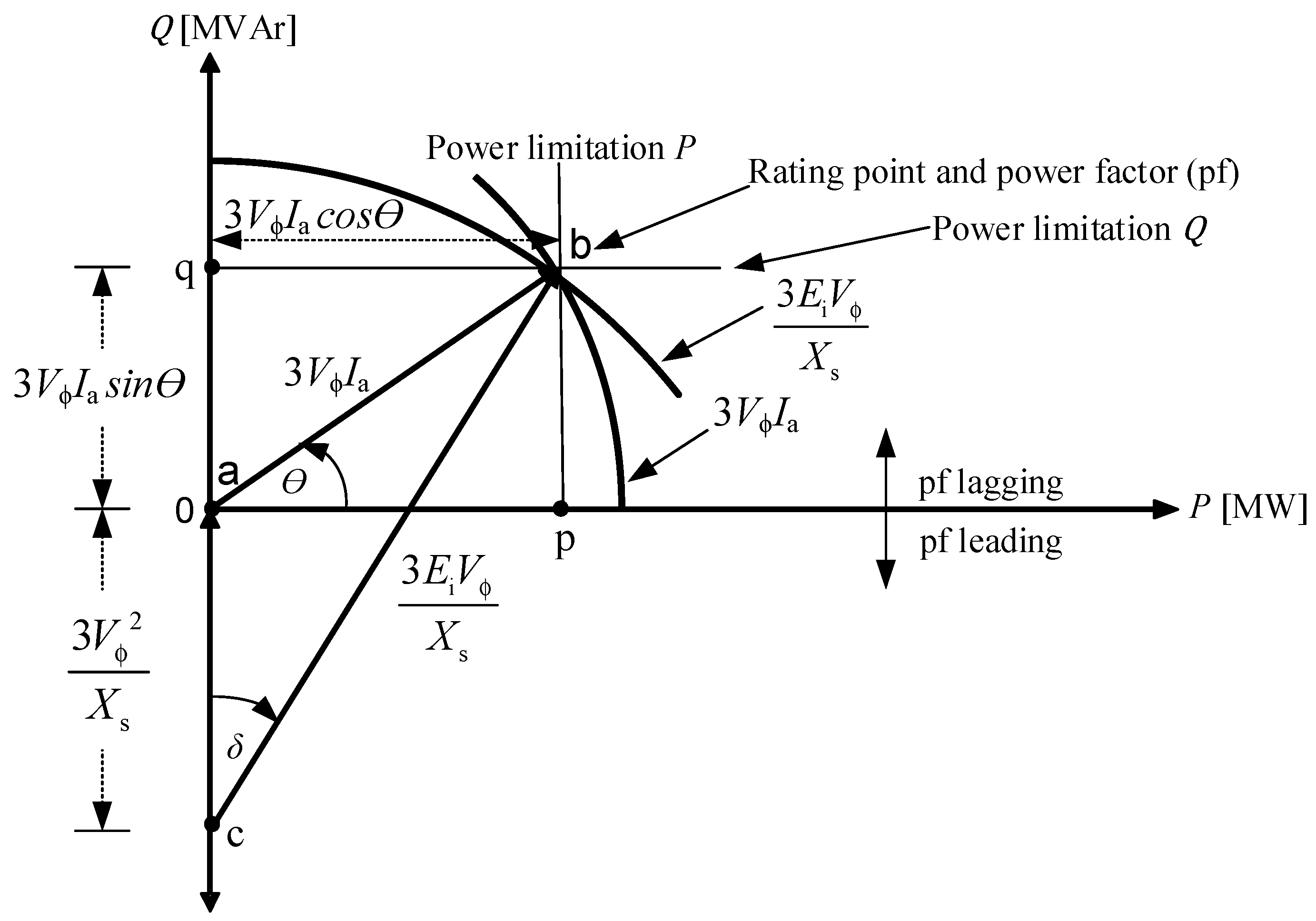
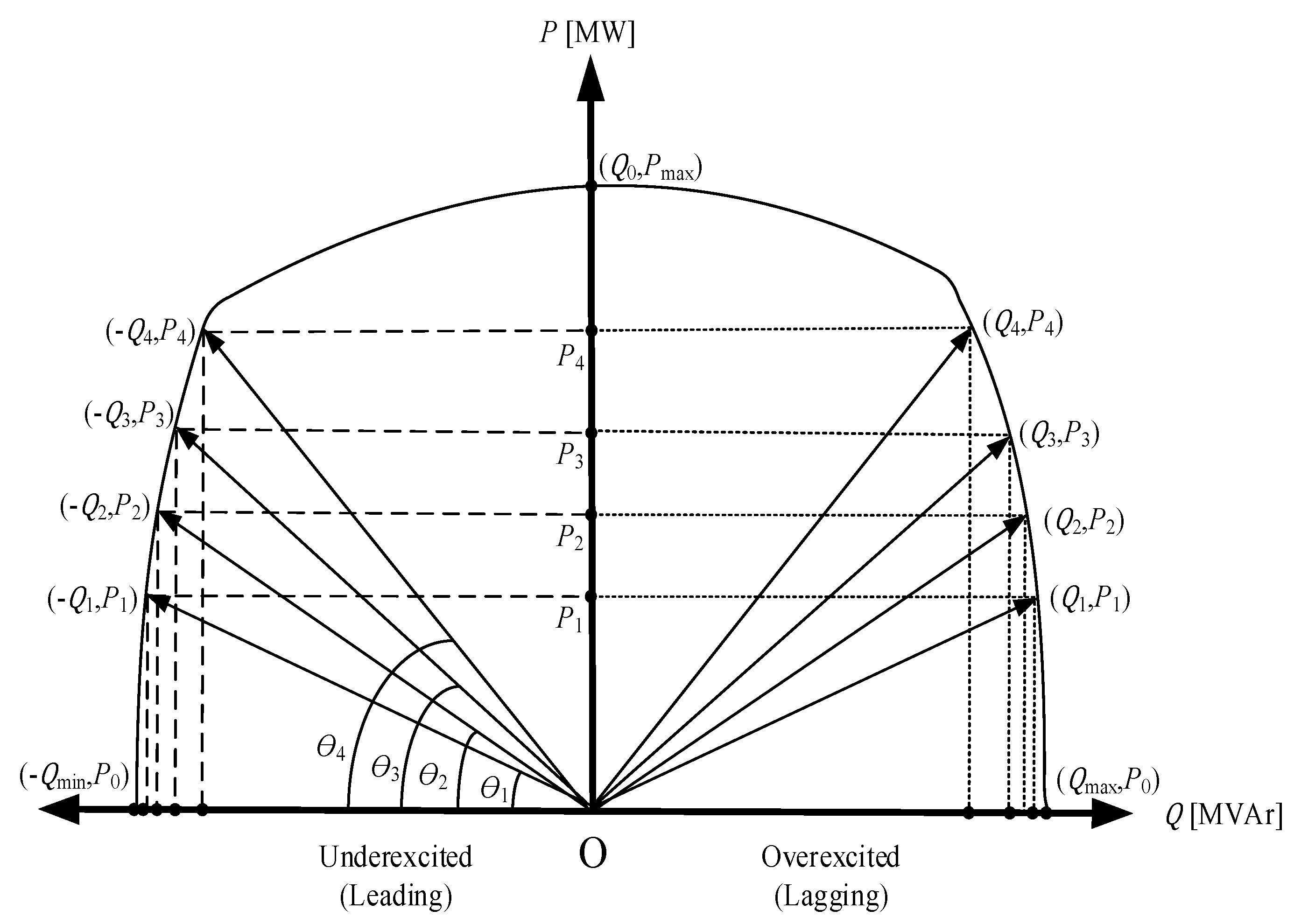
- In theory, the generator capability curve is formed with active power (MW) on the x-axis and reactive power (MVAr) on the y-axis. Therefore, the phasor diagram of Figure 3 is rotated towards the O-axis counterclockwise, producing a phasor diagram with active power (MW) on the -axis and reactive power (MVAr) on the -axis, as shown in Figure 4.
- Based on the power diagram of a synchronous engine, the generator working area is on the positive -axis while the motor work is on the negative -axis. Therefore, the phasor diagram from Figure 4 is mirrored against the -axis, resulting in a phasor diagram in Figure 5 which states the generator working area on the positive -axis.
2.2. Generator Operation Limits
- : active power (MW).
- : reactive power (MVAr).
- : apparent power (MVA).
- : stator current (A).
- : field current (A).
- : synchronous reactance (p.u).
- : terminal voltage (V).
- 3Vϕ Ia cos θ: active power limitation (MW).
- 3Vϕ Ia sin θ: reactive power limitation (MVAr).
- 3Vϕ Ia: stator current limitation (A).
- : rotor current limitation (A).
- Point b: generator rating (MVA).
- pf: power factor (p.u).
- 1.
- Generator power limit:
- 2.
- Armature current limit:
- Depicted as a circle
- Center of circle: at point a (0,0);
- Length of radius of circle: length of line a–b, which is the generator rating .
- 3.
- Field current limit:
- Depicted as a circle
- Center of circle point: at point c .
- 4.
- Length of radius of circle: length of line c-b
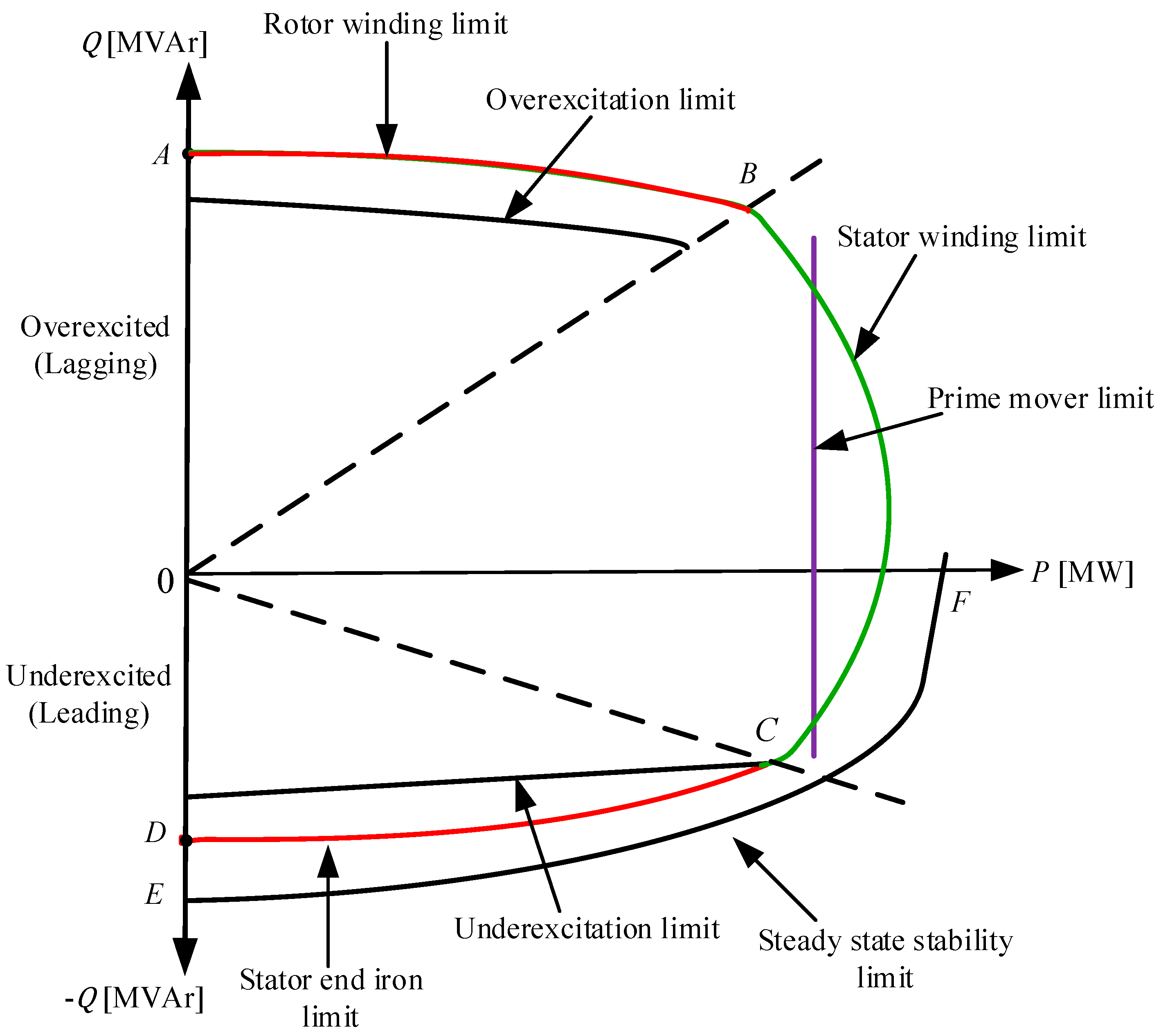
- 5.
- Stator-end region heating limit.
- 6.
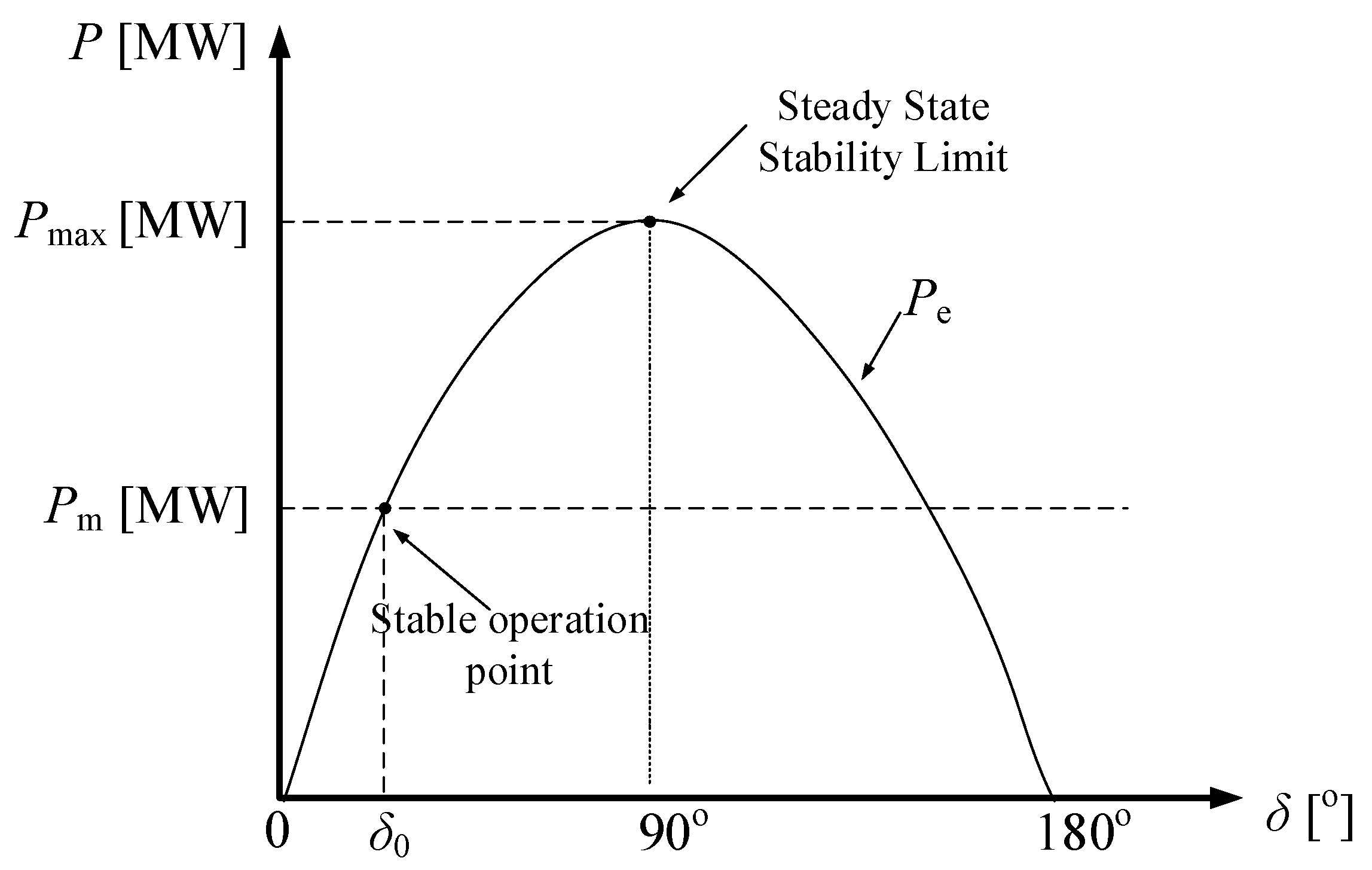
- Steady-state stability limit.
- If > or > , the rotor is decelerating;
- If = or = , stable operation point;
- If < or < , the rotor is accelerating.
- is the power angle between voltage and (engine torque angle);
- is the mechanical output power (MW);
- is the electrical output power generator (MW).
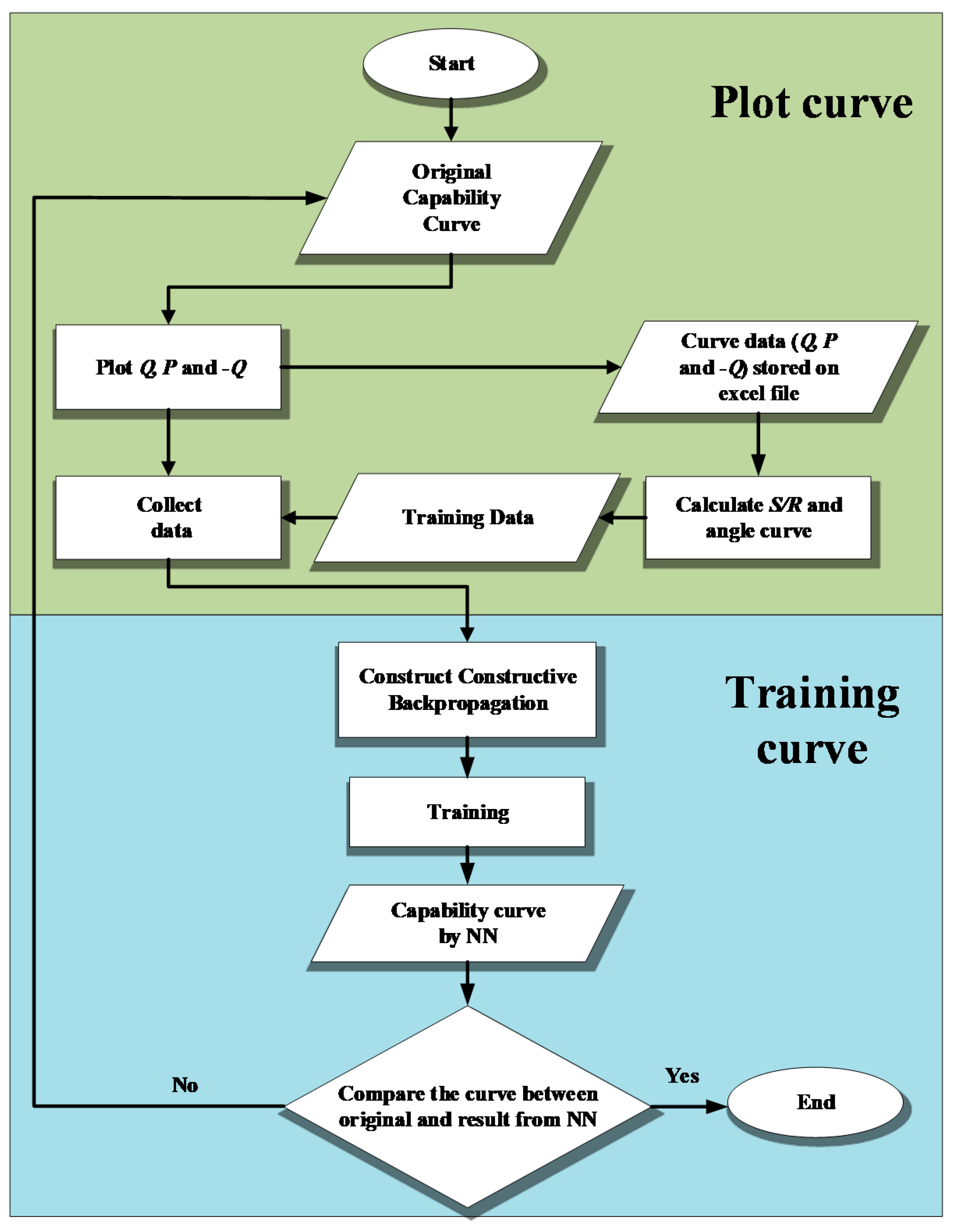
3. Proposed Method
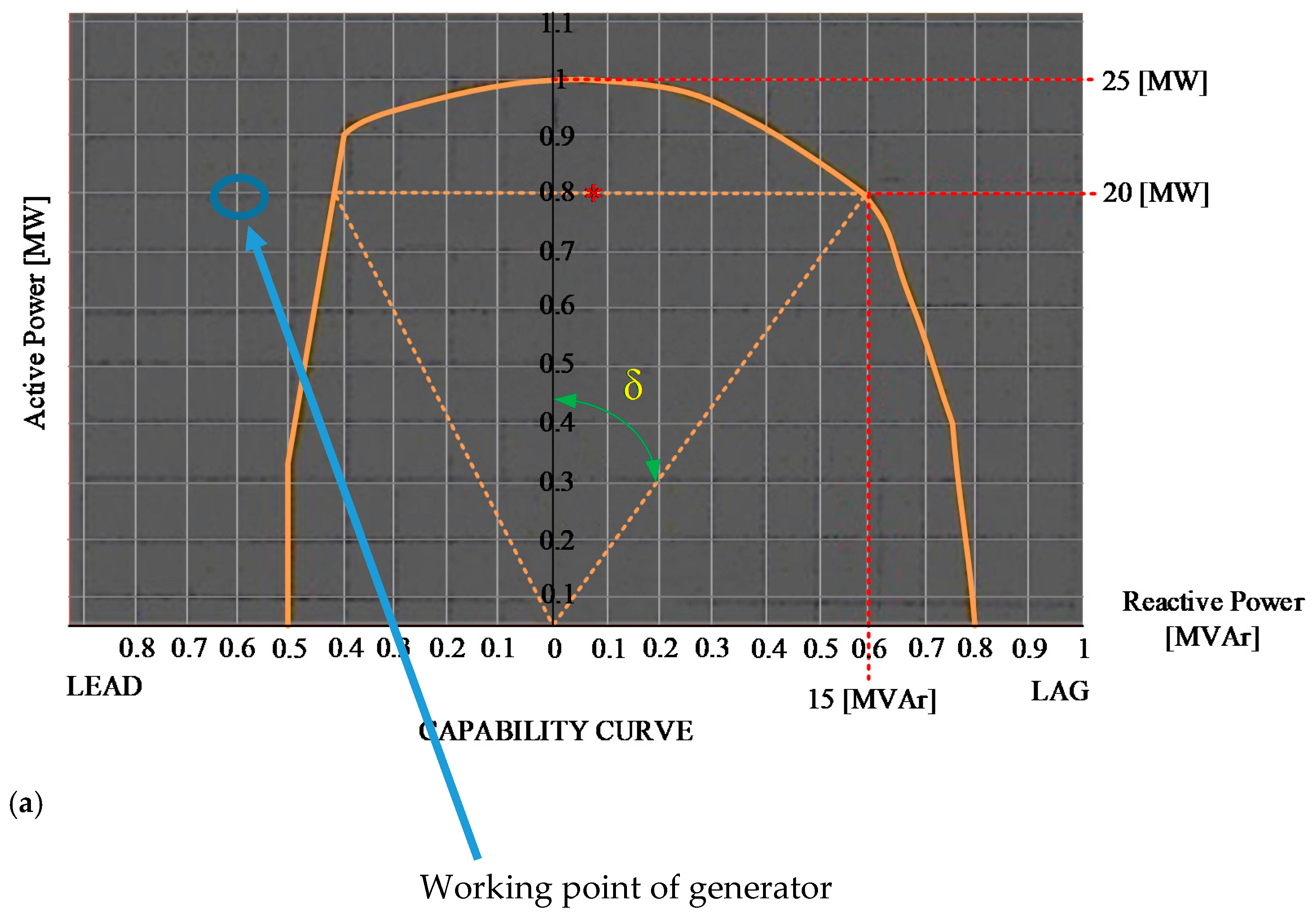
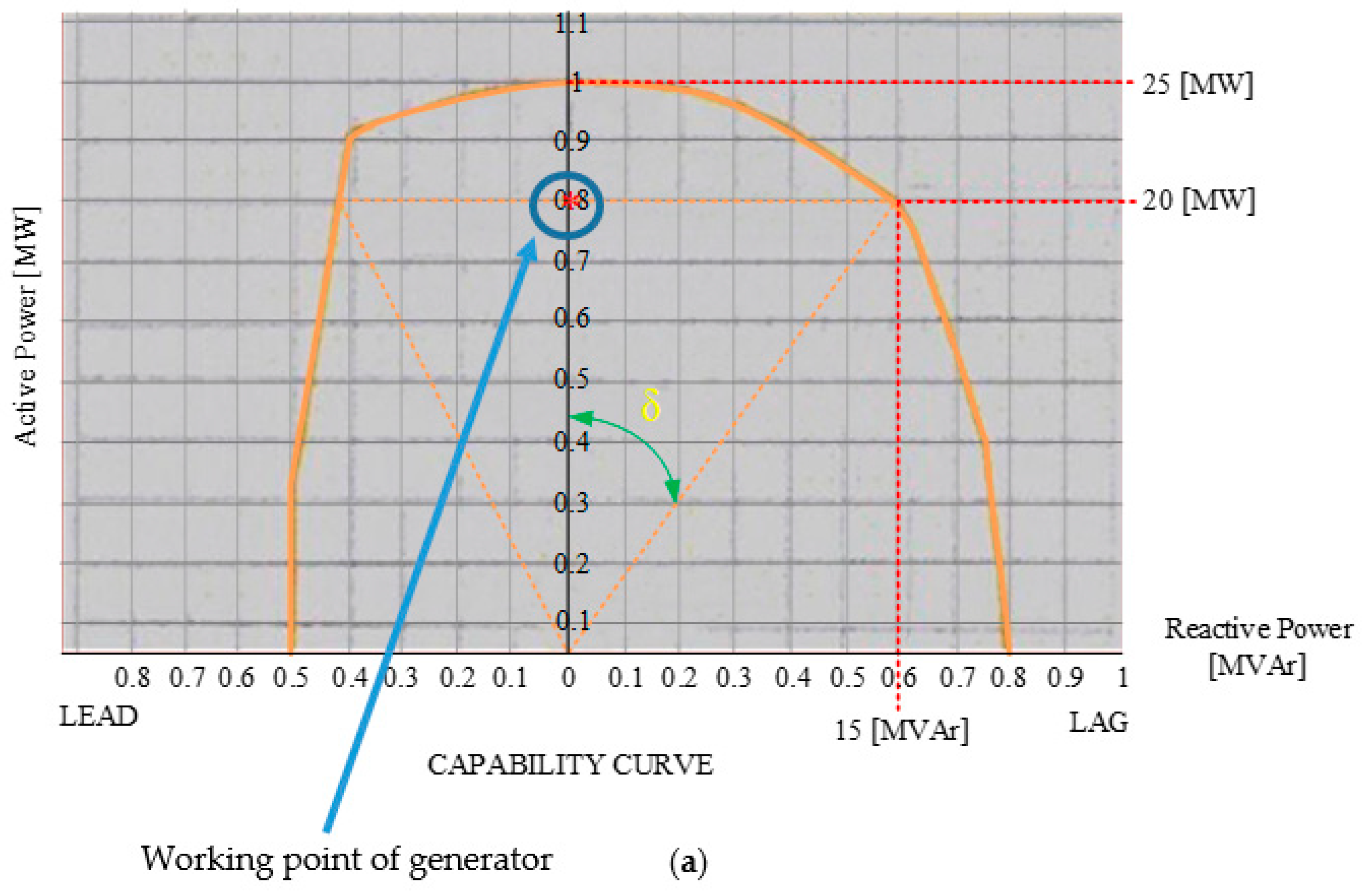
3.1. Plot the Original Capability Curve
- : maximum reactive power point (in overexcited condition/lagging area);
- : the power point is active when = 0;
- : minimum reactive power point (in underexcited/leading area);
- : the point of reactive power when = 0.
3.2. Training the Curve Data
- Load data: the data resulting from the generator capability curve plot is stored in Microsoft Excel, then is called using the Matlab program.
- When calculating the complex power and angle curve, the calculation is conducted with the Matlab program:
- 4.
- Construct the hidden unit layer.
- 5.
- Build a constructive backpropagation network.
- Initialization—namely, the initial formation of ANN in the form of ANN without hidden units. The weight of the initial configuration is calculated by minimizing the sum of squared error (SSE). Weights that have been found are fixed.
- New hidden unit training to connect the input to the new unit and connect the output to the output unit. All the weights connected to the new unit are adjusted by minimizing the SSE (modified SSE).
- Freezing of new hidden units—namely, permanently assigning weights to interconnect with new units.
- Convergence test—that is, if the number of hidden units has produced a viable solution, then the training is stopped. If not, go back to step 2.
- Determine training parameters.
- net.trainParam.show: used to display the change frequency of mse (mean square error).
- net.trainParam.lr: used to determine the rate of understanding (α = learning rate).
- net.trainParam.epochs: used to determine the maximum number of epochs of training.
- net.trainParam.goal: used to specify the mse value limit to stop iteration. The iteration will stop if the mse < limit specified in “net.trainParam.goal”.
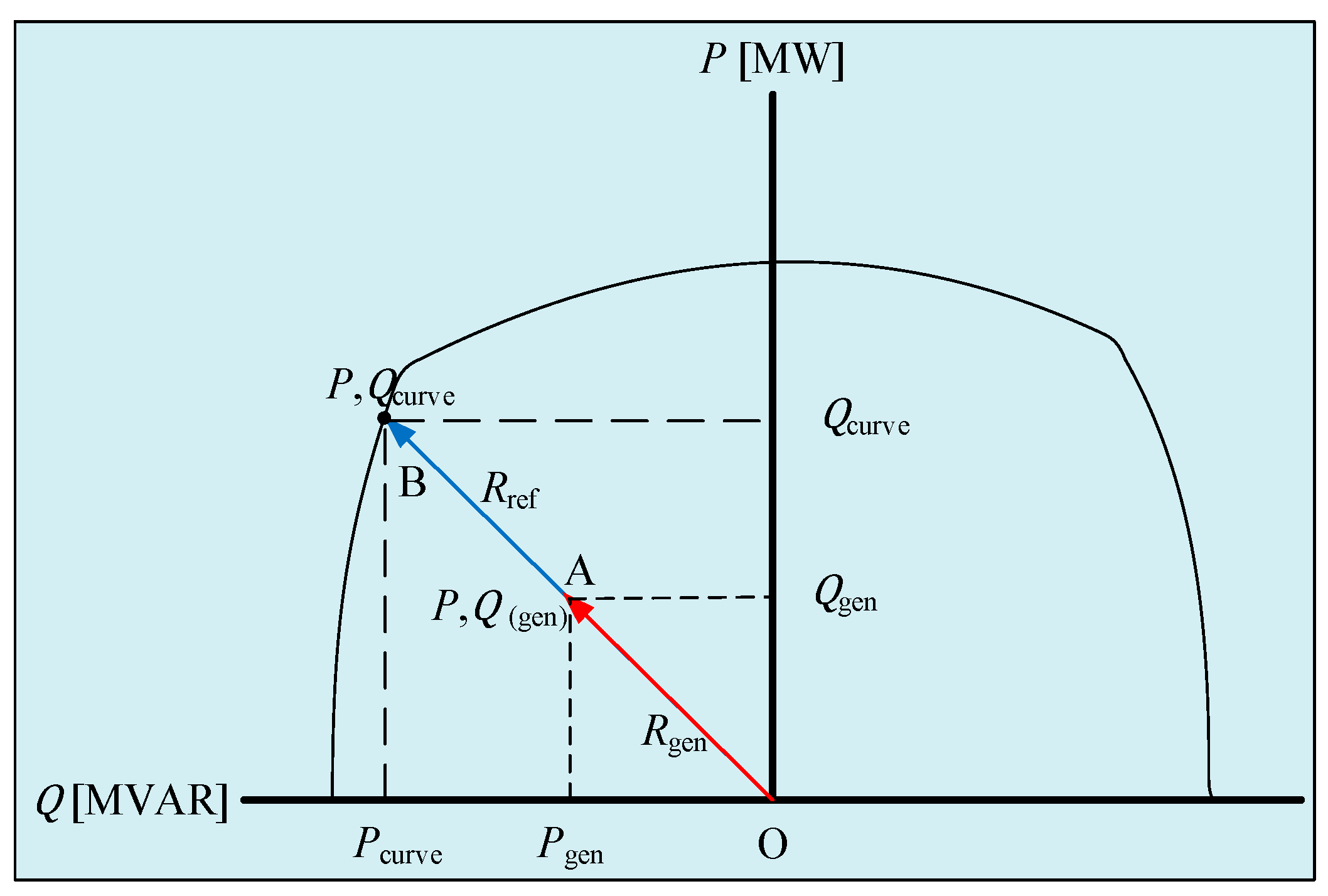
- Entering the active power () and reactive power () of the original capability curve as an input to the capability curve of the NN training results.
- From the and data of the original capability curve, the value and the magnitude of the are calculated (the power of the generator complex or the radius of the load curve).
- By entering the angle data as an input to the NN yield curve that has been previously generated, the output of the NN yield capability curve will be obtained in the form of (the radius of the NN yield curve).
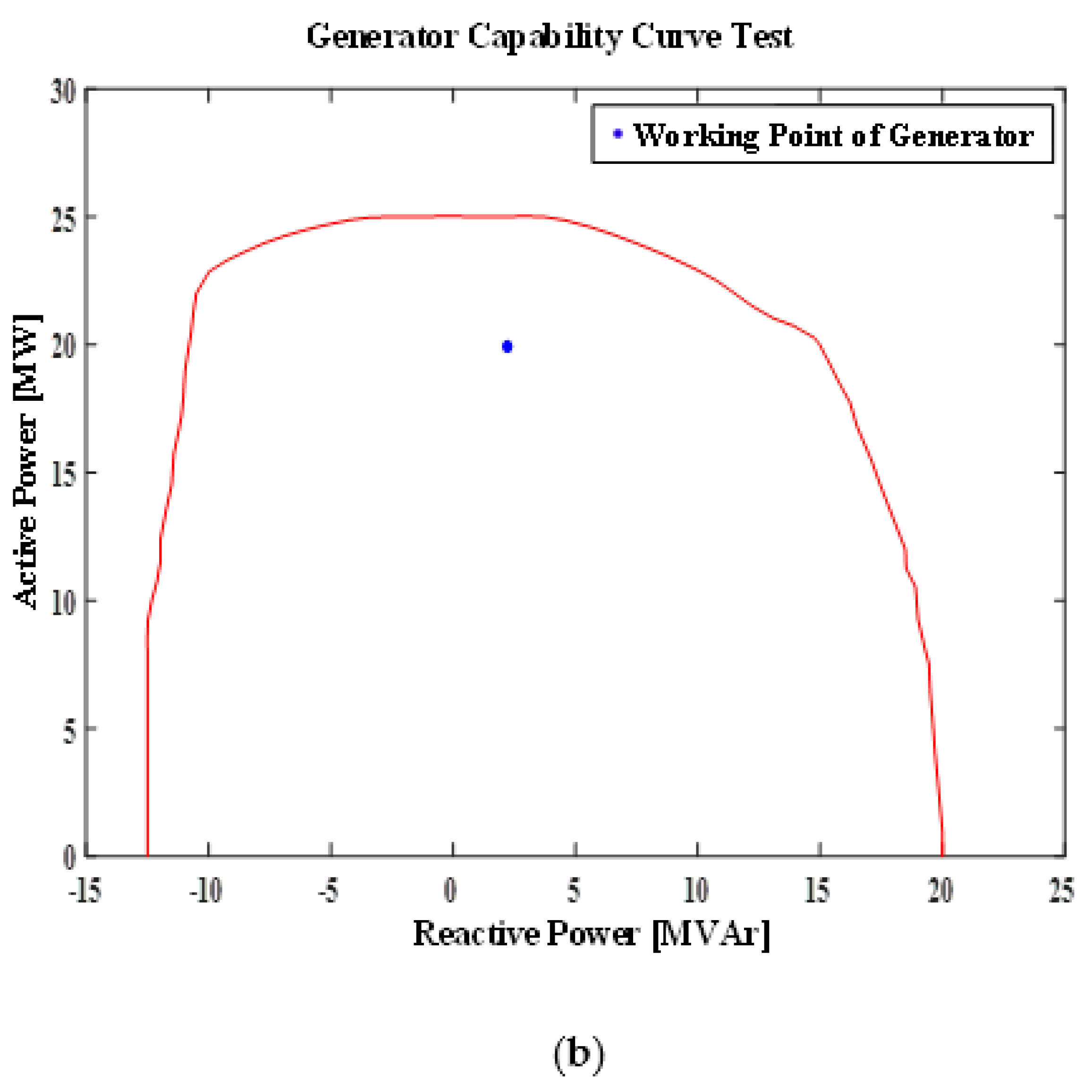
- Generator safety testing is carried out by comparing the and values. If ≤ and the difference between and (difference R) is positive, the generator status is safe. Otherwise, if > and the difference between and (difference ) is negative, the generator status is not safe.
4. Results of the Simulation
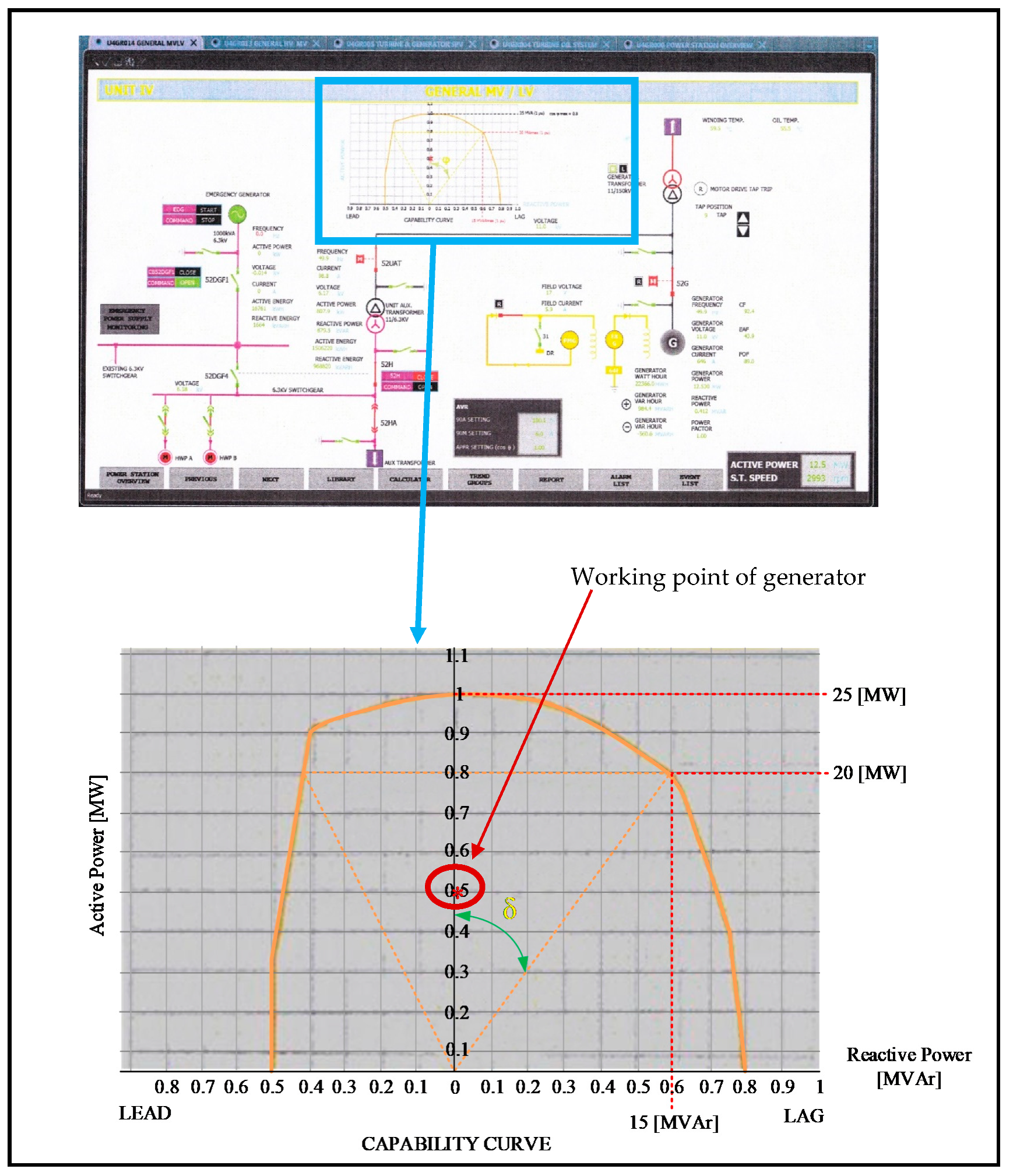
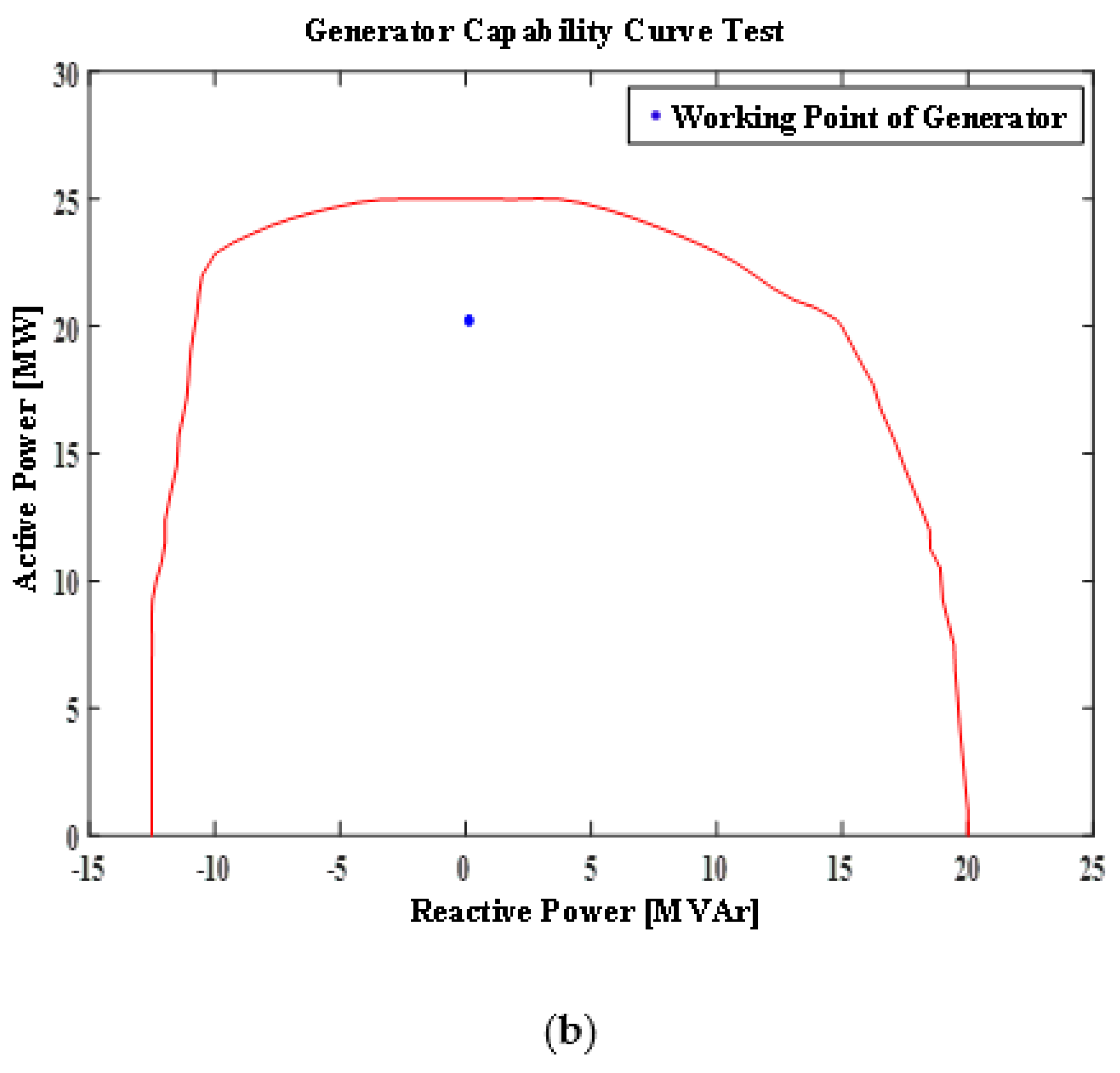
4.1. Case Study 1
- point: 81 points;
- point: 81 points.
4.2. Case Study 2
4.3. Case Study 3
4.4. Discussion
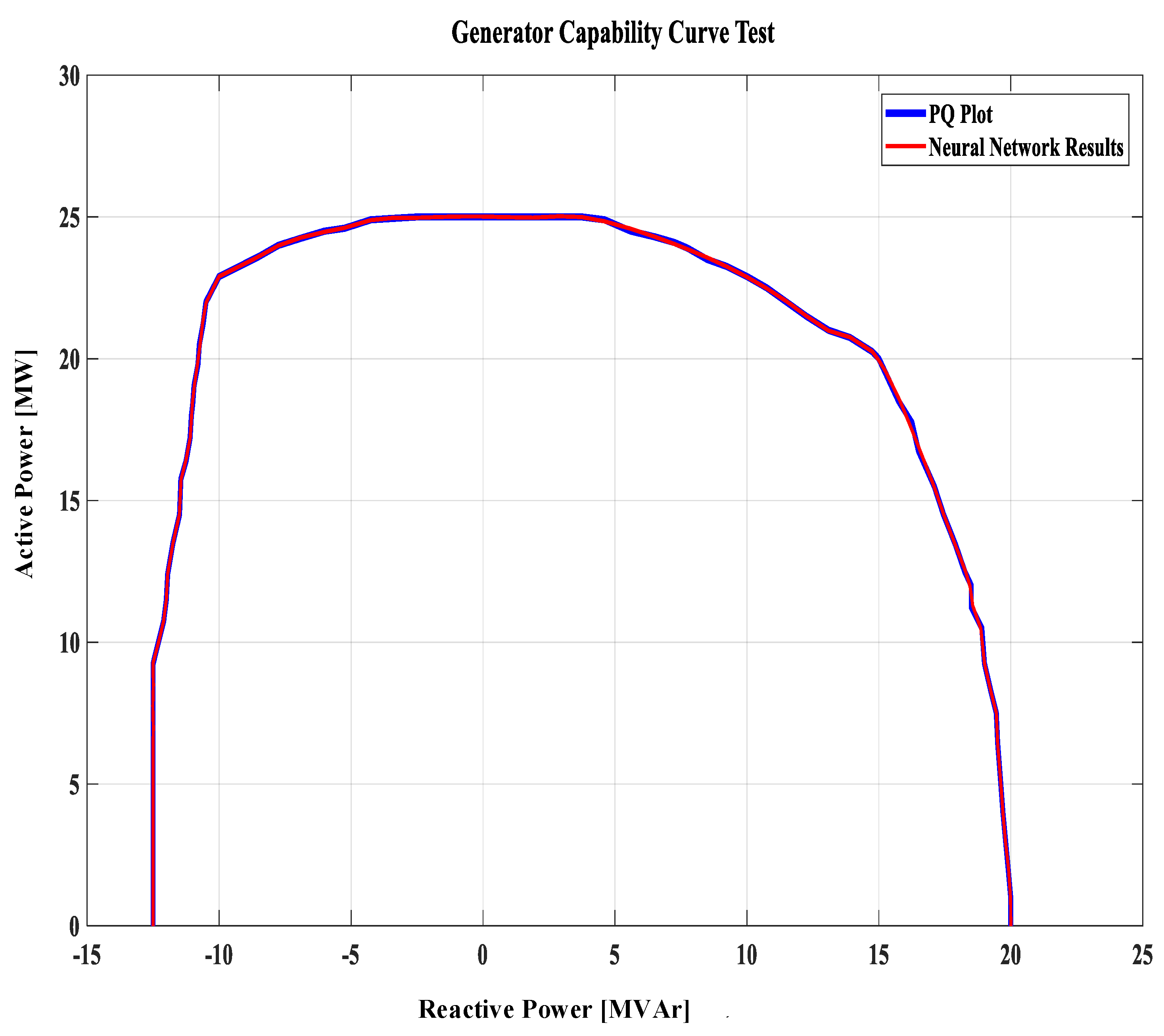
- Developing a virtual visualization of capability curve: Unlike some similar research to GCC, this study proposed a virtual visualization of GCC which can monitor the condition of generator during operation considering all the limitations of the generator.
- Shown an excellent performance: The proposed GCC is identical to the original GCC. The GCC visualization can monitor the operation condition of generator and ensure the safety of the generator through the working point of the generator.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shen, X.; Wu, G.; Wang, R.; Chen, H.; Li, H.; Shi, J. A self-adapted across neighborhood search algorithm with variable reduction strategy for solving non-convex static and dynamic economic dispatch problems. IEEE Access 2018, 6, 41314–41324. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Tuegeh, M. Optimal optimisation-based microgrid scheduling considering impacts of unexpected forecast errors due to the uncertainty of renewable generation and loads fluctuation. IET Renew. Power Gener. 2020, 14, 321–331. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, S.; Chao, K.H. Energy management of a power system for economic load dispatch using the artificial intelligent algorithm. Electronics 2020, 9, 108. [Google Scholar] [CrossRef]
- Yang, Y.; Wei, B.; Liu, H.; Zhang, Y.; Zhao, J.; Manla, E. Chaos firefly algorithm with self-adaptation mutation mechanism for solving large-scale economic dispatch with valve-point effects and multiple fuel options. IEEE Access 2018, 5, 45907–45922. [Google Scholar] [CrossRef]
- Nilsson, N.E.; Mercurio, J. Synchronous generator capability curve testing and evaluation. IEEE Trans. Power Deliv. 1994, 9, 414–424. [Google Scholar] [CrossRef]
- Painemal, H.P. Enforcement of current limits in DFIG-based wind turbine dynamic models through capability curve. IEEE Trans. Sustain. Energy 2019, 10, 318–320. [Google Scholar] [CrossRef]
- Thakar, S.; Vijay, A.S.; Doolla, S. Effect of p-q limits on microgrid reconfiguration: A capability curve perspective. IEEE Trans. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Fernandes, I.G.; Paucar, V.L.; Saavendra, O.R. Impacts of synchronous generator capability curve in power system analyses trough a convex optimal power flow. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Conference-Latin America (ISGT Latin America), Gramado, Brazil, 15–18 September 2019. [Google Scholar]
- Sangeetha, G.; Sherine, S.; Arputharaju, K.; Prakash, S. On line monitoring of higher rated alternator using automated generator capability curve administer. In Proceedings of the 2018 International Conference on Recent Trends in Electrical, Control and Communication (RTECC), Selangor, Malaysia, 20–22 March 2018. [Google Scholar]
- Morais, A.P. Adaptive Mho relay for synchronous generator loss-of-excitation protection: A capability curve limit-based approach. IET Gener. Transm. Distrib. 2016, 10, 3449–3457. [Google Scholar] [CrossRef]
- Park, B.; Tang, L.; Ferris, M.C.; DeMarco, C.L. Examination of three different ACOPF formulations with generator capability curves. IEEE Trans. Power Syst. 2017, 32, 2913–2923. [Google Scholar] [CrossRef]
- Sutherland, P.E. Safe operating limit. IEEE Ind. Appl. Mag. 2011, 17, 14–19. [Google Scholar] [CrossRef]
- Ahmadi, H.; Foroud, A.A. Design of joint active and reactive power reserve market: A multi-objective approach using NSGA II. IET Gener. Transm. Distrib. 2015, 10, 31–40. [Google Scholar] [CrossRef]
- Enrique, E.H. Generation capability curves for wind Farms. In Proceedings of the IEEE Conference on Technologies for Sustainability, Portland, OR, USA, 24–26 July 2014. [Google Scholar]
- Tan, Z.; Zhong, H.; Wang, X.; Tang, H. An Efficient Method for Estimating the Capability Curve of a Virtual Power Plant. CSEE J. Power Energy Syst. 2020. [Google Scholar] [CrossRef]
- Khazaei, J.; Nguyen, D.H.; Asrari, A. Consensus-based demand Response of PMSG wind turbines with distributed energy storage considering capability curves. IEEE Trans. Sustain. Energy 2019. [Google Scholar] [CrossRef]
- Shicong, Y.; Ukil, A.; Gupta, A.K. Development of low voltage ride-through capability curve for grid connected diesel engine generators. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Grainger, J.J.; Stevenson, W.D., Jr. Power System Analysis; McGraw-Hill, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Beaty, H.W.; Fink, D. Standard Handbook for Electrical Engineers, 16th ed.; McGraw-Hill, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Blackburn, J.L.; Domin, T.J. Protective Relaying Principles and Applications, 3rd ed.; CRC Press Taylor & Francis Group: New York, NY, USA, 2007. [Google Scholar]



| Reference | Type of Analysis | Advantages | Disadvantages |
|---|---|---|---|
| [5] | Conducting MVAR capability range tests on synchronous generators. | Validating the generator capability curves supplied by the manufacturers as well as the operating practices in the plants themselves. | Study based on theoretical aspects but not developing the capability curve. |
| [6] | Enforcing stator and rotor current limits in DFIG-based wind turbine models using the DFIG capability curve. | Accurate and effective in properly enforcing current limits in doubly fed induction generator (DFIG)-based Wind Turbine dynamic models. | Study based on theoretical aspects but not developing the capability curve. |
| [7] | Microgrid reconfiguration is revisited from the capability curve perspective. | Showing the effect of P-Q limits on microgrid reconfiguration from a capability curve perspective. | Study based on theoretical aspects but not developing the capability curve. |
| [8] | Solving the optimal power flow, including a synchronous generator capability curve. | Describing the main effects of including a synchronous generator capability curve in optimal power flow through a convex approach, considering also security constraints. | Study based on theoretical aspects but not developing the capability curve. |
| [9] | On-line monitoring of higher rated alternator using an automated generator capability curve. | Showing how to draw a capability curve manually. | Study based on theoretical aspects and developing the generator capability curves manually. |
| [10] | Using the generator capability curve to derive the adaptive Mho operating characteristics. | Showing the generator capability curve against impedance-based methods to obtain real-time derivation of Mho operating characteristics. | Study based on theoretical aspects but not developing the capability curve. |
| [11] | Presenting the “D-curves”, including options to enable the active and reactive limits dependent on the generator voltage. | Demonstrating a technique to construct capability curve constraints containing several assumptions on available data regarding generator parameters and their impact. | Study based on theoretical aspects but not developing the capability curve. |
| [12] | A study of generator capability for offshore oil platforms. | Determining the safe operating limits of the generator in case the entire load has to be carried by one generator. | Study based on theoretical aspects but not developing the capability curve. |
| [13] | Obtaining simultaneously optimal capacities of active and reactive power reserve as a solution in the market. | Analyzing mutual effects through the capability curve between the reactive and active power reserve markets. | Study based on theoretical aspects but not developing the capability curve. |
| [14] | Studying the maximum generating power given by the aggregate of the individual capability curve for each generator in the case of a wind farm. | Showing the required steps to determine the capability curve of a wind farm and all the factors affecting the form of this curve. | Study based on theoretical aspects but not developing the capability curve. |
| [15] | Studying the concept of the virtual power plant capability curve, which characterizes the allowable range explicitly. | The concept of the virtual power plant capability curve explicitly characterizes allowable active and reactive power flexibility in the distribution system. | Study based on theoretical aspects but not developing the capability curve. |
| [16] | Presenting how to deliver active and reactive powers to the load in varying wind speed conditions cooperatively. | Formulating a distributed consensus which provides active power sharing and reactive power support considering the capability curves of wind turbines and storage units. | Study based on theoretical aspects but not developing the capability curve. |
| [17] | Development and assessment of a low-voltage ride-through (LVRT) capability curve for a diesel engine generator. | Developing the LVRT capability curve of a diesel generator by plotting all the maximum fault clear times for different voltage dips at the point of common coupling. | Study based on theoretical aspects and developing the capability curve manually based on plotting all the maximum fault clear times. |
| Generator Name | LH4 |
|---|---|
| Type | GTLRI494/45–2 |
| Output [MVA] | 25 |
| Output [MW] | 20 |
| Voltage [kV] | 11 |
| Current [A] | 1312 |
| Excitation voltage [V] | 160 |
| Excitation current [A] | 808 |
| Phase | 3 |
| Power factor | 0.8 |
| Frequency [Hz] | 50 |
| Number of Poles | 2 |
| Speed [rpm] | 3000 |
| Production year | 2010 |
| Producer | Fuji Electric |
| No. | Pcurve | Qcurve | S | θ | No. | Pcurve | Qcurve | S | θ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 20.000 | 20.000 | 1.571 | 41 | 25.000 | 0.000 | 25.000 | 0.000 |
| 2 | 0.950 | 20.000 | 20.023 | 1.523 | 42 | 25.000 | −0.750 | 25.011 | −0.030 |
| 3 | 2.000 | 19.900 | 20.000 | 1.471 | 43 | 25.000 | −1.600 | 25.051 | −0.064 |
| 4 | 3.000 | 19.800 | 20.026 | 1.420 | 44 | 25.000 | −2.500 | 25.125 | −0.100 |
| 5 | 4.000 | 19.700 | 20.102 | 1.370 | 45 | 24.950 | −3.400 | 25.181 | −0.135 |
| 6 | 5.250 | 19.600 | 20.291 | 1.309 | 46 | 24.900 | −4.250 | 25.260 | −0.169 |
| 7 | 6.450 | 19.500 | 20.539 | 1.251 | 47 | 24.600 | −5.250 | 25.154 | −0.210 |
| 8 | 7.500 | 19.450 | 20.846 | 1.203 | 48 | 24.500 | −6.000 | 25.224 | −0.240 |
| 9 | 8.250 | 19.250 | 20.943 | 1.166 | 49 | 24.250 | −6.900 | 25.213 | −0.277 |
| 10 | 9.250 | 19.000 | 21.132 | 1.118 | 50 | 24.000 | −7.750 | 25.220 | −0.312 |
| 11 | 10.500 | 18.900 | 21.621 | 1.064 | 51 | 23.600 | −8.500 | 25.084 | −0.346 |
| 12 | 11.250 | 18.500 | 21.652 | 1.024 | 52 | 23.250 | −9.250 | 25.022 | −0.379 |
| 13 | 12.000 | 18.500 | 22.009 | 0.994 | 53 | 22.900 | −10.000 | 24.988 | −0.412 |
| 14 | 12.500 | 18.250 | 22.120 | 0.970 | 54 | 22.000 | −10.500 | 24.377 | −0.445 |
| 15 | 13.450 | 17.900 | 22.390 | 0.926 | 55 | 21.250 | −10.600 | 23.747 | −0.463 |
| 16 | 14.500 | 17.450 | 22.688 | 0.877 | 56 | 20.500 | −10.750 | 23.148 | −0.483 |
| 17 | 15.500 | 17.100 | 23.079 | 0.834 | 57 | 19.800 | −10.800 | 22.554 | −0.499 |
| 18 | 16.750 | 16.500 | 23.512 | 0.778 | 58 | 19.050 | −10.950 | 21.973 | −0.522 |
| 19 | 17.750 | 16.250 | 24.065 | 0.741 | 59 | 18.400 | −11.000 | 21.437 | −0.539 |
| 20 | 18.500 | 15.750 | 24.296 | 0.705 | 60 | 18.000 | −11.050 | 21.121 | −0.551 |
| 21 | 19.500 | 15.250 | 24.755 | 0.664 | 61 | 17.200 | −11.100 | 20.471 | −0.573 |
| 22 | 20.000 | 15.000 | 25.000 | 0.644 | 62 | 16.400 | −11.250 | 19.888 | −0.601 |
| 23 | 20.250 | 14.750 | 25.052 | 0.630 | 63 | 15.750 | −11.450 | 19.472 | −0.629 |
| 24 | 20.750 | 13.900 | 24.975 | 0.590 | 64 | 14.500 | −11.500 | 18.507 | −0.671 |
| 25 | 21.000 | 13.100 | 24.751 | 0.558 | 65 | 13.500 | −11.750 | 17.897 | −0.716 |
| 26 | 21.500 | 12.250 | 24.745 | 0.518 | 66 | 12.400 | −11.950 | 17.221 | −0.767 |
| 27 | 22.000 | 11.500 | 24.824 | 0.482 | 67 | 11.500 | −12.000 | 16.621 | −0.807 |
| 28 | 22.500 | 10.750 | 24.936 | 0.446 | 68 | 10.750 | −12.100 | 16.186 | −0.844 |
| 29 | 22.900 | 10.000 | 24.988 | 0.412 | 69 | 10.000 | −12.300 | 15.852 | −0.888 |
| 30 | 23.250 | 9.250 | 25.022 | 0.379 | 70 | 9.250 | −12.500 | 15.550 | −0.934 |
| 31 | 23.500 | 8.500 | 24.990 | 0.347 | 71 | 8.500 | −12.500 | 15.116 | −0.974 |
| 32 | 23.900 | 7.750 | 25.125 | 0.314 | 72 | 7.750 | −12.500 | 14.708 | −1.016 |
| 33 | 24.100 | 7.250 | 25.167 | 0.292 | 73 | 7.000 | −12.500 | 14.327 | −1.060 |
| 34 | 24.300 | 6.500 | 25.154 | 0.261 | 74 | 6.300 | −12.500 | 13.998 | −1.104 |
| 35 | 24.500 | 5.600 | 25.132 | 0.225 | 75 | 5.500 | −12.500 | 13.657 | −1.156 |
| 36 | 24.900 | 4.600 | 25.321 | 0.183 | 76 | 4.650 | −12.500 | 13.337 | −1.215 |
| 37 | 25.000 | 3.750 | 25.280 | 0.149 | 77 | 3.750 | −12.500 | 13.050 | −1.279 |
| 38 | 25.000 | 2.900 | 25.168 | 0.115 | 78 | 3.000 | −12.500 | 12.855 | −1.335 |
| 39 | 25.000 | 1.900 | 25.072 | 0.076 | 79 | 2.000 | −12.500 | 12.659 | −1.412 |
| 40 | 25.000 | 0.750 | 25.011 | 0.030 | 80 | 1.000 | −12.500 | 12.540 | −1.491 |
| 81 | 0.000 | −12.500 | 12.500 | −1.571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-Y.; Tuegeh, M. Virtual Visualization of Generator Operation Condition through Generator Capability Curve. Energies 2021, 14, 185. https://doi.org/10.3390/en14010185
Lee C-Y, Tuegeh M. Virtual Visualization of Generator Operation Condition through Generator Capability Curve. Energies. 2021; 14(1):185. https://doi.org/10.3390/en14010185
Chicago/Turabian StyleLee, Chun-Yao, and Maickel Tuegeh. 2021. "Virtual Visualization of Generator Operation Condition through Generator Capability Curve" Energies 14, no. 1: 185. https://doi.org/10.3390/en14010185
APA StyleLee, C.-Y., & Tuegeh, M. (2021). Virtual Visualization of Generator Operation Condition through Generator Capability Curve. Energies, 14(1), 185. https://doi.org/10.3390/en14010185






