Two-Dimensional Tomographic Simultaneous Multispecies Visualization—Part II: Reconstruction Accuracy
Abstract
1. Introduction
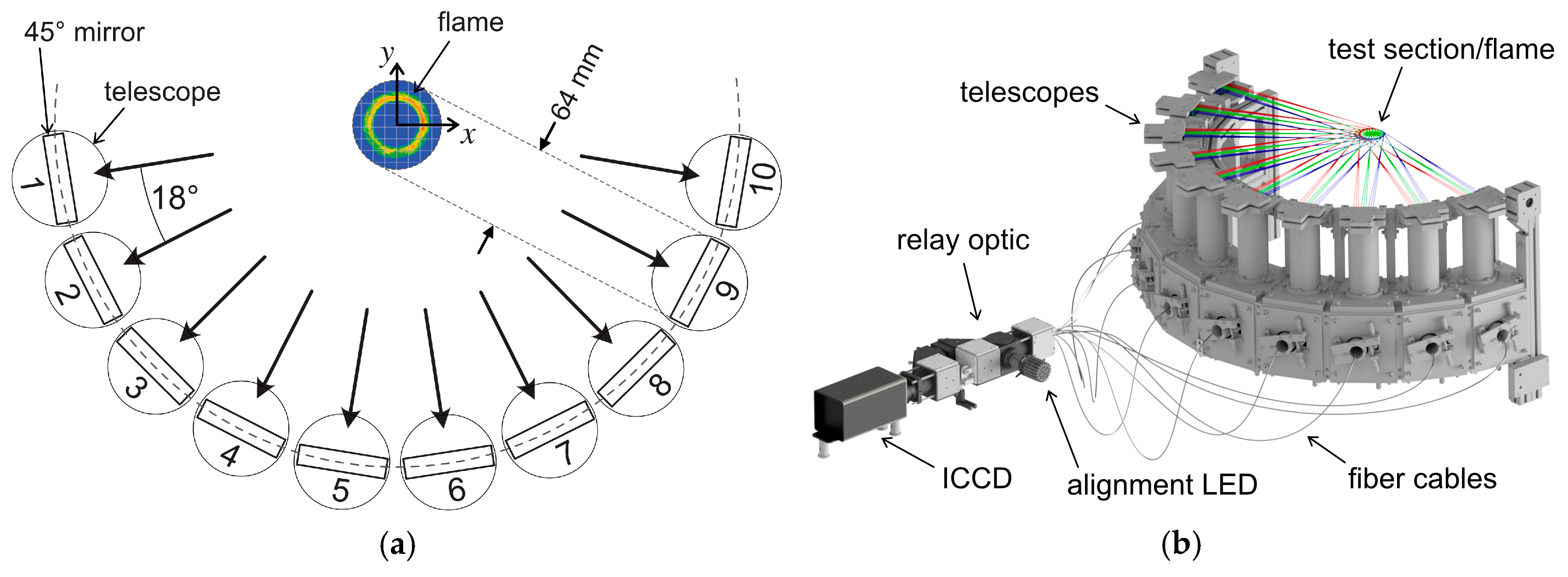
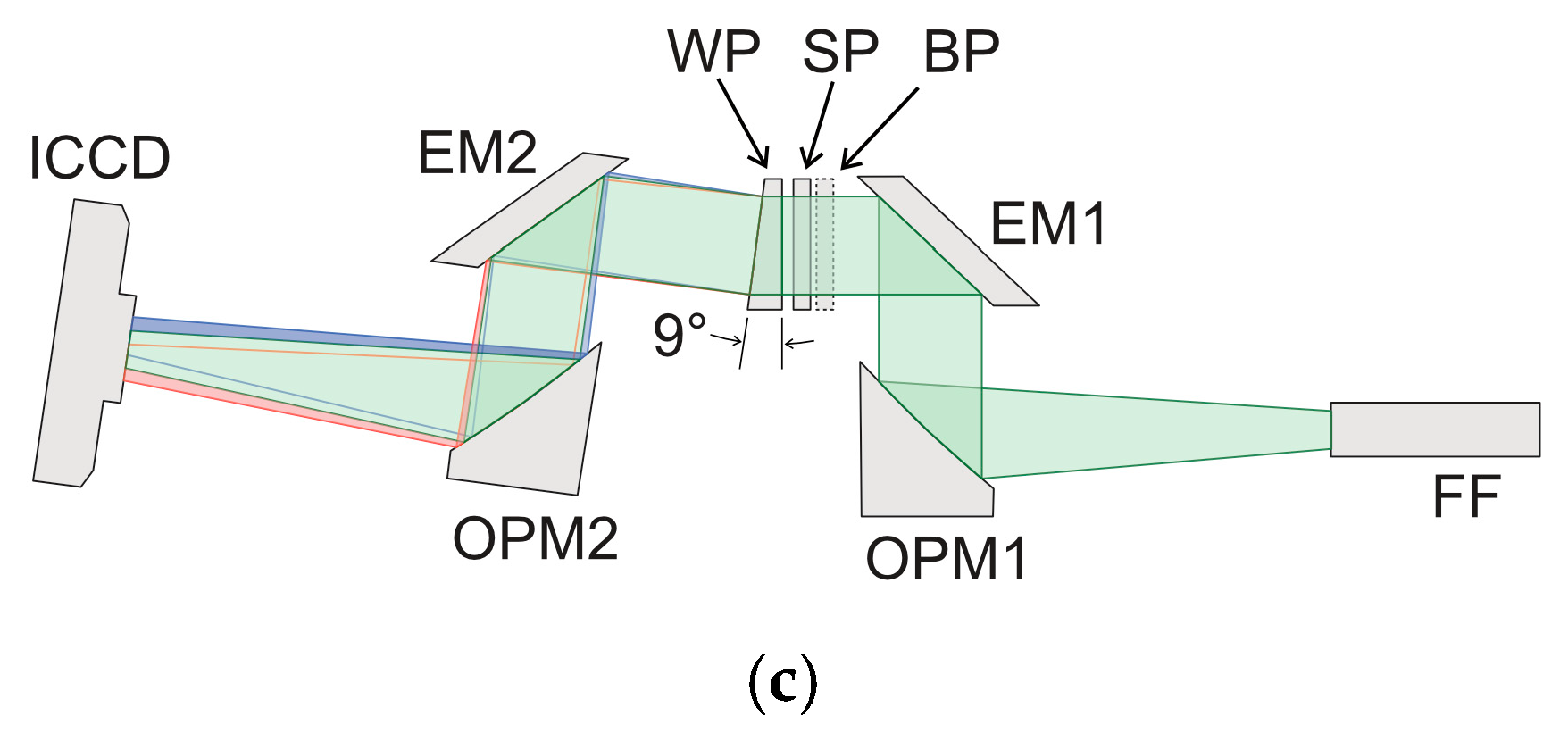
2. Materials and Methods
2.1. Tomographic Setup
2.2. Tomographic Reconstruction
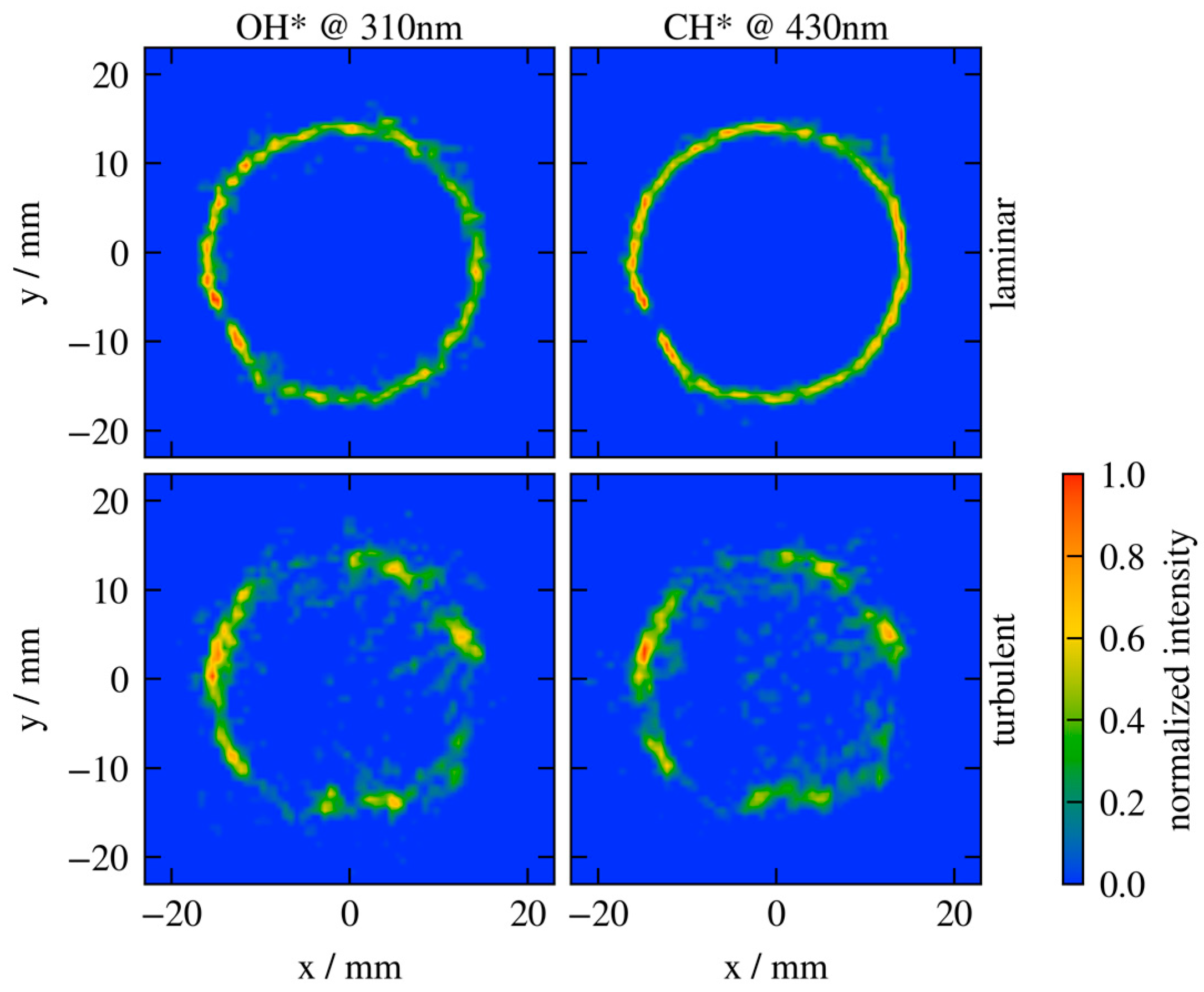
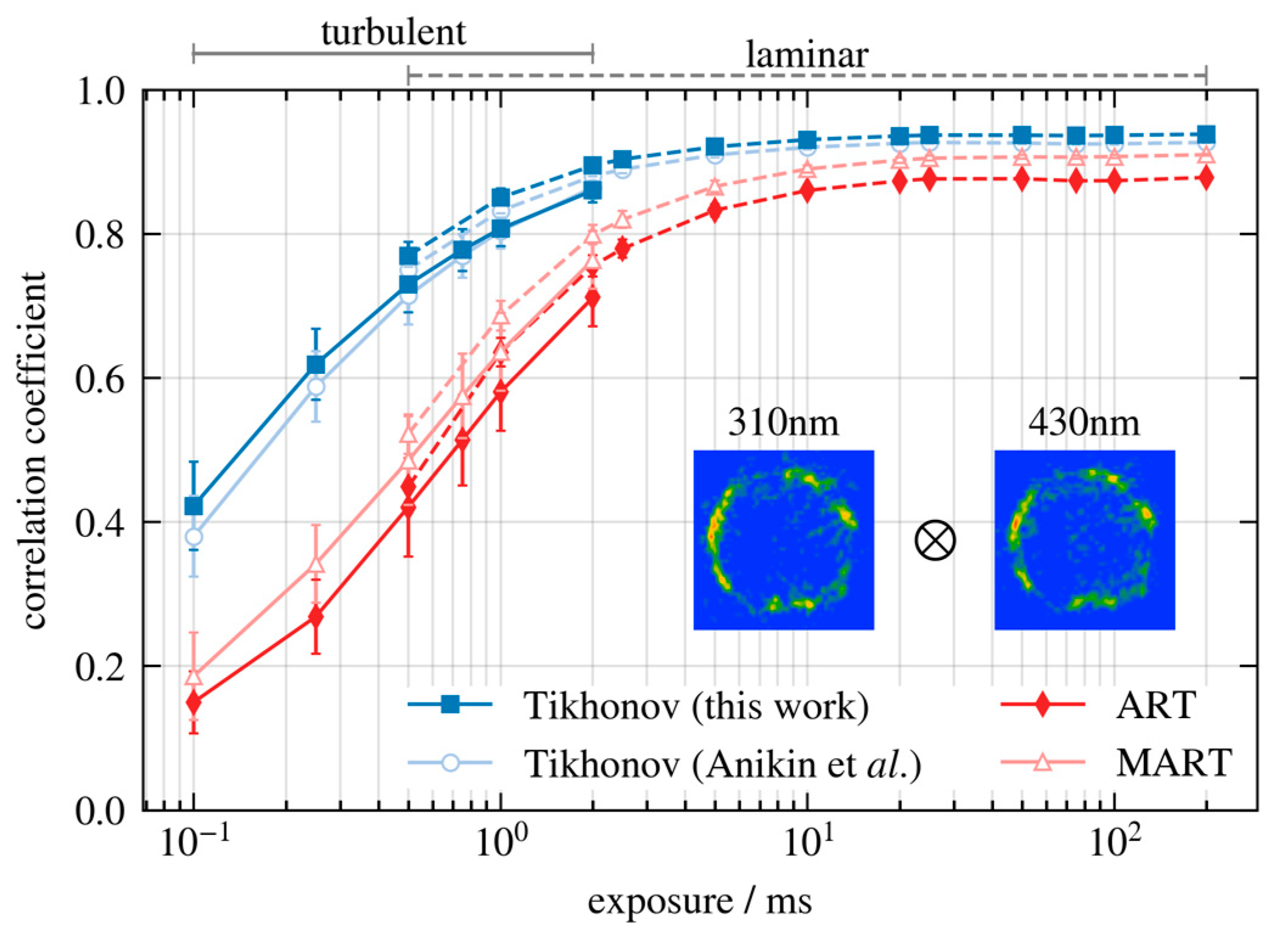
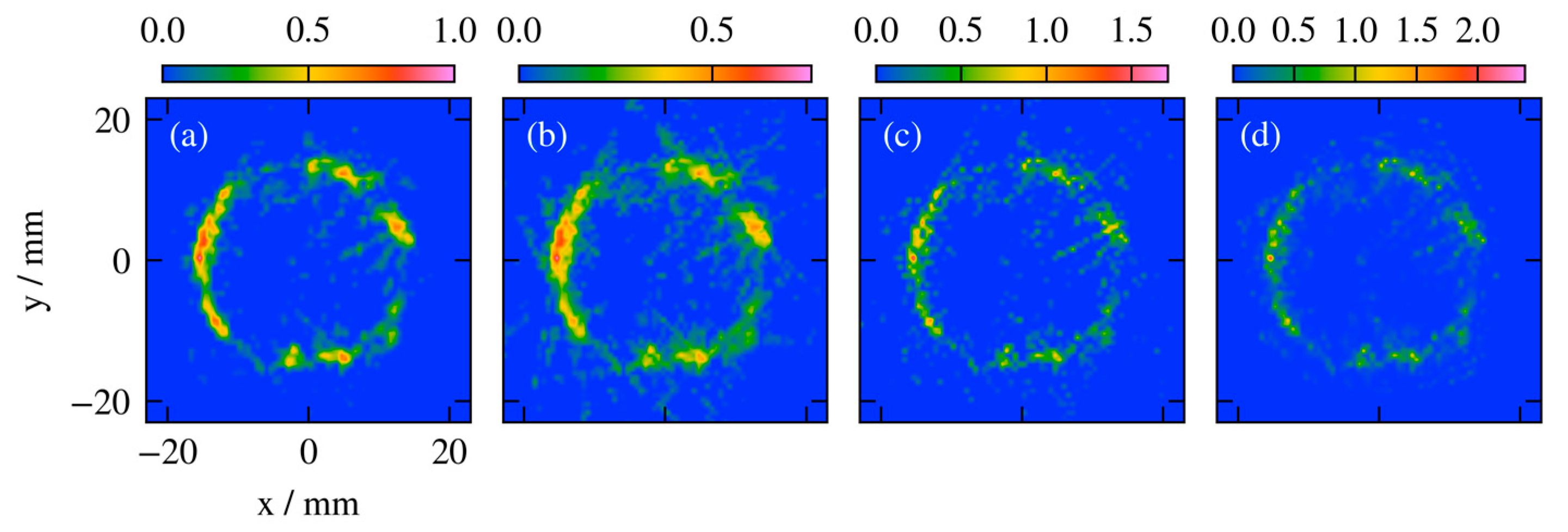
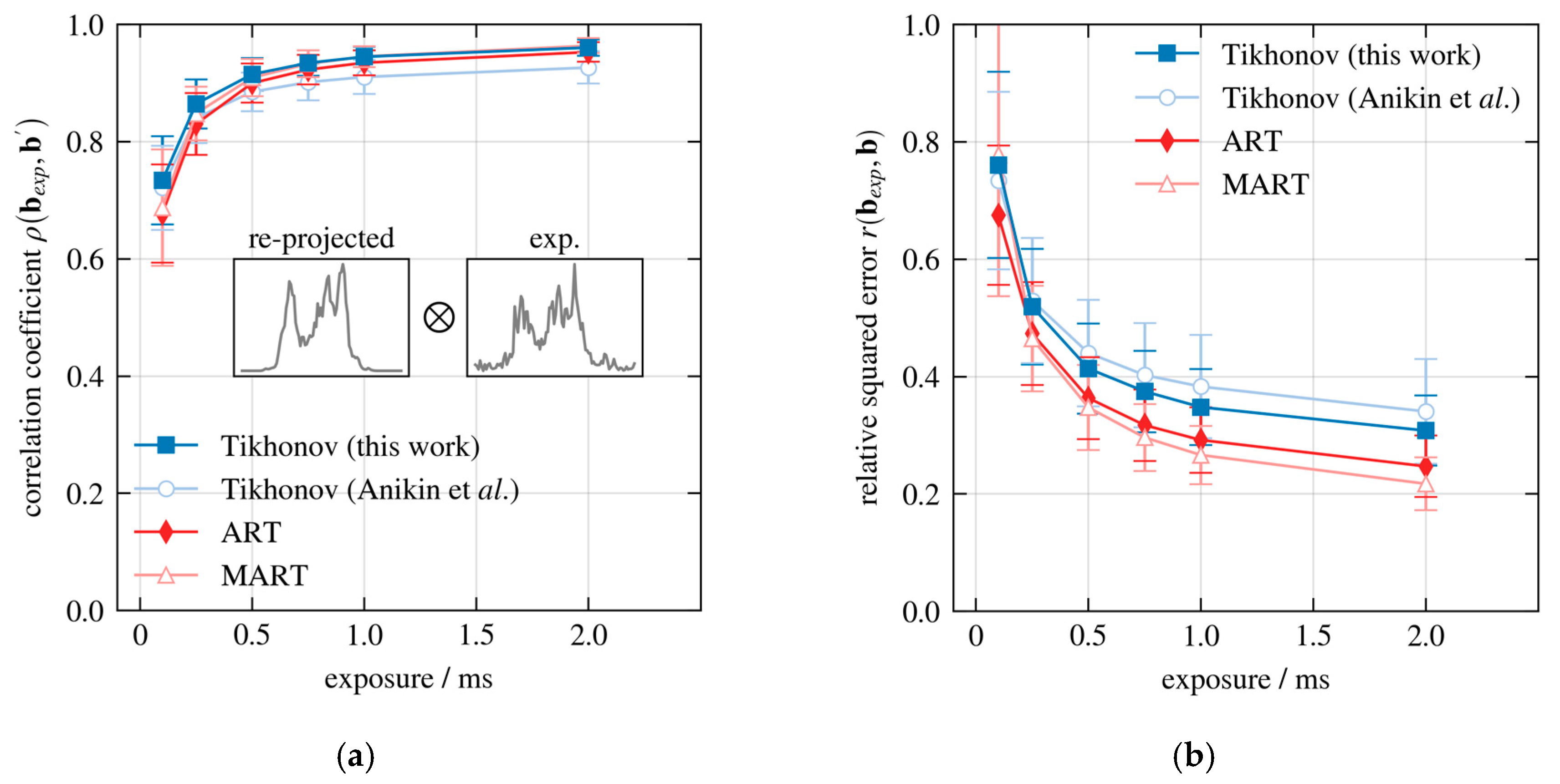
3. Results
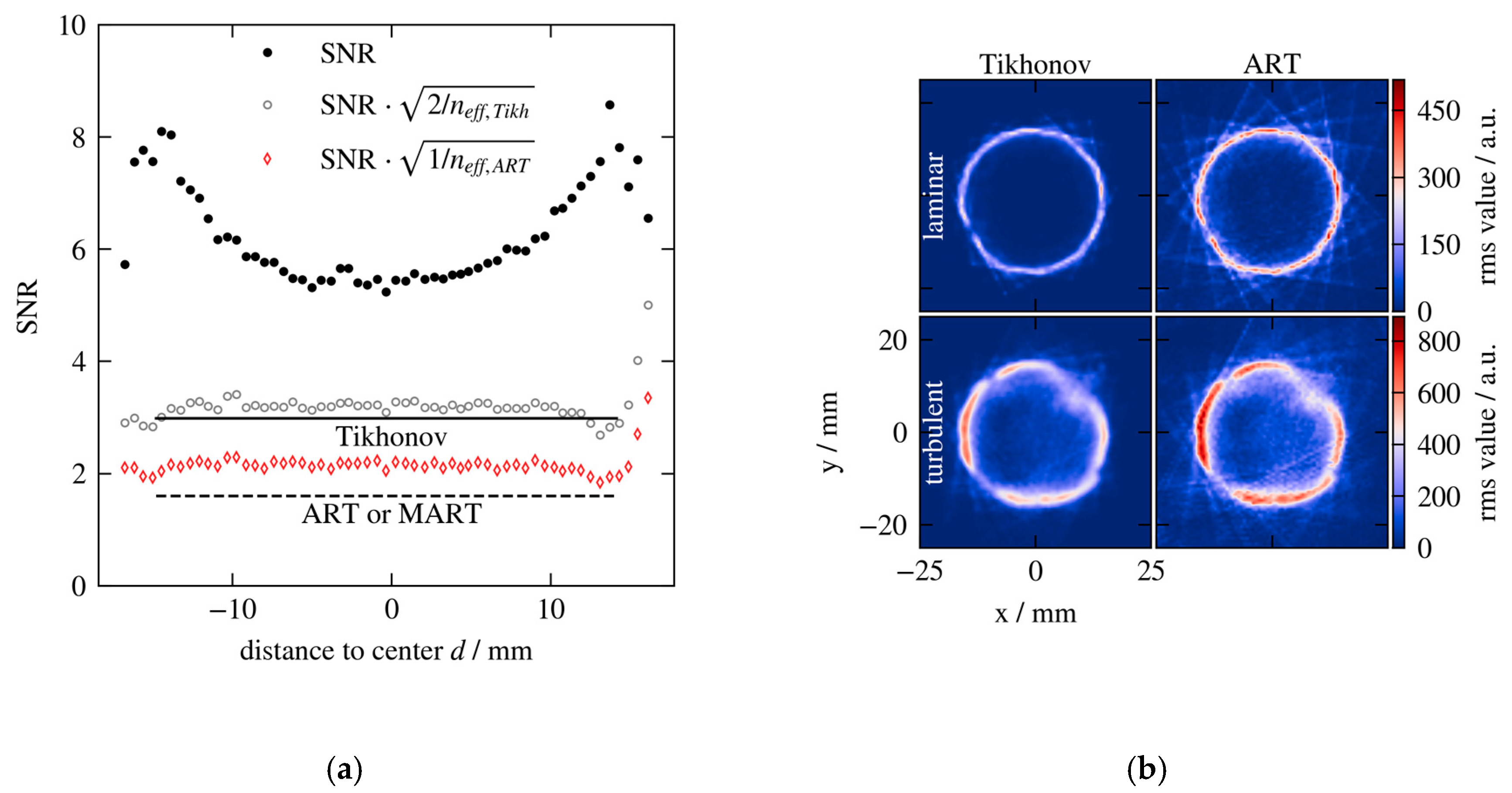
4. Discussion
4.1. Erroneous Validation Methods
4.2. Signal-to-noise Ratio Estimate
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ruan, C.; Chen, F.; Cai, W.; Qian, Y.; Yu, L.; Lu, X. Principles of non-intrusive diagnostic techniques and their applications for fundamental studies of combustion instabilities in gas turbine combustors: A brief review. Aerosp. Sci. Technol. 2019, 84, 585–603. [Google Scholar] [CrossRef]
- Scarano, F. Tomographic PIV: Principles and practice. Meas. Sci. Technol. 2013, 24, 12001. [Google Scholar] [CrossRef]
- Anikin, N.B.; Suntz, R.; Bockhorn, H. Tomographic reconstruction of 2D-OH∗-chemiluminescence distributions in turbulent diffusion flames. Appl. Phys. B 2012, 107, 591–602. [Google Scholar] [CrossRef]
- Anikin, N.B.; Suntz, R.; Bockhorn, H. Tomographic reconstruction of the OH*-chemiluminescence distribution in premixed and diffusion flames. Appl. Phys. B 2010, 100, 675–694. [Google Scholar] [CrossRef]
- Denisova, N. Plasma Diagnostics Using Computed Tomography Method. IEEE Trans. Plasma Sci. 2009, 37, 502–512. [Google Scholar] [CrossRef]
- Floyd, J.; Geipel, P.; Kempf, A.M. Computed Tomography of Chemiluminescence (CTC): Instantaneous 3D measurements and Phantom studies of a turbulent opposed jet flame. Combust. Flame 2011, 158, 376–391. [Google Scholar] [CrossRef]
- Floyd, J.; Kempf, A.M. Computed Tomography of Chemiluminescence (CTC): High resolution and instantaneous 3-D measurements of a Matrix burner. Proc. Combust. Inst. 2011, 33, 751–758. [Google Scholar] [CrossRef]
- Geraedts, B.D.; Arndt, C.M.; Steinberg, A.M. Rayleigh Index Fields in Helically Perturbed Swirl-Stabilized Flames Using Doubly Phase Conditioned OH* Chemiluminescence Tomography. Flow Turbul. Combust. 2016, 96, 1023–1038. [Google Scholar] [CrossRef]
- Goyal, A.; Chaudhry, S.; Subbarao, P.M.V. Direct three dimensional tomography of flames using maximization of entropy technique. Combust. Flame 2014, 161, 173–183. [Google Scholar] [CrossRef]
- Hossain, M.M.; Lu, G.; Yan, Y. Optical Fiber Imaging Based Tomographic Reconstruction of Burner Flames. IEEE Trans. Instrum. Meas. 2012, 61, 1417–1425. [Google Scholar] [CrossRef]
- Hossain, M.M.; Lu, G.; Yan, Y. Three-dimensional reconstruction of combustion flames through optical fiber sensing and CCD imaging. In Proceedings of the IEEE Instrumentation and Measurement Technology Conference (I2MTC), Hangzhou, China, 10–12 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1–7. [Google Scholar]
- Li, X.; Ma, L. Capabilities and limitations of 3D flame measurements based on computed tomography of chemiluminescence. Combust. Flame 2015, 162, 642–651. [Google Scholar] [CrossRef]
- Liu, H.; Sun, B.; Cai, W. kHz-rate volumetric flame imaging using a single camera. Opt. Commun. 2019, 437, 33–43. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Q.; Cai, W. Parametric study on single-camera endoscopic tomography. J. Opt. Soc. Am. B JOSAB 2020, 37, 271–278. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Shui, C.; Cai, W. Reconstruction and analysis of non-premixed turbulent swirl flames based on kHz-rate multi-angular endoscopic volumetric tomography. Aerosp. Sci. Technol. 2019, 91, 422–433. [Google Scholar] [CrossRef]
- Lv, L.; Tan, J.; Hu, Y. Numerical and Experimental Investigation of Computed Tomography of Chemiluminescence for Hydrogen-Air Premixed Laminar Flames. Int. J. Aerosp. Eng. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Ma, L.; Wu, Y.; Lei, Q.; Xu, W.; Carter, C.D. 3D flame topography and curvature measurements at 5 kHz on a premixed turbulent Bunsen flame. Combust. Flame 2016, 166, 66–75. [Google Scholar] [CrossRef]
- Song, J.; Hong, Y.; Wang, G.; Pan, H. Algebraic tomographic reconstruction of two-dimensional gas temperature based on tunable diode laser absorption spectroscopy. Appl. Phys. B 2013, 112, 529–537. [Google Scholar] [CrossRef]
- Unterberger, A.; Röder, M.; Giese, A.; Al-Halbouni, A.; Kempf, A.M.; Mohri, K. 3D Instantaneous Reconstruction of Turbulent Industrial Flames Using Computed Tomography of Chemiluminescence (CTC). J. Combust. 2018, 2018, 1–6. [Google Scholar] [CrossRef]
- Unterberger, A.; Kempf, A.M.; Mohri, K. 3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase. Energies 2019, 12, 2075. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Li, Z.-H.; Kempf, A.M.; He, A.-Z. Multi-directional 3D flame chemiluminescence tomography based on lens imaging. Opt. Lett. 2015, 40, 1231–1234. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Zhang, Y.; Yu, X. Camera calibration for multidirectional flame chemiluminescence tomography. Opt. Eng. 2017, 56, 41307. [Google Scholar] [CrossRef]
- Wang, K.; Li, F.; Zeng, H.; Yu, X. Three-dimensional flame measurements with large field angle. Opt. Express 2017, 25, 21008. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Li, F.; Zeng, H.; Zhang, S.; Yu, X. Computed tomography measurement of 3D combustion chemiluminescence using single camera. In Proceedings of the International Symposium on Optoelectronic Technology and Application 2016, Beijing, China, 9 May 2016; Han, S., Tan, J., Eds.; SPIE: Bellingham, WA, USA, 2016; p. 1015531. [Google Scholar]
- Wiseman, S.M.; Brear, M.J.; Gordon, R.L.; Marusic, I. Measurements from flame chemiluminescence tomography of forced laminar premixed propane flames. Combust. Flame 2017, 183, 1–14. [Google Scholar] [CrossRef]
- Worth, N.A.; Dawson, J.R. Tomographic reconstruction of OH* chemiluminescence in two interacting turbulent flames. Meas. Sci. Technol. 2013, 24, 24013. [Google Scholar] [CrossRef]
- Yu, T.; Liu, H.; Cai, W. On the quantification of spatial resolution for three-dimensional computed tomography of chemiluminescence. Opt. Express 2017, 25, 24093–24108. [Google Scholar] [CrossRef]
- Yu, T.; Ruan, C.; Chen, F.; Wang, Q.; Cai, W.; Lu, X. Measurement of the 3D Rayleigh index field via time-resolved CH* computed tomography. Aerosp. Sci. Technol. 2019, 105487. [Google Scholar] [CrossRef]
- Yu, T.; Ruan, C.; Liu, H.; Cai, W.; Lu, X. Time-resolved measurements of a swirl flame at 4 kHz via computed tomography of chemiluminescence. Appl. Opt. 2018, 57, 5962. [Google Scholar] [CrossRef]
- Halls, B.R.; Hsu, P.S.; Roy, S.; Meyer, T.R.; Gord, J.R. Two-color volumetric laser-induced fluorescence for 3D OH and temperature fields in turbulent reacting flows. Opt. Lett. 2018, 43, 2961–2964. [Google Scholar] [CrossRef]
- Halls, B.R.; Hsu, P.S.; Jiang, N.; Legge, E.S.; Felver, J.J.; Slipchenko, M.N.; Roy, S.; Meyer, T.R.; Gord, J.R. kHz-rate four-dimensional fluorescence tomography using an ultraviolet-tunable narrowband burst-mode optical parametric oscillator. Optica 2017, 4, 897. [Google Scholar] [CrossRef]
- Li, T.; Pareja, J.; Fuest, F.; Schütte, M.; Zhou, Y.; Dreizler, A.; Böhm, B. Tomographic imaging of OH laser-induced fluorescence in laminar and turbulent jet flames. Meas. Sci. Technol. 2018, 29, 15206. [Google Scholar] [CrossRef]
- Pareja, J.; Johchi, A.; Li, T.; Dreizler, A.; Böhm, B. A study of the spatial and temporal evolution of auto-ignition kernels using time-resolved tomographic OH-LIF. Proc. Combust. Inst. 2019, 37, 1321–1328. [Google Scholar] [CrossRef]
- Atkinson, C.; Soria, J. Algebraic Reconstruction Techniques for Tomographic Particle Image Velocimetry. In Proceedings of the 16th Australasian Fluid Mechanics Conference, Gold Coast, Australia, 2–7 December 2007. [Google Scholar]
- Atkinson, C.; Soria, J. An efficient simultaneous reconstruction technique for tomographic particle image velocimetry. Exp. Fluids 2009, 47, 553–568. [Google Scholar] [CrossRef]
- Elsinga, G.E.; Scarano, F.; Wieneke, B.; van Oudheusden, B.W. Tomographic particle image velocimetry. Exp. Fluids 2006, 41, 933–947. [Google Scholar] [CrossRef]
- Atkinson, C.; Coudert, S.; Foucaut, J.-M.; Stanislas, M.; Soria, J. The accuracy of tomographic particle image velocimetry for measurements of a turbulent boundary layer. Exp. Fluids 2011, 50, 1031–1056. [Google Scholar] [CrossRef]
- Liu, H.; Yu, T.; Zhang, M.; Cai, W. Demonstration of 3D computed tomography of chemiluminescence with a restricted field of view. Appl. Opt. 2017, 56, 7107. [Google Scholar] [CrossRef]
- Wan, X.; Zhang, F.; Chu, Q.; Zhang, K.; Sun, F.; Yuan, B.; Liu, Z. Three-dimensional reconstruction using an adaptive simultaneous algebraic reconstruction technique in electron tomography. J. Struct. Biol. 2011, 175, 277–287. [Google Scholar] [CrossRef]
- Daun, K.J.; Grauer, S.J.; Hadwin, P.J. Chemical species tomography of turbulent flows: Discrete ill-posed and rank deficient problems and the use of prior information. J. Quant. Spectrosc. Radiat. Transf. 2016, 172, 58–74. [Google Scholar] [CrossRef]
- Häber, T.; Bockhorn, H.; Suntz, R. Two-dimensional tomographic simultaneous multi-species visualization—Part I: Experimental methodology and application to laminar and turbulent flames. Energies 2020, 13, 2335. [Google Scholar] [CrossRef]
- Panoutsos, C.; Hardalupas, Y.; Taylor, A. Numerical evaluation of equivalence ratio measurement using OH∗ and CH∗ chemiluminescence in premixed and non-premixed methane–air flames. Combust. Flame 2009, 156, 273–291. [Google Scholar] [CrossRef]
- Kojima, J.; Ikeda, Y.; Nakajima, T. Detail distributions of OH*, CH* and C2* chemiluminescence in the reaction zone of laminar premixed methane/air flames. In Proceedings of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Las Vegas, NV, USA, 24–28 July 2000; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Kojima, J.; Ikeda, Y.; Nakajima, T. Basic aspects of OH(A), CH(A), and C2(d) chemiluminescence in the reaction zone of laminar methane–air premixed flames. Combust. Flame 2005, 140, 34–45. [Google Scholar] [CrossRef]
- Kathrotia, T.; Riedel, U.; Seipel, A.; Moshammer, K.; Brockhinke, A. Experimental and numerical study of chemiluminescent species in low-pressure flames. Appl. Phys. B 2012, 107, 571–584. [Google Scholar] [CrossRef]
- Deleo, M.; Saveliev, A.; Kennedy, L.; Zelepouga, S. OH and CH luminescence in opposed flow methane oxy-flames. Combust. Flame 2007, 149, 435–447. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.I. Solutions of Ill-Posed Problems; John, F., Ed.; Wiley: New York, NY, USA, 1977; ISBN 9780470991244. [Google Scholar]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1998; ISBN 978-0-89871-403-6. [Google Scholar]
- Gordon, R.; Bender, R.; Herman, G.T. Algebraic Reconstruction Techniques (ART) for three-dimensional electron microscopy and X-ray photography. J. Theor. Biol. 1970, 29, 471–481. [Google Scholar] [CrossRef]
- Hounsfield, G.N. Method of and Apparatus for Examining a Body by Radiation such as X or Gamma Radiation. U.S. Patent No. 3924131, 1975. [Google Scholar]
- Gilbert, P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theor. Biol. 1972, 36, 105–117. [Google Scholar] [CrossRef]
- Herman, G.T.; Lent, A. Iterative reconstruction algorithms. Comput. Biol. Med. 1976, 6, 273–294. [Google Scholar] [CrossRef]
- Mailloux, G.E.; Noumeir, R.; Lemieux, R. Deriving the multiplicative algebraic reconstruction algorithm (MART) by the method of convex projection (POCS). In Proceedings of the ICASSP-93, IEEE International Conference on Acoustics, Speech, and Signal Processing, Minneapolis, MN, USA, 27–30 April 1993; Volume 5, pp. 457–460. [Google Scholar]
- Daun, K.J. Infrared species limited data tomography through Tikhonov reconstruction. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 105–115. [Google Scholar] [CrossRef]
- Hadamard, J. Sur les problèmes aux dérivées partielles et leur signification physique. Princeton Univ. Bull. 1902, 13, 49–52. [Google Scholar]
- Jing, L.; Liu, S.; Zhihong, L.; Meng, S. An image reconstruction algorithm based on the extended Tikhonov regularization method for electrical capacitance tomography. Measurement 2009, 42, 368–376. [Google Scholar] [CrossRef]
- Dodge, Y.; Jurečková, J. Adaptive Regression; Springer: New York, NY, USA, 2000; ISBN 9780387989655. [Google Scholar]
- Hong, M.; Yu, Y.; Wang, H.; Liu, F.; Crozier, S. Compressed sensing MRI with singular value decomposition-based sparsity basis. Phys. Med. Biol. 2011, 56, 6311–6325. [Google Scholar] [CrossRef]
- Zdunek, R. Multigrid Regularized Image Reconstruction for Limited-Data Tomography. CMST 2007, 13, 67–77. [Google Scholar] [CrossRef]
- Song, J.; Hong, Y.; Xin, M.; Wang, G.; Liu, Z. Tomography system for measurement of gas properties in combustion flow field. Chin. J. Aeronaut. 2017, 30, 1697–1707. [Google Scholar] [CrossRef]
- Kaczmarz, S. Angenäherte Auflösung von Systemen linearer Gleichungen. Bull. Acad. Polon. Sci. Lett. A 1937, 35, 355–357. [Google Scholar]
- Herman, G.T. On modifications to the algebraic reconstruction techniques. Comput. Biol. Med. 1979, 9, 271–276. [Google Scholar] [CrossRef]
- Andersen, A.H.; Kak, A.C. Simultaneous algebraic reconstruction technique (SART): A superior implementation of the art algorithm. Ultrason. Imaging 1984, 6, 81–94. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Li, X.; Ma, L. Practical aspects of implementing three-dimensional tomography inversion for volumetric flame imaging. Appl. Opt. 2013, 52, 8106–8116. [Google Scholar] [CrossRef] [PubMed]
- Verhoeven, D. Limited-data computed tomography algorithms for the physical sciences. Appl. Opt. 1993, 32, 3736–3754. [Google Scholar] [CrossRef] [PubMed]
- Hardalupas, Y.; Orain, M. Local measurements of the time-dependent heat release rate and equivalence ratio using chemiluminescent emission from a flame. Combust. Flame 2004, 139, 188–207. [Google Scholar] [CrossRef]
- Ikeda, Y.; Kojima, J.; Nakajima, T. Local Chemiluminescence Measurements of OH*, CH* and C2* at Turbulent Premixed Flame-Fronts. In Smart Control of Turbulent Combustion; Yoshida, A., Ed.; Springer Japan: Tokyo, Japan, 2001; pp. 12–27. ISBN 978-4-431-66987-6. [Google Scholar]
- Eckbreth, A.C. Laser Diagnostics for Combustion Temperature and Species, 2nd ed.; Gordon and Breach Publ.: New York, NY, USA, 1996; ISBN 9782884492256. [Google Scholar]
- Lewis, J.P. Fast Normalized Cross-Correlation. 1995. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.21.6062 (accessed on 9 March 2020).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Proc. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Herbert, T.J. Statistical stopping criteria for iterative maximum likelihood reconstruction of emission images. Phys. Med. Biol. 1990, 35, 1221–1232. [Google Scholar] [CrossRef]
- Ma, L.; Wu, Y.; Xu, W.; Hammack, S.D.; Lee, T.; Carter, C.D. Comparison of 2D and 3D flame topography measured by planar laser-induced fluorescence and tomographic chemiluminescence. Appl. Opt. 2016, 55, 5310–5315. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Häber, T.; Suntz, R.; Bockhorn, H. Two-Dimensional Tomographic Simultaneous Multispecies Visualization—Part II: Reconstruction Accuracy. Energies 2020, 13, 2368. https://doi.org/10.3390/en13092368
Häber T, Suntz R, Bockhorn H. Two-Dimensional Tomographic Simultaneous Multispecies Visualization—Part II: Reconstruction Accuracy. Energies. 2020; 13(9):2368. https://doi.org/10.3390/en13092368
Chicago/Turabian StyleHäber, Thomas, Rainer Suntz, and Henning Bockhorn. 2020. "Two-Dimensional Tomographic Simultaneous Multispecies Visualization—Part II: Reconstruction Accuracy" Energies 13, no. 9: 2368. https://doi.org/10.3390/en13092368
APA StyleHäber, T., Suntz, R., & Bockhorn, H. (2020). Two-Dimensional Tomographic Simultaneous Multispecies Visualization—Part II: Reconstruction Accuracy. Energies, 13(9), 2368. https://doi.org/10.3390/en13092368




