An MPC Approach for Grid-Forming Inverters: Theory and Experiment
Abstract
1. Introduction
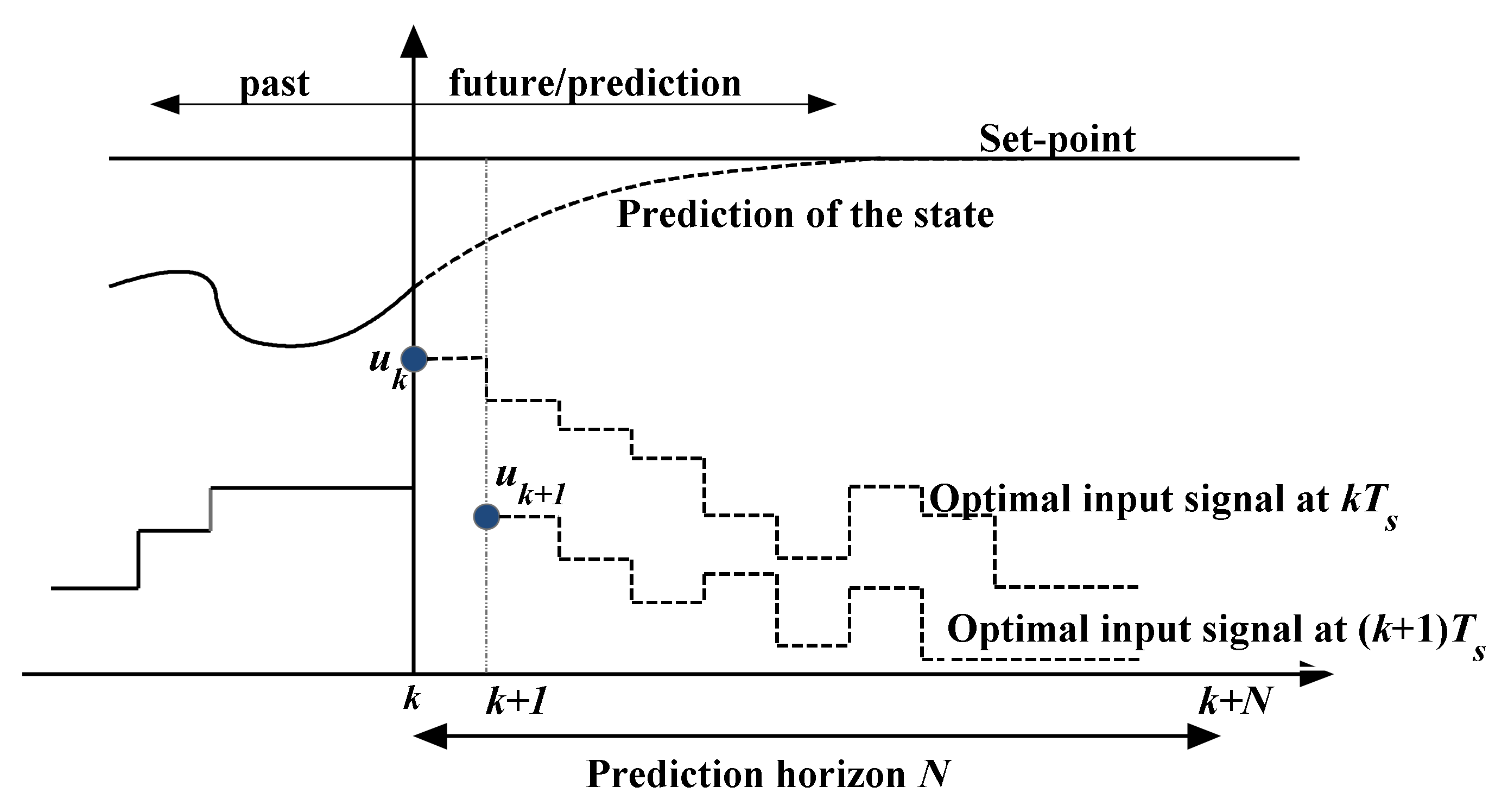
2. Some Remarks about the MPC Technique
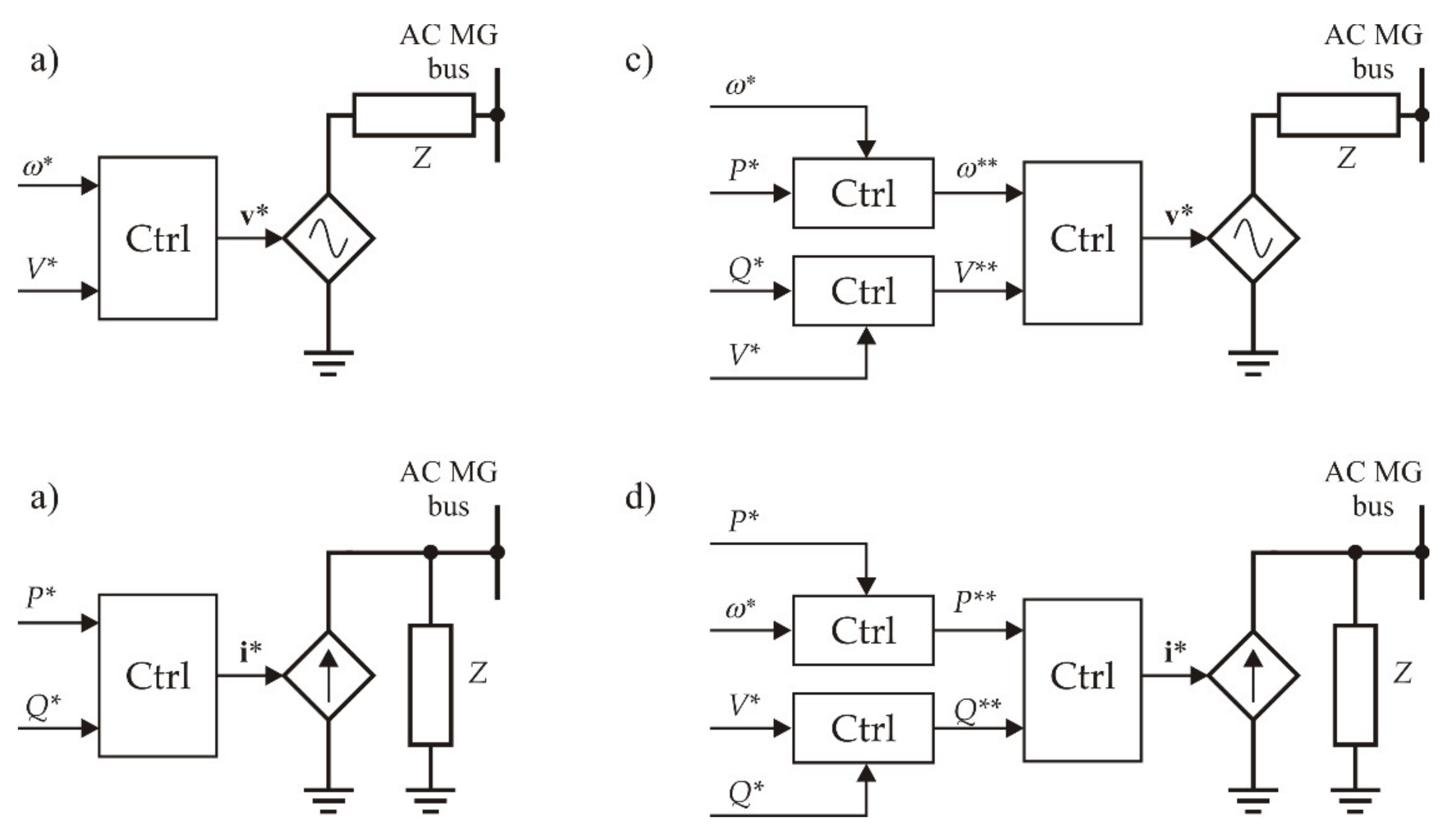
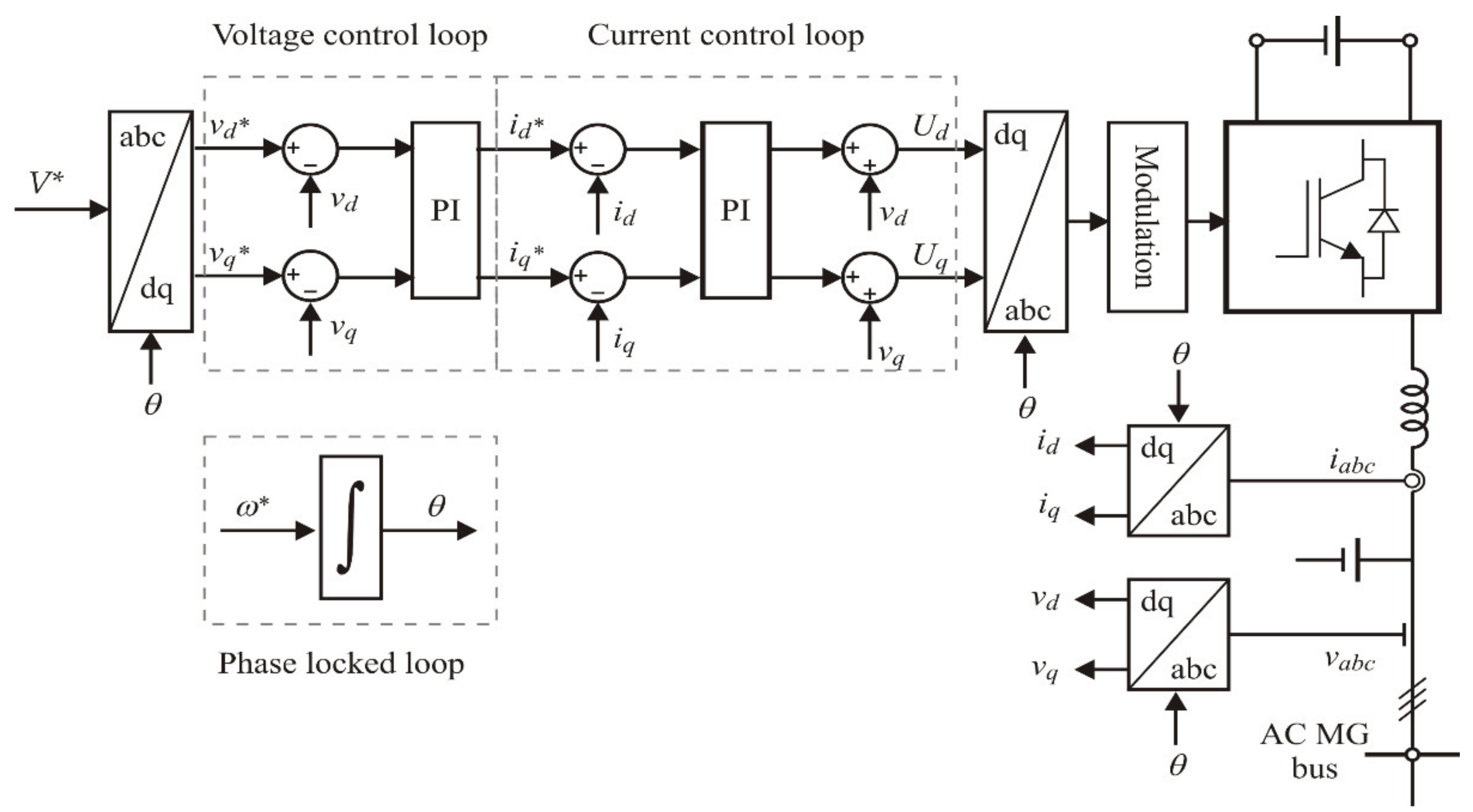
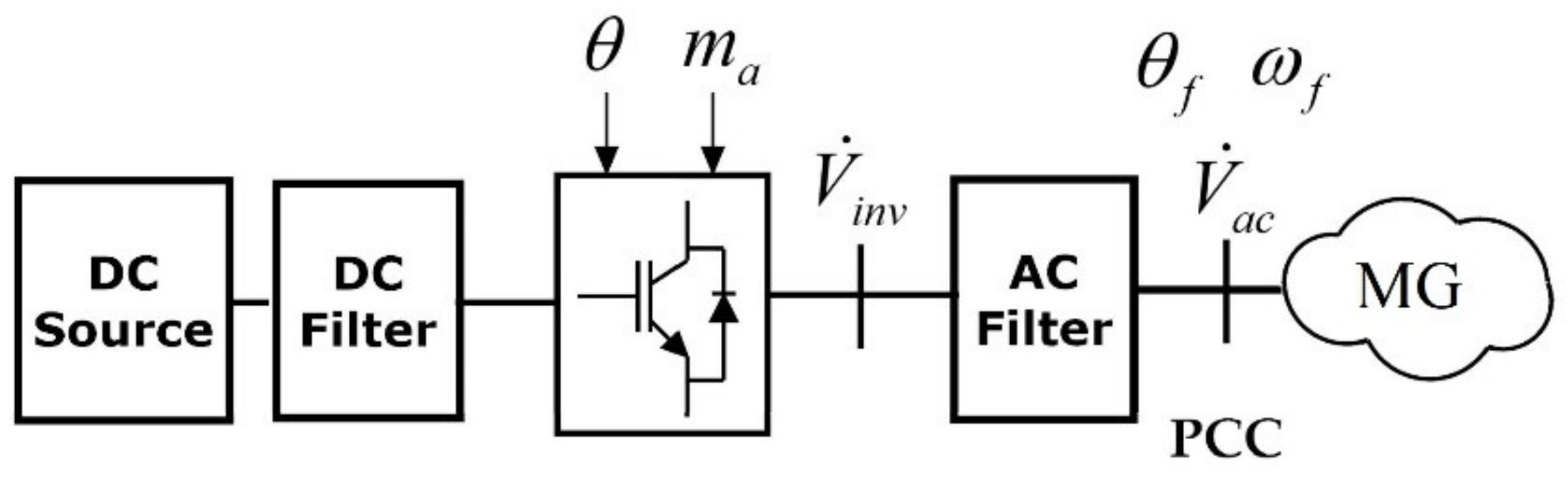
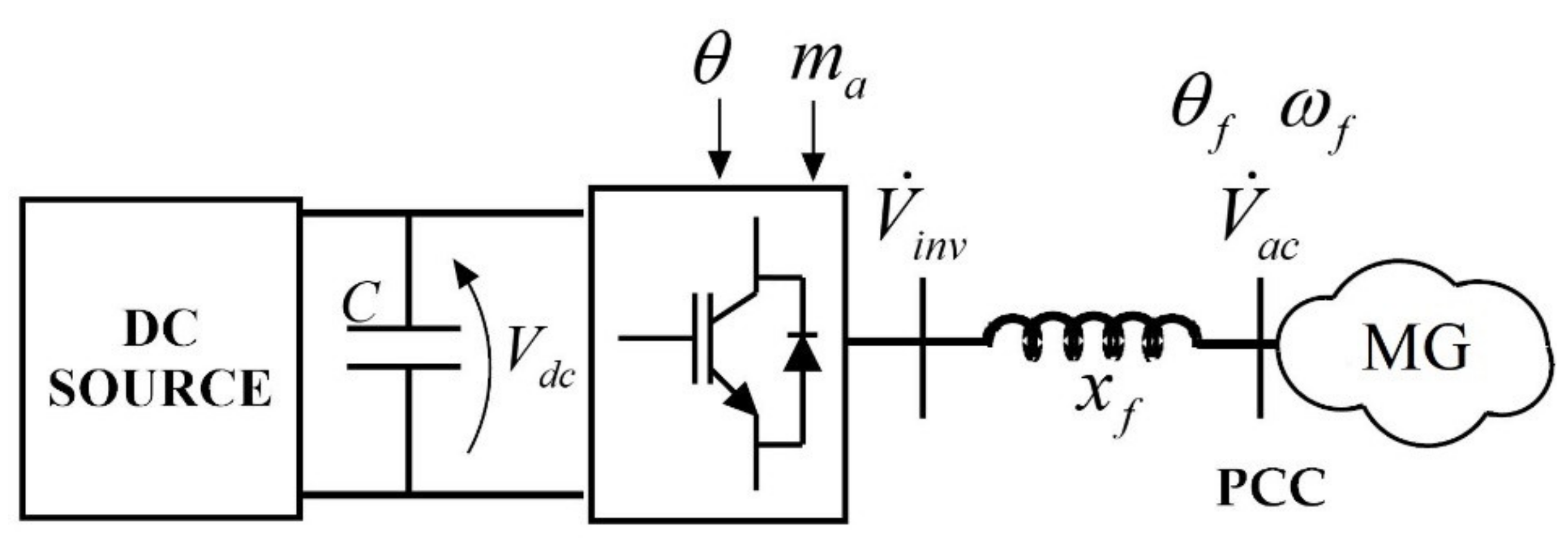
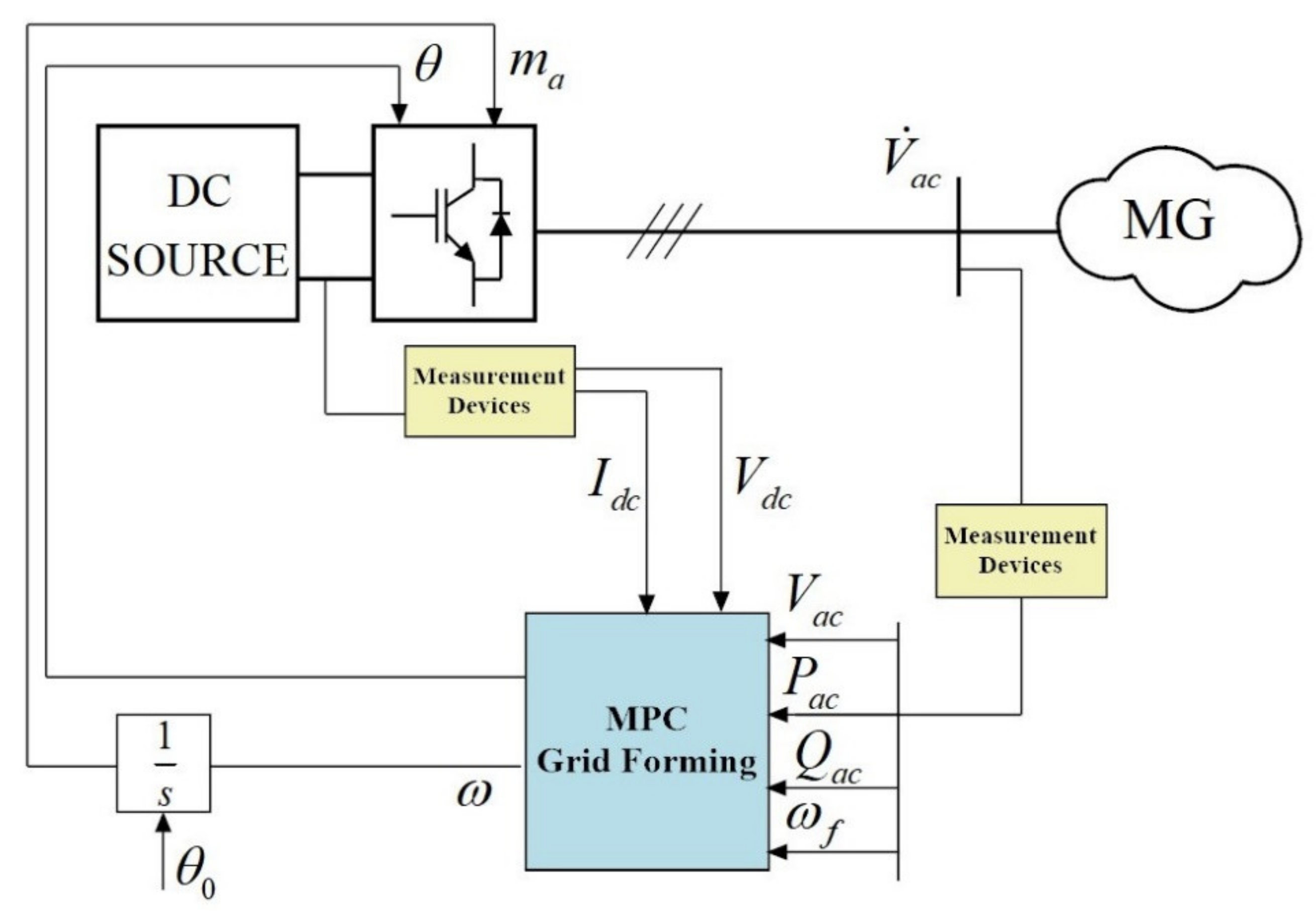
3. MPC Controller Design for Grid-Forming Inverters
- AC side of the MG is supposed to be at steady state while DC dynamics are fully considered;
- Higher-order harmonics are neglected;
- DC inductor is neglected;
- The shunt section of the AC filter is neglected.
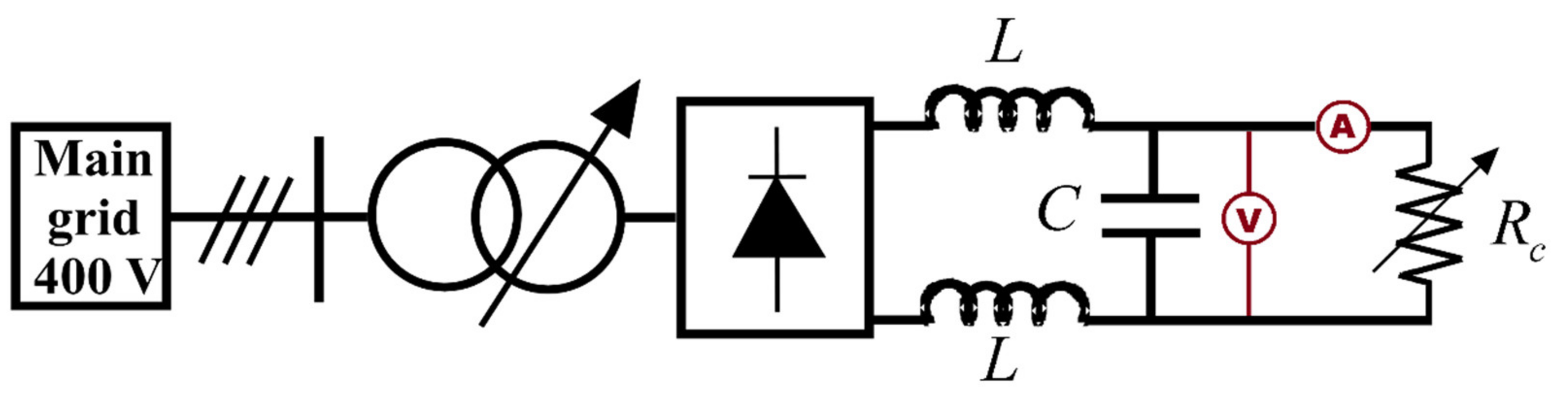
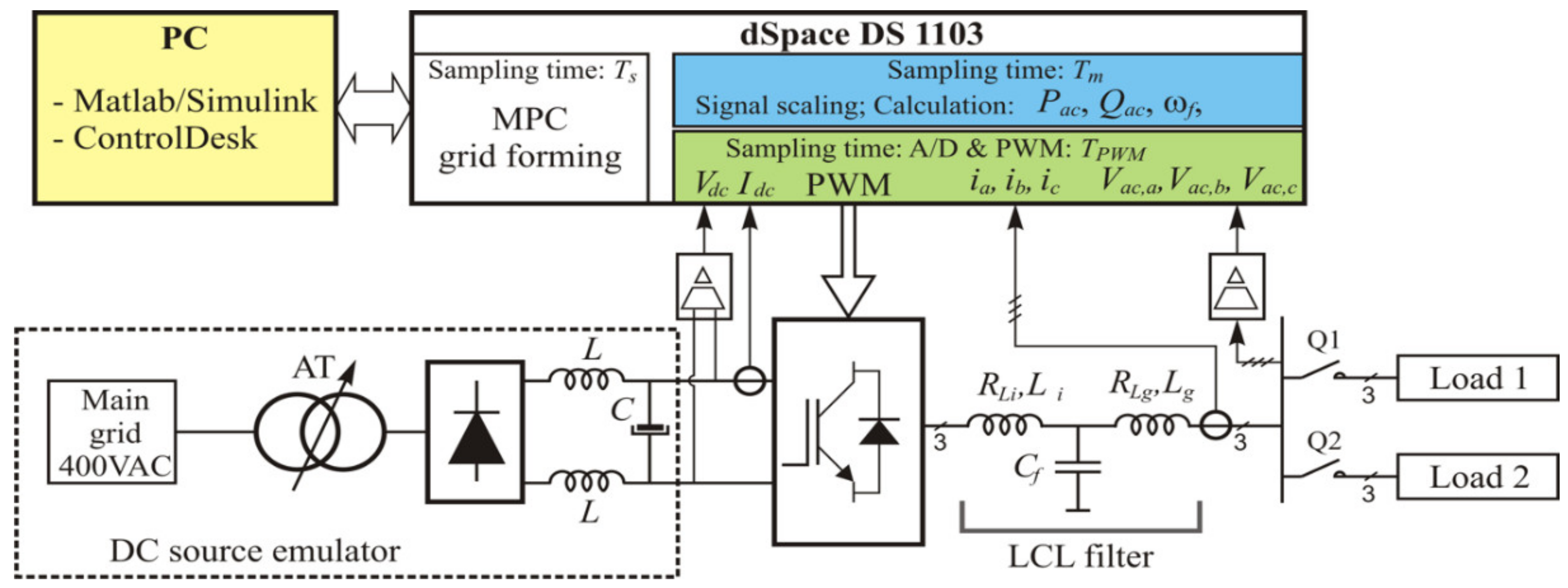
4. Experimental Setup
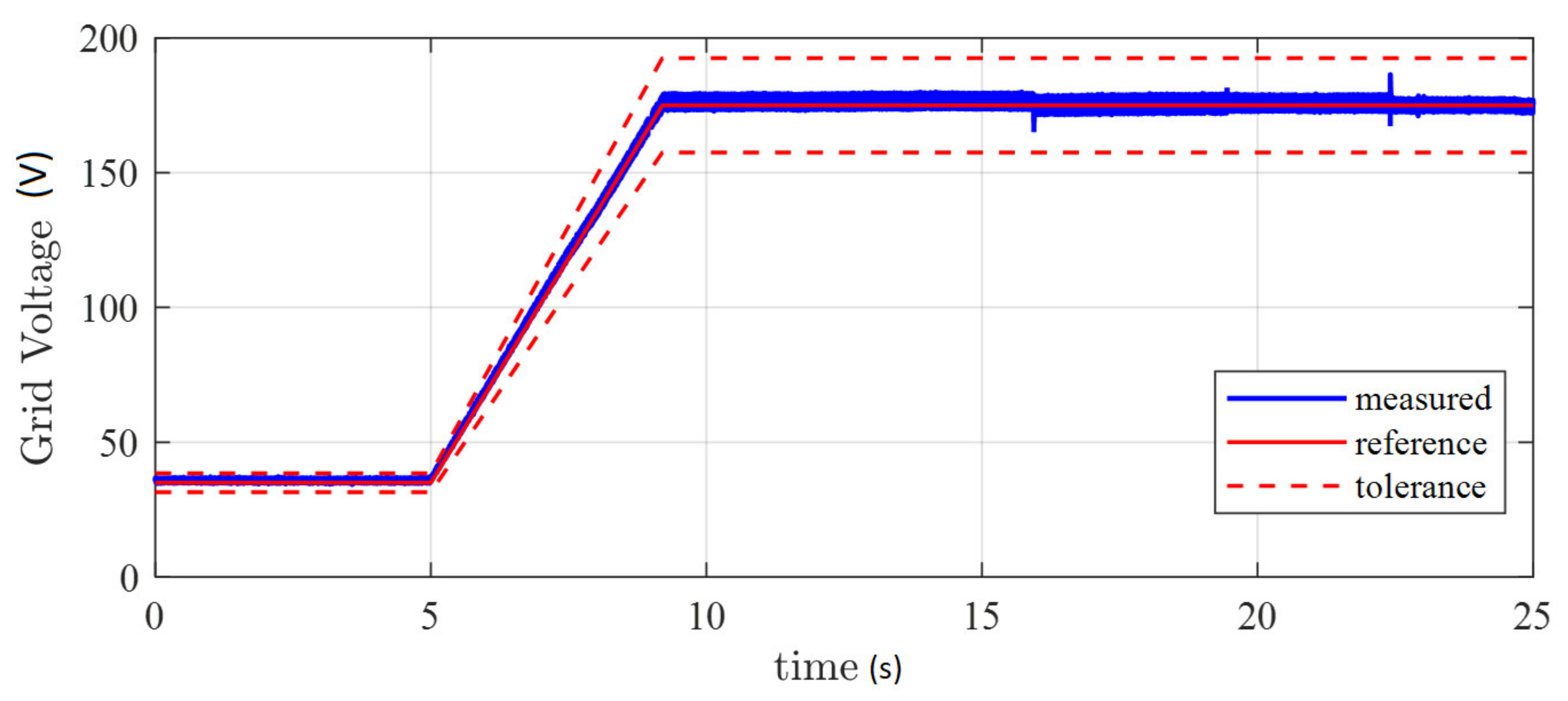
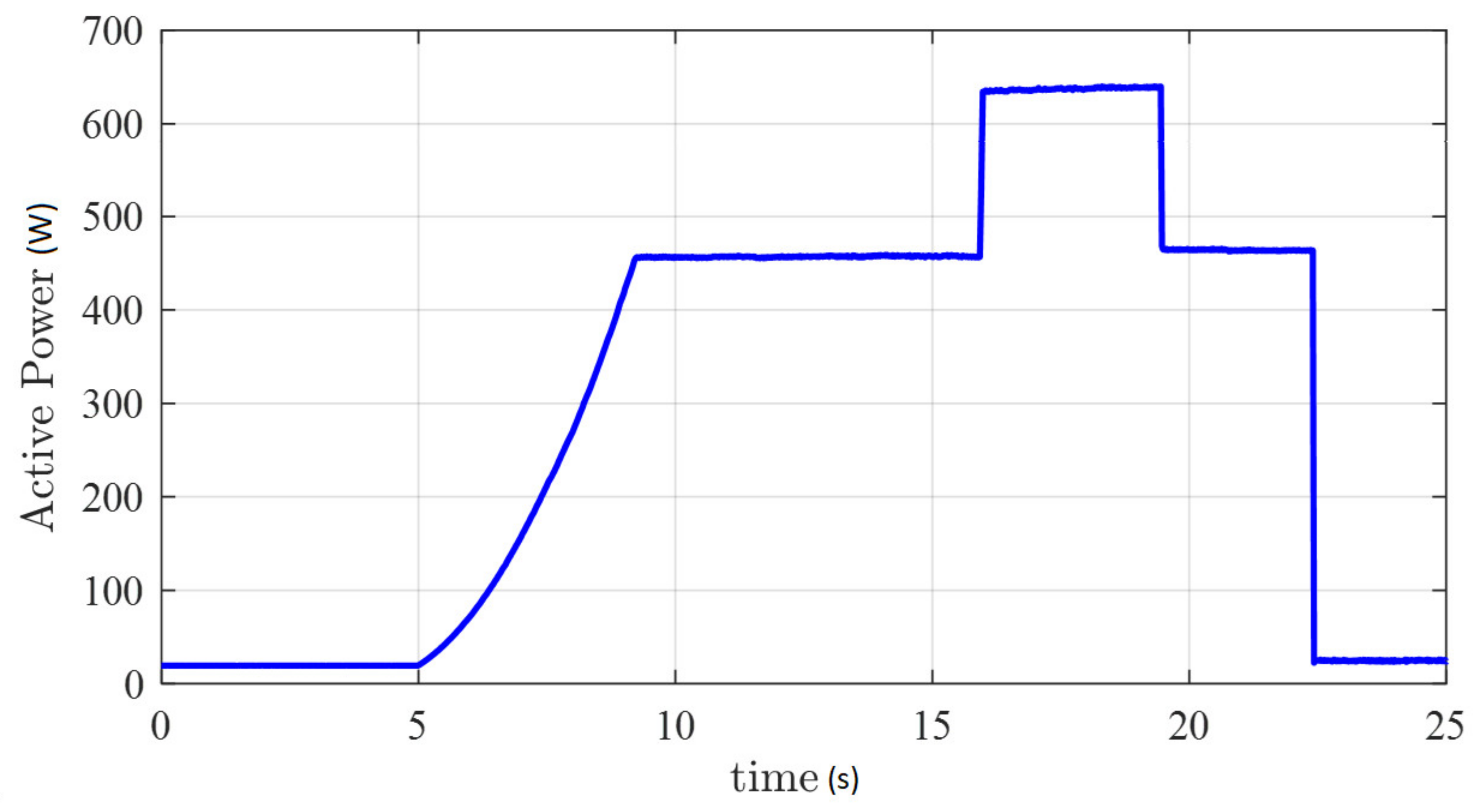
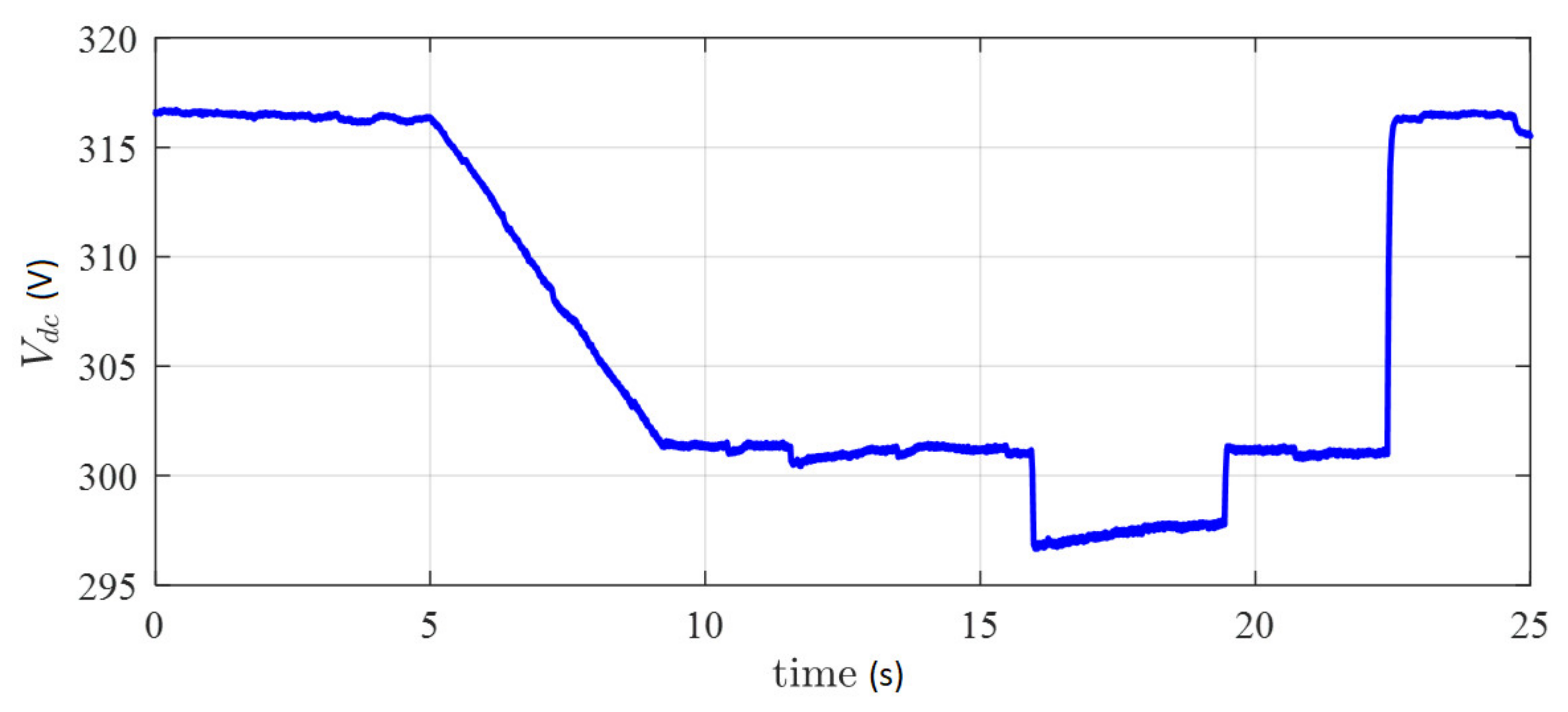
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
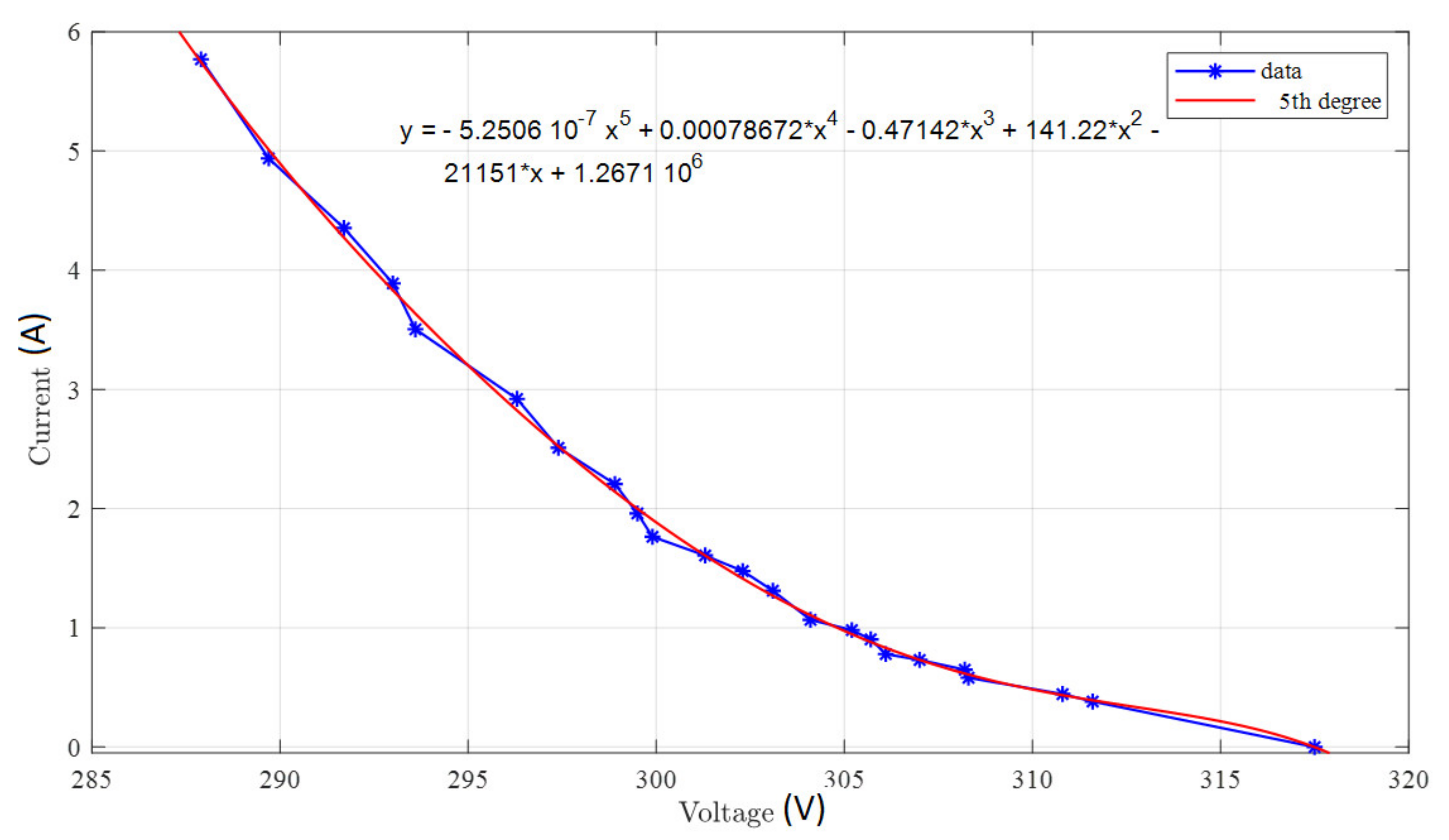
| 5th | 4th | 3th | 2th | 1th | 0 |
|---|---|---|---|---|---|
| −2.5 × 10−7 | 7.87 × 10−4 | −0.471 | 114 | −2.12 × 104 | 1.27 × 106 |
References
- Bendato, I.; Bonfiglio, A.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R. Definition and on-field validation of a microgrid energy management system to manage load and renewables uncertainties and system operator requirements. Electr. Power Syst. Res. 2017, 146, 349–361. [Google Scholar] [CrossRef]
- Bendato, I.; Bonfiglio, A.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R.; Rossi, M. Design criteria for the optimal sizing of integrated photovoltaic-storage systems. Energy 2018, 149, 505–515. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Brignone, M.; Delfino, F.; Invernizzi, M.; Pampararo, F.; Procopio, R. A technique for the optimal control and operation of grid-connected photovoltaic production units. In Proceedings of the 2012 47th International Universities Power Engineering Conference (UPEC), Middlesex, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in Microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Shrivastwa, R.; Hably, A.; Melizi, K.; Bacha, S. Understanding Microgrids and Their Future Trends. In Proceedings of the IEEE ICIT 2019, Melbourne, Australia, 13–15 February 2019. [Google Scholar]
- Bonfiglio, A.; Barillari, L.; Bendato, I.; Bracco, S.; Brignone, M.; Delfino, F.; Pampararo, F.; Procopio, R.; Robba, M.; Rossi, M. Day ahead microgrid optimization: A comparison among different models. In Proceedings of the OPT-i 2014—1st International Conference on Engineering and Applied Sciences Optimization, Kos, Greece, 4–6 June 2014; pp. 1153–1165. [Google Scholar]
- Fornari, F.; Procopio, R.; Bollen, M.H.J. SSC compensation capability of unbalanced voltage sags. IEEE Trans. Power Deliv. 2005, 20, 2030–2037. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.M.; Bonfiglio, A.; Procopio, R.; Verduci, B. Evaluation of inertial response controllers for full-rated power converter wind turbine (Type 4). In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Bonfiglio, A.; Invernizzi, M.; Labella, A.; Procopio, R. Design and Implementation of a Variable Synthetic Inertia Controller for Wind Turbine Generators. IEEE Trans. Power Syst. 2019, 34, 754–764. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Viinamäki, J.; Kuperman, A.; Suntio, T. Grid-Forming-Mode Operation of Boost-Power-Stage Converter in PV-Generator-Interfacing Applications. Energies 2017, 10, 1033. [Google Scholar] [CrossRef]
- IEEE Life Senior Member Daley PE DGCP; IEEE Member Houser PE. Assessment of DER Interconnection Installation for Conformance with IEEE Std 1547. In Assessment of DER Interconnection Installation for Conformance with IEEE Std 1547; IEEE: Piscataway, NJ, USA, 2018; pp. 1–18. [Google Scholar]
- Hou, X.; Sun, Y.; Yuan, W.; Han, H.; Zhong, C.; Guerrero, J. Conventional P-ω/Q-V Droop Control in Highly Resistive Line of Low-Voltage Converter-Based AC Microgrid. Energies 2016, 9, 943. [Google Scholar] [CrossRef]
- Italian Standard C. CEI 0-16—Technical Rules for the Connection of Active Passive Consumers to the HV MV Electrical Networks of Distribution Company; CEI: Milan, Italy, 2008. [Google Scholar]
- IEEE. IEEE. IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. In IEEE Std 1547-2018 (Revision of IEEE Std 1547–2003); IEEE: Piscataway, NJ, USA, 2018; pp. 1–138. [Google Scholar] [CrossRef]
- Bouzid, A.M.; Guerrero, J.M.; Cheriti, A.; Bouhamida, M.; Sicard, P.; Benghanem, M.J.R.; Reviews, S.E. A survey on control of electric power distributed generation systems for microgrid applications. Renew. Sustain. Energy Rev. 2015, 44, 751–766. [Google Scholar] [CrossRef]
- Serban, I.; Ion, C.P.; Systems, E. Microgrid control based on a grid-forming inverter operating as virtual synchronous generator with enhanced dynamic response capability. J. Electr. Power Energy Syst. 2017, 89, 94–105. [Google Scholar] [CrossRef]
- Hirase, Y.; Abe, K.; Sugimoto, K.; Sakimoto, K.; Bevrani, H.; Ise, T. A novel control approach for virtual synchronous generators to suppress frequency and voltage fluctuations in microgrids. Appl. Energy 2018, 210, 699–710. [Google Scholar] [CrossRef]
- Liu, J.; Miura, Y.; Ise, T. Comparison of Dynamic Characteristics between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators. IEEE Trans. Power Electron. 2016, 31, 3600–3611. [Google Scholar] [CrossRef]
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Huseinbegovic, S.; Perunicic-Drazenovic, B. A sliding mode based direct power control of three-phase grid-connected multilevel inverter. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012; pp. 790–797. [Google Scholar]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, S.; Bian, J. Control of a Grid-Forming Inverter Based on Sliding-Mode and Mixed ${H_2}/{H_\infty }$ Control. IEEE Trans. Ind. Electron. 2017, 64, 3862–3872. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Electron. 2017, 64, 935–947. [Google Scholar] [CrossRef]
- Hans, C.A.; Braun, P.; Raisch, J.; Grune, L.; Reincke-Collon, C. Hierarchical Distributed Model Predictive Control of Interconnected Microgrids. IEEE Trans. Sustain. Energy 2018, 10, 407–416. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.; Tan, R. Distributed Model Predictive Control for On-Connected Microgrid Power Management. IEEE Trans. Control Syst. Technol. 2018, 26, 1028–1039. [Google Scholar] [CrossRef]
- Morstyn, T.; Hredzak, B.; Aguilera, R.P.; Agelidis, V.G. Model Predictive Control for Distributed Microgrid Battery Energy Storage Systems. IEEE Trans. Control Syst. Technol. 2018, 26, 1107–1114. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Oliveri, A.; Procopio, R.; Delfino, F.; Denegrí, G.B.; Invernizzi, M.; Storace, M. Improving power grids transient stability via Model Predictive Control. In Proceedings of the 2014 Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]
- Babqi, A.J.; Etemadi, A.H. MPC-based microgrid control with supplementary fault current limitation and smooth transition mechanisms. IET Gener. Trans. Distrib. 2017, 11, 2164–2172. [Google Scholar] [CrossRef]
- Tavakoli, A.; Negnevitsky, M.; Muttaqi, K.M. A decentralized model predictive control for multiple distributed generators in the islanded mode of operation. In Proceedings of the 2015 IEEE Industry Applications Society Annual Meeting, Addison, TX, USA, 18–22 October 2015; pp. 1–8. [Google Scholar]
- Anderson, S.; Hidalgo-Gonzalez, P.; Dobbe, R.; Tomlin, C.J. Distributed Model Predictive Control for Autonomous Droop-Controlled Inverter-Based Microgrids. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 6242–6248. [Google Scholar]
- Dragicevic, T.; Alhasheem, M.; Lu, M.; Blaabjerg, F. Improved model predictive control for high voltage quality in microgrid applications. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4475–4480. [Google Scholar]
- Alhasheem, M.; Blaabjerg, F.; Davari, P. Performance Assessment of Grid Forming Converters Using Different Finite Control Set Model Predictive Control (FCS-MPC) Algorithms. Appl. Sci. 2019, 9, 3513. [Google Scholar] [CrossRef]
- Allgöwer, F.; Zheng, A. Nonlinear Model Predictive Control; Birkhäuser: Basel, Switzerland, 2012; Volume 26. [Google Scholar]
- Bonfiglio, A.; Brignone, M.; Invernizzi, M.; Labella, A.; Mestriner, D.; Procopio, R. A Simplified Microgrid Model for the Validation of Islanded Control Logics. Energies 2017, 10, 1141. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Delfino, F.; Labella, A.; Mestriner, D.; Pampararo, F.; Procopio, R.; Guerrero, J.M. Modeling and Experimental Validation of an Islanded No-Inertia Microgrid Site. IEEE Trans. Sustain. Energy 2018, 9, 1812–1821. [Google Scholar] [CrossRef]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. qpOASES: A parametric active-set algorithm for quadratic programming. Math. Programm. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Ferreau, H.J.; Bock, H.G.; Diehl, M. An online active set strategy to overcome the limitations of explicit MPC. Int. J. Robust Nonlinear Control IFAC-Affil. J. 2008, 18, 816–830. [Google Scholar] [CrossRef]



| C | 1.1 mF | RLg | 11 mΩ |
|---|---|---|---|
| L | 2.35 mH | Cf | 3.3 μF |
| Li | 28 mH | Lg | 1.3 mH |
| RLi | 0.17 Ω |
| QV | 3 | fmin | 49.5 Hz |
|---|---|---|---|
| Rω | 10 | fmax | 50.5 Hz |
| RJ | 5 | ma,min | 0.18 |
| N | 3 | ma,max | 1.156 |
| ωn | 314.159 rad/s | Amax | 4 kVA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Labella, A.; Filipovic, F.; Petronijevic, M.; Bonfiglio, A.; Procopio, R. An MPC Approach for Grid-Forming Inverters: Theory and Experiment. Energies 2020, 13, 2270. https://doi.org/10.3390/en13092270
Labella A, Filipovic F, Petronijevic M, Bonfiglio A, Procopio R. An MPC Approach for Grid-Forming Inverters: Theory and Experiment. Energies. 2020; 13(9):2270. https://doi.org/10.3390/en13092270
Chicago/Turabian StyleLabella, Alessandro, Filip Filipovic, Milutin Petronijevic, Andrea Bonfiglio, and Renato Procopio. 2020. "An MPC Approach for Grid-Forming Inverters: Theory and Experiment" Energies 13, no. 9: 2270. https://doi.org/10.3390/en13092270
APA StyleLabella, A., Filipovic, F., Petronijevic, M., Bonfiglio, A., & Procopio, R. (2020). An MPC Approach for Grid-Forming Inverters: Theory and Experiment. Energies, 13(9), 2270. https://doi.org/10.3390/en13092270








