Coarse-Grained Model of Underground Thermal Energy Storage Applied to Efficiency Optimization
Abstract
1. Introduction
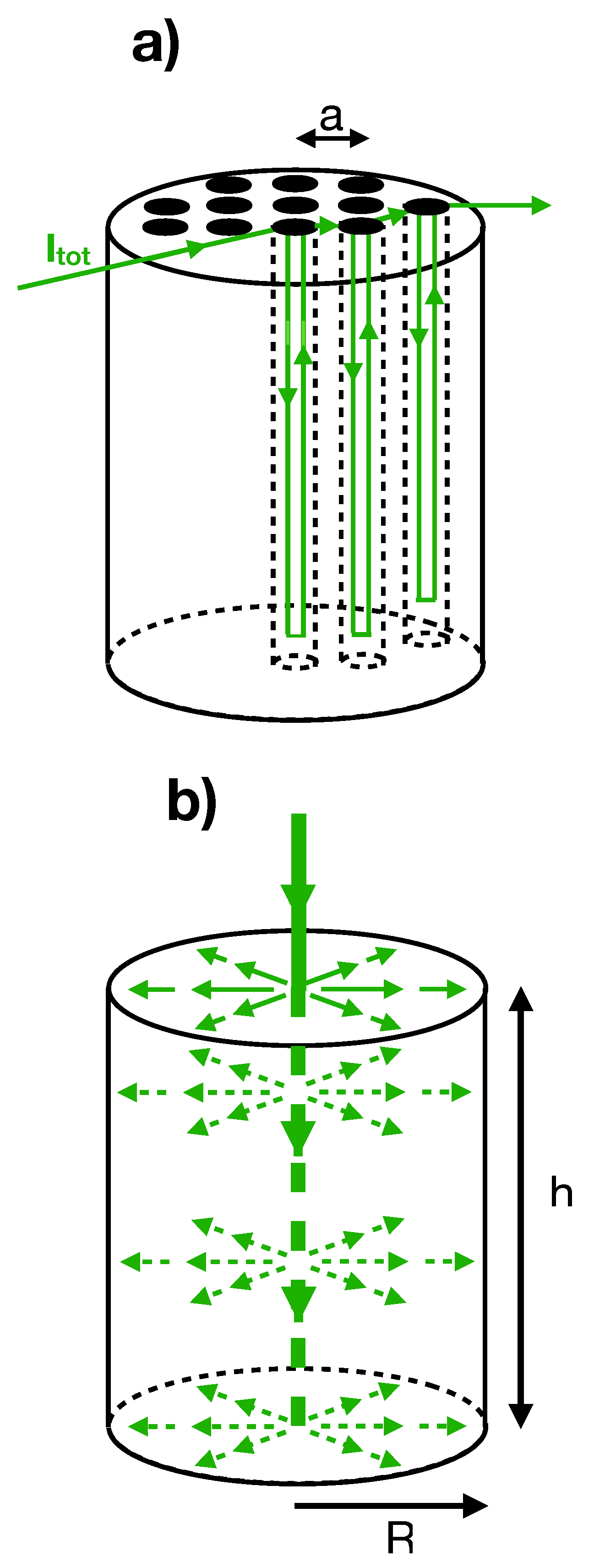
2. Methodology
3. Results and Discussion
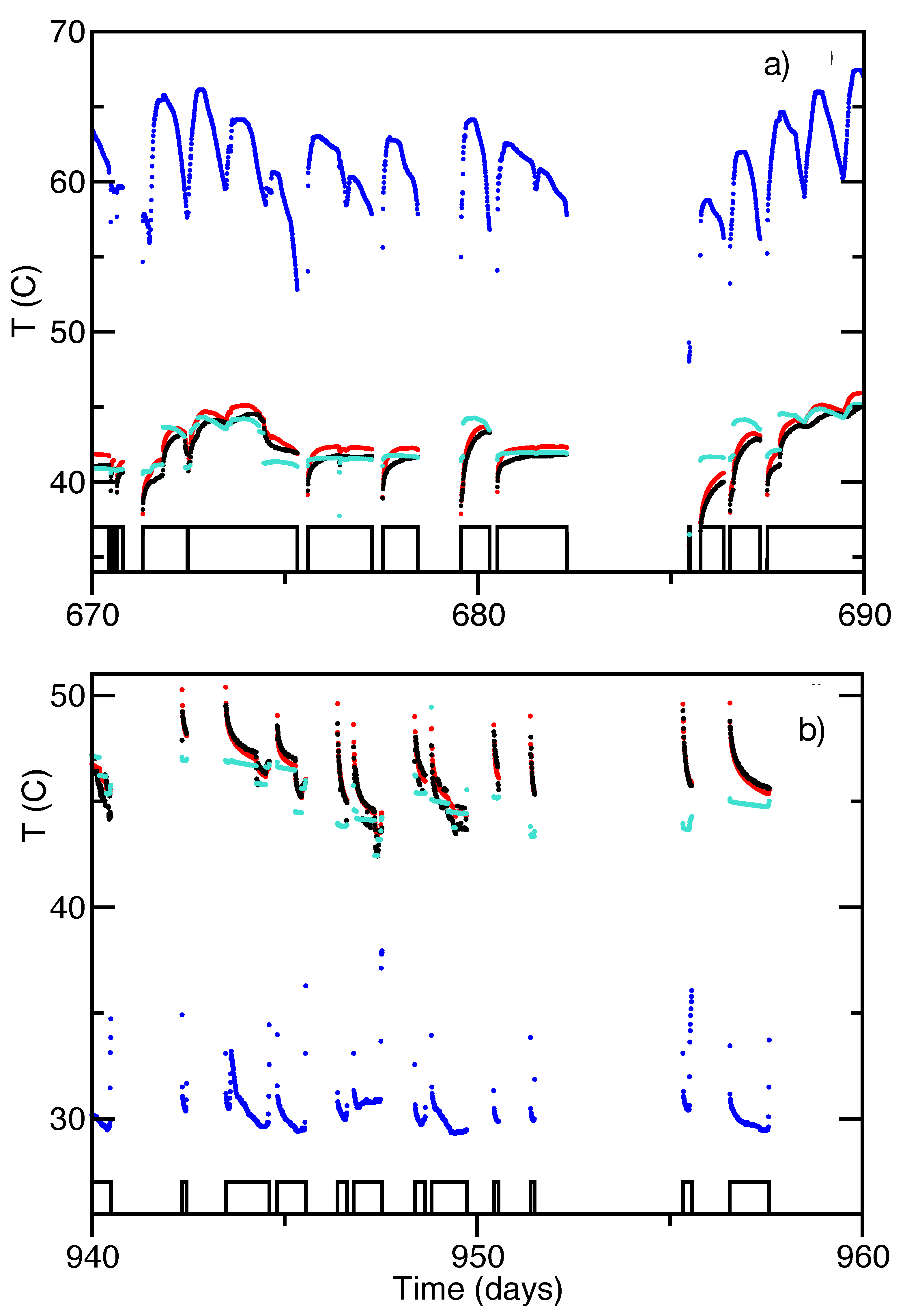
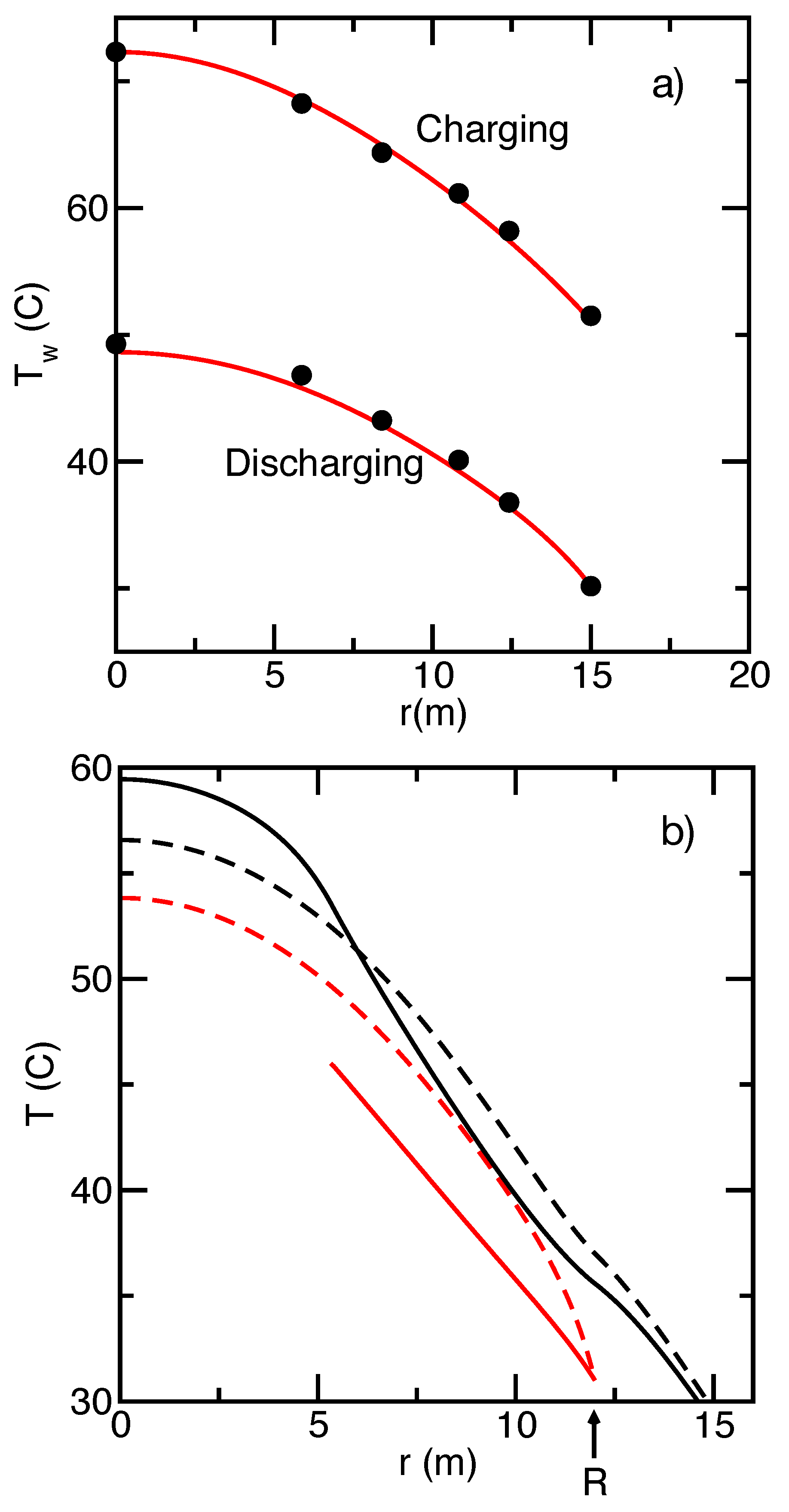
3.1. Description of Drake Landing data
3.2. Exploration of Potential Improvements to Model
- (i)
- A nonuniform borehole spacing, treated via an r-dependent w. Conservation of water then requires that . Several possible shapes of were tried, including both increasing and decreasing Gaussians, and step-function shapes with either a higher or lower central value of w. A decreasing Gaussian, for example, would describe a borehole spacing that is larger near the edge of the array. None of these shapes increased by more than 2%, thus a constant borehole spacing seems to be nearly optimal.
- (ii)
- Discharging heated water before it reaches the array center. Water entering at is discharged not at , but already at the point defined by at a particular time. Thus, at all times. The varying demand is met by taking . During charging, water enters at and leaves at . could be varied by placing outlet valves at various radii in the array, and adding pipes to connect different circuits at a given radius. This procedure “sculpts” the soil–temperature profile, removing heat preferentially from the edge of the array. This is denoted the “constant-temperature” discharge strategy.
4. Conclusions and Future Work
- (i)
- A conceptually simple and physically transparent model of a BTES array, treating only outward flow of water, heat transfer between soil and water, and thermal diffusion of water, gives an accurate description of the water-temperature dynamics. This physically transparent model, based on Equations (3), (4), (6), (A4), (A11) and (A13), runs quickly and is simple enough that it can be straightforwardly coded within generally available packages such as MATLAB, Fortran, and C. This greatly expands the range of possible users, and simplifies the simulation of new types of system configurations, such as the recently proposed “zone” strategy [22,26]. Application of the model to the Drake Landing BTES installation [4,12] gives a fit to the measured temperature data, for both the long-term trends and more rapid fluctuations, with an rms error of less than 1 C. This quality of fit equals or exceeds those of previous models. The model provides a useful complement to more complete approaches such as TRNSYS [11] and finite-element calculations.
- (ii)
- The model predicts that a modified discharge strategy for water heated by the soil can increase the energy-storage capacity significantly. This strategy involves removing water heated by the array at a point where it has been heated by a fixed degree difference rather than using the conventional approach of removing the water at the array center. This new strategy reduces diffusive losses and increases the energy put into the system during charging. The storage capacity is increased by 25% in systems that are 20% smaller in radius than the Drake Landing one, 15% in systems with twice the borehole density of the Drake Landing system, and 29% in systems with both reduced system size and increased borehole density. This may enhance the practicality of smaller BTES systems, which are particularly sensitive to thermal diffusion. This is an important improvement, since BTES size is limited by available land, and these findings may shift the balance toward smaller systems with a higher density of boreholes. It also enhances the likelihood of a BTES system being practical for a single multiunit building. Since the market for underground thermal energy storage could be several hundred billion dollars in the US alone [1], even small efficiency improvements could be very significant.
- (i)
- The coarse-graining and symmetrization of the borehole field give a description of the temperature field that is in principle less accurate than can be obtained by finite-element simulations. However, finite-element simulations at this point do not appear to be fast enough to treat the rapid flow and temperature fluctuations that occur in typical BTES installations. Therefore, the method presented here seems to be a good choice for describing these rapid variations.
- (ii)
- The coarse-graining of the model means that the identification of points in the model with particular boreholes, for temperature comparisons, is imprecise. However, the temperature variation from borehole to borehole is quite slow, so this is probably not a major concern.
- (iii)
- The model is limited to installations with near-cylindrical symmetry. This is likely not a major limitation, since systems with other symmetries, such as rectangular or triangular, would likely lose more heat by diffusion and thus be less efficient. In principle, a spherical system might have smaller diffusive losses because it minimizes surface area, but this appears to be impossible given that only straight boreholes can be drilled.
- (iv)
- The model is only applicable to installations with a large number of boreholes. In smaller systems, the coarse-graining approximation will not be accurate.
- (v)
- Since the model does not treat water flow in the soil induced by temperature gradients, it is only applicable to cases where this flow has small thermal effects. This is believed the case for the Drake Landing system [16], but further study is needed.
- (vi)
- The model does not treat the effects of changes in individual borehole properties, such as the thermal properties of the U-tubes. It only has a two global parameters describing heat transfer, which are fitted to the experimental data.
- (vii)
- The validity of the assumptions made in embedding the two-dimensional diffusion inside the cylinder into the three-dimensional surrounding soil is not known. However, the insensitivity of the results to the details of the embedding, in particular to the embedding radius, suggests that this is not a large problem.
- (viii)
- The “constant-temperature” discharging approach has been tested only on a scenario based on two constant input temperatures, one for charging and one for discharging. To qualitatively evaluate the effectiveness of the approach in more complicated scenarios, it is worth noting that the importance of the soil-sculpting effect depends strongly on the combination of the exponential decay rate characterizing the convergence of water temperature to the soil temperature, and the cylinder radius. According to Equation (6), this combination is captured by the dimensionless parameter . If discharging is turned on and off frequently, will be enhanced immediately after the times when discharging is turned on, suggesting the the effect will be more important during those times. Thus, the overall effect could to enhance the boost in storage capacity from the constant-temperature discharging scenario, although the effect should be small because it only occurs during the transients before the steady-state is reached.
- (i)
- Systematic testing of the “constant-temperature” discharging approach using more complex input temperatures profiles.
- (ii)
- Inclusion of soil permeability and water flow effects. It may be possible to treat soil permeability via an enhancement of the thermal diffusion coefficient, so that one number treats both thermal diffusion and permeability effects. This should be a useful approximation since a temperature gradient generates a pressure gradient that drives a flow of water, which in turn generates a flow of heat—a process parallel to the direct diffusion of heat. Effects of directed water flow across the entire system could be approximately treated by adding a non-radial component to . For example, for water flow in the x-direction, one could write . Then, starting with an initially circularly symmetric state (), water flow in the x-direction would cause to build up. Once has built up, further water flow would result in feeding back on .
- (iii)
- Relating the global heat-transfer parameters and D to the detailed properties of the boreholes and the pipes. This could be done by fitting the model to more complete results obtained via finite-element methods, for shorter run times and/or smaller systems.
- (iv)
- Further analysis and simplification to obtain an explicit formula for the energy-storage capacity. A reasonable scale for the energy-storage capacity is , where is the average input water temperature during charging, is the average input water temperature during discharging, and V is the volume of the system. This is the energy that would be stored if all of the the soil temperature reached the incoming water temperature, and if the discharging water brought the final soil temperature down to the input water temperature during discharging. It is clearly an overestimate. An accurate expression for the energy-storage capacity for a cylindrical BTES might have the form , where g is a dimensionless function and and are the times spent charging and discharging, respectively. Extensive simulation runs using a model of the type described here, along with further efforts toward simplification, will help pin down the form of this function.
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition | Drake Landing or Baseline Value |
| R | Array radius | 15 m |
| Baseline R | 15 m | |
| Water discharge radius | varies | |
| h | Array height (borehole depth) | 35 m |
| w | Water volume fraction | 0.000206 |
| Water volume specific heat | C | |
| Soil volume specific heat | C | |
| Total water current | Varies | |
| Water current density | Varies | |
| D | Soil thermal diffusion coefficient | |
| Coarse-grained water temperature | Varies | |
| Coarse-grained soil temperature | Varies | |
| Asymptotic soil temperature | ||
| Incoming water temperature in simplified model | , | |
| Outgoing water temperature in simplified model | Varies | |
| Minimum temperature increase in constant-volume discharge strategy | ||
| Time required for water to reach radius r | Varies | |
| Time required for water quasi-steady-state to be reached | 6 h | |
| Time width of discharge peak in simplified model | days | |
| Time of peak discharge in simplified model | years | |
| Start time of discharge in simplified model | years | |
| Stop time of discharge in simplified model | years | |
| Water heat-transfer coefficient | Varies | |
| Soil heat-transfer coefficient | Varies | |
| Steady-state soil heat-transfer coefficient | ||
| Steady-state water heat-transfer coefficient | ||
| Enhancement factor for and | Varies | |
| Power demand at time t in simplified model | Varies | |
| Peak power value in simplified model | Varies |
Appendix A
Appendix A.1. Validity of Equation (1)
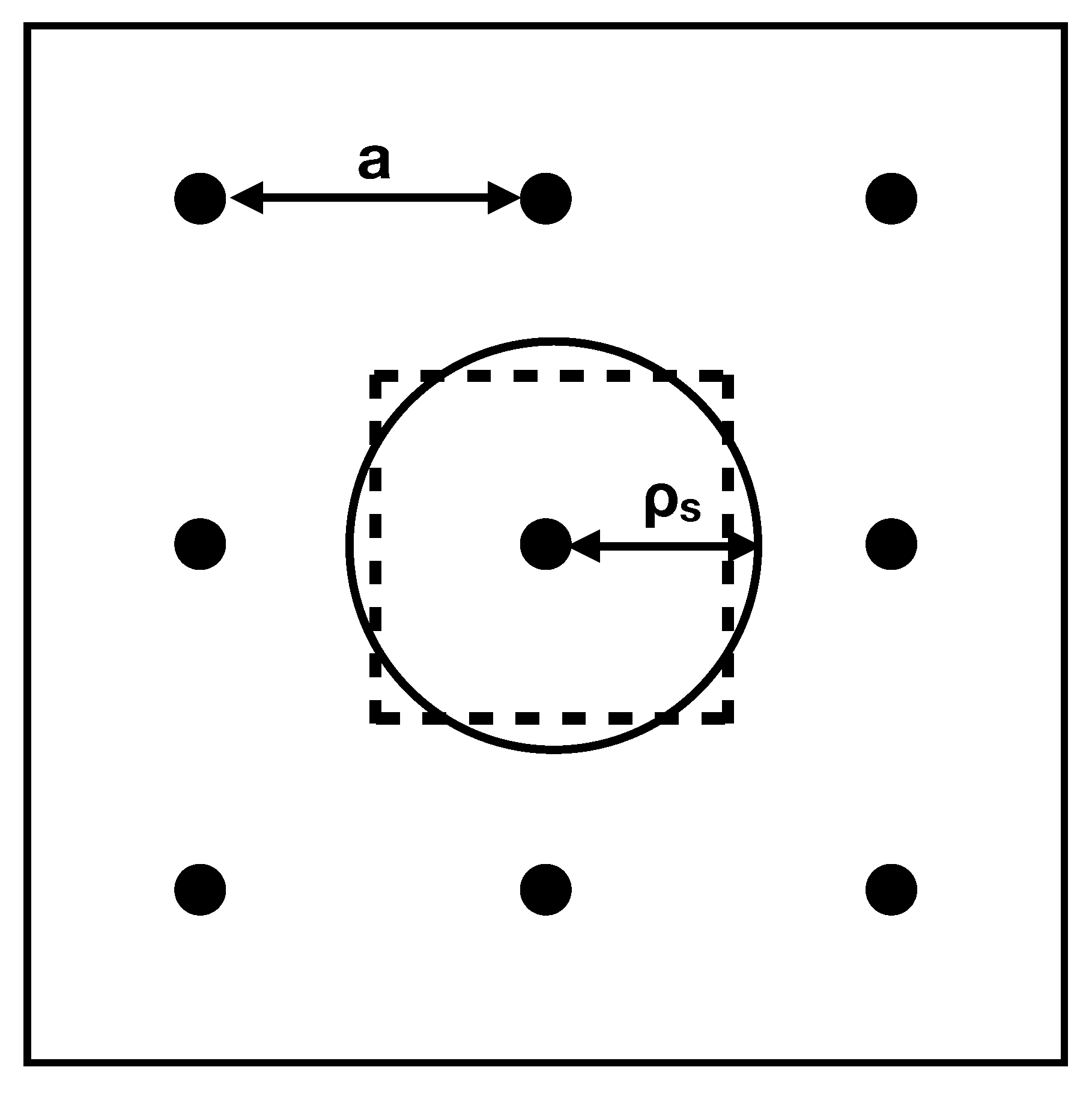
- Discrete approach using actual 3D borehole geometry with boreholes in a square array of spacing a and height h, laid out in circuits starting at the center. If , then the number of boreholes inside r is . Since , the total length of pipe inside r is well approximated as (the factor of 2 accounts for the upward-flowing and downward-flowing pipes in each borehole). The average length of each circuit going out from the center to the radius r is then , where is the number of circuits. If the velocity of water in the pipes is , then the average time for the water to reach r is thus
- Continuous model approach based on radial flow (Equation 1). The flow velocity is obtained from the total current carried by the pipes. The fractional water density is , where the factor of 2 again comes from the “upward” and “downward” pipes in each borehole and is the pipe radius. Then, from , one finds . The average time required to reach r is thus
Appendix A.2. Validity of Equation (2) and Implementation of Equation (3)
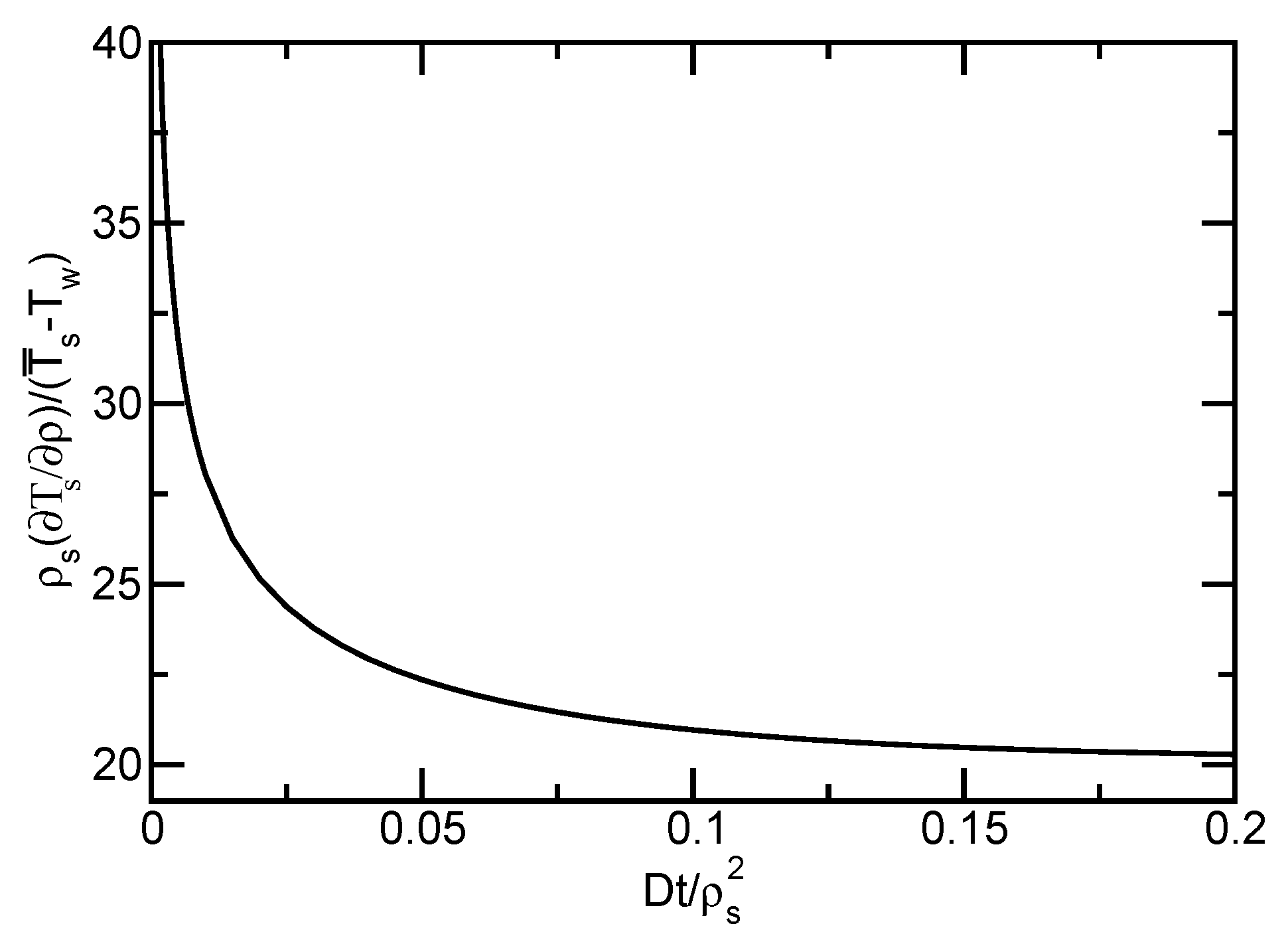
Appendix A.3. Corrections to Cylindrical-Diffusion Model
Appendix A.4. Additional Details of Calculations
- (1)
- Thermal diffusion. The thermal properties of the borehole grout are assumed to be similar to those of the soil. The soil at Drake Landing is probably wet clay [16], with a thermal conductivity of roughly [25]. Cementitious grouts containing twice as much sand as cement have [29]. The grout at Drake Landing has a slightly lower proportion of sand, which increases the thermal conductivity. Thus, should be less than 2.4 , supporting the assumption. Convective heat transfer in the soil is ignored. The analysis of Ref. [16] indicated that thermal diffusion, as opposed to convection, is the dominant mode of heat dispersion.
- (2)
- Numerical procedures and fitting. Equation (6) was integrated by using a local linear approximation to in each interval . This gives an analytic solution on the interval involving an exponential. The end value of on each interval was used as the starting point for the next interval. A step size of m was found to give good convergence. The diffusion equation was solved using a nearest-neighbor approximation to the 2D Laplacian, using a time step of 10 min. The optimal values of D and were found by calculating the root-mean-square error over a 2D mesh of possible values. The total squared error was obtained by adding up the squares of the residuals between the theoretical predictions and the experimental data (97,358 charging data points and 49,870 discharging data points). Data for were taken from the “23-1” sensor; was from the “23-7” sensor in the dataset [12]. Data in Figure 4a were taken from sensors “23-1” to “23-7”.
References
- Jacobson, M.Z.; Delucchi, M.A.; Cameron, M.A.; Frew, B.A. Low-cost solution to the grid reliability problem with 100% penetration of intermittent wind, water, and solar for all purposes. Proc. Natl. Acad. Sci. USA 2015, 112, 15060–15065. [Google Scholar] [CrossRef] [PubMed]
- Rad, F.M.; Fung, A.S. Solar community heating and cooling system with borehole thermal energy storage–Review of systems. Renew. Sustain. Energy Rev. 2016, 60, 1550–1561. [Google Scholar] [CrossRef]
- Lanahan, M.; Tabares-Velasco, P. Seasonal thermal-energy storage: A critical review on BTES systems, modeling, and system design for higher system efficiency. Energies 2017, 10, 743. [Google Scholar] [CrossRef]
- Mesquita, L.; McClenahan, D.; Thornton, J.; Carriere, J.; Wong, B. Drake Landing Solar Community: 10 Years of Operation. In Proceedings of the ISES Solar World Congress 2017, Abu Dhabi, UAE, 29 October–2 November 2017. [Google Scholar]
- Reed, A.; Novelli, A.; Doran, K.; Ge, S.; Lu, N.; McCartney, J. Solar district heating with underground thermal energy storage: Pathways to commercial viability in North America. Renew. Energy 2018, 126, 1–13. [Google Scholar] [CrossRef]
- McDowell, T.P.; Thornton, J.W. Simulation and model calibration of a large-scale solar seasonal storage system. Proc. SimBuild 2008, 3, 174–181. [Google Scholar]
- Chapuis, S.; Bernier, M. Seasonal storage of solar energy in borehole heat exchangers. In Proceedings of the Eleventh International IBPSA Conference, Glasgow, UK, 27–30 July 2009. [Google Scholar]
- Sibbitt, B.; McClenahan, D.; Djebbar, R.; Thornton, J.; Wong, B.; Carriere, J.; Kokko, J. The performance of a high solar fraction seasonal storage district heating system—Five years of operation. Energy Procedia 2012, 30, 856–865. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, P.; Mao, J.; Tang, X.; Li, Z.; Shi, J. A low cost seasonal solar soil heat storage system for greenhouse heating: Design and pilot study. Appl. Energy 2015, 156, 213–222. [Google Scholar] [CrossRef]
- Rad, F.M.; Fung, A.S.; Rosen, M.A. An integrated model for designing a solar community heating system with borehole thermal storage. Energy Sustain. Dev. 2017, 36, 6–15. [Google Scholar] [CrossRef]
- Klein, S.; Beckman, W.; Mitchell, J.; Duffie, J.; Duffie, N.; Freeman, T.; Mitchell, J.; Braun, J.; Evans, B.; Kummer, J.; et al. TRNSYS 17: A Transient System Simulation Program; Solar Energy Laboratory, University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]
- Natural Resources Canada (Ottawa, ON, Canada); CanmetENERGY (1615 Boulevard Lionel-Boulet, Varennes, QC J3X 1P7, Canada). Personal communication, 2018.
- Rad, F.M.; Fung, A.S.; Leong, W.H. Effects of weather parameters on vertical ground heat exchanger design. ASHRAE Trans. 2014, 120, 184–195. [Google Scholar]
- Zhang, R.; Lu, N.; Wu, Y.s. Efficiency of a community-scale borehole thermal energy storage technique for solar thermal energy. In Proceedings of the GeoCongress 2012: State of the Art and Practice in Geotechnical Engineering, Oakland, CA, USA, 25–29 March 2012; pp. 4386–4395. [Google Scholar]
- Pruess, K.; Oldenburg, C.M.; Moridis, G. TOUGH2 User’s Guide Version 2; Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 1999.
- Catolico, N.; Ge, S.; McCartney, J.S. Numerical modeling of a soil-borehole thermal energy storage system. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Başer, T.; Lu, N.; McCartney, J.S. Operational response of a soil-borehole thermal energy storage system. J. Geotech. Geoenviron. Eng. 2015, 142, 04015097. [Google Scholar] [CrossRef]
- COMSOL Inc. COMSOL Multiphysics Version 5.4; COMSOL Inc.: Stockholm, Sweden, 2018. [Google Scholar]
- Welsch, B.; Ruehaak, W.; Schulte, D.O.; Baer, K.; Sass, I. Characteristics of medium deep borehole thermal energy storage. Int. J. Energy Res. 2016, 40, 1855–1868. [Google Scholar] [CrossRef]
- Diersch, H.J.G. FEFLOW: Finite Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: Berlin, Germany, 2013. [Google Scholar]
- Hellström, G.; Sanner, B. Earth Energy Designer; Blocon AB: Lund, Sweden, 2000. [Google Scholar]
- Skarphagen, H.; Banks, D.; Frengstad, B.S.; Gether, H. Design Considerations for Borehole Thermal Energy Storage (BTES): A Review with Emphasis on Convective Heat Transfer. Geofluids 2019, 2019, 4961781. [Google Scholar] [CrossRef]
- Borehole Thermal Energy Storage (BTES). Available online: http://https://www.dlsc.ca/borehole.htm (accessed on 22 November 2019).
- Hellstrom, G. Ground Heat Storage Thermal Analysis of Duct Storage Systems. Ph.D. Thesis, Department of Mathematics Physics, Lund University, Lund, Sweden, 1991. [Google Scholar]
- Chesworth, W. Encyclopedia of Soil Science; Springer: Berlin, Germany, 2007; p. 167. [Google Scholar]
- Borehole Thermal Energy Storage. Available online: https://www.phcppros.com/articles/6989-borehole-thermal-energy-storage (accessed on 18 February 2019).
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Lienhard, J.H. A Heat Transfer Textbook; Courier Corporation: North Chelmsford, MA, USA, 2013. [Google Scholar]
- Allan, M.; Philippacopoulos, A. Performance characteristics and modelling of cementitious grouts for geothermal heat pumps. In Proceedings of the World Geothermal Congress, Kyushu, Tohoku, Japan, 28 May–10 June 2000; Volume 28. [Google Scholar]

| (a) Baseline w value | |||
|---|---|---|---|
| Strategy | |||
| Baseline | 207 | 439 | 666 |
| CT | 259 | 486 | 707 |
| Percent increase | 25% | 11% | 6% |
| (b) Doubled | |||
| Strategy | |||
| Baseline | 364 | 648 | 964 |
| CT | 467 | 775 | 1112 |
| Percent increase | 29% | 20% | 15% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlsson, A.E. Coarse-Grained Model of Underground Thermal Energy Storage Applied to Efficiency Optimization. Energies 2020, 13, 1918. https://doi.org/10.3390/en13081918
Carlsson AE. Coarse-Grained Model of Underground Thermal Energy Storage Applied to Efficiency Optimization. Energies. 2020; 13(8):1918. https://doi.org/10.3390/en13081918
Chicago/Turabian StyleCarlsson, Anders E. 2020. "Coarse-Grained Model of Underground Thermal Energy Storage Applied to Efficiency Optimization" Energies 13, no. 8: 1918. https://doi.org/10.3390/en13081918
APA StyleCarlsson, A. E. (2020). Coarse-Grained Model of Underground Thermal Energy Storage Applied to Efficiency Optimization. Energies, 13(8), 1918. https://doi.org/10.3390/en13081918






