1. Introduction
Hydro power is the largest renewable energy resource in Europe, accounting for 325,000 GWh of generation in 2017, equivalent to approximately 42% of EU renewable energy generation or 10.8% of European total net electricity generation [
1]. Hydro power, in particular through reservoir-based power plants, plays a critical role in providing flexibility to the European power systems. With the EU renewable energy target of 32% by 2030 [
2], the role of hydro power will be even more important in a low-carbon scenario, where the capacity of non-dispatchable electricity sources (mostly wind and solar) will be much higher than today [
3].
Like wind and solar power, hydro power is a climate-dependent energy source. To date, its power generation has been mostly modelled by means of physical models with technical parameters specified for individual power plants. There are several explanations for this approach: (i) modelling tends to be thought of as a bottom-up approach, therefore starting from individual power plants (to e.g., assist with their operations) rather than at the entire country or pan-European level; (ii) the impacts of climate variables on hydro power are varied and complex, and many factors contribute to these impacts such as watershed characteristics, the river flow rate, the evaporation process, and human factors, and hence, using only climate data is not sufficient to predict hydro power generation at the desired accuracy for plant-level operational purposes; (iii) hydro power generation at the European level has only recently started to become publicly available (as further discussed below); (iv) the quality of climate data as provided by reanalysis (i.e., climate reconstructions), and particularly precipitation, has been improving significantly only in recent years.
Wind and solar power play an increasingly important role in a low-carbon energy plan. However, their weather-dependent nature requires a more stable energy source, together with storage solutions, to cope with climate variability. Hydro power is a good candidate with its ability to dispatch or store electricity according to demand. For example, [
4] showed that integrating run-of-river power with wind and solar power, for 12 European areas, increases the penetration rate of wind and solar power by a few to several percentage points.
Moreover, understanding and predicting hydro power generation at a scale larger than individual power plants could be beneficial to Transmission System Operators (TSOs)—the primary role of which is to ensure the balance of power networks at a large scale. Thus, understanding the impacts of climate variability on hydro power can assist with ensuring a stable pan European electricity network in time. In addition, other specialists such as energy traders require and utilize large-scale power production estimations for their bidding. An accessible homogenous hydro power dataset for Europe over several decades, by extending the short periods (normally a few years) of publicly available power generation data, would therefore provide an invaluable input to pan-European network assessment and planning. This is one of the goals of the Copernicus Climate Change Service (C3S) for the Energy Sector (C3S Energy) [
5].
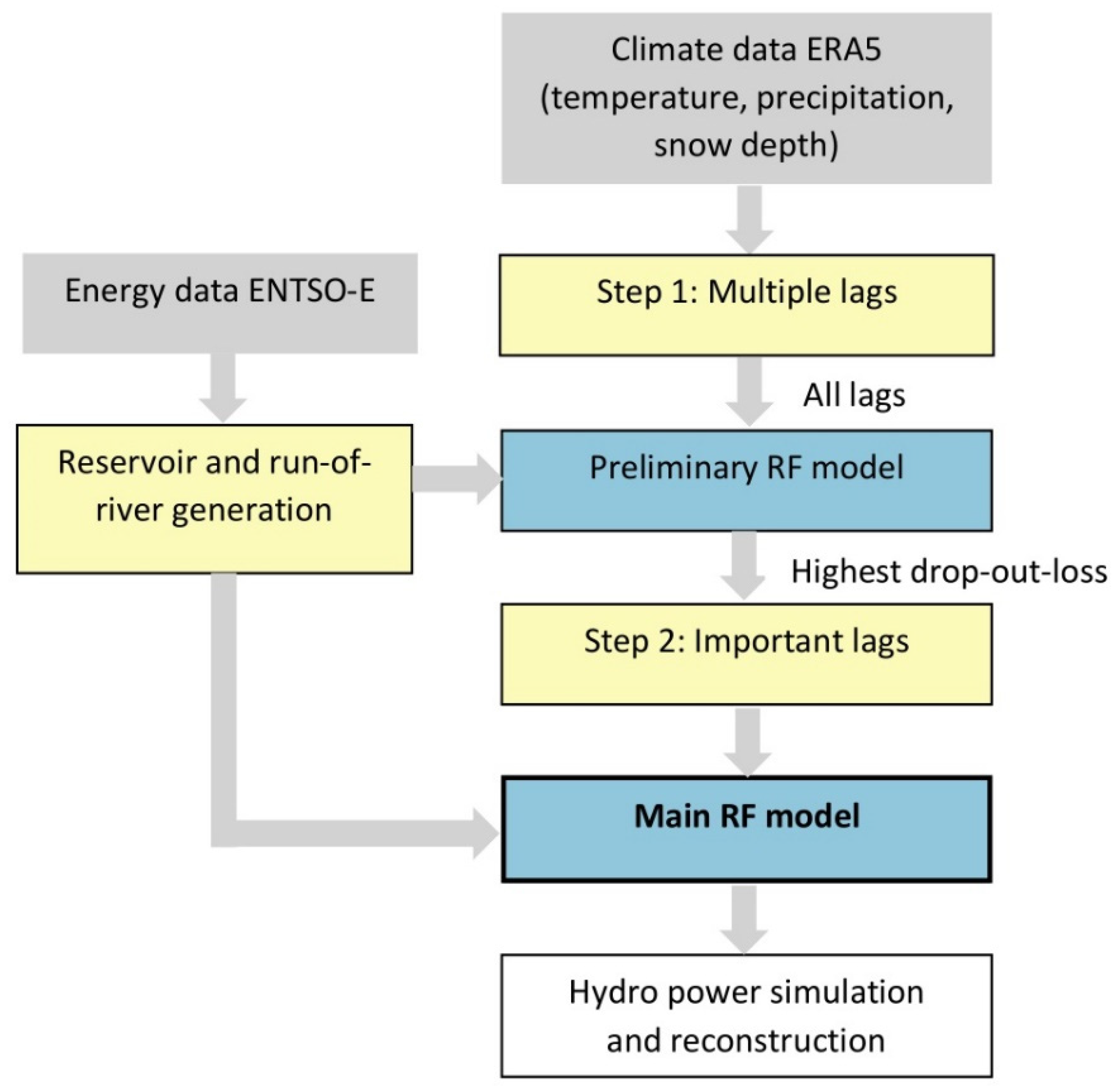
Here, we introduce a dataset of hydro power generation for 12 European countries using a machine learning model, the random forest. While the model we propose is highly simplified and uses only two climate variables (2 metre temperature and precipitation) as predictors, it is capable of reproducing with high accuracy observed power generation data at the country level and at the sub-country level (snow depth was also used for testing purposes as described later, but it is not included in the final model). One of the features of this model is that instead of their instantaneous values (for temperature) or daily accumulated values (for precipitation), we mimic the latency of the system by using their lagged values. The lag time is designed to account for processes which usually take longer than the daily timescale to produce an effect on electricity generation, e.g., snow melting, river run-off and underground water processes. In the case of reservoir-based hydro power production, these relationships are even more complex due to human intervention, which controls electricity demand as well as for other competing uses of water (agricultural, domestic, etc.). In this paper, two methods of lag calculation—optimal lag and multiple lags—are compared to each other and against a baseline model with daily climate values.
Two types of hydro power generation are considered: (i) reservoir-based generation, where water is stored behind a dam to be dispatched when needed; (ii) run-of-river generation, where there is no or minimal storage mechanism. Hydro pump storage was not considered as it contributes only a very small proportion and heavily depends on human management rather than climate conditions. Since energy generation data for specific hydro power plants in Europe are not publicly available, we used the aggregated publicly available data obtained from the European Network of Transmission System Operators for Electricity (ENTSO-E) Transparency Platform [
6]. The focus here is mainly at the country level, a large enough spatial scale to cover relevant climate characteristics such as precipitation or snow contributing to hydro power plants. The country average level is also a relevant scale for many applications (European-scale optimisation models for instance), including adequacy outlooks run by TSOs and European-level investments studies. Naturally, however, the countries considered have different sizes, and hence our model provides an indirect measure of its ability to reproduce hydro power generation at different scales. In addition, however, an explicit sub-country test for Italy is also presented.
This paper is structured as follows.
Section 2 describes the data used in this work and how the machine learning model was setup.
Section 3 shows the model results, including a comparison with measured power data and further validation tests with independent datasets. Finally,
Section 4 presents a summary together with a discussion on how to use the model and dataset efficiently.
3. Results
Our methodology is tested in three different ways. Firstly, a 5-fold cross-validation is applied to compare the optimal lag and multiple lag approaches in modelling hydro power generation. Secondly, the selected best model from the previous test is assessed against independent and longer datasets for three countries (France, Sweden, and Finland) to examine the robustness of the model and its ability to extrapolate in time. Thirdly, the model is also implemented at the sub-country level using the Italian bidding zones to test our methodology at a more local, regional scale.
3.1. The 5-Fold Cross-Validation
The 5-fold cross-validation approach was used to evaluate the performance of the model for reservoir-based and run-of-river generation separately, using five configurations: (1) daily data of temperature, precipitation, and snow depth (Baseline_TATPSD); (2) daily and optimal lags of temperature and precipitation (Opt_TATP); (3) daily and optimal lags of temperature, precipitation, and snow depth (Opt_TATPSD); (4) daily and multiple lags of temperature and precipitation (Mult_TATP); (5) daily and multiple lags of temperature, precipitation, and snow depth (Mult_TATPSD); see
Table 2.
In examining the performance of these five model configurations we also address the following two questions: (1) Could lag times of climate factors improve performance of hydro power model compared to daily values? (2) Can snow depth data be replaced by lagged series of temperature and precipitation?
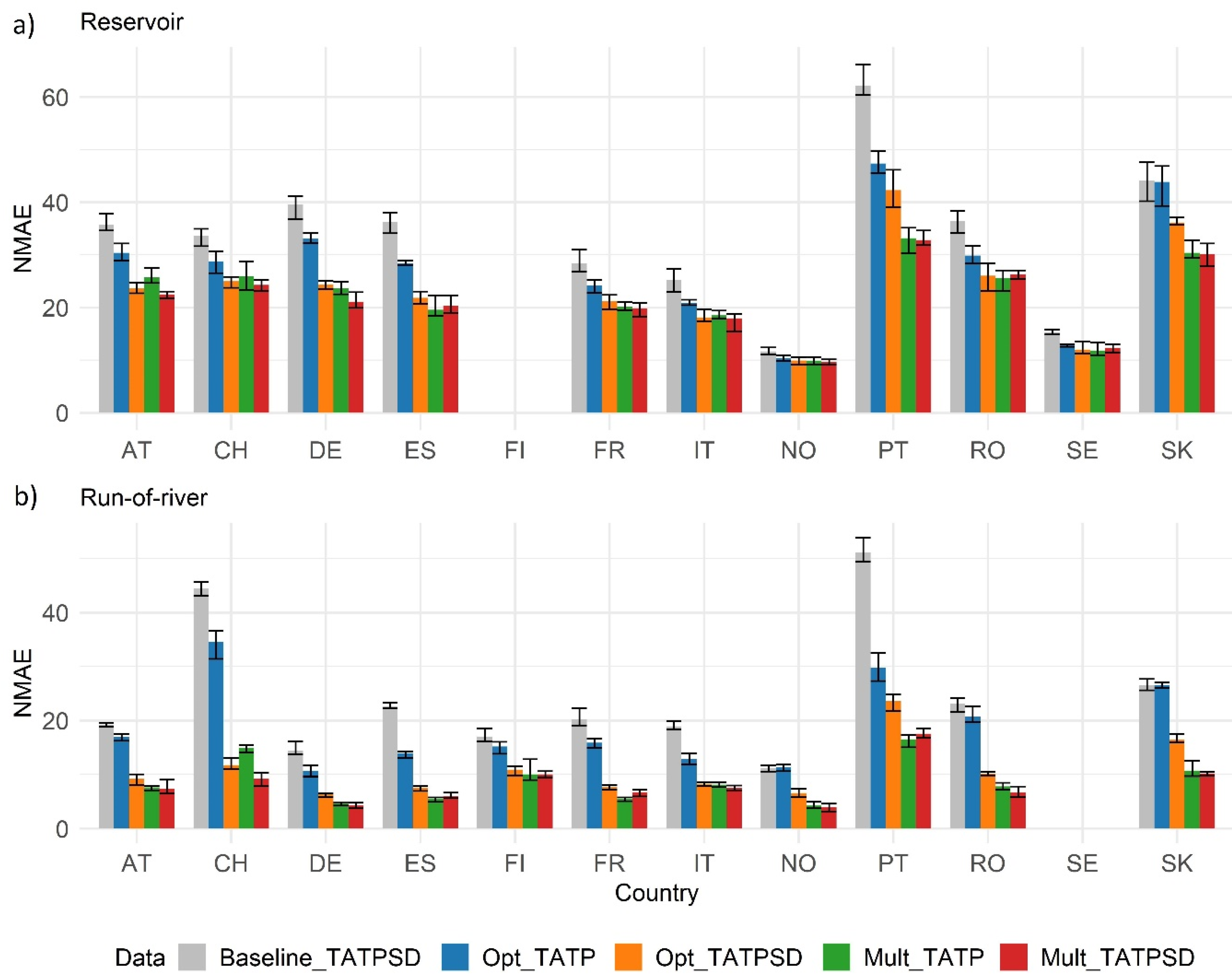
Figure 2 shows the normalised mean absolute error (NMAE) of the five model configurations under consideration. The normalisation is done by dividing the MAE by the average of all observed data. Firstly, we can see that run-of-river (lower panel) is reproduced better than reservoir-based generation (upper panel). This is expected, as run-of-river generation is influenced less by human intervention and management due to limited or none water storage. On the contrary, reservoirs are operated with optimization tools depending on situational factors such as energy market prices. Reservoir-based generation is also mechanically more difficult to simulate when considering only climate variables. The effect of climate variability, e.g., the North Atlantic Oscillation, on reservoir-based hydro power generation is weaker than on inflows due to power plant design and operator decision [
15]. This impact is expected to be higher in run-of-river generation. For the same reason, snow depth impacts are more prominent in run-of-river than in reservoir-based hydro power generation.
Second, it is also noticeable that using lagged values, both optimal lag and multiple lags, improves the model performance in all cases, confirming that climate factors have a delayed effect on hydro power generation.
Figure 2 also shows that adding snow depth (orange bars) improves the optimal lag (blue bars) model significantly in most countries, except for Sweden reservoir-based generation. However, in the multiple lag approach case, snow depth (red bars) improves the model performance only marginally, and in less than half of the countries, compared to when only temperature and precipitation data are used (green bars). Overall, the performance of the multiple lag configuration is essentially the same in most countries regardless of whether snow depth is included or not (statistical significance test results are shown in
Table 3).
With only temperature and precipitation data, the multiple lag approach outperforms the optimal lag approach, even when snow depth is used (
Figure 3). This result indicates that a combination of important multiple lags of temperature and precipitation can efficiently serve as a proxy for the effect of snow melting, and at the same time, importantly, yield a good simulation of hydro power production, as further discussed below.
Since the multiple lags approach is more robust than the optimal lag approach with respect to the length of the training dataset, and since multiple lags of temperature and precipitation are able to capture the impact of snow on hydro power, we retain the multiple lags of temperature and precipitation as our final model (model (4)—green bars in
Figure 2). This is also considering that in the second phase of the C3S Energy service, the same model is applied to climate projections and seasonal forecast, for which snow depth is not always available (and in any case, snow depth quality in long-range predictions is worse than temperature and precipitation).
Table 4 presents the correlation coefficient of the modelled versus observed generation values with the chosen model, resulting from the 5-fold cross-validation process (the cross-validation columns). The mean correlation among all twelve countries is 0.81 for reservoir-based generation, with a range of [0.73; 0.90]; and 0.95 for run-of-river generation, with a range of [0.85; 0.98].
Table 4 also shows the NMAE decrease with respect to the optimal lag model (model 2). The average improvement is 5.99% and 10.22%, respectively, for reservoir-based and run-of-river generation.
Furthermore, a leave-one-out test was also implemented in order to assess the model performance using an alternate assessment procedure. Each year in the period 2015–2019 was left aside for validating the model trained on the rest of the dataset. The average results of this leave-one-out test are presented in
Table 4 and are compared to the 5-fold cross-validation method. Overall, the model performance is considerably lower when using the leave-one-out test, and again lower in reservoir-based than in run-of-river generation, with an average correlation of 0.47 and NMAE decrease of 0.53% for reservoir-based, and 0.67 and 3.77% for run-of-river generation, respectively. Nevertheless, some countries are more robust than the others. For example, Spain and Italy perform well under the leave-one-out test. This highlights the fact that not only can the hydrological and climate regimes vary from year to year, but the interannual variability in hydro power generation strongly depends on non-climate factors related to power-dispatching decisions which depend on a variety of factors such as electricity price, competing water usage, and power plant maintenance regimes. Further discussion on the ability of our model to extrapolate hydro power beyond the training dataset using independent datasets is presented in
Section 3.2.
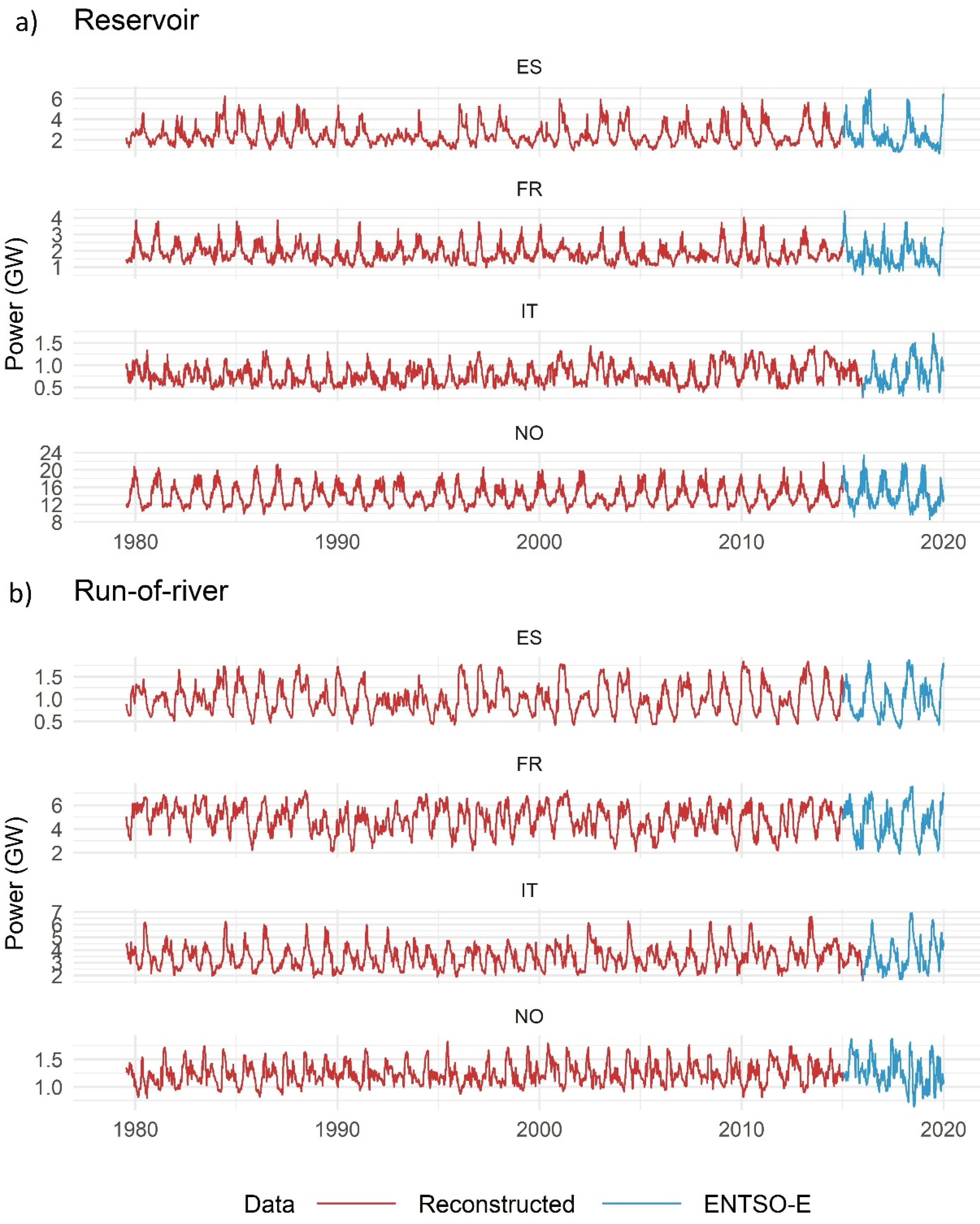
In order to produce a dataset of hydro power generation for the twelve countries of interest, country-specific models were trained again with the full observed ENTSO-E dataset for the period 2015–2019 using model 4 (multiple lags with temperature and precipitation). The model was then used with the full ERA5 time series data to extend the hydro power generation simulation to the historical period from 1979 to present—so called reconstructed data. While the focus of this paper is on the historical reconstruction over the past ca. 40 years, it is worth noting that the C3S Energy service is also developing similar datasets for two other cases: seasonal forecasts, up to six months ahead, and projections, up to 2100. The same model developed for the historical period is implemented in both of these cases.
Figure 4 illustrates time series of reconstructed hydro power generation using our selected model configuration compared against data from ENTSO-E for the four countries selected as representatives. The output data show similar patterns of seasonality as ENTSO-E data but somewhat smoother, especially in the case of reservoir-based generation, due to operation regulation according to electricity demand. However, we are confident that the main features of hydro power generation are well reproduced, in particular high- and low-generation events corresponding to low-frequency precipitation variability.
3.2. Validation with Independent Datasets
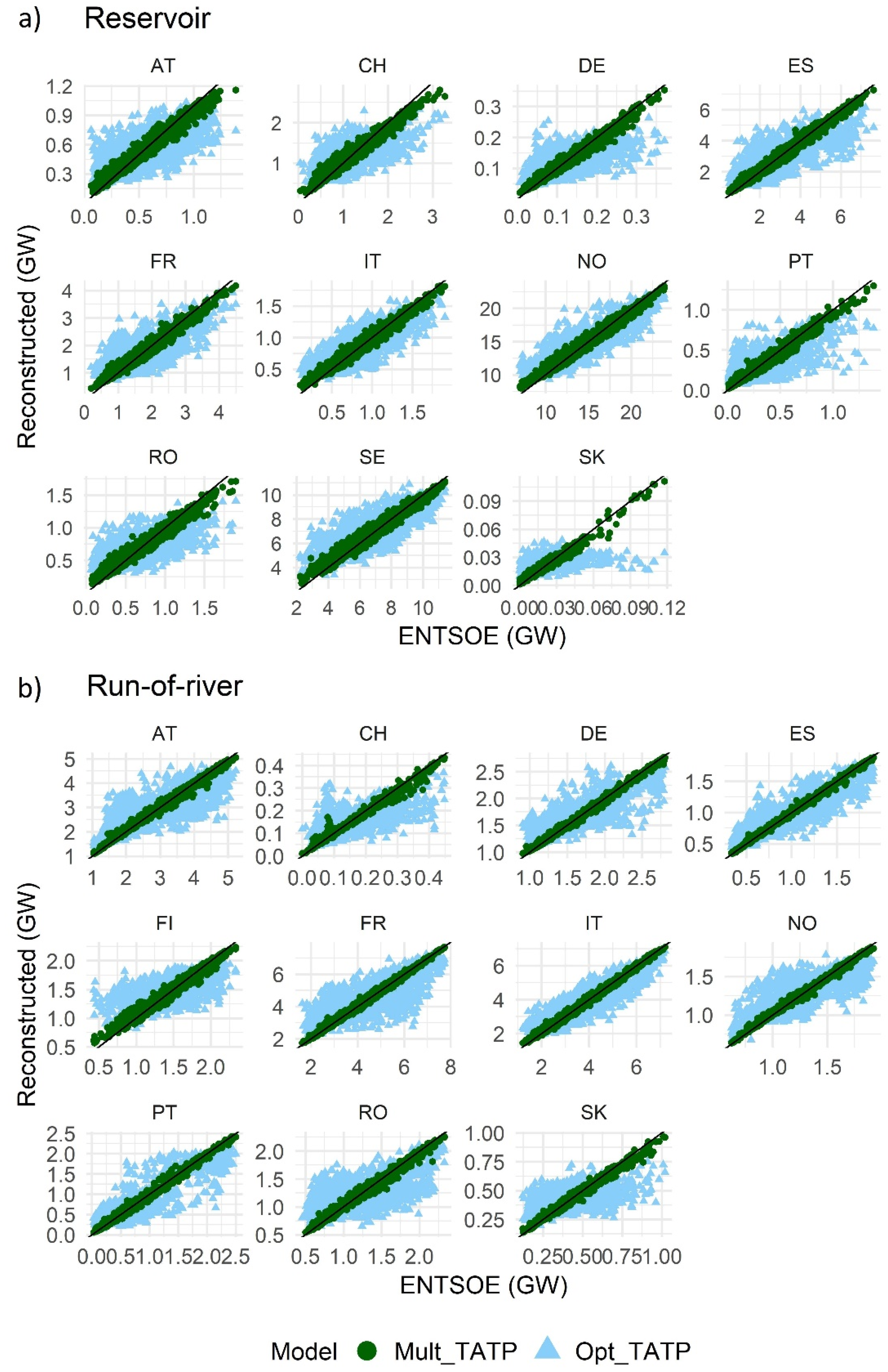
Although the two-step random forest model showed good performance, especially for Spain (Pearson’s correlation coefficient of 0.90 for reservoir-based and 0.98 for run-of-river generation from 5-fold cross-validation), this validation method usually gives optimistic results [
16]. One possible explanation is that despite being randomly permuted, the validation dataset in each cross-validation is still an average of multiple random samples from the same dataset, and thus the prediction is not totally independent of the training set. As the model’s skill for extrapolation is important in producing historical (and eventually seasonal forecast, and projections) data, we conducted further tests with additional datasets from Réseau de Transport d’Électricité (RTE) for French hydro power generation in 2013–2014, and from Open Power System Data (OPSD) [
17] data for Finland and Sweden in 2010–2014 (
Figure 5).
Considering that the model only uses climate data and does not include any power plant information, these reconstructed time series show very encouraging results (see correlation coefficient indicated on each subplot). Specifically, the reconstruction for run-of-river generation captures the year-to-year variability in hydro power production remarkably well, with relatively high correlations (0.65 for FI, and 0.83 for FR) and relatively low NMAE values (13.7 for FI, and 10.2 for FR). While the performance is lower for reservoir-based hydro power generation, the difference is not large and, in any case, it is in line with that seen during the training period. The fact that our model is able to reconstruct the interannual variability of hydro power production reasonably well can be a very useful piece of information for system adequacy and extreme events assessments.
We can again see that the model performs better for run-of-river compared to reservoir-based generation here in the case of France. Reservoir time series have noticeably higher short-term variations. This is most likely due to reservoir operations managed by plant dispatchers to account for daily energy market dynamics. A model based on only climate data cannot capture these features, and hence the smoother predicted time series. However, the model is able to simulate the upward and downward trends of both hydro power generation types quite well, but it tends to underestimate the amplitude of the signal. As with every statistical model, it can only reproduce features that are embedded in the training period and, as such, it is limited in its ability to reproduce more extreme episodes. This is a common limitation of non-physical models which do not perform well in extreme cases.
3.3. The Sub-Country Level
One limitation of modelling hydro power is that averaging over a large domain such as country-size can smooth the characteristics of hydro power generation and neglect many physical aspects of the relevant water pathways. For instance, the river flow providing water for a given hydro power plant may come from a river basin in a neighbouring country and is therefore not considered. In addition, we consider country average temperature and precipitation, which could be a rough approximation, as a particular power plant will receive only water falling in the surrounding area, and not from the entire country. However, it is also the case that these considerations are very much country dependent, and different extensions and orography would need to be properly assessed in order to draw stronger conclusions.
To estimate the impact of geographical scales on our model, here, we test the model using the six Italian geographical bidding power zones. A geographical bidding zone is defined by ENTSO-E as a geographical area where market participants are able to exchange energy without transmission capacity allocation. Generation data at the bidding zone level is also available on the ENTSO-E Transparency Platform.
We chose Italy due to several factors. Firstly, only a few European countries have multiple bidding zones (for most of the countries, the bidding zone coincides with the country borders). Secondly, the Italian bidding zones provide a good mix of different installed hydro power capacities, orographic features, climatic characteristics, and zone sizes.
Italian bidding zones can be represented with an aggregation of nomenclature of territorial units for statistics [
18] (NUTS) level 2 (or NUTS-2) regions. Since temperature and precipitation are provided at NUTS-2, these are first averaged (using a simple average; area-weights are assumed to be second-order effects) according to the bidding zone aggregation (see
Table 5). To assess the spatial scale effect, we aggregated the bidding zones into regions and country level and trained model accordingly to test its performance in these cases. The regional scale, i.e., North (IT_North in
Table 5) and South Italy (the remaining 5 zones in
Table 5), is based on geography and especially the different distribution of hydro power plants in Italy, with the North of Italy presenting the majority of the hydro power production. One of the corollaries is that the North and South of Italy are also considered as the main geographical subdivision of Italy as used in power trading (a discussion on the configuration of Italian bidding zones can be found at the following URL:
https://docstore.entsoe.eu/Documents/cep/implementation/BZ/A4_BZR_ED_CSI_SQ.pdf). Areas corresponding to bidding zones as well as to regions and their average generation are shown in
Table 5.
Figure 6 shows the NMAE of the model implemented in these spatial scales. In general, the performance of the model for individual bidding zones is comparable to, or slightly worse than, that at the country level. Notable differences are for IT_SUD and IT_SICI, but especially for IT_SARD, for run-of-river generation. The main reason for this low performance is the very low installed capacities in these zones. Noting that the model performance at the country average level is very good (NMAE less than 10%) and therefore it is difficult to improve on it. It is also interesting to see that when bidding zones are aggregated in North and South Italy, the results are similar to the country average. These sub-country results demonstrate that a highly simplified hydro power model such as that used in our study has the potential to effectively simulate hydro power, therefore offering a credible complement to much more sophisticated physical models.
4. Summary and Discussion
We developed a new dataset of hydro power generation for reservoir-based and run-of-river generation using only two essential climate variables—temperature and precipitation—and a machine learning methodology, based on random forests, selected for its flexibility and accuracy. Model training was performed over the period 2015–2019. The reconstruction dataset was then developed for the historical period from 1979 to present, corresponding to the available period of the ERA5 climate reanalysis dataset (it will also be extended to seasonal forecast and climate projections). Snow melt has an important impact on river flow and, thus, on hydro power generation, but it is generally not available in seasonal climate forecast or climate projection outputs. Therefore, an approach was suggested using lagged values of temperature and precipitation to replace snow depth in the model. After testing two approaches with the optimal lag and multiple lags of temperature and precipitation, we found that multiple lags with a two-step approach to select the most important variables for each country and each hydro power type produced the best performance.
In general, the multiple lag approach yields better results than the optimal lag approach, particularly for run-of-river hydro power generation. In this case, we obtained a high average correlation of 0.95 and an average NMAE decrease of 10.23% compared to the optimal lag approach. Meanwhile, the model performance is expectedly lower in the case of reservoir hydro power generation, but still with a high correlation of 0.81 and an NMAE decrease of 5.98%. We also demonstrated that the inclusion of snow depth as an additional predictor does not, in general, lead to statistically better results. This model is inevitably subject to limitations.
An important limitation is that our methodology assumes constant installed capacities in all countries—both during training and reconstructed periods. This assumption does not take into account the periods in which plants are not available (e.g., for maintenance or due to temporary failures): in those periods, the actual generation data shows a drop that is not caused by meteorological factors. This information would be necessary to achieve better training of the machine learning models, thus for improving the simulation of the generation. In particular, in a cross-validation approach like that detailed in
Section 3.1, this may explain some differences between the training and validation periods. Assuming constant installed capacity also ignores variations in other sources of energy. For instance, a newly installed wind farm might make the operator reduce electricity generated from a reservoir, but this effect is not captured by our model as it is not weather driven.
In addition, due to the complexity of hydro power plants, a statistical model cannot outcompete a physical model, especially when extrapolating to periods with climate characteristics outside of the observed range. Further, in our case, the training period is relatively short with five-year data for the period 2015–2019. In any case, one should keep in mind that the primary objective, developed in the context of C3S Energy is to provide a realistic method which can be readily implemented with publicly accessible datasets such as ENTSO-E. For example, [
19] has produced a time series of reservoir-based generation in China using basin and power plant information. However, it is the first time a dataset of hydro power, which is also complemented by electricity demand, wind and solar power, has been produced at the European scale for both historical and future periods [
20]. It is important to emphasize that the approach taken by C3S Energy is to model electricity demand and power generation over the ca. 40 year period, 1979 to present, assuming a fixed EU energy system based on available power data, which normally cover the last several years. From this dataset, actual energy generation and demand can be derived using simple arithmetic to rescale mean energy demand and generation based on actual installed capacity and annual energy consumption.
In terms of data quality, there is confidence in the model’s input data: [
21] shows that precipitation and temperature variables from the ERA5 dataset can produce results equivalent to observational data in hydrological modelling from North-American catchments; [
6] on the ENTSO-E dataset also highlights that it is the most ambitious global open source dataset for energy data.
Hydro power depends strongly on water availability, for which five years of training data could not accurately represent all the impacts of interannual climate variability. Bootstrap aggregation in random forest helps to avoid high-variance estimators from decision trees, i.e., a small change in input can alter the prediction results. Nonetheless, the fact that the model simulates hydro power production well (relatively low NMAEs and high correlations), especially over the extended periods available for France, Sweden and Finland, demonstrates that even a simple model, trained over a relatively short period, can capture essential (interannual) variability processes. It is also planned to update the models on a yearly basis, when an additional year of ENTSO-E data becomes available. This extension of the model training period is expected to improve the quality of the models over time.
Although random forest is known for its robustness against outliers, this feature reduces its ability to extrapolate to extreme events or to values outside of the training dataset, as shown in
Section 3.2. In addition, when input variable deviation is large compared to their mean value, it is more difficult to differentiate between signal and noise, hence the lower performance in countries with smaller installed capacity such as run-of-river generation in Switzerland or both hydro power types in Slovakia.
Nevertheless, the model performance is encouraging, considering its simplicity and versatility. The presented results will be available in the C3S Climate Data Store later in 2020 and can serve as a benchmark for further studies on the impact of climate variability on hydro power.