An Insight into Practical Solutions for Electric Vehicle Charging in Smart Grid
Abstract
1. Introduction
2. EV Battery Charging Strategies and Infrastructure
3. EV Charging Strategies
3.1. Impact of Uncoordinated Charging—High EV Penetrations
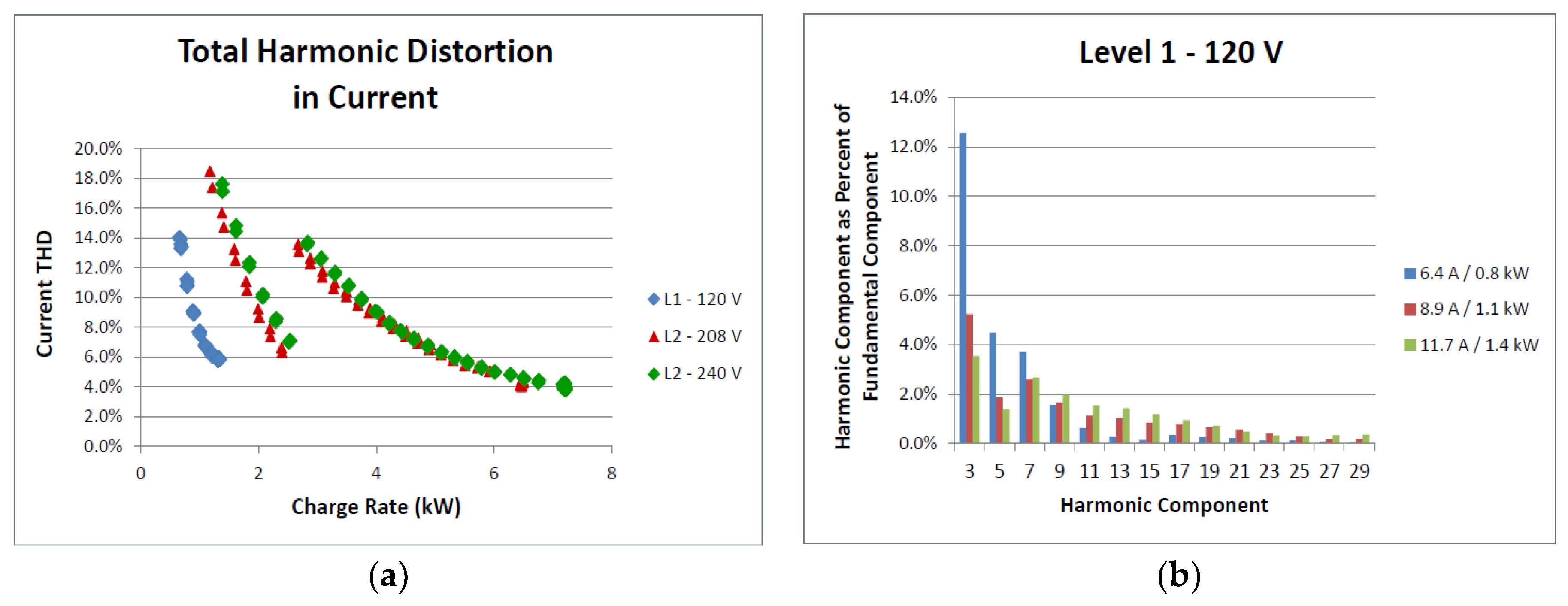
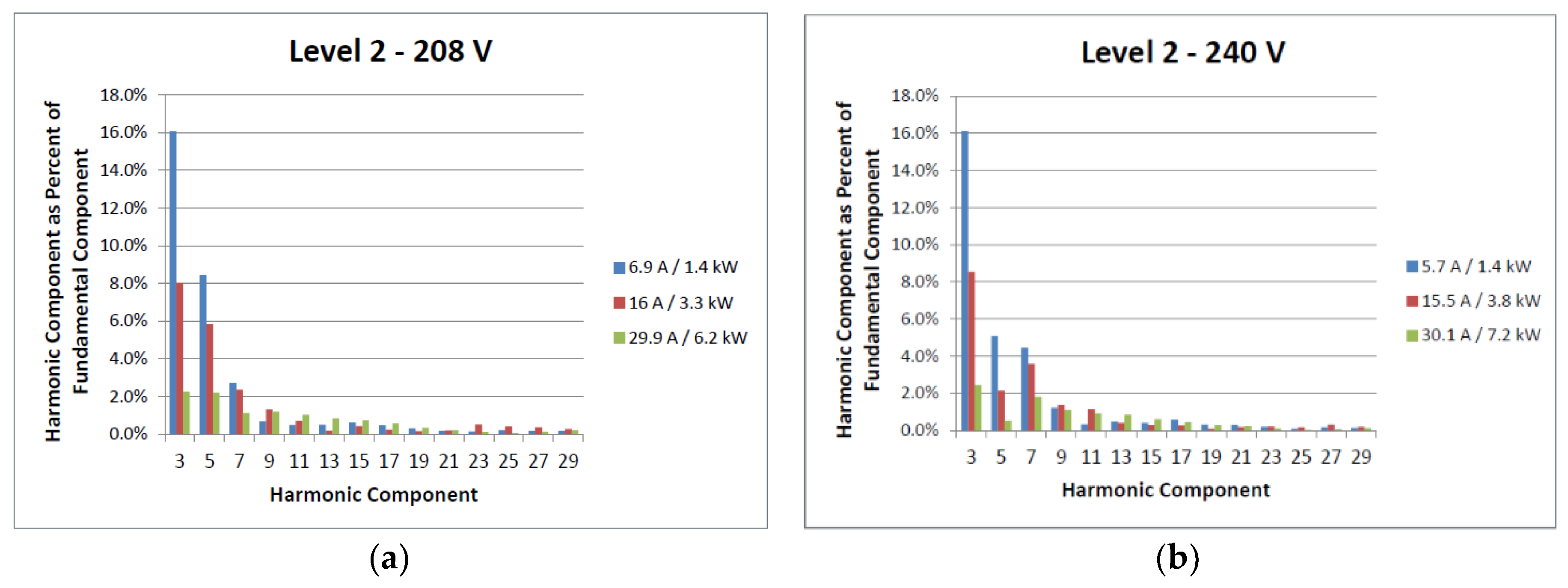
3.1.1. Power Quality
3.1.2. Voltage Stability
3.1.3. Peak Demand
3.1.4. Reliability
4. EV Coordinated Charging Approach
- Introducing the infrastructure, such as large-scale batteries, vehicle-to-grid (V2G) opportunities, or increased network capacity [35].
- Control chargers installed in the car: Many EV manufacturers have developed their own controlled device to control their charging and prevent any high peak prices, such as Nissan Leaf. Controlling the charging device can also be done remotely by sending signals to the charger.
- EV Coordination: Controlling/introducing a different tariff for peak hours and off-peak hours to the customers and encouraging people to charge their vehicle when required during off-peak hours. This can be done dynamically/statically or by smart charging, where the active control of the EV charging can be handled by the utilities or EV charging provider. Smart charging is centralized or decentralized.
- EV coordination (load sifting with the integration of RERs) is another possible solution that has been constantly proposed and discussed. There have been many studies in EV controlled charging strategies with the integration of wind generation or RERs.
- Intelligent/smart controlling scheme is another approach. Load shedding and load shaving have been discussed and investigated as possible solutions.
4.1. Online MSS Optimization with EV Battery Chargers
4.2. Online GA Optimization with EV Battery Chargers
4.3. Application of SSC and Optimal Dispatch in Online EV MSS Optimization
4.4. Problem Formulation of the Objective Function Optimization Problems
5. Comparative Analysis
- The uncontrolled EV approach leads to high THDv and voltage deviations beyond the acceptable standard limits, especially with high EV penetration. In this controlled strategy, EV owners can easily charge their vehicles at any time.
- The online GA optimization with EV battery chargers: This approach was tested and implemented on the modified system. As shown in Table 6, GA optimization is not able to fully charge the EVs till 8am in the morning and therefore all EVs will not be ready for their trip in the morning. The computational time of this approach is slower than the MSS optimization strategy. However, this approach is still able to satisfy the grid power quality and grid performance requirement even for high EV penetrations.
6. Conclusions and Future Directions
- The review analysis on EV battery infrastructure and charging technologies presents the basics of the EV structure, EV industry, and connection to the power grid. The study also explored the existing challenges and opportunities associated with uncontrolled EV charging methods.
- The uncontrolled charging of EV batteries can lead to severe impacts on the performance, power quality, and stability of the power network. The paper studied the important issues associated with uncontrolled EV charging and the main grid factors affected by this EV charging method.
- To address the existing issues and number of priority problems, the research provided an overview of practical solution approaches and enables the readers to determine the relevant research works and their own practices.
- The suitability and validity of the solution approaches were discussed and compared in a practical case study.
Author Contributions
Funding
Conflicts of Interest
References
- Grid Modernization and Smart Grid. 2007. Available online: https://www.energy.gov/oe/activities/technology-development/grid-modernization-and-smart-grid (accessed on 19 February 2020).
- Preparing the Grid for the Uptake of Electric Vehicles. Available online: https://www.lek.com/insights/ei/preparing-grid-uptake-electric-vehicles (accessed on 18 February 2020).
- Global EV Outlook 2018. Available online: http://centrodeinnovacion.uc.cl/assets/uploads/2018/12/global_ev_outlook_2018 (accessed on 18 February 2020).
- Stijn, V.; Claessens, B.; Hommelberg, M.; Holvoet, T.; Deconinck, G. A Scalable Three-Step Approach for Demand Side Management of Plug-in Hybrid Vehicles. IEEE Trans. Smart Grid 2013, 4, 720–728. [Google Scholar]
- Basu, M. Optimal Dispatch in Smart Power Grids with Partially Known Deviation. Master’s Thesis, In Electrical and Computer Engineering, The University of Iowa, Iowa City, IA, USA, 2015. [Google Scholar]
- Chen, H.; Guo, Z.; Xin, Y.; Zhao, Y.; Jia, Y. Coordination of PEV Charging across Multiple Stations in Distribution Networks Using Aggregate PEV Charging Load Model. In Proceedings of the 2017 International Smart Cities Conference (ISC2), Wuxi, China, 14–17 September 2017. [Google Scholar]
- Sergio, B.; Lamonaca, S.; Scala, M.L.; Rotondo, G.; Stecchi, U. Load control through smart metering on distribution networks. In Proceedings of the IEEE Bucharest Power-Tech, Bucharest, Romania, 28 June–2 July August 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Deilami, S.; Masoum, A.S.; Moses, P.; Masoum, M.A.S. Realtime Coordination of Plug-In Electric Vehicle Charging in Smart Grids to Minimize Power Losses and Improve Voltage Profile. IEEE Trans. Smart Grid 2011, 2, 456–467. [Google Scholar] [CrossRef]
- Bahrami, S.; Wong, V.W.S.; Huang, J. An Online Learning Algorithm for Demand Response in Smart Grid. IEEE Trans. Smart Grid 2017, 9, 4712–4725. [Google Scholar] [CrossRef]
- Ma, J.; Deng, J.; Song, L.; Han, Z. Incentive mechanism for demand side management in smart grid using auction. IEEE Trans. Smart Grid 2014, 5, 1379–1388. [Google Scholar] [CrossRef]
- Fakeha, S.; Manisa, P.; Rahman, S. Demand management to mitigate impacts of plug-in electric vehicle fast charge in buildings with renewables. Energy 2017, 120, 642–651. [Google Scholar]
- Pouresmaeil, E.; Mehrasa, M.; Catalao, J.P.S. A multifunction control strategy for the stable operation of DG units in smart grids. IEEE Trans. Smart Grid 2015, 6, 598–607. [Google Scholar] [CrossRef]
- Zhang, Y.; Cai, L. Dynamic Charging Scheduling for EV Parking Lots with Photovoltaic Power System. IEEE Access 2018, 6, 56995–57005. [Google Scholar] [CrossRef]
- Masoum, A.S.; Deilami, S.; Masoum, M.A.S.; Abu-Siada, A.; Islam, S.M. Overnight Coordinated Charging of Plug-In Electric Vehicles based on Maximum Sensitivities Selections. In Applied Engineering Sciences; Deng, W., Ed.; CRC Press: London, UK, 2014; pp. 65–70. [Google Scholar]
- Masoum, A.S.; Deilami, S.; Moses, P.S.; Masoum, M.A.S.; Abu-Siada, A. Smart Load Management of Plug-In Electric Vehicles in Distribution and Residential Networks with Charging Stations for Peak Shaving and Loss Minimization Considering Voltage Regulation. IET Proc. Gener. Transm. Distrib. 2011, 5, 877–888. [Google Scholar] [CrossRef]
- Deilami., S.; Masoum, A.S.; Jabalameli, N.; Masoum, M.A.S. Optimal Scheduling of LTC and Switched Shunt Capacitors in Smart Grid with Electric Vehicles and Charging Station. In Proceedings of the 8th International Conference on Electrical and Electronics Engineering (ELECO 2013), Bursa, Turkey, 28–30 November 2003; pp. 162–166. [Google Scholar]
- Deilami, S. Online Coordination of Plug-In Electric Vehicles Considering Grid Congestion and Smart Grid Power Quality. Energies 2018, 11, 2187. [Google Scholar] [CrossRef]
- Jiang, C.; Torquato, R.; Salles, D.; Xu, W. Method to assess the power-quality impact of plug-in electric vehicles. IEEE Trans. Power Deliv. 2014, 29, 958–965. [Google Scholar] [CrossRef]
- Staats, P.T.; Grady, W.M.; Arapostathis, A.; Thallam, R.S. A statistical analysis of the effect of electric vehicle battery charging on distribution system harmonic voltages. IEEE Trans. Power Deliv. 1998, 13, 640–646. [Google Scholar] [CrossRef]
- Gómez, J.C.; Medhat, M.M. Impact of EV battery chargers on the power quality of distribution systems. IEEE Trans. Power Deliv. 2003, 18, 975–981. [Google Scholar]
- Basu, M.; Gaughan, K.; Coyle, E. Harmonic distortion caused by EV battery chargers in the distribution systems network and its remedy. In Proceedings of the 39th International Universities Power Engineering Conference, Bristol, UK, 6–8 September 2004; pp. 1–6. [Google Scholar]
- Engel, H.; Russell Hensley, R.; Shivika Sahdev, S. Charging Ahead: Electric Vehicle Infrastructure Demand. Available online: https://www.mckinsey.com/industries/automotive-and-assembly/our-insights/charging-ahead-electric-vehicle-infrastructure-demand (accessed on 19 February 2020).
- Watson, N.R.; Watson, J.D.; Watson, R.M.; Sharma, K.; Miller, A. Impact of Electric Vehicle Chargers on a Low Voltage Distribution System. In Proceedings of the EEA Conference & Exhibition, Wellington, New Zealand, 24–26 June 2015; Available online: http://hdl.handle.net/10092/12059 (accessed on 19 February 2020).
- Ronanki, D.; Kelkar, A.; Williamson, S.S. Extreme Fast Charging Technology—Prospects to Enhance Sustainable Electric Transportation. Energies 2019, 12, 3721. [Google Scholar] [CrossRef]
- SAE Electric Vehicle, 2010–2017. Available online: http://www.fveaa.org/fb/J1772_386.pdf (accessed on 19 February 2020).
- Yilmaz, M.; Krein, P.H.T. Review of Battery Charger Topologies, Charging Power Levels, and Infrastructure for Plug-In Electric and Hybrid Vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Vasiladiotis, M.; Rufer, A.; Béguin, A. Modular converter architecture for medium voltage ultra-fast EV charging stations: Global system considerations. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–7. [Google Scholar]
- Gao, Y.; Zhang, X.; Cheng, Q.; Guo, B.; Yang, J. Classification and Review of the Charging Strategies for Commercial Lithium-Ion Batteries. IEEE Access 2019, 7, 43511–43524. [Google Scholar] [CrossRef]
- Alam, M.M.; Mekhilef, S.; Seyedmahmoudian, M.; Horan, B. Dynamic Charging of Electric Vehicle with Negligible Power Transfer Fluctuation. Energies 2017, 10, 701. [Google Scholar] [CrossRef]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid—The new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2011, 14, 944–980. [Google Scholar] [CrossRef]
- Dubey, A.; Santoso, S. Electric Vehicle Charging on Residential Distribution Systems: Impacts and Mitigations. IEEE Access 2015, 3, 1871–1893. [Google Scholar] [CrossRef]
- Masoum, M.A.S.; Fuchs, E.F. Power Quality in Power Systems and Electrical Machines, 2nd ed.; Elsevier: Amsterdam, The Netherlands; Academic Press: Burlington, MA, USA, 2015. [Google Scholar]
- Steady State Vehicle Charging Fact Sheet: BWMi3. Available online: https://avt.inl.gov/sites/default/files/pdf/fsev/SteadyStateLoadCharacterization2014BMWi3.pdf (accessed on 17 February 2020).
- Idaho National Laboratory. Available online: https://inl.gov/article/inl-releases-new-open-source-software-projects/ (accessed on 26 March 2020).
- Managing the Impacts of Renewably Powered Electric Vehicles on Distribution Networks. Available online: https://arena.gov.au/assets/2019/03/managing-the-impacts-of-renewably-powered-electric-vehicles-on-distribution-networks.pdf (accessed on 12 February 2020).
- Zhang, M.; Zheng, J.H.; Wang, W.Z.; Dai, M.T. Research on static voltage stability based on EV charging station load modelling. In Proceedings of the 2011 International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of Electric Vehicle Charging Station Load on Distribution Network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Kong, P.Y.; Karagiannidis, G.K. Charging Schemes for Plug-In Hybrid Electric Vehicles in Smart Grid: A Survey. IEEE Access 2016, 4, 6846–6875. [Google Scholar] [CrossRef]
- Deb, S.; Kalita, K.; Mahanta, P. Review of impact of electric vehicle charging station on the power grid. In Proceedings of the 2017 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017. [Google Scholar] [CrossRef]
- Chowdhury, A.; Koval, D. Power Distribution System Reliability: Practical Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Billinton, R.; Alen, R. Reliability Evaluation of Power Systems, 2nd ed.; Plenum: New York, NY, USA, 1994; pp. 400–442. [Google Scholar]
- Zhang, Q.; Zhu, Y.; Wang, Z.; Su, Y.; Li, C. Reliability Assessment of Distribution Network and Electric Vehicle Considering Quasi-Dynamic Traffic Flow and Vehicle-to-Grid. IEEE Access 2019, 7, 131201–131213. [Google Scholar] [CrossRef]
- Bhadra, J.; Chattopadhyay, T.K. Analysis of distribution network by reliability indices. In Proceedings of the International Conference on Energy, Power, and Environment: Towards Sustainable Growth (ICEPE), Shillong, India, 12–13 June 2015; pp. 1–5. [Google Scholar]
- Gaurav Gaur, G.; Mehta, N.; Khanna, R.; Kaur, S. Demand Side Management in a Smart Grid Environment. In Proceedings of the 2017 IEEE International Conference on Smart Grid and Smart Cities, Singapore, 23–26 July 2017. [Google Scholar]
- Khaldi, M.R. Sensitivity matrices for reactive power dispatch and voltage control of large-scale power systems. WSEAS Trans. Circuits Syst. 2004, 3, 1918–1923. [Google Scholar]
- Deilami, S. Online Coordination of Plugged-In Electric Vehicles and Optimal Rescheduling of Switched Shunt Capacitors in Smart Grid Considering Battery Charger Harmonics. IEEE Power Energy Technol. Syst. J. 2018, 5, 148–156. [Google Scholar] [CrossRef]
- Ulinuha, A.; Masoum, M.A.S.; Islam, S.M. Optimal Scheduling of LTC and Shunt Capacitors in Large Distorted Distribution Systems using Evolutionary-Based Algorithms. IEEE Trans. Power Deliv. 2008, 23, 434–441. [Google Scholar] [CrossRef]
- Ladjevardi, M.; Masoum, M.A.S. Genetically optimized fuzzy placement and sizing of capacitor banks indistorted distribution networks. IEEE Trans. Power Deliv. 2008, 23, 449–456. [Google Scholar] [CrossRef]
- Zhang, N.; Liu, D.; Zhao, J.; Wang, Z.; Sun, Y.; Li, Z. A repair Dispatching algorithm based on fog computing in smart grid. In Proceedings of the 28th Wireless and Optical Communications Conference (WOCC 2019), Beijing, China, 9–10 May 2019. [Google Scholar]
- Deilami, S.; Masoum, M.A.S. Optimal Dispatch of LTC and Switched Shunt Capacitors in Smart Grid with Plug-In Electric Vehicles. In Proceedings of the IEEE Power Engineering Society General Meeting PES GM, Vancouver, BC, Canada, 21–25 July 2013; pp. 1–7. [Google Scholar]
- Deilami, S. LTC and Shunt Capacitor Switching in Smart Grid: Sensitivity to Plug-In Electric Vehicle Forecasts. Int. J. Electr. Electron. Data Commun. 2015, 3, 102–106. [Google Scholar]
- Jabalameli, N.; Su, X.; Deilami, S. An Online Coordinated Charging/Discharging Strategy of Plug-in Electric Vehicles in Unbalanced Active Distribution Networks with Ancillary Reactive Service in the Energy Market. Energies 2019, 12, 1350. [Google Scholar] [CrossRef]
- Steady State Vehicle Charging Fact Sheet: Nissan Leaf. Available online: http/avt.inl.gov/sites/default/files/pdf/fsev/SteadyStateLoadCharacterization2015Leaf (accessed on 17 February 2020).
- Civanlar, S.; Grainger, J.J. Volt/Var control on distribution systems with lateral branches using shunt capacitors and voltage regulators part III: The numerical results. IEEE Trans. Power Appar. Syst. 1985, 104, 3291–3297. [Google Scholar] [CrossRef]
- Smart Power Tariff. Available online: https://www.synergy.net.au/Your-home/Manage-account/Solarconnections-and-upgrades (accessed on 19 February 2020).
- IEEE. Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; IEEE Standard; IEEE: New York, NY, USA, 2014. [Google Scholar]
| Publications | Detailed Description/Contribution |
|---|---|
| [1,2,3,4,5,6,7,8] | Smart grid, Grid modernization, Integration of EVs, EV chargers, and infrastructure—Centralized and decentralized controlled algorithm, Challenge, Load control through smart metering |
| [9,10,11] | Demand side management, Three steps- approach (offline/online optimization), online learning, EVs and integration of renewable energy |
| [12,13,14,15,16] | Optimal scheduling of LTC and SSC, Real time coordination of EV charging, EV charging impacts, charging schemes and strategies, Smart Load Management, EVs and integration of renewable energy |
| [17,18,19,20,21] | Power quality concerns, Impact of EV battery chargers on residential networks, Harmonics. |
| [22,23,24,25] | EV charging impacts, charging schemes and strategies, EV Standard SAE 2010-2017 |
| [26,27,28,29,30,31] | Smart grid- Integration of EVs, survey and analysis, Fast charging, Dynamic charging EV charging impacts and mitigation, |
| [32] | Power quality, Harmonics in power systems |
| [33,34] | EV charging fact sheets online datasheet- BWMi3, Idaho national laboratory |
| [35,36,37,38,39,40,41,42,43] | EV charging impacts, charging schemes and strategies, Electric vehicle infrastructure, Fast charging technology, Reliability of power system |
| [44,45,46,47,48,49,50,51,52,53,54] | Optimal scheduling of LTC and SSC, Capacitor sizing, EV charging, Volt/Var control. nonlinear loads in Residential and distribution networks Fuzzy and GA optimization, sensitivity analysis and MSS optimization, EV charging fact sheets online datasheet- Nissan Leaf |
| [55,56] | Price List Standard Fees and charges, IEEE standard 519. |
| EV Type | Input Voltage | Input Current | Typical Use | Charging Time |
|---|---|---|---|---|
| Level l- AC | 120 single phase) | 15 A–1.9 kW | House or office | 10–13 h |
| Level 2- AC | 208–240 Three phase) | 40 A–20 kW | Private or Commercial | 1–3 h |
| Level 3- DC Fast charging | 200–500 (Three phase) | 80 A–40 kW | Public | 0.5–1.44 h |
| Network Level | Typical Size | Charger | 10 EV Charging | 100 EVs Charging |
|---|---|---|---|---|
| Transformers | 50–250 kVA | 7.4 kW/22 kW | 30%–150%/Exceed capacity | Exceed capacity/Exceed capacity |
| Feeders | 5–10 MVA | 7.4 kW/22 kW | 0.7%–1.5%/2%–4% | 7%–15%/22%–44% |
| Zone Substations | 30–60 MVA | 7.4 kW/22 kW | 0.1%–0.2%/0.4%–0.7% | 1.2%–2.5%/4%–7% |
| Index | Definition | Significance |
|---|---|---|
| SAIFI | Units of interruptions over a certain time period per customer | Condition of the system, units of interruption per customer. |
| SAIDI | Average interruption during per customer served | Shows the duration of interruption as the condition of the system. |
| CAIDI | Average interruption time for those customers interrupted over a year | Offers the average outage duration that any given customer would experience. |
| ENS | The total energy not supplied by the system | An indicator of Energy deficiency of the system |
| AENS | Average system load curtailment index | Represent how much energy is not served over a certain time. |
| Harmonic Order | EV | Six-Pulse VFD | PWM-ASD | |||
|---|---|---|---|---|---|---|
| Mag. [%] | Phase [deg] | Mag. [%] | Phase [deg] | Mag. [%] | Phase [deg] | |
| 1 | 100 | 0 | 100 | 0 | 100 | 0 |
| 5 | 2 | −67 | 23.52 | 111 | 23.52 | 111 |
| 7 | 2 | −67 | 6.08 | 109 | 6.08 | 109 |
| 9 | 1.5 | −46 | 4.57 | −158 | 4.57 | −158 |
| 11 | 1.8 | −46 | 4.20 | −178 | 4.20 | −178 |
| THDi | 18.9% | 25.2% | 7.1% | |||
| EV Charging Approach | EV Penetration (%) | Voltage Deviations (%) | THDv at Worst Bus (%) | Number of EVs Left Uncharged |
|---|---|---|---|---|
| Uncontrolled | 32 47 63 | 8.27 13.2 16.1 | 6.3 11.3 15.4 | 0 0 0 |
| GA- Approach | 32 47 63 32 | 0.99 0.99 1.12 0.97 | 5.5 5.4 5.6 5.1 | 0 0 12 0 |
| MSS- Approach | 47 63 | 0.97 0.98 | 5.3 5.3 | 0 0 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deilami, S.; Muyeen, S.M. An Insight into Practical Solutions for Electric Vehicle Charging in Smart Grid. Energies 2020, 13, 1545. https://doi.org/10.3390/en13071545
Deilami S, Muyeen SM. An Insight into Practical Solutions for Electric Vehicle Charging in Smart Grid. Energies. 2020; 13(7):1545. https://doi.org/10.3390/en13071545
Chicago/Turabian StyleDeilami, Sara, and S. M. Muyeen. 2020. "An Insight into Practical Solutions for Electric Vehicle Charging in Smart Grid" Energies 13, no. 7: 1545. https://doi.org/10.3390/en13071545
APA StyleDeilami, S., & Muyeen, S. M. (2020). An Insight into Practical Solutions for Electric Vehicle Charging in Smart Grid. Energies, 13(7), 1545. https://doi.org/10.3390/en13071545






