Transient Flow of a Horizontal Well with Multiple Fracture Wings in Coalbed Methane Reservoirs
Abstract
1. Introduction
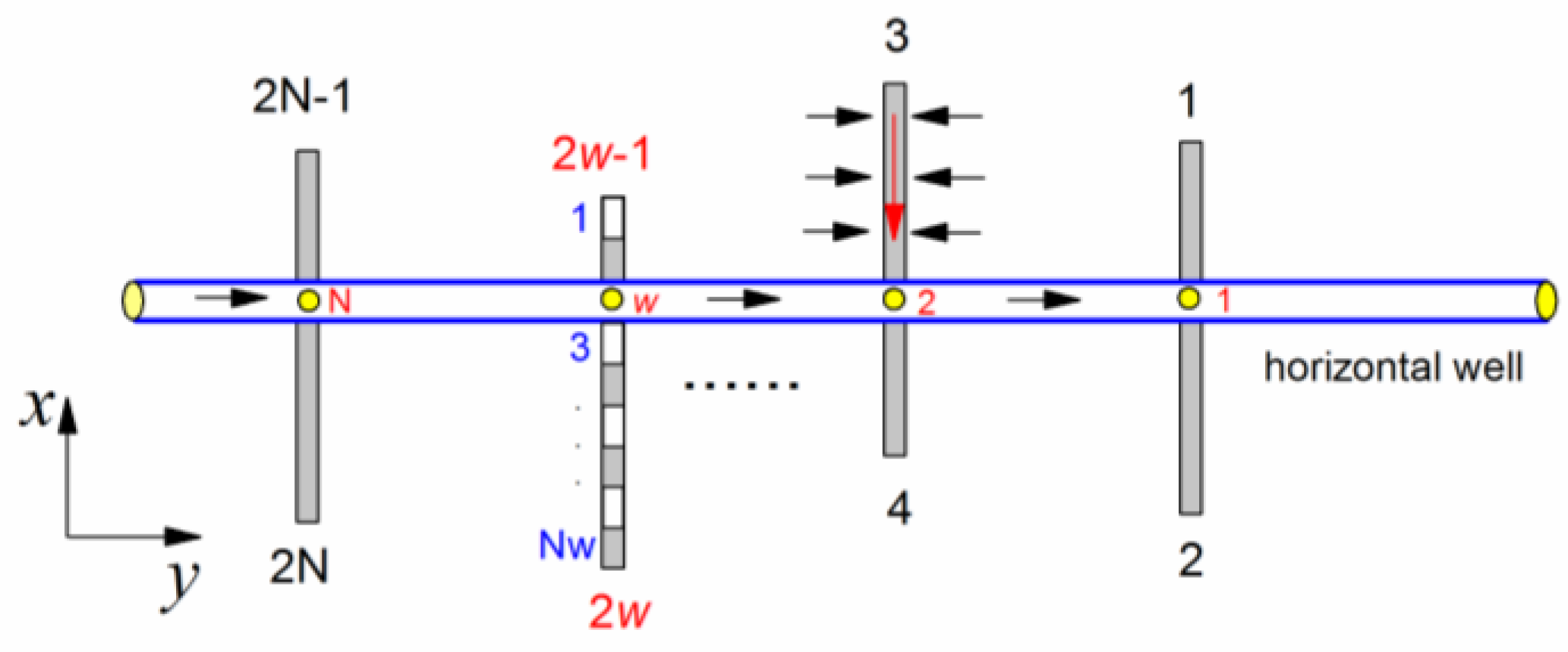
2. Mathematical Models
2.1. Fluid Flow in Coalbed Methane Reservoir
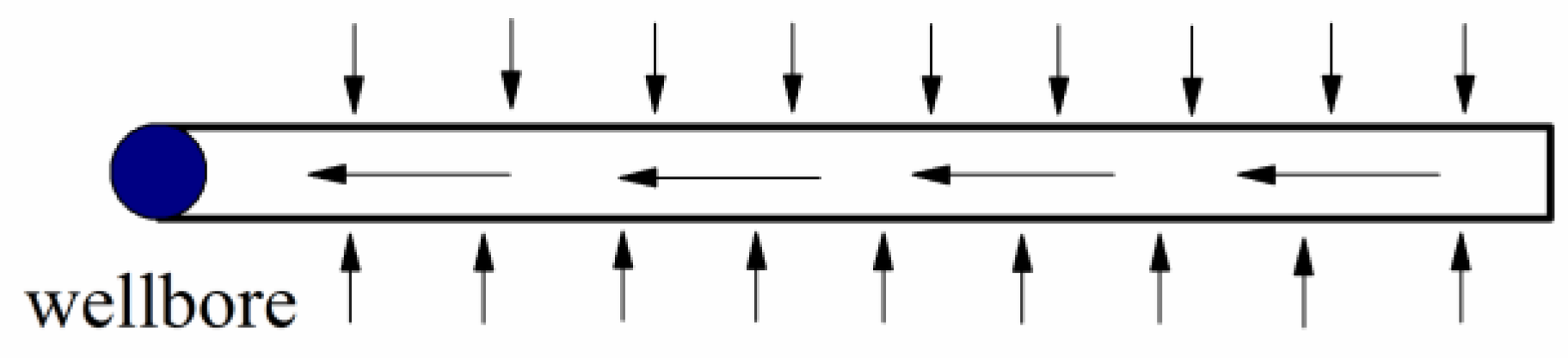
2.2. Fluid Flow in the Fracture
2.3. The Semi-Analytical Solution
3. Results and Discussions
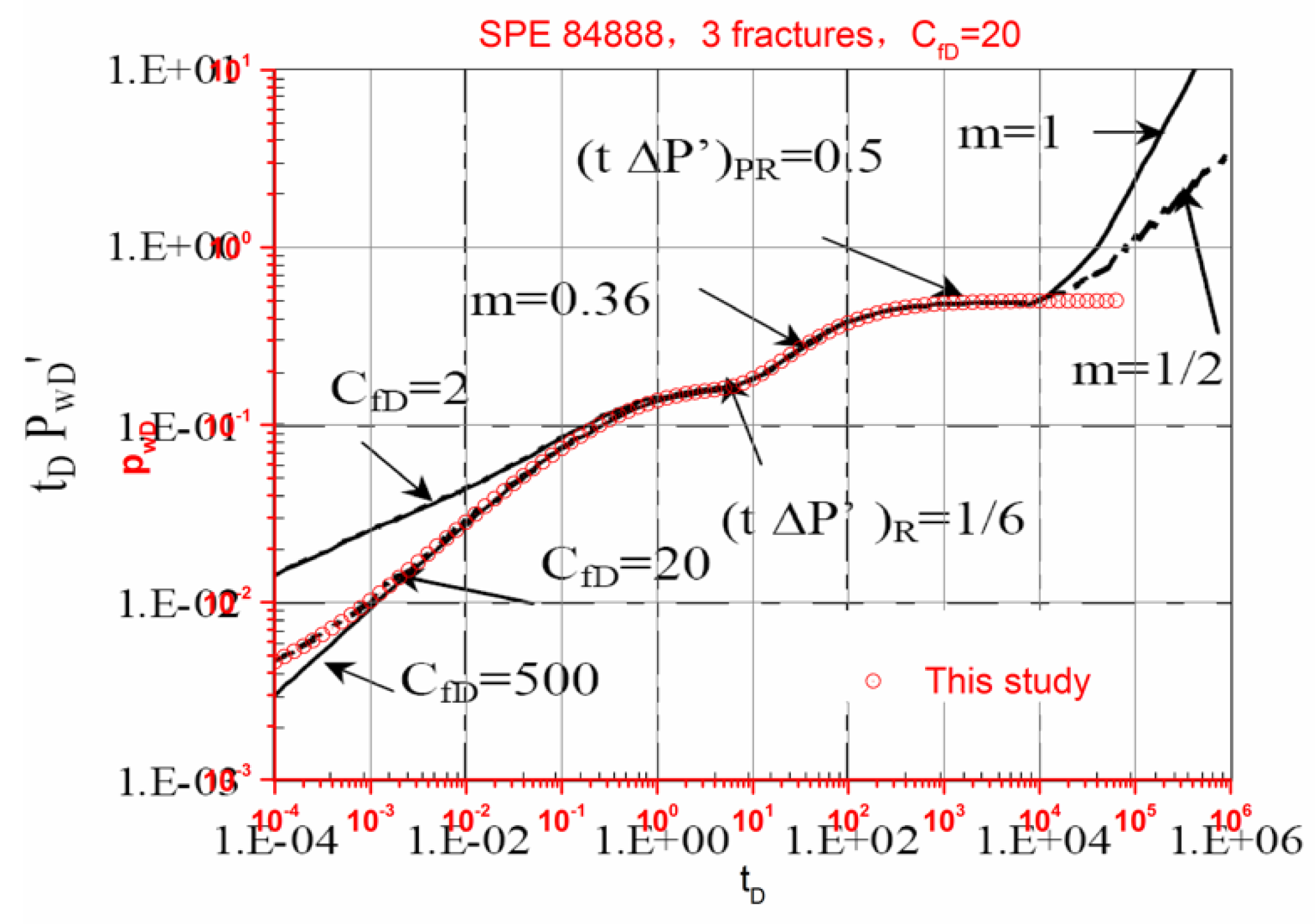
3.1. Model Validation
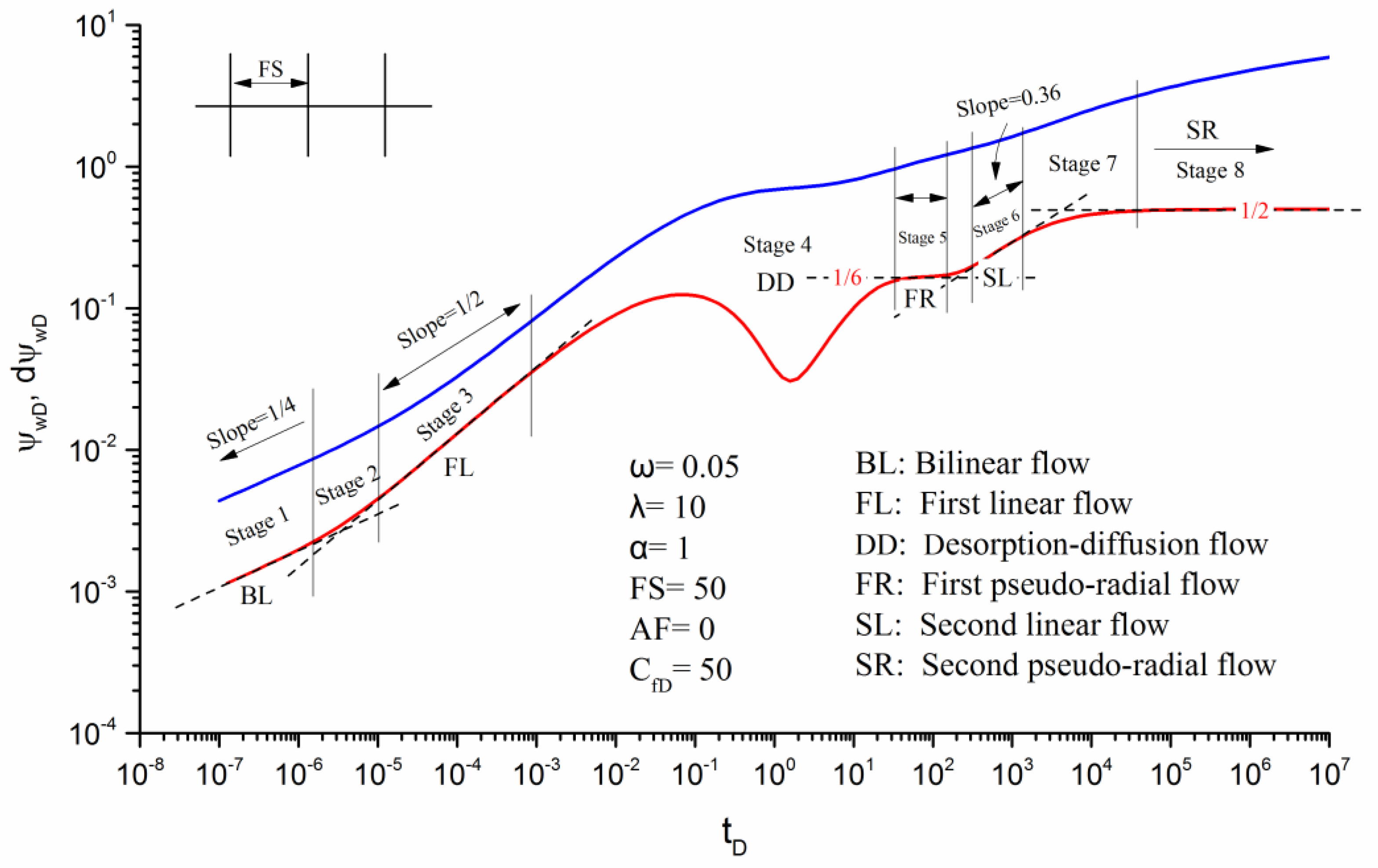
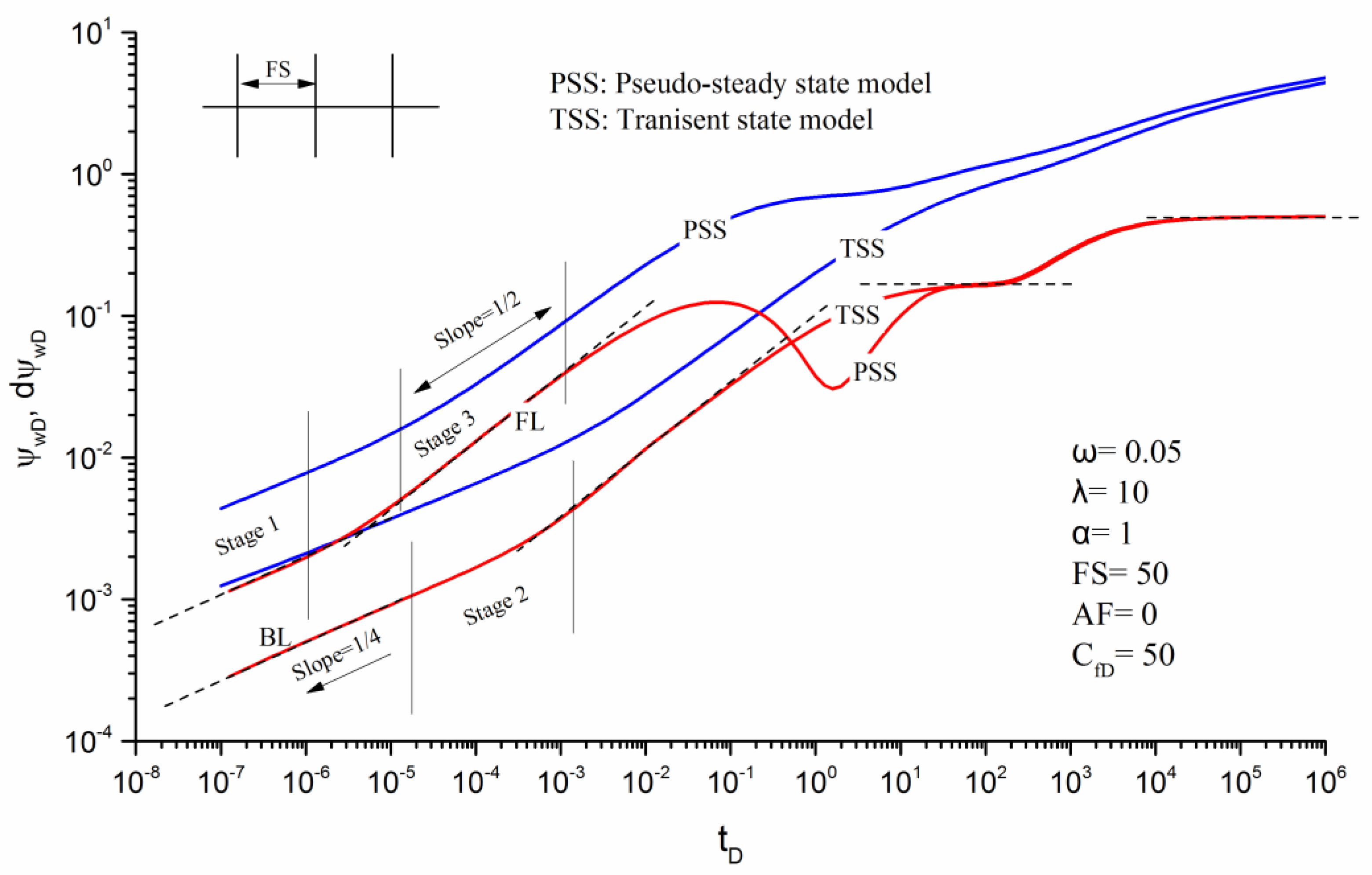
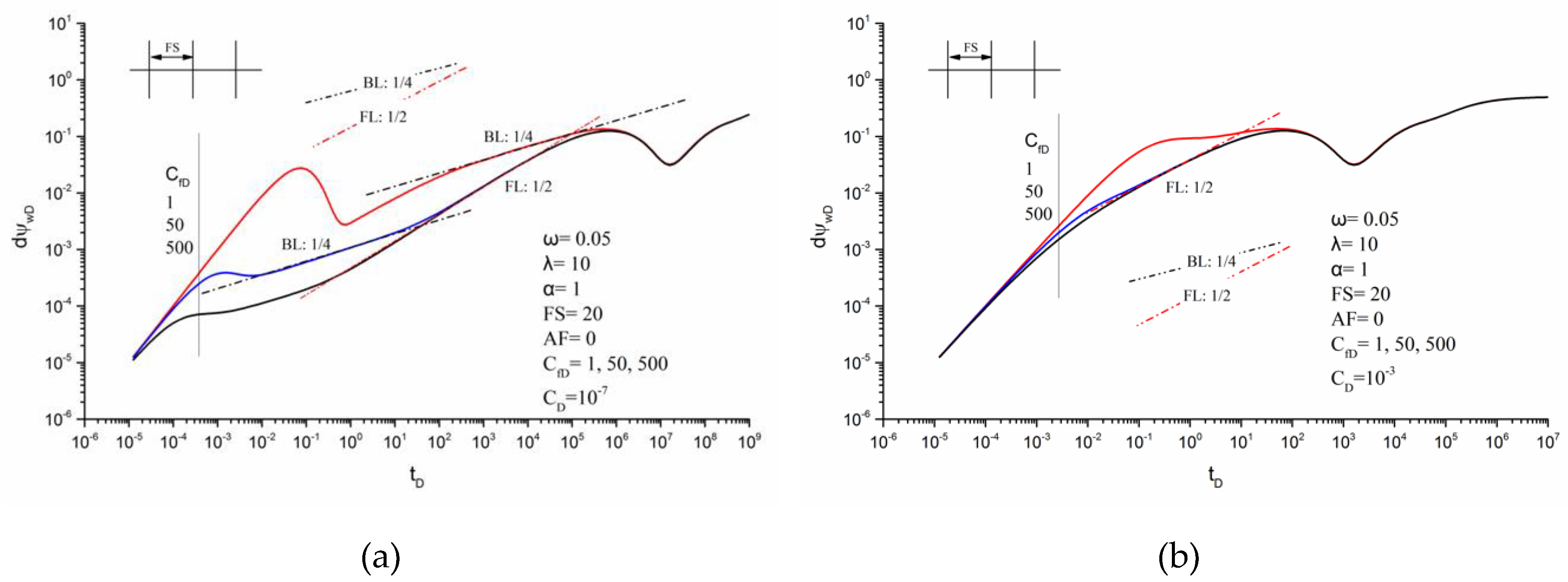
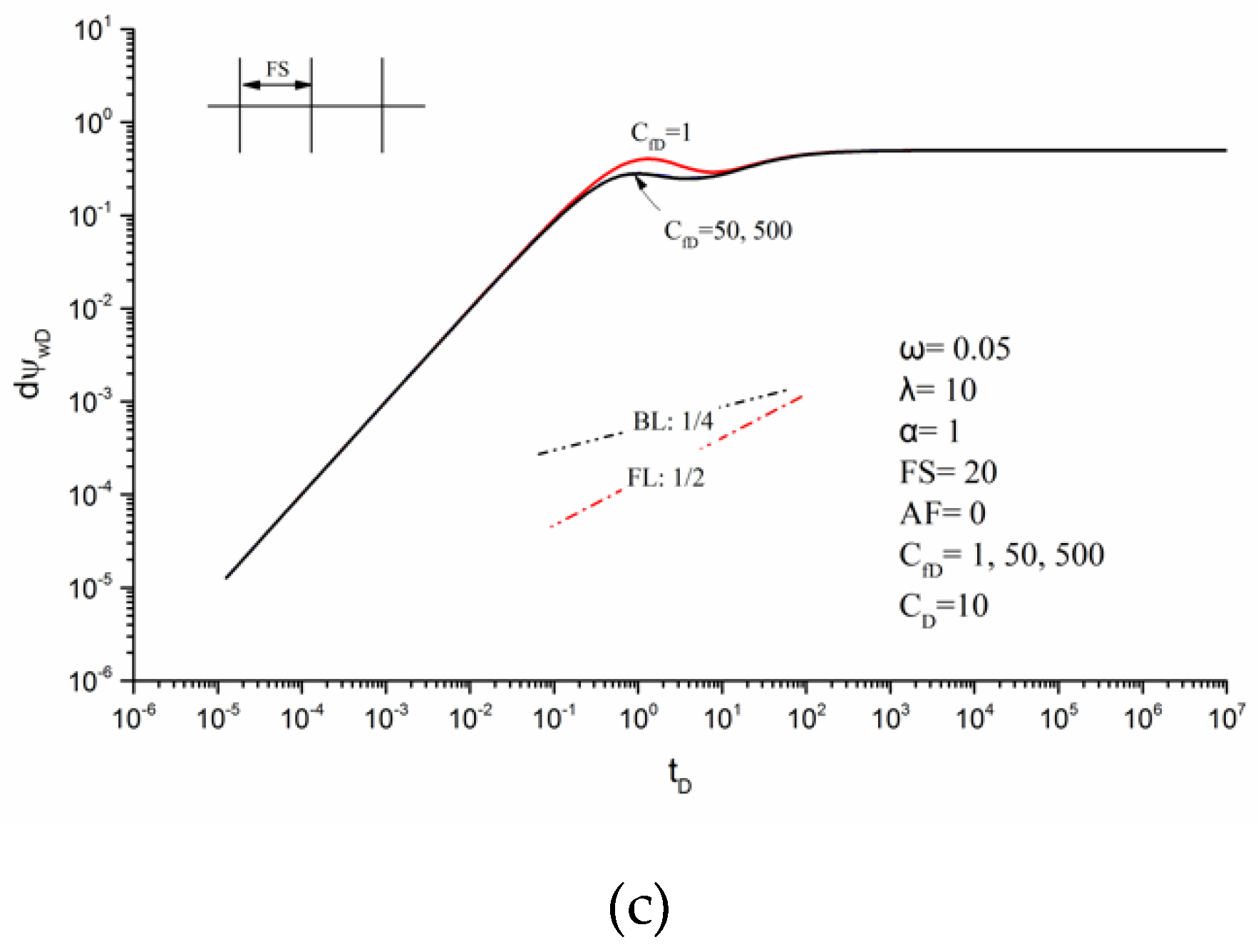
3.2. Flow Characteristics Analysis
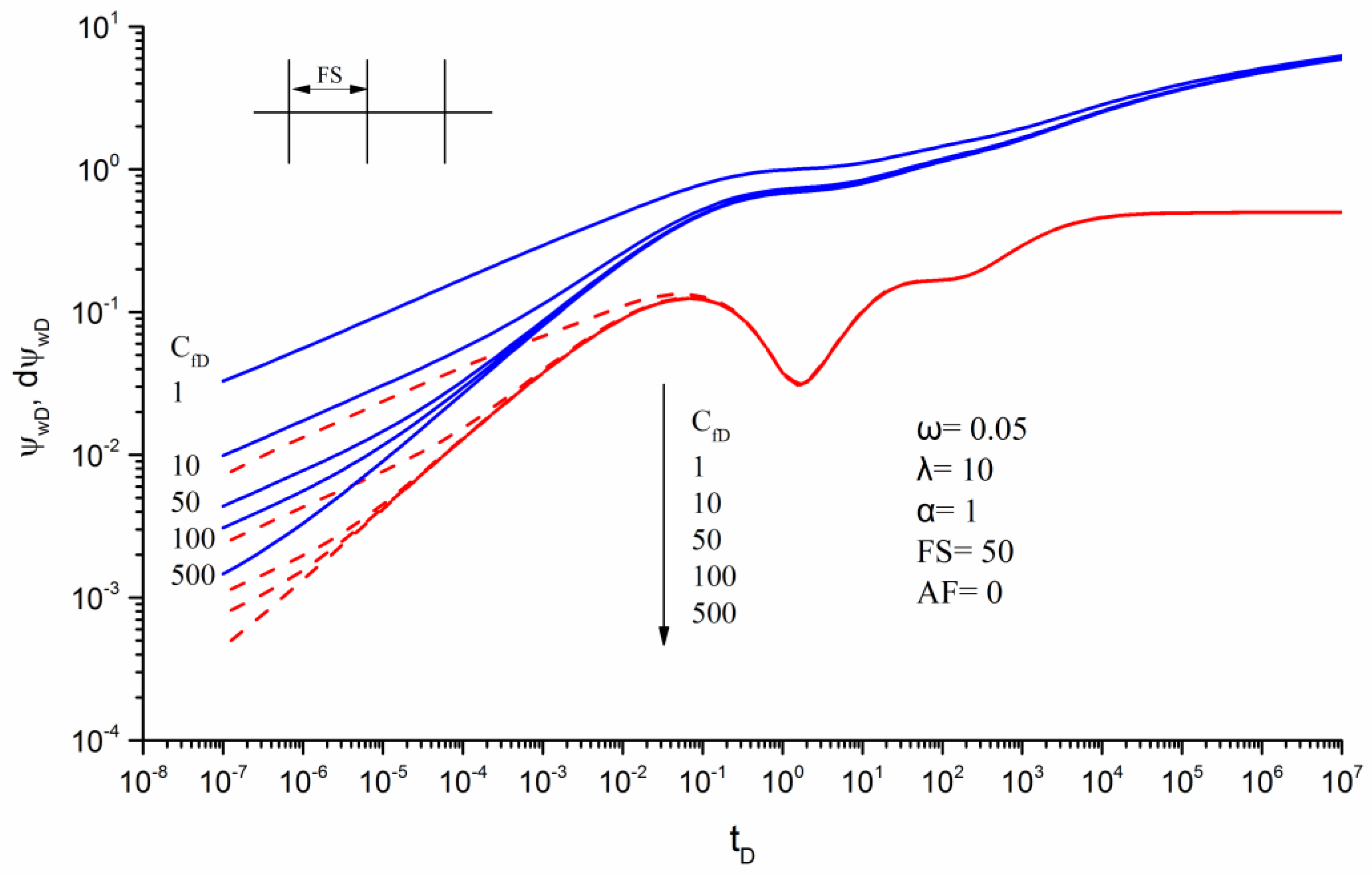
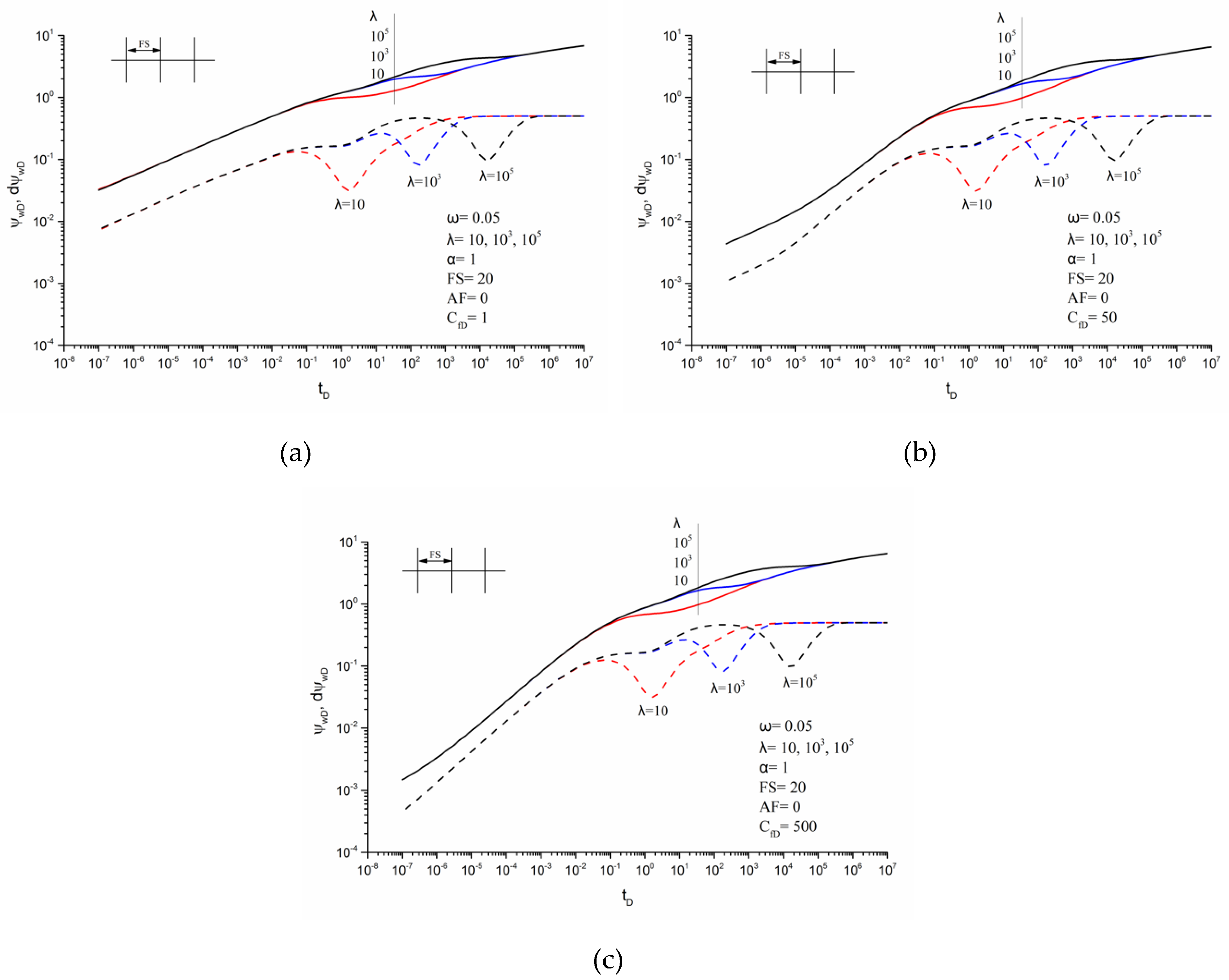
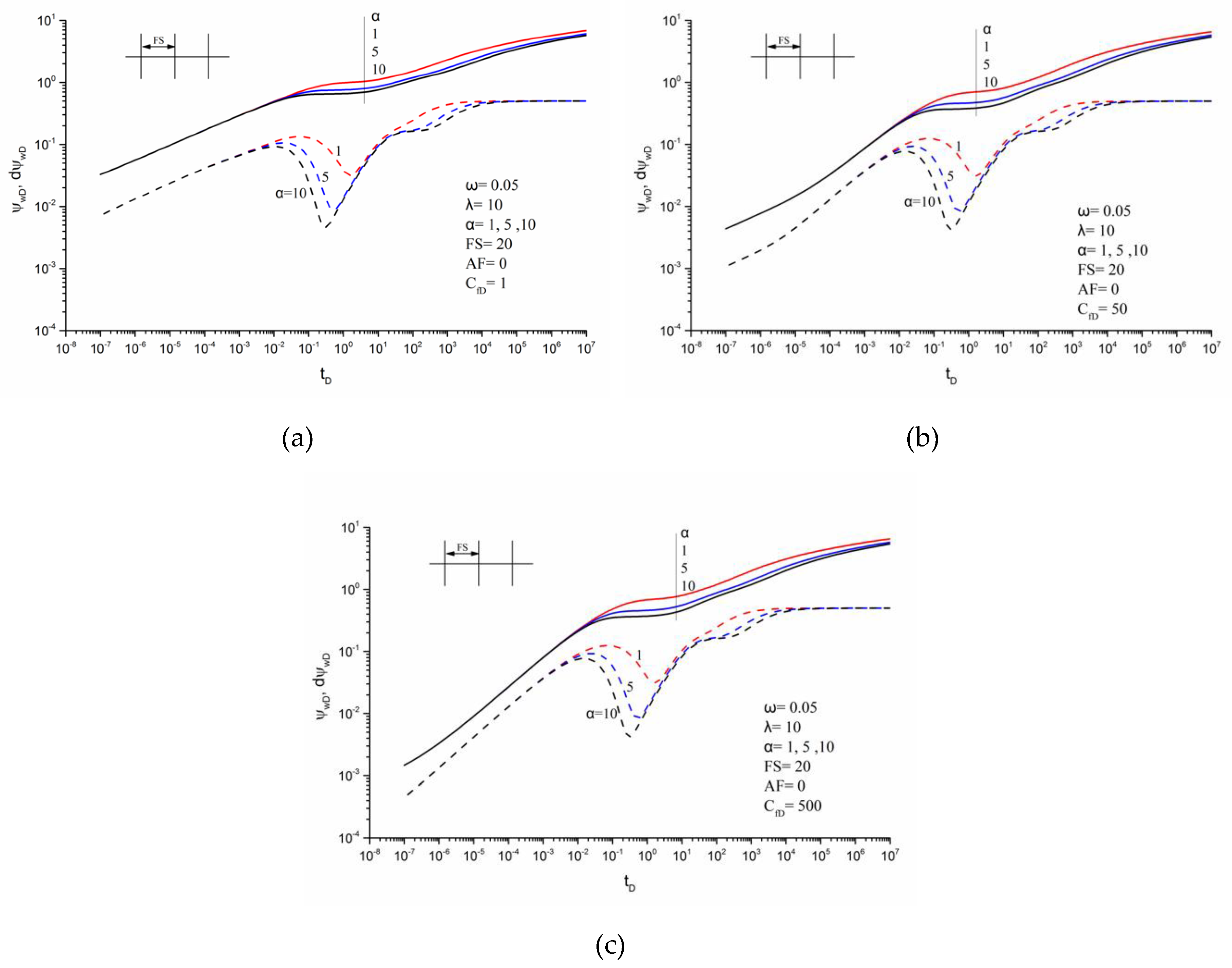
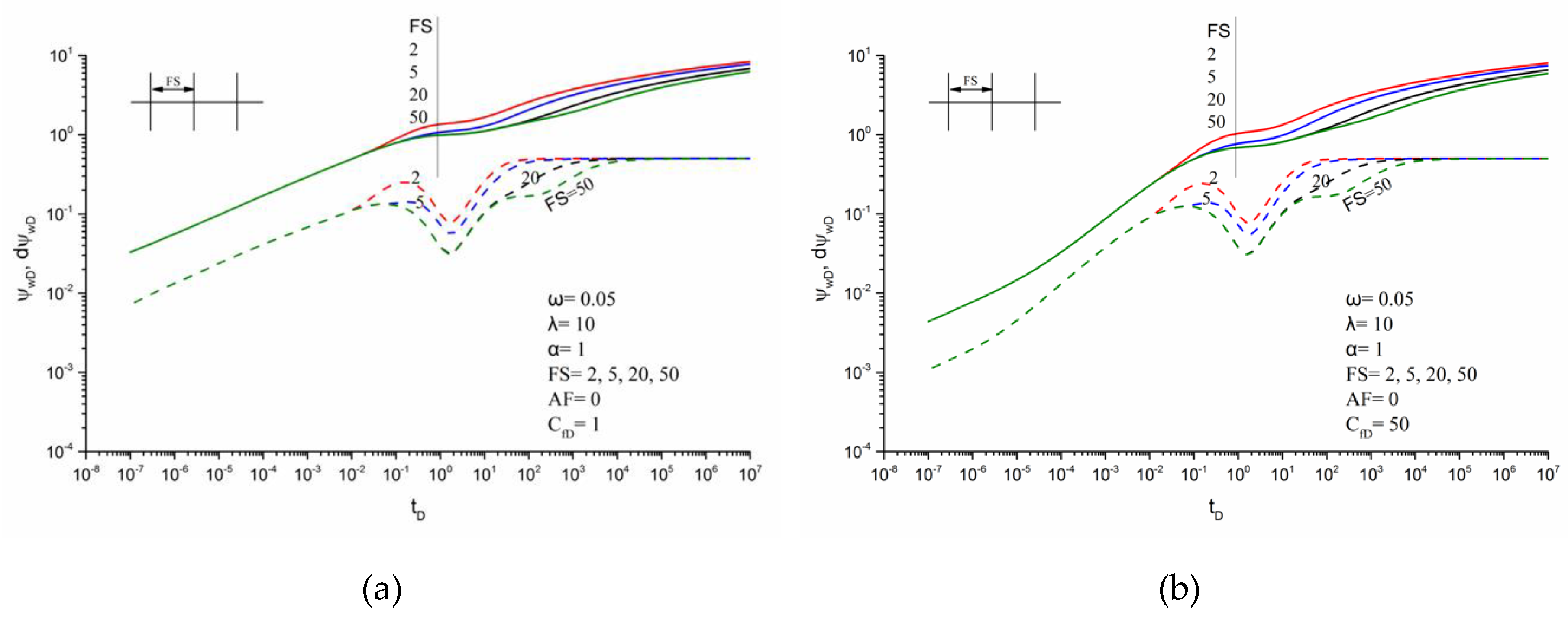
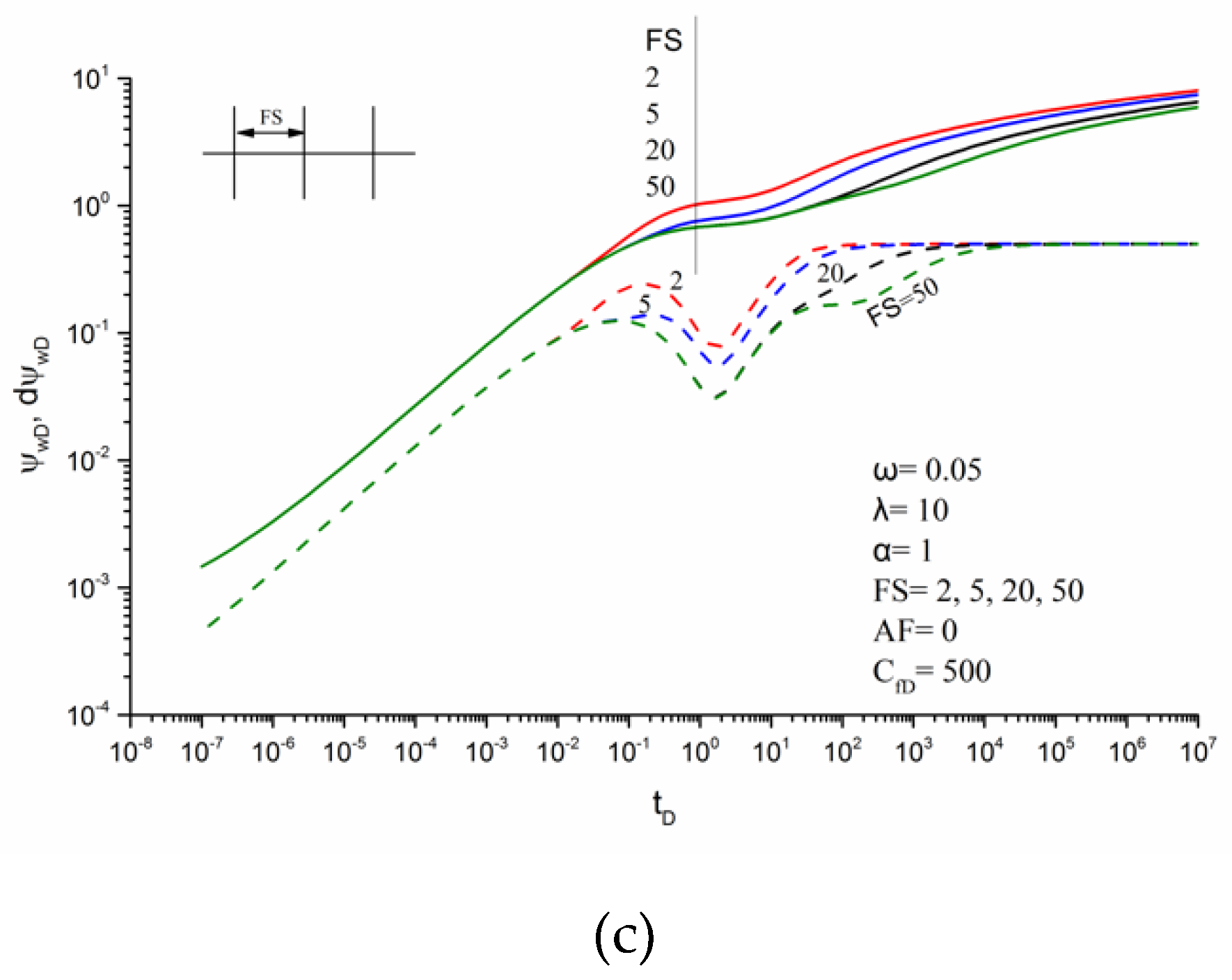
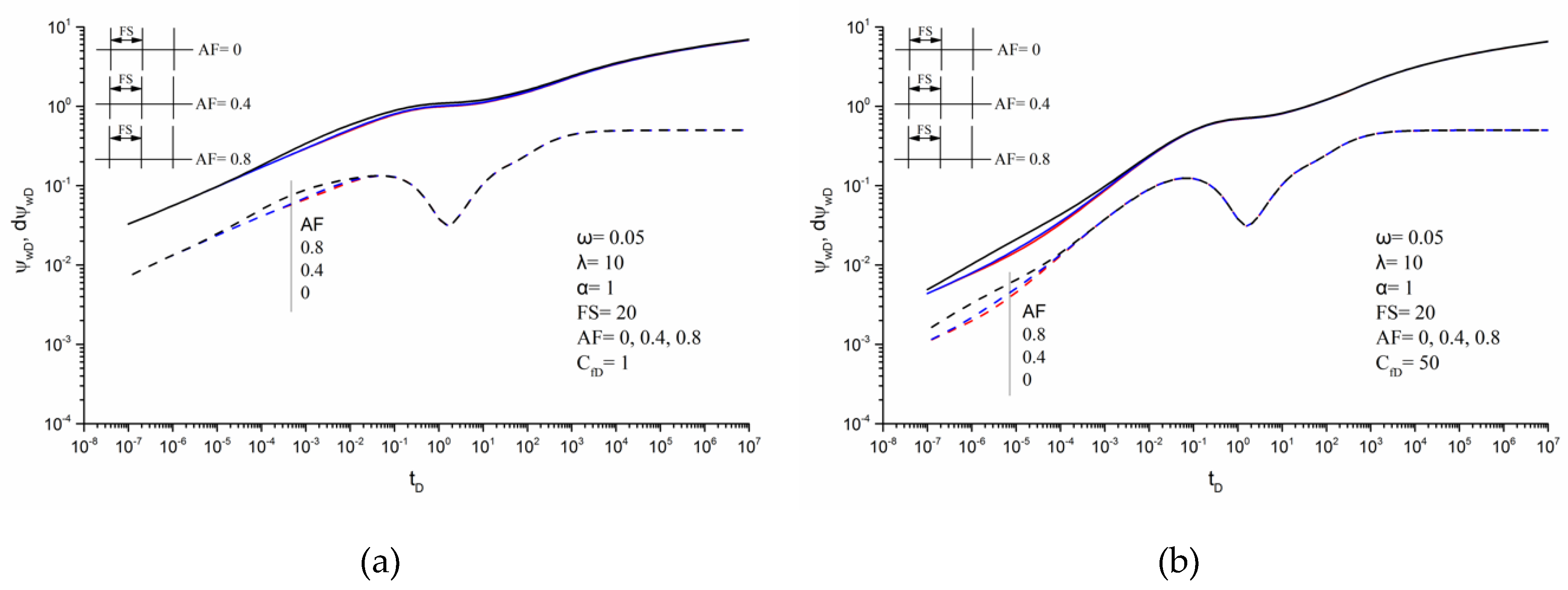
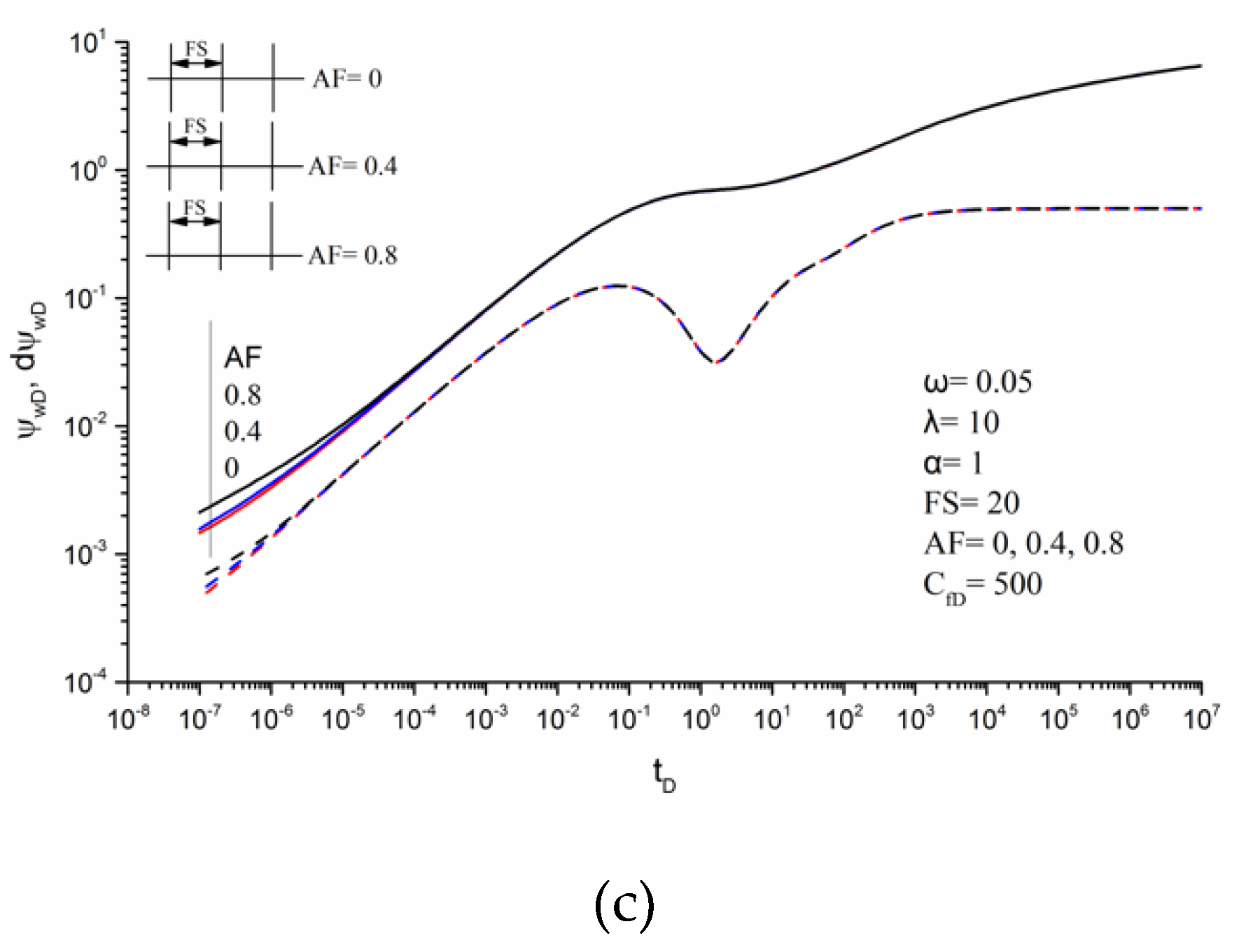
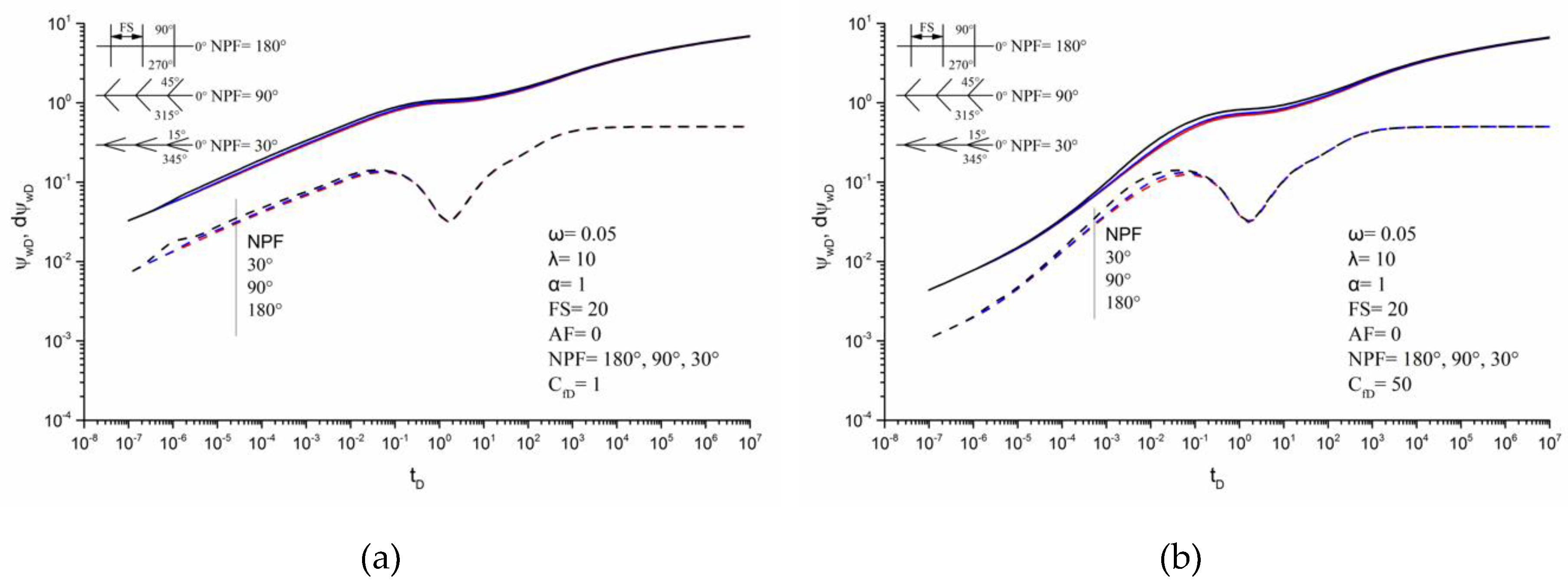
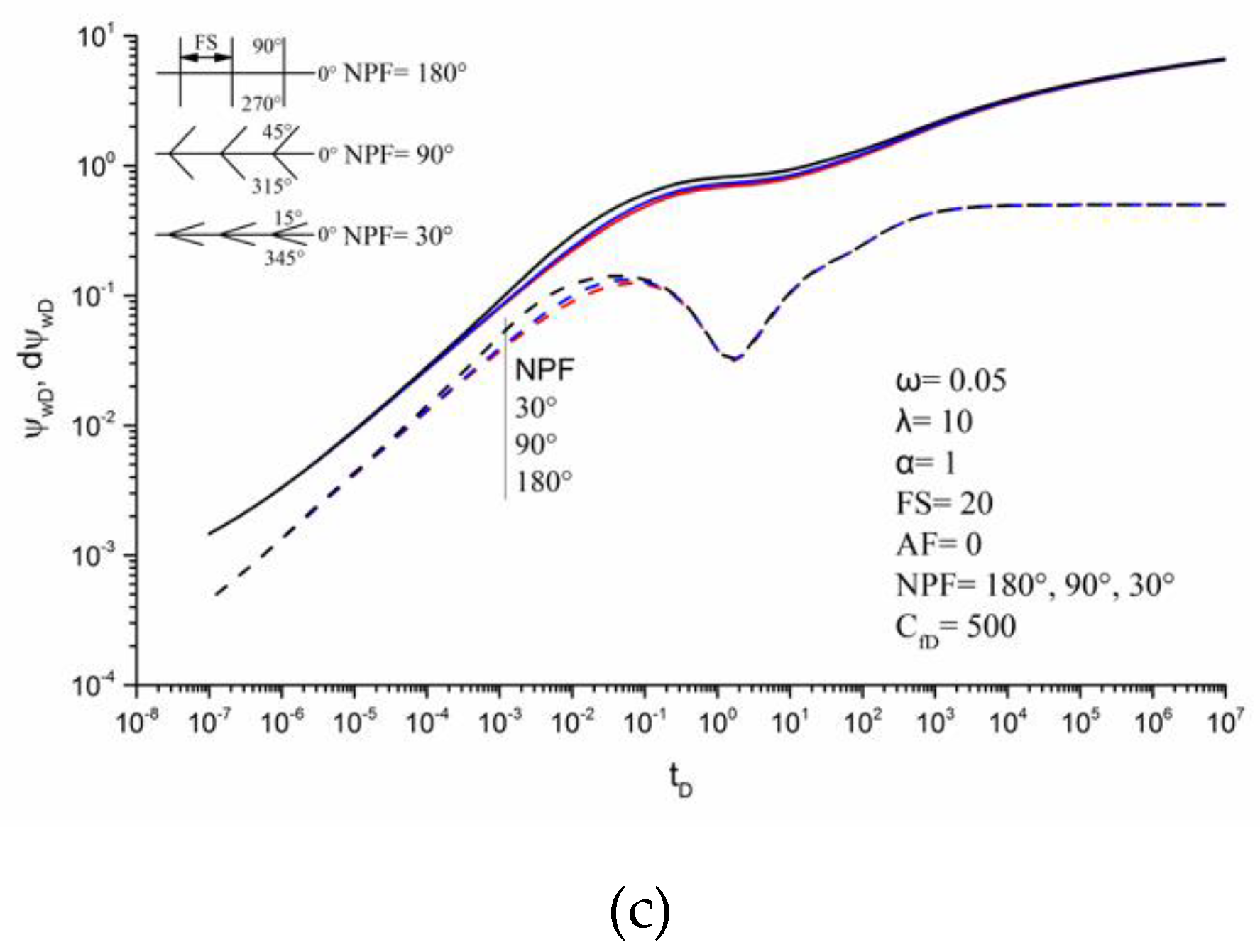
3.3. Effects of Parameters on Transient Pseudo-Pressure Responses
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Dimensionless Variables: Real Domain | |
| CfD | dimensionless fracture conductivity |
| tD | dimensionless time |
| CD | dimensionless wellbore storage coefficient |
| ψwD | dimensionless well bottom pseudo pressure |
| ψD | dimensionless pseudo pressure |
| dψD | dimensionless pseudo pressure derivative |
| ψfD | dimensionless pseudo fracture pressure |
| AF | fracture asymmetry factor |
| FS | dimensionless fracture spacing |
| λ | inter-porosity flow coefficient |
| ω | storability ratio |
| α | adsorption index |
| Dimensionless Variables: Laplace Domain | |
| s | time variable in Laplace domain, dimensionless |
| dimensionless pseudo pressure ψD in Laplace domain | |
| bottom pressure ψwD in Laplace domain | |
| dimensionless pseudo fracture pressure ψfD in Laplace domain | |
| dimensionless fracture rate qfD in Laplace domain | |
| Field Variables | |
| ct | total compressibility, 1/psi |
| k | effective permeability, mD |
| pf | fracture pressure, psi |
| pi | initial formation pressure, psi |
| qf | rate of per unit fracture length from formation, MMscf/d |
| Q | total rate of all fracture wings in the wellbore, MMscf/d |
| µ | fluid viscosity, cp |
| h | formation thickness, ft |
| φ | porosity, fraction |
| t | initial time variable, h |
| h | formation thickness, ft |
| T | temperature, R |
| Z | gas compressibility factor, fraction |
| Zi | initial gas compressibility factor, fraction |
| Bgi | initial volume factor, fraction |
| Lf | fracture wing length, ft |
| wf | width of the fracture, ft |
| Special Functions | |
| f | fracture property |
| D | dimensionless |
| g | gas property |
| sc | standard condition |
| i | initial condition |
| w | wellbore property |
Appendix A. Derivation of Fracture-Wing Model in a Coalbed Methane Reservoir
References
- Gentzis, T. Review of the hydrocarbon potential of the Steele Shale and Niobrara Formation in Wyoming, USA: A major unconventional resource play? Int. J. Coal Geol. 2016, 166, 118–127. [Google Scholar] [CrossRef]
- Adiya, Z.I.S.G.; Dupont, V.; Mahmud, T. Steam reforming of shale gas in a packed bed reactor with and without chemical looping using nickel based oxygen carrier. Int. J. Hydrog. Energy 2018, 43, 6904–6917. [Google Scholar] [CrossRef]
- Dong, G.J.; Chen, P. A comparative experiment investigate of strength parameters for Longmaxi shale at the macro- and mesoscales. Int. J. Hydrog. Energy 2017, 42, 20082–20091. [Google Scholar] [CrossRef]
- Yao, Y.B.; Liu, D.M.; Tang, D.Z.; Tang, S.H.; Che, Y.; Huang, W.H. Preliminary evaluation of the coalbed methane production potential and its geological controls in the Weibei Coalfield, Southeastern Ordos Basin, China. Int. J. Coal Geol 2009, 78, 1–15. [Google Scholar] [CrossRef]
- Lin, F.; Sheng, P.; Li, C.Y. Fracture parameter optimization of fractured horizontal well of coal bed gas reservoir. Zhongzhou Coal 2016, 2, 126–128. [Google Scholar]
- Zhou, J.J. Development and utilization status and technical progress of coalbed methane in China. Petrochem. Ind. Appl. 2017, 36, 1–4. [Google Scholar]
- Wang, G.Y.; Feng, Q.T.; Li, P. Research on mining technology of coalbed gas through staged fracturing horizontal well along the roof of coal seam. J. Shanxi Datong Univ. 2013, 29, 68–70. [Google Scholar]
- Ji, Y.; He, B.S.; Liu, S.J.; Cao, S.F.; Zhang, B.H. Improvement technology of CBM horizontal well fracturing in Qinshui Basin. Coal Sci. Technol. 2016, 44, 173–178. [Google Scholar]
- Wang, J.; Yao, T.Q. Study on CBM horizontal well sectional fracturing parameters optimization in Zhaozhuang Minefield. Coal Geol. China 2017, 29, 35–39. [Google Scholar]
- Cinco-Ley, H.; Samaniego, V.F.; Dominguez, A.N. Transient pressure behavior for a well with a finite-conductivity vertical fracture. SPE J. 1978, 18, 253–264. [Google Scholar]
- Luo, W.J.; Tang, C.F. Pressure-transient analysis of multiwing fractures connected to a vertical wellbore. SPE J. 2015, 20, 360–367. [Google Scholar] [CrossRef]
- Tian, Q.; Liu, P.C.; Jiao, Y.W.; Bie, A.F.; Xia, J.; Li, B.Z.; Liu, Y. Pressure transient analysis of non-planar asymmetric fractures connected to vertical wellbores in hydrocarbon reservoirs. Int. J. Hydrog. Energy 2017, 42, 18146–18155. [Google Scholar] [CrossRef]
- Liu, Q.G.; Xu, Y.J.; Peng, X.; Liu, Y.C.; Qi, S.Z. Pressure transient analysis for multi-wing fractured wells in dual-permeability hydrocarbon reservoirs. J. Petrol. Sci. Eng. 2019, 180, 278–288. [Google Scholar] [CrossRef]
- Larsen, L.; Hegre, T.M. Pressure-transient behavior of horizontal wells with finite-conductivity vertical fractures. In Proceedings of the International Arctic Technology Conference, Anchorage, AK, USA, 29–31 May 1991. Paper No. SPE-22076. [Google Scholar] [CrossRef]
- Guo, G.L.; Evans, R.D. A systematic methodology for production modelling of naturally fractured reservoirs intersected by horizontal wells. In Proceedings of the SPE/CIM/CANMET International Conference on Recent Advances in Horizontal Well Applications, Calgary, AB, Canada, 20–23 March 1994. Paper No. PETSOC-HWC-94-40. [Google Scholar] [CrossRef]
- Horne, R.N.; Temeng, K.O. Relative productivities and pressure transient modeling of horizontal wells with multiple fractures. In Proceedings of the Middle East Oil Show, Bahrain, 11–14 March 1995. Paper No. SPE-29891. [Google Scholar] [CrossRef]
- Chen, C.C.; Rajagopal, R. A multiply-fractured horizontal well in a rectangular drainage region. SPE J. 1997, 2, 455–465. [Google Scholar] [CrossRef]
- Wan, J.; Aziz, K. Semi-analytical well model of horizontal wells with multiple hydraulic fractures. SPE J. 2002, 7, 437–445. [Google Scholar] [CrossRef]
- Zerzar, A.; Bettam, Y. Interpretation of multiple hydraulically fractured horizontal wells in closed systems. In Proceedings of the Canadian International Petroleum Conference, Calgary, AB, Canada, 8–10 June 2004. Paper No. PETSOC-2004-027. [Google Scholar] [CrossRef]
- Al-Kobaisi, M.; Ozkan, E.; Kazemi, H. A hybrid numerical-analytical model of finite-conductivity vertical fractures intercepted by a horizontal well. In Proceedings of the SPE International Petroleum Conference in Mexico, Puebla Pue., Mexico, 7–9 November 2004. Paper No. SPE-92040. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Practical analytical model to simulate production of horizontal wells with branch fractures. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. Paper No. SPE-162515. [Google Scholar] [CrossRef]
- Al-Rbeawi, S.J.H.; Djebbar, T. Transient pressure analysis of a horizontal well with multiple inclined hydraulic fractures using type-curve matching. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2012. Paper No. SPE-149902. [Google Scholar] [CrossRef]
- Wang, H.; Ran, Q.Q.; Liao, X.W. Pressure transient responses study on the hydraulic volume fracturing vertical well in stress-sensitive tight hydrocarbon reservoirs. Int. J. Hydrog. Energy 2017, 42, 18343–18349. [Google Scholar] [CrossRef]
- Yuan, B.; Zheng, D.; Moghanloo, R.G.; Wang, K. A novel integrated workflow for evaluation, optimization, and production predication in shale plays. Int. J. Coal Geol. 2017, 180, 18–28. [Google Scholar] [CrossRef]
- Xing, G.Q.; Wang, M.X.; Wu, S.H.; Li, H.; Dong, J.Y.; Zhao, W.Q. Pseudo-steady-state parameters for a well penetrated by a fracture with an azimuth angle in an anisotropic reservoir. Energies 2019, 12, 2449. [Google Scholar] [CrossRef]
- Wang, M.X.; Xing, G.Q.; Fan, Z.F.; Zhao, W.Q.; Lun, Z.; Heng, S. A novel model incorporating geomechanics for a horizontal well in a naturally fractured reservoir. Energies 2018, 11, 2584. [Google Scholar] [CrossRef]
- Xing, G.Q.; Wu, S.H.; Wang, J.H.; Wang, M.X.; Wang, B.H.; Cao, J.J. Pressure transient performance for a horizontal well intercepted by multiple reorientation fractures in a tight reservoir. Energies 2019, 12, 4232. [Google Scholar] [CrossRef]
- Venart, J.E.S.; Prasad, R.C.; Wang, G. Knudsen-effect errors with transient line-source measurement in fluids. Int. J. Thermophys. 1987, 8, 39–46. [Google Scholar] [CrossRef]
- Alata, M.; Al-Nimr, M.A.; Naji, M. Transient behavior of a thermoelectric device under the hyperbolic heat conduction model. Int. J. Thermophys. 2003, 24, 1753–1768. [Google Scholar] [CrossRef]
- Khadrawi, A.F.; Othman, A.; Al-Nimr, M.A. Transient free convection fluid flow in a vertical microchannel as described by the hyperbolic heat conduction model. Int. J. Thermophys. 2005, 26, 905–918. [Google Scholar] [CrossRef]
- Minea, A.A.; Buonomo, B.; Burggraf, J.; Ercole, D.; Karpaiya, K.R.; Pasqua, A.D.; Sekrani, G.; Steffens, J.; Tibaut, J.; Wichmann, N.; et al. NanoRound: A benchmark study on the numerical approach in nanofluids’ simulation. Int. Commun. Heat Mass. 2019, 108, 104292. [Google Scholar] [CrossRef]
- Sung, W.; Ertekin, T.; Schwerer, F.C. The development, testing, and application of a comprehensive coal seam degasification model. In Proceedings of the SPE Unconventional Gas Technology Symposium, Louisville, KY, USA, 18–21 May 1986. Paper No. SPE-15247. [Google Scholar] [CrossRef]
- Ertekin, T.; Sung, W. Pressure transient analysis of coal seams in the presence of multi-mechanistic flow and sorption phenomena. In Proceedings of the SPE Gas Technology Symposium, Dallas, TX, USA, 7–9 June 1989. Paper No. SPE-19102. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. A comprehensive study of pressure transient analysis with sorption phenomena for single-phase gas flow in coal seams. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 23–26 September 1990. Paper No. SPE-20568. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. A simplified approach for in-situ characterization of desorption properties of coal seams. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 15–17 April 1991. Paper No. SPE-21808. [Google Scholar] [CrossRef]
- Anbarci, K.; Ertekin, T. Pressure transient behavior of fractured wells in coalbed reservoirs. In Proceedings of the SPE Annual Technical Conference and Exhibition, Washington, DC, USA, 4–7 October 1992. Paper No. SPE-24703. [Google Scholar] [CrossRef]
- Guo, X.; Du, Z.M.; Li, S.L. Computer modeling and simulation of coalbed methane reservoir. In Proceedings of the SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 6–10 September 2003. Paper No. SPE-84815. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Jordan, C.L.; Ilk, D.; Blasingame, T.A. Production data analysis of fractured and horizontal CBM wells. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 23–25 September 2009. Paper No. SPE-125929. [Google Scholar] [CrossRef]
- Aminian, K.; Ameri, S. Predicting production performance of CBM reservoirs. J. Nat. Gas Sci. Eng. 2009, 1, 25–30. [Google Scholar] [CrossRef]
- Nie, R.S.; Meng, Y.F.; Guo, J.C.; Jia, Y.L. Modeling transient flow behavior of a horizontal well in a coal seam. Int. J. Coal Geol. 2012, 92, 54–68. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.D.; Li, J.Q.; Wang, J.H. Simulation of pressure transient behavior for asymmetrically finite-conductivity fractured wells in coal reservoirs. Transp. Porous Med. 2013, 97, 353–372. [Google Scholar] [CrossRef]
- Zhang, L.H.; Kou, Z.H.; Wang, H.T.; Zhao, Y.L.; Dejam, M.; Guo, J.J.; Du, J. Performance analysis for a model of a multi-wing hydraulically fractured vertical well in a coalbed methane gas reservoir. J. Petrol. Sci. Eng. 2018, 166, 104–120. [Google Scholar] [CrossRef]
- Chen, X.X.; Wang, L.; Xue, L. A gaseous compound of hydrogen and carbon production performance model in coalbed reservoir with horizontal fractures. Int. J. Hydrog. Energy 2019, 44, 5262–5269. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]

| CfD = 1 | ω = 0.05 | ω = 0.1 | ω = 0.5 | |||
| tD | ΨwD | dΨwD | ΨwD | dΨwD | ΨwD | dΨwD |
| 10−6 | 0.0559 | 0.0133 | 0.0474 | 0.0111 | 0.0329 | 0.0072 |
| 10−5 | 0.0971 | 0.0237 | 0.0821 | 0.0198 | 0.0559 | 0.0133 |
| 10−4 | 0.1701 | 0.0411 | 0.1439 | 0.0350 | 0.0971 | 0.0237 |
| 10−3 | 0.2933 | 0.0677 | 0.2497 | 0.0586 | 0.1702 | 0.0411 |
| 10−2 | 0.4940 | 0.1102 | 0.4229 | 0.0953 | 0.2934 | 0.0677 |
| 10−1 | 0.7861 | 0.1287 | 0.6951 | 0.1341 | 0.4948 | 0.1112 |
| 100 | 0.9890 | 0.0385 | 0.9606 | 0.0756 | 0.7982 | 0.1419 |
| 101 | 1.1113 | 0.1047 | 1.1109 | 0.1046 | 1.0999 | 0.1268 |
| 102 | 1.5094 | 0.2453 | 1.5090 | 0.2455 | 1.5056 | 0.2474 |
| 103 | 2.3140 | 0.4382 | 2.3140 | 0.4383 | 2.3138 | 0.4386 |
| 104 | 3.4063 | 0.4930 | 3.4063 | 0.4930 | 3.4063 | 0.4930 |
| 105 | 4.5513 | 0.4993 | 4.5513 | 0.4993 | 4.5513 | 0.4993 |
| 106 | 5.7020 | 0.5000 | 5.7020 | 0.5000 | 5.7020 | 0.5000 |
| CfD = 50 | ω = 0.05 | ω = 0.1 | ω = 0.5 | |||
| tD | ΨwD | dΨwD | ΨwD | dΨwD | ΨwD | dΨwD |
| 10−6 | 0.0078 | 0.0020 | 0.0065 | 0.0016 | 0.0044 | 0.0011 |
| 10−5 | 0.0146 | 0.0045 | 0.0119 | 0.0034 | 0.0078 | 0.0020 |
| 10−4 | 0.0330 | 0.0131 | 0.0253 | 0.0094 | 0.0146 | 0.0045 |
| 10−3 | 0.0867 | 0.0376 | 0.0643 | 0.0276 | 0.0330 | 0.0131 |
| 10−2 | 0.2286 | 0.0902 | 0.1725 | 0.0718 | 0.0867 | 0.0376 |
| 10−1 | 0.4911 | 0.1231 | 0.4052 | 0.1242 | 0.2292 | 0.0911 |
| 100 | 0.6894 | 0.0380 | 0.6611 | 0.0746 | 0.5021 | 0.1357 |
| 101 | 0.8092 | 0.1029 | 0.8088 | 0.1028 | 0.7972 | 0.1253 |
| 102 | 1.2046 | 0.2449 | 1.2041 | 0.2451 | 1.2007 | 0.2470 |
| 103 | 2.0077 | 0.4375 | 2.0077 | 0.4376 | 2.0075 | 0.4379 |
| 104 | 3.0992 | 0.4929 | 3.0992 | 0.4929 | 3.0992 | 0.4929 |
| 105 | 4.2441 | 0.4993 | 4.2441 | 0.4993 | 4.2441 | 0.4993 |
| 106 | 5.3948 | 0.5000 | 5.3948 | 0.5000 | 5.3948 | 0.5000 |
| CfD = 500 | ω = 0.05 | ω = 0.1 | ω = 0.5 | |||
| tD | ΨwD | dΨwD | ΨwD | dΨwD | ΨwD | dΨwD |
| 10−6 | 0.0033 | 0.0013 | 0.0025 | 0.0010 | 0.0015 | 0.0005 |
| 10−5 | 0.0090 | 0.0042 | 0.0066 | 0.0030 | 0.0033 | 0.0013 |
| 10−4 | 0.0268 | 0.0129 | 0.0193 | 0.0092 | 0.0090 | 0.0042 |
| 10−3 | 0.0801 | 0.0373 | 0.0578 | 0.0274 | 0.0268 | 0.0129 |
| 10−2 | 0.2211 | 0.0898 | 0.1654 | 0.0714 | 0.0801 | 0.0374 |
| 10−1 | 0.4829 | 0.1229 | 0.3971 | 0.1239 | 0.2217 | 0.0906 |
| 100 | 0.6810 | 0.0380 | 0.6527 | 0.0745 | 0.4938 | 0.1355 |
| 101 | 0.8008 | 0.1029 | 0.8003 | 0.1028 | 0.7888 | 0.1253 |
| 102 | 1.1960 | 0.2449 | 1.1956 | 0.2451 | 1.1922 | 0.2470 |
| 103 | 1.9992 | 0.4375 | 1.9991 | 0.4375 | 1.9989 | 0.4379 |
| 104 | 3.0906 | 0.4929 | 3.0906 | 0.4929 | 3.0906 | 0.4929 |
| 105 | 4.2355 | 0.4993 | 4.2355 | 0.4993 | 4.2355 | 0.4993 |
| 106 | 5.3862 | 0.5000 | 5.3862 | 0.5000 | 5.3862 | 0.5000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Cui, Y.; Luo, W.; Liu, P.; Ning, B. Transient Flow of a Horizontal Well with Multiple Fracture Wings in Coalbed Methane Reservoirs. Energies 2020, 13, 1498. https://doi.org/10.3390/en13061498
Tian Q, Cui Y, Luo W, Liu P, Ning B. Transient Flow of a Horizontal Well with Multiple Fracture Wings in Coalbed Methane Reservoirs. Energies. 2020; 13(6):1498. https://doi.org/10.3390/en13061498
Chicago/Turabian StyleTian, Qing, Yudong Cui, Wanjing Luo, Pengcheng Liu, and Bo Ning. 2020. "Transient Flow of a Horizontal Well with Multiple Fracture Wings in Coalbed Methane Reservoirs" Energies 13, no. 6: 1498. https://doi.org/10.3390/en13061498
APA StyleTian, Q., Cui, Y., Luo, W., Liu, P., & Ning, B. (2020). Transient Flow of a Horizontal Well with Multiple Fracture Wings in Coalbed Methane Reservoirs. Energies, 13(6), 1498. https://doi.org/10.3390/en13061498





