Experimental Performance of a Solar Air Collector with a Perforated Back Plate in New Zealand
Abstract
1. Introduction
2. Materials and Methods
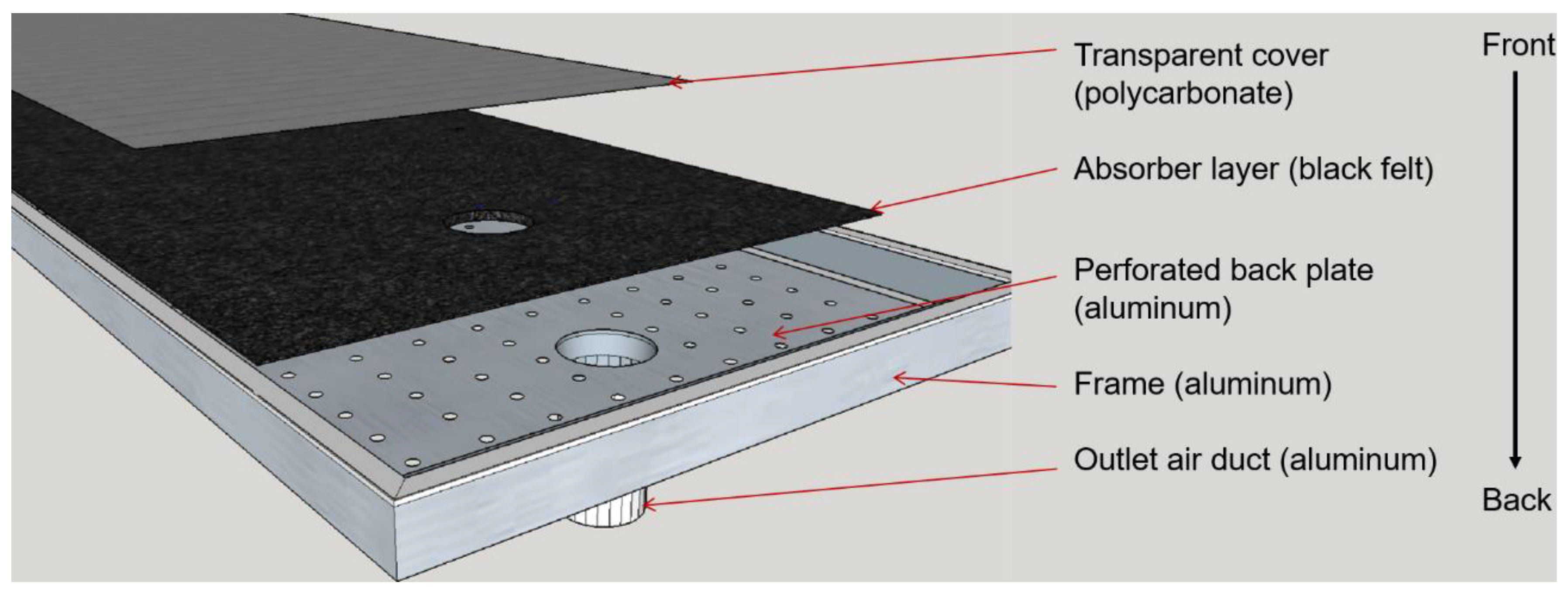
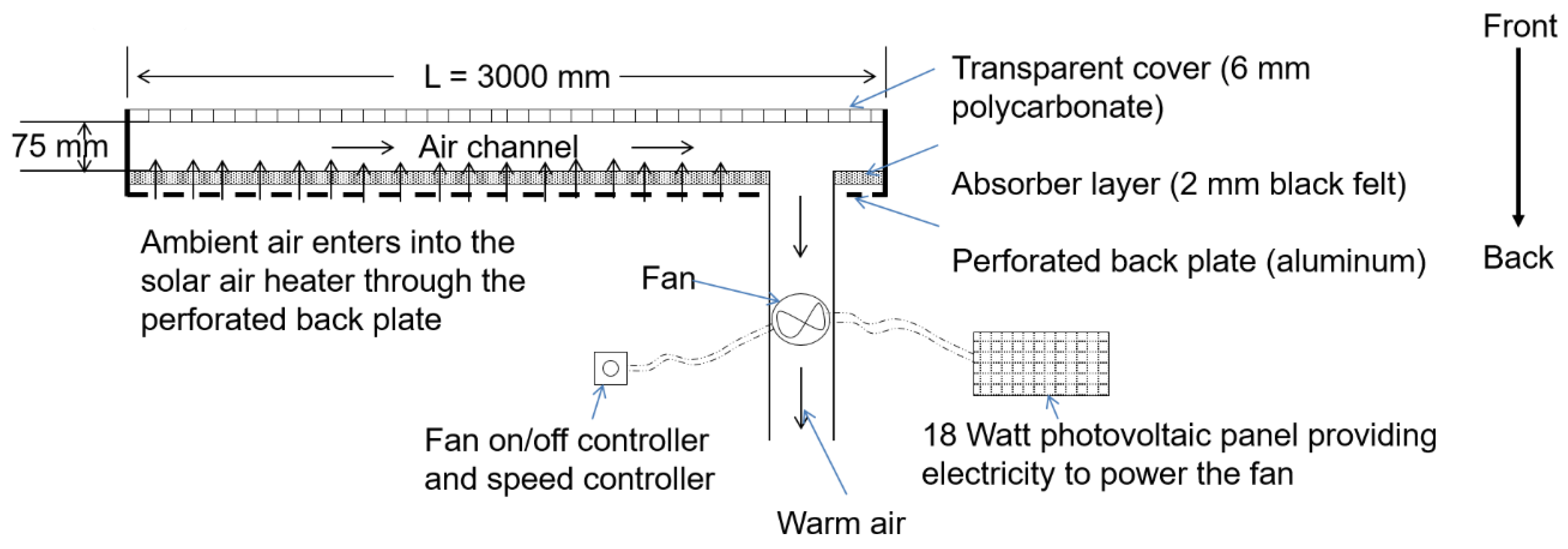
2.1. Structure of the Studied Solar Air Heater
2.2. Experiment Setup and Test Procedure
2.3. Thermal Efficiency Calculation
| Solar air heater effective area (m2) | |
| Outlet duct cross section area (m2) | |
| Specific heat capacity of air [J/(kg*K)] | |
| Solar radiation on the tilted solar air heater surface (W/m2) | |
| Inlet air temperature (K) | |
| Outlet air temperature (K) | |
| Air mass flow rate (kg/s) | |
| Efficiency (%) | |
| Density of air (kg/m3) | |
| Air velocity (m/s) |
2.4. Effective Efficiency Calculation
| Effective efficiency of the solar air heater (%) | |
| Useful thermal energy gained by the solar air heater (W) | |
| Mechanical power that required to force the air through the solar air collector (W) | |
| the conversion factor | |
| Solar radiation on the tilted solar air heater surface (W/m2) | |
| Solar air heater effective area (m2) |
| Mechanical power that required to force the air through the solar air collector (W) | |
| Volume flow rate (m3/s) | |
| Pressure drop inside the air channel (N/m2) |
| Pressure drop inside the air channel (N/m2) | |
| Density of air (kg/m3) | |
| Friction factor | |
| Air velocity (m/s) | |
| Length of the solar air heater (m) | |
| Hydraulic diameter (m) |
| Hydraulic diameter (m) | |
| Width of the air channel (m) | |
| Depth of the air channel (m) |
| Porosity | |
| Diameter of the holes (1.5 mm) | |
| Spaces between the evenly distributed holes (15 mm) |
| Reynolds number | |
| Dynamic viscosity (kg/(m*s)) |
2.5. The Uncertainty Calculation
| Uncertainty of the variable x |
| Uncertainty of the variable x | |
| Standard deviation of the variable x | |
| Uncertainty of the instrument |
3. Results and Discussion
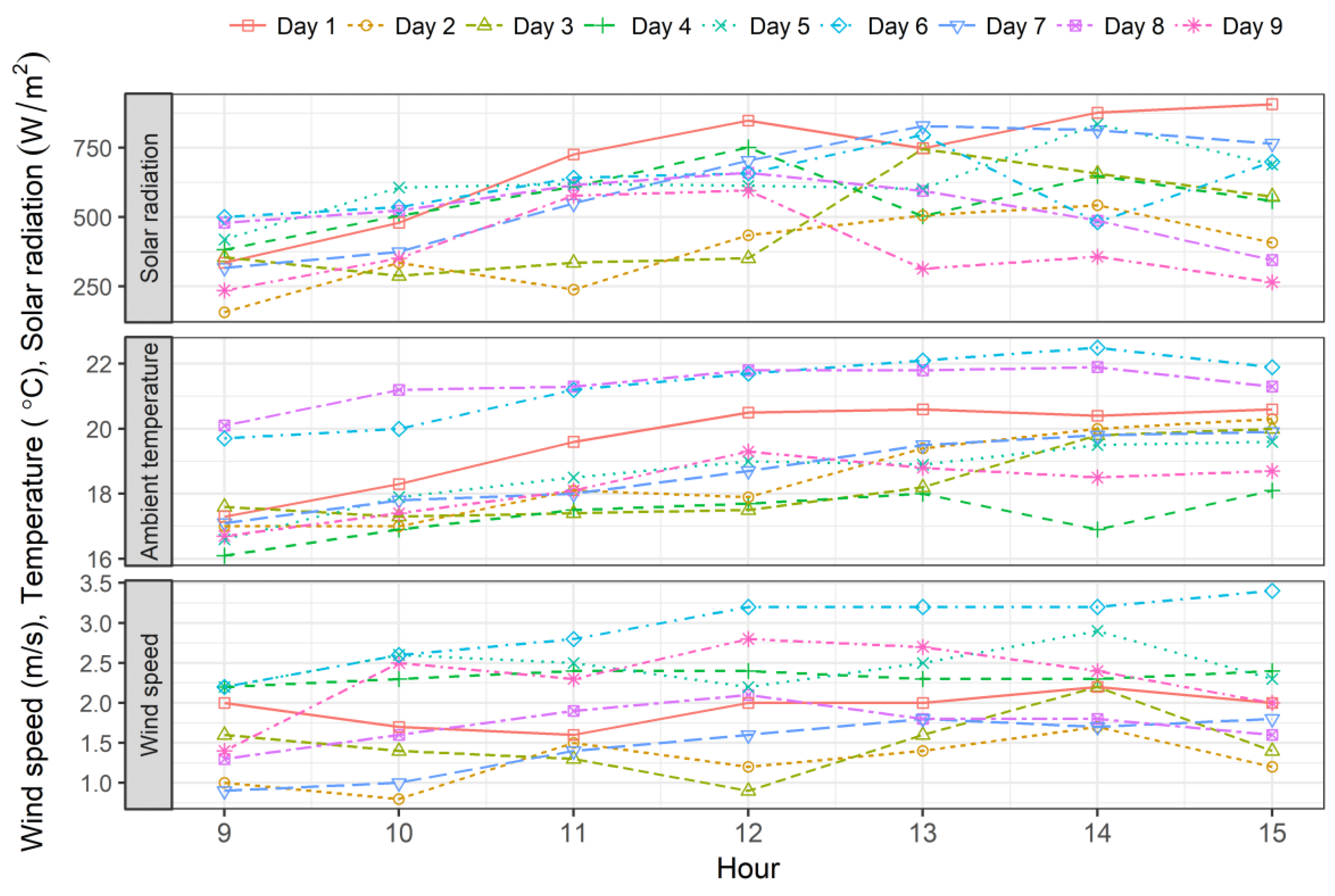
3.1. Ambient Weather Conditions during Experiment
3.2. Outlet Air Temperature of the Studied SAH
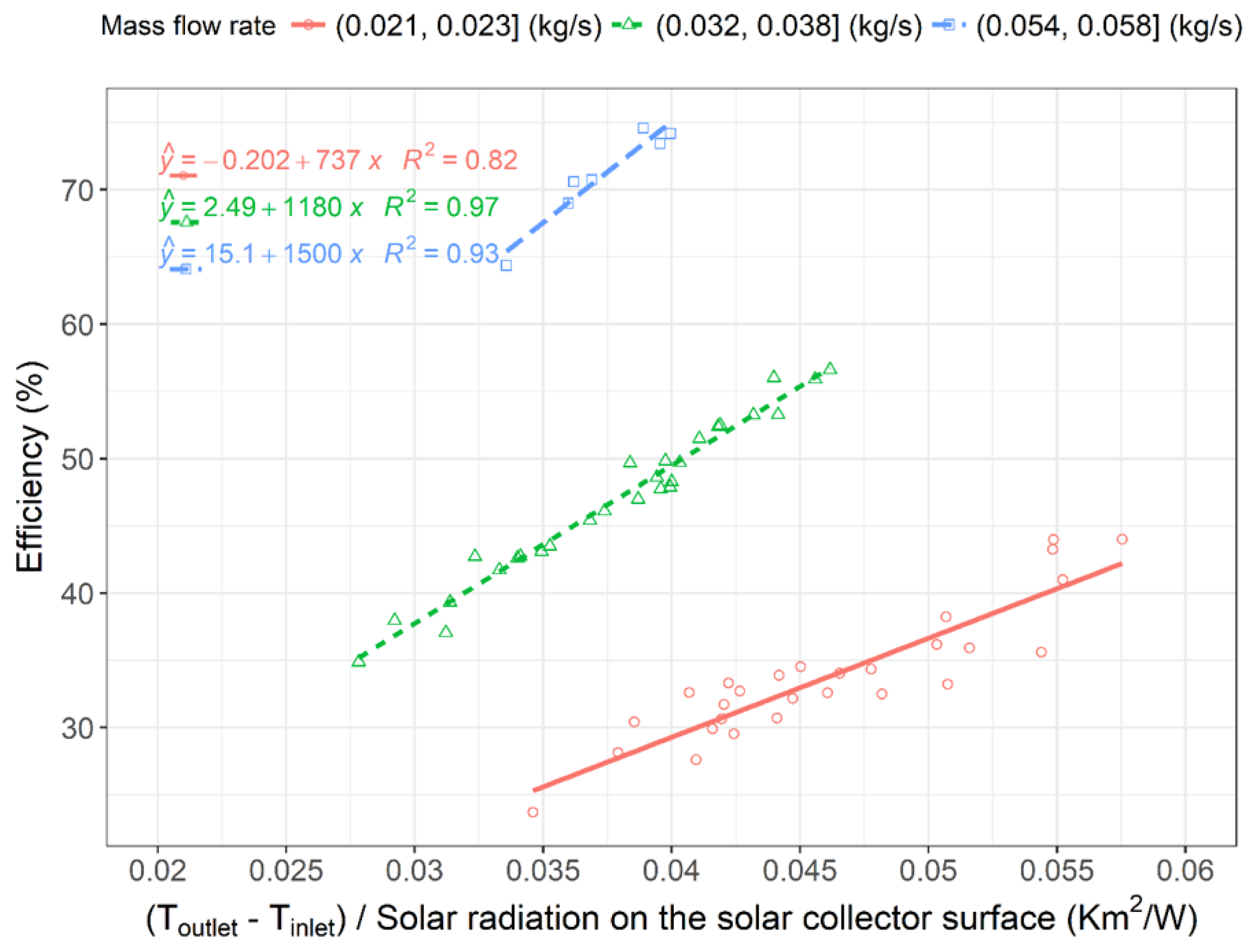
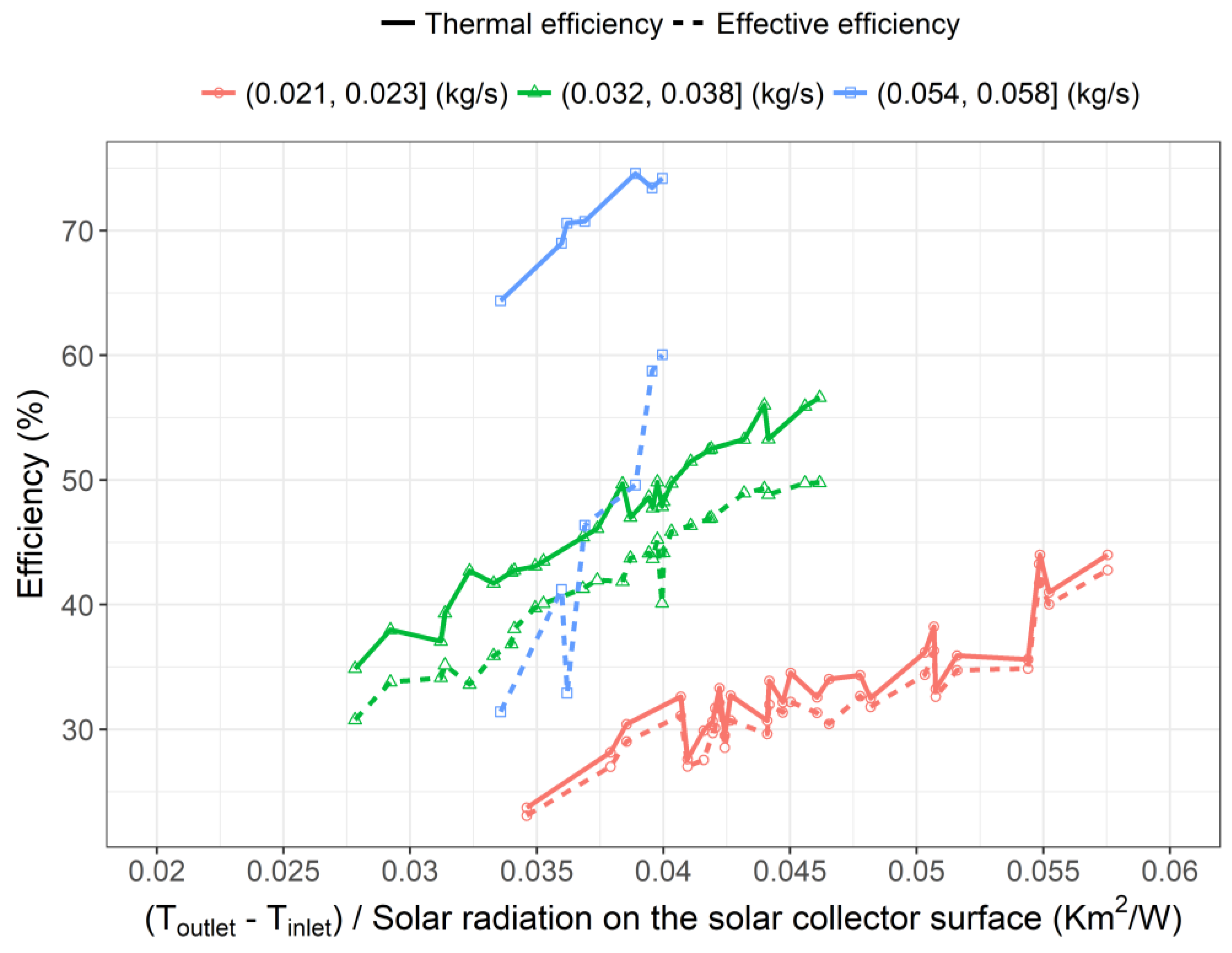
3.3. Thermal Efficiency and Effective Efficiency of the Studied Solar Air Heater
3.4. Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| the declination angle | |
| the nth day of the year |
| the extra-terrestrial radiation incident on the plane | |
| the solar constant |
| Diffuse fraction | |
| Hourly horizontal diffuse solar radiation | |
| Hourly horizontal global solar radiation | |
| Hourly clearness index | |
| Apparent solar time | |
| Solar angle in degrees | |
| Daily clearness index | |
| Error or residual values | |
| Hourly extraterrestrial radiation |
| Diffuse solar irradiance for an inclined surface | |
| Diffuse sky irradiance | |
| Radiant intensity at normal incidence | |
| Solar constant | |
| Angle of incidence between Sun and normal to the surface | |
| Solar zenith angle | |
| Panel tilted angle (slope angle) |
References
- Esen, H.; Ozgen, F.; Esen, M.; Sengur, A. Modelling of a new solar air heater through least-squares support vector machines. Expert Syst. Appl. 2009, 36, 10673–10682. [Google Scholar] [CrossRef]
- Sopian, K.; Supranto; Daud, W.R.W.; Othman, M.Y.; Yatim, B. Thermal performance of the double-pass solar collector with and without porous media. Renew. Energy 1999, 18, 557–564. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Koçyiğit, F. Energy and exergy analysis of a new flat-plate solar air heater having different obstacles on absorber plates. Appl. Energy 2010, 87, 3438–3450. [Google Scholar] [CrossRef]
- Promvonge, P.; Khanoknaiyakarn, C.; Kwankaomeng, S.; Thianpong, C. Thermal behavior in solar air heater channel fitted with combined rib and delta-winglet. Int. Commun. Heat Mass Transf. 2011, 38, 749–756. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Aboul-Enein, S.; Ramadan, M.R.I.; El-Bialy, E. Year round performance of double pass solar air heater with packed bed. Energy Convers. Manag. 2007, 48, 990–1003. [Google Scholar] [CrossRef]
- Jaurker, A.R.; Saini, J.S.; Gandhi, B.K. Heat transfer and friction characteristics of rectangular solar air heater duct using rib-grooved artificial roughness. Solar Energy 2006, 80, 895–907. [Google Scholar] [CrossRef]
- Skullong, S.; Kwankaomeng, S.; Thianpong, C.; Promvonge, P. Thermal performance of turbulent flow in a solar air heater channel with rib-groove turbulators. Int. Commun. Heat Mass Transf. 2014, 50, 34–43. [Google Scholar] [CrossRef]
- Naphon, P. On the performance and entropy generation of the double-pass solar air heater with longitudinal fins. Renew. Energy 2005, 30, 1345–1357. [Google Scholar] [CrossRef]
- Chabane, F.; Moummi, N.; Benramache, S. Experimental study of heat transfer and thermal performance with longitudinal fins of solar air heater. J. Adv. Res. 2014, 5, 183–192. [Google Scholar] [CrossRef] [PubMed]
- Bahrehmand, D.; Ameri, M.; Gholampour, M. Energy and exergy analysis of different solar air collector systems with forced convection. Renew. Energy 2015, 83, 1119–1130. [Google Scholar] [CrossRef]
- Yang, M.; Yang, X.; Li, X.; Wang, Z.; Wang, P. Design and optimization of a solar air heater with offset strip fin absorber plate. Appl. Energy 2014, 113, 1349–1362. [Google Scholar] [CrossRef]
- Dhiman, P.; Thakur, N.S.; Chauhan, S.R. Thermal and thermohydraulic performance of counter and parallel flow packed bed solar air heaters. Renew. Energy 2012, 46, 259–268. [Google Scholar] [CrossRef]
- Hernández, A.L.; Quiñonez, J.E. Analytical models of thermal performance of solar air heaters of double-parallel flow and double-pass counter flow. Renew. Energy 2013, 55, 380–391. [Google Scholar] [CrossRef]
- Yeh, H.M.; Lin, T.T. Efficiency improvement of flat-plate solar air heaters. Energy 1996, 21, 435–443. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Aboul-Enein, S.; Ramadan, M.R.I.; Shalaby, S.M.; Moharram, B.M. Thermal performance investigation of double pass-finned plate solar air heater. Appl. Energy 2011, 88, 1727–1739. [Google Scholar] [CrossRef]
- El-Sebaii, A.A.; Aboul-Enein, S.; Ramadan, M.R.I.; Shalaby, S.M.; Moharram, B.M. Investigation of thermal performance of-double pass-flat and v-corrugated plate solar air heaters. Energy 2011, 36, 1076–1086. [Google Scholar] [CrossRef]
- Karim, M.; Hawlader, M. Performance investigation of flat plate, v-corrugated and finned air collectors. Energy 2006, 31, 452–470. [Google Scholar] [CrossRef]
- Ozgen, F.; Esen, M.; Esen, H. Experimental investigation of thermal performance of a double-flow solar air heater having aluminium cans. Renew. Energy 2009, 34, 2391–2398. [Google Scholar] [CrossRef]
- Omojaro, A.P.; Aldabbagh, L.B.Y. Experimental performance of single and double pass solar air heater with fins and steel wire mesh as absorber. Appl. Energy 2010, 87, 3759–3765. [Google Scholar] [CrossRef]
- El-khawajah, M.F.; Aldabbagh, L.B.Y.; Egelioglu, F. The effect of using transverse fins on a double pass flow solar air heater using wire mesh as an absorber. Solar Energy 2011, 85, 1479–1487. [Google Scholar] [CrossRef]
- Esen, H. Experimental energy and exergy analysis of a double-flow solar air heater having different obstacles on absorber plates. Build. Environ. 2008, 43, 1046–1054. [Google Scholar] [CrossRef]
- Aldabbagh, L.B.Y.; Egelioglu, F.; Ilkan, M. Single and double pass solar air heaters with wire mesh as packing bed. Energy 2010, 35, 3783–3787. [Google Scholar] [CrossRef]
- Mahmood, A.J.; Aldabbagh, L.B.Y.; Egelioglu, F. Investigation of single and double pass solar air heater with transverse fins and a package wire mesh layer. Energy Convers. Manag. 2015, 89, 599–607. [Google Scholar] [CrossRef]
- Nowzari, R.; Aldabbagh, L.B.Y.; Egelioglu, F. Single and double pass solar air heaters with partially perforated cover and packed mesh. Energy 2014, 73, 694–702. [Google Scholar] [CrossRef]
- Cengel, Y.A. Thermodynamics: An Engineering Approach, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2015; p. 996. [Google Scholar]
- Lamigueiro, P.O. solaR: Solar Radiation and Photovoltaic Systems with R. J. Stat. Softw. 2012, 50, 1–32. [Google Scholar]
- Spencer, J.W. Fourier Series Representation of the Position of the Sun. Search 1971, 2, 172. [Google Scholar]
- Ridley, B.; Boland, J.; Lauret, P. Modelling of diffuse solar fraction with multiple predictors. Renew. Energy 2010, 35, 478–483. [Google Scholar] [CrossRef]
- Boland, J. Tools for Estimating Solar Radiation on Inclined Surfaces. Available online: http://www.lowcarbonlivingcrc.com.au/sites/all/files/event_file_attachments/session_2_-_estimating_solar_radiation_prof_j_boland.pdf (accessed on 13 March 2016).
- Hay, J.E.; McKay, D.C. Estimating Solar Irradiance on Inclined Surfaces: A Review and Assessment of Methodologies. Int. J. Solar Energy 1985, 3, 203. [Google Scholar] [CrossRef]
- Cortés, A.; Piacentini, R. Improvement of the efficiency of a bare solar collector by means of turbulence promoters. Appl. Energy 1990, 36, 253–261. [Google Scholar] [CrossRef]
- Mittal, M.K.; Varshney, L. Optimal thermohydraulic performance of a wire mesh packed solar air heater. Solar Energy 2006, 80, 1112–1120. [Google Scholar] [CrossRef]
- Sopian, K.; Alghoul, M.A.; Alfegi, E.M.; Sulaiman, M.Y.; Musa, E.A. Evaluation of thermal efficiency of double-pass solar collector with porous–nonporous media. Renew. Energy 2009, 34, 640–645. [Google Scholar] [CrossRef]
- McGowan, P. A Thermal Model for a Solar Ventilation System Used in NZ Schools. Master’s Dissertation, Massey University, Auckland, New Zealand, 2016. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2016. [Google Scholar]
- Tyagi, V.V.; Panwar, N.L.; Rahim, N.A.; Kothari, R. Review on solar air heating system with and without thermal energy storage system. Renew. Sustain. Energy Rev. 2012, 16, 2289–2303. [Google Scholar] [CrossRef]
- Wang, Y.; Boulic, M.; Phipps, R.; Plagmann, M.; Cunningham, C.; Theobald, C.; Howden-Chapman, P.; Baker, M. Impacts of a solar ventilation unit on temperature and ventilation rate in New Zealand schools: An intervention study. In Proceedings of the 14th International Conference of Indoor Air Quality and Climate, Ghent, Belgium, 3–7 July 2016. [Google Scholar]
- Boulic, M.; Wang, Y.; Phipps, R.; Plagmann, M.; Cunningham, C.; Theobald, C.; Howden-Chapman, P.; Baker, M. Increasing the ventilation rate and temperature in New Zealand classrooms using a solar roof collector. In Proceedings of the Central European towards Sustainable Building, Prague, Czech Repubic, 2–4 July 2019. [Google Scholar]
- Prasad, S.B.; Saini, J.S.; Singh, K.M. Investigation of heat transfer and friction characteristics of packed bed solar air heater using wire mesh as packing material. Solar Energy 2009, 83, 773–783. [Google Scholar] [CrossRef]

| Study | Air Mass Flow Rate (kg/s) | Cover | Flow Type | Absorber Layer | Efficiency (%) | Reference |
|---|---|---|---|---|---|---|
| 1 | 0.010 kg/s; 0.020 kg/s; 0.030 kg/s; 0.040 kg/s; 0.050 kg/s; 0.060 kg/s. | Double glazed | Double parallel pass; Placing the absorber plate in the middle of the air channel forming the equal upper and lower flow channel. | Type 1: flat plate; Type 2: longitudinal fins below and above the absorber layer; Type 3: V-corrugated shaped absorber layer. | Type 3 was 11% to 14% more efficiency than Type 1; Type 3 was 9% to 12% more efficient than Type 2; Maximum efficiencies at air mass flow rate of 0.060 kg/s: Type 1: 58%; Type 2: 56%; Type 3: 65%. | [15,16] |
| 2 | 0.010 kg/s; 0.020 kg/s; 0.030 kg/s; 0.040 kg/s; 0.050 kg/s; 0.060 kg/s. | Single glazed | Type 1, 2, 3 single pass under the absorber layer; Type 4, 5, 6 double counter pass. First channel was formed by the glass cover and the absorber layer. Second channel was formed by the absorber layer and the insulation layer. | Type 1 and Type 4: flat plate; Type 2 and Type 5: longitudinal fins below the absorber layer; Type 3 and Type 6: V-corrugated shape absorber layer. | Maximum efficiencies at air mass flow rate of 0.060 kg/s: Type 1: 65%; Type 2: 69%; Type 3: 75%; Type 4: 78%; Type 5: 79%; Type 6: 82%. | [17] |
| 3 | 0.012 kg/s; 0.016 kg/s. | Single glazed | Single pass | Type 1: galvanized iron sheet with 0.5 mm thick black chrome selective coating, without fins; Type 2: five longitudinal and hollow semi-cylindrical fins located below the absorber layer | Maximum efficiencies at air mass flow rate of 0.012 kg/s and 0.016 kg/s: Type 1: 35% and 44% respectively; Type 2: 40% and 52% respectively. | [9] |
| 4 | 0.030 kg/s; 0.050 kg/s. | Single glazed | Double parallel pass; Placing the absorber layer in the middle of the air channel forming the upper and lower flow channel. | Absorber layer was formed by aluminum cans. Type 1: flat aluminum plate with zag-zig staggered arranged aluminum cans on both sides; Type 2: flat aluminum plate with orderly arranged aluminum cans on both side; Type 3: flat aluminum plate with no cans on both sides. | The maximum efficiency (73%) was found in Type 1 SAH at air mass flow rate of 0.050 kg/s. Mean efficiencies at air mass flow rate 0.030 kg/s and 0.050 kg/s respectively: Type 1: 41% and 55%; Type 2: 36% and 47%; Type 3: 31% and 43%. | [18] |
| 5 | 0.012 kg/s to 0.038 kg/s | Double glazed; | Type 1: Single pass through wire mesh; Type 2: Double counter pass through wire mesh. | A steel wire mesh with fins. | Maximum efficiencies at air mass flow rate of 0.038 kg/s: Type 1: 60%; Type 2: 64%. | [19] |
| 6 | 0.012 kg/s to 0.042 kg/s | Double glazed; | Double pass; First flow channel was formed by the two glass layers; Second flow channel was formed by the lower glass cover and the absorber layer. | Wire mesh layers between the fins; Type 1: With 2 fins attached; Type 2: With 4 fins attached; Type 3: With 6 fins attached. | Maximum efficiencies at air mass flow rate of 0.042 kg/s: Type 1: 75%; Type 2: 82%; Type 3: 86%. | [20] |
| Device | Monitored Parameters | Range | Accuracy |
|---|---|---|---|
| HP2000 weather station | Solar irradiance (W/m2) | 0–3000 W/m2 | ±15% |
| Ambient air temperature (°C) | −30–65 °C | ±1 °C | |
| Wind speed (m/s) | 0–50 m/s | ± 1 m/s (wind speed <5 m/s); ± 10% (wind speed >5 m/s) | |
| AM4214SD hot wire anemometer | Outlet air velocity (m/s) | 0.2–25 m/s | ±5% of reading |
| Outlet air temperature (°C) | 0–50 °C | ±0.8 °C |
| Air Temperature (K) | Air Density (kg/m3) | Air specific Heat Capacity (J/(kg*K)) | Air Dynamic Viscosity × 10−5 (kg/(m*s)) |
|---|---|---|---|
| [273.15, 283.15] | 1.269 | 1006 | 1.748 |
| [283.15, 293.15] | 1.225 | 1007 | 1.797 |
| [293.15, 303.15] | 1.184 | 1007 | 1.844 |
| [303.15, 313.15] | 1.145 | 1007 | 1.892 |
| [313.15, 323.15] | 1.109 | 1007 | 1.938 |
| [323.15, 333.15] | 1.076 | 1007 | 1.984 |
| [333.15, 343.15] | 1.044 | 1007 | 2.029 |
| Test Day | Solar Radiation (W/m2) | Ambient Temperature (°C) | Wind Speed (m/s) |
|---|---|---|---|
| Day 1 | 703.3 ± 286.6 | 19.6 ± 1.3 | 1.9 ± 1.1 |
| Day 2 | 374.8 ± 161.6 | 18.5 ± 1.3 | 1.3 ± 1.0 |
| Day 3 | 473.6 ± 255.8 | 18.3 ± 1.1 | 1.5 ± 1.1 |
| Day 4 | 566.7 ± 277.9 | 17.3 ± 0.8 | 2.3 ± 1.3 |
| Day 5 | 626.5 ± 299.2 | 18.6 ± 1.0 | 2.5 ± 1.4 |
| Day 6 | 616.5 ± 252.2 | 21.3 ± 1.0 | 3.0 ± 1.5 |
| Day 7 | 622.0 ± 314.3 | 18.7 ± 1.0 | 1.5 ± 1.0 |
| Day 8 | 529.6 ± 152.8 | 21.3 ± 0.6 | 1.7 ± 1.0 |
| Day 9 | 385.3 ± 180.3 | 18.2 ± 0.9 | 2.3 ± 1.3 |
| Percent of Maximum Speed of the Ventilator (%) | Test Day | Velocity (m/s) | Air Mass Flow Rate (kg*s−1) | IT1 (W/m2) | T 2 Outlet Air (°C) | T Difference 3 (°C) |
|---|---|---|---|---|---|---|
| 50% | Day 1 | 1.5 ± 0.1 | 0.014 ± 0.006 | 552 ± 178 | 45.2 ± 9.3 | 25.5 ± 8.3 |
| Day 2 | 1.5 ± 0.1 | 0.021 ± 0.001 | 297 ± 113 | 31.6 ± 6.4 | 13.1 ± 5.6 | |
| Day 3 | 1.6 ± 0.1 | 0.021 ± 0.004 | 376 ± 153 | 34.6 ± 8.3 | 16.3 ± 7.8 | |
| Day 4 | 1.7 ± 0.1 | 0.019 ± 0.006 | 451 ± 106 | 39.5 ± 8.9 | 22.2 ± 8.7 | |
| 75% | Day 5 | 2.6 ± 0.1 | 0.034 ± 0.005 | 490 ± 112 | 37.1 ± 6.1 | 18.6 ± 5.7 |
| Day 6 | 2.7 ± 0.1 | 0.035 ± 0.004 | 478 ± 111 | 39.1 ± 5.5 | 17.8 ± 5.3 | |
| Day 7 | 2.7 ± 0.1 | 0.036 ± 0.005 | 494 ± 175 | 36.9 ± 8.9 | 18.3 ± 8.3 | |
| Day 8 | 2.7 ± 0.1 | 0.036 ± 0.002 | 414 ± 92 | 36.9 ± 5.0 | 15.5 ± 4.9 | |
| 100% | Day 9 | 4.0 ± 0.1 | 0.056 ± 0.005 | 304 ± 117 | 29.7 ± 6.3 | 11.5 ± 5.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Boulic, M.; Phipps, R.; Plagmann, M.; Cunningham, C. Experimental Performance of a Solar Air Collector with a Perforated Back Plate in New Zealand. Energies 2020, 13, 1415. https://doi.org/10.3390/en13061415
Wang Y, Boulic M, Phipps R, Plagmann M, Cunningham C. Experimental Performance of a Solar Air Collector with a Perforated Back Plate in New Zealand. Energies. 2020; 13(6):1415. https://doi.org/10.3390/en13061415
Chicago/Turabian StyleWang, Yu, Mikael Boulic, Robyn Phipps, Manfred Plagmann, and Chris Cunningham. 2020. "Experimental Performance of a Solar Air Collector with a Perforated Back Plate in New Zealand" Energies 13, no. 6: 1415. https://doi.org/10.3390/en13061415
APA StyleWang, Y., Boulic, M., Phipps, R., Plagmann, M., & Cunningham, C. (2020). Experimental Performance of a Solar Air Collector with a Perforated Back Plate in New Zealand. Energies, 13(6), 1415. https://doi.org/10.3390/en13061415






