Dynamic Stall Control around Practical Airfoil Using Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators
Abstract
1. Introduction
2. Experiments
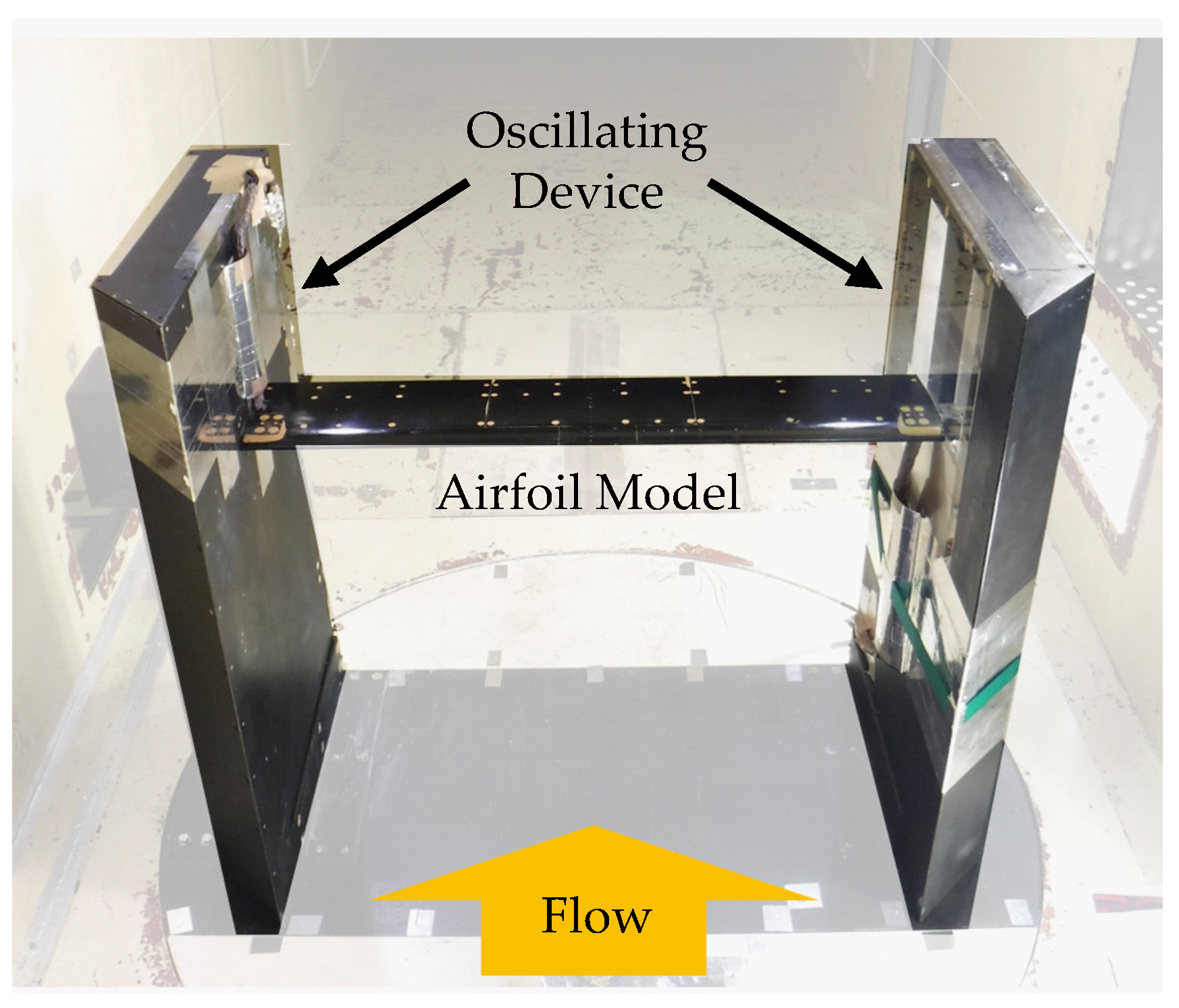
2.1. Experimental Apparatus
2.2. Experimental Conditions
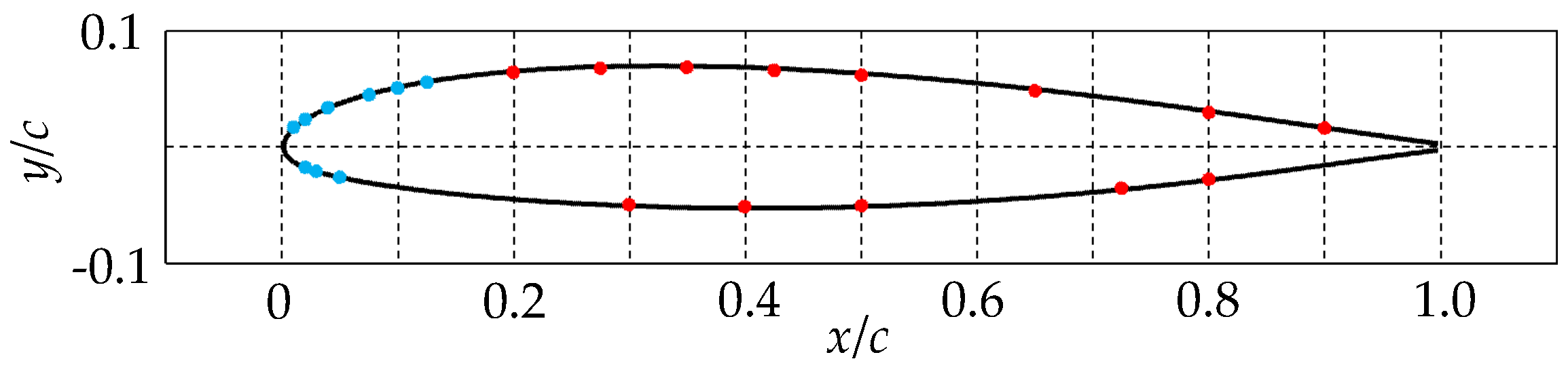
2.3. Data Processing Method
3. Results and Discussion
3.1. Reliability of Aerodynamic Coefficients
3.2. Flow Control Effect
3.3. Flow Control Effect Sensitivity of Parameters
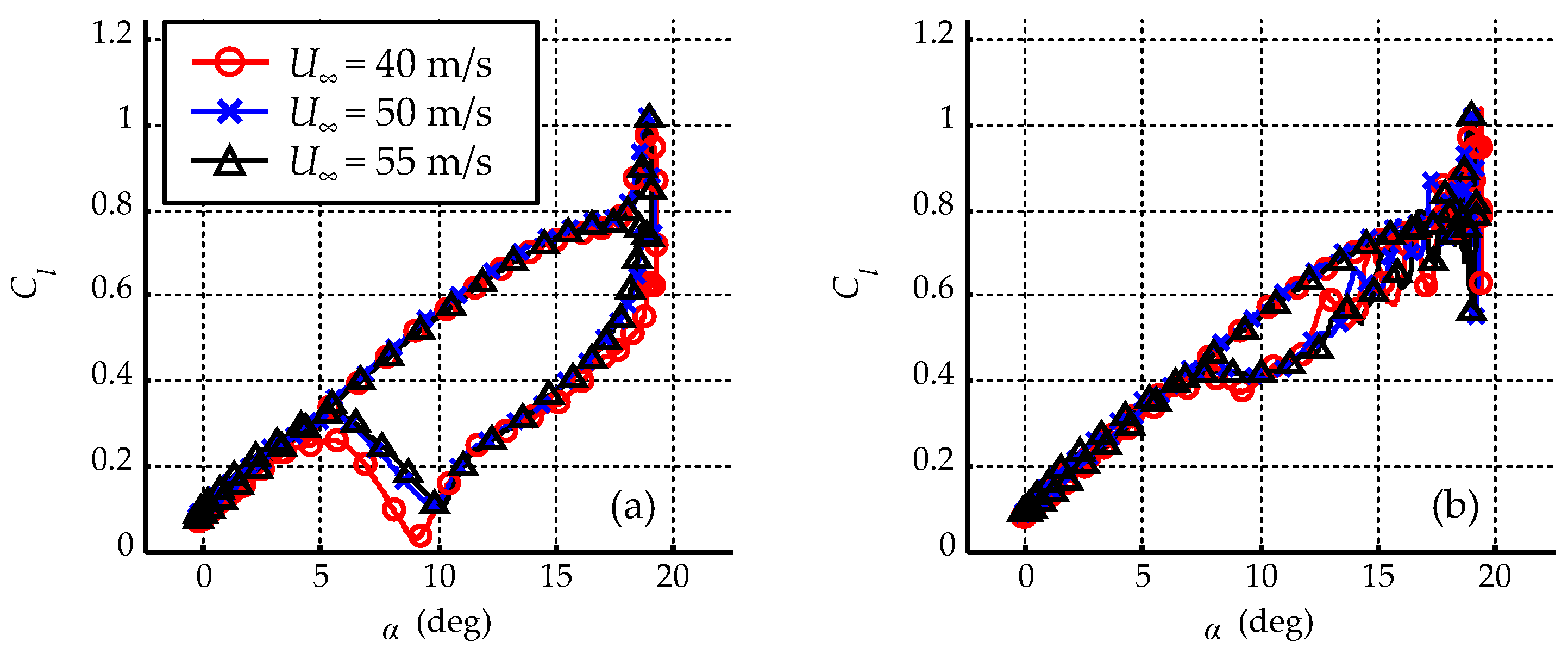
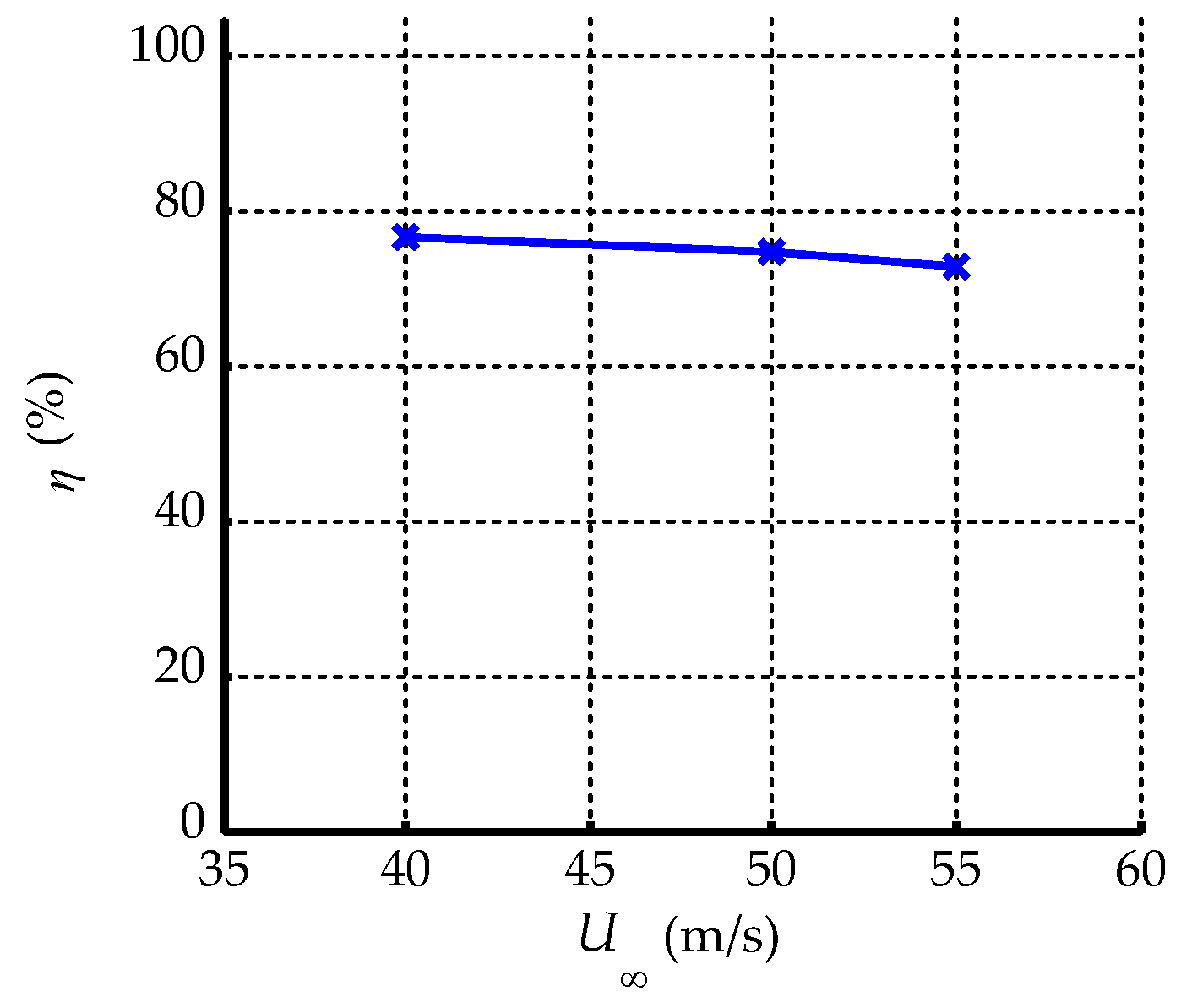
3.3.1. Freestream Velocity
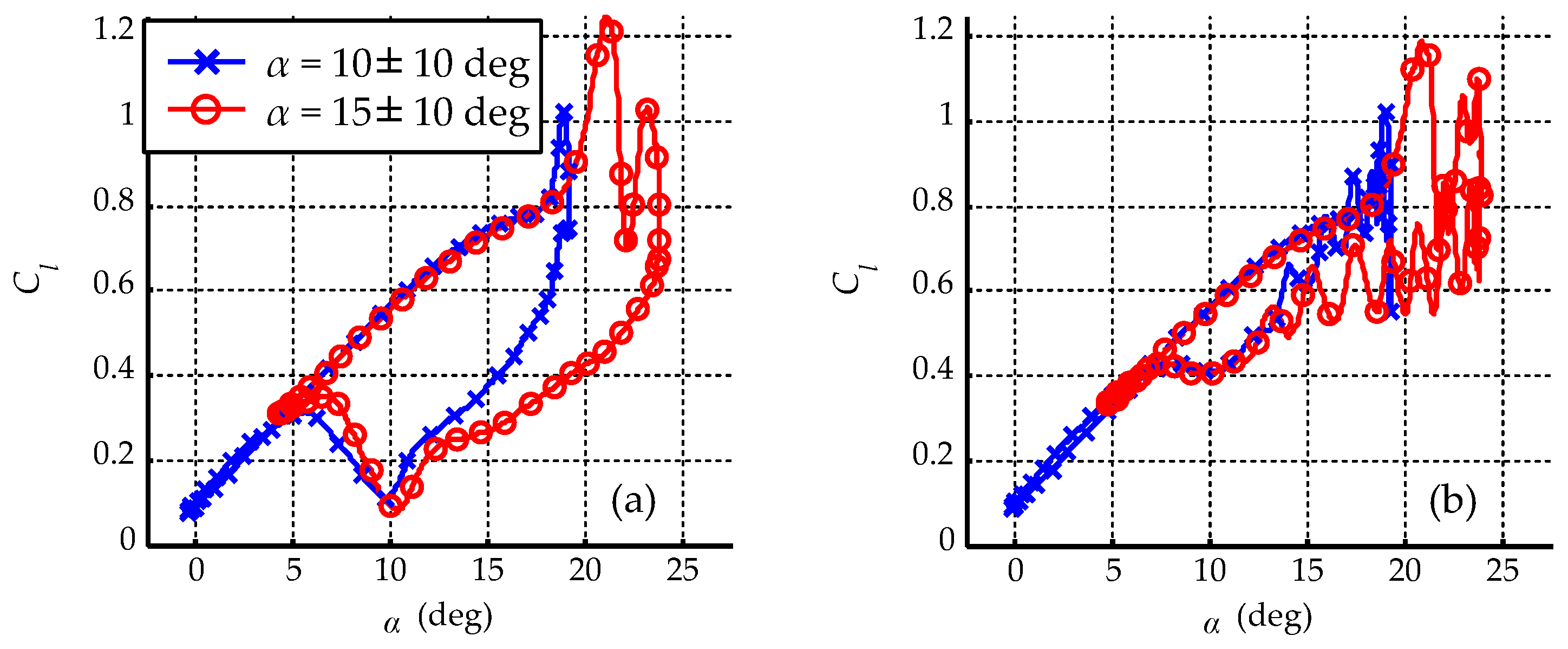
3.3.2. Mean of the Angle of Attack
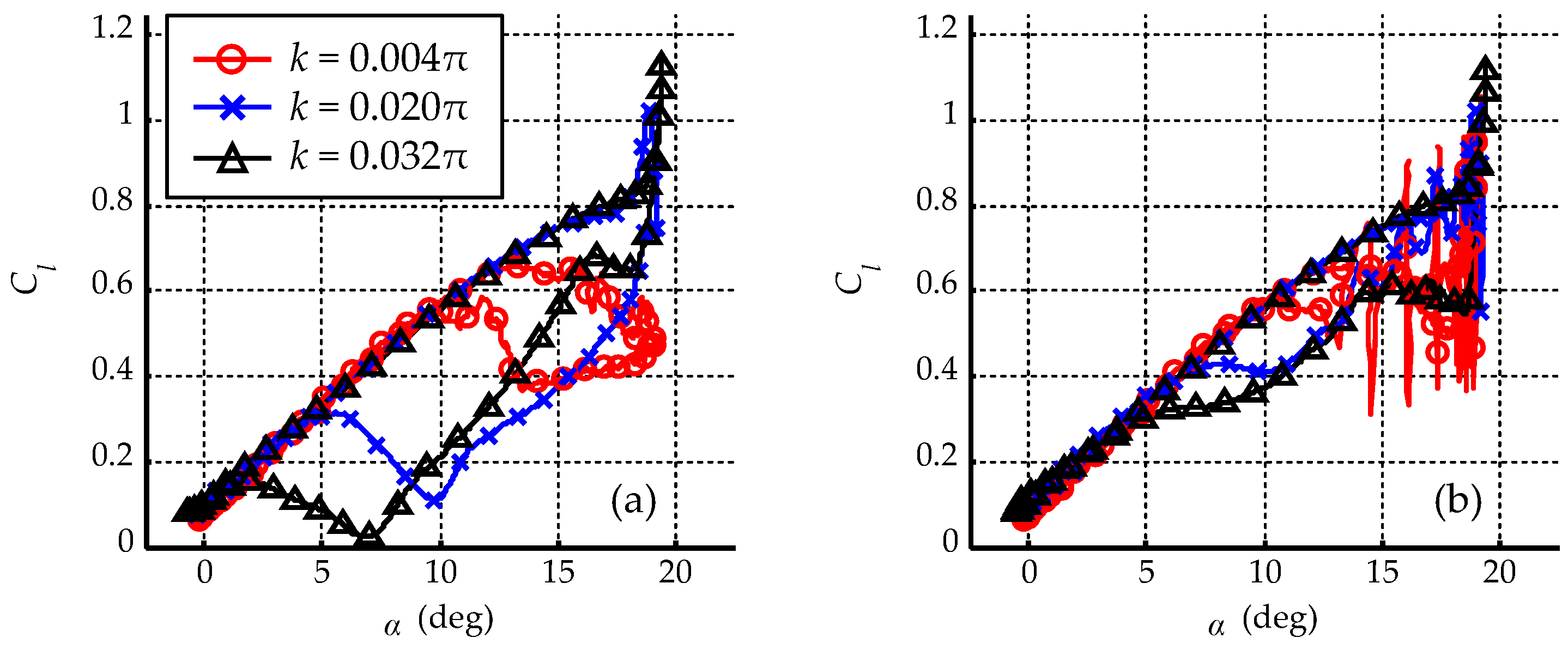
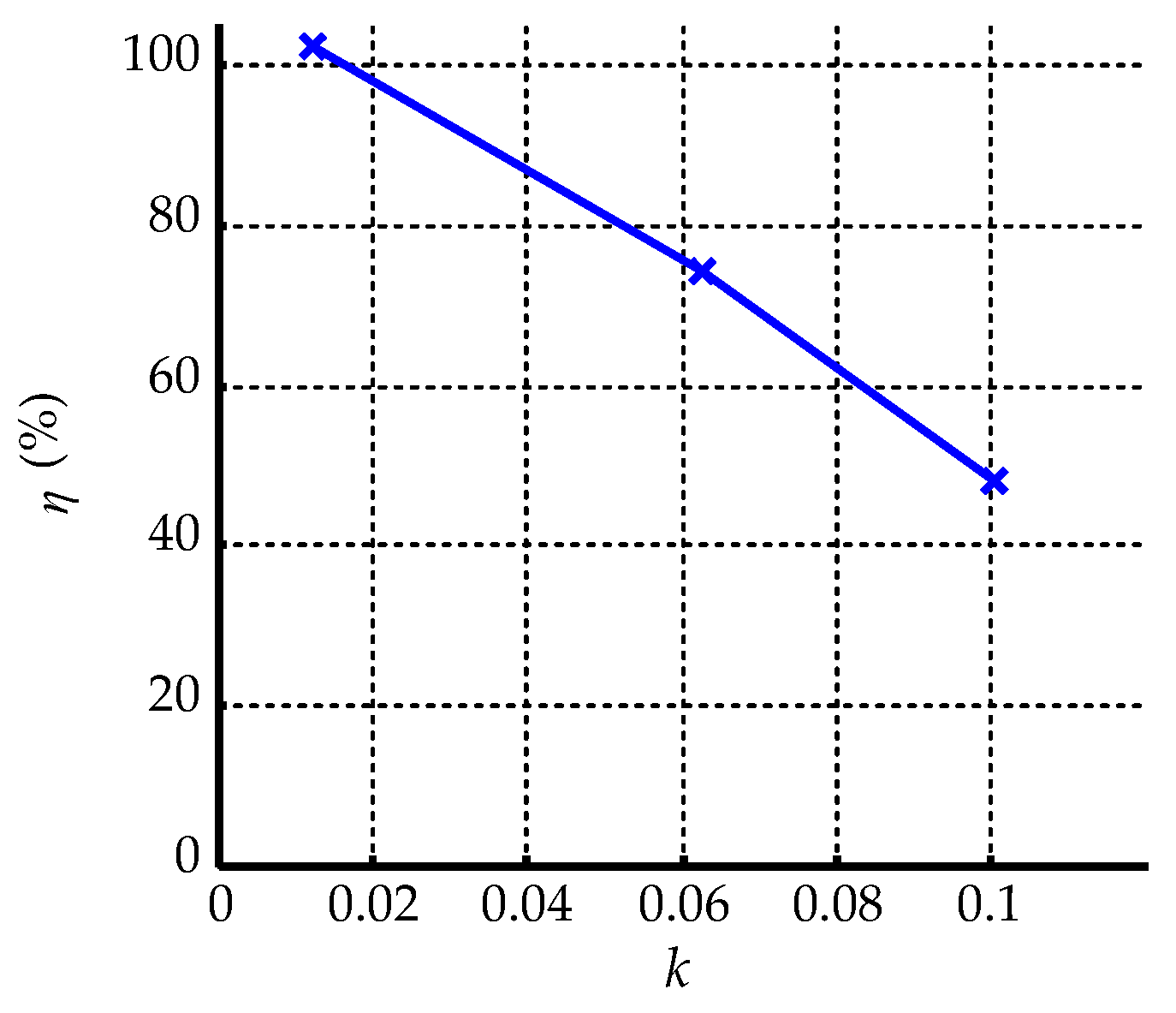
3.3.3. Reduced Frequency
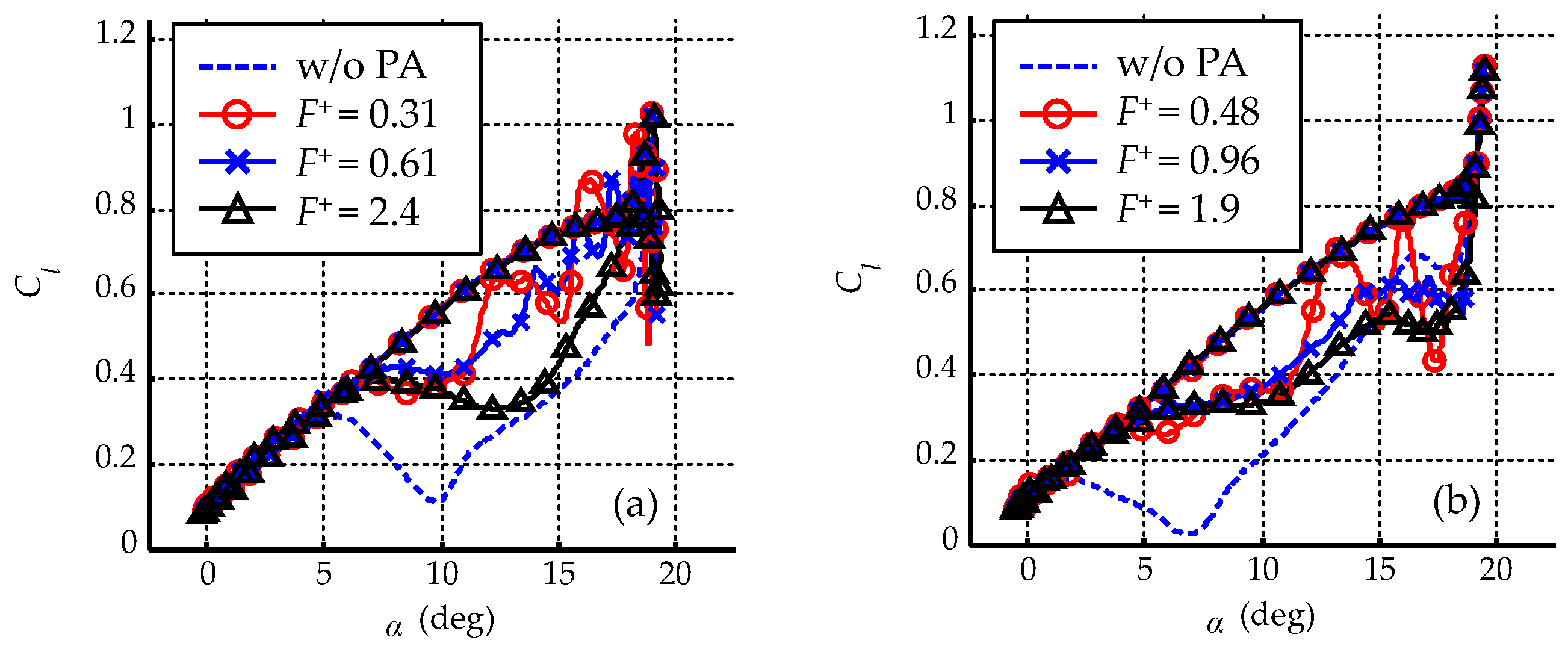
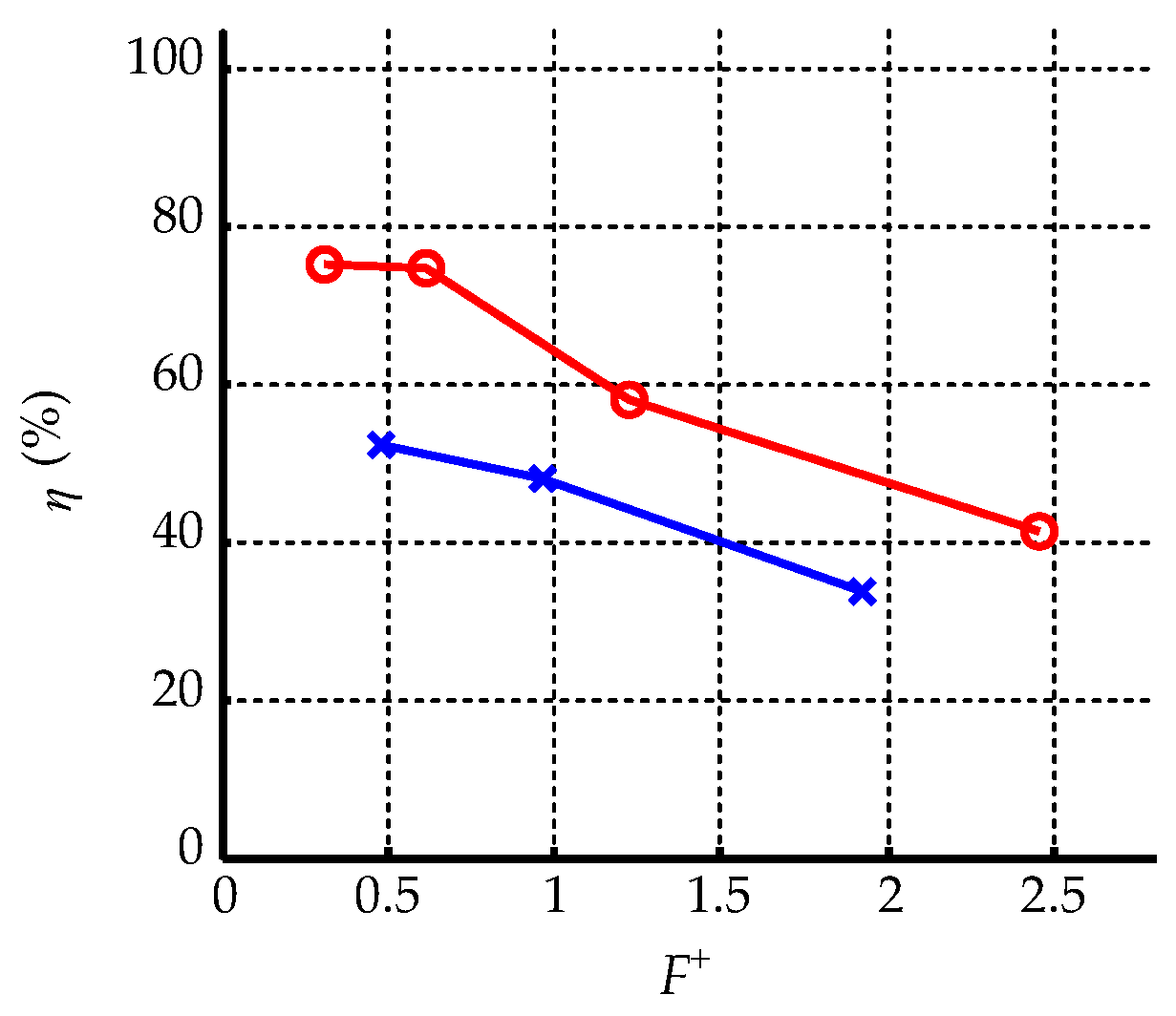
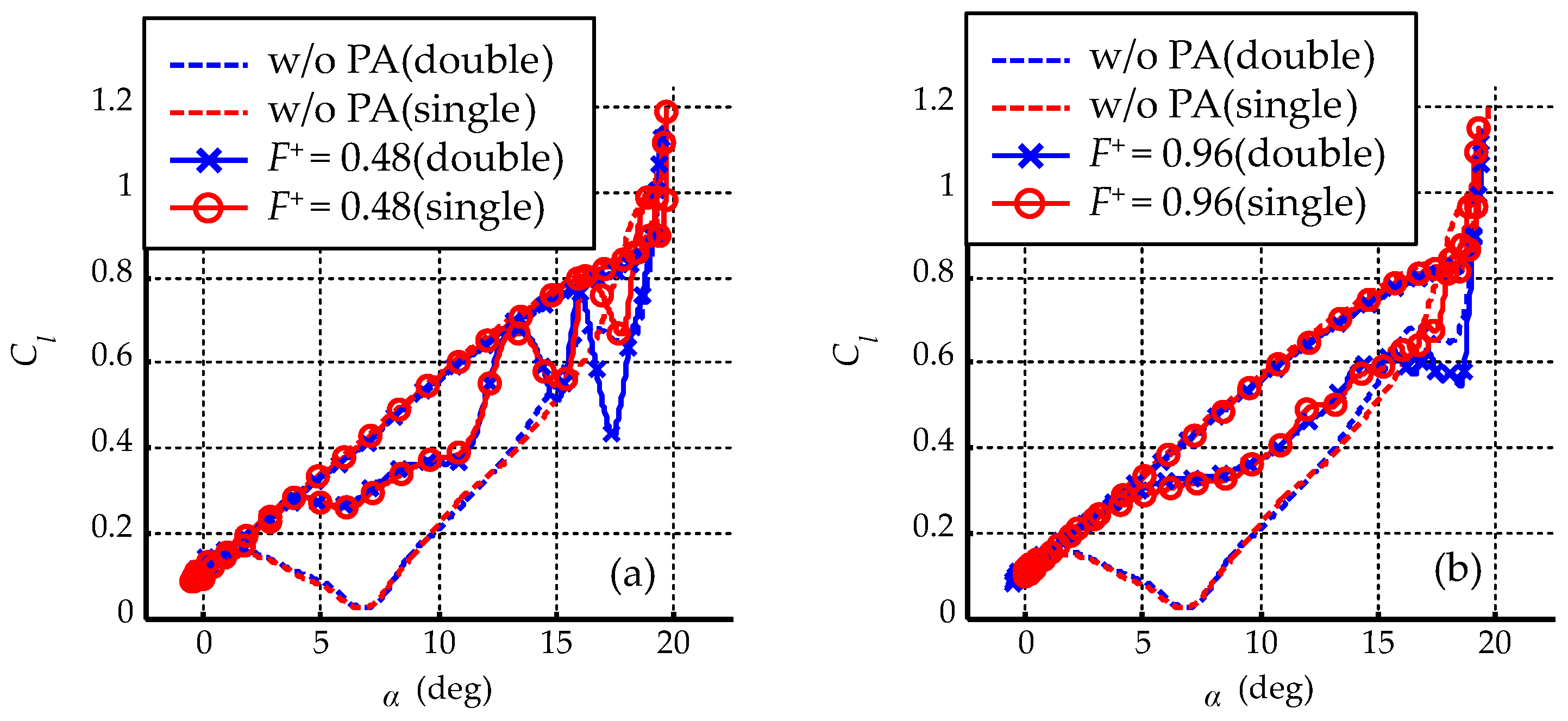
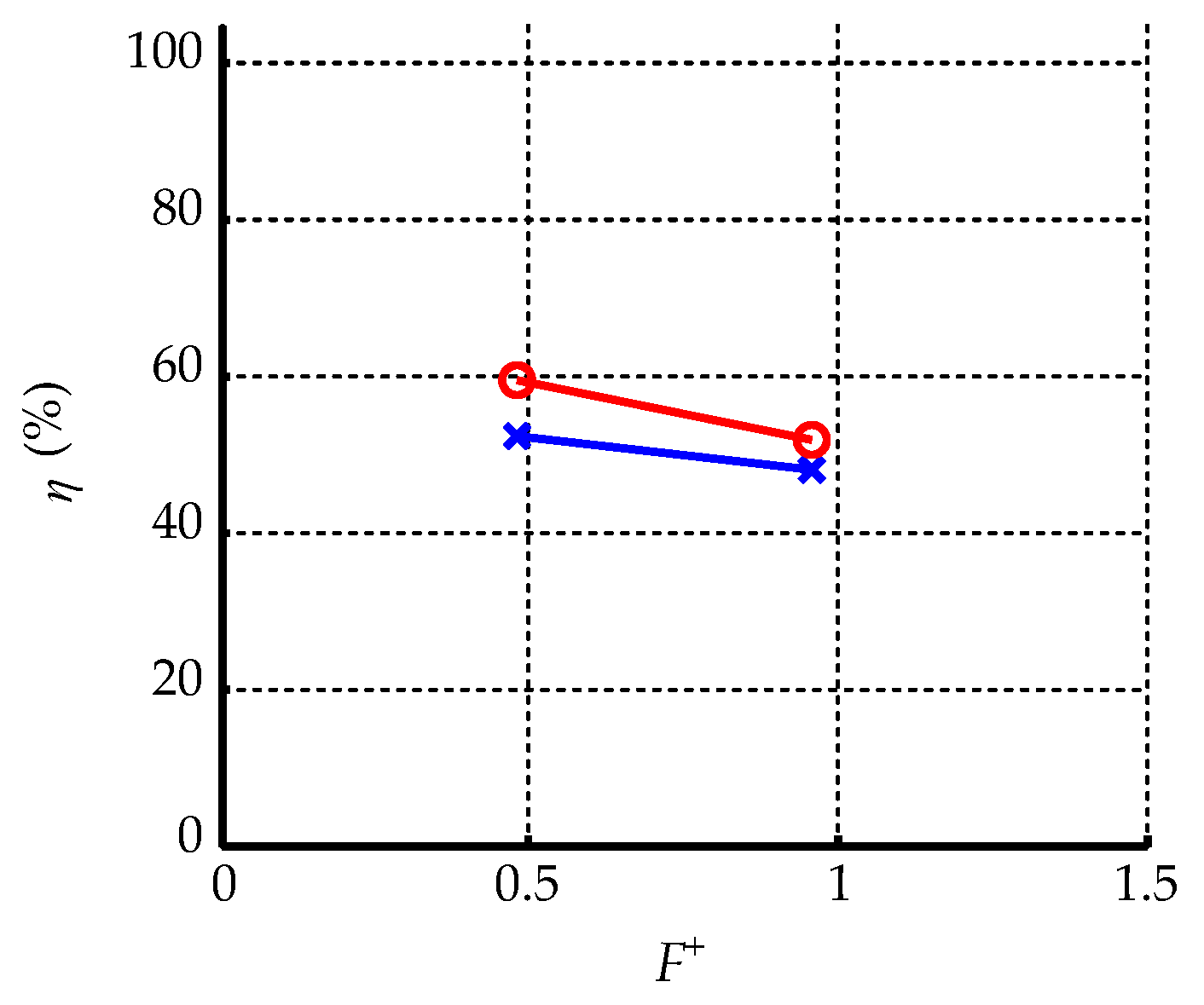
3.3.4. Nondimensional Frequency of Pulse Voltage
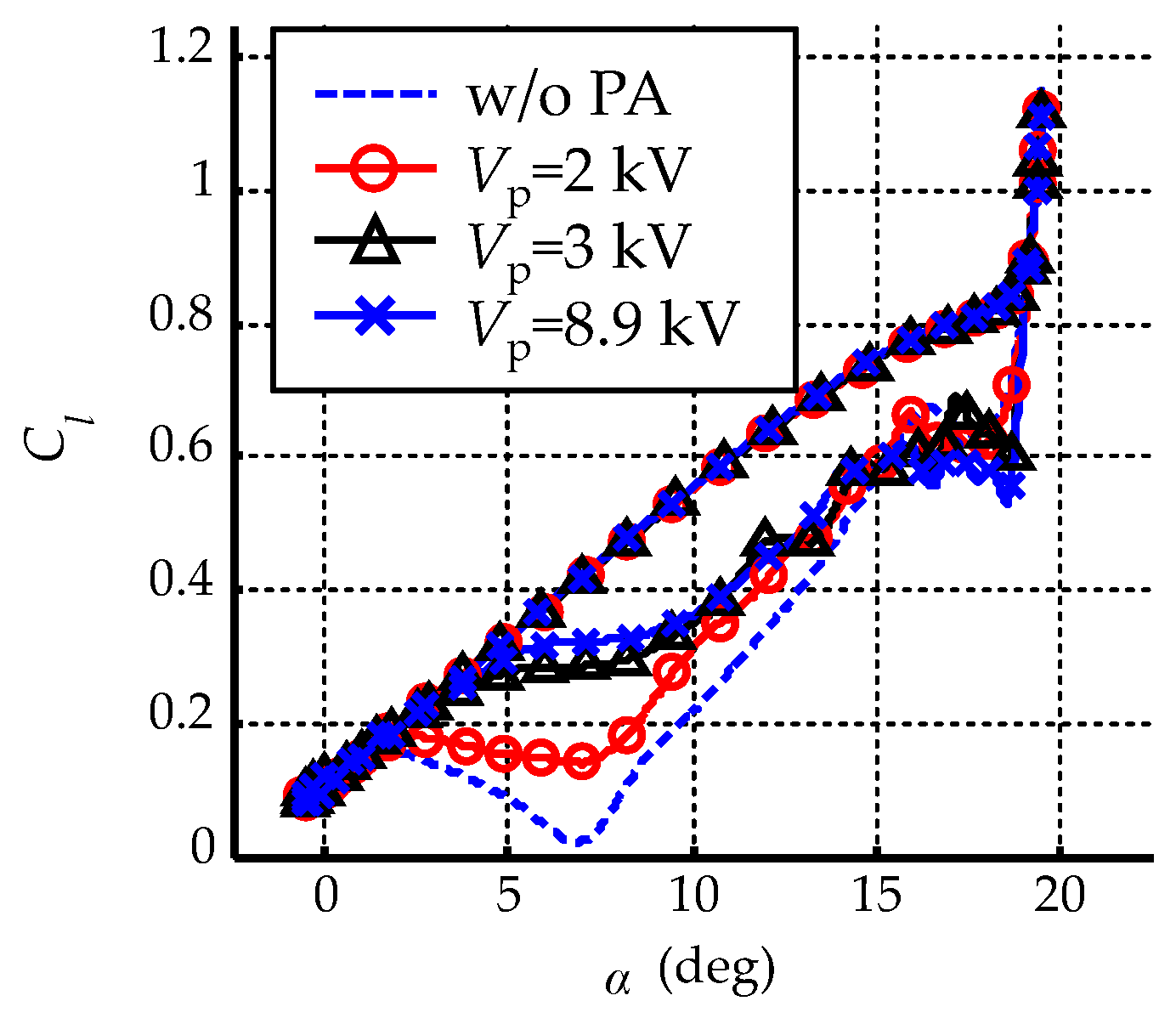
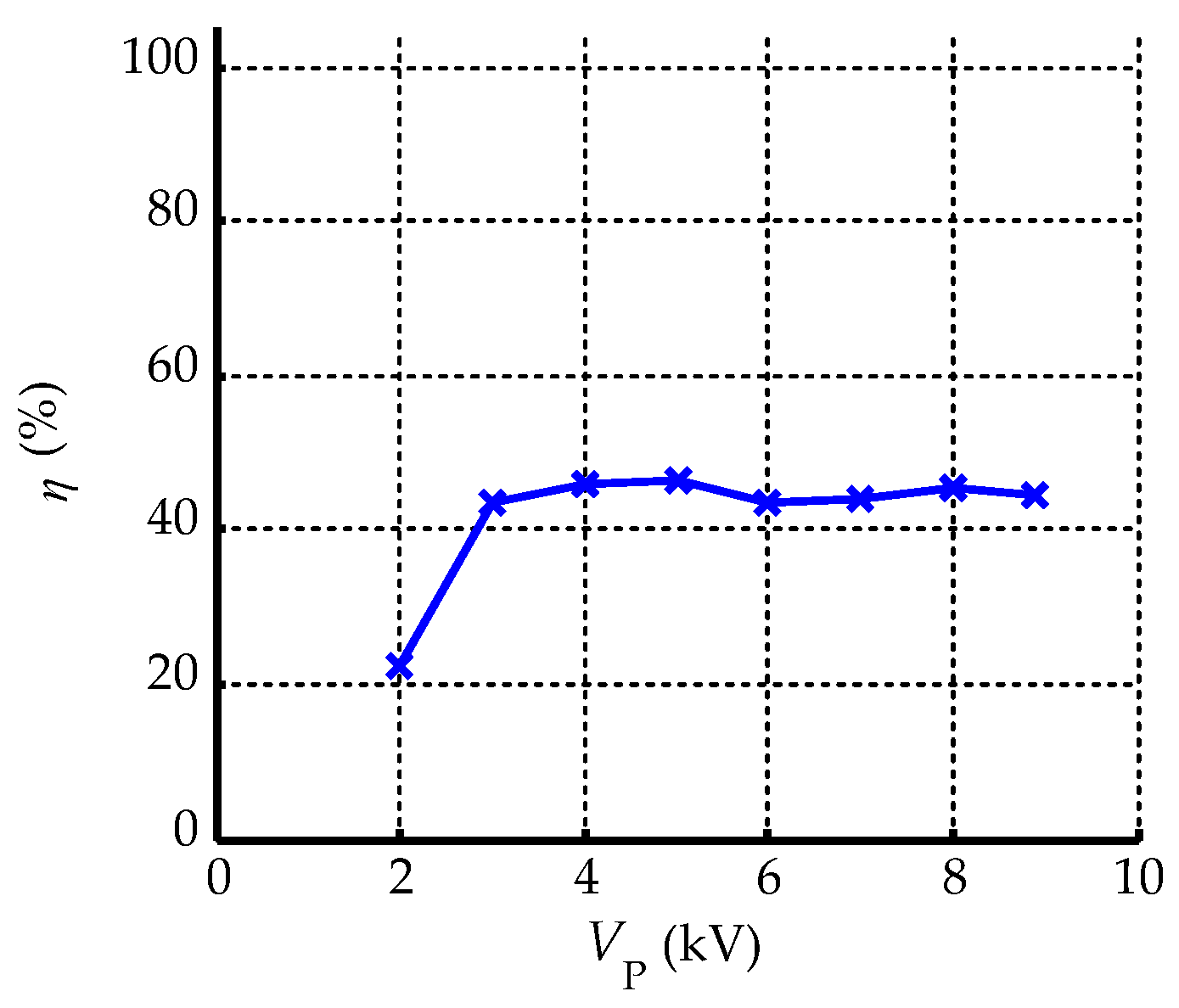
3.3.5. Peak Pulse Voltage
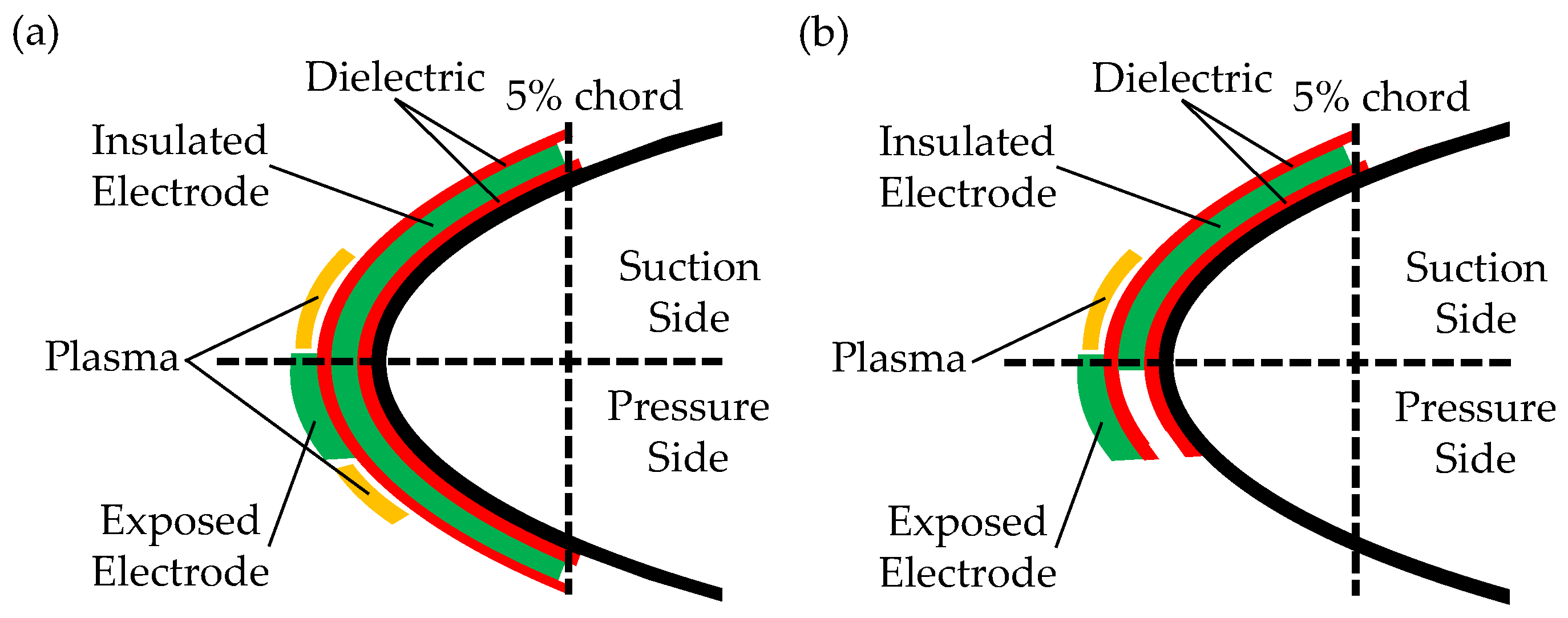
3.3.6. Type of ns-DBDPA
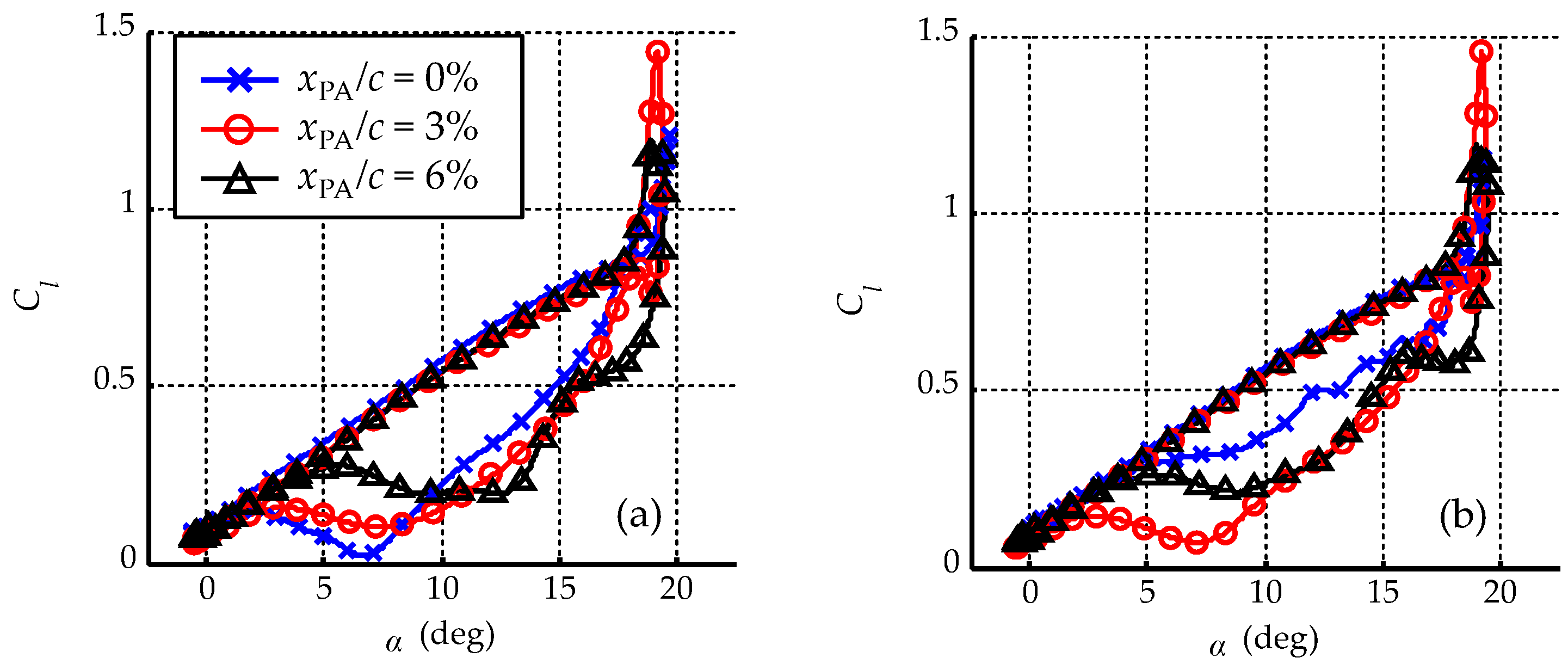
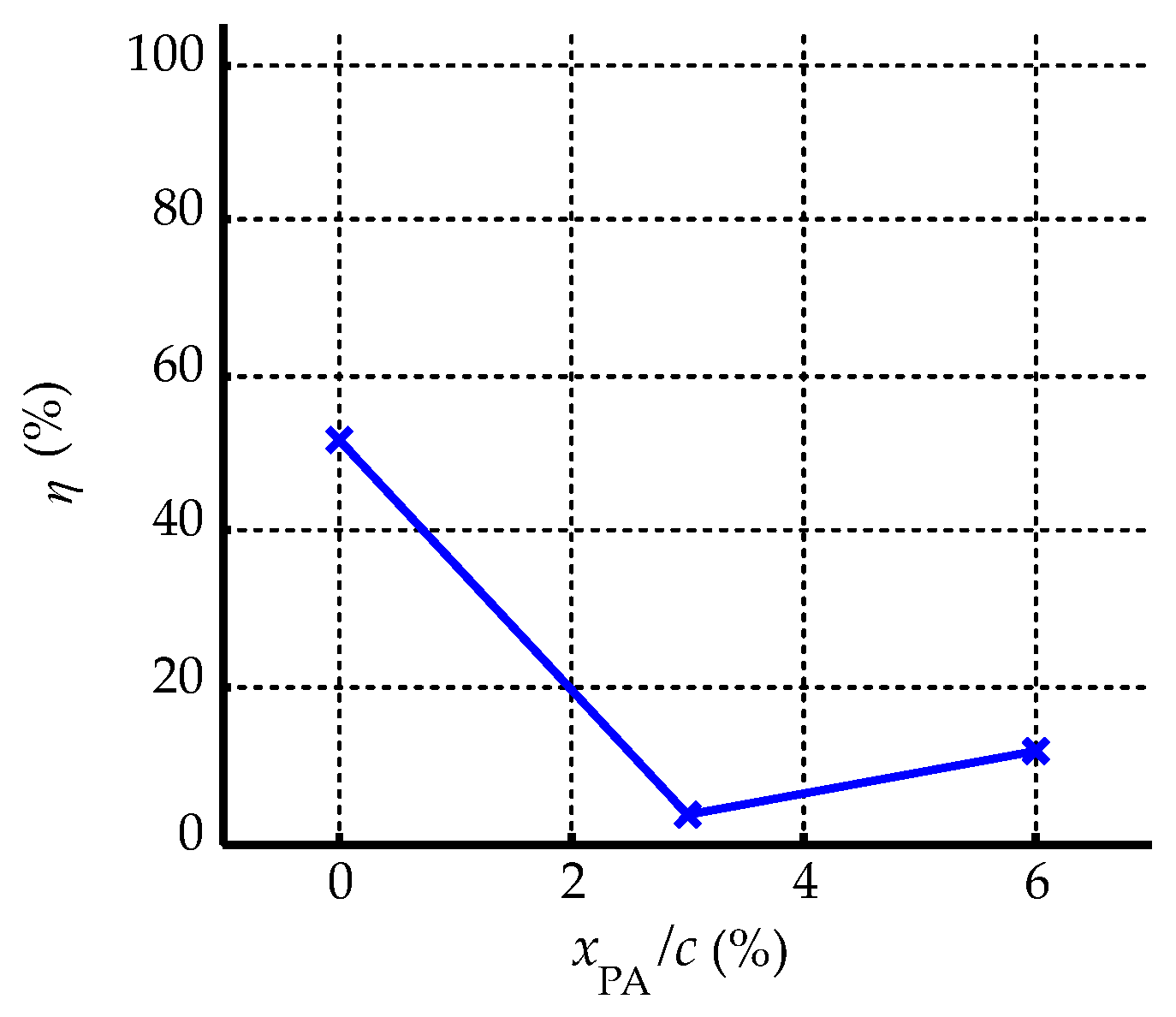
3.3.7. Position of ns-DBDPA
4. Conclusions
- The lift coefficient increases by driving the ns-DBDPA when the model is pitching down;
- The aerodynamic coefficients corresponding to the frequency of the pulse voltage fluctuate when the ns-DBDPA is applied.
- The flow control effect appears under all conditions in which the freestream velocity, the angle of attack, and the reduced frequency were set to be from 40 m/s to 55 m/s, from 10 ± 10 deg to 15 ± 10 deg, and from 0.004 to 0.032, respectively;
- Changes in the freestream velocity have little effect on the flow control effect in the range we investigated;
- The flow control effect increases as the mean of the angle of attack and the reduced frequency decrease.
- The flow control effect increases as the nondimensional frequency of the pulse voltage decreases in the range we investigated, but the amplitude of the lift coefficient fluctuation increases;
- A sufficient flow control effect is obtained when the peak pulse voltage is greater than or equal to 3 kV;
- The flow control effect is sensitive to the shape of the leading edge. The best flow control effect is obtained when the position of the ns-DBDPA is 0% in the single-discharge type in the range we investigated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
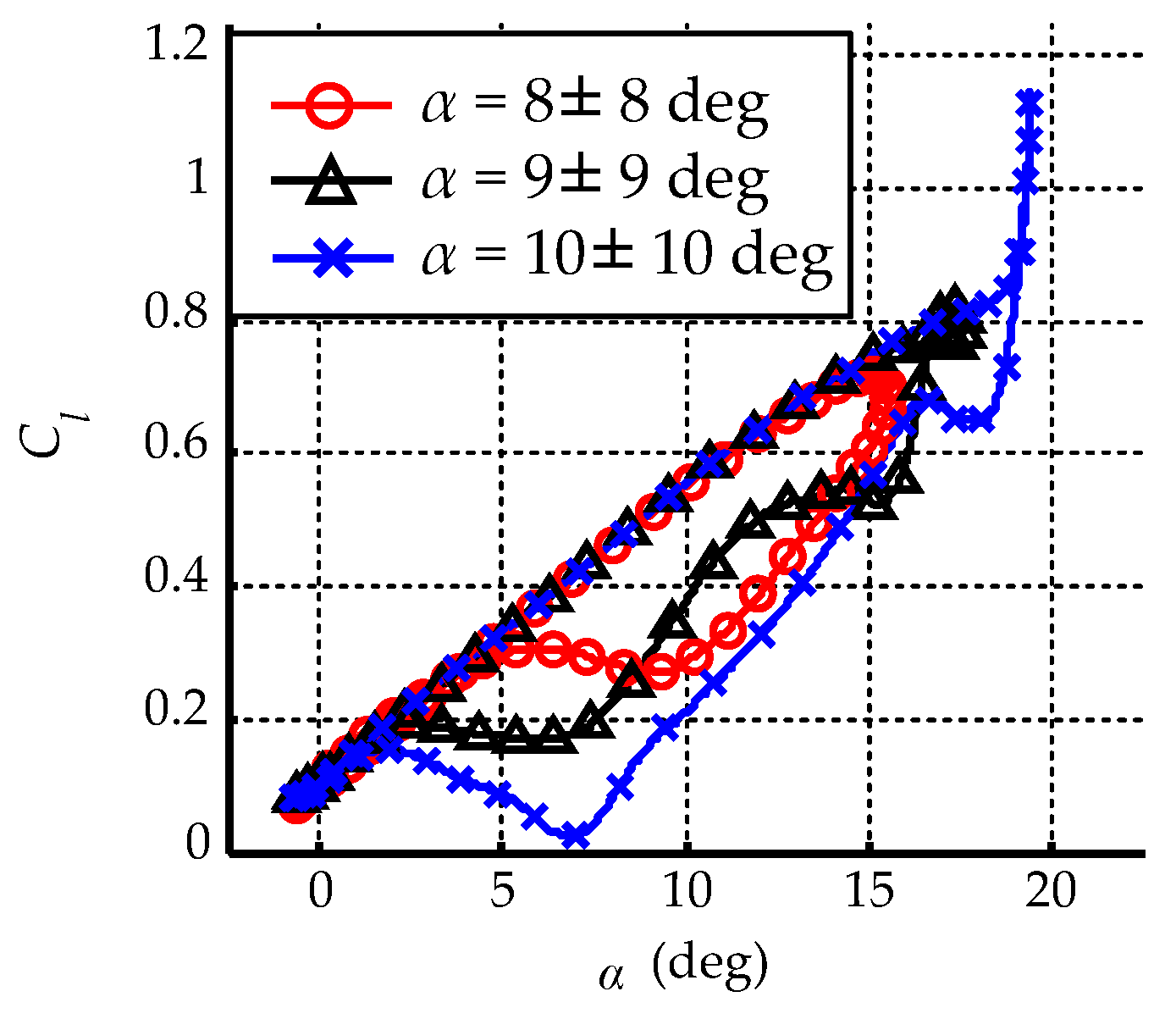
Appendix A. Selection of Oscillating Amplitude
| (m/s) | (deg) | (deg) | k |
|---|---|---|---|
| 50 | 8–10 | 8–10 | 0.032 |
References
- McCroskey, W.J. The Phenomenon of Dynamic Stall; Technical Report; National Aeronuatics and Space Administration Moffett Field Ca Ames Research Center: Washington, DC, USA, 1981. [Google Scholar]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Airc. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Wang, S.; Ingham, D.B.; Ma, L.; Pourkashanian, M.; Tao, Z. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils. Comput. Fluids 2010, 39, 1529–1541. [Google Scholar] [CrossRef]
- Corke, T.C.; Thomas, F.O. Dynamic stall in pitching airfoils: Aerodynamic damping and compressibility effects. Annu. Rev. Fluid Mech. 2015, 47, 479–505. [Google Scholar] [CrossRef]
- Nankai, K.; Ozawa, Y.; Nonomura, T.; Asai, K. Linear Reduced-order Model Based on PIV Data of Flow Field around Airfoil. Trans. Jpn. Soc. Aeronaut. Space Sci. 2019, 62, 227–235. [Google Scholar] [CrossRef]
- Zong, H.; Chiatto, M.; Kotsonis, M.; de Luca, L. Plasma synthetic jet actuators for active flow control. Actuators 2018, 7, 77. [Google Scholar] [CrossRef]
- Zong, H.; Kotsonis, M. Formation, evolution and scaling of plasma synthetic jets. J. Fluid Mech. 2018, 837, 147–181. [Google Scholar] [CrossRef]
- Roth, J.R. Aerodynamic flow acceleration using paraelectric and peristaltic electrohydrodynamic effects of a one atmosphere uniform glow discharge plasma. Phys. Plasmas 2003, 10, 2117–2126. [Google Scholar] [CrossRef]
- Post, M.L.; Corke, T.C. Separation control on high angle of attack airfoil using plasma actuators. AIAA J. 2004, 42, 2177–2184. [Google Scholar] [CrossRef]
- Forte, M.; Leger, L.; Pons, J.; Moreau, E.; Touchard, G. Plasma actuators for airflow control: Measurement of the non-stationary induced flow velocity. J. Electrostat. 2005, 63, 929–936. [Google Scholar] [CrossRef]
- Sato, M.; Aono, H.; Yakeno, A.; Nonomura, T.; Fujii, K.; Okada, K.; Asada, K. Multifactorial effects of operating conditions of dielectric-barrier-discharge plasma actuator on laminar-separated-flow control. AIAA J. 2015, 53, 2544–2559. [Google Scholar] [CrossRef]
- Sekimoto, S.; Nonomura, T.; Fujii, K. Burst-mode frequency effects of dielectric barrier discharge plasma actuator for separation control. AIAA J. 2017, 1385–1392. [Google Scholar] [CrossRef]
- Post, M.L.; Corke, T.C. Separation control using plasma actuators: Dynamic stall vortex control on oscillating airfoil. AIAA J. 2006, 44, 3125–3135. [Google Scholar] [CrossRef]
- Greenblatt, D.; Ben-Harav, A.; Mueller-Vahl, H. Dynamic stall control on a vertical-axis wind turbine using plasma actuators. AIAA J. 2014, 52, 456–462. [Google Scholar] [CrossRef]
- Mitsuo, K.; Watanabe, S.; Atobe, T.; Kato, H.; Tanaka, M.; Uchida, T. Lift Enhancement of a Pitching Airfoil in Dynamic Stall by DBD Plasma Actuators. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013; p. 1119. [Google Scholar]
- Guoqiang, L.; Weiguo, Z.; Yubiao, J.; Pengyu, Y. Experimental investigation of dynamic stall flow control for wind turbine airfoils using a plasma actuator. Energy 2019, 185, 90–101. [Google Scholar] [CrossRef]
- Roupassov, D.; Nikipelov, A.; Nudnova, M.; Starikovskii, A.Y. Flow separation control by plasma actuator with nanosecond pulsed-periodic discharge. AIAA J. 2009, 47, 168–185. [Google Scholar] [CrossRef]
- Little, J.; Takashima, K.; Nishihara, M.; Adamovich, I.; Samimy, M. Separation control with nanosecond-pulse-driven dielectric barrier discharge plasma actuators. AIAA J. 2012, 50, 350–365. [Google Scholar] [CrossRef]
- Kelley, C.L.; Bowles, P.O.; Cooney, J.; He, C.; Corke, T.C.; Osborne, B.A.; Silkey, J.S.; Zehnle, J. Leading-edge separation control using alternating-current and nanosecond-pulse plasma actuators. AIAA J. 2014, 52, 1871–1884. [Google Scholar] [CrossRef]
- Little, J.; Singh, A.; Ashcraft, T.; Durasiewicz, C. Post-stall flow control using nanosecond pulse driven dielectric barrier discharge plasma actuators. Plasma Sources Sci. Technol. 2018, 28, 014002. [Google Scholar] [CrossRef]
- Zhang, C.; Huang, B.; Luo, Z.; Che, X.; Yan, P.; Shao, T. Atmospheric-pressure pulsed plasma actuators for flow control: Shock wave and vortex characteristics. Plasma Sources Sci. Technol. 2019, 28, 064001. [Google Scholar] [CrossRef]
- Starikovskiy, A.; Meehan, K.; Persikov, N.; Miles, R. Static and dynamic stall control by NS SDBD actuators. Plasma Sources Sci. Technol. 2019, 28, 054001. [Google Scholar] [CrossRef]
- Komuro, A.; Takashima, K.; Konno, K.; Tanaka, N.; Nonomura, T.; Kaneko, T.; Ando, A.; Asai, K. Schlieren visualization of flow-field modification over an airfoil by near-surface gas-density perturbations generated by a nanosecond-pulse-driven plasma actuator. J. Phys. D Appl. Phys. 2017, 50, 215202. [Google Scholar] [CrossRef]
- Frankhouser, M.W.; Gregory, J.W. Nanosecond Dielectric Barrier Discharge Plasma Actuator Flow Control of Compressible Dynamic Stall. In Proceedings of the 46th AIAA Plasmadynamics and Lasers Conference, Dallas, TX, USA, 22–26 June 2015; p. 2341. [Google Scholar]
- Fukumoto, H.; Aono, H.; Watanabe, T.; Tanaka, M.; Matsuda, H.; Osako, T.; Nonomura, T.; Oyama, A.; Fujii, K. Control of dynamic flowfield around a pitching NACA633- 618 airfoil by a DBD plasma actuator. Int. J. Heat Fluid Flow 2016, 62, 10–23. [Google Scholar] [CrossRef]
- Komuro, A.; Takashima, K.; Suzuki, K.; Kanno, S.; Nonomura, T.; Kaneko, T.; Ando, A.; Asai, K. Influence of discharge energy on the lift and drag forces induced by a nanosecond-pulse-driven plasma actuator. Plasma Sources Sci. Technol. 2019, 28, 065006. [Google Scholar] [CrossRef]
- Singhal, A.; Castañeda, D.; Webb, N.; Samimy, M. Control of dynamic stall over a NACA 0015 airfoil using plasma actuators. AIAA J. 2017, 78–89. [Google Scholar] [CrossRef]

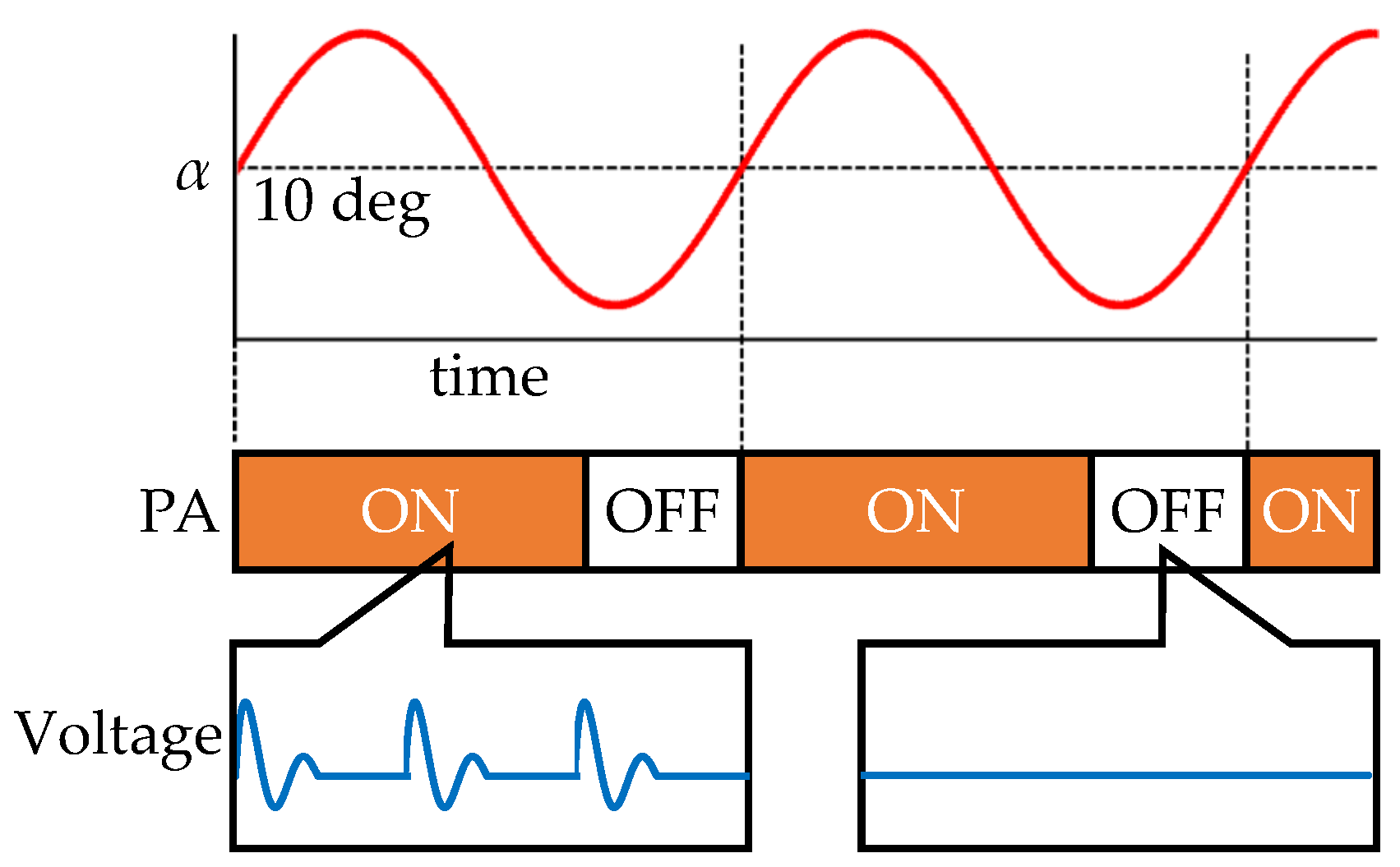
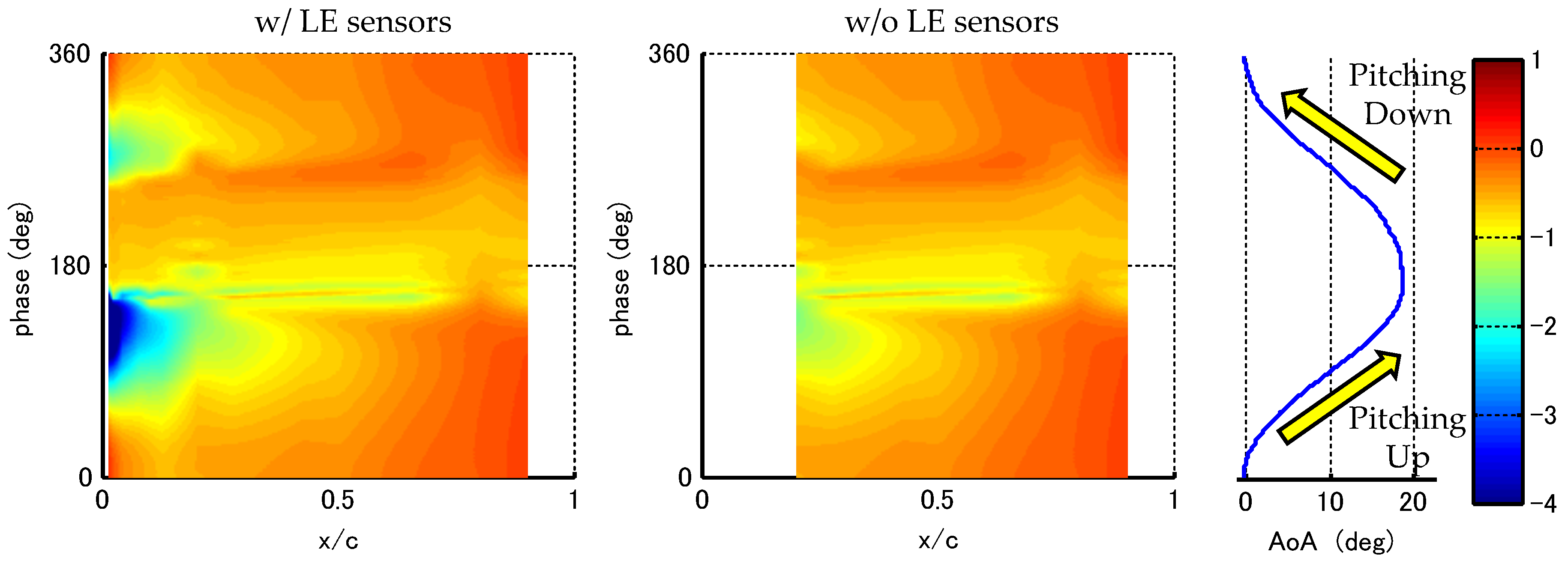
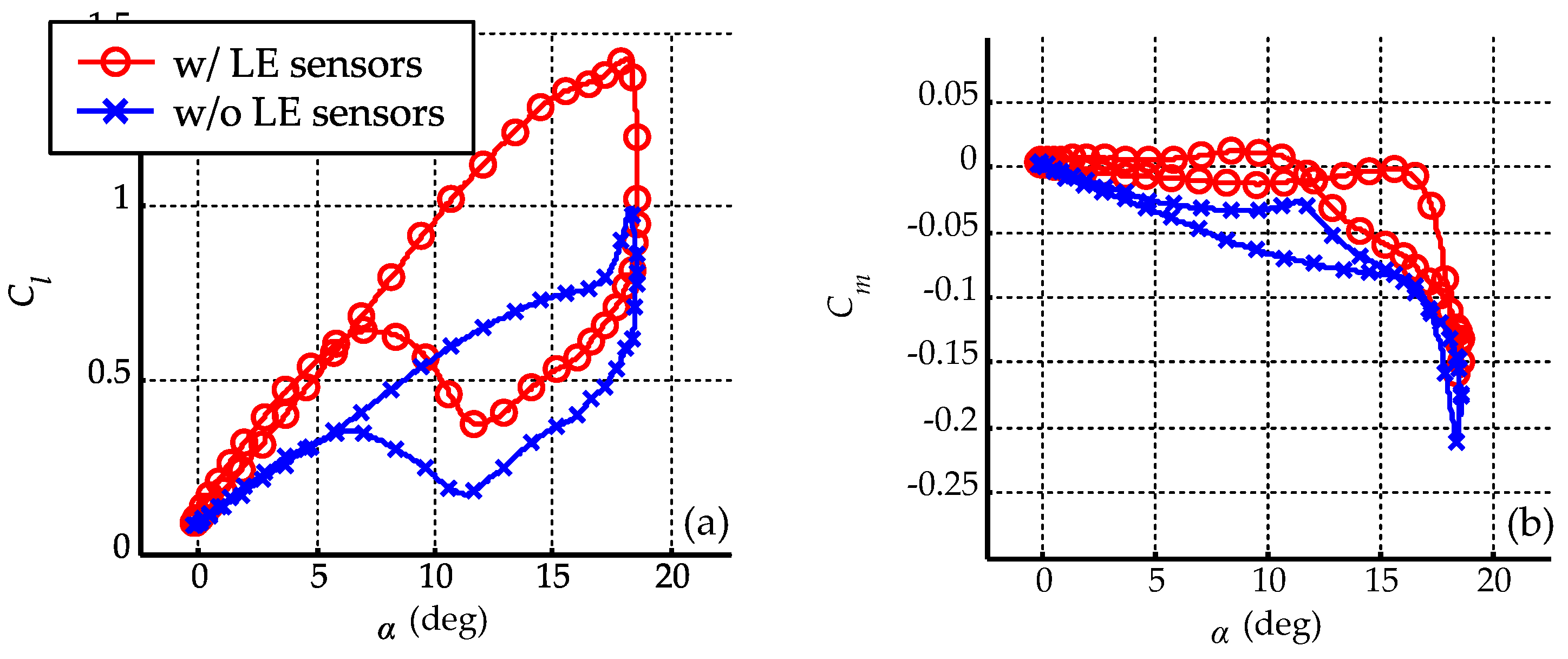
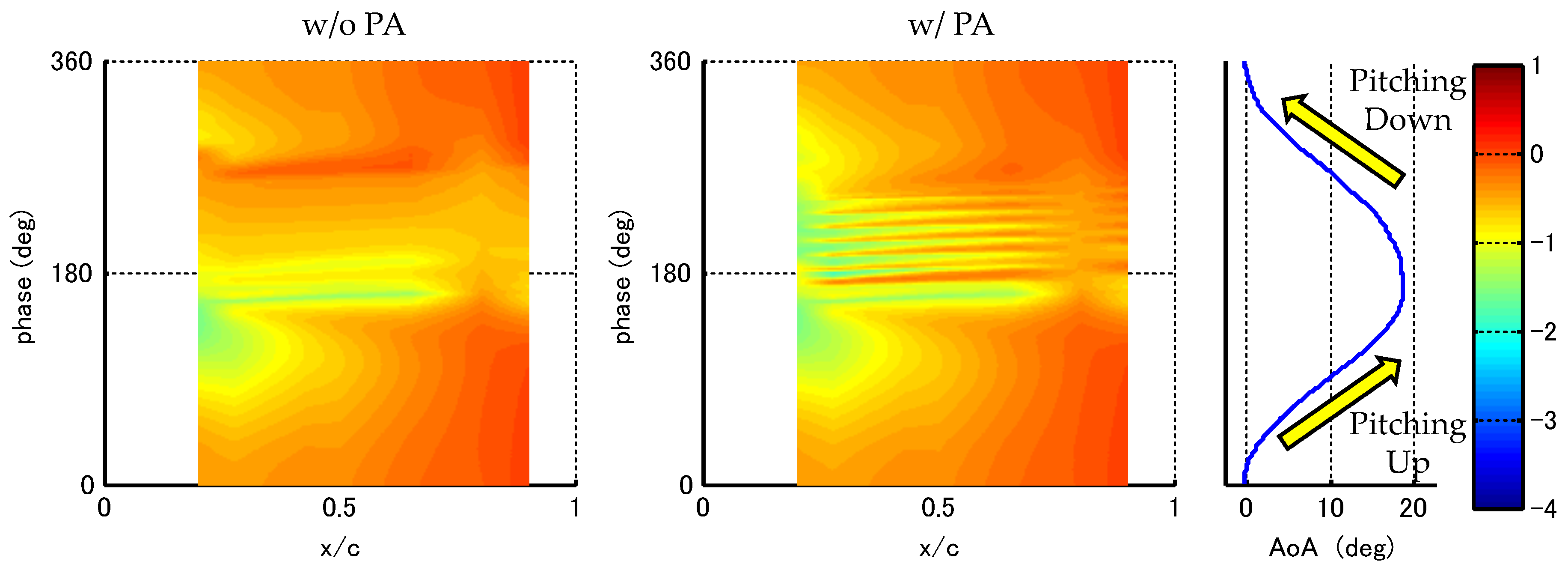


| Case | (m/s) | (deg) | (deg) | k | (kV) | Type | (%) | |
|---|---|---|---|---|---|---|---|---|
| 1 | 50 | 10 | 10 | 0.020 | - | - | - | - |
| 2 | 50 | 10 | 10 | 0.020 | 0.61 | 8.9 | Double | 0 |
| 3 | 40–55 | 10 | 10 | 0.020 | 0.61 | 8.9 | Double | 0 |
| 4 | 50 | 10–15 | 10 | 0.020 | 0.61 | 8.9 | Double | 0 |
| 5 | 50 | 10 | 10 | 0.004–0.032 | 0.13–0.96 | 8.9 | Double | 0 |
| 6 | 50 | 10 | 10 | 0.020 | 0.31–2.5 | 8.9 | Double | 0 |
| 7 | 50 | 10 | 10 | 0.032 | 0.48–1.9 | 8.9 | Double | 0 |
| 8 | 50 | 10 | 10 | 0.032 | 0.96 | 2–8.9 | Double | 0 |
| 9 | 50 | 10 | 10 | 0.032 | 0.48 | 8.9 | Double, single | 0 |
| 10 | 50 | 10 | 10 | 0.032 | 0.96 | 8.9 | Double, single | 0 |
| 11 | 50 | 10 | 10 | 0.032 | 0.96 | 8.9 | Single | 0–6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iwasaki, Y.; Nonomura, T.; Nankai, K.; Asai, K.; Kanno, S.; Suzuki, K.; Komuro, A.; Ando, A.; Takashima, K.; Kaneko, T.; et al. Dynamic Stall Control around Practical Airfoil Using Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators. Energies 2020, 13, 1376. https://doi.org/10.3390/en13061376
Iwasaki Y, Nonomura T, Nankai K, Asai K, Kanno S, Suzuki K, Komuro A, Ando A, Takashima K, Kaneko T, et al. Dynamic Stall Control around Practical Airfoil Using Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators. Energies. 2020; 13(6):1376. https://doi.org/10.3390/en13061376
Chicago/Turabian StyleIwasaki, Yuto, Taku Nonomura, Koki Nankai, Keisuke Asai, Shoki Kanno, Kento Suzuki, Atsushi Komuro, Akira Ando, Keisuke Takashima, Toshiro Kaneko, and et al. 2020. "Dynamic Stall Control around Practical Airfoil Using Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators" Energies 13, no. 6: 1376. https://doi.org/10.3390/en13061376
APA StyleIwasaki, Y., Nonomura, T., Nankai, K., Asai, K., Kanno, S., Suzuki, K., Komuro, A., Ando, A., Takashima, K., Kaneko, T., Yasuda, H., Hayama, K., Tsujiuchi, T., Nakajima, T., & Nakakita, K. (2020). Dynamic Stall Control around Practical Airfoil Using Nanosecond-Pulse-Driven Dielectric Barrier Discharge Plasma Actuators. Energies, 13(6), 1376. https://doi.org/10.3390/en13061376





