Heavy Oil Laminar Flow in Corrugated Ducts: A Numerical Study Using the Galerkin-Based Integral Method
Abstract
:1. Introduction
2. Mathematical Formulation
- (a)
- The laminar flow is fully developed, isothermal, single-phase, and steady-state;
- (b)
- The cross-sectional area of the tube, along the z-axis, is constant;
- (c)
- The properties of the fluid, thermal and physical, are considered constant;
- (d)
- There is a condition of not-slipping on the duct wall.
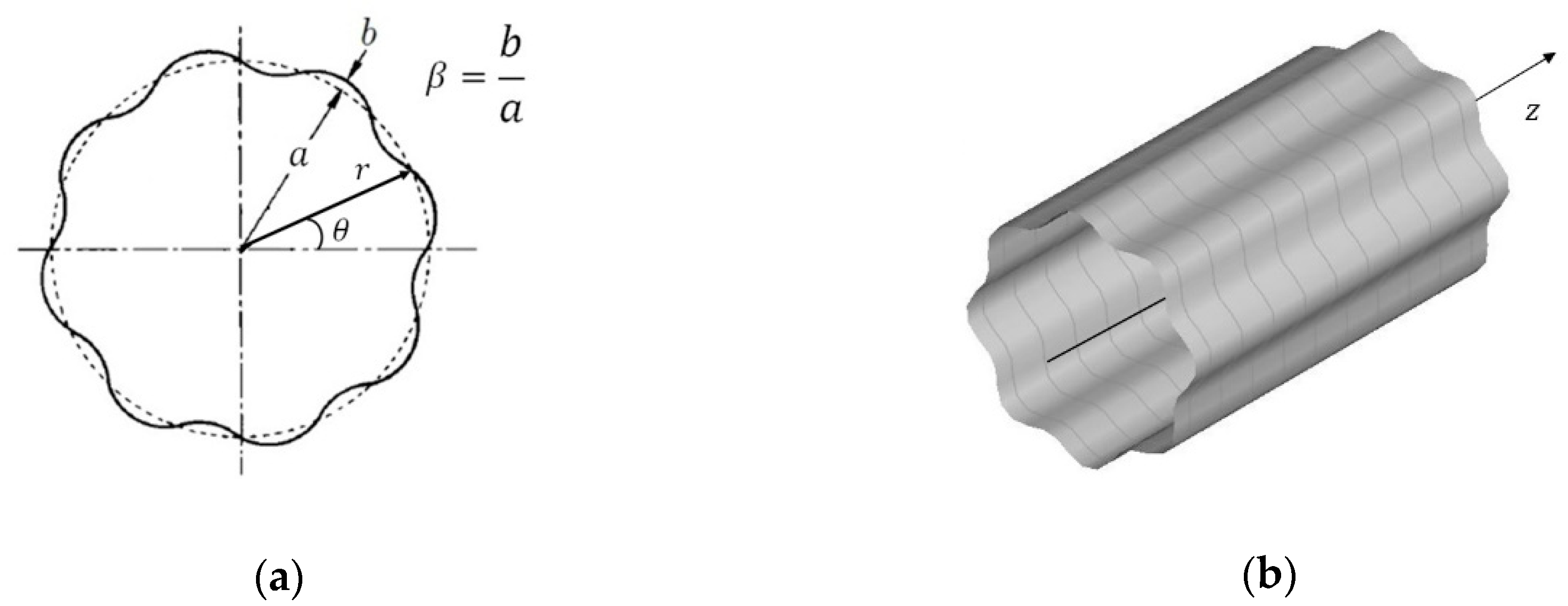
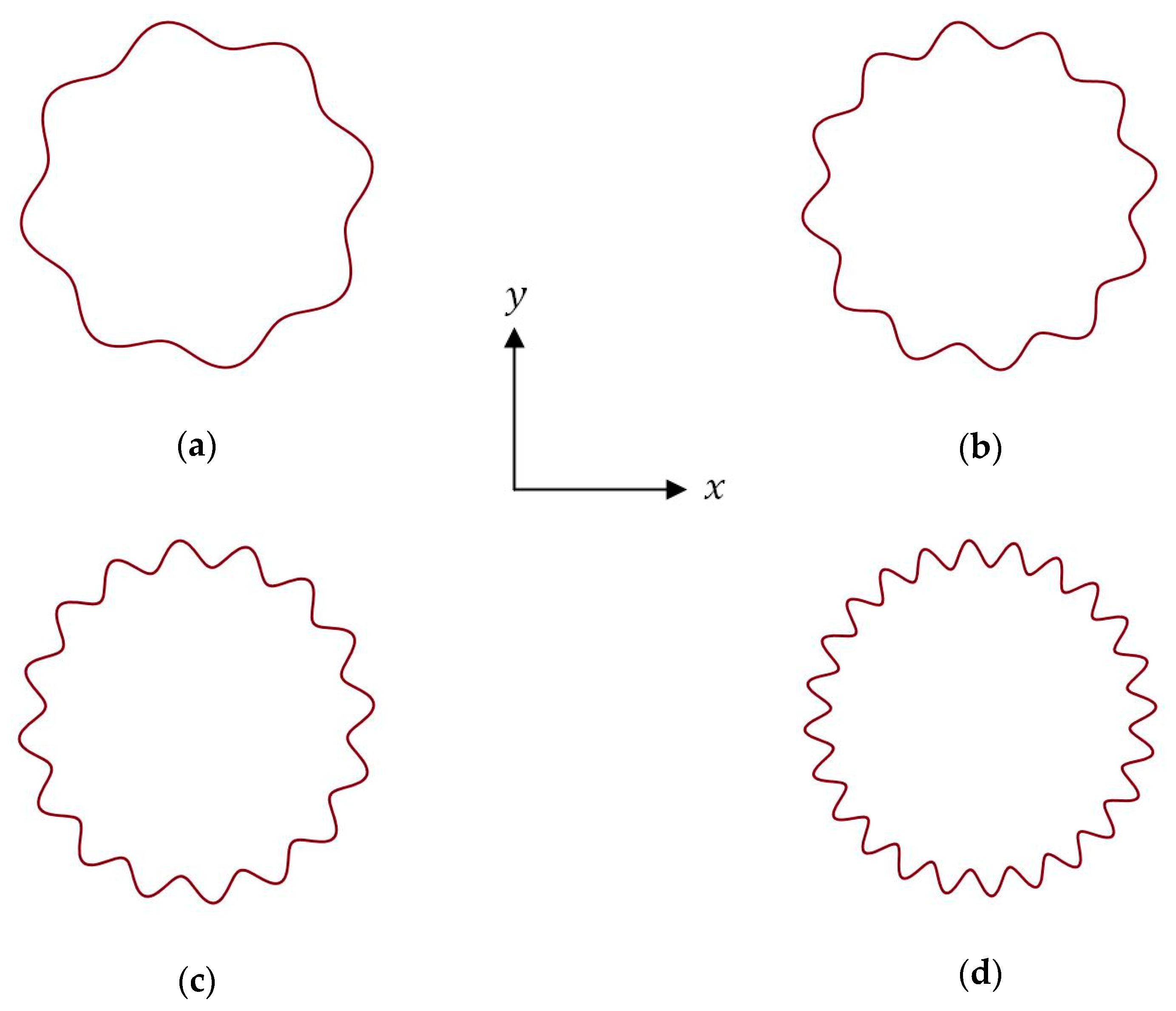
2.1. The Geometry
2.2. Momentum Equation
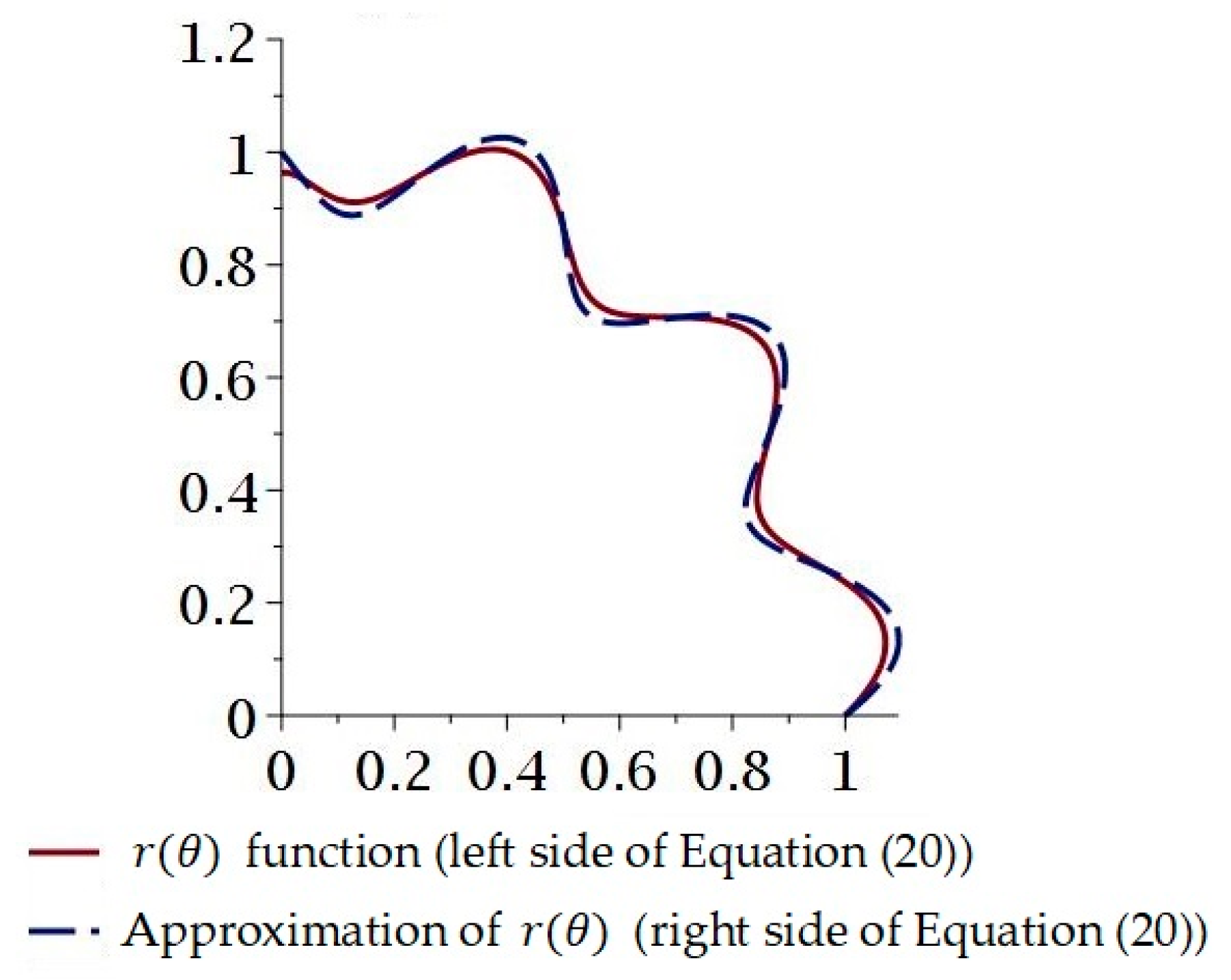
2.3. Solution Methodology
2.4. Heavy Oil Flow Application
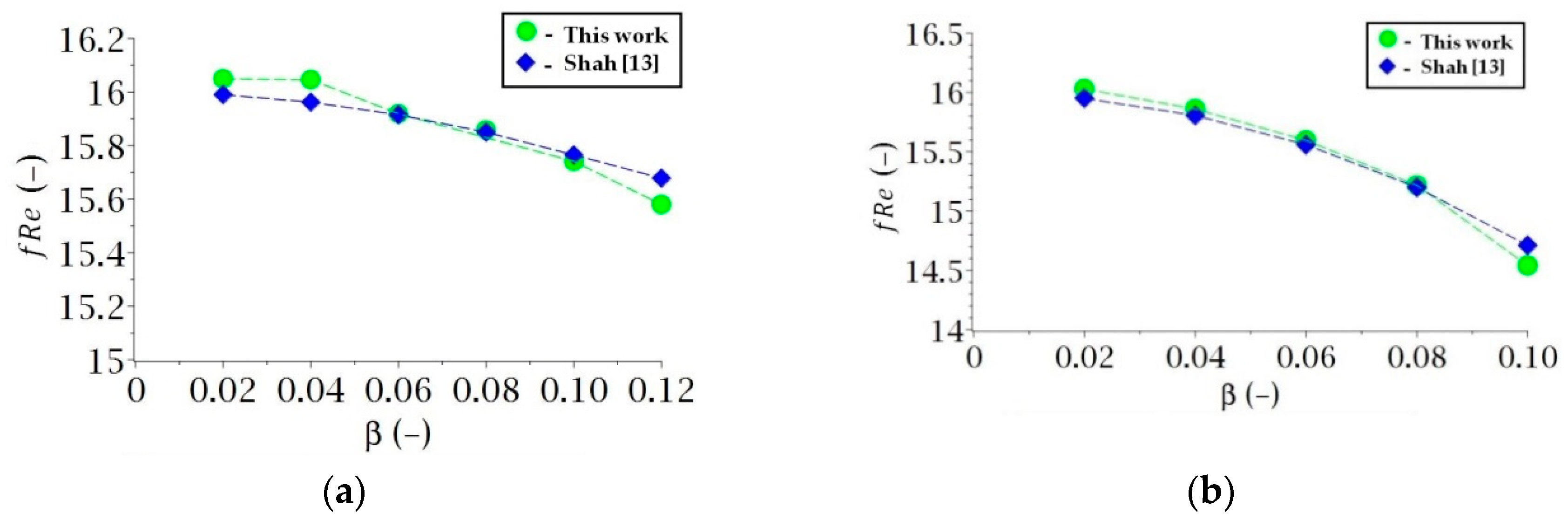
3. Results and Discussion
4. Conclusions
- The Galerkin-based integral method assisted by symbolic manipulation software is an effective tool for investigating the fully developed laminar flow fluid in a corrugated cross-section cylindrical duct. Fully developed velocity profiles for any duct shape can be predicted by this method.
- The Poiseuille number, , obtained for different aspect ratios of the pipe was compared with the existing literature, and a good concordance was obtained in all studied cases.
- The appropriate number of base functions is different depending on the aspect ratio and the number of corrugations of the studied geometry. Such variation altered the computational time significantly. The smaller the number of base functions, the lower the computational time.
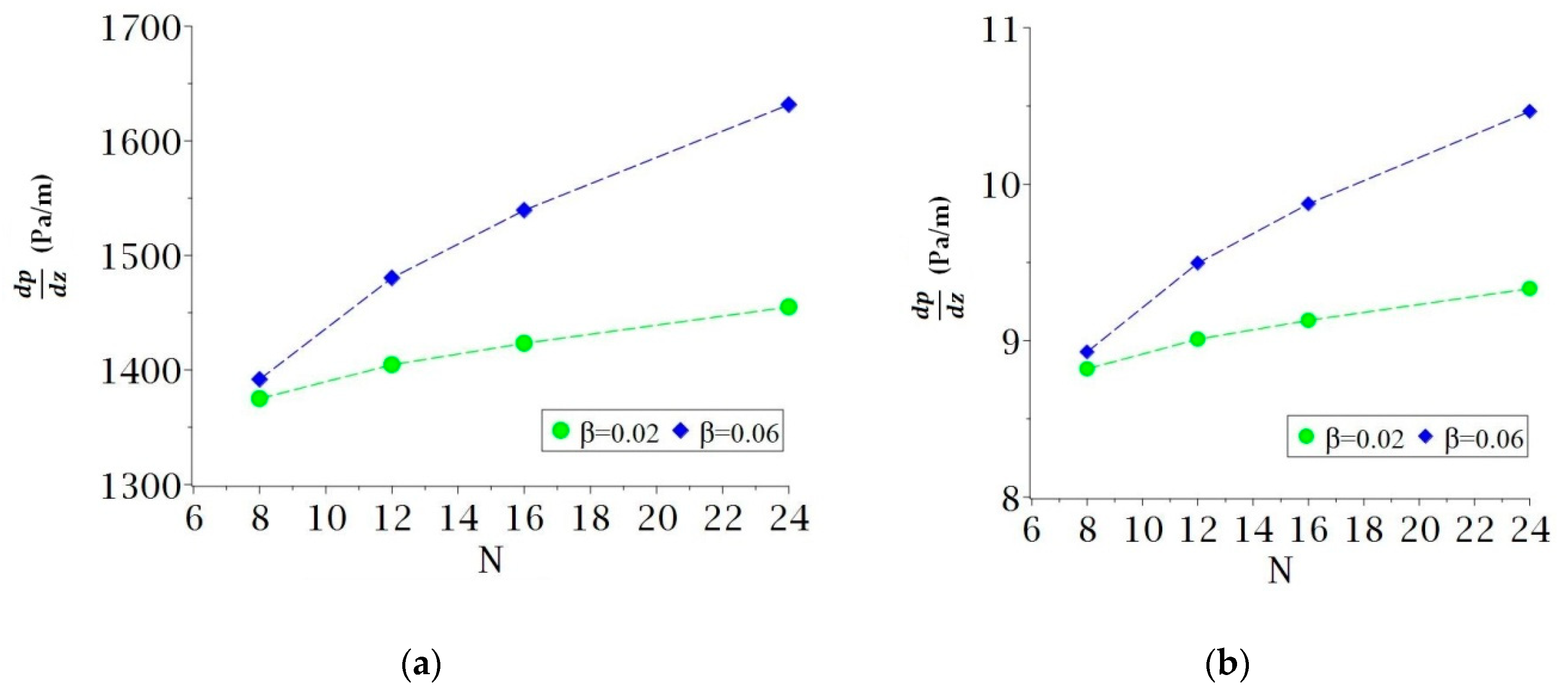
- The pressure gradient increases with the number of corrugations and the aspect ratio of the pipe and decreases with the increase in the fluid temperature.
- Values for the Reynolds number, Fanning friction factor, shear stress, and pressure gradient for heavy oil flow, with temperature-dependent viscosity, were presented. These results make it possible to better understand the behavior of heavy oil in corrugated cross-section ducts.
Author Contributions
Acknowledgments
Conflicts of Interest
List of Symbols
| Geometric dimensions (m) | |
| Element of matrix | |
| Cross-section area of the duct (m2) | |
| Inverse matrix of | |
| Matrix | |
| Element of matrix (constants) | |
| Hydraulic diameter (m) | |
| Constants to be evaluated (constants) | |
| Dimensionless hydraulic diameter | |
| Fanning friction factor (dimensionless) | |
| Base functions; Galerkin functions | |
| Poiseuille number (dimensionless) | |
| Characteristic length (m) | |
| Number of base functions | |
| Nusselt number for the constant flux boundary condition | |
| Perimeter (m) | |
| Pressure (Pa) | |
| Cylindrical coordinates | |
| Reynolds number [dimensionless] | |
| Local axial velocity (m/s) | |
| Temperature (°C) | |
| Mean velocity (m/s) | |
| Normalized velocity (dimensionless) | |
| Cartesian coordinates (m/s) | |
| Dimensionless coordinates (dimensionless) | |
| Dimensionless velocity (dimensionless) | |
| Dimensionless mean velocity (dimensionless) | |
| Aspect ratio (dimensionless) | |
| Dynamic viscosity (Pa·s) | |
| Kinematic viscosity (cS) | |
| Density (kg/m3) | |
| Shear stress (Pa) | |
| Boundary of duct | |
| Laplacian operator |
Abbreviations
| GBI | Galerkin-based integral |
References
- Jadidi, A.; Saleh, S.J. Lubricated Transport of Heavy Oil Investigated by CFD. Ph.D. Thesis, Department of Engineering, University of Leicester, Leicester, UK, 2017. [Google Scholar]
- Andrade, T.H.F.; Damacena, Y.T.; Crivelaro, K.C.O.; Farias Neto, S.R.; Lima, A.G.B. Friction Reduction in Two-Phase Water-Oil Flow in Horizontal Tubes, XV Brazilian Congress of Mechanical Engineering; Águas de Lindóia: São Paulo, Brazil, 2010. (In Portuguese) [Google Scholar]
- Moharana, M.K.; Khandekar, S. Generalized formulation for estimating pressure drop in fully developed laminar flow in singly and doubly connected channels of non-circular cross-sections. Comput. Methods Appl. Mech. Eng. 2013, 259, 64–76. [Google Scholar] [CrossRef]
- Aparecido, J.B.; Cotta, R.M. Thermally developing laminar flow inside rectangular ducts. Int. J. Heat Mass Transf. 1990, 33, 341–347. [Google Scholar] [CrossRef]
- Syrjälä, S. Laminar flow of viscoelastic fluids in rectangular ducts with heat transfer: A finite element analysis. Int. Commun. Heat Mass Transf. 1998, 25, 191–204. [Google Scholar] [CrossRef]
- Aparecido, J.B.; Lindquist, C. Laminar Forced Convection through Rectangular Ducts with Uniform Axial and Peripheral Heat Flux; Brazilian Congress of Mechanical Engineering: Águas de Lindóia, Brazil, 1999. [Google Scholar]
- Lee, Y.M.; Kuo, Y.M. Laminar flow in annuli ducts with constant wall temperature. Int. Commun. Heat Mass Transf. 1998, 25, 227–236. [Google Scholar] [CrossRef]
- Venegas Prada, J.W. Experimental Study of Annular Oil-Water Flow (Core Flow) in the Elevation of Ultra-Hazardous Oils. Master’s Thesis, Petroleum Sciences, and Engineering, State University of Campinas, Campinas, Brazil, 1999. (In Portuguese). [Google Scholar]
- Bensakhria, A.; Peysson, Y.; Antonini, G. Experimental study of the pipeline lubrication for heavy oil transport. Oil Gas Sci. Technol. 2004, 59, 523–533. [Google Scholar] [CrossRef]
- Casarella, M.J.; Laura, P.A.; Chi, M. On the approximate solution of flow and heat transfer through non-circular conduits with uniform wall temperature. Br. J. Appl. Phys. 1967, 18, 1327. [Google Scholar] [CrossRef]
- Hu, M.H.; Chang, Y.P. Optimization of finned tubes for heat transfer in laminar flow. J. Heat Transf. 1973, 95, 332–338. [Google Scholar] [CrossRef]
- Shah, R.K. Laminar flow friction and forced convection heat transfer in ducts of arbitrary geometry. Int. J. Heat Mass Transf. 1975, 18, 849–862. [Google Scholar] [CrossRef]
- Courant, R.; David, H. Methods of Mathematical Physics: Partial Differential Equations; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Petrovsky, I.G. Lectures on Partial Differential Equations; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Browder, F.E. Problemes Non-Lineaires; Presses de l’Université de Montréal: Montréal, QC, Canada, 1966; Volume 15. [Google Scholar]
- Dautray, R.; Lions, J.L. Mathematical Analysis and Numerical Methods for Science and Technology; Evolution Problems II; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 6. [Google Scholar]
- Assan, A.E. Finite Elements Methods-First Steps; Unicamp: Campinas, Brazil, 2003. [Google Scholar]
- Cooper, J.M. Introduction to Partial Differential Equations with MATLAB; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Thomas, J.E. Fundamentals of Petroleum Engineering, 2nd ed.; Interciência, Petrobras: Rio de Janeiro, Brazil, 2004. (In Portuguese) [Google Scholar]
- Franco, C.M.R.; Barbosa de Lima, A.G.; Silva, J.V.; Nunes, A.G. Applying liquid diffusion model for continuous drying of rough rice in fixed bed. Defect Diffus. Forum 2016, 369, 152–156. [Google Scholar] [CrossRef]
- Santos, J.P.S.; Santos, I.B.; Pereira, E.M.A.; Silva, J.V.; de Lima, A.G.B. Wheat convective drying: An analytical investigation via galerkin-based integral method. Defect Diffus. Forum 2015, 365, 82–87. [Google Scholar] [CrossRef]
- Haji-Sheikh, A.; Mashena, M.; Haji-Sheikh, M.J. Heat transfer coefficient in ducts with constant wall temperature. J. Heat Transf. 1983, 105, 878–883. [Google Scholar] [CrossRef]
- Lakshminarayanan, R.; Haji-Sheikh, A. Entrance heat transfer in isosceles and right triangular ducts. J. Thermophys. Heat Transf. 1992, 6, 167–171. [Google Scholar] [CrossRef]
- Lee, Y.M.; Lee, P.C. Laminar flow in elliptic ducts with and without central circular cores for constant wall temperature. Int. Commun. Heat Mass Transf. 2001, 28, 1115–1124. [Google Scholar] [CrossRef]


| Oil | |
|---|---|
| T °C | (cS) |
| 29.22 | 180.21 |
| 51.16 | 70.786 |
| 81.11 | 25.526 |
| 108.5 | 11.840 |
| 137.9 | 6.3270 |
| 155.5 | 4.4980 |
| 199.6 | 2.3870 |
| 228.5 | 1.6520 |
| 260.3 | 1.1560 |
| This Work | Ref [13] | This Work | Ref [13] | ||||
|---|---|---|---|---|---|---|---|
| 8 | 0.02 | 16.049 | 15.990 | 16 | 0.02 | 16.269 | 15.887 |
| 0.04 | 16.046 | 15.962 | 0.04 | 15.894 | 15.542 | ||
| 0.06 | 15.918 | 15.915 | 0.06 | 15.015 | 14.943 | ||
| 0.08 | 15.858 | 15.850 | 0.08 | 14.218 | 14.051 | ||
| 0.10 | 15.741 | 15.765 | |||||
| 0.12 | 15.579 | 15.678 | |||||
| 12 | 0.02 | 16.029 | 15.952 | 24 | 0.02 | 16.043 | 15.679 |
| 0.04 | 15.860 | 15.806 | 0.04 | 14.868 | 14.671 | ||
| 0.06 | 15.595 | 15.559 | 0.06 | 12.839 | 12.872 | ||
| 0.08 | 15.216 | 15.200 | |||||
| 0.10 | 14.541 | 14.711 |
| 8 | 0.02 | 12 | 16 | 0.02 | 12 |
| 0.04 | 13 | 0.04 | 15 | ||
| 0.06 | 11 | 0.06 | 15 | ||
| 0.08 | 7 | 0.08 | 5 | ||
| 0.10 | 5 | ||||
| 0.12 | 5 | ||||
| 12 | 0.02 | 30 | 24 | 0.02 | 15 |
| 0.04 | 52 | 0.04 | 15 | ||
| 0.06 | 10 | 0.06 | 6 | ||
| 0.08 | 11 | ||||
| 0.10 | 10 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 11.0295 | 1.4413 | 686.20 | 1374.98 |
| 51.17 | 67.400 | 28.0809 | 0.5661 | 269.52 | 540.061 |
| 81.11 | 24.305 | 77.8710 | 0.2041 | 97.192 | 194.750 |
| 108.5 | 11.273 | 167.883 | 0.0946 | 45.082 | 90.3333 |
| 137.9 | 6.0244 | 314.167 | 0.0506 | 24.090 | 48.2718 |
| 155.5 | 4.2828 | 441.915 | 0.0359 | 17.126 | 34.3175 |
| 199.6 | 2.2728 | 832.734 | 0.0190 | 9.0887 | 18.2116 |
| 228.5 | 1.5729 | 1203.23 | 0.0132 | 6.2901 | 12.6039 |
| 260.3 | 1.1007 | 1719.49 | 0.0092 | 4.4015 | 8.81970 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 10.9438 | 1.4341 | 682.77 | 1404.52 |
| 51.16 | 67.400 | 27.8627 | 0.5632 | 268.17 | 551.666 |
| 81.11 | 24.305 | 77.2661 | 0.2031 | 96.707 | 198.935 |
| 108.5 | 11.273 | 166.579 | 0.0942 | 44.856 | 92.2744 |
| 137.9 | 6.0244 | 311.726 | 0.0503 | 23.970 | 49.3091 |
| 155.5 | 4.2828 | 438.482 | 0.0357 | 17.041 | 35.0549 |
| 199.6 | 2.2728 | 826.265 | 0.0189 | 9.0433 | 18.6029 |
| 228.5 | 1.5729 | 1193.88 | 0.0131 | 6.2587 | 12.8747 |
| 260.3 | 1.1007 | 1706.13 | 0.0091 | 4.3795 | 9.00922 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 29.22 | 10.82772 | 1.4482 | 689.49 | 1423.29 |
| 51.16 | 51.16 | 27.56704 | 0.5688 | 270.81 | 559.040 |
| 81.11 | 81.11 | 76.44601 | 0.2051 | 97.658 | 201.594 |
| 108.5 | 108.5 | 164.8108 | 0.0951 | 45.298 | 93.5076 |
| 137.9 | 137.9 | 308.4180 | 0.0508 | 24.206 | 49.9681 |
| 155.5 | 155.5 | 433.8285 | 0.0361 | 17.208 | 35.5234 |
| 199.6 | 199.6 | 817.4951 | 0.0191 | 9.1323 | 18.8515 |
| 228.5 | 228.5 | 1181.211 | 0.0132 | 6.3203 | 13.0468 |
| 260.3 | 260.3 | 1688.028 | 0.0092 | 4.4226 | 9.12963 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 10.51788 | 1.4104 | 671.50 | 1454.98 |
| 51.16 | 67.400 | 26.77820 | 0.5539 | 263.75 | 571.485 |
| 81.11 | 24.305 | 74.25849 | 0.1997 | 95.110 | 206.082 |
| 108.5 | 11.273 | 160.0947 | 0.0926 | 44.116 | 95.5893 |
| 137.9 | 6.0244 | 299.5925 | 0.0495 | 23.574 | 51.0805 |
| 155.5 | 4.2828 | 421.4144 | 0.0352 | 16.759 | 36.3142 |
| 199.6 | 2.2728 | 794.1023 | 0.0186 | 8.8940 | 19.2712 |
| 228.5 | 1.5729 | 1147.410 | 0.0129 | 6.1553 | 13.3372 |
| 260.3 | 1.1007 | 1147.410 | 0.0090 | 4.3072 | 9.33287 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 10.5343 | 1.3965 | 664.89 | 1391.80 |
| 51.16 | 67.400 | 26.8200 | 0.5485 | 261.15 | 546.670 |
| 81.11 | 24.305 | 74.3745 | 0.1978 | 94.174 | 197.133 |
| 108.5 | 11.273 | 160.344 | 0.0917 | 43.682 | 91.4386 |
| 137.9 | 6.0244 | 300.060 | 0.0490 | 23.342 | 48.8625 |
| 155.5 | 4.2828 | 422.072 | 0.0348 | 16.594 | 34.7374 |
| 199.6 | 2.2728 | 795.342 | 0.0184 | 8.8065 | 18.4344 |
| 228.5 | 1.5729 | 1149.20 | 0.0128 | 6.0948 | 12.7581 |
| 260.3 | 1.1007 | 1642.28 | 0.0089 | 4.2649 | 8.92762 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 9.93330 | 1.3399 | 637.91 | 1480.35 |
| 51.16 | 67.400 | 25.2898 | 0.5262 | 250.55 | 581.447 |
| 81.11 | 24.305 | 70.1312 | 0.1897 | 90.353 | 209.674 |
| 108.5 | 11.273 | 151.196 | 0.0880 | 41.909 | 97.2556 |
| 137.9 | 6.0244 | 282.941 | 0.0470 | 22.395 | 51.9710 |
| 155.5 | 4.2828 | 397.992 | 0.0334 | 15.921 | 36.9473 |
| 199.6 | 2.2728 | 749.966 | 0.0177 | 8.4491 | 19.6072 |
| 228.5 | 1.5729 | 1083.63 | 0.0122 | 5.8475 | 13.5697 |
| 260.3 | 1.1007 | 1548.58 | 0.0085 | 4.0918 | 9.49557 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 9.25648 | 1.2723 | 605.76 | 1539.44 |
| 51.16 | 67.400 | 23.5667 | 0.4997 | 237.92 | 604.658 |
| 81.11 | 24.305 | 65.3527 | 0.1802 | 85.799 | 218.044 |
| 108.5 | 11.273 | 140.894 | 0.0830 | 39.797 | 101.138 |
| 137.9 | 6.0244 | 263.662 | 0.0440 | 21.266 | 54.0456 |
| 155.5 | 4.2828 | 370.874 | 0.0310 | 15.118 | 38.4222 |
| 199.6 | 2.2728 | 698.866 | 0.0168 | 8.0233 | 20.3899 |
| 228.5 | 1.5729 | 1009.80 | 0.0116 | 5.5527 | 14.1114 |
| 260.3 | 1.1007 | 1443.07 | 0.0081 | 3.8856 | 9.87463 |
(°C) | (Pa·s) | (-) | (-) | (Pa) | (Pa/m) |
|---|---|---|---|---|---|
| 29.22 | 171.60 | 7.92614 | 1.1217 | 534.036 | 1631.59 |
| 51.16 | 67.400 | 20.1797 | 0.4405 | 209.757 | 640.854 |
| 81.11 | 24.305 | 55.9603 | 0.1588 | 75.6402 | 231.097 |
| 108.5 | 11.273 | 120.645 | 0.0736 | 35.0850 | 107.192 |
| 137.9 | 6.0244 | 225.769 | 0.0393 | 18.7485 | 57.28089 |
| 155.5 | 4.2828 | 317.572 | 0.0279 | 13.3287 | 40.7222 |
| 199.6 | 2.2728 | 598.425 | 0.0148 | 7.07330 | 21.6104 |
| 228.5 | 1.5729 | 864.674 | 0.0102 | 4.89530 | 14.9562 |
| 260.3 | 1.1007 | 1235.67 | 0.0071 | 3.42553 | 10.4657 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves dos Santos Júnior, V.; Rodrigues de Farias Neto, S.; Gilson Barbosa de Lima, A.; Fernandes Gomes, I.; Buriti Galvão, I.; Maria Rufino Franco, C.; Evangelista Franco do Carmo, J. Heavy Oil Laminar Flow in Corrugated Ducts: A Numerical Study Using the Galerkin-Based Integral Method. Energies 2020, 13, 1363. https://doi.org/10.3390/en13061363
Alves dos Santos Júnior V, Rodrigues de Farias Neto S, Gilson Barbosa de Lima A, Fernandes Gomes I, Buriti Galvão I, Maria Rufino Franco C, Evangelista Franco do Carmo J. Heavy Oil Laminar Flow in Corrugated Ducts: A Numerical Study Using the Galerkin-Based Integral Method. Energies. 2020; 13(6):1363. https://doi.org/10.3390/en13061363
Chicago/Turabian StyleAlves dos Santos Júnior, Valdecir, Severino Rodrigues de Farias Neto, Antonio Gilson Barbosa de Lima, Igor Fernandes Gomes, Israel Buriti Galvão, Célia Maria Rufino Franco, and João Evangelista Franco do Carmo. 2020. "Heavy Oil Laminar Flow in Corrugated Ducts: A Numerical Study Using the Galerkin-Based Integral Method" Energies 13, no. 6: 1363. https://doi.org/10.3390/en13061363
APA StyleAlves dos Santos Júnior, V., Rodrigues de Farias Neto, S., Gilson Barbosa de Lima, A., Fernandes Gomes, I., Buriti Galvão, I., Maria Rufino Franco, C., & Evangelista Franco do Carmo, J. (2020). Heavy Oil Laminar Flow in Corrugated Ducts: A Numerical Study Using the Galerkin-Based Integral Method. Energies, 13(6), 1363. https://doi.org/10.3390/en13061363







