Energy, Exergy and Economic Analyses of a Combined Heating and Power System with Turbine-Driving Fans and Pumps in Northeast China
Abstract
1. Introduction
2. Materials and Methods
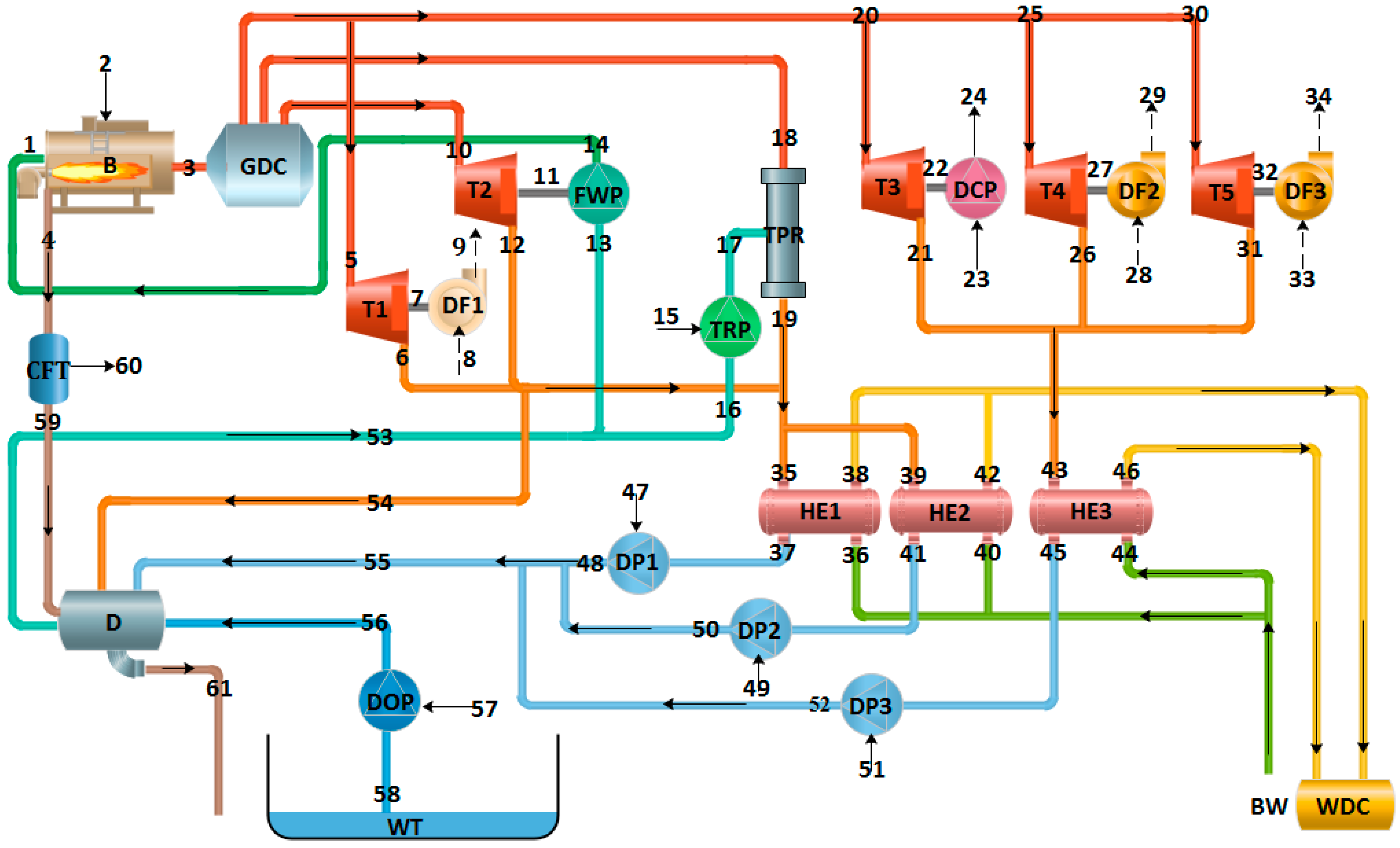
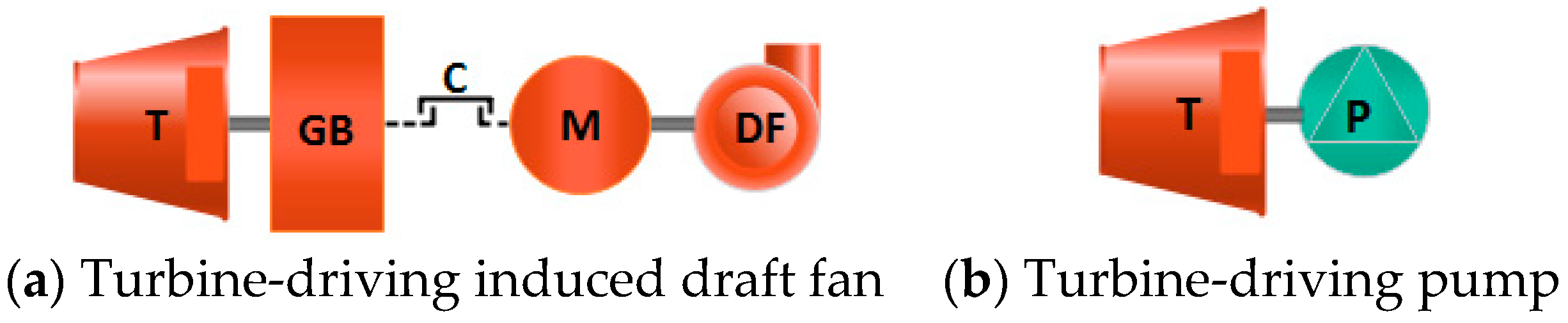
2.1. System Description
2.2. Data Preparation
2.3. Analytical Methods
- (1)
- A steady-state operational condition is assumed for the whole process.
- (2)
- The kinetic and potential exergies of flows are neglected.
- (3)
- The fresh air and flue gas are considered as ideal gases.
- (4)
- The pressure losses in piping and ducts are neglected.
- (5)
- The basic analysis is based on the reference state of 298.15 K and 0.10 MPa.
- (6)
- The standard molar fractions of species in the reference state are taken according to those of Szargut et al. [35].
2.3.1. Energy Analysis
2.3.2. Exergy Analysis
2.3.3. Economic Analysis
2.3.4. Uncertainty Analysis
3. Results and Discussion
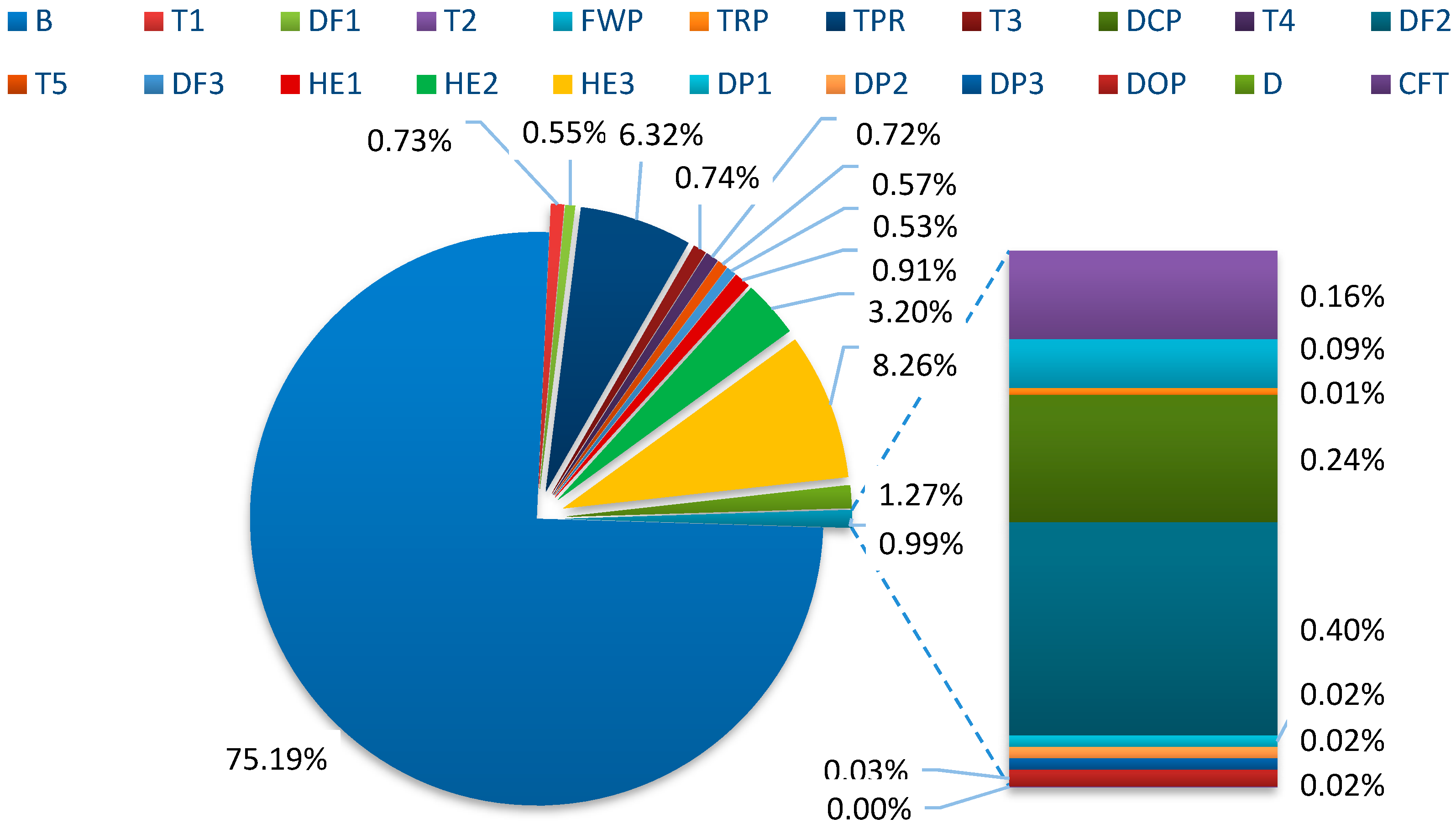
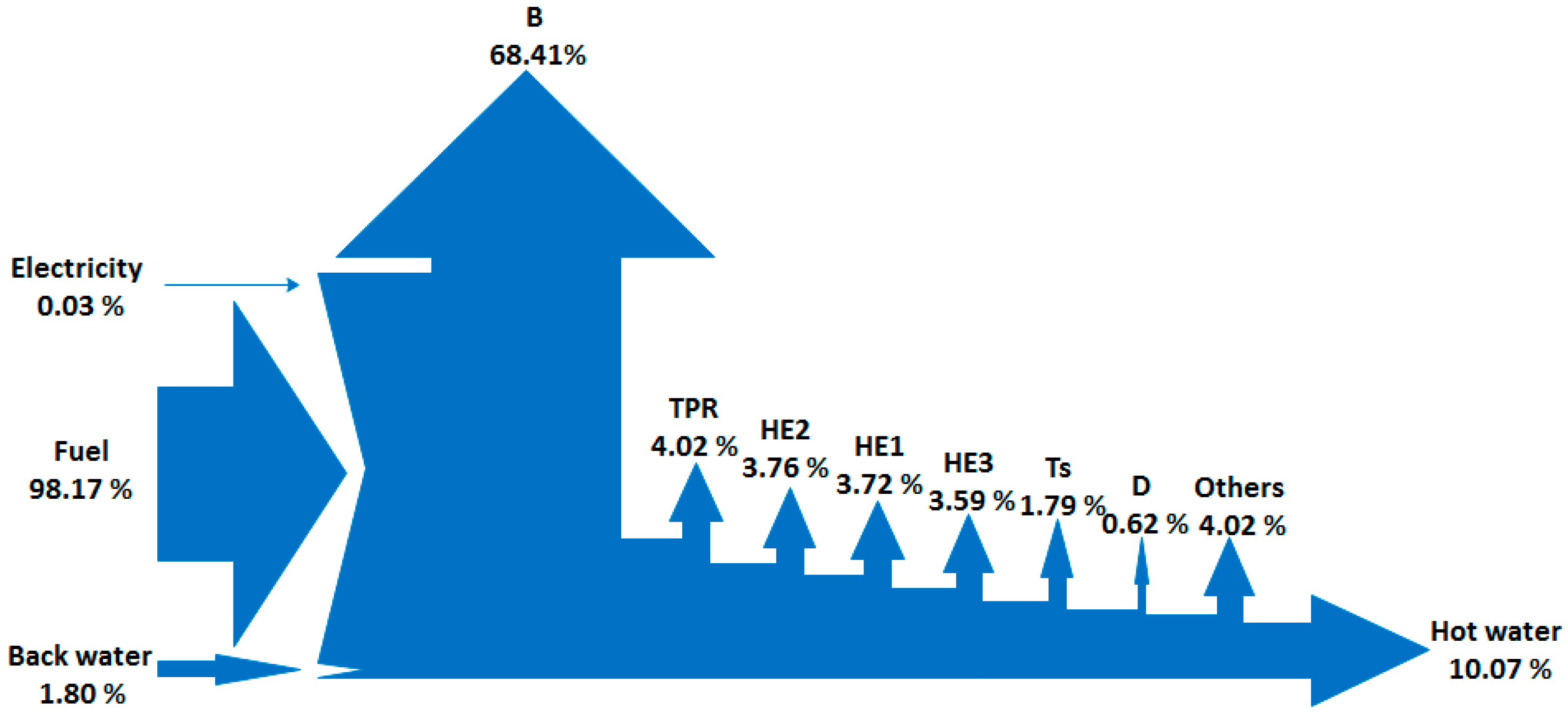
3.1. Energy Loss
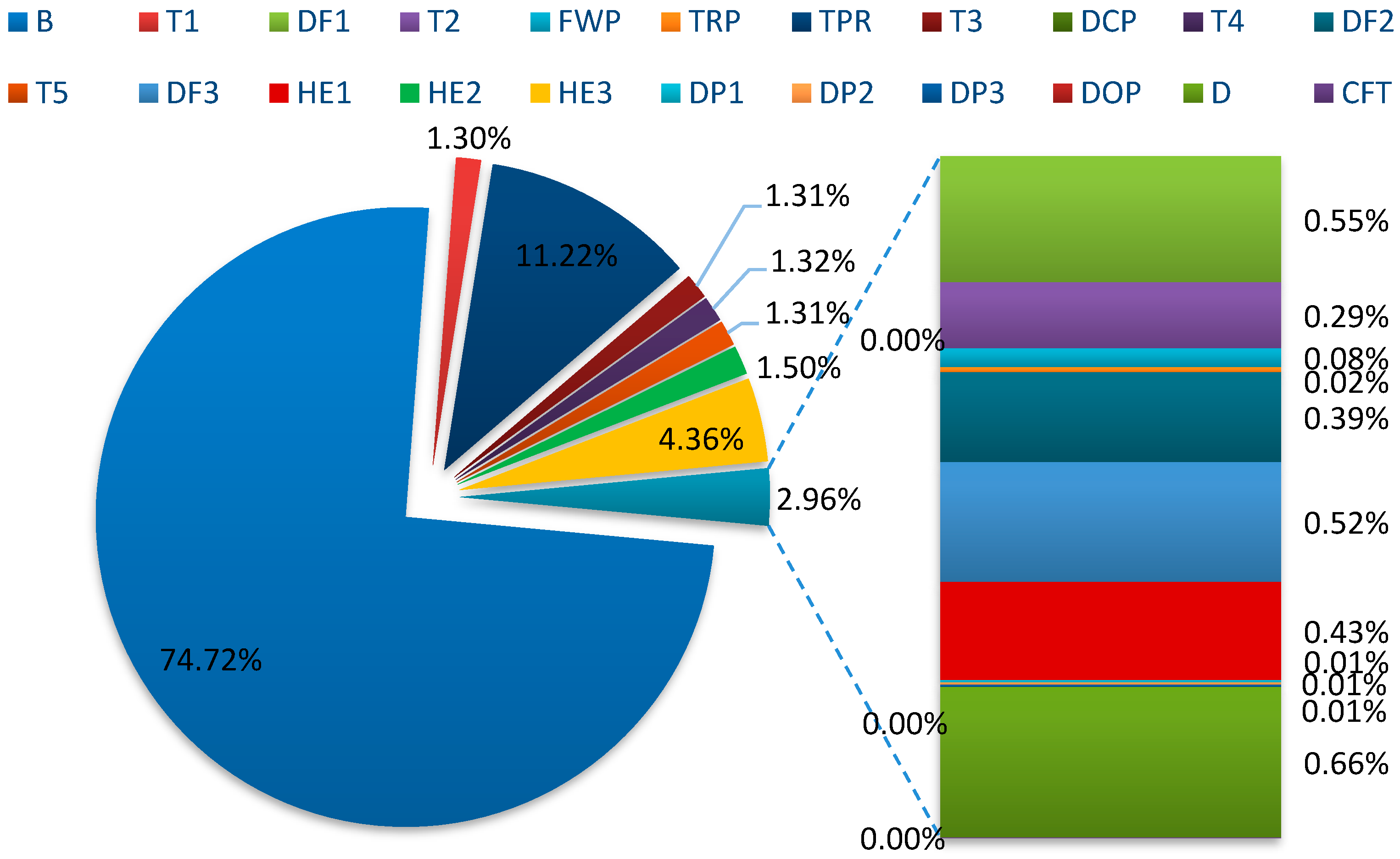
3.2. Exergy Loss
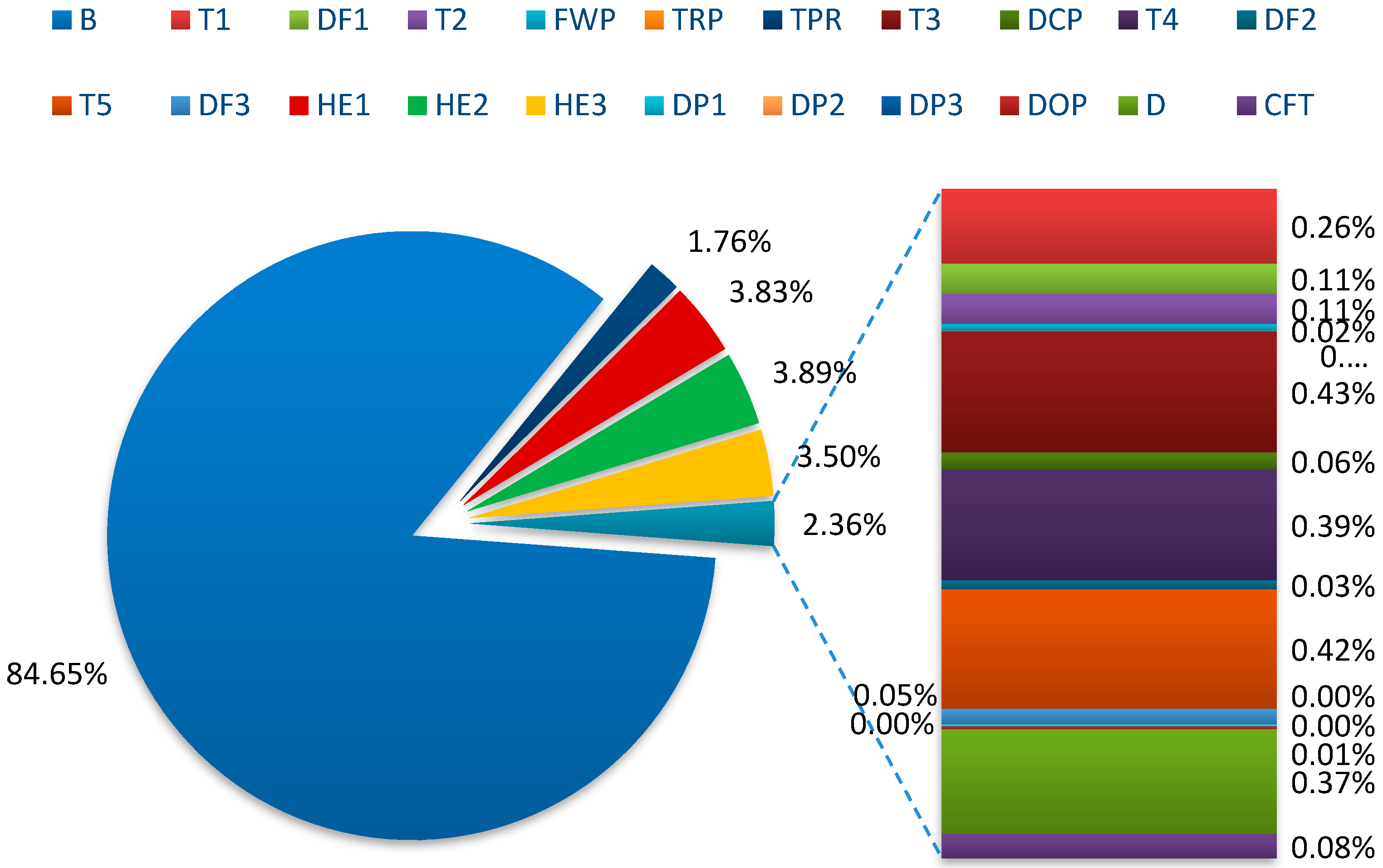
3.3. Exergy Destruction
3.4. Energy and Exergy Efficiencies
3.5. Exergy Improvement Potential
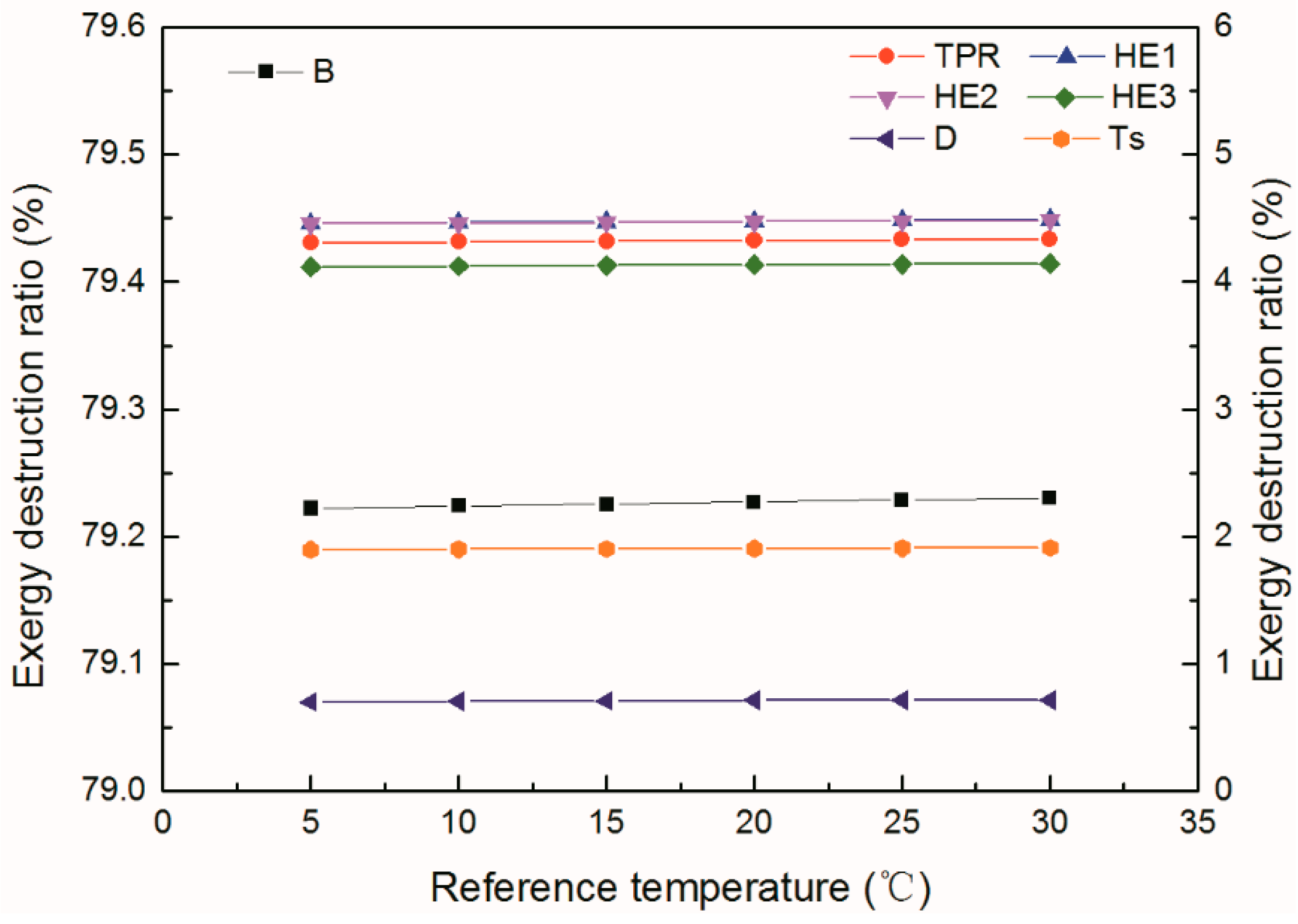
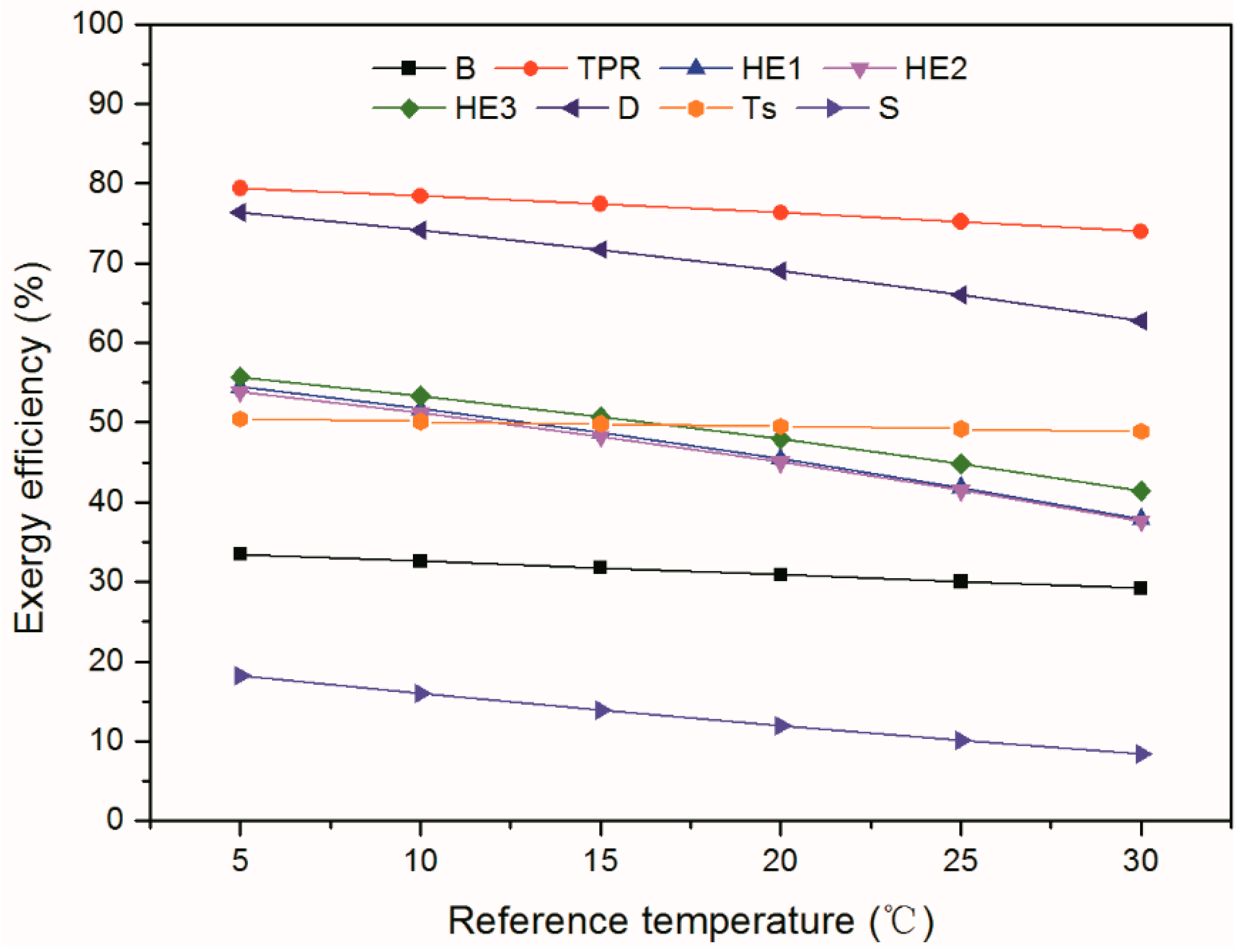
3.6. Effect of the Reference Temperature
3.7. Economic Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Component | Energy Balance | Energy Efficiency (×100%) |
|---|---|---|
| B | ||
| T1 | ||
| DF1 | ||
| T2 | ||
| FWP | ||
| TRP | ||
| TPR | ||
| T3 | ||
| DCP | ||
| T4 | ||
| DF2 | ||
| T5 | ||
| DF3 | ||
| HE1 | ||
| HE2 | ||
| HE3 | ||
| DP1 | ||
| DP2 | ||
| DP3 | ||
| DOP | ||
| D | ||
| CFT |
Appendix B
| Component | Exergy Balance | Exergy Efficiency (×100%) |
|---|---|---|
| B | ||
| T1 | ||
| DF1 | ||
| T2 | ||
| FWP | ||
| TRP | ||
| TPR | ||
| T3 | ||
| DCP | ||
| T4 | ||
| DF2 | ||
| T5 | ||
| DF3 | ||
| HE1 | ||
| HE2 | ||
| HE3 | ||
| DP1 | ||
| DP2 | ||
| DP3 | ||
| DOP | ||
| D | ||
| CFT |
Appendix C
| No. | Pressure (Mpa) | Temperature (K) | Fluid Type | Mass Flow Rate (kg·s−1) | Exergy Rate (kJ·kg−1) | Energy (kW) | Exergy (kW) |
|---|---|---|---|---|---|---|---|
| 1 | 1.78 | 373.79 | Water | 36.25 | 36.16 | 15,334.39 | 1310.68 |
| 2 | 0.10 | 273.15 | Fuel | 6.81 | 16,243.50 | 105,118.61 | 110,546.04 |
| 3 | 1.73 | 579.63 | Steam | 34.43 | 1002.31 | 104,909.94 | 34,514.53 |
| 4 | 1.73 | 478.23 | Water | 1.81 | 170.72 | 1586.50 | 309.41 |
| 5 | 1.25 | 562.88 | Steam | 3.25 | 947.78 | 9821.77 | 3079.72 |
| 6 | 0.30 | 454.67 | Steam | 3.25 | 676.44 | 9188.56 | 2198.01 |
| 7 | Work of T1 | 497.07 | 497.07 | ||||
| 8 | 0.10 | 388.40 | Flue gas | 82.59 | 15.40 | 1073.83 | |
| 9 | 0.11 | 388.40 | Flue gas | 82.59 | 19.89 | 1387.00 | |
| 10 | 1.24 | 549.18 | Steam | 0.93 | 933.10 | 2769.19 | 863.43 |
| 11 | Work of T2 | 111.18 | 111.18 | ||||
| 12 | 0.29 | 460.36 | Steam | 0.93 | 675.63 | 2627.56 | 625.18 |
| 13 | 0.12 | 377.93 | Water | 36.25 | 38.13 | 15,923.40 | 1382.04 |
| 14 | 1.78 | 378.26 | Water | 36.25 | 40.07 | 16,017.65 | 1452.51 |
| 15 | Electric power of TRP | 94.84 | 94.84 | ||||
| 16 | 0.12 | 377.93 | Water | 1.17 | 38.13 | 516.15 | 44.80 |
| 17 | 1.26 | 378.03 | Water | 1.17 | 39.32 | 517.62 | 46.20 |
| 18 | 1.23 | 566.70 | Steam | 19.17 | 950.12 | 58,103.56 | 18,210.70 |
| 19 | 0.30 | 452.95 | Steam | 20.34 | 675.21 | 57,448.75 | 13,734.92 |
| 20 | 1.21 | 557.88 | Steam | 3.91 | 938.65 | 11,792.57 | 3674.05 |
| 21 | 0.28 | 464.30 | Steam | 3.91 | 674.48 | 11,150.68 | 2640.05 |
| 22 | Work of T3 | 503.88 | 503.88 | ||||
| 23 | 0.10 | 298.15 | Water | 1069.72 | 0.00 | 112,245.95 | 0.00 |
| 24 | 0.44 | 298.16 | Water | 1069.72 | 0.34 | 112,705.93 | 364.30 |
| 25 | 1.22 | 559.98 | Steam | 3.84 | 942.28 | 11,587.10 | 3618.86 |
| 26 | 0.30 | 468.10 | Steam | 3.84 | 685.90 | 10,962.90 | 2634.20 |
| 27 | Work of T4 | 490.00 | 490.00 | ||||
| 28 | 0.10 | 388.04 | Flue gas | 90.92 | 15.29 | 1389.87 | |
| 29 | 0.11 | 388.04 | Flue gas | 90.92 | 19.60 | 1781.74 | |
| 30 | 1.23 | 556.35 | Steam | 3.34 | 939.43 | 10,045.66 | 3136.52 |
| 31 | 0.28 | 470.27 | Steam | 3.34 | 678.92 | 9552.26 | 2266.74 |
| 32 | Work of T5 | 387.32 | 387.32 | ||||
| 33 | 0.10 | 386.10 | Flue gas | 62.91 | 14.69 | 923.87 | |
| 34 | 0.11 | 386.10 | Flue gas | 62.91 | 19.00 | 1195.03 | |
| 35 | 0.28 | 452.56 | Steam | 11.00 | 666.01 | 31,063.24 | 7324.48 |
| 36 | 0.52 | 319.45 | Water | 217.57 | 3.43 | 42,277.94 | 746.99 |
| 37 | 0.04 | 337.69 | Water | 11.00 | 10.02 | 2971.20 | 110.23 |
| 38 | 0.42 | 350.15 | Water | 217.57 | 17.31 | 70,200.70 | 3766.89 |
| 39 | 0.28 | 452.37 | Steam | 11.00 | 665.89 | 31,058.95 | 7323.14 |
| 40 | 0.52 | 319.45 | Water | 216.62 | 3.43 | 42,093.35 | 743.73 |
| 41 | 0.04 | 330.97 | Water | 11.00 | 6.97 | 2661.84 | 76.63 |
| 42 | 0.41 | 350.15 | Water | 216.62 | 17.32 | 69,896.36 | 3752.61 |
| 43 | 0.28 | 459.41 | Steam | 11.09 | 670.92 | 31,491.26 | 7442.83 |
| 44 | 0.52 | 319.40 | Water | 155.52 | 3.43 | 30,188.29 | 533.76 |
| 45 | 0.04 | 336.89 | Water | 11.09 | 9.62 | 2959.96 | 106.77 |
| 46 | 0.42 | 360.88 | Water | 155.52 | 24.59 | 57,186.83 | 3823.96 |
| 47 | Electric power of DP1 | 10.00 | 10.00 | ||||
| 48 | 0.56 | 337.72 | Water | 11.00 | 10.54 | 2977.25 | 115.95 |
| 49 | Electric power of DP2 | 10.00 | 10.00 | ||||
| 50 | 0.56 | 331.00 | Water | 11.00 | 7.46 | 2667.89 | 82.02 |
| 51 | Electric power of DP3 | 10.09 | 10.09 | ||||
| 52 | 0.56 | 336.92 | Water | 11.09 | 10.14 | 2966.06 | 112.54 |
| 53 | 0.12 | 377.93 | Water | 37.42 | 38.13 | 16,439.55 | 1426.84 |
| 54 | 0.28 | 452.56 | Steam | 2.52 | 666.01 | 7121.60 | 1679.22 |
| 55 | 0.56 | 334.60 | Water | 33.09 | 9.06 | 8525.91 | 299.83 |
| 56 | 0.58 | 298.18 | Water | 1.73 | 0.48 | 182.47 | 0.83 |
| 57 | Electric power of DOP | 6.75 | 6.75 | ||||
| 58 | 0.10 | 298.15 | Water | 1.73 | 0.00 | 181.48 | 0.00 |
| 59 | 0.12 | 377.93 | Steam | 0.35 | 511.83 | 945.07 | 180.29 |
| 60 | 0.12 | 377.93 | Water | 1.46 | 38.13 | 641.43 | 55.67 |
| 61 | 0.12 | 373.27 | Steam | 0.04 | 511.83 | 100.41 | 19.15 |
Appendix D
| Component | Energy Loss (kW) | Energy Efficiency (%) | Exergy Loss (kW) | Exergy Destruction (kW) | Exergy Efficiency (%) | Exergy Improvement Potential (kW) |
|---|---|---|---|---|---|---|
| B | 13,956.56 | 85.21 | 3243.00 | 73,789.79 | 30.04 | 53,895.05 |
| T1 | 136.14 | 78.5 | 56.36 | 328.28 | 56.38 | 167.80 |
| DF1 | 102.4 | 79.4 | 23.8 | 160.11 | 49.46 | 92.95 |
| T2 | 30.45 | 78.5 | 12.46 | 114.6 | 46.67 | 67.80 |
| FWP | 16.94 | 84.77 | 3.58 | 37.13 | 63.38 | 14.91 |
| TRP | 2.23 | 39.69 | 0.92 | 1.39 | 37.8 | 1.43 |
| TPR | 1172.42 | 98 | 486.78 | 4035.2 | 75.23 | 1120.03 |
| T3 | 138.01 | 78.5 | 56.72 | 473.4 | 48.73 | 271.80 |
| DCP | 43.9 | 91.29 | 0 | 139.58 | 72.30 | 38.67 |
| T4 | 134.2 | 78.5 | 57.18 | 437.49 | 49.76 | 248.51 |
| DF2 | 73.49 | 85 | 17.02 | 81.1 | 62.78 | 36.52 |
| T5 | 106.08 | 78.5 | 57.06 | 425.4 | 44.53 | 267.62 |
| DF3 | 99.12 | 74.41 | 22.58 | 93.58 | 54.96 | 52.32 |
| HE1 | 169.28 | 99.4 | 18.53 | 4175.82 | 41.86 | 2438.59 |
| HE2 | 594.1 | 97.91 | 65.04 | 4172.6 | 41.52 | 2478.1 |
| HE3 | 1532.76 | 94.63 | 189.23 | 3856.63 | 44.85 | 2231.3 |
| DP1 | 3.95 | 60.49 | 0.46 | 3.82 | 57.21 | 1.83 |
| DP2 | 3.95 | 60.49 | 0.39 | 4.22 | 53.93 | 2.12 |
| DP3 | 3.99 | 60.47 | 0.46 | 3.86 | 57.19 | 1.85 |
| DOP | 5.76 | 14.61 | 0 | 5.92 | 12.31 | 5.19 |
| D | 235.1 | 98 | 49.63 | 663.72 | 66.05 | 242.17 |
| CFT | 0 | 59.57 | 0 | 129.12 | 58.27 | 53.89 |
| Total | 18,560.83 | 89.72 | 4361.20 | 93,132.76 | 10.07 | 63,730.45 |
References
- Hepbasli, A.; Erbay, Z.; Icier, F.; Colak, N.; Hancioglu, E. A review of gas engine driven heat pumps (GEHPs) for residential and industrial applications. Renew. Sust. Energy Rev. 2009, 13, 85–99. [Google Scholar] [CrossRef]
- Kaushik, S.C.; Reddy, V.S.; Tyagi, S.K. Energy and exergy analyses of thermal power plants: A review. Renew. Sust. Energy Rev. 2011, 15, 1857–1872. [Google Scholar] [CrossRef]
- Saidur, R.; Ahamed, J.U.; Masjuki, H.H. Energy, exergy and economic analysis of industrial boilers. Energy Policy 2010, 38, 2188–2197. [Google Scholar] [CrossRef]
- Zhang, Q.; Yi, H.; Yu, Z.; Gao, J.; Wang, X.; Lin, H.; Shen, B. Energy-exergy analysis and energy efficiency improvement of coal-fired industrial boilers based on thermal test data. Appl. Therm. Eng. 2018, 144, 614–627. [Google Scholar] [CrossRef]
- Koroglu, T.; Sogut, O.S. Conventional and advanced exergy analyses of a marine steam power plant. Energy 2018, 163, 392–403. [Google Scholar] [CrossRef]
- Elhelw, M.; Al Dahma, K.S.; el Hamid Attia, A. Utilizing exergy analysis in studying the performance of steam power plant at two different operation mode. Appl. Therm. Eng. 2019, 150, 285–293. [Google Scholar] [CrossRef]
- Ahmadi, G.R.; Toghraie, D. Energy and exergy analysis of Montazeri Steam Power Plant in Iran. Renew. Sustain. Energy Rev. 2016, 56, 454–463. [Google Scholar] [CrossRef]
- Xu, C.; Li, X.; Xu, G.; Xin, T.; Yang, Y.; Liu, W.; Wang, M. Energy, exergy and economic analyses of a novel solar-lignite hybrid power generation process using lignite pre-drying. Energy Convers. Manag. 2018, 170, 19–33. [Google Scholar] [CrossRef]
- Menberg, K.; Heo, Y.; Choi, W.; Ooka, R.; Choudhary, R.; Shukuya, M. Exergy analysis of a hybrid ground-source heat pump system. Appl. Energy 2017, 204, 31–46. [Google Scholar] [CrossRef]
- Vakilabadi, M.A.; Bidi, M.; Najafi, A.F.; Ahmadi, M.H. Exergy analysis of a hybrid solar-fossil fuel power plant. Energy Sci. Eng. 2019, 7, 146–161. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, J.; Lubell, M.; Qiu, L.; Kang, K. Design and simulation of a novel hybrid solar-biomass energy supply system in northwest China. J. Clean. Prod. 2019, 233, 1221–1239. [Google Scholar] [CrossRef]
- Koroneos, C.J.; Fokaides, P.A.; Christoforou, E.A. Exergy analysis of a 300 MW lignite thermoelectric power plant. Energy 2014, 75, 304–311. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, Q.; Fang, M.; Luo, Z.; Cen, K. Thermodynamic and economic analysis of polygeneration system integrating atmospheric pressure coal pyrolysis technology with circulating fluidized bed power plant. Appl. Energy 2014, 113, 1301–1314. [Google Scholar] [CrossRef]
- Ahmadi, G.; Toghraie, D.; Akbari, O. Energy, exergy and environmental (3E) analysis of the existing CHP system in a petrochemical plant. Renew. Sust. Energy Rev. 2019, 99, 234–242. [Google Scholar] [CrossRef]
- Gürtürk, M.; Oztop, H.F. Exergy analysis of a circulating fluidized bed boiler cogeneration power plant. Energy Convers. Manag. 2016, 120, 346–357. [Google Scholar] [CrossRef]
- Karellas, S.; Braimakis, K. Energy–exergy analysis and economic investigation of a cogeneration and trigeneration ORC–VCC hybrid system utilizing biomass fuel and solar power. Energy Convers. Manag. 2016, 107, 103–113. [Google Scholar] [CrossRef]
- Ozdil, N.F.T.; Tantekin, A.; Erbay, Z. Energy and exergy analyses of a fluidized bed coal combustor steam plant in textile industry. Fuel 2016, 183, 441–448. [Google Scholar] [CrossRef]
- Zeng, Z.; Hong, M.; Li, J.; Man, Y.; Liu, H.; Li, Z.; Zhang, H. Integrating process optimization with energy-efficiency scheduling to save energy for paper mills. Appl. Energy 2018, 225, 542–558. [Google Scholar] [CrossRef]
- Zhao, H.; Lin, B. Will agglomeration improve the energy efficiency in China’s textile industry: Evidence and policy implications. Appl. Energy 2019, 237, 326–337. [Google Scholar] [CrossRef]
- Mojarab Soufiyan, M.; Dadak, A.; Hosseini, S.S.; Nasiri, F.; Dowlati, M.; Tahmasebi, M.; Aghbashlo, M. Comprehensive exergy analysis of a commercial tomato paste plant with a double-effect evaporator. Energy 2016, 111, 910–922. [Google Scholar] [CrossRef]
- Mojarab Soufiyan, M.; Aghbashlo, M. Application of exergy analysis to the dairy industry: A case study of yogurt drink production plant. Food Bioprod. Process. 2017, 101, 118–131. [Google Scholar] [CrossRef]
- Mojarab Soufiyan, M.; Aghbashlo, M.; Mobli, H. Exergetic performance assessment of a long-life milk processing plant: A comprehensive survey. J. Clean. Prod. 2017, 140, 590–607. [Google Scholar] [CrossRef]
- Kubule, A.; Zogla, L.; Rosa, M. Resource and Energy Efficiency in Small and Medium Breweries. Energy Procedia 2016, 95, 223–229. [Google Scholar] [CrossRef]
- Hepbasli, A. A review on energetic, exergetic and exergoeconomic aspects of geothermal district heating systems (GDHSs). Energy Convers. Manag. 2010, 51, 2041–2061. [Google Scholar] [CrossRef]
- Ozgener, L.; Hepbasli, A.; Dincer, I. Energy and exergy analysis of the Gonen geothermal district heating system, Turkey. Geothermics 2005, 34, 632–645. [Google Scholar] [CrossRef]
- Li, H.; Svendsen, S. Energy and exergy analysis of low temperature district heating network. Energy 2012, 45, 237–246. [Google Scholar] [CrossRef]
- Ozgener, L.; Ozgener, O. Monitoring of energy exergy efficiencies and exergoeconomic parameters of geothermal district heating systems (GDHSs). Appl. Energy 2009, 86, 1704–1711. [Google Scholar] [CrossRef]
- Zhu, L. Analysis of Market Status and Development Trend of CHP Industry in 2018. Available online: https://www.qianzhan.com/analyst/detail/220/190104-9eb67de3.html (accessed on 4 January 2019).
- National Development and Reform Commission. 13th Five Year Plan for Electric Power Development; National Energy Administration: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Heberle, F.; Brüggemann, D. Exergy based fluid selection for a geothermal Organic Rankine Cycle for combined heat and power generation. Appl. Therm. Eng. 2010, 30, 1326–1332. [Google Scholar] [CrossRef]
- Kanoglu, M.; Dincer, I. Performance assessment of cogeneration plants. Energy Convers. Manag. 2009, 50, 76–81. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y. Energy, exergy and environmental analysis of a hybrid combined cooling heating and power system utilizing biomass and solar energy. Energy Convers. Manag. 2016, 124, 566–577. [Google Scholar] [CrossRef]
- Al-Sulaiman, F.A.; Hamdullahpur, F.; Dincer, I. Greenhouse gas emission and exergy assessments of an integrated organic Rankine cycle with a biomass combustor for combined cooling, heating and power production. Appl. Therm. Eng. 2011, 31, 439–446. [Google Scholar] [CrossRef]
- Khaljani, M.; Khoshbakhti Saray, R.; Bahlouli, K. Comprehensive analysis of energy, exergy and exergo-economic of cogeneration of heat and power in a combined gas turbine and organic Rankine cycle. Energy Convers. Manag. 2015, 97, 154–165. [Google Scholar] [CrossRef]
- Szargut, J.; Morris, D.R.; Steward, F.R. Exergy Analysis of Thermal, Chemical, and Metallurgical Processes, 1st ed.; Hemisphere: New York, NY, USA, 1988. [Google Scholar]
- Yin, W.Z.; Qi, J.F.; Yuan, S. The Energy-Saving Status of the Industrial Boilers and Reduce Consumption Measures; Destech Publications: Lancaster, PA, USA, 2015; pp. 2746–2750. [Google Scholar]
- Gürtürk, M.; Oztop, H.F.; Hepbaslı, A. Energy and exergy assessments of a perlite expansion furnace in a plaster plant. Energy Convers. Manag. 2013, 75, 488–497. [Google Scholar] [CrossRef]
- Terhan, M.; Comakli, K. Energy and exergy analyses of natural gas-fired boilers in a district heating system. Appl. Therm. Eng. 2017, 121, 380–387. [Google Scholar] [CrossRef]
- Ohijeagbon, I.O.; Waheed, M.A.; Jekayinfa, S.O. Methodology for the physical and chemical exergetic analysis of steam boilers. Energy 2013, 53, 153–164. [Google Scholar] [CrossRef]
- Erdem, H.H.; Akkaya, A.V.; Cetin, B.; Dagdas, A.; Sevilgen, S.H.; Sahin, B.; Teke, I.; Gungor, C.; Atas, S. Comparative energetic and exergetic performance analyses for coal-fired thermal power plants in Turkey. Int. J. Therm. Sci. 2009, 48, 2179–2186. [Google Scholar] [CrossRef]
- Gümüş, M.; Atmaca, M. Energy and Exergy Analyses Applied to a CI Engine Fueled with Diesel and Natural Gas. Energy Sour. Part A 2013, 35, 1017–1027. [Google Scholar] [CrossRef]
- Xu, N. Study on Evaluation Method of Steam System Energy Efficiency in Iron and Steel Enterprises; Shandong University: Jinan, China, 2014. (In Chinese) [Google Scholar]
- Dowlati, M.; Aghbashlo, M.; Mojarab Soufiyan, M. Exergetic performance analysis of an ice-cream manufacturing plant: A comprehensive survey. Energy 2017, 123, 445–459. [Google Scholar] [CrossRef]
- Zhu, W. Flow Characteristic Analysis of Turbine Control Valve Based on Data Mining; Zhejiang University: Hangzhou, China, 2019. (In Chinese) [Google Scholar]
- Mambro, A.; Galloni, E.; Congiu, F.; Maraone, N. Modelling of low-pressure steam turbines operating at very low flowrates: A multiblock approach. Appl. Therm. Eng. 2019, 158, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Han, W.; Zhang, N.; Su, B.; Liu, M.; Jin, H. Assessment of off-design performance of a combined cooling, heating and power system using exergoeconomic analysis. Energy Convers. Manag. 2018, 171, 188–195. [Google Scholar] [CrossRef]
- Tian, Z.; Niu, J.; Lu, Y.; He, S.; Tian, X. The improvement of a simulation model for a distributed CCHP system and its influence on optimal operation cost and strategy. Appl. Energy 2016, 165, 430–444. [Google Scholar] [CrossRef]
- Sun, H.; Feng, D.; Zhao, Y.; Guo, D.; Ma, Y.; Tan, H.; Sun, S. Characteristics of Gas–Liquid–Solid Products in Corn Straw Gasification: Effect of the Char–Tar–H2O Interaction. Energy Fuels 2019, 33, 9974–9984. [Google Scholar] [CrossRef]
- Aljundi, I.H. Energy and exergy analysis of a steam power plant in Jordan. Appl. Therm. Eng. 2009, 29, 324–328. [Google Scholar] [CrossRef]



| Dry Ash-Free Basis | Unit | Value |
|---|---|---|
| Cdaf | % | 66.72 |
| Hdaf | % | 4.59 |
| Odaf | % | 26.67 |
| Ndaf | % | 1.07 |
| Sdaf | % | 0.95 |
| LHV0 1 | kJ·kg−1 | 15,446 |
| Composition | Unit | Value |
|---|---|---|
| CO2 | % | 12.25 |
| O2 | % | 7.95 |
| CO | % | 0.03 |
| N2 | % | 79.77 |
| Reference State | Section | Energy Efficiency % | Exergy Efficiency % | Reference | ||
|---|---|---|---|---|---|---|
| Boiler | Turbine | Boiler | Turbine | |||
| 298.15 K, 0.10 MPa | Industrial | 72.46 | 24.89 | [3] | ||
| 80.80 | 25.00 | [3] | ||||
| 66.00 | 26.00 | [37] | ||||
| 82.21 | 32.77 | [38] | ||||
| 84.65 | 29.43 | [15] | ||||
| 69.56 | 38.57 | [39] | ||||
| Power plant | 40.84 | 80.10 | [40] | |||
| 36.75 | 85.45 | |||||
| 45.47 | 88.60 | |||||
| 48.23 | 90.03 | |||||
| 36.45 | 84.19 | |||||
| 39.00 | 86.16 | |||||
| 84.89 | 78.50 | 30.04 | 49.21 | This work | ||
| Economic Analysis | Electricity-Driving Mode | Turbine-Driving Mode |
|---|---|---|
| Power consumption (kW) | 2121.13 | 131.68 |
| Electricity cost (yuan) | 34,343.22 | 94.46 |
| Electricity income (yuan) | 17,594.69 | 0.00 |
| Capital saved (yuan) | 16,654.08 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Gao, J.; Zhang, Y.; Zhang, Y.; Du, Q.; Wu, S.; Qin, Y. Energy, Exergy and Economic Analyses of a Combined Heating and Power System with Turbine-Driving Fans and Pumps in Northeast China. Energies 2020, 13, 878. https://doi.org/10.3390/en13040878
Li X, Gao J, Zhang Y, Zhang Y, Du Q, Wu S, Qin Y. Energy, Exergy and Economic Analyses of a Combined Heating and Power System with Turbine-Driving Fans and Pumps in Northeast China. Energies. 2020; 13(4):878. https://doi.org/10.3390/en13040878
Chicago/Turabian StyleLi, Ximei, Jianmin Gao, Yaning Zhang, Yu Zhang, Qian Du, Shaohua Wu, and Yukun Qin. 2020. "Energy, Exergy and Economic Analyses of a Combined Heating and Power System with Turbine-Driving Fans and Pumps in Northeast China" Energies 13, no. 4: 878. https://doi.org/10.3390/en13040878
APA StyleLi, X., Gao, J., Zhang, Y., Zhang, Y., Du, Q., Wu, S., & Qin, Y. (2020). Energy, Exergy and Economic Analyses of a Combined Heating and Power System with Turbine-Driving Fans and Pumps in Northeast China. Energies, 13(4), 878. https://doi.org/10.3390/en13040878






