Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction
Abstract
1. Introduction
2. Pricing Strategy Using the Thermal Response of HVAC Systems in Commercial Buildings
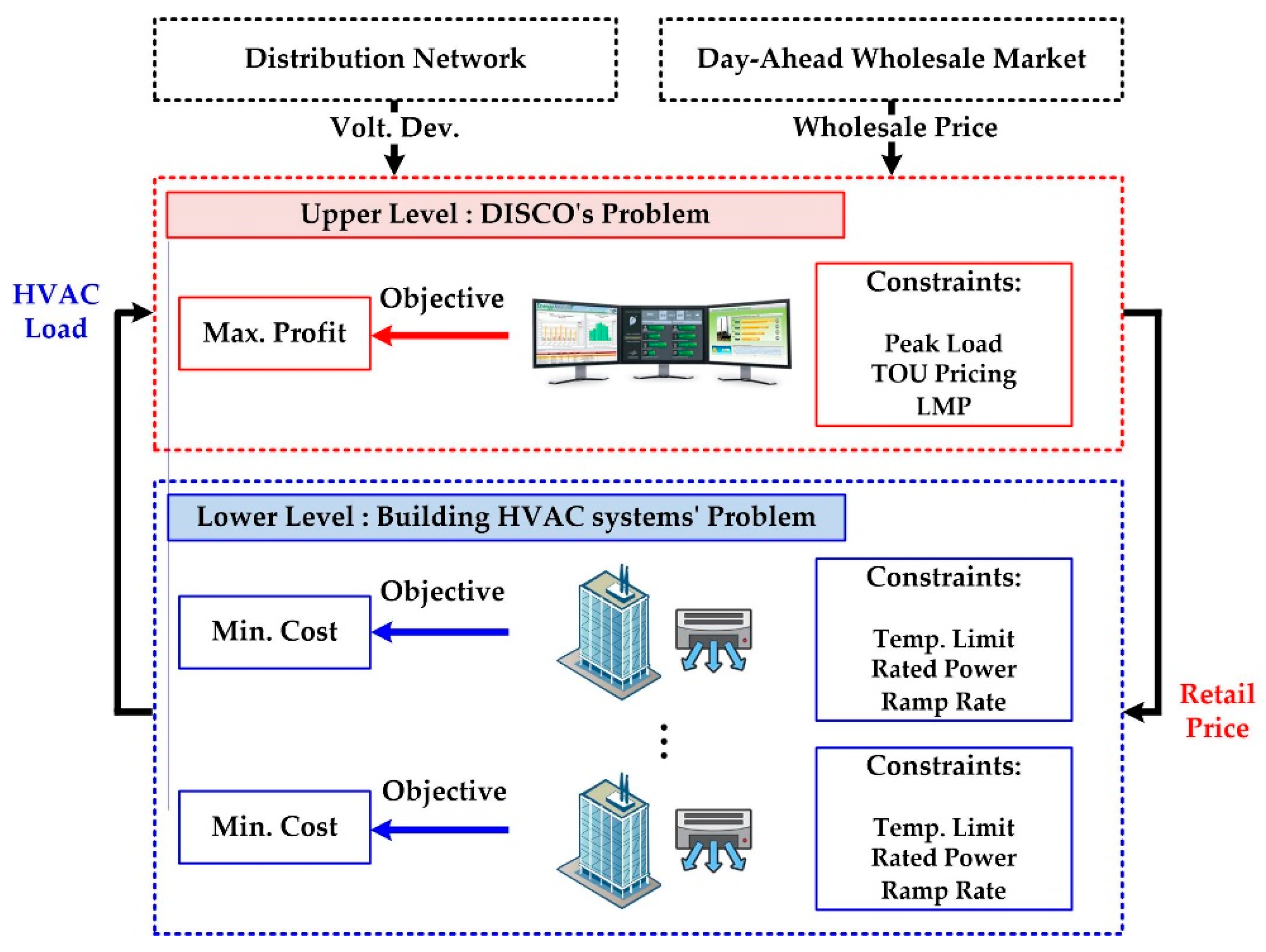
2.1. Framework of the Proposed Pricing Strategy
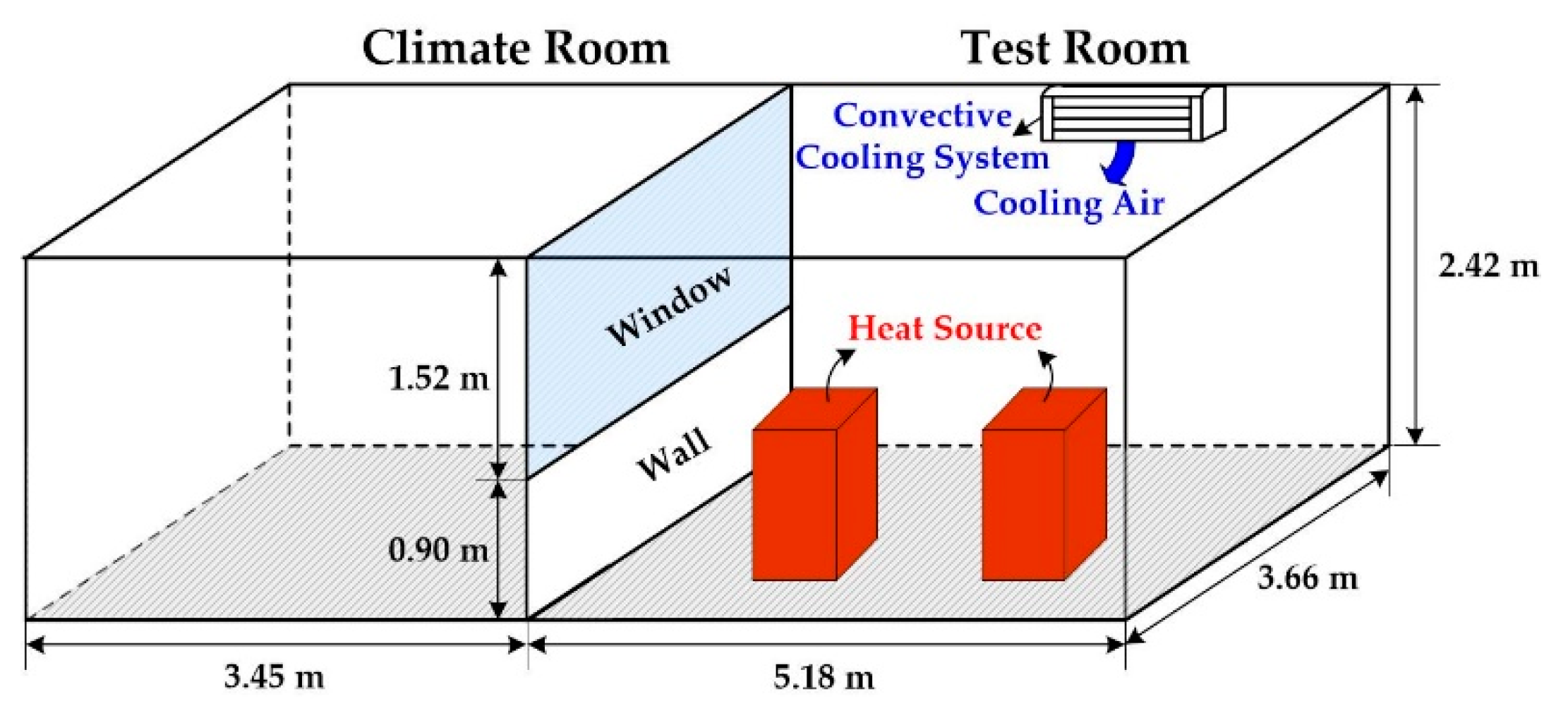
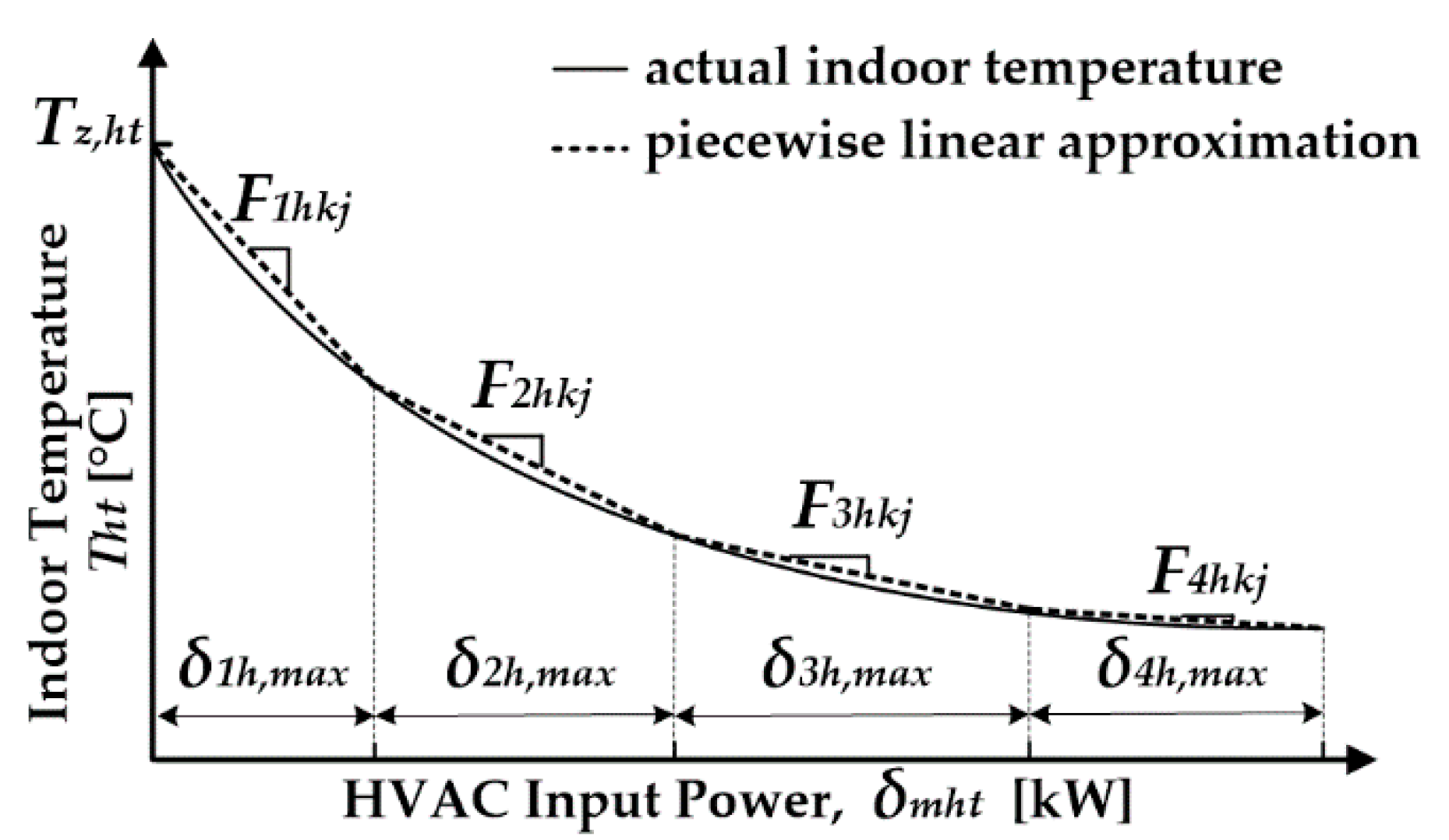
2.2. Modeling the Thermal Response of HVAC Systems in Commercial Buildings
3. Optimization Problem Formulation
3.1. Upper-Level Problem
3.2. Lower-Level Problem
3.3. Equivalent Single-Level Problem
4. Simulation Case Studies and Results
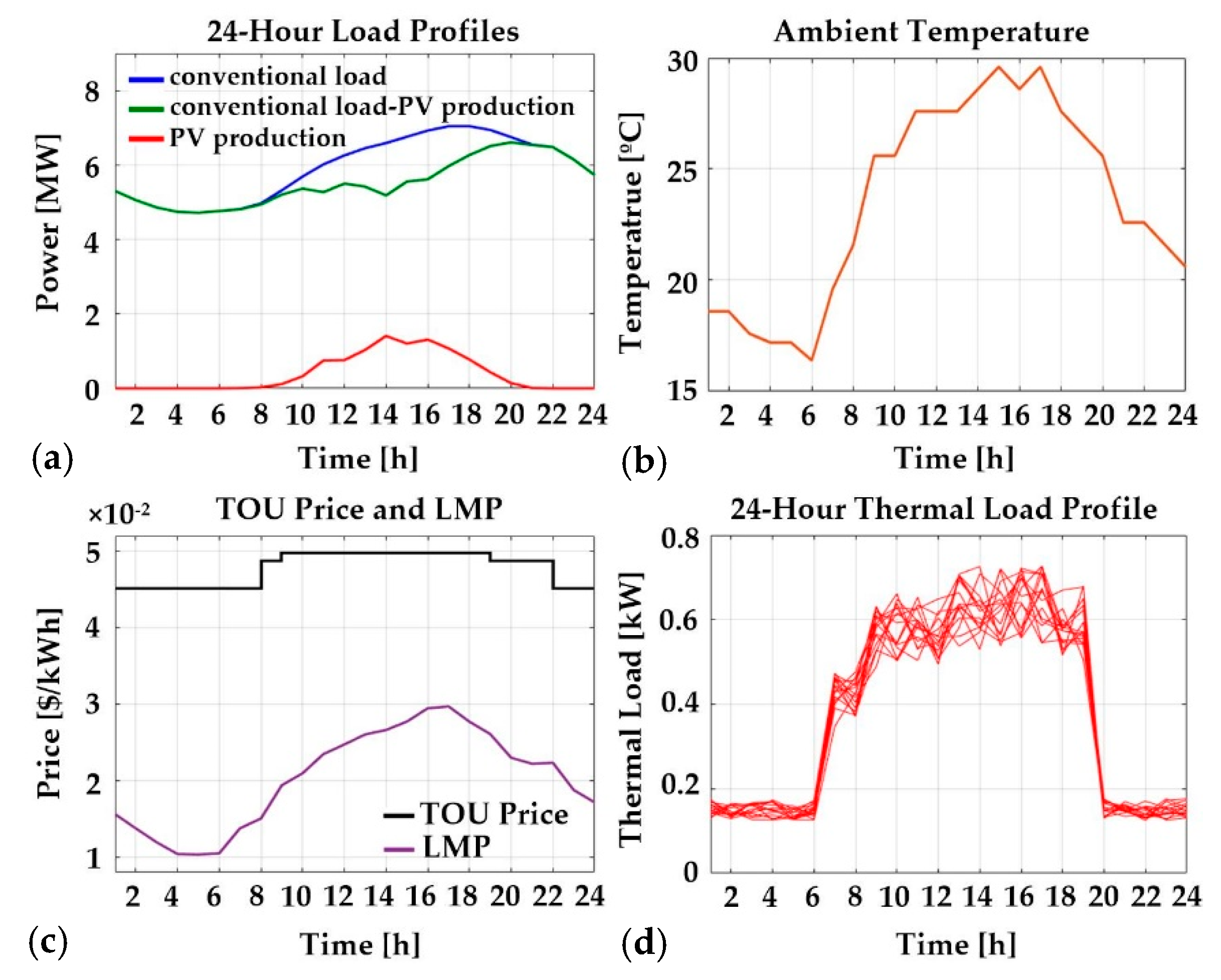
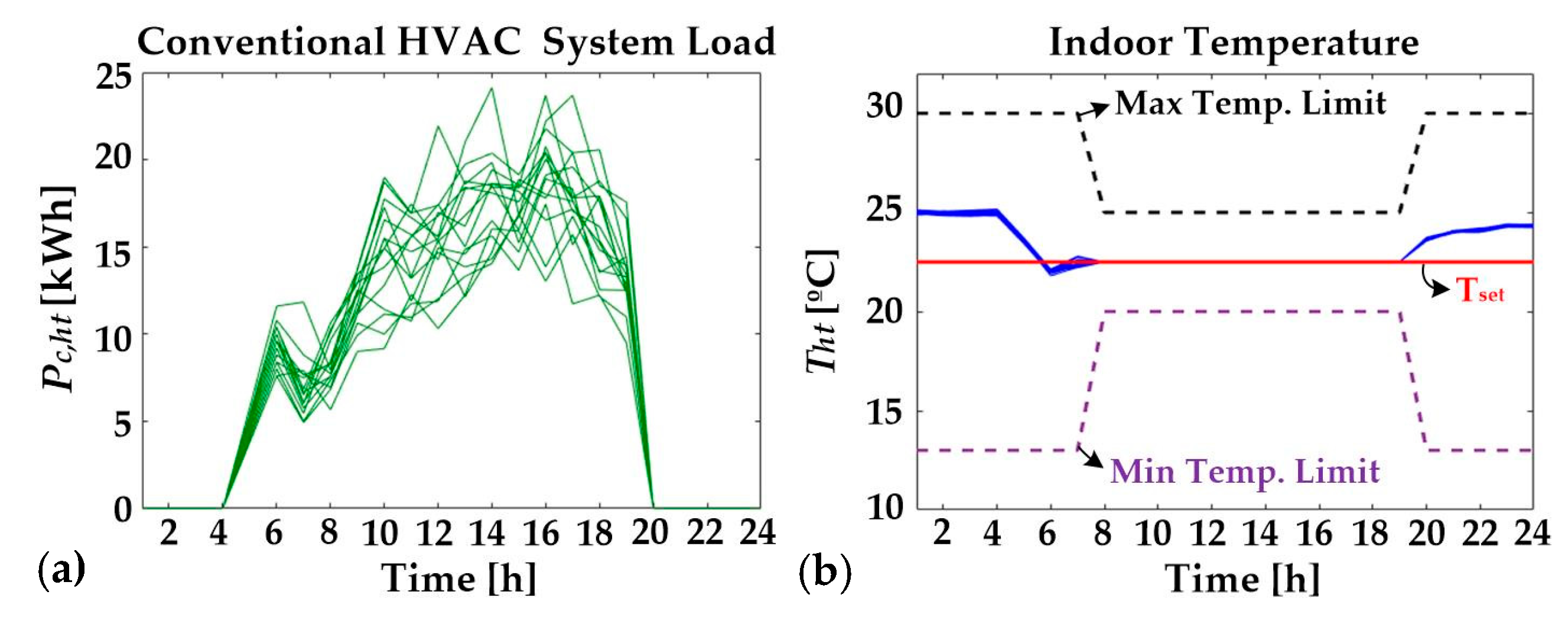
4.1. Test System and Simulation Conditions
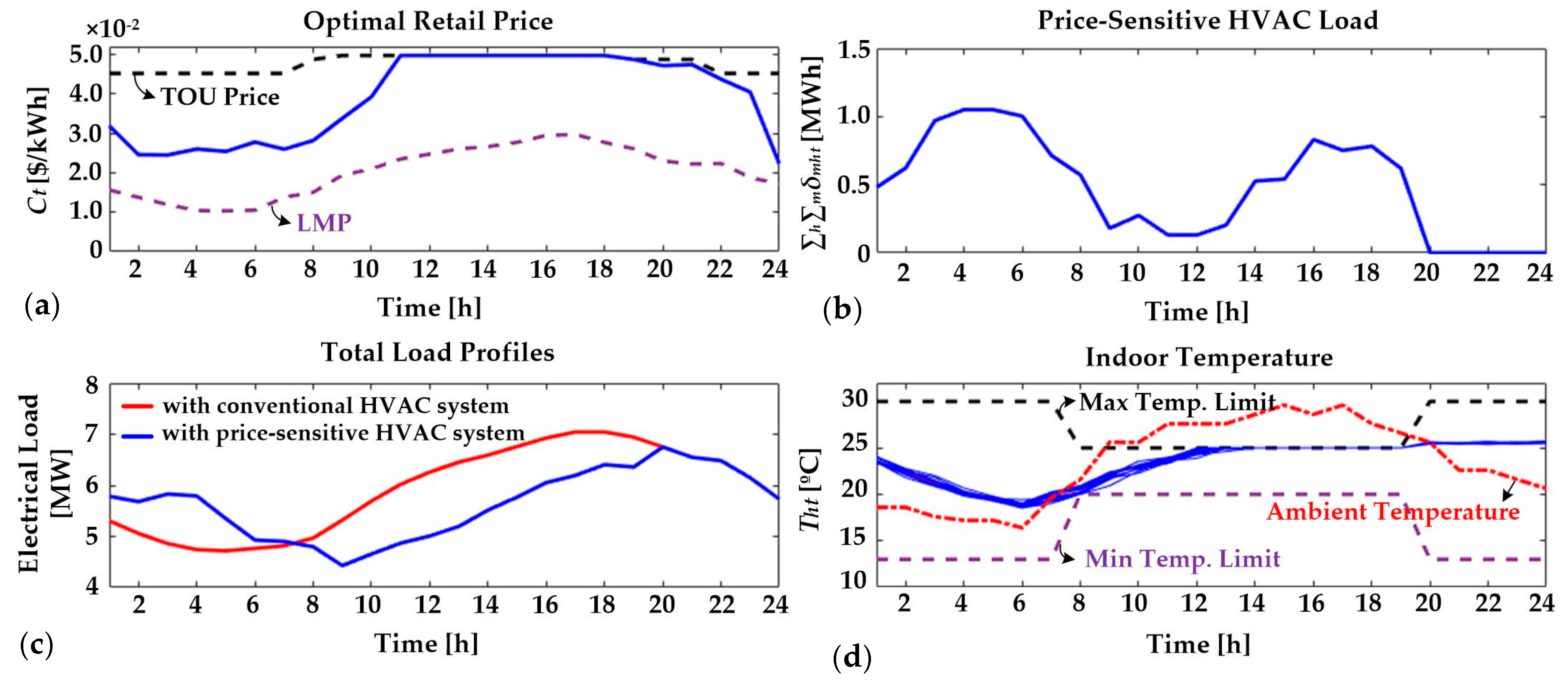
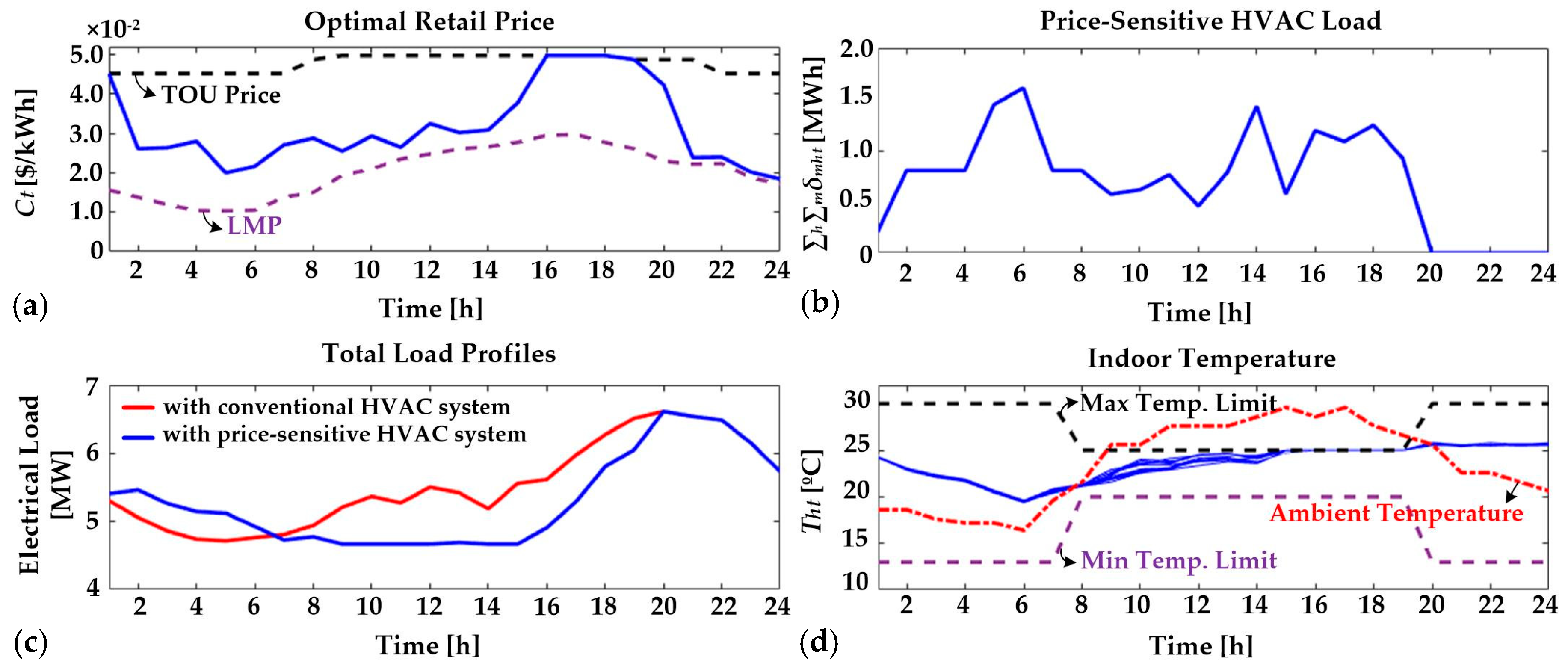
4.2. Case Study A: Two Types of Load Profiles
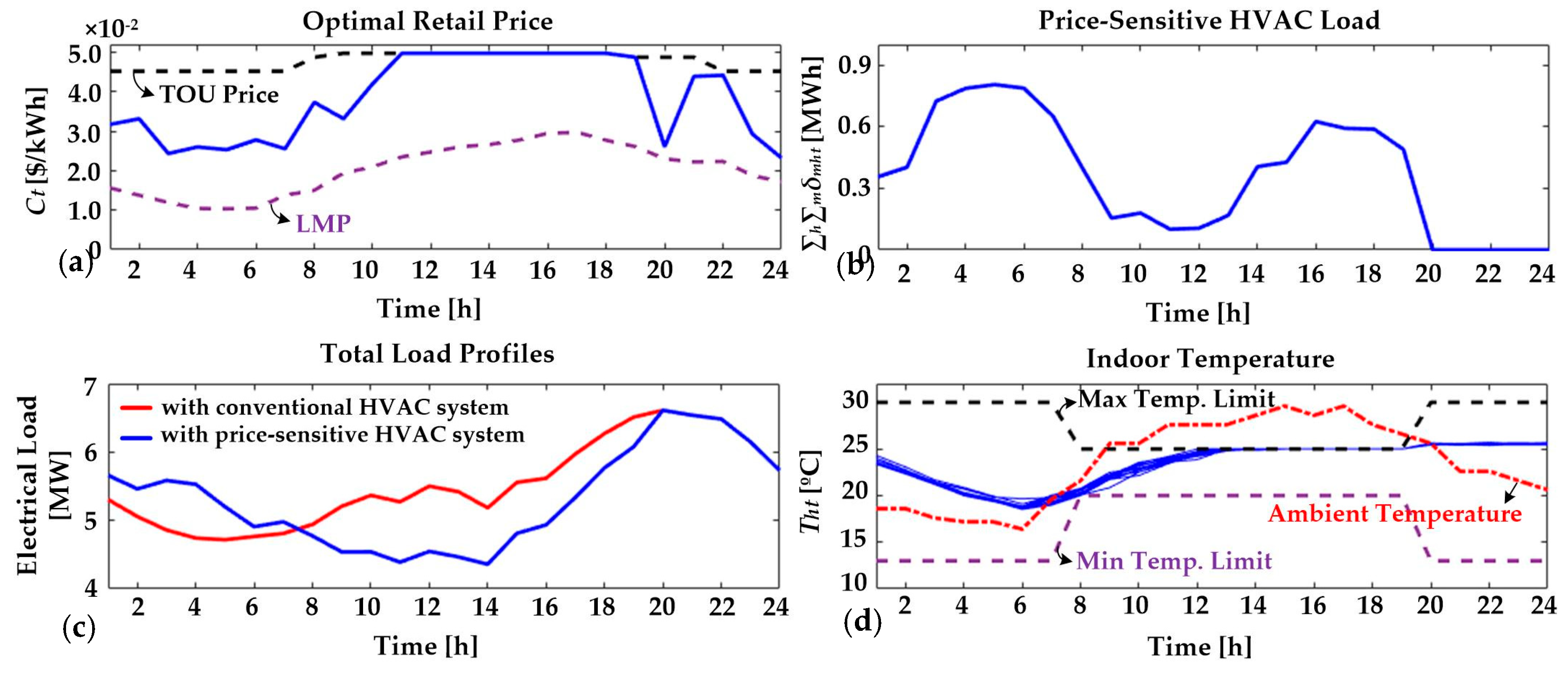
4.3. Case Study B: Purpose of Demand Response
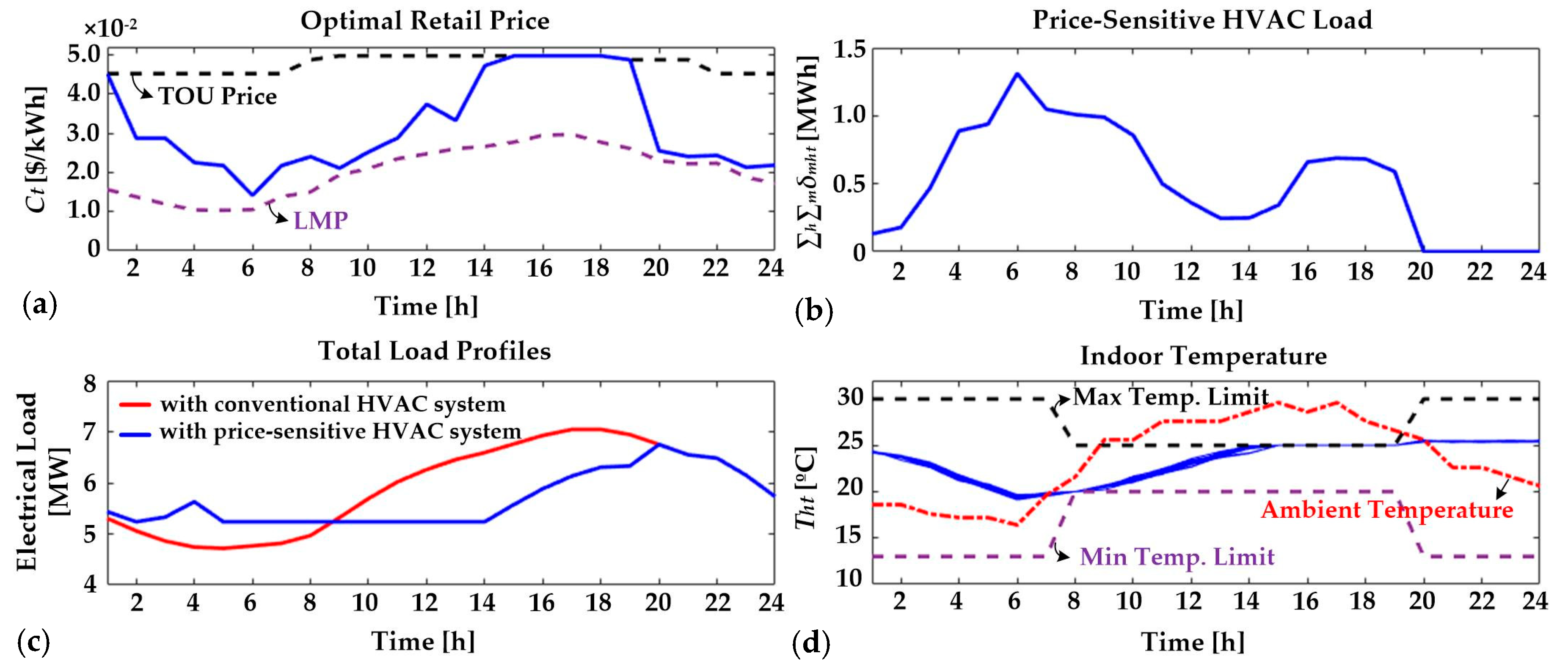
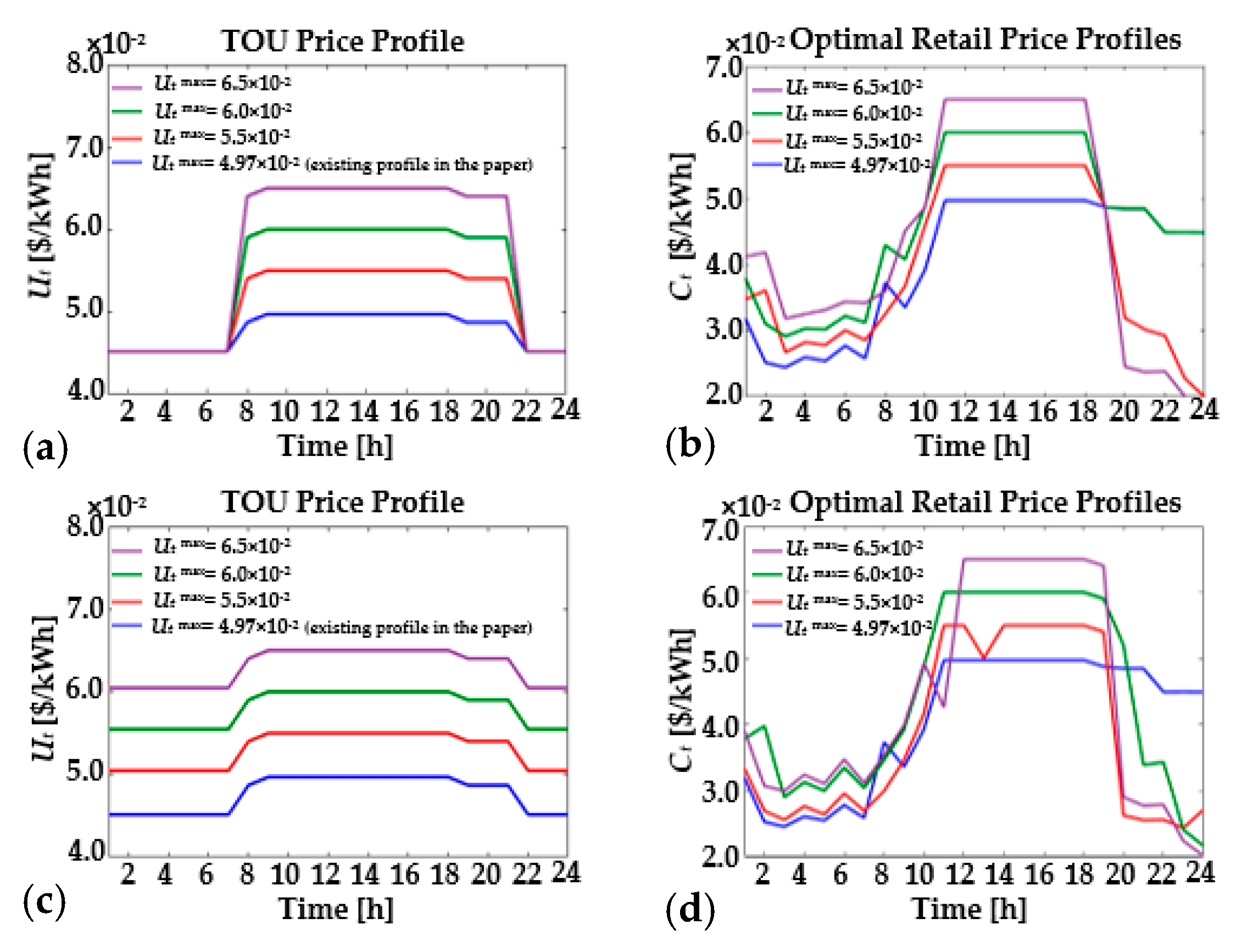
4.4. Case Study C: Parameter Sensitivity
4.5. Discussion
5. Conclusions
- The EUC induced the pre-cooling of HVAC systems, considering that the consumers minimize the operating cost of HVAC units. To compensate for the reduction of the EUC’s profit because of the pre-cooling, the EUC determined high retail price during on-peak times. In addition, the building operators scheduled small input power of HVAC system during the on-peak hours to minimize the electricity bills.
- For the conventional load curve, the peak load could be successfully reduced using the pre-cooling of HVAC units. The corresponding reduction of the EUC’s profit can be justified by the opportunity cost of installing an additional line or substation and the reduction in consumers’ electricity bills.
- For the duck curve, as participation in DR of the commercial HVAC systems does not result in peak load reduction or load leveling, residential HVAC systems will also need to be addressed by inducing participation in DR. In addition, we will research additional case studies on the application of the proposed pricing strategy to large-scale, multi-zone buildings.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| A. Acronyms: | |||
| DR | Demand response | ESS | Energy storage system |
| ETP | Equivalent thermal parameter | EUC | Electric utility company |
| HVAC | Heating, ventilation, and air-conditioning | LMP | Locational marginal pricing |
| PV | Photovoltaic | TOU | Time-of-use |
| VSHP | Variable speed heat pump | VSD | Variable speed drive |
| B. Sets and Indices: | |||
| t, h, m | Subscripts for time, HVAC units, and piecewise linear | ω, ψ, ρ, λ | Subscripts for Lagrangian multipliers |
| Ntime | number of scheduling time intervals in a day | ||
| C. Parameters: | |||
| NL | Total number of piecewise linear blocks | NT | Total number of scheduling time intervals in a day |
| NH | Total number of price-sensitive HVAC units in the distribution network | NHVAC | Total number of HVAC systems in the distribution network divided NH |
| RH | the ratio of the power consumption of HVAC systems in the commercial buildings to the total power consumption in the distribution network | Fmhtj | Linear gradient of Tht at time t = j resulting from power segment m of HVAC unit h at time t |
| aht, sht, dht, fht, ght, kht, | Coefficients used for the thermal dynamic model of the building including HVAC unit h at time t | Tz,ht | Indoor temperature at time t when no cooling is supplied by HVAC unit h for the period from 1 to t |
| z0,h t –z3,ht | Coefficients of the cooling rate supplied by HVAC unit h at time t | Txt, Tat | Ambient and adjacent room temperatures at time t |
| PR,t | Total power consumption minus conventional HVAC systems’ power consumption | PC,ht | Input power of conventional HVAC unit h in the distribution network at time t |
| Ph,max | Maximum input power of HVAC unit h | π | Penalty factor value |
| δmh,max | Maximum input power of segment m of HVAC unit h | Ut, Mt | TOU price and wholesale market price at time t |
| DL, DU | Upward and downward ramp rates of price-sensitive HVAC unit h | PT,t | Total power consumption in the distribution network at time t |
| Ppeak, Pmin | Peak upper and lower limit | ∆tunit | Unit time interval |
| Tht,min, Tht,max | Minimum and maximum limits of indoor temperature controlled by HVAC unit h at time t | Nω, Nψ, Nρ, Nλ | Number of Lagrangian multipliers |
| Qct, Qrt | Internal convective and radiative heat gains at time t | ||
| D. Variables: | |||
| Tht | Indoor temperature controlled by HVAC unit h at time t [°C] | δmht | Power input of price-sensitive HVAC unit h in segment m at time t |
| Qht | Cooling rate of HVAC unit h at time t | Ct | Day-ahead retail price at time t |
| bmht | Binary variables for piecewise linear approximation to indoor temperature variation by the power input of HVAC unit h in segment m at time t | JDC, JDP | EUC’s profits from the sales of electricity to conventional and price-sensitive HVAC units |
| μωht, αψht, βρmht, ηλmht | Lagrangian multipliers | ϑ | Upper bound of the sum of complementary slackness terms |
| JD, JB | Total profit of EUC and electricity bills of HVAC units | JBC,(h),JBP,(h) | Electricity bills of conventional and (hth) price-sensitive HVAC units |
References
- Strrbac, G.; Gan, C.K.; Aunedi, M. Benefits of advanced smart metering for demand response based control of distribution networks. Rep. Energy Netw. Assoc. UK 2010, 2, 1–46. [Google Scholar]
- Wilks, M. Demand Side Response: Conflict between Supply and Network Driven Optimisation. A Report to DECC; POYRY: Vantaa, Finland, 2010. [Google Scholar]
- Hou, Q.; Zhang, N.; Du, E. Probabilistic duck curve in high PV penetration power system: Concept, modeling, and empirical analysis in China. Appl. Energy 2019, 242, 205–215. [Google Scholar] [CrossRef]
- Rowe, M.; Yunusov, T.; Haben, S. A Peak Reduction Scheduling Algorithm for Storage Devices on the Low Voltage Network. IEEE Trans. Smart Grid 2014, 5, 2115–2124. [Google Scholar] [CrossRef]
- Qdr, Q. Benefits of Demand Response in Electricity Markets and Recommendations for Achieving Them; Technical Report; US Department of Energy: Washington, DC, USA, 2006.
- Hassan, N.U.; Khalid, Y.I.; Yuen, C. Customer engagement plans for peak load reduction in residential smart grids. IEEE Trans. Smart Grid 2015, 6, 3029–3041. [Google Scholar] [CrossRef]
- Yoon, J.H.; Baldick, R. Dynamic Demand Response Controller Based on Real-time Retail Price for Residential Buildings. IEEE Trans. Smart Grid 2014, 5, 121–129. [Google Scholar] [CrossRef]
- Perez, K.X.; Baldea, M.; Edgar, T.F. Integrated HVAC management and optimal scheduling of smart appliances for community peak load reduction. Energy Build. 2016, 123, 34–40. [Google Scholar] [CrossRef]
- Jeong, M.G.; Moon, S.I.; Hwang, P.I. Indirect load control for energy storage systems using incentive pricing under time-of-use tariff. Energies 2016, 9, 558. [Google Scholar] [CrossRef]
- Doostizadeh, M.; Ghasemi, H. A day-ahead electricity pricing model based on smart metering and demand-side management. Energy 2012, 46, 221–230. [Google Scholar] [CrossRef]
- US Energy Information Administration. Annual Energy Outlook 2016 (DOE/EIA-0383). Available online: www.eia.gov/outlooks/aeo/pdf/0383(2016).pdf (accessed on 7 November 2019).
- Kim, Y.J.; Wang, J. Power Hardware-in-the-Loop Simulation Study on Frequency Regulation through Direct Load Control of Thermal and Electrical Energy Storage Resources. IEEE Trans. Smart Grid 2018, 9, 2786–2796. [Google Scholar] [CrossRef]
- Kim, Y.; Norford, L.K. Optimal use of thermal energy storage resources in commercial buildings through price-based demand response considering distribution network operation. Appl. Energy 2017, 193, 308–324. [Google Scholar] [CrossRef]
- Vasudevan, J.; Swarup, K.S. Price based demand response strategy considering load priorities. In Proceedings of the IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Chen, Z.; Wu, L.; Fu, Y. Real-time Price-based Demand Response Management for Residential Appliances via Stochastic Optimization and Robust Optimization. IEEE Trans. Smart Grid 2012, 3, 1822–1831. [Google Scholar] [CrossRef]
- Hanif, S.; Gooi, H.B.; Massier, T. Distributed Congestion Management of Distribution Grids under Robust Flexible Buildings Operations. IEEE Trans. Power Syst. 2017, 32, 4600–4613. [Google Scholar] [CrossRef]
- Huang, S.; Wu, Q.; Oren, S.S. Distribution Locational Marginal Pricing through Quadratic Programming for Congestion Management in Distribution Networks. IEEE Trans. Power Syst. 2015, 30, 2170–2178. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.; Wang, J. Real-time Trading Strategies of Proactive DISCO with Heterogeneous DG Owners. IEEE Trans. Smart Grid 2018, 9, 1688–1697. [Google Scholar]
- Nguyen, D.T.; Nguyen, H.T.; Le, L.B. Dynamic Pricing Design for Demand Response Integration in Power Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 3457–3472. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.; Wang, J. Real-time Procurement Strategies of a Proactive Distribution Company with Aggregator-Based Demand Response. IEEE Trans. Smart Grid 2018, 9, 766–776. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.; Wang, J. Strategy-making for a proactive distribution company in the real-time market with demand response. Appl. Energy 2016, 181, 540–548. [Google Scholar] [CrossRef]
- Heydt, G.T.; Chowdhury, B.H.; Crow, M.L. Pricing and Control in the Next Generation Power Distribution System. IEEE Trans. Smart Grid 2012, 3, 907–914. [Google Scholar] [CrossRef]
- Yuan, Z.; Hesamzadeh, M.R. Implementing Zonal Pricing in Distribution Network: The Concept of Pricing Equivalence. In Proceedings of the IEEE Power Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Hu, Z.; Kim, J.; Wang, J. Review of dynamic pricing programs in the U.S. and Europe: Status quo and policy recommendations. Renew. Sustain. Energy Rev. 2015, 42, 743–751. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q.; Wen, F. Day-ahead congestion management in distribution systems through household demand respond and distribution congestion prices. IEEE Trans. Smart Grid 2014, 5, 2739–2747. [Google Scholar] [CrossRef]
- Dehghanpour, K.; Nehrir, M.H.; Sheppard, J.W. Agent-based modeling of retail electrical energy markets with demand response. IEEE Trans. Smart Grid 2018, 9, 3465–3475. [Google Scholar] [CrossRef]
- Lasaulce, S.; Tembine, H. Game Theory and Learning for Wireless Networks; Academic Press: Waltham, MA, USA, 2011; pp. 69–71. [Google Scholar]
- Zakula, T. Model Predictive Control for Energy Efficient Cooling and Dehumidification. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, June 2013. [Google Scholar]
- Gayeski, N.; Gange, J.; Armstrong, P. Development of a Low-Lift Chiller Controller and Simplified Precooling Control Algorithm: Final Report; U.S. Department of Energy: Washington, DC, USA, 2011.
- Kim, Y.; Norford, L.K.; Kirtley, J.L. Modeling and analysis of a variable speed heat pump for frequency regulation through direct load control. IEEE Trans. Power Syst. 2015, 30, 397–408. [Google Scholar] [CrossRef]
- Wei, W.; Feng, L.; Shengwei, M. Energy pricing and dispatch for smart grid retailers under demand response and market price uncertainty. IEEE Trans. Smart Grid 2015, 6, 1364–1374. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004; pp. 561–562. [Google Scholar]
- Benson, H.Y.; Sen, A.; Shannon, D.F. Interior-point algorithms, penalty methods and equilibrium problems. Comput. Optim. Appl. 2006, 34, 155–182. [Google Scholar] [CrossRef]
- Sharma, D.D.; Singh, S.N. Electrical load profile analysis and peak load assessment using clustering technique. In Proceedings of the IEEE Power Energy Society General Meeting (PESGM), National Harbor, MD, USA, 27–31 July 2014; pp. 1–5. [Google Scholar]
- Tsikalakis, A.G.; Hatziargyriou, N.D. Centralized control for optimizing microgrids operation. IEEE Trans. Energy Convers. 2008, 23, 241–248. [Google Scholar] [CrossRef]
- Weather History for Cambridge. Available online: http://www.wunderground.com/weatherstation/WXDailyHistory.asp?ID=KMACAMBR4&month=7&day=21&year=2012 (accessed on 7 November 2019).
- Day Ahead Market Zonal LBMP; NYISO. Available online: http://www.nyiso.com/public/markets_operations/market_data/maps/index.jsp?load=DAM (accessed on 7 November 2019).
- RATES & TARIFFS; Eversource. Available online: http://www.eversource.com/Content/emac/residential/my-account/billing-payment/rates-tariffs (accessed on 7 November 2019).
- Zakula, T.; Armstrong, P.; Norford, L.K. Modeling environment for model predictive control of buildings. Energy Build. 2014, 85, 549–559. [Google Scholar] [CrossRef]
- Chiu, W.Y.; Hsieh, J.T.; Chen, C.M. Pareto optimal demand response based on energy costs and load factor in smart grid. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Kim, H.T.; Jin, Y.G.; Yoon, Y.T. Energy storage systems (BESS) in an electricity market environment: The Korean case. Energies 2019, 12, 1608. [Google Scholar] [CrossRef]
| ah(t–3) | ah(t−2) | ah(t−1) | sh(t−3) | sh(t−2) | sh(t−1) | sht | |
| −5.08 × 10−1 | 6.84 × 10−1 | 8.13 × 10−1 | 1.07 × 10−3 | 1.07 × 10−3 | 1.07 × 10−3 | 1.07 × 10−3 | |
| dh(t−3) | dh(t−2) | dh(t−1) | dht | fh(t−3) | fh(t−2) | fh(t−1) | fht |
| −9.31 × 10−3 | −1.06 × 10−2 | 1.34 × 10−2 | 1.32 × 10−2 | 1.46 × 10−3 | −3.54 × 10−3 | −1.25 × 10−3 | 3.75 × 10−3 |
| gh(t−3) | gh(t−2) | gh(t−1) | ght | kh(t−3) | kh(t−2) | kh(t−1) | kht |
| 1.46 × 10−3 | −3.54 × 10−3 | −1.25 × 10−3 | 3.75 × 10−3 | 4.08× 10−5 | −1.24 × 10−3 | 1.49 × 10−4 | 1.44× 10−3 |
| No | Ph,max [kW] | Qh,max [kW] | (Qc + Qr)max [W] | No | Ph,max [kW] | Qh,max [kW] | (Qc + Qr)max [W] |
|---|---|---|---|---|---|---|---|
| 1 | 26 | 118 | 708 | 9 | 27 | 123 | 727 |
| 2 | 24 | 109 | 725 | 10 | 29 | 132 | 639 |
| 3 | 26 | 118 | 675 | 11 | 25 | 114 | 653 |
| 4 | 24 | 109 | 698 | 12 | 19 | 86 | 709 |
| 5 | 21 | 95 | 721 | 13 | 22 | 100 | 721 |
| 6 | 19 | 86 | 723 | 14 | 20 | 91 | 717 |
| 7 | 23 | 105 | 704 | 15 | 24 | 109 | 701 |
| 8 | 21 | 95 | 713 |
| HVAC unit | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) JBP,h [$] | 4.85 | 4.92 | 4.15 | 4.75 | 5.30 | 4.58 | 4.28 | 4.44 | 4.70 | 4.61 | 3.52 | 4.35 | 5.26 | 3.59 | 3.81 |
| (2) JBC,h [$] | 10.72 | 11.11 | 9.14 | 10.38 | 11.74 | 10.33 | 9.42 | 10.00 | 10.41 | 10.22 | 7.99 | 9.51 | 11.80 | 7.94 | 8.36 |
| ((2)-(1))/(2) [%] | 54.78 | 55.67 | 54.62 | 54.24 | 54.88 | 55.67 | 54.58 | 55.54 | 54.80 | 54.91 | 55.96 | 54.29 | 55.42 | 54.79 | 54.48 |
| Case A: Conventional Load Curve | Reduction Rate | ||||
|---|---|---|---|---|---|
| (a) Conventional | (b) Peak Reduction | (c) Load Leveling | [(a)–(b)]/[a] | [(a)–(c)]/[a] | |
| peak [MW] | 7.04 | 6.75 | 6.75 | 4.12% | 4.12% |
| peak–min. [MW] | 2.33 | 2.32 | 1.51 | 0.43% | 35.19% |
| load factor | 0.8396 | 0.8341 | 0.8388 | 0.66% | 0.10% |
| MSE load leveling [%] | 6911.12 | 4175.25 | 2571.28 | 39.59% | 62.80% |
| JDP [$] | 457.21 | 198.82 | 149.14 | 56.51% | 67.38% |
| total profit [$] | 3795.47 | 3537.08 | 3493.97 | 6.81% | 7.94% |
| Case B: Duck Curve | Reduction Rate | ||||
|---|---|---|---|---|---|
| (a) Conventional | (b) Peak Reduction | (c) Load Leveling | [(a)–(b)]/[a] | [(a)–(c)]/[a] | |
| peak [MW] | 6.61 | 6.61 | 6.61 | 0% | 0% |
| peak-min. [MW] | 1.89 | 2.25 | 1.94 | −19.05% | −2.65% |
| load factor | 0.8358 | 0.8029 | 0.8012 | 3.94% | 4.14% |
| MSE load leveling [%] | 3753.35 | 4877.88 | 4208.09 | −29.96% | −12.12% |
| JDP [$] | 350.53 | 159.45 | 109.58 | 54.51% | 68.74% |
| total profit [$] | 3580.88 | 3389.79 | 3339.93 | 5.34% | 6.73% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, A.-Y.; Kang, H.-K.; Moon, S.-I. Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction. Energies 2020, 13, 862. https://doi.org/10.3390/en13040862
Yoon A-Y, Kang H-K, Moon S-I. Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction. Energies. 2020; 13(4):862. https://doi.org/10.3390/en13040862
Chicago/Turabian StyleYoon, Ah-Yun, Hyun-Koo Kang, and Seung-II Moon. 2020. "Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction" Energies 13, no. 4: 862. https://doi.org/10.3390/en13040862
APA StyleYoon, A.-Y., Kang, H.-K., & Moon, S.-I. (2020). Optimal Price Based Demand Response of HVAC Systems in Commercial Buildings Considering Peak Load Reduction. Energies, 13(4), 862. https://doi.org/10.3390/en13040862





