Numerical Study on the Elastic Deformation and the Stress Field of Brittle Rocks under Harmonic Dynamic Load
Abstract
1. Introduction
2. The 3D Uniaxial Compression Simulation
3. Numerical Model of Indenter Intrusion
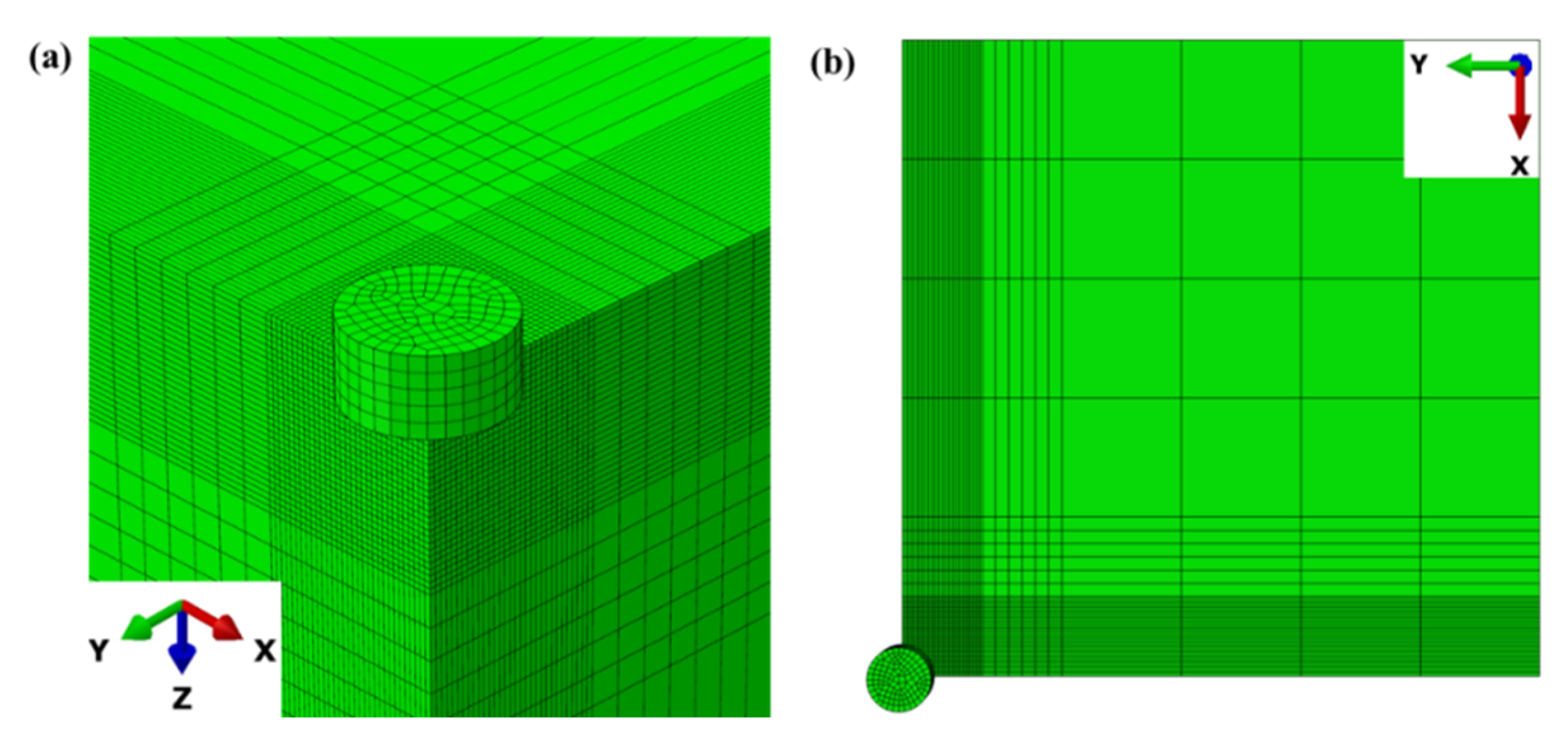
3.1. The 3D Finite Element Modeling
3.2. Parameter Settings
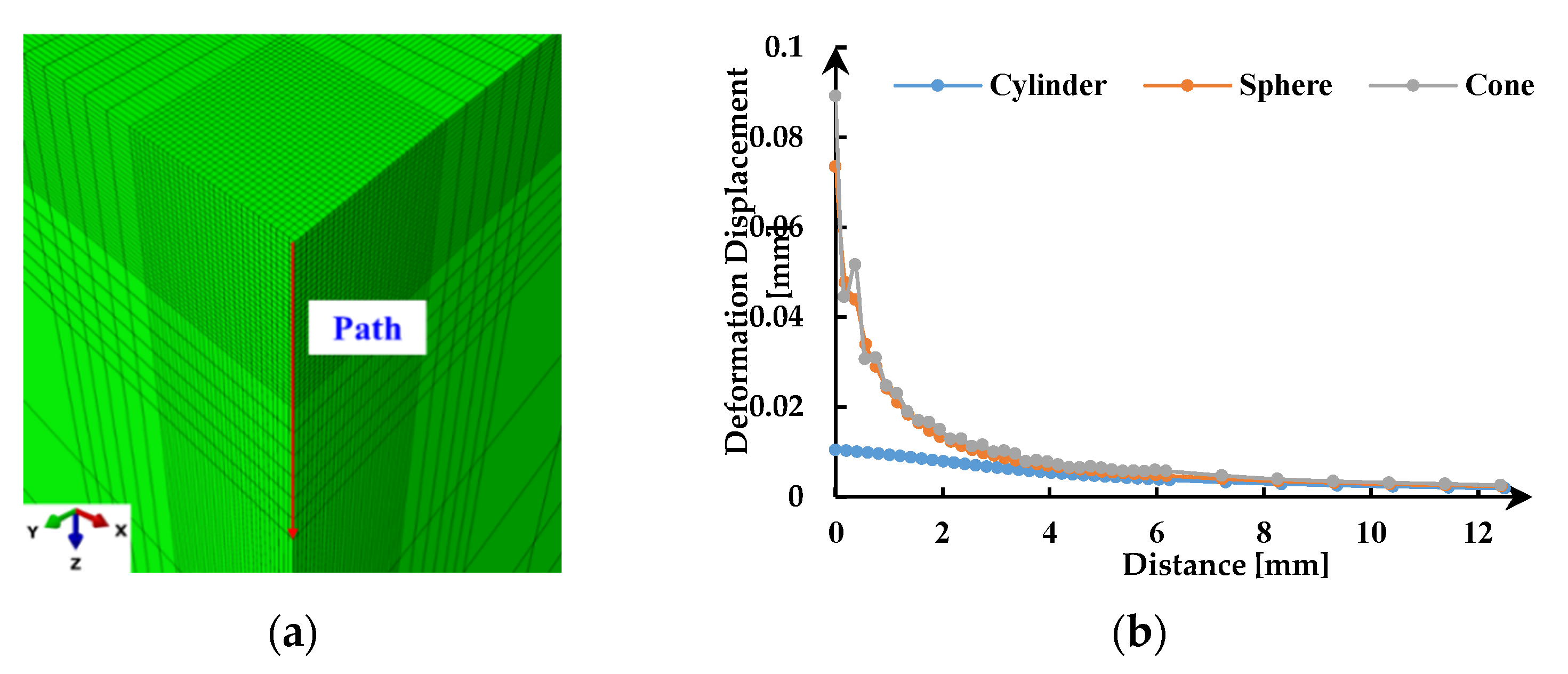
3.3. Mesh Size Sensitivity Analysis
4. Results and Analysis
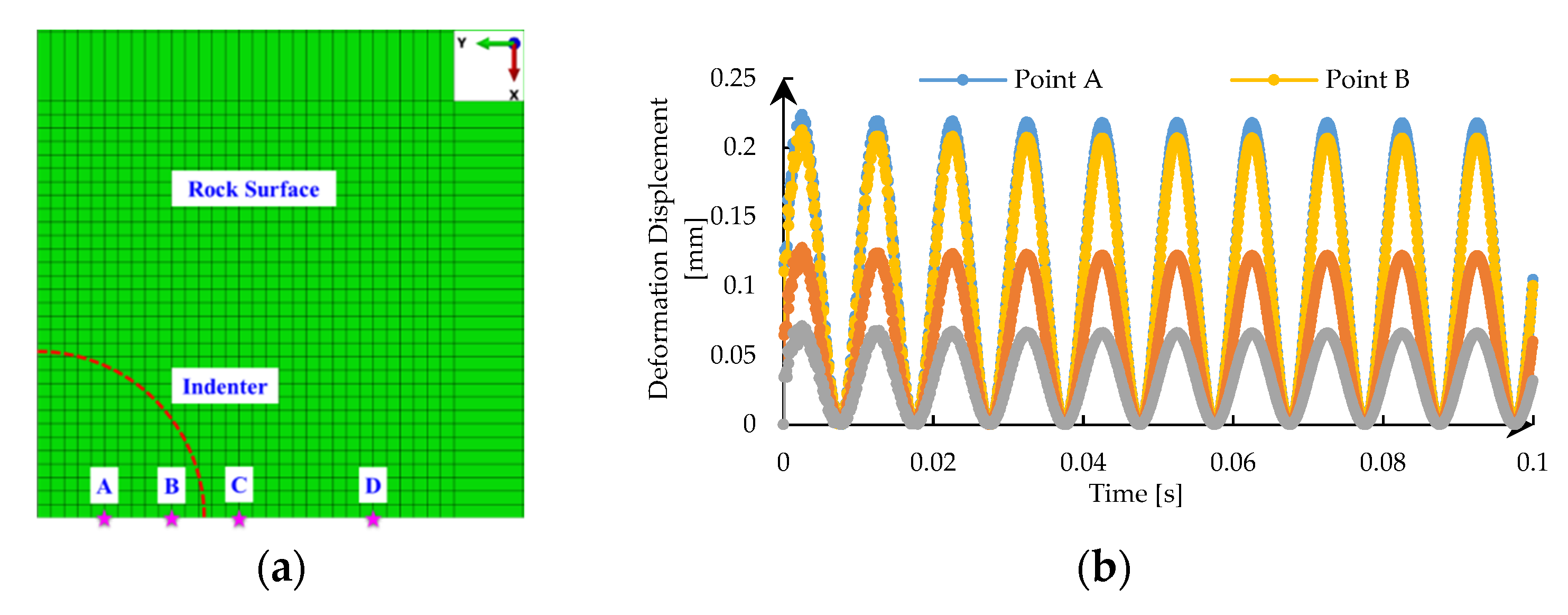
4.1. Influence of the Position on the Rock
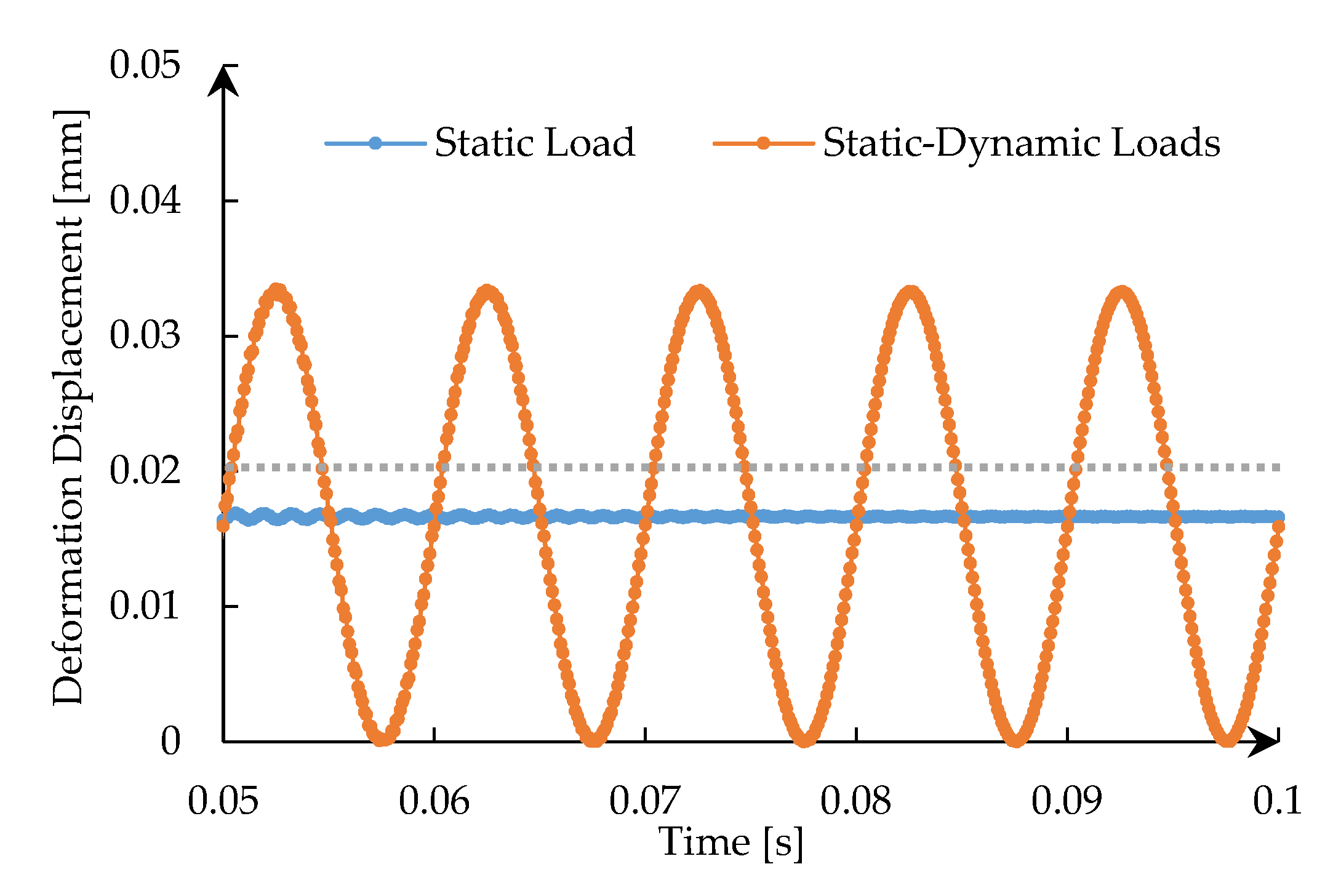
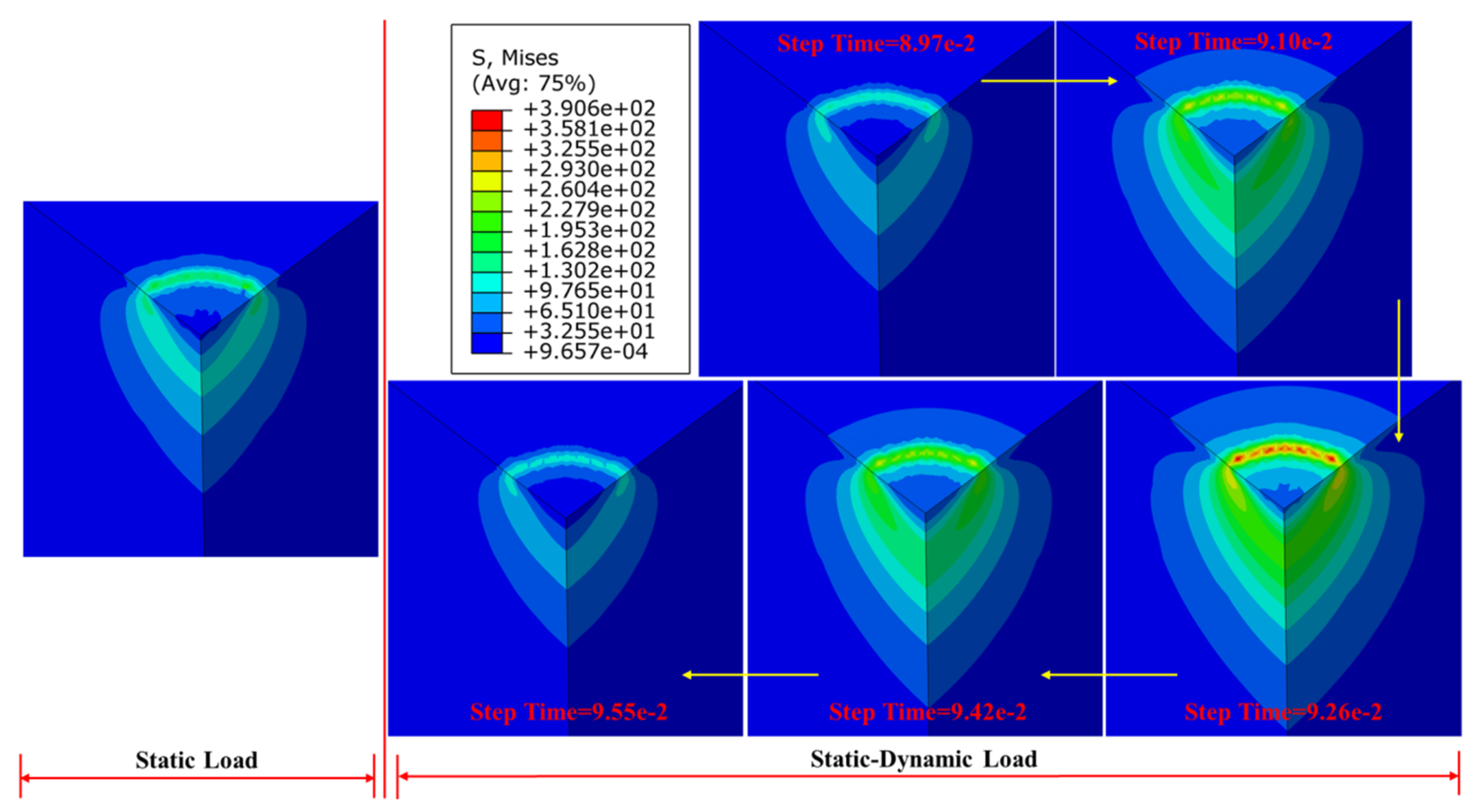
4.2. Static Load vs. Static-Dynamic Loads
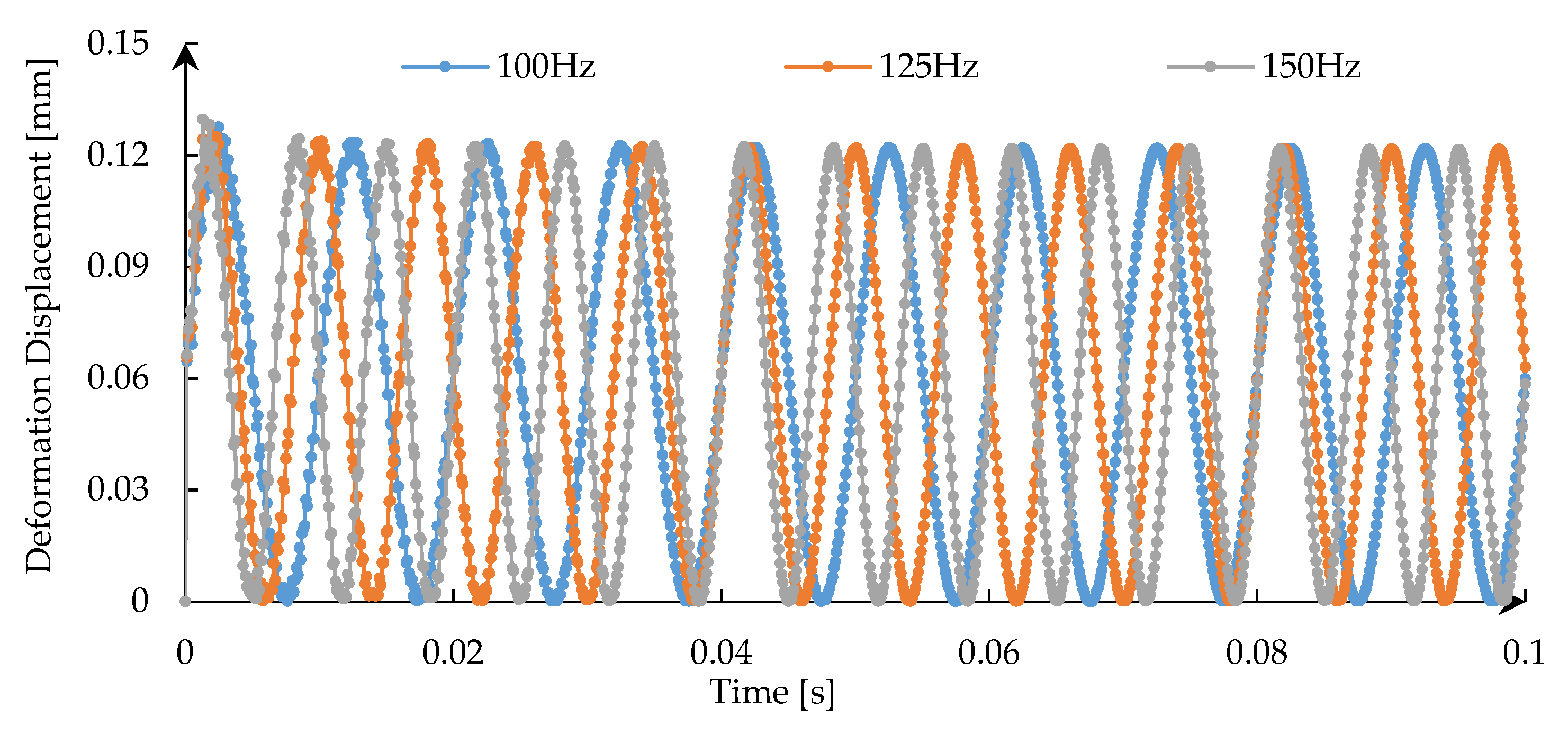
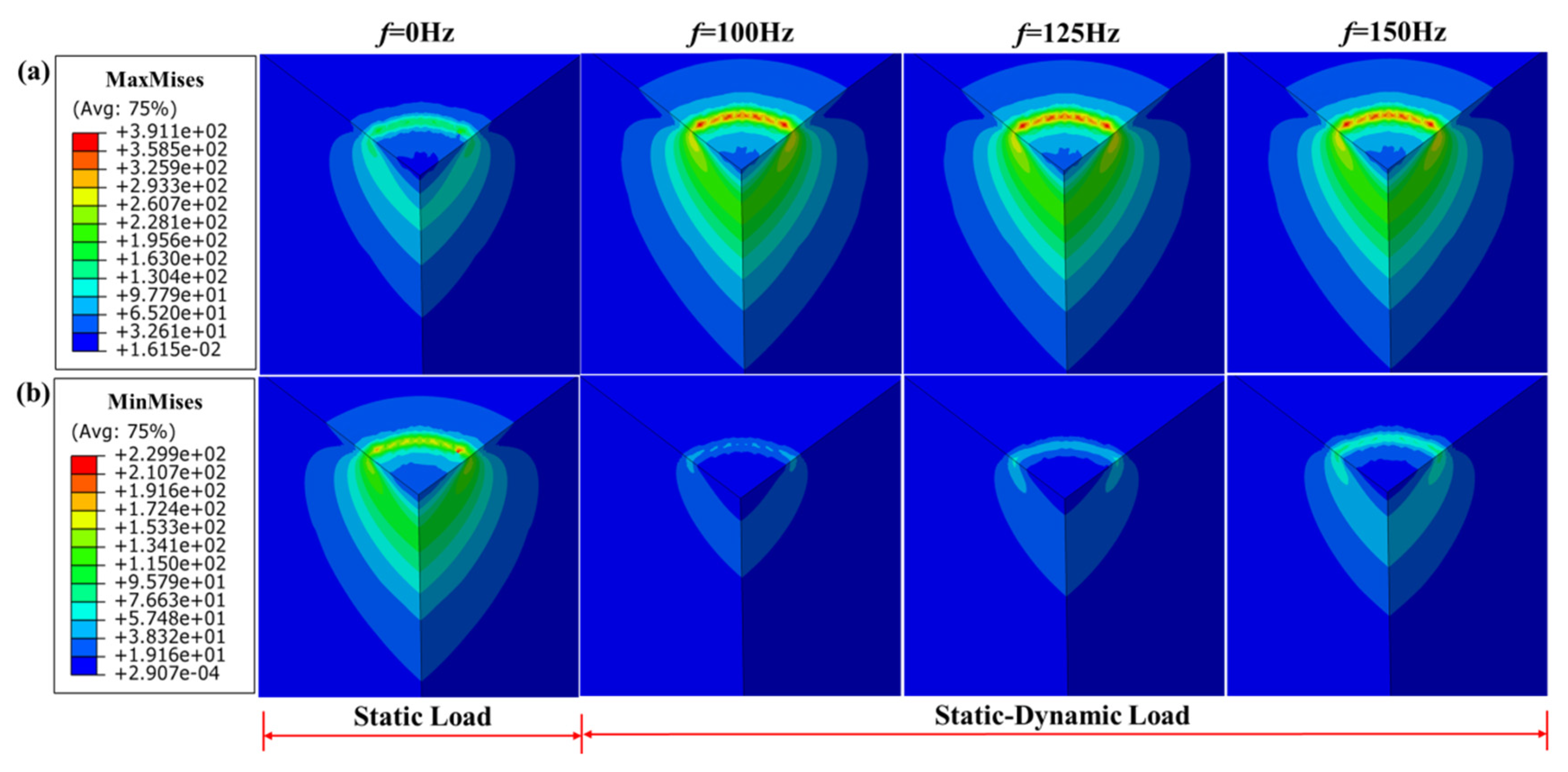
4.3. Influence of the Frequency of Dynamic Load
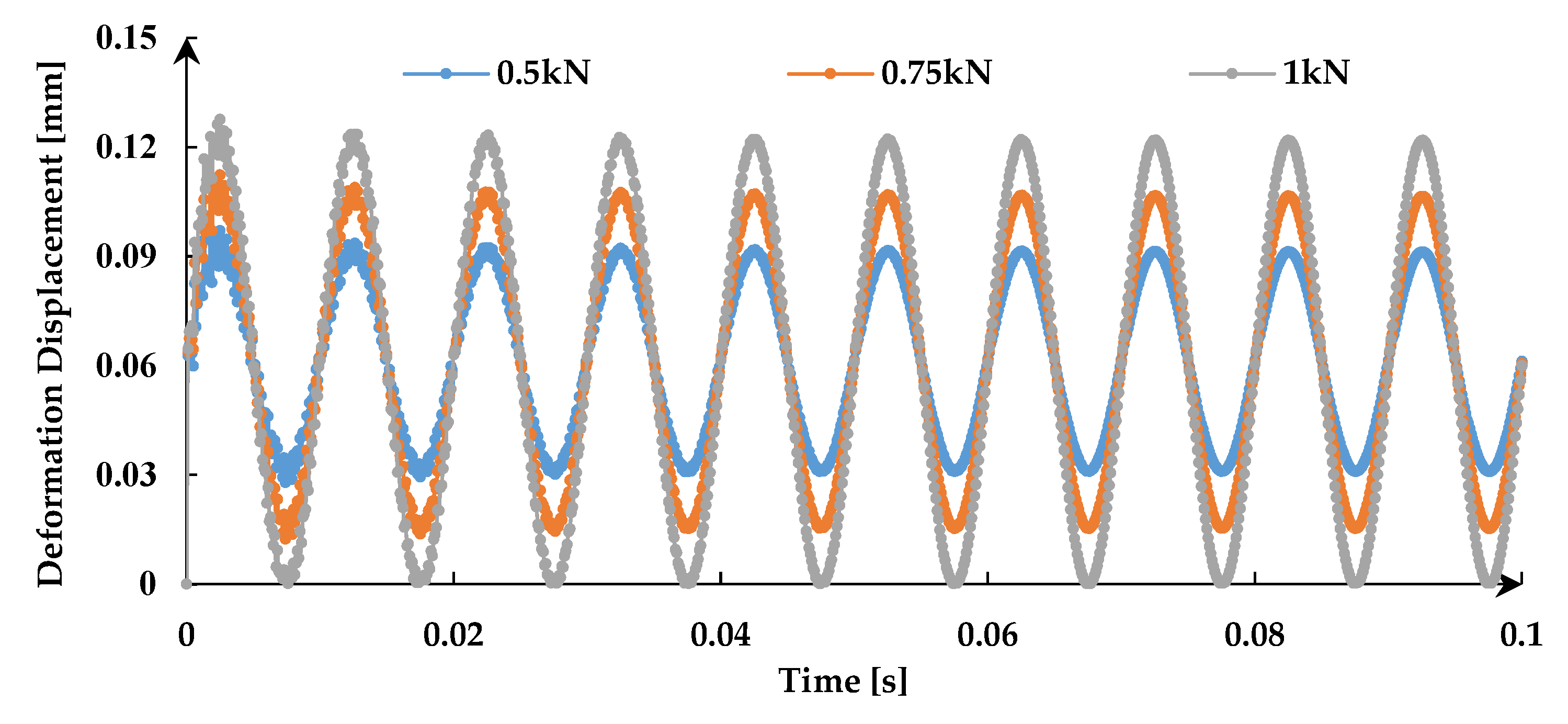
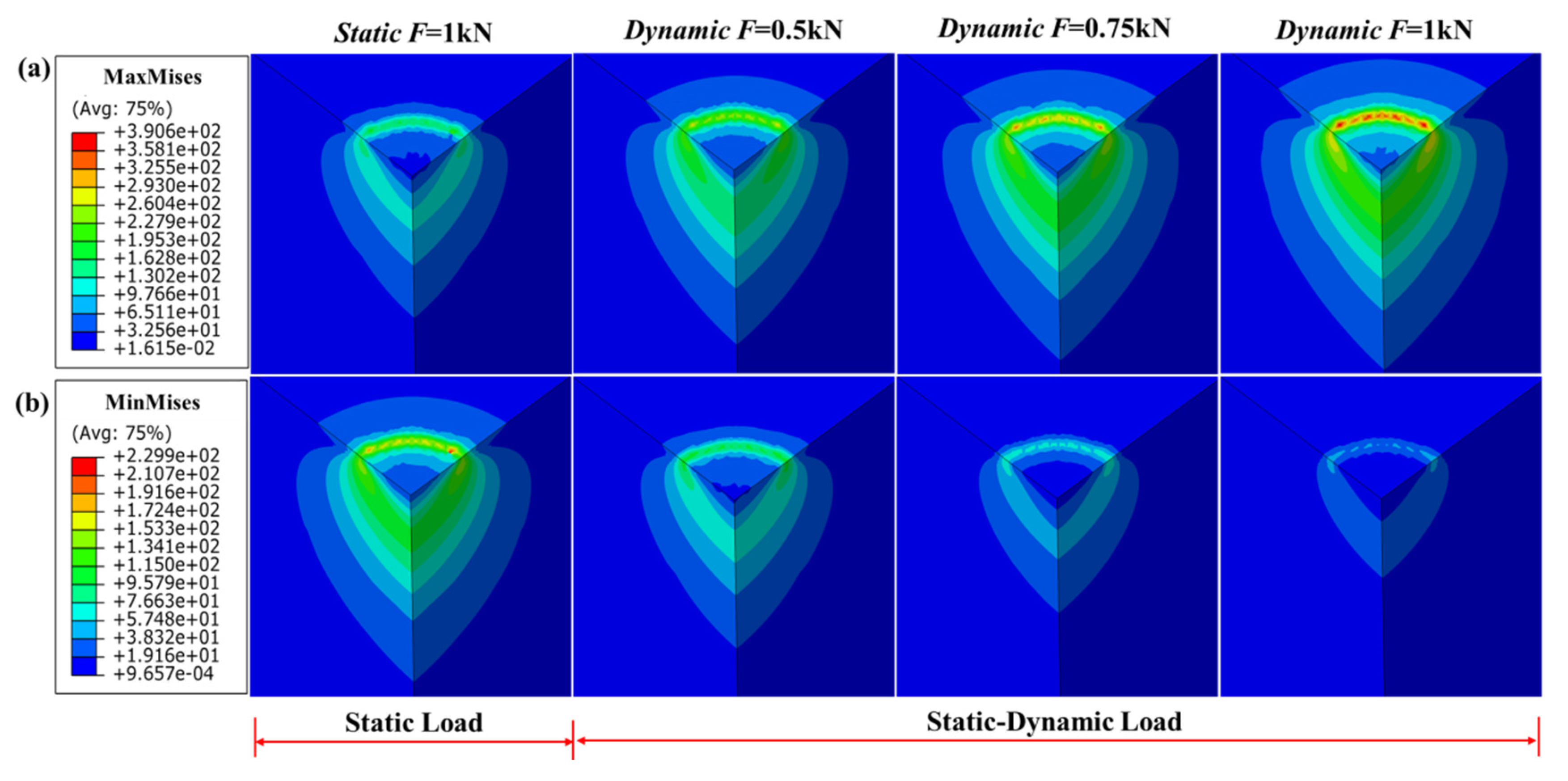
4.4. Influence of the Amplitude of Dynamic Load
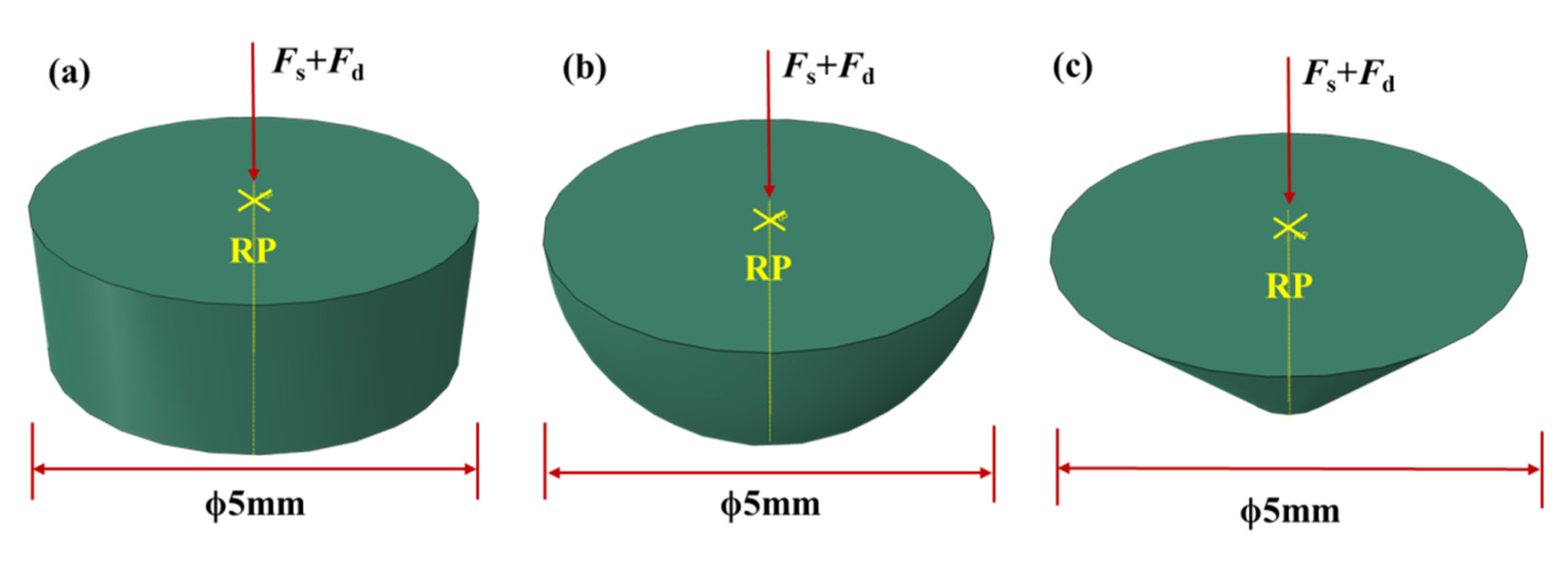
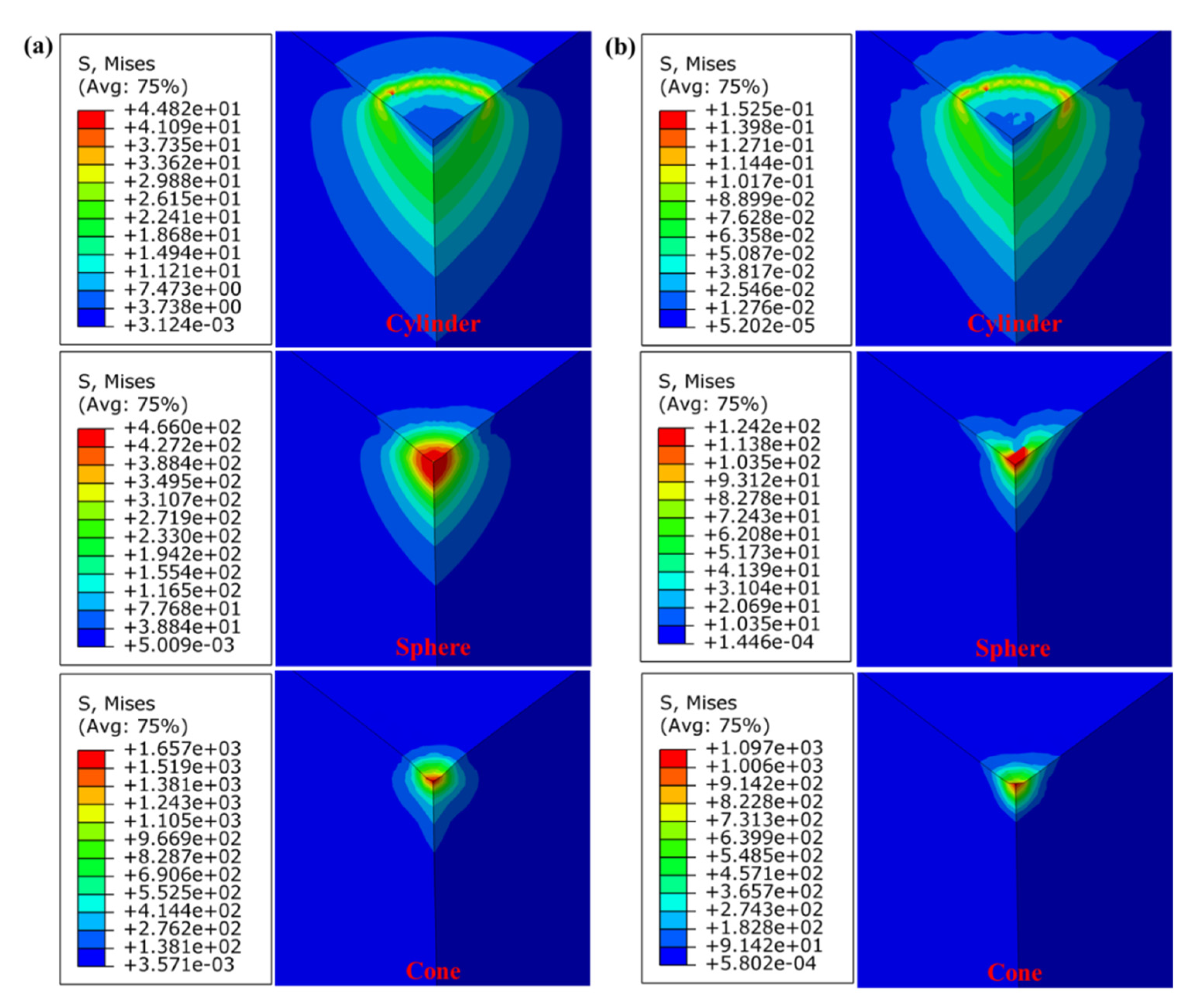
4.5. Influence of the Type of Indenter
4.6. Discussion
5. Conclusions
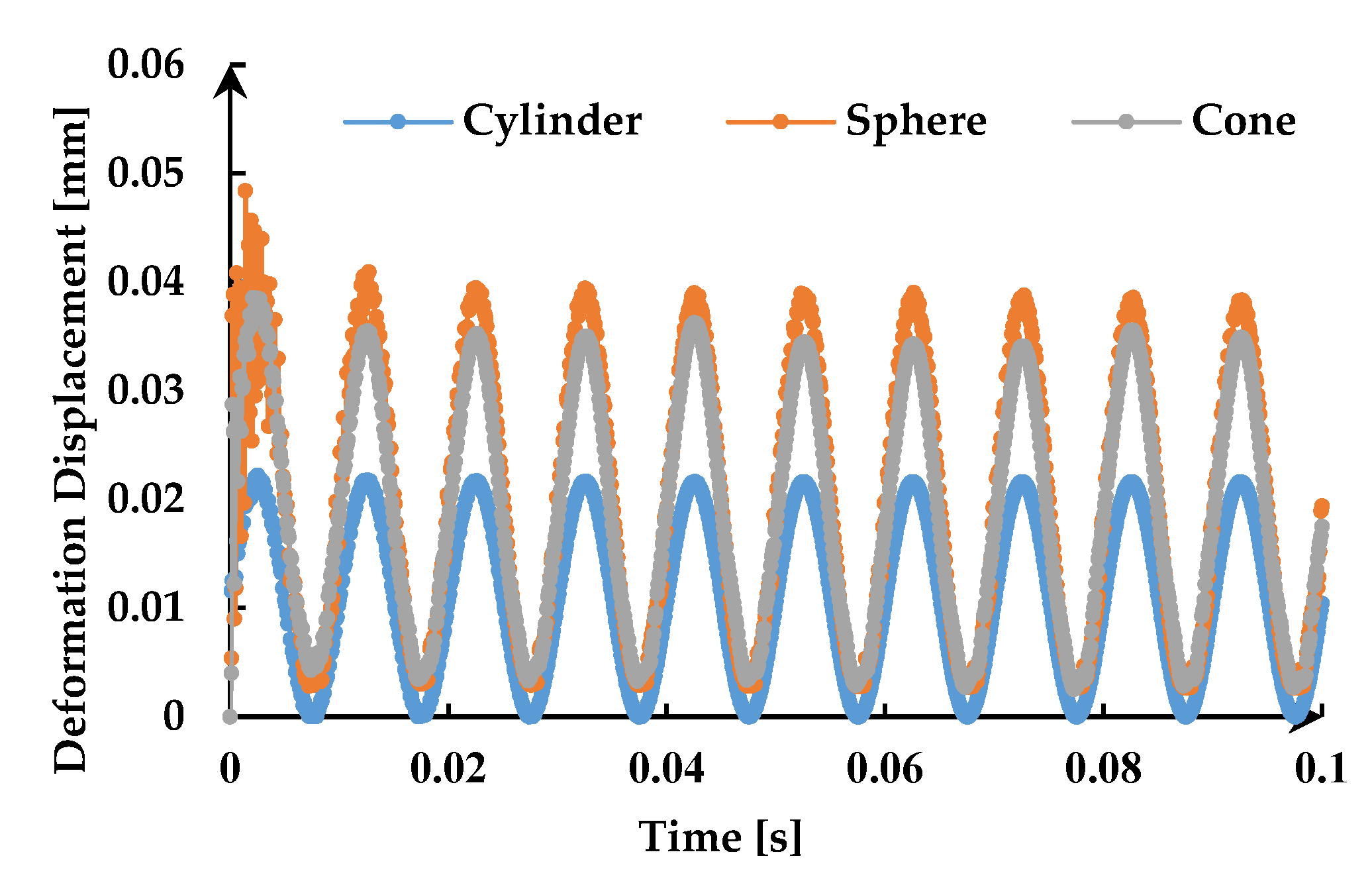
- The deformation displacement of the rock presents a harmonic variation under static-dynamic loads and decreases as the distance from the center of the indenter increases. The frequency of dynamic load only changes the fluctuation period of the deformation displacement of the rock without changing its amplitude, while the amplitude of dynamic load has the opposite effect on it. Besides, the deformation displacement of the rock increase with the decrease of the contact area between the rock and the indenter.
- The stress field of the rock also presents periodic changes due to the existence of harmonic dynamic load. The magnitude of the stress field of the rock increases with the increase of the amplitude of dynamic load and does not change with the change of the frequency of dynamic load. In addition, a small contact area between the rock and the indenter creates a large stress field but a small response range of the rock.
- Compared with the deformation displacement and the stress field of the rock under the same static load, the deformation displacement of the rock is more likely to exceed its failure level and the maximum stress generated is also larger, and the response degree and range of the rock is wider under static-dynamic loads.
Author Contributions
Funding
Conflicts of Interest
List of Symbols
| μ | Poisson’s ratio |
| E | Elastic modulus, Pa |
| a | Radius of the indenter, m |
| r | Distance from the center of the indenter, m |
| q | Static load per unit area, N/m2 |
| q(t) | Dynamic load per unit area, N/m2 |
References
- Jia, B.; Tsau, J.S.; Barati, R. A review of the current progress of CO2 injection EOR and carbon storage in shale oil reservoirs. Fuel 2019, 236, 404–427. [Google Scholar] [CrossRef]
- Aguiar, R.R.; Weber, H.I. Mathematical modeling and experimental investigation of an embedded vibro-impact system. Nonlinear Dyn. 2011, 65, 317–334. [Google Scholar] [CrossRef]
- Pavlovskaia, E.; Hendry, D.C.; Wiercigroch, M. Modelling of high frequency vibro-impact drilling. Int. J. Mech. Sci. 2015, 91, 110–119. [Google Scholar] [CrossRef]
- Wiercigroch, M.; Vaziri, V.; Kapitaniak, M. RED: Revolutionary Drilling Technology for Hard Rock Formations. In Proceedings of the 2017 SPE/IADC Drilling Conference, The Hague, The Netherlands, 14–16 March 2017; pp. 1234–1241. [Google Scholar]
- Potthast, C.; Twiefel, J.; Wallaschek, J. Modelling approaches for an ultrasonic percussion drill. J. Sound Vib. 2007, 308, 405–417. [Google Scholar] [CrossRef]
- Bai, D.; Quan, Q.; Wang, Y.; Tang, D.; Deng, Z. A longitudinal & longitudinal-torsional vibration actuator for rotary-percussive ultrasonic planetary drills. Adv. Space Res. 2019, 63, 1065–1072. [Google Scholar]
- Li, S.Q.; Yan, T.; Li, W.; Bi, F.Q. Modeling of vibration response of rock by harmonic impact. J. Nat. Gas Sci. Eng. 2015, 23, 90–96. [Google Scholar] [CrossRef]
- Dong, G.; Chen, P. 3D numerical simulation and experiment validation of dynamic damage characteristics of anisotropic shale for percussive-rotary drilling with a full-scale PDC bit. Energies 2018, 11, 1326. [Google Scholar] [CrossRef]
- Bilgin, N.; Copur, H.; Balci, C. Effect of replacing disc cutters with chisel tools on performance of a TBM in difficult ground conditions. Tunn. Undergr. Space Technol. 2012, 27, 41–51. [Google Scholar] [CrossRef]
- Bejari, H.; Hamidi, J.K. Simultaneous effects of joint spacing and orientation on TBM cutting efciency in jointed rock masses. Rock Mech. Rock Eng. 2013, 46, 897–907. [Google Scholar] [CrossRef]
- Souissi, S.; Hamdi, E.; Sellami, H. Microstructure effect on hard rock damage and fracture during indentation process. Geotech. Geol. Eng. 2015, 33, 1539–1550. [Google Scholar] [CrossRef]
- Zhao, X.B.; Yao, X.H.; Gong, Q.M.; Ma, H.S.; Li, X.Z. Comparison study on rock crack pattern under a single normal and inclined disc cutter by linear cutting experiments. Tunn. Undergr. Space Technol. 2015, 50, 479–489. [Google Scholar] [CrossRef]
- Alehossein, H.; Detournay, E.; Huang, H. An analytical model for the indentation of rocks by blunt tools. Rock Mech. Rock Eng. 2000, 33, 267–284. [Google Scholar] [CrossRef]
- Momber, A.W. Deformation and fracture of rocks loaded with spherical indenters. Int. J. Fract. 2004, 125, 263–279. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Song, H.; Kang, Y. Experimental investigation of deformation and failure mechanisms in rock under indentation by digital image correlation. Eng. Fract. Mech. 2012, 96, 667–675. [Google Scholar] [CrossRef]
- Huang, H.; Detournay, E. Discrete element modeling of tool-rock interaction II: Rock indentation. Int. J. Numer. Anal. Met. 2013, 37, 1930–1947. [Google Scholar] [CrossRef]
- Liu, T.; Lin, B.; Yang, W.; Zou, Q.; Kong, J.; Yan, F. Cracking process and stress field evolution in specimen containing combined flaw under uniaxial compression. Rock Mech. Rock Eng. 2016, 49, 3095–3113. [Google Scholar] [CrossRef]
- Wang, X.; Wen, Z.J.; Jiang, Y.J. Time–space effect of stress field and damage evolution law of compressed coal-rock. Geotech. Geol. Eng. 2016, 34, 1933–1940. [Google Scholar] [CrossRef]
- Ma, L.F.; Yari, N.; Wiercigroch, M. Shear stress triggering brittle shear fracturing of rock-like materials. Int. J. Mech. Sci. 2018, 146, 295–302. [Google Scholar] [CrossRef]
- Hogan, J.D.; Boonsue, S.; Spray, J.G.; Rogers, R.J. Micro-scale deformation of gypsum during micro-indentation loading. Int. J. Rock Mech. Min. 2012, 54, 140–149. [Google Scholar] [CrossRef]
- Ajibose, O.K.; Wiercigroch, M.; Akisanya, A.R. Experimental studies of the resultant contact forces in drill bit–rock interaction. Int. J. Mech. Sci. 2015, 91, 3–11. [Google Scholar] [CrossRef]
- Kitamura, M.; Hirose, T. Strength determination of rocks by using indentation tests with a spherical indenter. J. Struct. Geol. 2017, 98, 1–11. [Google Scholar] [CrossRef]
- Shariati, H.; Saadati, M.; Bouterf, A.; Weddfelt, K.; Larsson, P.L.; Hild, F. On the inelastic mechanical behavior of granite: Study based on quasi-oedometric and indentation tests. Rock Mech. Rock Eng. 2019, 52, 645–657. [Google Scholar] [CrossRef]
- Yoffe, E.H. Elastic stress fields caused by indenting brittle materials. Philos. Mag. A 1982, 46, 617–628. [Google Scholar] [CrossRef]
- Feng, G.; Qu, S.; Huang, Y.; Nix, W.D. An analytical expression for the stress field around an elastoplastic indentation/contact. Acta Mater. 2007, 55, 2929–2938. [Google Scholar] [CrossRef]
- Weddfelt, K.; Saadati, M.; Larsson, P.L. On the load capacity and fracture mechanism of hard rocks at indentation loading. Int. J. Rock Mech. Min. 2017, 100, 170–176. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, W.; He, X. The investigation of rock indentation simulation based on discrete element method. KSCE J. Civ. Eng. 2017, 21, 1201–1212. [Google Scholar] [CrossRef]
- Liu, H.Y.; Kou, S.Q.; Lindqvist, P.A.; Tang, C.A. Numerical simulation of the rock fragmentation process induced by indenters. Int. J. Rock Mech. Min. 2002, 39, 491–505. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Ge, S. Numerical simulation of rock fragmentation during cutting by conical picks under confining pressure. Compt. Rendus Mec. 2017, 345, 890–902. [Google Scholar] [CrossRef]
- Yari, N.; Kapitaniak, M.; Vaziri, V.; Ma, L.F.; Wiercigroch, M. Calibrated FEM Modelling of Rock Cutting with PDC Cutter. MATEC Web Conf. 2018, 148, 16006. [Google Scholar] [CrossRef]
- Li, H.S.; Liu, S.Y.; Xu, P.P. Numerical simulation on interaction stress analysis of rock with conical picks. Tunn. Undergr. Space Tech. 2019, 85, 231–242. [Google Scholar] [CrossRef]
- Liu, W.; Qian, X.; Li, T.; Zhou, Y.; Zhu, X. Investigation of the tool-rock interaction using Drucker-Prager failure criterion. J. Petrol. Sci. Eng. 2019, 173, 269–278. [Google Scholar] [CrossRef]
- Zhang, H.; Song, H.; Kang, Y.; Huang, G.; Qu, C. Experimental analysis on deformation evolution and crack propagation of rock under cyclic indentation. Rock Mech. Rock Eng. 2013, 46, 1053–1059. [Google Scholar] [CrossRef]
- Li, X.; Wang, S.; Wang, S. Experimental investigation of the influence of confining stress on hard rock fragmentation using a conical pick. Rock Mech. Rock Eng. 2018, 51, 255–277. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Du, K.; Wang, S. Experimental investigation of hard rock fragmentation using a conical pick on true triaxial test apparatus. Tunn. Undergr. Space Tech. 2018, 79, 210–223. [Google Scholar] [CrossRef]
- Fang, K.; Zhao, T.; Zhang, Y.; Qiu, Y.; Zhou, J. Rock cone penetration test under lateral confining pressure. Int. J. Rock Mech. Min. 2019, 119, 149–155. [Google Scholar] [CrossRef]
- Shan, R.; Jiang, Y.; Li, B. Obtaining dynamic complete stress-strain curves for rock using the Split Hopkinson Pressure Bar technique. Int. J. Rock Mech. Min. 2000, 37, 983–992. [Google Scholar] [CrossRef]
- Saksala, T. Damage-viscoplastic consistency model with a parabolic cap for rocks with brittle and ductile behavior under low-velocity impact loading. Int. J. Numer. Anal. Meth. Geomech. 2010, 34, 1362–1386. [Google Scholar] [CrossRef]
- Wang, S.Y.; Sloan, W.; Liu, H.Y.; Tang, C.A. Numerical simulation of the rock fragmentation process induced by two drill bits subjected to static and dynamic (impact) loading. Rock Mech. Rock Eng. 2011, 44, 317–332. [Google Scholar] [CrossRef]
- Duan, K.; Kwo, C.Y.; Tham, L.G. Micromechanical analysis of the failure process of brittle rock. Int. J. Numer. Anal. Met. 2015, 39, 618–634. [Google Scholar] [CrossRef]
- Chen, G.; Li, T.; Guo, F.; Wang, Y. Brittle mechanical characteristics of hard rock exposed to moisture. Bull. Eng. Geol. Environ. 2017, 76, 219–230. [Google Scholar] [CrossRef]
- Liu, G.; Cai, M.; Huang, M. Mechanical properties of brittle rock governed by micro-geometric heterogeneity. Comput. Geotech. 2018, 104, 358–372. [Google Scholar] [CrossRef]
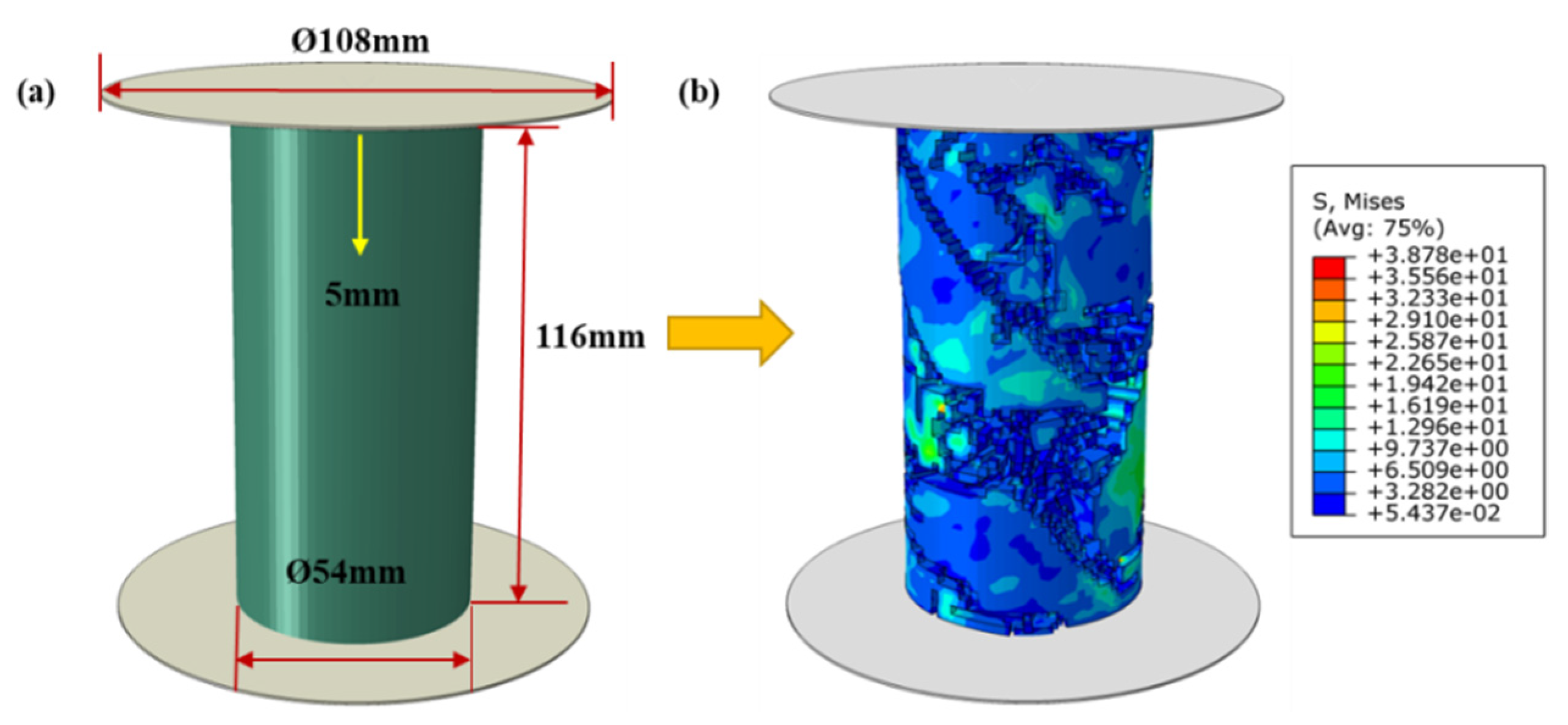
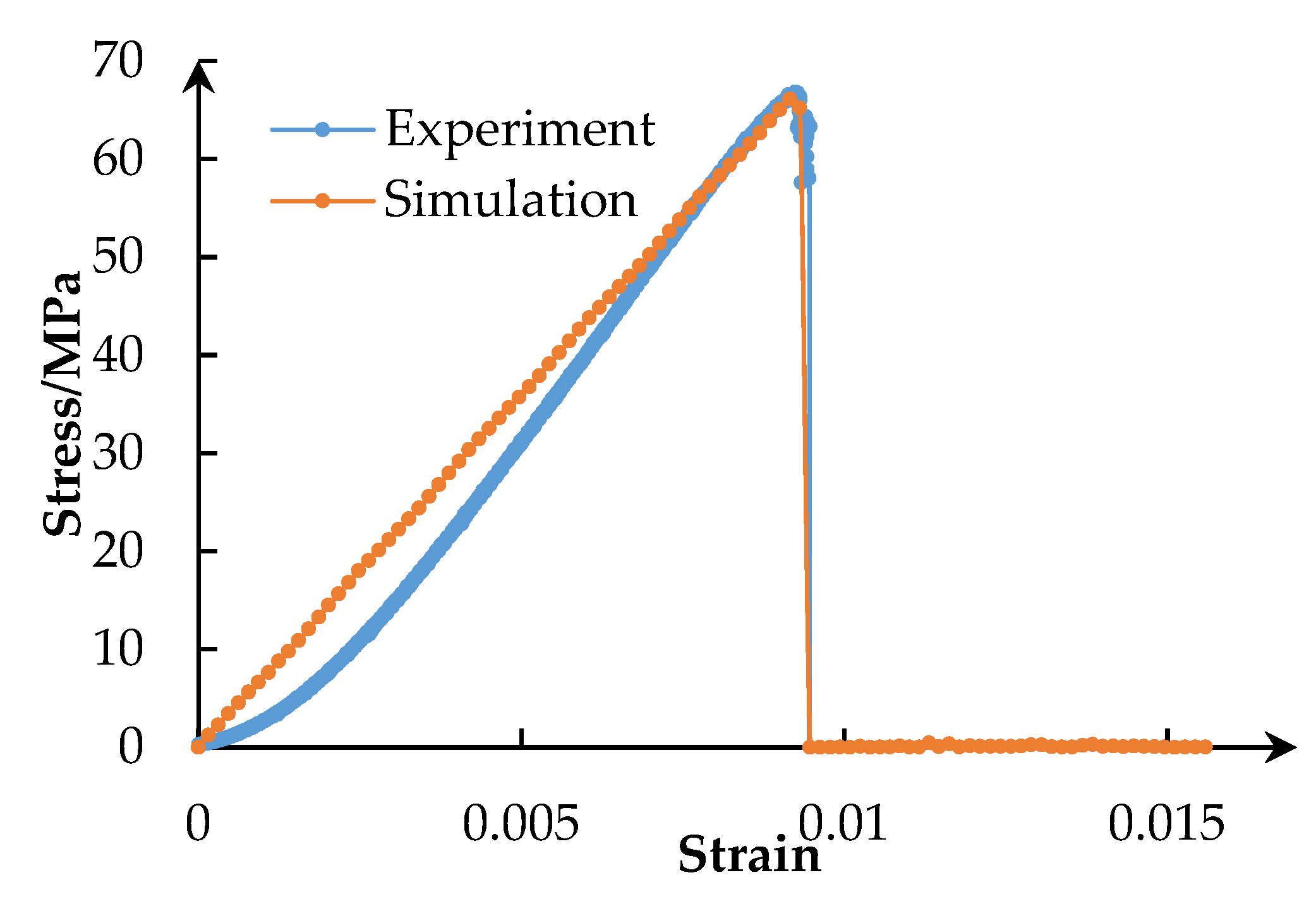
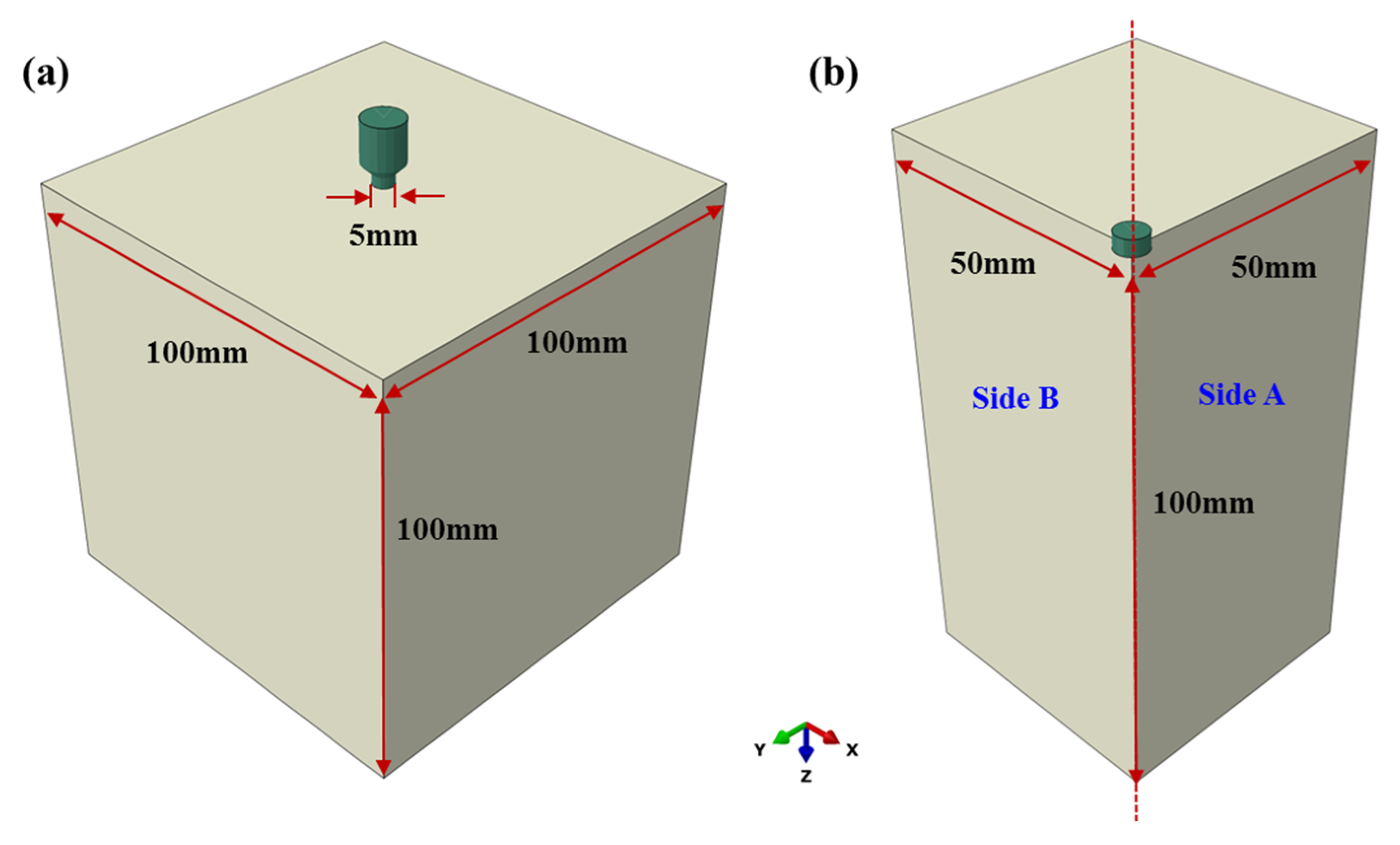
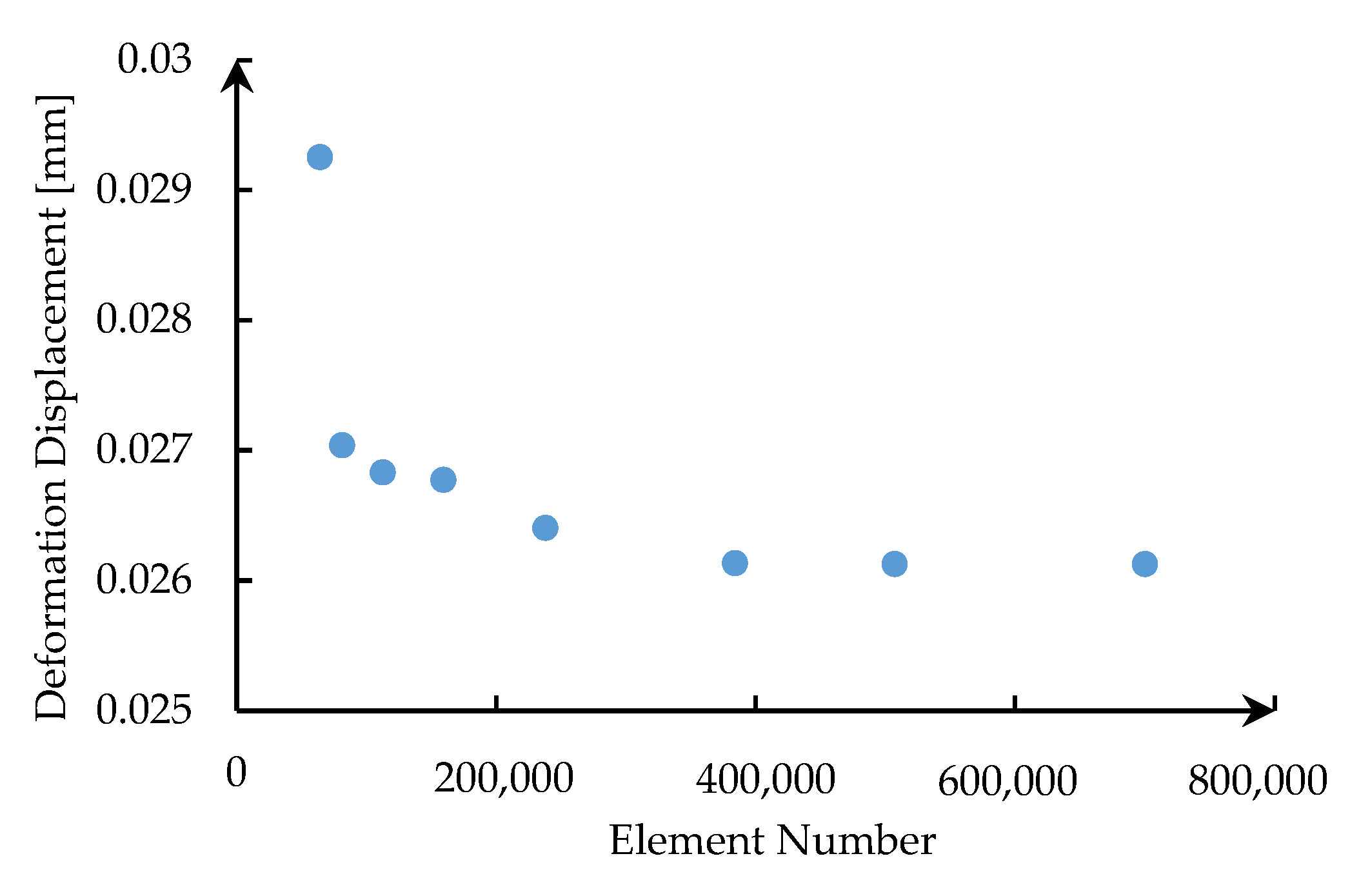
| Material | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Sandstone | Density (t/mm3) | 2.7 × 10−9 | Angle of Friction (°) | 50 |
| Elastic Modulus (MPa) | 7228 | Dilation Angle (°) | 8 | |
| Poisson’s Ratio | 0.3 | Flow Stress Ratio | 0.8 | |
| Failure Displacement (mm) | 0.02 | Yield Stress (MPa) | 67 | |
| Fracture Strain | 5 × 10−4 |
| Material | Parameter | Value | Parameter | Value |
|---|---|---|---|---|
| Sandstone | Density (t/mm3) | 2.7 × 10−9 | Elastic Modulus (MPa) | 7228 |
| Poisson’s Ratio | 0.3 | |||
| Indenter | Density (t/mm3) | 7.85 × 10−9 | Elastic Modulus (MPa) | 2.06 × 10−5 |
| Poisson’s Ratio | 0.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Tian, S.; Li, W.; Ling, X.; Kapitaniak, M.; Vaziri, V. Numerical Study on the Elastic Deformation and the Stress Field of Brittle Rocks under Harmonic Dynamic Load. Energies 2020, 13, 851. https://doi.org/10.3390/en13040851
Li S, Tian S, Li W, Ling X, Kapitaniak M, Vaziri V. Numerical Study on the Elastic Deformation and the Stress Field of Brittle Rocks under Harmonic Dynamic Load. Energies. 2020; 13(4):851. https://doi.org/10.3390/en13040851
Chicago/Turabian StyleLi, Siqi, Shenglei Tian, Wei Li, Xin Ling, Marcin Kapitaniak, and Vahid Vaziri. 2020. "Numerical Study on the Elastic Deformation and the Stress Field of Brittle Rocks under Harmonic Dynamic Load" Energies 13, no. 4: 851. https://doi.org/10.3390/en13040851
APA StyleLi, S., Tian, S., Li, W., Ling, X., Kapitaniak, M., & Vaziri, V. (2020). Numerical Study on the Elastic Deformation and the Stress Field of Brittle Rocks under Harmonic Dynamic Load. Energies, 13(4), 851. https://doi.org/10.3390/en13040851





