Linear-Gompertz Model-Based Regression of Photovoltaic Power Generation by Satellite Imagery-Based Solar Irradiance
Abstract
1. Introduction
2. Data
2.1. Solar Irradiance Data
2.2. PV Power Generation Data
3. Methods
3.1. Regression Model
3.1.1. Gompertz Function
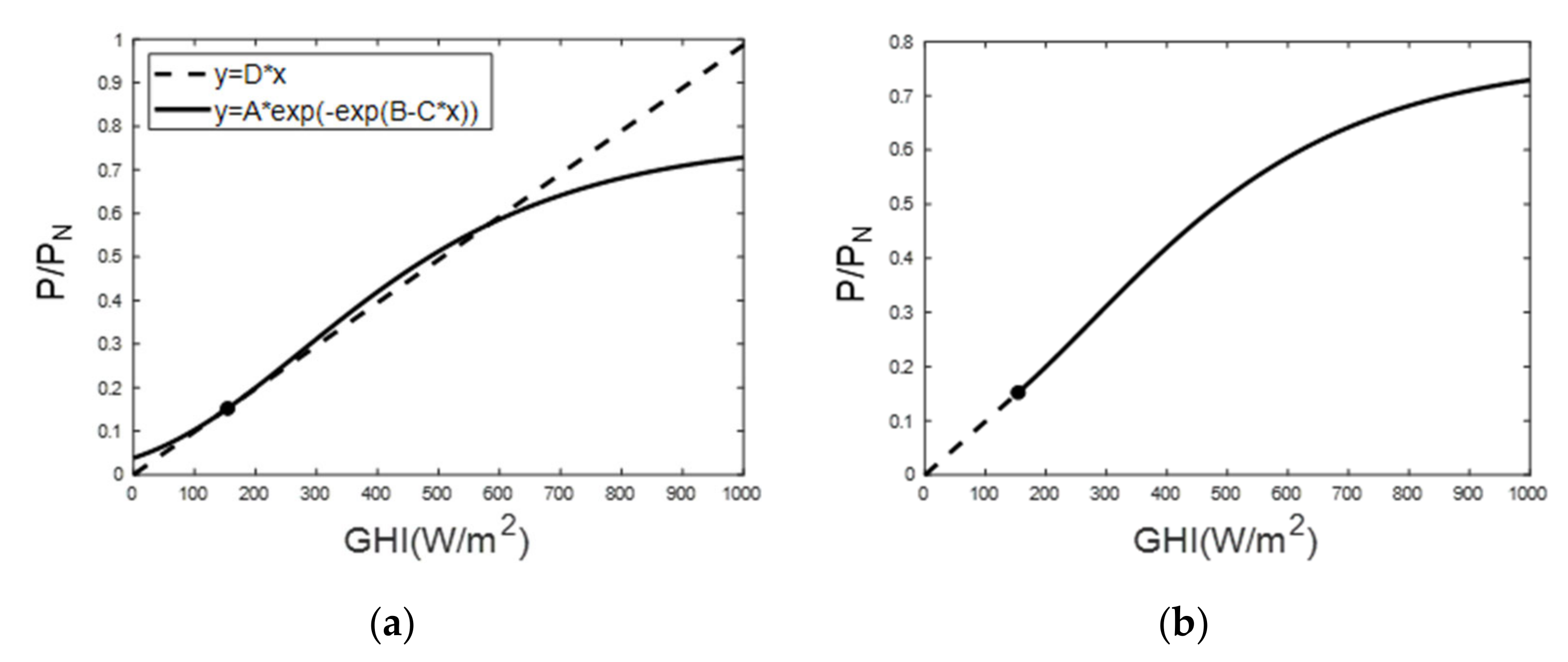
3.1.2. Linear-Gompertz Conjoint Function
3.2. Evaluation of Regression
4. Results and Discussions
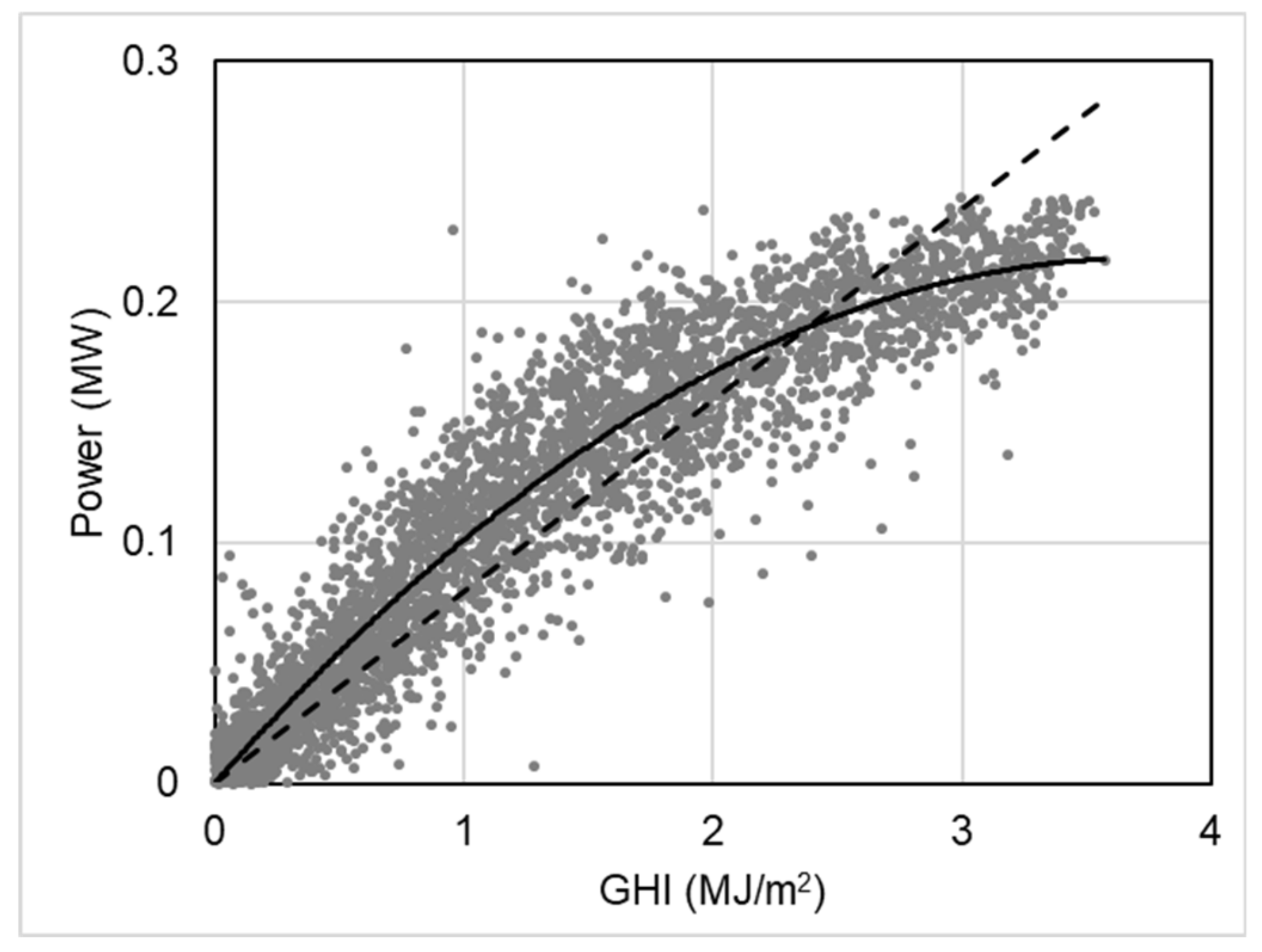
4.1. Comparison of the Regression Models
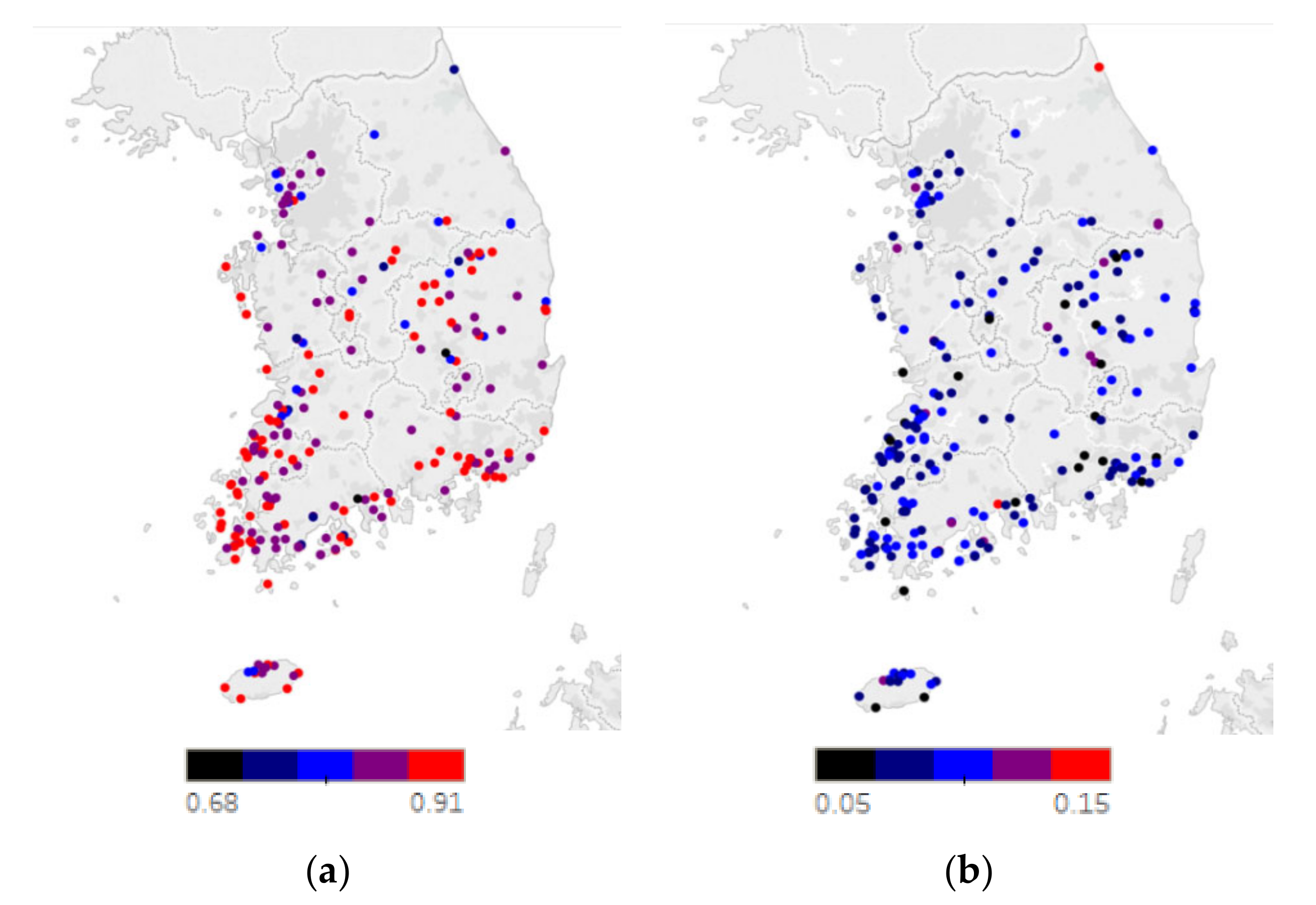
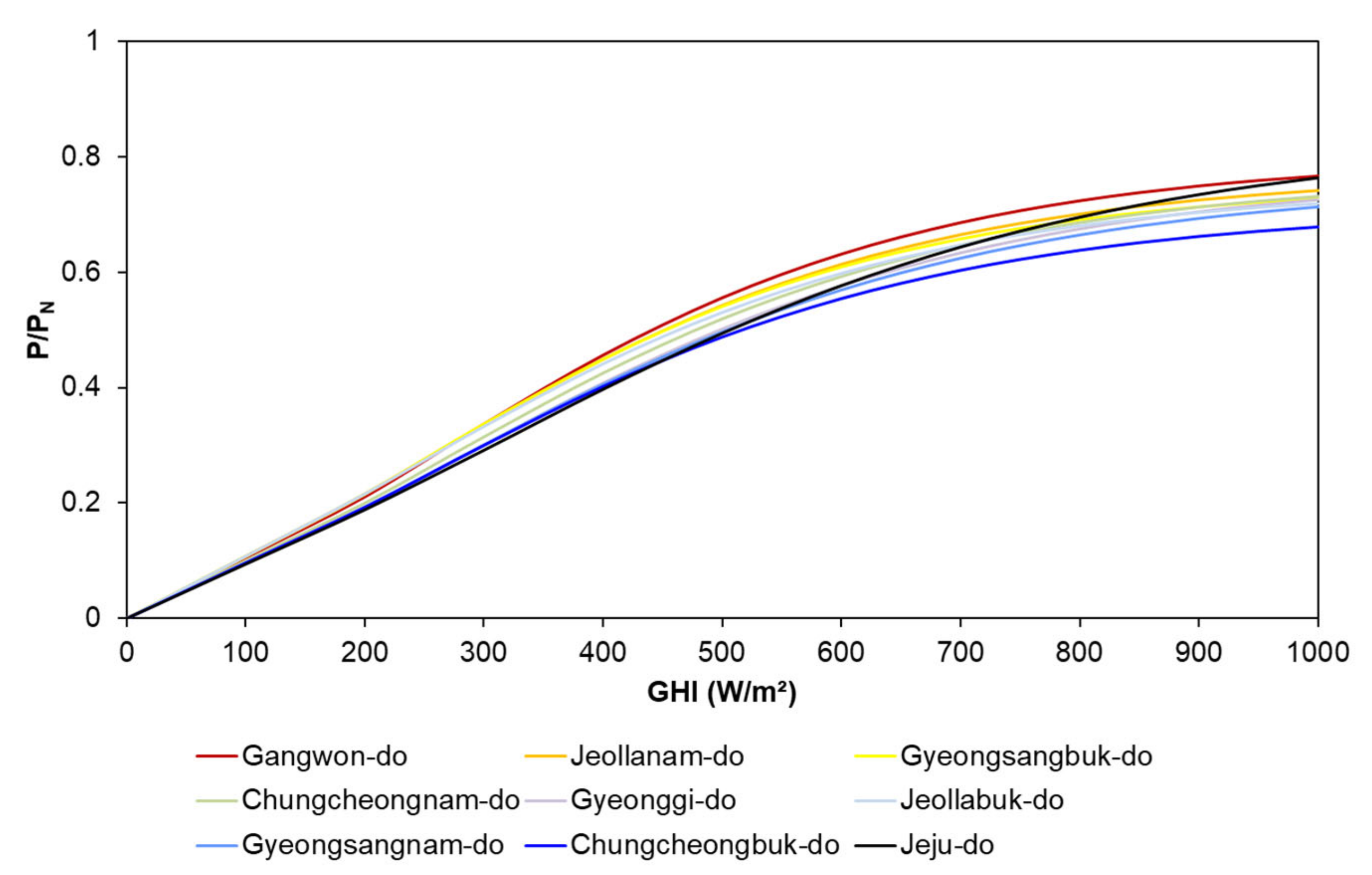
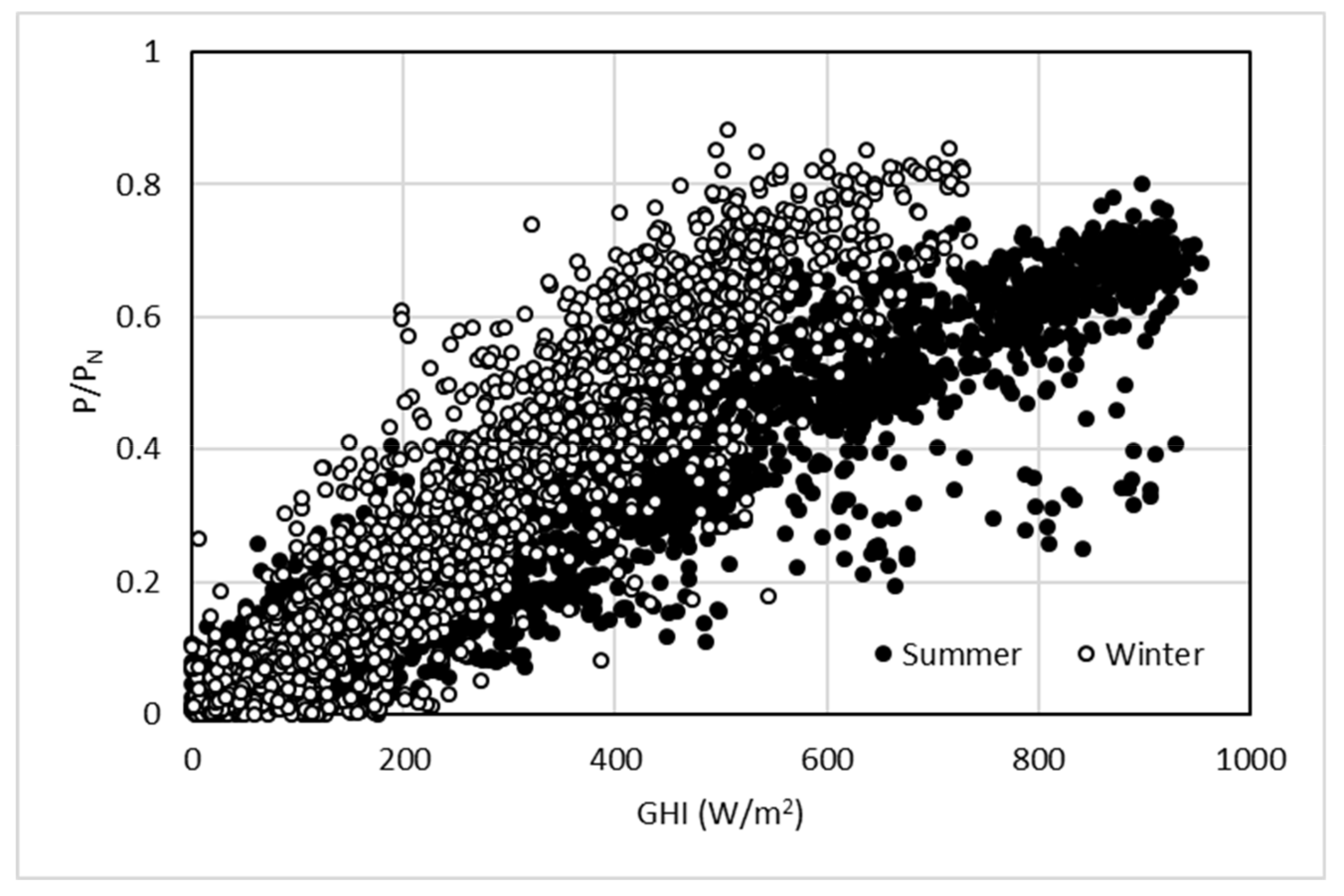
4.2. Gompertz Model Coefficients
4.3. Validation of the Model
5. Conclusions
- (1)
- The Linear-Gompertz model successfully expressed the sigmoidal characteristics of the PV system performance countrywide as a single function of GHI, which is the simplest regression form adequate for machine learning needed to develop a forecasting model. The nonphysical trend of the Gompertz model in the low GHI range was fixed by combining a linear equation having the same slope at the conjoint point. The fitness of the Linear-Gompertz regression was R2 = 0.85, and the nRMSE of normalized power output ratio was 0.09.
- (2)
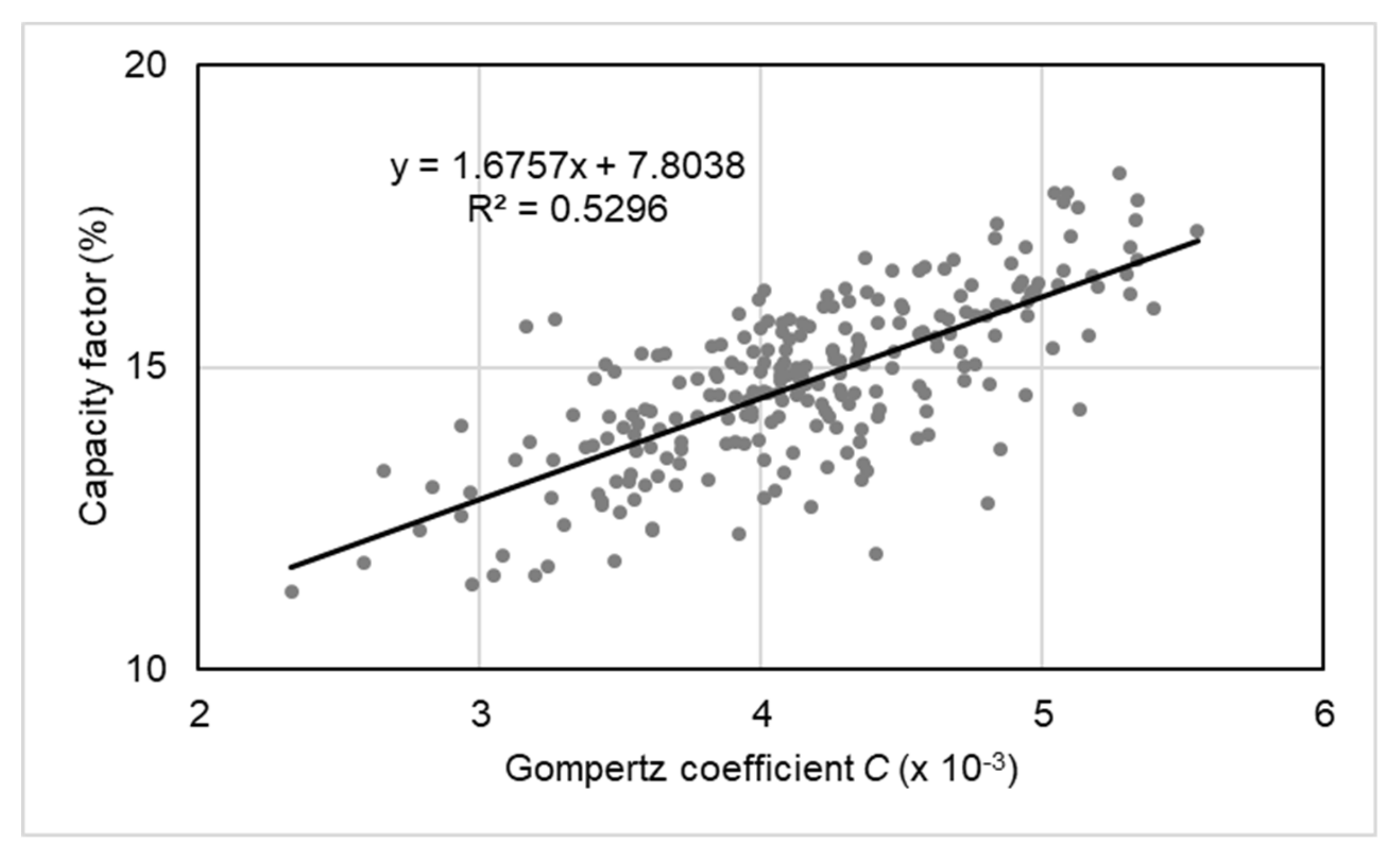
- The three Gompertz coefficients A, B, and C were calculated by year, by season, and by province, and it was found that they had normal distributions and equivariances, meaning that the Gompertz coefficients were the general parameters for the entire country. Moreover, the Gompertz coefficient of the growth rate C showed a strong correlation (R2 = 0.53) with the capacity factor of the PV power plant. Therefore, it was possible to derive the capacity factor equation as a function of A, B, and C, that showed a fitness of R2 = 0.88.
- (3)
- In order to use the Linear-Gompertz model to obtain South Korea’s general PV performance curve for PV power forecasting, it will be necessary to increase the fitness of the model to over R2 > 0.9 by including significant environmental variables such as ambient temperature. Future research will consist of securing long-term PV power output data and analyzing the aging effect of the PV panel to correct the degradation effect. In addition, the accuracy of the Linear-Gompertz model will be improved by calculating and applying the POA, the primary input variable, instead of GHI. To that end, the solar irradiance decomposition algorithm should be improved in the UASIBS-KIER model, and verification and compensation steps using actual measurement data should be implemented in advance.
- (4)
- Because the solar irradiance in most regions of South Korea is less than 1300 W/m2, an additional verification of the conditions of high solar irradiance is needed to apply this result to regions with high solar irradiance. In addition, since PV power generation is significantly influenced by climate conditions, there will be some differences compared to regions in which the climate zone is completely different from that of South Korea. However, South Korea has four distinct seasons and a wide temperature distribution ranging from −15 °C to +35 °C throughout the year. Thus, the effect of climate conditions on PV power generation is relatively significant, which means the prediction error that occurred when the present regression model was applied to other climate zone is expected to be smaller in a relative sense.
Author Contributions
Funding
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Global warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty, 1st ed.; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Greenhouse Gas Inventory and Research Center. Second Biennial Update Report of the Republic of Korea Under the United Nations Framework Convention on Climate Change, 1st ed.; The Government of the Republic of Korea: Seoul, Korea, 2017; pp. 25–33.
- Maennel, A.; Kim, H.-G. Comparison of greenhouse gas reduction potential through renewable energy transition in South Korea and Germany. Energies 2018, 11, 206. [Google Scholar] [CrossRef]
- Korea Energy Agency. 2018 New & Renewable Energy White Paper, 1st ed.; Korea Ministry of Trade, Industry and Energy: Seoul, Korea, 2019.
- SolarPower Europe. Global Market Outlook for Solar Power/2018–2022, 1st ed.; SolarPower Europe: Brussels, Belgium, 2018; p. 64. [Google Scholar]
- Wirth, H. Recent Facts about Photovoltaics in Germany, 1st ed.; Fraunhofer Institute for Solar Energy Systems: Freiburg, Germany, 2019. [Google Scholar]
- Das, U.K.; Tey, K.S.; Seyedmahmoudian, M.; Mekhilef, S.; Idris, M.Y.I.; van Deventer, W.; Horan, B.; Stojcevski, A. Forecasting of photovoltaic power generation and model optimization: A review. Renew. Sustain. Energy Rev. 2018, 81, 912–928. [Google Scholar] [CrossRef]
- Ruiz-Ariasa, J.A.; Gueymard, C.A. Worldwide inter-comparison of clear-sky solar radiation models: Consensus based review of direct and global irradiance components simulated at the earth surface. Solar Energy 2018, 168, 10–29. [Google Scholar] [CrossRef]
- Kim, C.K.; Holmgren, W.F.; Stovern, M.; Betterton, E.A. Toward improved solar irradiance forecasts: Derivation of downwelling surface shortwave radiation in Arizona from satellite. Pure Appl. Geophys. 2016, 173, 2535–2553. [Google Scholar] [CrossRef]
- Bocca, A.; Bergamasco, L.; Fasano, M.; Bottaccioli, L.; Chiavazzo, E.; Macii, A.; Asinari, P. Multiple-Regression Method for Fast Estimation of Solar Irradiation and Photovoltaic Energy Potentials over Europe and Africa. Energies 2018, 11, 3477. [Google Scholar] [CrossRef]
- Sharma, N.; Gummeson, J.; Irwin, D.; Shenoy, P. Cloudy computing: Leveraging weather forecasts in energy harvesting sensor systems. In Proceedings of the 7th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Boston, MA, USA, 21–25 June 2010; pp. 1–9. [Google Scholar]
- Zhanga, W.; Danga, H.; Simoes, R. A new solar power output prediction model based on a hybrid forecast engine and a decomposition model. ISA Trans. 2018, 81, 105–120. [Google Scholar] [CrossRef] [PubMed]
- Gan, L.K.; Shek, J.K.H.; Mueller, M.A. Hybrid wind–photovoltaic–diesel–battery system sizing tool development using empirical approach, life-cycle cost and performance analysis: A case study in Scotland. Energy Conv. Manag. 2015, 106, 479–494. [Google Scholar] [CrossRef]
- Field, D.A.; Rogers, T.; Sealy, A. Dust accumulation and PV power output in the tropical environment of Barbados. In Proceedings of the 14th International Conference on Sustainable Energy Technologies, Nottingham, UK, 25–27 August 2015; pp. 276–278. [Google Scholar]
- Chou, M.-D.; Suárez, M.J. A solar radiation parameterization for atmospheric studies. NASA Tech. Rep. Series Global Model. Data Assim. 1999, 15, 1–40. [Google Scholar]
- Kim, C.K.; Kim, H.-G.; Kang, Y.-H.; Yun, C.-Y. Toward improved solar irradiance forecasts: Comparison of the global horizontal irradiances derived from the COMS satellite imagery over the Korean Peninsula. Pure Appl. Geophys. 2017, 174, 2773–2792. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1977; pp. 72–88. [Google Scholar]
- Jordan, D.C.; Kurtz, S.R. Photovoltaic degradation rates—An analytical review. Prog. Photovol. Res. Appl. 2013, 21, 12–29. [Google Scholar] [CrossRef]
- King, D.L.; Boyson, W.E.; Kratochvil, J.A. Photovoltaic Array Performance Model, SAND2004-3535; Sandia National Laboratories: Albuquerque, NM, USA, 2004. [Google Scholar]
- Molina-Garcia, A.; Guerrero-Pérez, J.; Bueso, M.C.; Kessler, M.; Gómez-Lázaro, E. A new solar module modeling for PV applications based on a symmetrized and shifted Gompertz model. IEEE Trans. Energy Conv. 2015, 30, 51–59. [Google Scholar] [CrossRef]
- Kim, B.Y.; Vilanova, A.; Kim, C.K.; Kang, Y.H.; Yun, C.Y.; Kim, H.G. Non-linear regression model between solar irradiation and PV power generation using the Gompertz curve. J. Korean Solar Energy Soc. 2019, 39, 113–125. [Google Scholar] [CrossRef]
- Georg, O.; Szegö, G. Aufgaben und Lehrsätze aus der Analysis; Springer-Verlag: Heidelberg, Germany, 2013; Volume 74. [Google Scholar]
- Anderson, T.W.; Darling, D.A. A Test of goodness of fit. J. Am. Stat. Assoc. 1954, 49, 765–769. [Google Scholar] [CrossRef]
- Shravanth, V.M.; Srinivasan, J.; Ramasesha, S.K. Performance of solar photovoltaic installations: effect of seasonal variations. Solar Energy 2016, 131, 39–46. [Google Scholar] [CrossRef]
- Cheon, J.H.; Lee, J.T.; Kim, H.G.; Kang, Y.H.; Yun, C.Y.; Kim, C.K.; Kim, B.Y.; Kim, J.Y.; Park, Y.Y.; Kim, T.H.; et al. Review of the trend of solar energy forecasting techniques. J. Korean Solar Energy Soc. 2019, 39, 41–54. [Google Scholar] [CrossRef]
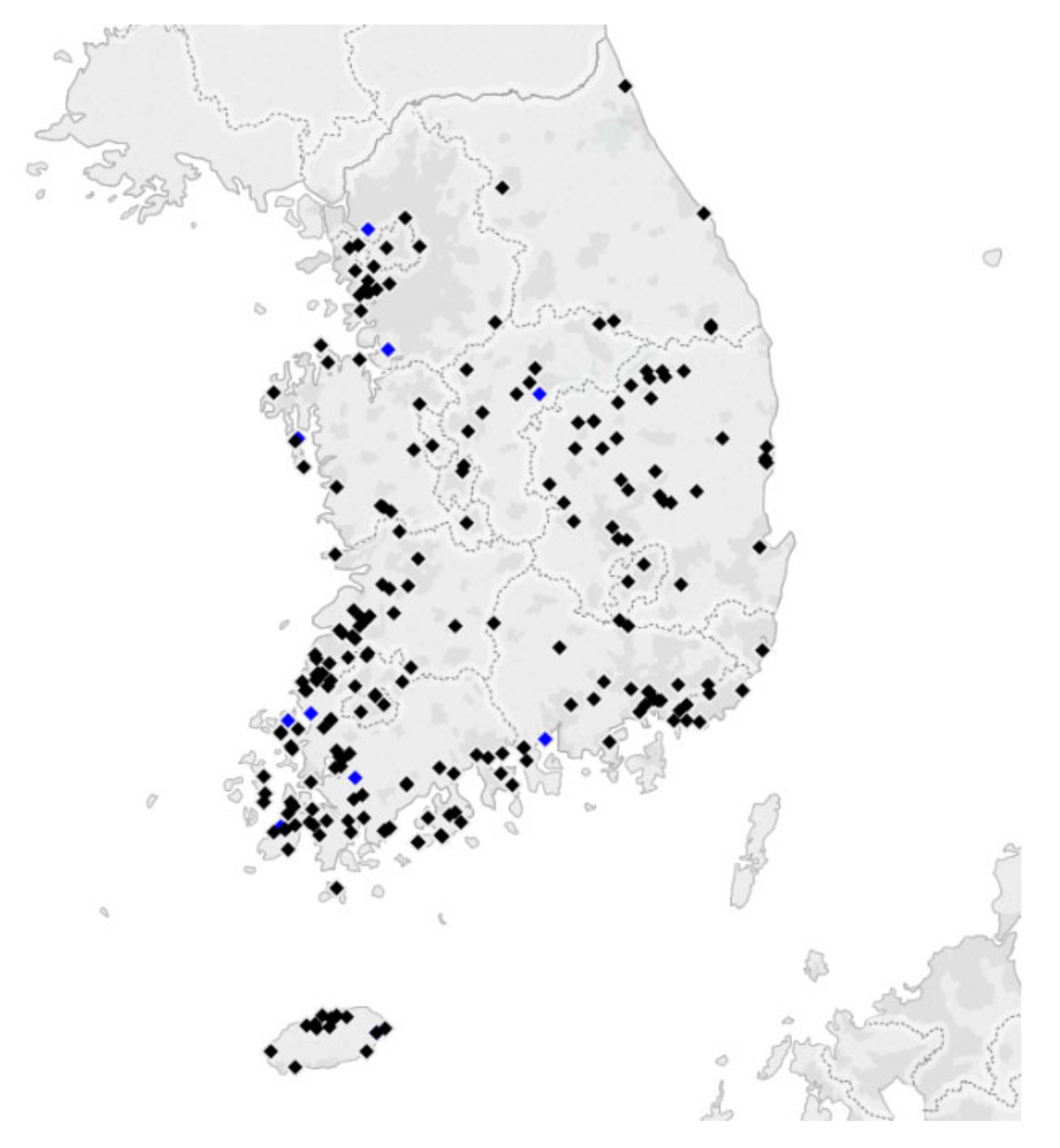

| Province | Sampling | PV Plants (>50 kWp) | Total No. of PV Plants |
|---|---|---|---|
| Jeollanam-do | 86 | 218 | 6728 |
| Jeollabuk-do | 28 | 71 | 9040 |
| Gyeongsangnam-do | 29 | 72 | 2398 |
| Gyeongsangbuk-do | 37 | 91 | 3847 |
| Chungcheongnam-do | 16 | 39 | 4323 |
| Chungcheongbuk-do | 6 | 13 | 2144 |
| Gyeonggi-do | 17 | 39 | 3435 |
| Gangwon-do | 9 | 23 | 2320 |
| Jeju-do | 14 | 34 | 590 |
| Sum | 242 | 600 | 34,825 |
| Year | 2014 | 2015 | 2016 | 2014~2016 | ||||
|---|---|---|---|---|---|---|---|---|
| Model | L | L-G | L | L-G | L | L-G | L | L-G |
| R2 | 0.83 | 0.85 | 0.84 | 0.86 | 0.82 | 0.85 | 0.83 | 0.85 |
| nRMSE | 0.10 | 0.09 | 0.10 | 0.09 | 0.10 | 0.09 | 0.10 | 0.09 |
| Year | 2014 | 2015 | 2016 | 2014~2016 | |
|---|---|---|---|---|---|
| A | μ | 0.77 | 0.78 | 0.76 | 0.77 |
| σ | 0.05 | 0.05 | 0.05 | 0.05 | |
| B | μ | 1.09 | 1.10 | 1.10 | 1.10 |
| σ | 0.06 | 0.06 | 0.06 | 0.06 | |
| C | μ (×10−3) | 4.20 | 4.09 | 4.15 | 4.14 |
| σ (×10−3) | 0.64 | 0.62 | 0.60 | 0.61 | |
| Coefficient | Season | 2014 | 2015 | 2016 | 2014~2016 |
|---|---|---|---|---|---|
| A | Winter | 0.82 | 0.87 | 0.83 | 0.84 |
| Spring | 0.87 | 0.86 | 0.86 | 0.86 | |
| Summer | 0.74 | 0.78 | 0.79 | 0.77 | |
| Autumn | 0.70 | 0.75 | 0.73 | 0.73 | |
| B | Winter | 1.16 | 1.17 | 1.15 | 1.16 |
| Spring | 1.06 | 1.07 | 1.09 | 1.07 | |
| Summer | 0.96 | 0.93 | 0.96 | 0.95 | |
| Autumn | 0.84 | 1.00 | 1.11 | 0.98 | |
| C (×10−3) | Winter | 4.85 | 4.62 | 4.71 | 4.73 |
| Spring | 3.57 | 3.63 | 3.55 | 3.59 | |
| Summer | 3.72 | 3.33 | 3.27 | 3.44 | |
| Autumn | 4.57 | 4.21 | 4.50 | 4.43 |
| Year | 2014 | 2015 | 2016 | 2014~2016 | ||||
|---|---|---|---|---|---|---|---|---|
| Code | R2 | nRMSE | R2 | nRMSE | R2 | nRMSE | R2 | nRMSE |
| 1730 | 0.83 | 0.10 | 0.85 | 0.09 | 0.84 | 0.09 | 0.84 | 0.09 |
| 1837 | 0.87 | 0.09 | 0.89 | 0.09 | 0.87 | 0.09 | 0.88 | 0.09 |
| 1882 | 0.88 | 0.08 | 0.89 | 0.08 | 0.87 | 0.08 | 0.88 | 0.08 |
| 1947 | 0.87 | 0.09 | 0.88 | 0.09 | 0.87 | 0.09 | 0.87 | 0.09 |
| 1996 | 0.81 | 0.10 | 0.82 | 0.10 | 0.82 | 0.10 | 0.82 | 0.10 |
| 8877 | 0.86 | 0.10 | 0.86 | 0.10 | 0.84 | 0.10 | 0.85 | 0.10 |
| 8907 | 0.85 | 0.09 | 0.89 | 0.09 | 0.86 | 0.09 | 0.87 | 0.09 |
| 9577 | 0.88 | 0.10 | 0.88 | 0.09 | 0.87 | 0.09 | 0.88 | 0.09 |
| 9617 | 0.89 | 0.08 | 0.89 | 0.08 | 0.90 | 0.08 | 0.89 | 0.08 |
| 9927 | 0.89 | 0.09 | 0.89 | 0.09 | 0.89 | 0.09 | 0.89 | 0.09 |
| Mean | 0.86 | 0.09 | 0.87 | 0.09 | 0.86 | 0.09 | 0.87 | 0.09 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilanova, A.; Kim, B.-Y.; Kim, C.K.; Kim, H.-G. Linear-Gompertz Model-Based Regression of Photovoltaic Power Generation by Satellite Imagery-Based Solar Irradiance. Energies 2020, 13, 781. https://doi.org/10.3390/en13040781
Vilanova A, Kim B-Y, Kim CK, Kim H-G. Linear-Gompertz Model-Based Regression of Photovoltaic Power Generation by Satellite Imagery-Based Solar Irradiance. Energies. 2020; 13(4):781. https://doi.org/10.3390/en13040781
Chicago/Turabian StyleVilanova, Alba, Bo-Young Kim, Chang Ki Kim, and Hyun-Goo Kim. 2020. "Linear-Gompertz Model-Based Regression of Photovoltaic Power Generation by Satellite Imagery-Based Solar Irradiance" Energies 13, no. 4: 781. https://doi.org/10.3390/en13040781
APA StyleVilanova, A., Kim, B.-Y., Kim, C. K., & Kim, H.-G. (2020). Linear-Gompertz Model-Based Regression of Photovoltaic Power Generation by Satellite Imagery-Based Solar Irradiance. Energies, 13(4), 781. https://doi.org/10.3390/en13040781








