Dynamic and Economic Investigation of a Solar Thermal-Driven Two-Bed Adsorption Chiller under Perth Climatic Conditions
Abstract
1. Introduction
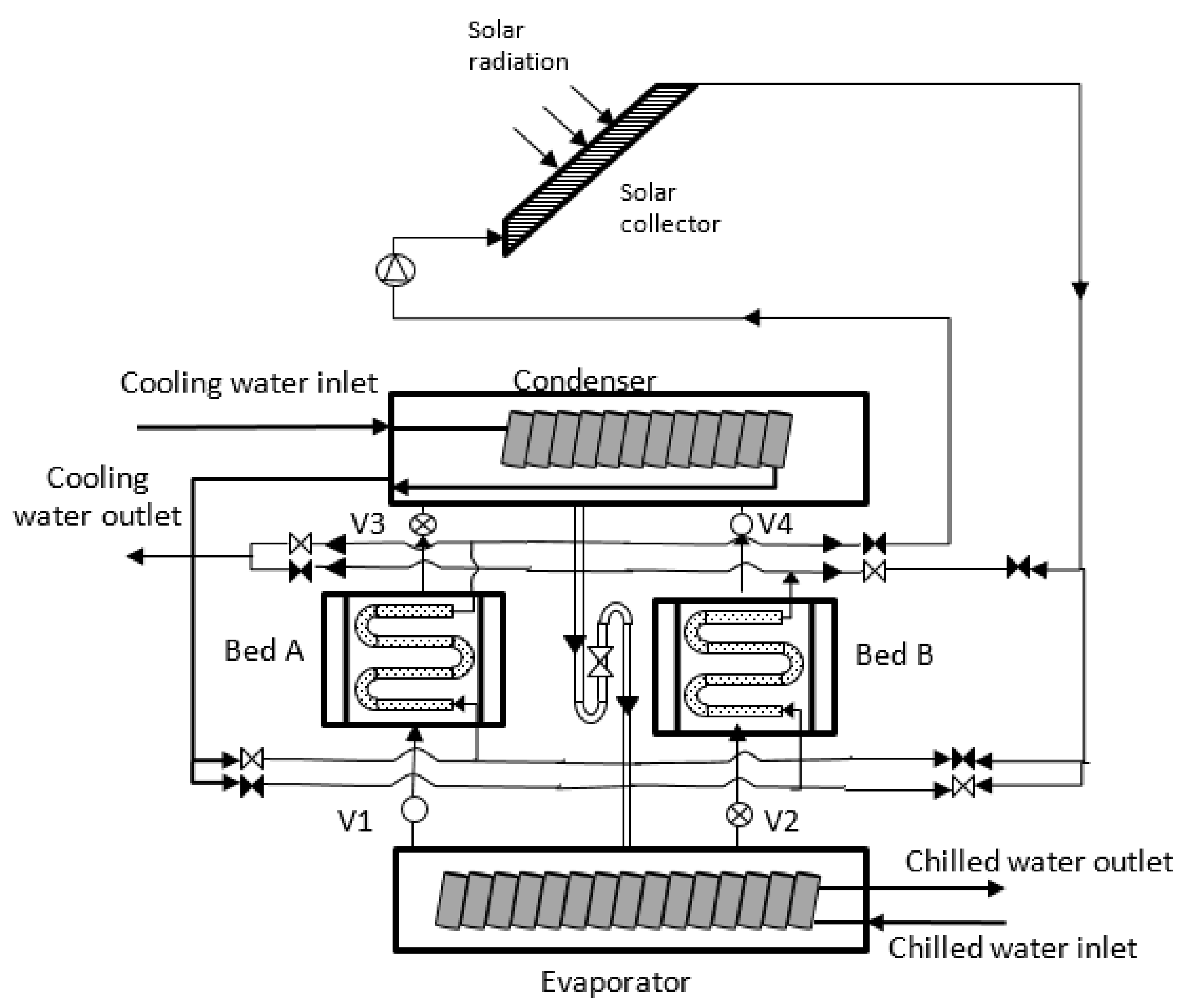
2. System Description
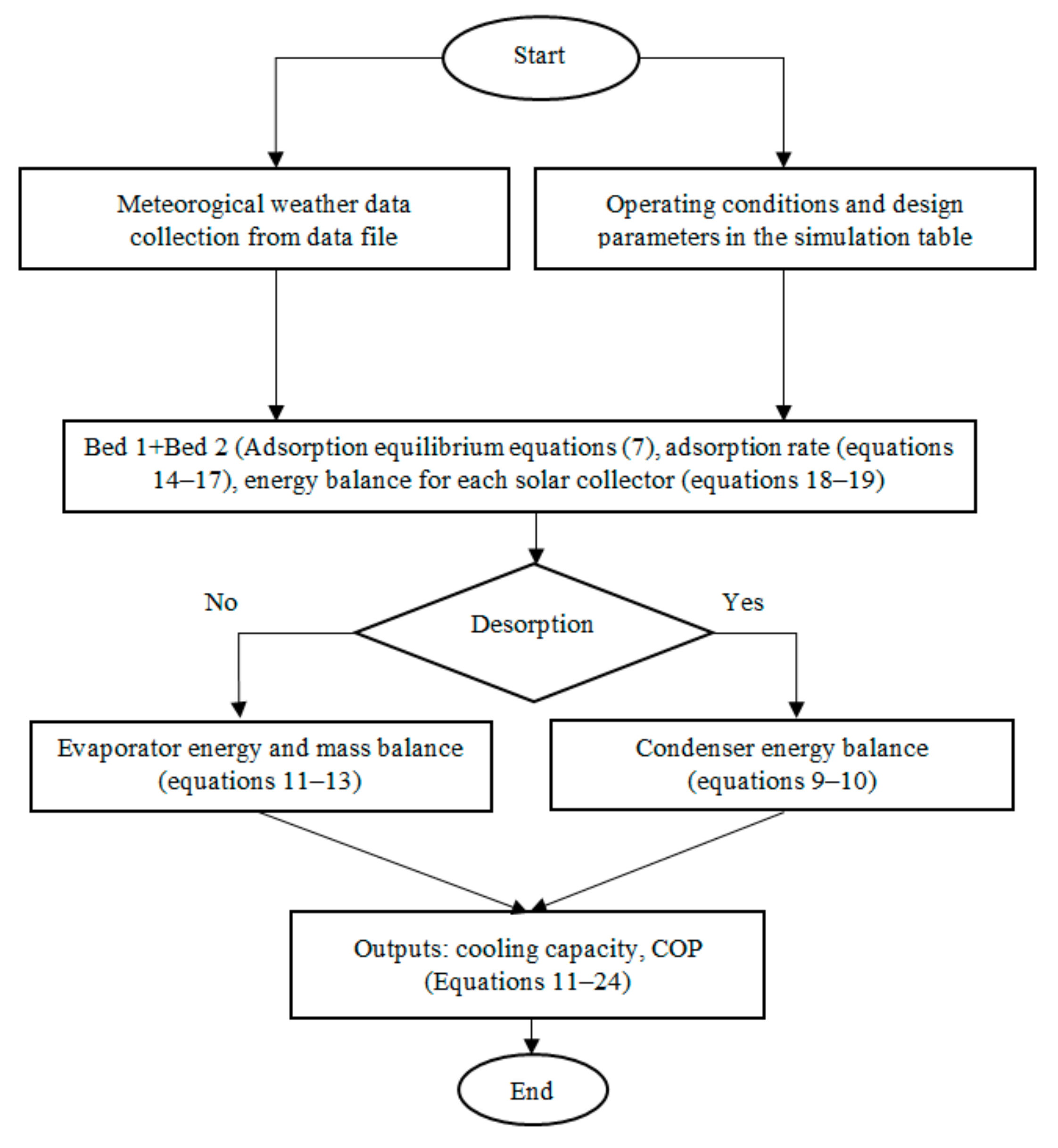
3. Mathematical Modelling
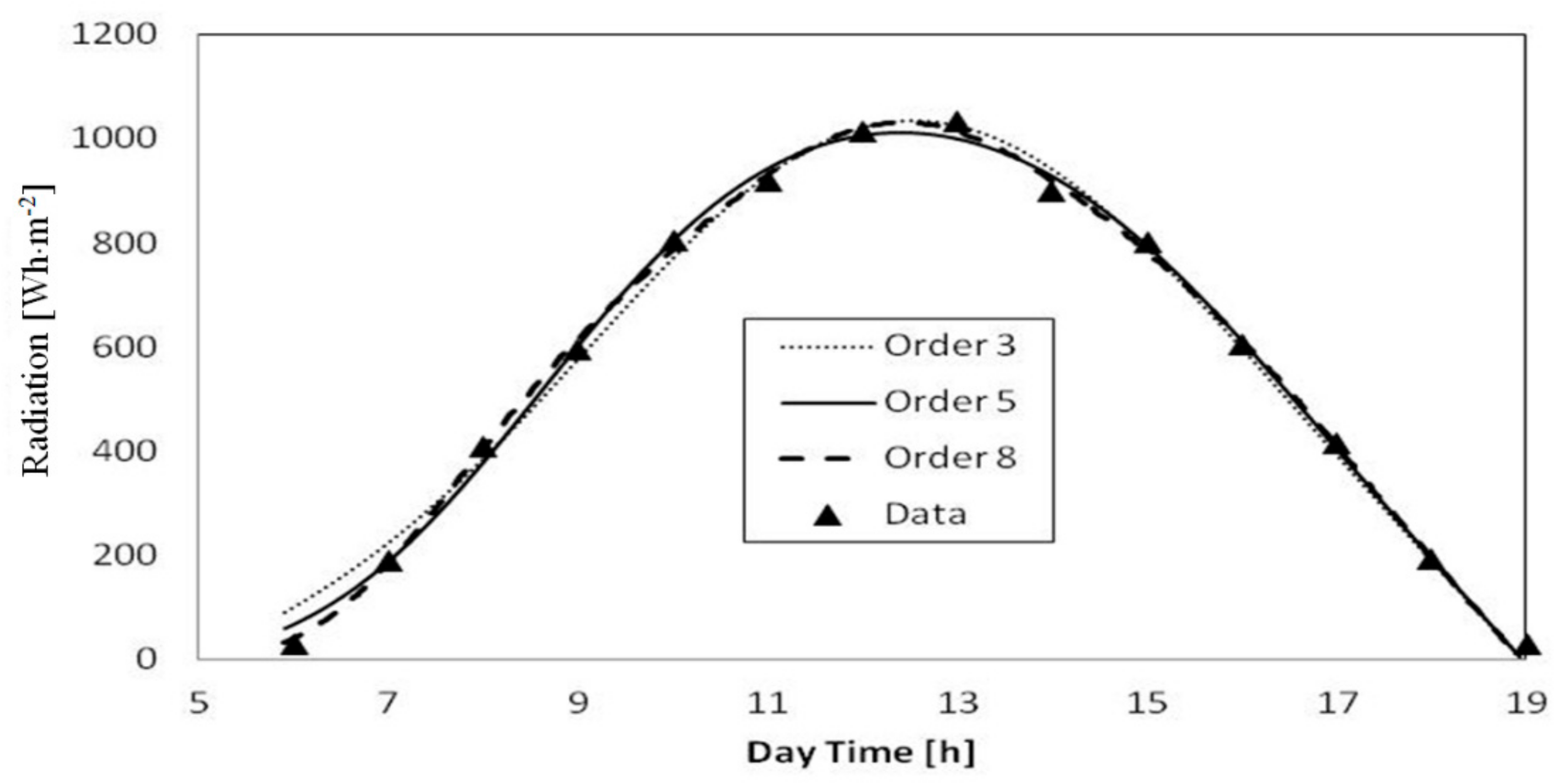
3.1. Correlation Equation of Solar Radiation Data
3.2. Empirical Equation for Day Temperature Data
3.3. Energy Balance for Adsorption Chiller
- = −6.5314 kg × kg−1 of dry adsorbent
- = 0.72452 × 10−1 kg×kg−1 of dry adsorbent K−1
- = −0.23951 × 10−3 kg×kg−1 of dry adsorbent K−2
- = 0.25493 × 10−6 kg×kg−1 of dry adsorbent K−3
- = −15.587
- = 015915 K−1
- = −0.50612 ×10−3 K−2
- = 0.5329 ×10−6 K−3
3.4. Performance Analysis
3.5. Economic Analysis
- The life span of the cooling system is set as 20 years according to available products in the market
- The period of the loan is 15 years
- In Australian markets, the inflation rate in fuel price and the interest rate is around 2.8% and 12 %, respectively
- The salvage factor for the auxiliary cooling system is assumed to be 20% of the capital cost
- The maintenance factor is assumed to be 1.1% of the capital cost for the auxiliary cooling system
- The electricity price is 0.33 USD kWh−1 in the Perth market
4. Results and Analysis
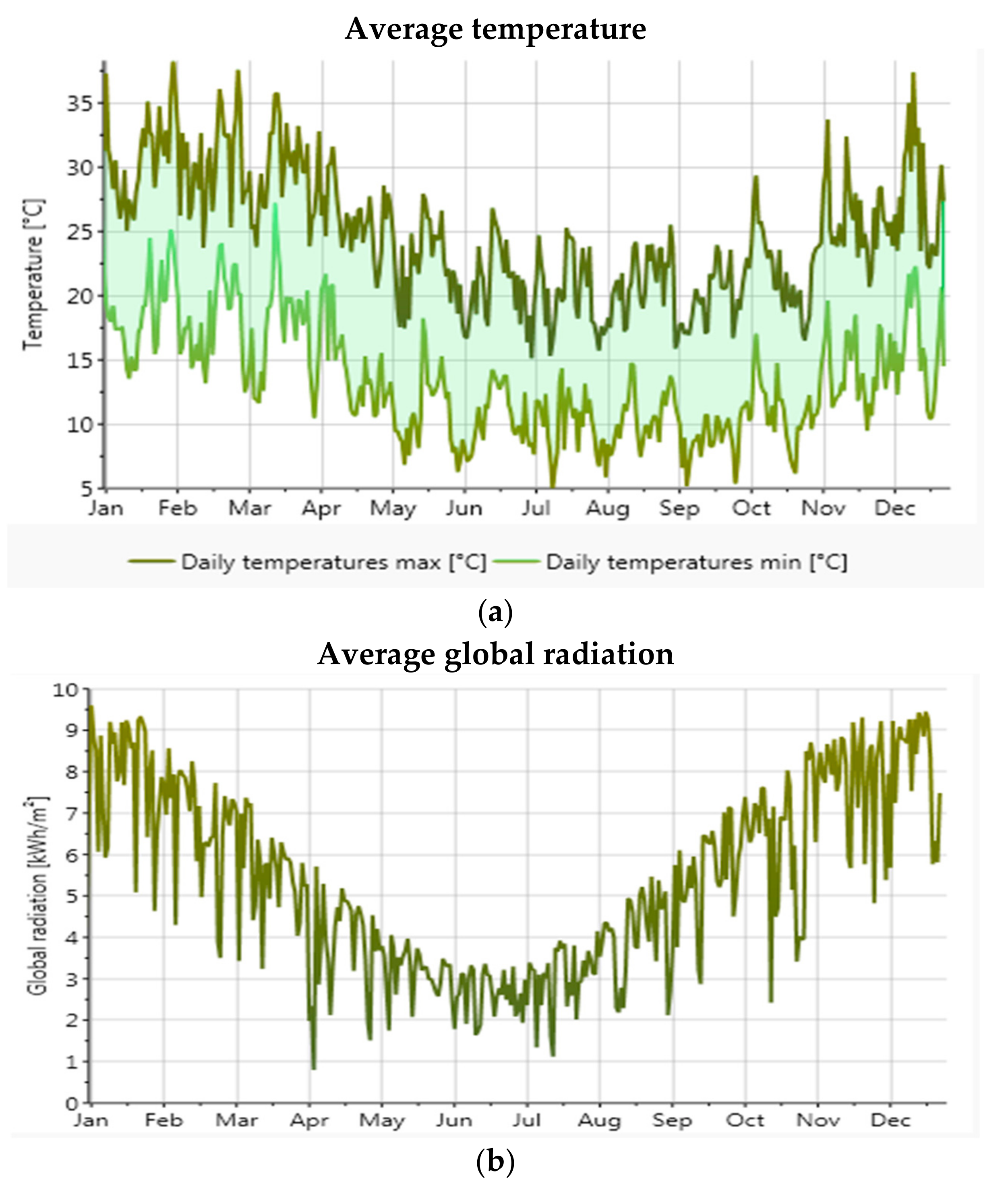
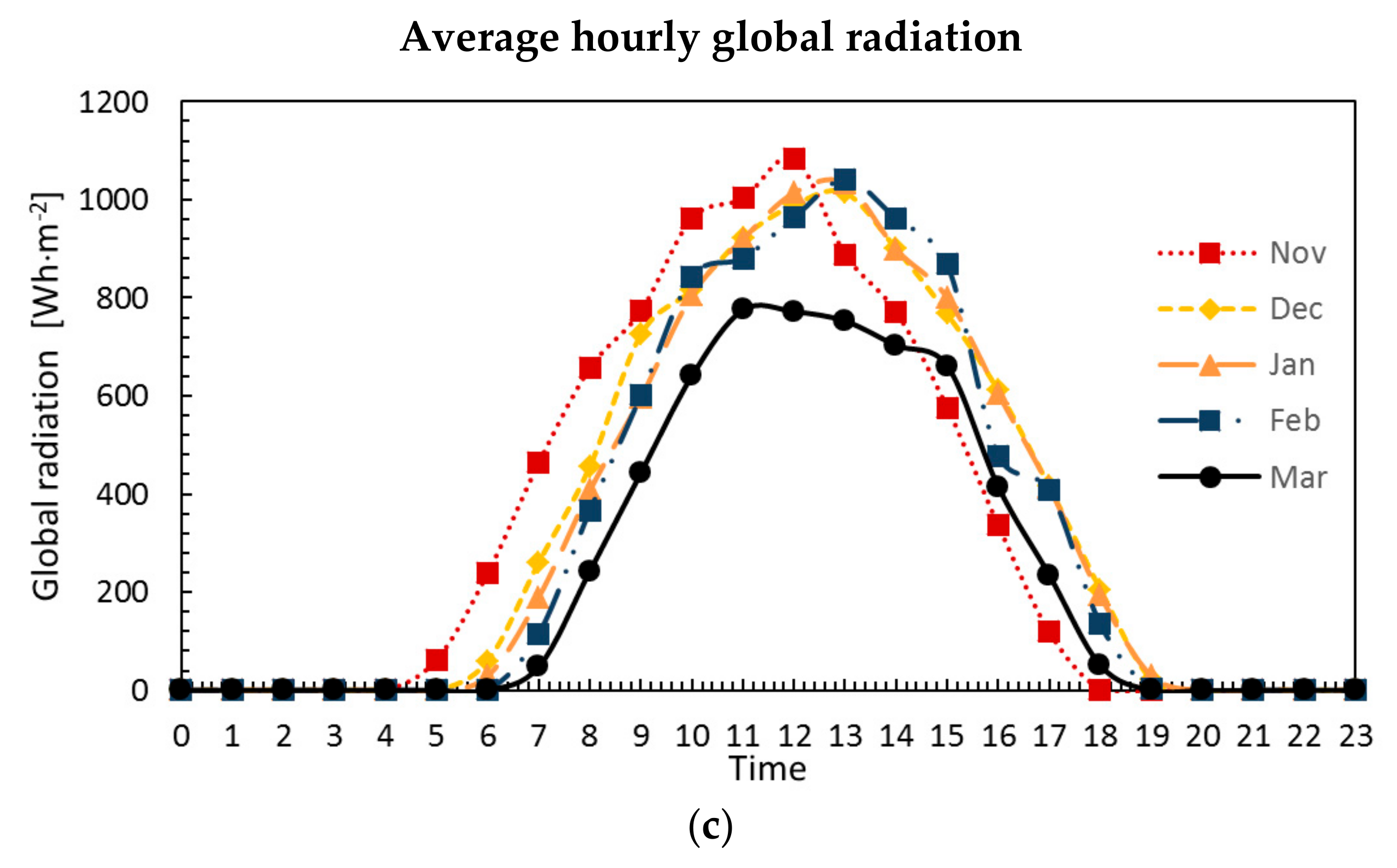
4.1. Ambient Temperature and Global Radiation of Perth City
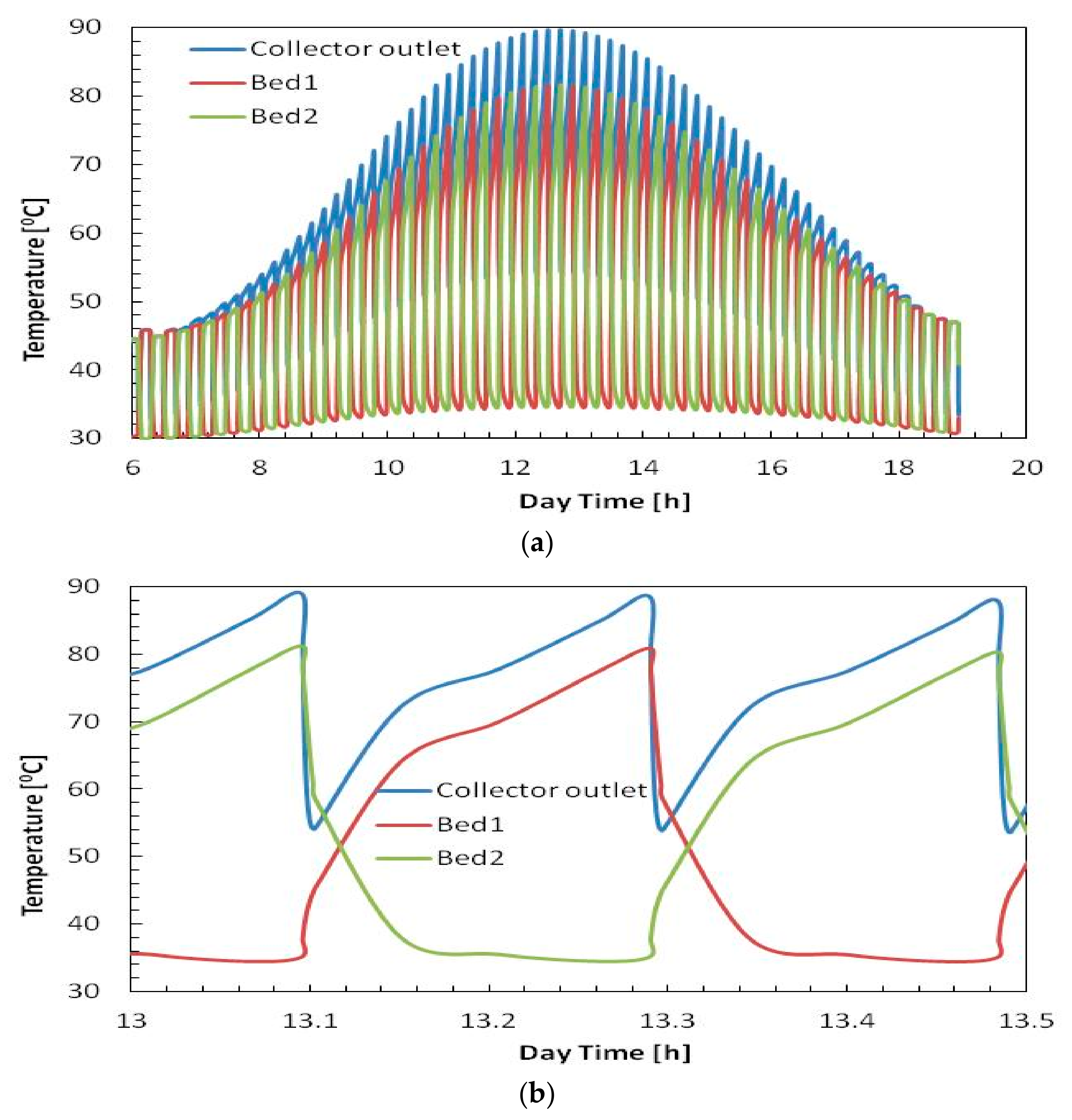
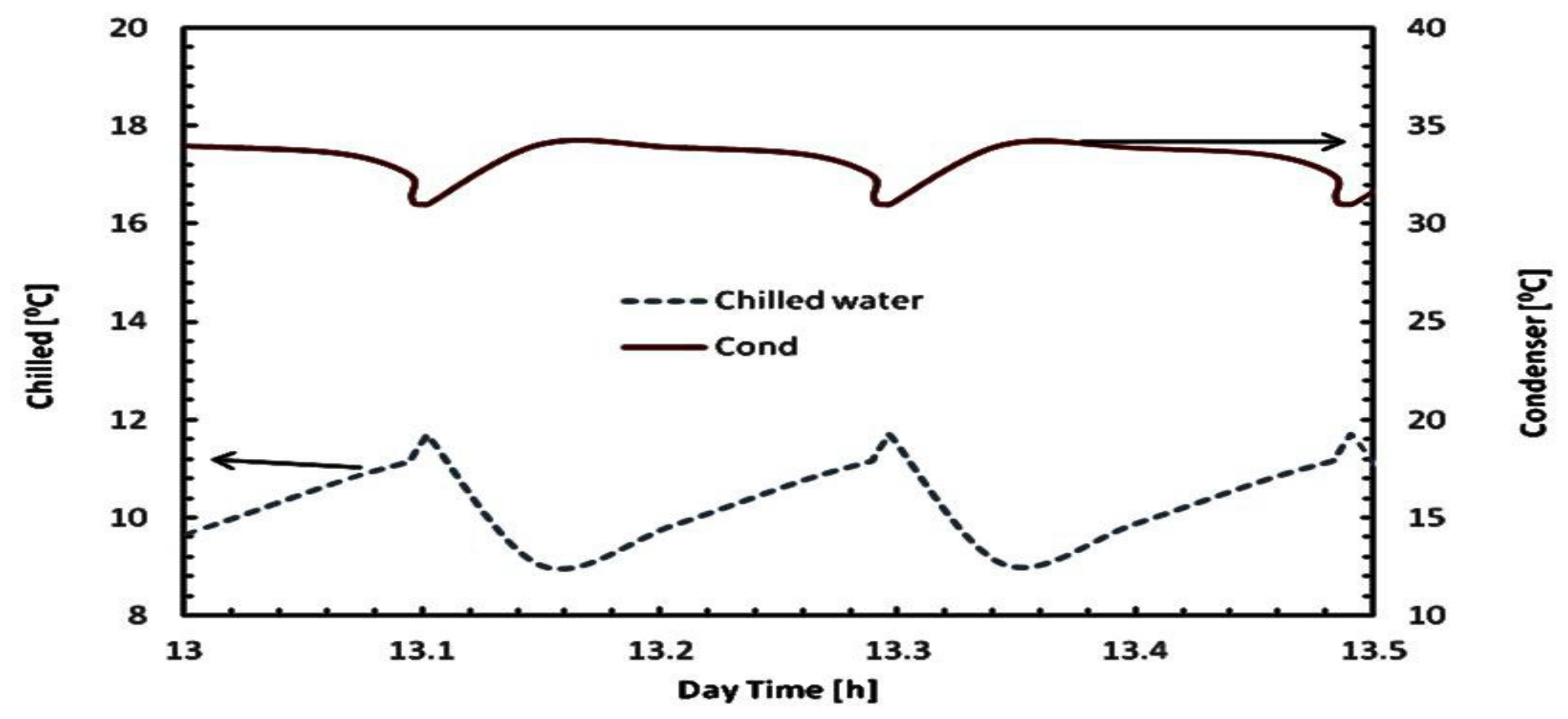
4.2. Outlet Temperatures History
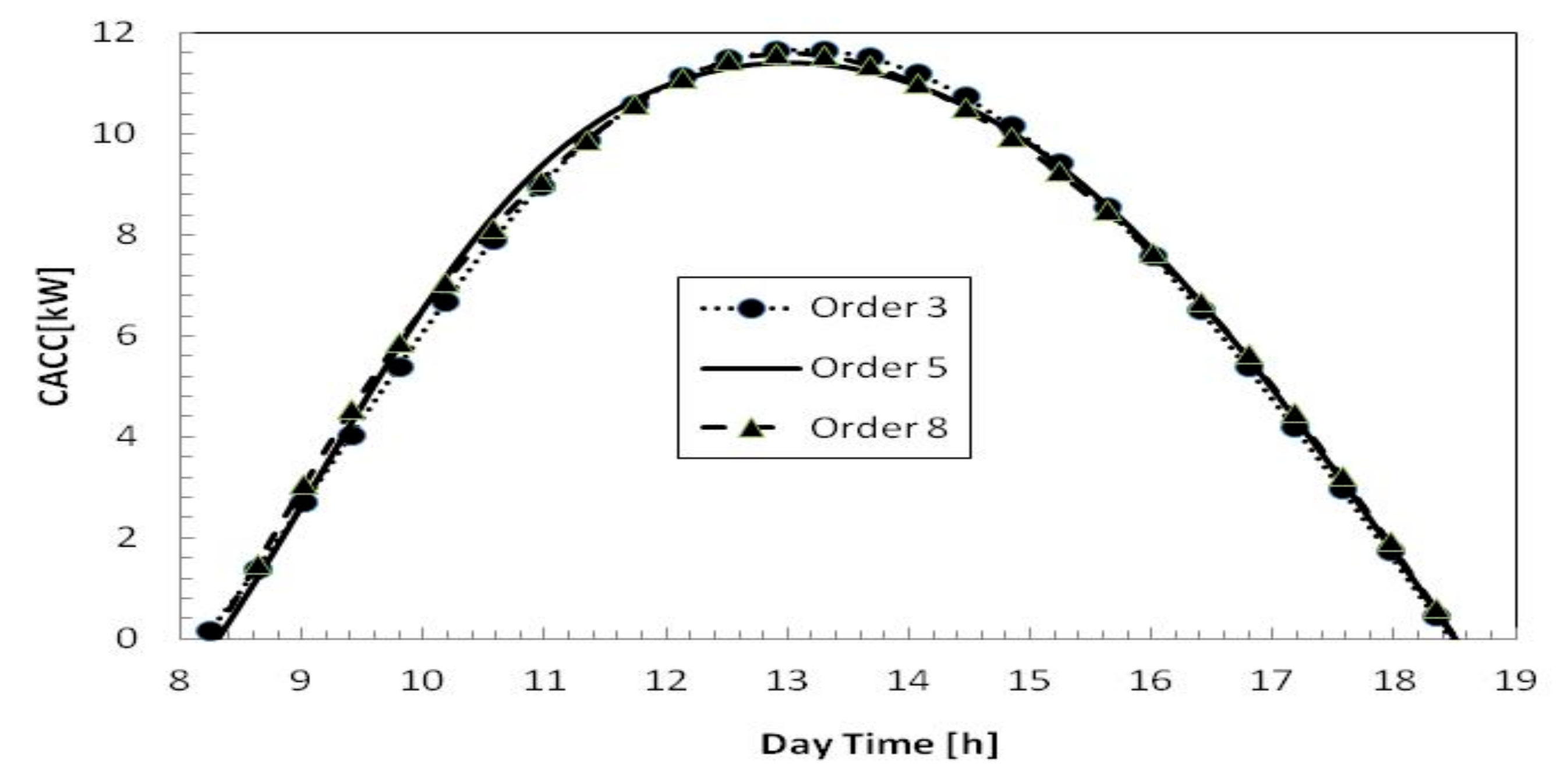
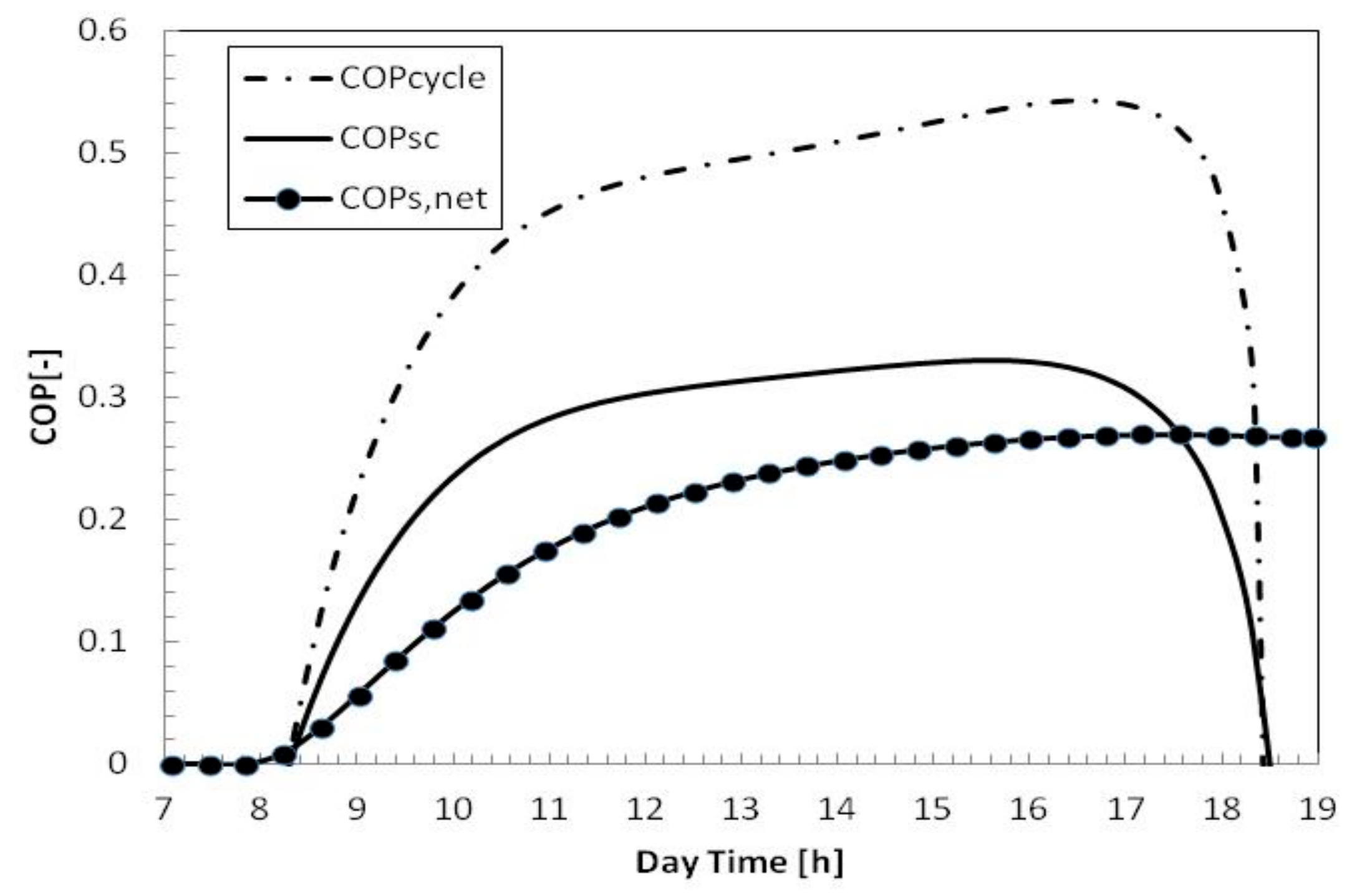
4.3. Performance Assessment
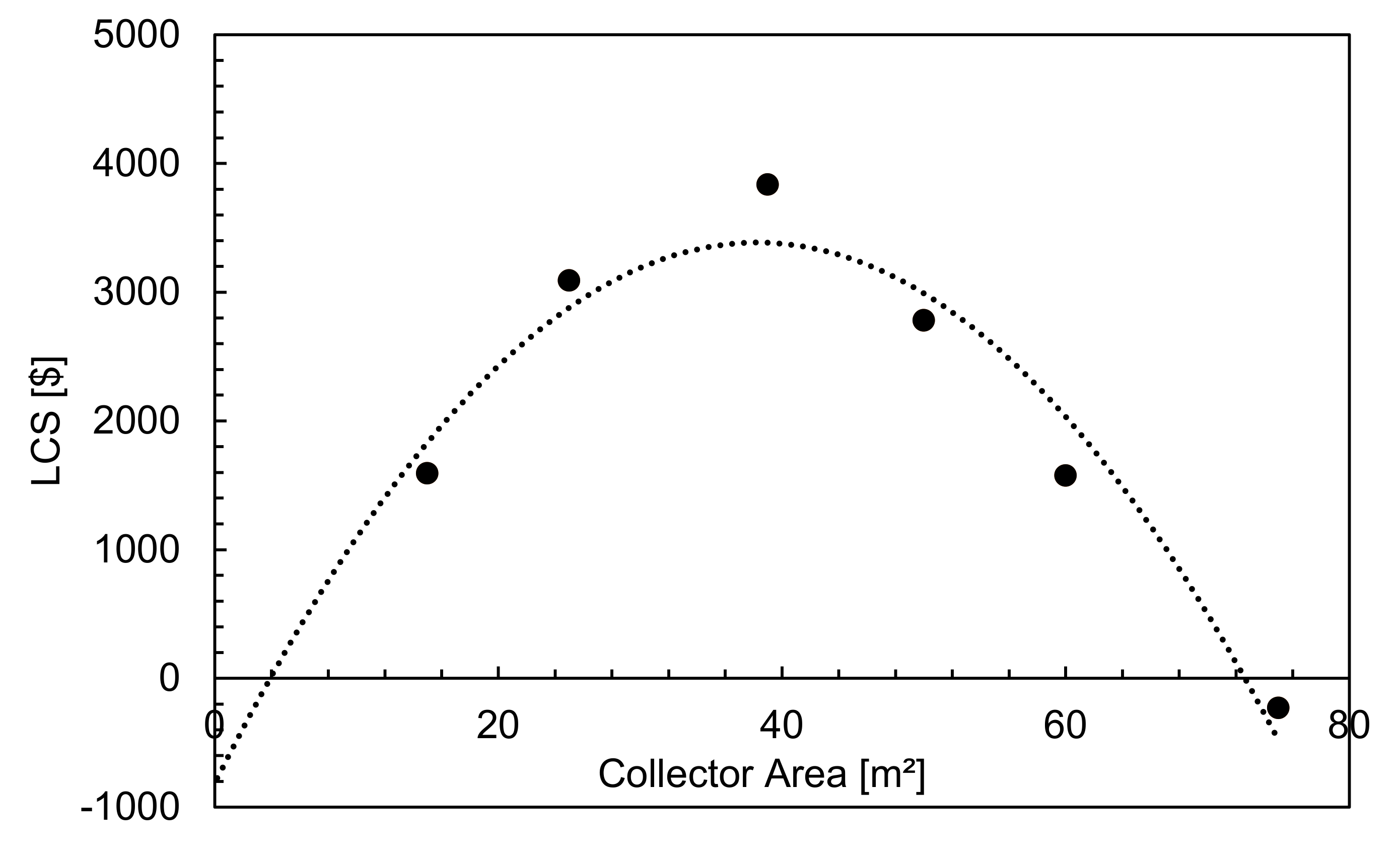
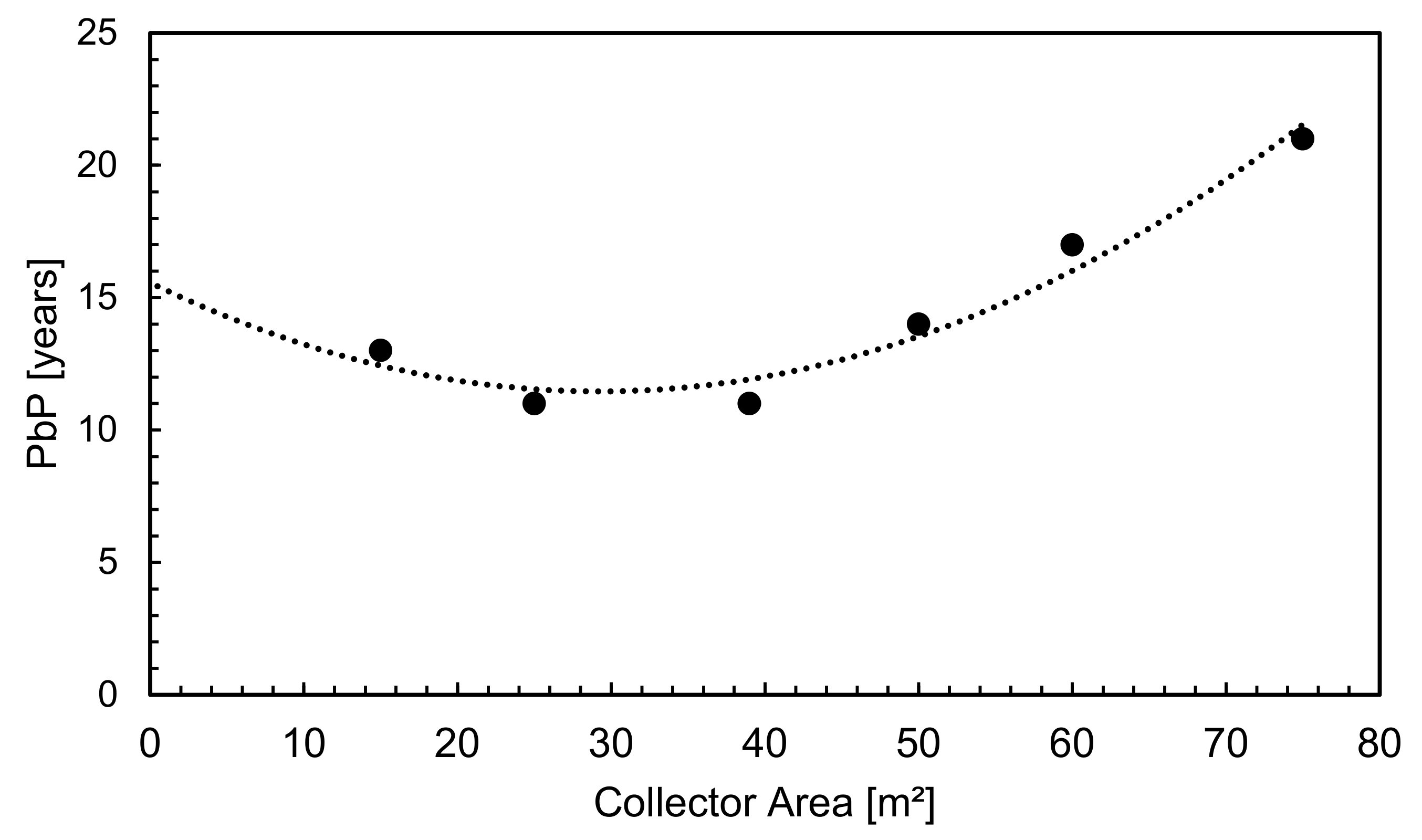
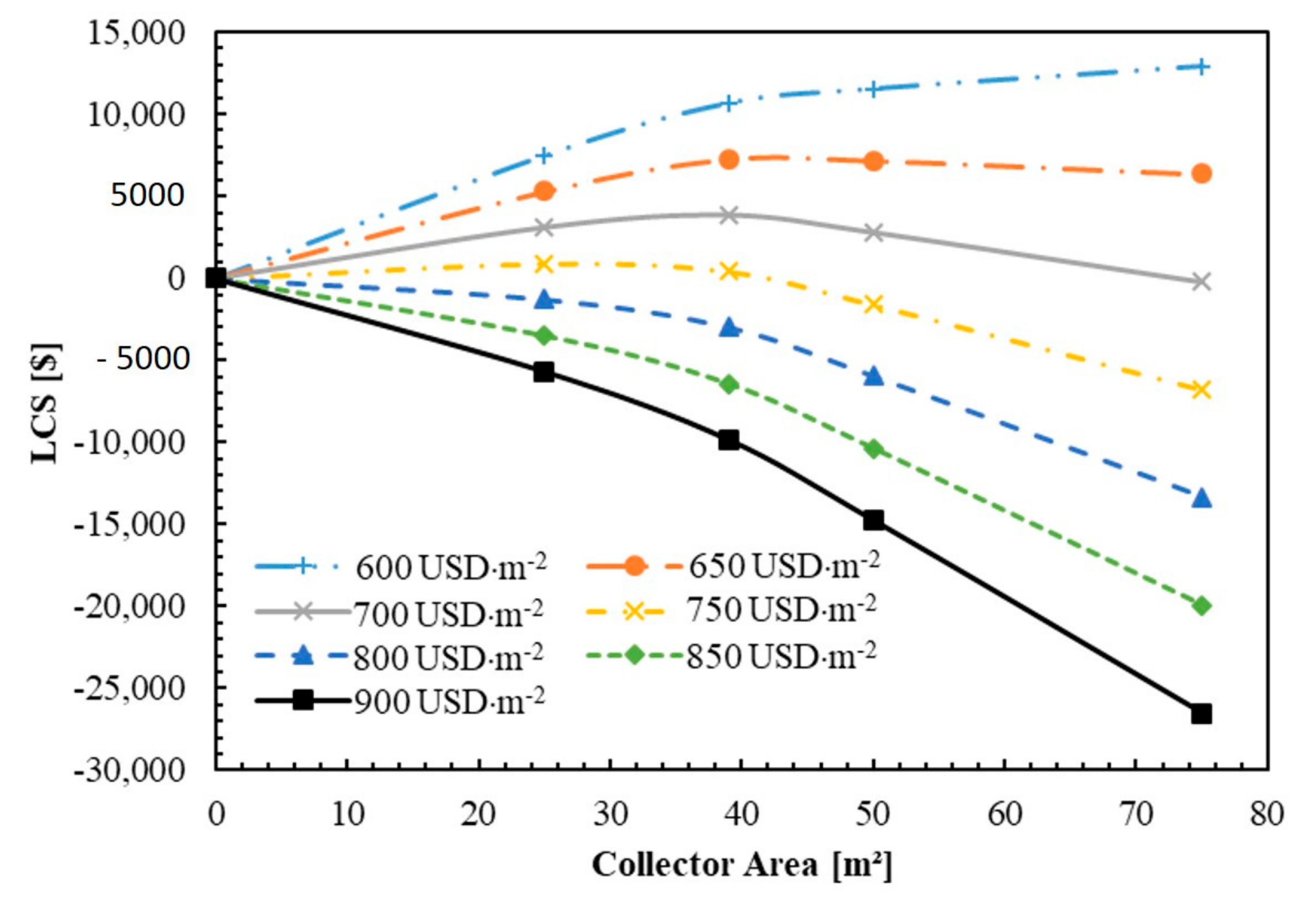
4.4. Feasibility Studies
5. Conclusions
- The order of the Fourier series function did not have a strong impact on the simulation of the global radiation profile for performance evaluation of the solar cooling system
- The solar thermally driven adsorption chiller system showed a relatively good performance for the period between 10:00 and 17:00. During the period 10:00 and 17:00, the system cycle COP ranges between 0.4 and 0.55, and the solar COP ranges between 0.25 and 0.32. This indicated that solar adsorption cooling could provide effective cooling for residential or commercial buildings
- Both life-cycle savings and payback period economic methods showed that the solar cooling system had an optimal solar collector area of 38 m2 in this study. For this collector area, the life-cycle savings were around $3500 and the payback period was about 11 years for a residential building application. This demonstrated that solar-adsorption cooling has promising potential
- The solar cooling system was found to be feasible for a collector unit cost lower than $700 per m2 and an interest rate of less than 16%
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | area, m2 | PV | photovoltaic |
| ACF | activated carbon fibre | q | adsorption capacity, kg kg−1 |
| Acr | each collector area, m2 | Qst | heat of adsorption, J·kg−1 |
| C | specific heat, J·kg−1·K−1; cost of installing solar cooling equipment (USD) | R | gas constant, J·kg−1·K−1 |
| CA | solar energy investment cost which is directly proportional to the collector area | Rp | silica gel particle diameter, m |
| CACC | cyclic average cooling capacity | SAR | solar-driven adsorption refrigeration |
| CC | cooling capacity | SCP | specific cooling capacity |
| CE | solar energy investment cost which is independent of collector area | T | temperature, K |
| CF | the unit cost of delivered conventional energy for the first year of analysis | t | time, s |
| COP | coefficient of performance | U | overall heat transfer coefficient, W·m−2·K−1 |
| CPC | compound parabolic concentrator | δ | flag functions |
| CTAR | constant temperature adsorption refrigeration | Subscripts | |
| Dso | diffusion coefficient, m2·s−1 | am | ambient |
| E | energy saving per year in USD | aux | auxiliary |
| Ea | activation energy, J·kg−1 | bed | adsorbent bed |
| ETC | evacuated tube solar collecting | chill | chilled water |
| FPC | flat plate solar collector | cool | cool water |
| Ft | total solar fraction of the solar system | con | condenser |
| I | solar radiation, W·m−2 | eva | evaporator |
| i | the change in energy prices relative to general inflation in the country, or energy inflation | l | liquid phase |
| L | latent heat of vaporization, J·kg−1; total load | M | metal |
| LCS | Life-Cycle Saving ($) | cr | collector |
| LMTD | log mean temperature difference, °C | hot | hot water |
| M | mass, kg | in | inlet |
| mass flow rate, kg·s−1 | s | silica gel or saturation | |
| n | number of collectors | r | water |
| NPV | net present value | out | outlet |
| OA | optimal solar collector area (m2) | r | refrigerant |
| P1 | the factor relating life cycle fuel cost to first-year fuel cost savings | ret | return |
| P2 | the factor relating life cycle by additional capital investment to initial investment | SC | solar |
| PbP | Payback Period (years) | v | vapour phase |
References
- Desideri, U.; Proietti, S.; Sdringola, P. Solar-powered cooling systems: Technical and economic analysis on industrial refrigeration and air-conditioning applications. Appl. Energy 2009, 86, 1376–1386. [Google Scholar] [CrossRef]
- Hassan, H.Z.; Mohamad, A.A.; Alyousef, Y.; Al-Ansary, H.A. A review on the equations of state for the working pairs used in adsorption cooling systems. Renew. Sustain. Energy Rev. 2015, 45, 600–609. [Google Scholar] [CrossRef]
- Al-Rbaihat, R.; Sakhrieh, A.; Al-Asfar, J.; Alahmer, A.; Ayadi, O.; Al-Salaymeh, A.; Al_hamamre, Z.; Al-bawwab, A.; Hamdan, M. Performance Assessment and Theoretical Simulation of Adsorption Refrigeration System Driven by Flat Plate Solar Collector. Jordan J. Mech. Ind. Eng. 2017, 11, 1–11. [Google Scholar]
- El Fadar, A.; Mimet, A.; Pérez-García, M. Modelling and performance study of a continuous adsorption refrigeration system driven by parabolic trough solar collector. Sol. Energy 2009, 83, 850–861. [Google Scholar] [CrossRef]
- Sah, R.P.; Choudhury, B.; Das, R.K. A review on adsorption cooling systems with silica gel and carbon as adsorbents. Renew. Sustain. Energy Rev. 2015, 45, 123–134. [Google Scholar] [CrossRef]
- Ajib, S.; Alahmer, A. Solar Cooling Technologies. In Energy Conversion-Current Technologies and Future Trends; InTechOpen: London, UK, 2018. [Google Scholar]
- Wang, X.; Chua, H.T.; Ng, K.C. Experimental investigation of silica gel–water adsorption chillers with and without a passive heat recovery scheme. Int. J. Refrig. 2005, 28, 756–765. [Google Scholar] [CrossRef]
- Wang, X.; He, Z.; Chua, H.T. Performance simulation of multi-bed silica gel-water adsorption chillers. Int. J. Refrig. 2015, 52, 32–41. [Google Scholar] [CrossRef]
- Alahmer, A.; Ajib, S.; Wang, X. Comprehensive strategies for performance improvement of adsorption air conditioning systems: A review. Renew. Sustain. Energy Rev. 2019, 99, 138–158. [Google Scholar] [CrossRef]
- Wang, X.; Chua, H.T. Two bed silica gel–water adsorption chillers: An effectual lumped parameter model. Int. J. Refrig. 2007, 30, 1417–1426. [Google Scholar] [CrossRef]
- Wang, X.; Chua, H.T. A comparative evaluation of two different heat recovery schemes as applied to a two-bed adsorption chiller. Int. J. Heat Mass Transf. 2007, 50, 433–443. [Google Scholar] [CrossRef]
- Rezk, A.R.; Al-Dadah, R.K. Physical and operating conditions effects on silica gel-water adsorption chiller performance. Appl. Energy 2012, 89, 142–149. [Google Scholar] [CrossRef]
- Deshmukh, H.; Maiya, M.P.; Murthy, S.S. Continuous vapour adsorption cooling system with three adsorber beds. Appl. Therm. Eng. 2015, 82, 380–389. [Google Scholar] [CrossRef]
- Alsaqoor, S.; Alahmer, A.; Chorowski, M.; Pyrka, P.; Rogala, Z. Performance evaluation for a low-temperature heat powered for 3-beds with dual evaporators silica gel water adsorption chillers. In Proceedings of the 8th International Renewable Energy Congress (IREC), Amman, Jordan, 21–23 March 2017; pp. 1–6. [Google Scholar]
- Chang, W.S.; Wang, C.C.; Shieh, C.C. Design and performance of a solar-powered heating and cooling system using silica gel-water adsorption chiller. Appl. Therm. Eng. 2009, 29, 2100–2105. [Google Scholar] [CrossRef]
- Hassan, H.Z.; Mohamad, A.A.; Al-Ansary, H.A.; Alyousef, Y.M. Dynamic analysis of the CTAR (constant temperature adsorption refrigeration) cycle. Energy 2014, 77, 852–858. [Google Scholar] [CrossRef]
- Hassan, H.Z.; Mohamad, A.A. Thermodynamic analysis and theoretical study of a continuous operation solar-powered adsorption refrigeration system. Energy 2013, 61, 167–178. [Google Scholar] [CrossRef]
- Habib, K.; Saha, B.B.; Koyama, S. Study of various adsorbent–refrigerant pairs for the application of solar driven adsorption cooling in tropical climates. Appl. Therm. Eng. 2014, 72, 266–274. [Google Scholar] [CrossRef]
- Habib, K.; Choudhury, B.; Chatterjee, P.K.; Saha, B.B. Study on a solar heat driven dual-mode adsorption chiller. Energy 2013, 63, 133–141. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Wang, R.Z.; Wu, J.Y.; Dai, Y.J.; Ma, Q. Design and performance of a solar-powered air-conditioning system in a green building. Appl. Energy 2008, 85, 297–311. [Google Scholar] [CrossRef]
- Sumathy, K.; Yong, L.; Muller Steinhagen, H.; Kerskes, H. Performance analysis of a modified two-bed solar-adsorption air-conditioning system. Int. J. Energy Res. 2009, 33, 675–686. [Google Scholar] [CrossRef]
- Tsoutsos, T.; Anagnostou, J.; Pritchard, C.; Karagiorgas, M.; Agoris, D. Solar cooling technologies in Greece. An economic viability analysis. Appl. Therm. Eng. 2003, 23, 1427–1439. [Google Scholar] [CrossRef]
- Al-Ugla, A.A.; El-Shaarawi, M.A.; Said, S.A.; Al-Qutub, A.M. Techno-economic analysis of solar-assisted air-conditioning systems for commercial buildings in Saudi Arabia. Renew. Sustain. Energy Rev. 2016, 54, 1301–1310. [Google Scholar] [CrossRef]
- Alahmer, A.; Wang, X.; Al-Rbaihat, R.; Alam, K.A.; Saha, B.B. Performance evaluation of a solar adsorption chiller under different climatic conditions. Appl. Energy 2016, 175, 293–304. [Google Scholar] [CrossRef]
- Carr, A.J.; Pryor, T.L. A comparison of the performance of different PV module types in temperate climates. Sol. Energy 2004, 76, 285–294. [Google Scholar] [CrossRef]
- Alam, K.A.; Saha, B.B.; Akisawa, A. Adsorption cooling driven by solar collector: A case study for Tokyo solar data. Appl. Therm. Eng. 2013, 50, 1603–1609. [Google Scholar] [CrossRef]
- Jaiswal, A.K.; Mitra, S.; Dutta, P.; Srinivasan, K.; Murthy, S.S. Influence of cycle time and collector area on solar driven adsorption chillers. Sol. Energy 2016, 136, 450–459. [Google Scholar] [CrossRef]
- Clausse, M.; Alam, K.C.; Meunier, F. Residential air conditioning and heating by means of enhanced solar collectors coupled to an adsorption system. Sol. Energy 2008, 82, 885–892. [Google Scholar] [CrossRef]
- Sayfikar, M.; Behbahani-nia, A. Study of the performance of a solar adsorption cooling System. Energy Equip. Syst. 2013, 1, 75–90. [Google Scholar]
- Ghoneim, A.A.; Abdullah, A.H. Feasibility Study of Solar Heating and Cooling Systems in Kuwait. Destin. Renew. ANZSES 2003, 239–248. [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Process, 4th ed.; Wiley Interscience: New York, NY, USA, 2013. [Google Scholar]
- Wang, X.; Bierwirth, A.; Christ, A.; Whittaker, P.; Regenauer-Lieb, K.; Chua, H.T. Application of geothermal absorption air-conditioning system: A case study. Appl. Therm. Eng. 2013, 50, 71–80. [Google Scholar] [CrossRef]
- Lu, Z.S.; Wang, R.Z. Experimental performance investigation of small solar air-conditioning systems with different kinds of collectors and chillers. Sol. Energy 2014, 110, 7–14. [Google Scholar] [CrossRef]
- Al-Alili, A.; Hwang, Y.; Radermacher, R.; Kubo, I. Optimization of a solar powered absorption cycle under Abu Dhabi’s weather conditions. Sol. Energy 2010, 84, 2034–2040. [Google Scholar] [CrossRef]
- Gebreslassie, B.H.; Guillén-Gosálbez, G.; Jiménez, L.; Boer, D. Design of environmentally conscious absorption cooling systems via multi-objective optimization and life cycle assessment. Appl. Energy 2009, 86, 1712–1722. [Google Scholar] [CrossRef]
- Chang, W.S.; Wang, C.C.; Shieh, C.C. Experimental study of a solid adsorption cooling system using flat-tube heat exchangers as adsorption bed. Appl. Therm. Eng. 2007, 27, 2195–2199. [Google Scholar] [CrossRef]

| Symbol | Parameter | Nominal Value |
|---|---|---|
| Abed | Sorbent bed heat transfer area | 2.415 m2 |
| Ubed | Heat transfer coefficient of the bed | 1724.14 W·m−2·K−1 |
| Aeva | Heat transfer area of the evaporator | 1.91 m2 |
| Ueva | Heat transfer coefficient of the evaporator | 2557.54 W·m−2·K−1 |
| Meva,M | Heat exchanger tube weight inside the evaporator | 12.45 kg |
| Acon | Heat transfer area of the condenser | 3.73 m2 |
| Ucon | Heat transfer coefficient of the condenser | 4115.23 W·m−2·K−1 |
| Wcon,M | Heat exchanger tube weight inside the condenser | 24.28 kg |
| Acr | One collector area | 2.415 m2 |
| Mcp | Weight of each pipe including absorber sheet | 0.4913 kg |
| Np | Number of pipes in each collector | 9 |
| ṁf, hot | Total mass flow rate to the CPC panel or the desorber | 1.3 kg·s−1 |
| ṁf, cool | Cooling water mass flow rate to the adsorber | 1.3 kg·s−1 |
| Ms | Silica gel weight in each bed | 47 kg |
| Meva;r | Liquid refrigerant mass in the evaporator initially | 50 kg |
| ṁf;cond | Cold water mass flow rate to the condenser | 1.3 kg·s−1 |
| ṁf;chill | Chilled water mass flow rate | 0.7 kg·s−1 |
| Wcon,r | Condensed refrigerant inside the condenser | 1.0 kg |
| Cr,l | Specific heat of the water in the liquid phase | 4.18 × 103 J·kg−1·K−1 |
| Cr,v | Specific heat of the water in the vapor phase | 1.89 × 103 J·kg−1·K−1 |
| Cs | Specific heat of the silica gel | 924 J·kg−1·K−1 |
| L | Latent heat of water | 2.6 × 106 J·kg−1 |
| Qst | Adsorption or isosteric heat | 2.81 × 106 J·kg−1 |
| R | Gas constant of the water | 462 J·kg−1·K−1 |
| Ea | Activation energy | 2.33 × 106 J·kg−1 |
| DS0 | Diffusion coefficient | 2.54 × 10−4 m2·s−1 |
| Rp | Diameter of the silica gel particle | 0.35 × 10−3 m |
| Tcool | Cooling source temperature | 30 °C |
| Tchill,in | Chilled water inlet temperature | 14 °C |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alahmer, A.; Wang, X.; Alam, K.C.A. Dynamic and Economic Investigation of a Solar Thermal-Driven Two-Bed Adsorption Chiller under Perth Climatic Conditions. Energies 2020, 13, 1005. https://doi.org/10.3390/en13041005
Alahmer A, Wang X, Alam KCA. Dynamic and Economic Investigation of a Solar Thermal-Driven Two-Bed Adsorption Chiller under Perth Climatic Conditions. Energies. 2020; 13(4):1005. https://doi.org/10.3390/en13041005
Chicago/Turabian StyleAlahmer, Ali, Xiaolin Wang, and K. C. Amanul Alam. 2020. "Dynamic and Economic Investigation of a Solar Thermal-Driven Two-Bed Adsorption Chiller under Perth Climatic Conditions" Energies 13, no. 4: 1005. https://doi.org/10.3390/en13041005
APA StyleAlahmer, A., Wang, X., & Alam, K. C. A. (2020). Dynamic and Economic Investigation of a Solar Thermal-Driven Two-Bed Adsorption Chiller under Perth Climatic Conditions. Energies, 13(4), 1005. https://doi.org/10.3390/en13041005






