1. Introduction
The efficiency of Combined Cycle Power Plants (CCPPs) is a key issue in the penetration of this technology in the electricity mix. A recent report [
1] has estimated that, in the next decade, the number of projects involving combined cycle technology will increase by a
, and this estimation is mainly based on the high efficiency of CCPPs. The electrical power production prediction in CCPPs encompasses numerous factors that should be considered to achieve an accurate estimation. The operators of a power grid often predict the power demand based on historical data and environmental factors, such as temperature, pressure, and humidity. Then, they compare these predictions with available resources, such as coal, natural gas, nuclear, solar, wind, or hydro power plants. Power generation technologies (e.g., solar and wind) are highly dependent on environmental conditions, and all generation technologies are subject to planned and unplanned maintenance. Thus, the challenge for a power grid operator is how to handle a shortfall in available resources versus actual demand. The power production of a peaker power plant varies depending on environmental conditions, so the business problem is to predict the power production of the peaker as a function of meteorological conditions—since this would enable the grid operator to make economic trade-offs about the number of peaker plants to turn on (or whether to buy usually expensive power from another grid).
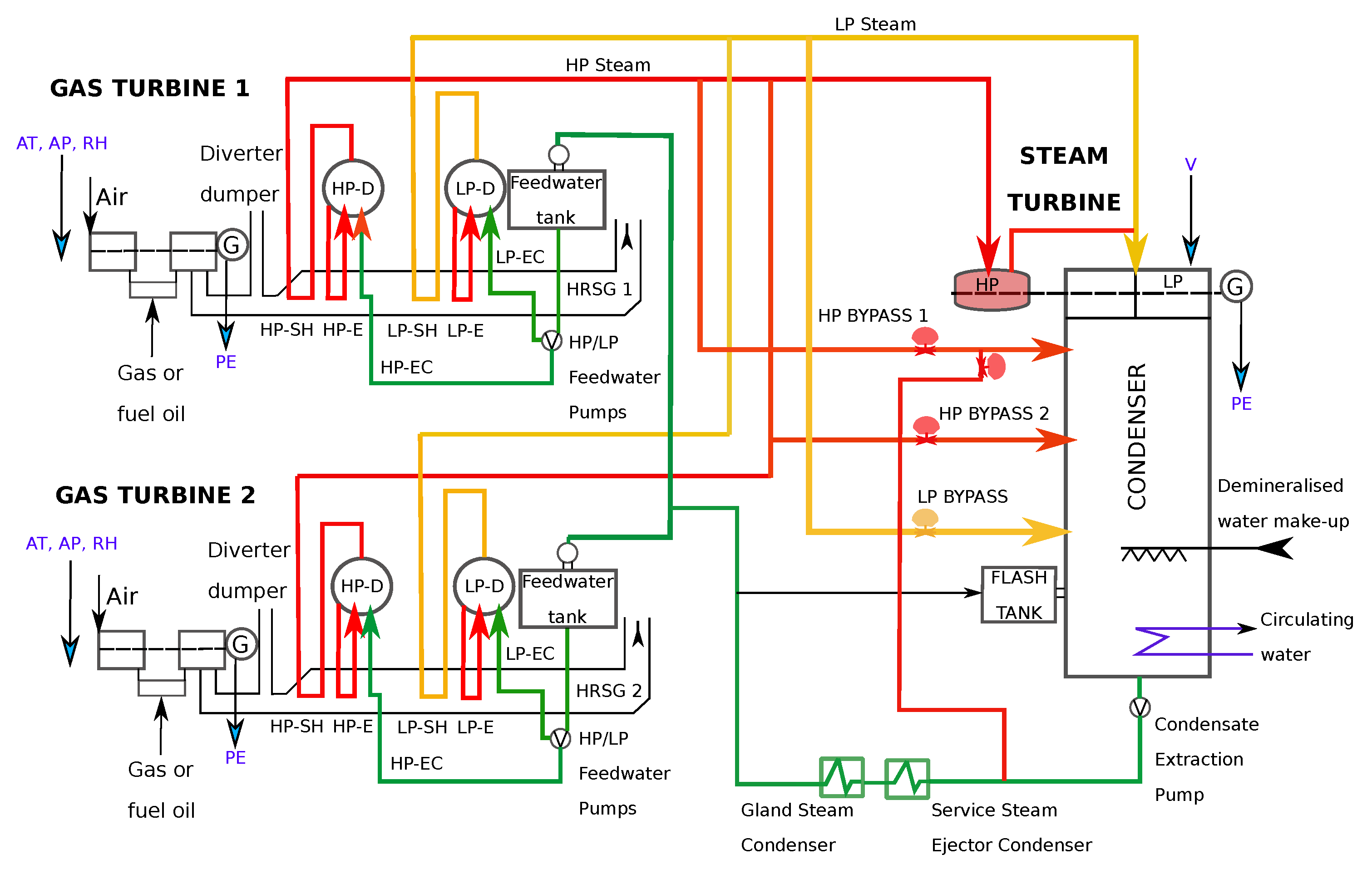
The referred CCPP in this work uses two gas turbines (GT) and one steam turbine (ST) together to produce up to
more electricity from the same fuel than a traditional simple-cycle plant. The waste heat from the GTs is routed to the nearby two STs, which generate extra power. In this real environment, a thermodynamical analysis compels thousands of nonlinear equations whose solution is near unfeasible, taking too many computational memory and time costs. This barrier is overcome by using a Machine Learning based approach, which is a frequent alternative instead of thermodynamical approaches [
2]. The correct prediction of its electrical power production is very relevant for the efficiency and economic operation of the plant, and maximizes the income from the available megawatt hours. The sustainability and reliability of the GTs depend highly on this electrical power production prediction, mainly when it is subjected to constraints of high profitability and contractual liabilities.
This work applies stream regression (SR) algorithms for a prediction analysis of a thermodynamic system, which is the mentioned CCPP. Our work uses some of the most known SR learning algorithms to successfully predict (in an online manner, as opposed to [
3] where a traditional non-streaming view is considered) the electrical power production by using a combination of input parameters defined by for GTs and STs (ambient temperature, vacuum, atmospheric pressure, and relative humidity). This work shows how the application of real-time analytics or Stream Learning (SL) fits the purposes of a modern industry in which data flow constantly, analyzing the impact of several streaming factors (which should be considered before the streaming process starts) on the production prediction. It also compares the results represented by several error metrics and time processing of several SRs under different experiments, finding the most recommendable ones in the electrical power production prediction, aside from carrying out a statistical significance study. Therefore, the contributions of this work can be summarized as follows:
We present a work closer to reality, where fast data can be huge, they are in motion, and closely connected, and where there are limited resources (e.g., time, memory) to process them, such as in an IoT application.
We follow and present a complete procedure about how to tackle SL challenges in energy IoT systems.
We offer a comparison of stream learners, due to the fact that under these real-time machine learning conditions we need regression methods that learn incrementally
Finally, we identify the best technique to be applied in the presented scenario, a real-time electrical power production prediction in a CCPP.
The rest of this work is organized as follows:
Section 2 provides a background about the topics of the manuscript. Specifically, it introduces the field of SL and presents the field of power production prediction. In
Section 3 materials and methods are presented, whereas
Section 4 describes the experimental work.
Section 5 presents the results of such experiments.
Section 6 provides a discussion of the work, and then
Section 7 finalizes by presenting the final conclusions of the work.
2. Related Work
There are different works in the literature undertaken related problems by using Machine Learning approaches. In [
3,
4] the authors successfully applied several regression methods to predict the full load electrical power production of a CCPP. A different approach for the same goal was investigated in [
5], where the authors presented a novel approach using a Particle Swarm Optimization algorithm [
6] for training feed-forward neural network to predict the power plant production. In line with this last study, the work in [
7] developed a new artificial neural network optimized by particle swarm optimization for dew point pressure prediction. In [
8] the authors applied forecasting methodologies, including linear and nonlinear regression, to predict GT behavior over time, which allows planning maintenance actions and saving costs, and also because unexpected stops can be avoided. This work [
9] presents a comparison of two strategies for GT performance prediction, using statistical regression as technique to analyze dynamic plant signals. The prognostic approach to estimate the remaining useful life of GT engines before their next major overhaul was overcome in [
10], where a combination of regression techniques was proposed to predict the remaining useful life of GT engines. In [
11] it was showed that regression models were good estimators of the response variables to carry out parametric based thermo-environmental and exergoeconomic analyses of CCPPs. The same authors were involved in [
12] when using multiple polynomial regression models to correlate the response variables and predictor variables in a CCPP to carry out a thermo-environmental analysis. More recently, in [
13] it is presented a real-time derivative-driven regression method for estimating the performance of GTs under dynamic conditions. A scheme for performance-based prognostics of industrial GTs operating under dynamic conditions is proposed and developed in [
14], where a regression method is implemented to locally represent the diagnostic information for subsequently forecasting the performance behavior of the engine.
Regarding the SL topic, many researches have focused on it due to its mentioned relevance, such as [
15,
16,
17,
18,
19], and more recently in [
20,
21,
22,
23]. The application of regression techniques to SL has been recently addressed in [
24], where the authors cover the most important online regression methods. The work [
25] deals with ensemble learning from data streams, and specifically it focused on regression ensembles. The authors of [
26] propose several criteria for efficient sample selection in case of SL regression problems within an online active learning context. In general, we can say that regression tasks in SL have not received as much attention as classification tasks, and this was spotlighted in [
27], where researchers carried out an study and an empirical evaluation of a set of online algorithms for regression, which includes the baseline Hoeffding-based regression trees, online option trees, and an online least mean squares filter.
2.1. Stream Learning in the Big Data Era
The Big Data paradigm has gained momentum last decade, because of its promise to deliver valuable insights to many real-world applications [
28]. With the advent of this emerging paradigm comes not only an increase in the volume of available data, but also the notion of its arrival velocity, that is, these real-world applications generate data in real-time at rates faster than those that can be handled by traditional systems. One particular case of the Big Data paradigm is real-time analytics or SL, where sequences of items (data streams), possibly infinite, arrive continuously, and where each item has a timestamp and so a temporal order. Data streams arrive one by one, and we would like to build and maintain models (e.g., predictors) of these items in real-time.
This situation leads us to assume that we have to deal with a potentially infinite and ever-growing datasets that may arrive continuously in batches of instances, or instance by instance, in contrast to traditional systems (batch learning) where there is free access to all historical data. These traditional processing systems assume that data are at rest and simultaneously accessed. For instance, database systems can store large collections of data and allow users to run queries or transactions. The models based on batch processing do not continuously integrate new information into already constructed models but, instead, regularly reconstruct new models from the scratch. However, the incremental learning that is carried out by SL presents advantages for this particular stream processing by continuously incorporating information into its models, and traditionally aim at minimal processing time and space. Because of its ability of continuous large-scale and real-time processing, incremental learning has recently gained more attention in the context of Big Data [
29]. SL also presents many new challenges and poses stringent conditions [
30]: only a single sample (or a small batch of instances) is provided to the learning algorithm at every time instant, a very limited processing time, a finite amount of memory, and the necessity of having trained models at every scan of the streams of data. In addition, these streams of data may evolve over time and may be occasionally affected by a change in their data distribution (
concept drift) [
31], forcing the system to learn under non-stationary conditions.
We can find many examples of real-world SL applications [
32], such as mobile phones, industrial process controls, intelligent user interfaces, intrusion detection, spam detection, fraud detection, loan recommendation, monitoring and traffic management, among others [
33]. In this context, the Internet of Things (IoT) has become one of the main applications of SL [
34], since it is producing huge quantity of data continuously in real-time. The IoT is defined as sensors and actuators connected by networks to computing systems [
35], which monitors and manages the health and actions of connected objects or machines in real-time. Therefore, stream data analysis is becoming a standard to extract useful knowledge from what is happening at each moment, allowing people or organizations to react quickly when inconveniences emerge or when new trends appear, helping them increase their performance.
A Fog Computing Perspective
Nowadays, cloud computing is already more than a promising paradigm in IoT Big Data analytics. Instead of being only on the cloud, the idea of bringing computing and analytics closer to the end-users/devices was proposed under the name of Fog Computing [
36]. Relying on fog-based analytics, we can benefit from the advantages of cloud computing while reducing or avoiding some of its drawbacks, such as network latency or security risks. It has been confirmed [
37] that, by hosting data analytics on fog computing nodes, the overall performance can be improved due to the avoidance of transmitting large amounts of raw data to distant cloud nodes. It is also possible to perform real-time analytics to some extent since the fog is hosted locally close to the source of data. Smart application gateways are the core elements in this new fog technology, performing some of the tasks currently done by cloud computing such as data aggregation, classification, integration, and interpretation, thus facilitating the use of IoT local computing resources [
38].
2.2. CCPPs and Stream Learning Regression
We have presented in the introduction of this Section how some problems in a CCPP have been tackled by using Machine Learning approaches, concretely applying regression techniques, and mostly from a batch learning perspective. Since the emergence of the SL field, many modern industrial processes based on these approaches are migrating from the traditional batch learning perspective to this real-time Machine Learning paradigm. And it is not surprising due to its benefits in many real cases, where the number of sensors producing data is huge, and the training of the Machine Learning models become unmanageable. Some processes need to be interrupted until Machine learning models are updated or retrained, which may lead to some operational drawbacks such as a loss of efficiency or an increase in costs. However, by applying a SL perspective, it is not required to store all historical data, and the Machine learning models can be trained incrementally every time new data instances arrive without interrupting any industrial process. The power production prediction process based on Machine learning models is not exempt from this inconveniences, and finds in the SL paradigm the suitable solution in a IoT environment.
Therefore the task of power production prediction can be seen as a process based on data streams, as we will show in this work. Even though the work [
3] is perfectly adequate under specific conditions which allow a batch processing, and where the author assumed the possibility of storing all the historical data to process it and predict the electrical power generation with a Machine Learning regression algorithms, we tackle the same problem from a contemporary streaming perspective. In this work we have considered a CCPP as a practical case of IoT application, where different sensors provide the required data to efficiently predict in real-time the full load electrical power generation (see
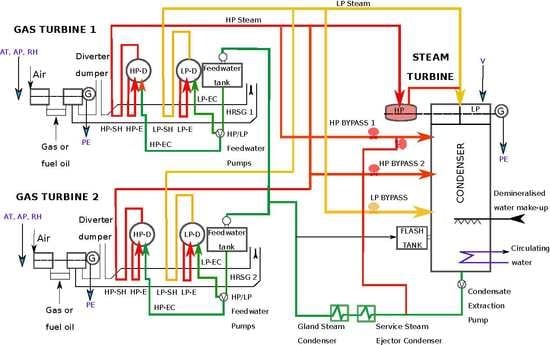
Figure 1). In fact, all the data generated by IoT applications can be considered as streaming data since they are obtained in specific intervals of time. Power generation is a complex process, and understanding and predicting power production is an important element in managing a CCPP, and its connection to the power grid.
Our view is close to real system where fast data can be huge, it is in motion, it is closely connected, and where there are limited resources (e.g., time, memory) to process it. While it does not seem appropriate to retrain the learning algorithms every time new instances are available (what occurs in batch processing), a streaming perspective introduces significant enhancements in terms of data processing (less time and computational costs), algorithms training (they are updated every time new instances come), and presents a modernized vision of a CCPP considering it as an IoT application, and as a part of the Industry
paradigm [
39]. To the best of our knowledge, this is the first time that a SL approach is applied to CCPPs for electrical production prediction. This work could be widely replicated for other streaming prediction purposes in CCPPs, even more, it can serve as a practical example of SL application for modern electrical power industries that need to obtain benefits from the Big Data and IoT paradigms.
3. Materials and Methods
3.1. System Description
The proposed CCPP is composed of two GTs, one ST and two heat recovery steam generators. In a CCPP, the electricity is generated by GTs and STs, which are combined in one cycle, and is transferred from one turbine to another [
40]. The CCPP captures waste heat from the GT to increase efficiency and the electrical production. Basically, how a CCPP works can be described as follows (see
Figure 1):
Gas turbine burns fuel: the GT compresses air and mixes it with fuel that is heated to a very high temperature. The hot air-fuel mixture moves through the GT blades, making them spin. The fast-spinning turbine drives a generator that converts a portion of the spinning energy into electricity
Heat recovery system captures exhaust: a Heat Recovery Steam Generator captures exhaust heat from the GT that would otherwise escape through the exhaust stack. The Heat Recovery Steam Generator creates steam from the GT exhaust heat and delivers it to the ST
Steam turbine delivers additional electricity: the ST sends its energy to the generator drive shaft, where it is converted into additional electricity
This type of CCPP is being installed in an increasing number of plants around the world, where there is access to substantial quantities of natural gas [
41]. As it was reported in [
3], the proposed CCPP is designed with a nominal generating capacity of 480 megawatts, made up of
megawatts ABB
GTs,
dual pressure Heat Recovery Steam Generators and
megawatts ABB ST. GT load is sensitive to the ambient conditions; mainly ambient temperature (AT), atmospheric pressure (AP), and relative humidity (RH). However, ST load is sensitive to the exhaust steam pressure (or vacuum, V). These parameters of both GTs and STs are used as input variables, and the electrical power generating by both GTs and STs is used as a target variable in the dataset of this study. All of them are described in
Table 1 and correspond to average hourly data received from the measurement points by the sensors denoted in
Figure 1.
3.2. The Stream Learning Process
We define a SL process as one that generates on a given stream of training data
a sequence of models
. In our case
stands for labeled training data
and
is a model function solely depending on
and the recent
p instances
with
p being strictly limited (in this work
, representing a real case with a very stringent use case of online learning). The learning process in streaming is incremental [
15], which means that we have to face the following challenges:
The stream algorithm adapts/learns gradually (i.e., is constructed based on without a complete retraining),
Retains the previously acquired knowledge avoiding the effect of catastrophic forgetting [
42], and
Only a limited number of p training instances are allowed to be maintained. In this work we have applied a real SL approach under stringent conditions in which instance storing is not allowed.
Therefore, data-intensive applications often work with transient data: some or all of the input instances are not available from memory. Instances in the stream arrive online (frequently one instance at a time) and can be read at most once, which constitutes the strongest constraint for processing data streams, and the system has to decide whether the current instance should be discarded or archived. Only selected past instances (e.g., a sliding window) can be accessed by storing them in memory, which is typically small relative to the size of the data streams.
A widespread approach for SL is the use of a sliding window to keep only a representative portion of the data, because we are not interested in storing all the historical data, particularly when we must meet the memory space constraint required for algorithms working. This technique is capable of dealing with
concept drift, removing those instances that belong to an old concept. According to [
43], the training window size can be fixed or variable over time, what can be a challenging task. On the one hand, a short window reflects the current distribution more accurately, thus it can assure a fast adaptation when drift occurs, but during stable periods a too short window worsens the performance of the algorithm. On the other hand, a large window shows a better performance in stable periods, however it reacts to drifts slower. Sliding windows of a fixed size store in memory a fixed number of the
w most recent instances. Whenever a new instance arrives, it is stored in memory and the oldest one is discarded. This is a simple adaptive learning method, often referred as forgetting strategy. However, sliding windows of variable size vary the number of instances in a window over time, usually depending on the indications of a change detector. A straightforward approach is to shrink the window whenever a change is detected, such that the training data reflects the most recent concept, and grow the window otherwise. This work is not focused on
concept drift, so we do not use any sliding window (except in the case of
RHAT as we will see in
Section 3.3), but we train and test our algorithms only with the arriving instance by using a
test-then-train evaluation (see
Section 4.2). This is the so-called online learning where only one instance is processed at each time.
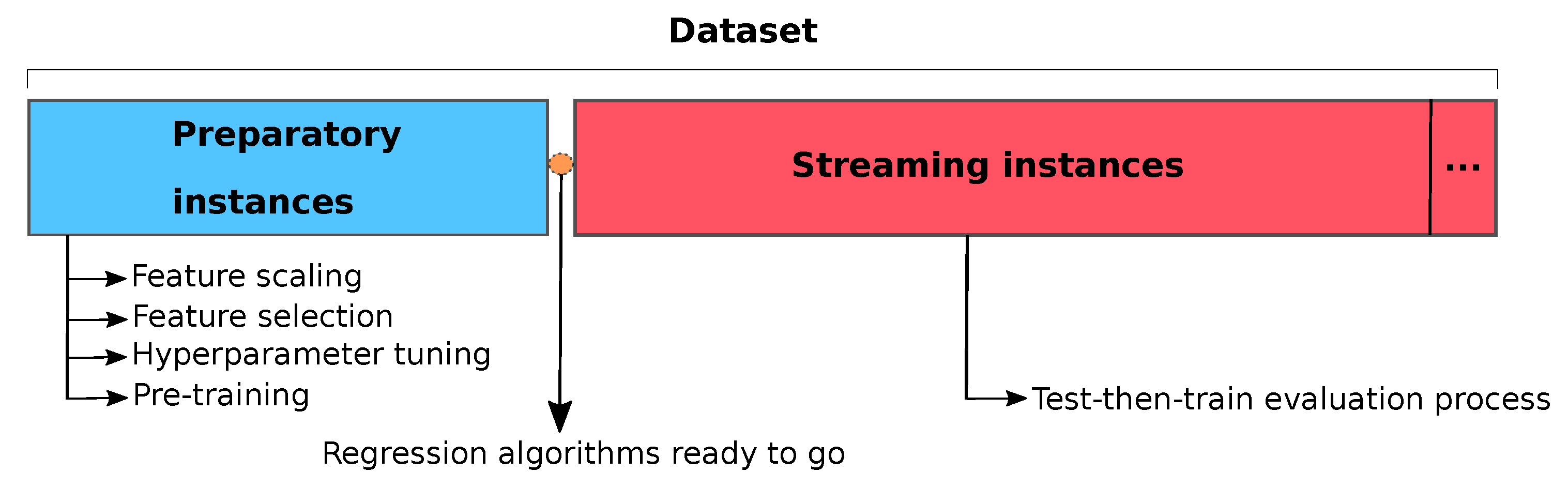
When designing SL algorithms, we have to take several algorithmic and statistical considerations into account. For example, we have to face the fact that, as we cannot store all the inputs, we cannot unwind a decision made on past data. In batch learning processing we have free access to all historical data gathered during the process, and then we can apply “preparatory techniques” such as pre-processing, variable selection or statistical analysis to the dataset, among others (see
Figure 2). Yet the problem with stream processing is that there is no access to the whole past dataset, and we have to opt for one of the following strategies. The first one is to carry out the preparatory techniques every time a new batch of instances or one instance is received, which increments the computational cost and time processing; it may occur that the process flow cannot be stopped to carry out this preparatory process because new instances continue arriving, which can be a challenging task. The second one is to store a first group of instances (preparatory instances) and carry out those preparatory techniques and data stream analysis, applying the conclusions to the incoming instances. This latter case is very common when streaming is applied to a real environment and it has been adopted by this work. We will show later how the selection of the size of this first group of instances (it might depend on the available memory or the time we can take to collect or process these data) can be crucial to achieve a competitive performance in the rest of the stream.
Once these first instances have been collected, in this work we will apply three common preparatory techniques before the streaming process starts in order to prepare our SRs:
Variable selection: it is one of the core concepts in machine learning that hugely impacts on the performance of models; irrelevant or partially relevant features can negatively impact model performance. Variable selection can be carried out automatically or manually, and selects those features which contribute most to the target variable. Its goal is to reduce overfitting, to improve the accuracy, and to reduce time training. In this work we will show how the variable selection impacts on the final results
Hyper-parameter tuning: a hyper-parameter is a parameter whose value is set before the learning process begins, and this technique tries to choose a set of optimal hyper-parameters for a learning algorithm in order to prevent overfitting and to achieve the maximum performance. There are two main different methods for optimizing hyper-parameters: grid search and random search. The first one works by searching exhaustively through a specified subset of hyper-parameters, guaranteeing to find the optimal combination of parameters supplied, but the drawback is that it can be very time consuming and computationally expensive. The second one searches the specified subset of hyper-parameters randomly instead of exhaustively, being its major benefit that decreases processing time, but without guaranteeing to find the optimal combination of hyper-parameters. In this work we have opted for a random search strategy considering a real scenario where computational resources and time are limited
Pre-training: once we have isolated a set of instances to carry out the previous techniques, why do not we also use these instances to train our SRs before the streaming process starts? As we will see in
Section 4.2, where the
test-then-train evaluation is explained, by carrying out a pre-training process our algorithms will obtain a better prediction than if they were tested after being trained by one single instance
3.3. Stream Regression Algorithms
A SL algorithm, like every Machine Learning method, estimates an unknown dependency between the independent input variables, and a dependent target variable, from a dataset. In our work, SRs predict the electrical power generation of a CCPP from a dataset which consists of couples (i.e., an instance), and they build a mapping function by using these couples. Their goal is to select the best function that minimizes the error between the actual production of a system and predicted production based on instances of the dataset (training instances).
The prediction of a real value (regression) is a very frequent problem researched in Machine Learning [
44], thus they are used to control response of a system for predicting a numeric target feature. Many real-world challenges are solved as regression problems, and evaluated using Machine Learning approaches to develop predictive models. Specifically, the following proposed algorithms have been designed to run on real-time, being capable of learning incrementally every time a new instance arrives. They have been selected due to their wide use by the SL community, and because their implementation can be easily found in three well-known Python frameworks, scikit-multiflow [
45], scikit-garden (
https://github.com/scikit-garden/scikit-garden), and scikit-learn [
46].
Passive-Aggressive Regressor (
PAR): the Passive-Aggressive technique focuses on the target variable of linear regression functions,
, where
is the incrementally learned vector. When a prediction is made, the algorithm receives the true target value
and suffers an instantaneous loss (
-insensitive hinge loss function). This loss function was specifically designed to work with stream data and it is analogous to a standard hinge loss. The role of
is to allow a low tolerance of prediction errors. Then, when a round finalizes, the algorithm uses
and the instance
to produce a new weight vector
, which will be used to extend the prediction on the next round. In [
47] the adaptation to learn regression is explained in detail
Stochastic Gradient Descent Regressor (
SGDR): linear model fitted by minimizing a regularized empirical loss with stochastic gradient descent (SGD) [
48] is one of the most popular algorithms to perform optimization for machine learning methods. There are three variants of gradient descent: batch gradient descent (BGD), SGD, and mini-batch gradient descent (mbGD). They differ in how much data we use to compute the gradient of the objective function; depending on the amount of data, we make a trade-off between the accuracy of the parameter update and the time it takes to perform an update. BGD and mbGD perform redundant computations for large datasets, as they recompute gradients for similar instances before each parameter update. SGD does away with this redundancy by performing one update at a time; it is therefore usually much faster and it is often used to learn online [
49]
Multi-Layer Perceptron Regressor (
MLPR): Multi-layer Perceptron (MLP) [
50] learns a non-linear function approximator for either classification or regression. MLPR uses a MLP that trains using backpropagation with no activation function in the output layer, which can also be seen as using the identity function as activation function. It uses the square error as the loss function, and the output is a set of real values
Regression Hoeffding Tree (
RHT): it is a regression tree that is able to perform regression tasks. A Hoeffding Tree (HT) or a Very Fast Decision Tree (VFDT) [
51] is an incremental anytime decision tree induction algorithm that is capable of learning from massive data streams, assuming that the distribution generating instances does not change over time, and exploiting the fact that a small instance can often be enough to choose an optimal splitting attribute. The idea is supported mathematically by the Hoeffding bound, which quantifies the number of instances needed to estimate some statistics within the goodness of an attribute. A RHT can be seen as a Hoeffding Tree with two modifications: instead of using information gain to split, it uses variance reduction; and instead of using majority class and naive bayes at the leaves, it uses target mean, and the perceptron [
52]
Regression Hoeffding Adaptive Tree (
RHAT): in this case,
RHAT is like
RHT but using ADWIN [
53] to detect drifts and perceptron to make predictions. As it has been previously mentioned, streams of data may evolve over time and may show a change in their data distribution, what provokes that learning algorithms become obsolete. By detecting these drifts we are able to suitably update our algorithms to the new data distribution [
16]. ADWIN is a popular two-time sliding window-based drift detection algorithm which does not require users to define the size of the compared windows in advance; it only needs to specify the total size
n of a "sufficiently large’ window
w.
Mondrian Tree Regressor (MTR): the MTR, unlike standard decision tree implementations, does not limit itself to the leaf in making predictions. It takes into account the entire path from the root to the leaf and weighs it according to the distance from the bounding box in that node. This has some interesting properties such as falling back to the prior mean and variance for points far away from the training data. This algorithm has been adapted by the scikit-garden framework to serve as a regressor algorithm
Mondrian Forest Regressor (
MFR): a
MFR [
54] is an ensemble of
MTRs. As in any ensemble of learners, the variance in predictions is reduced by averaging the predictions from all learners (Mondrian trees). Ensemble-based methods are among the most widely used techniques for data streaming, mainly due to their good performance in comparison to strong single learners while being relatively easy to deploy in real-world applications [
18]
Finally, we would like to underline the importance of including RHAT in the experimentation. As we mentioned previously, data streams may evolve generally over time and may be occasionally suffer from concept drift. Then, the data generation process may become affected by a non-stationary event such as eventual changes in the users’ habits, seasonality, periodicity, sensor errors, etc. This causes that predictive models trained over these streaming data become obsolete and do not adapt suitably to the new distribution. Therefore, learning and adaptation to drift in these evolving environments requires modeling approaches capable of monitoring, tracking and adapting to eventual changes in the produced data. Being aware of these circumstances, there is no evidence of the existence of any drift in the considered dataset for the experiments. As we cannot firmly assume the stationarity of the dataset, and as it is recommended in these real cases where the existence of a drift is unknown but probable, we have opted for considering the appearance of drifts by including a stream learning algorithm (RHAT) to deal with such a circumstance.
4. Experiments
We have designed an extensive experimental benchmark in order to find out the most suitable SR method for electrical power prediction in CCPPs, by comparing in terms of error metrics and time processing, 7 widely used SRs. We have also carried out an ANOVA test to know about the statistical significance of the experiments, and a Tukey’s test to measure the differences between SR pair-wises.
The experimental benchmark has been divided into four different experiments (see
Table 2) which have considered two preparatory sizes and two variable selection options, and it is explained in Algorithm 1. The idea is to observe the impact of the number of instances selected for the preparatory phase when the streaming process finalizes, and also to test the relevance of the variable selection process in this streaming scenario. Each experiment has been run 25 times, and the experimental benchmark has followed the scheme depicted in
Figure 2.
The experiments have been carried out under the scikit-multiflow framework [
45], which has been implemented in Python language [
55] due to its current popularity in the Machine Learning community. Inspired by the most popular open source Java framework for data stream mining, Massive Online Analysis (MOA) [
56], scikit-multiflow includes a collection of widely used SRs (
RHT and
RHAT have been selected for this work), among other streaming algorithms (classification, clustering, outlier detection, concept drift detection and recommender systems), datasets, tools, and metrics for SL evaluation. It complements scikit-learn [
46], whose primary focus is batch learning (despite the fact that it also provides researchers with some SL methods:
PAR,
SGDR and
MLPR have been selected for this work) and expands the set of machine learning tools on this platform. The scikit-garden framework in turn complements the experiments by proving the
MTR and
MFR SRs.
Regarding the variable selection process, in contrast to the study carried out in [
3] where different subsets of features were tested manually, we have opted for an automatic process. It is based on the feature importance, which stems from its Pearson correlation [
57] with the target variable: if it is higher than a threshold (
), then it will be considered for the streaming process. As this is a streaming scenario, and thus we do not know the whole dataset beforehand, we have carried out the variable selection process only with the preparatory instances in each of the 25 runs for Exp1 and Exp3 experiments. After that, we have assumed this selection of features for the rest of the streaming process.
Finally, for the hyper-parameter tuning process, we have optimized the parameters by using a randomized and cross-validated search on hyper-parameters provided by scikit-learn (
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html). In contrast to other common option called cross-validated grid-search, not all parameter values are tried out, but rather a fixed number of parameter settings is sampled from the specified distributions. The result in parameter settings is quite similar in both cases, while the run time for randomized search is drastically lower. As in the previous case, we have also carried out the hyper-parameter tuning process only with the preparatory instances in each of the 25 runs for all experiments. After that, we have assumed again the set of tuned parameters for the rest of the streaming process.
4.1. Dataset Description
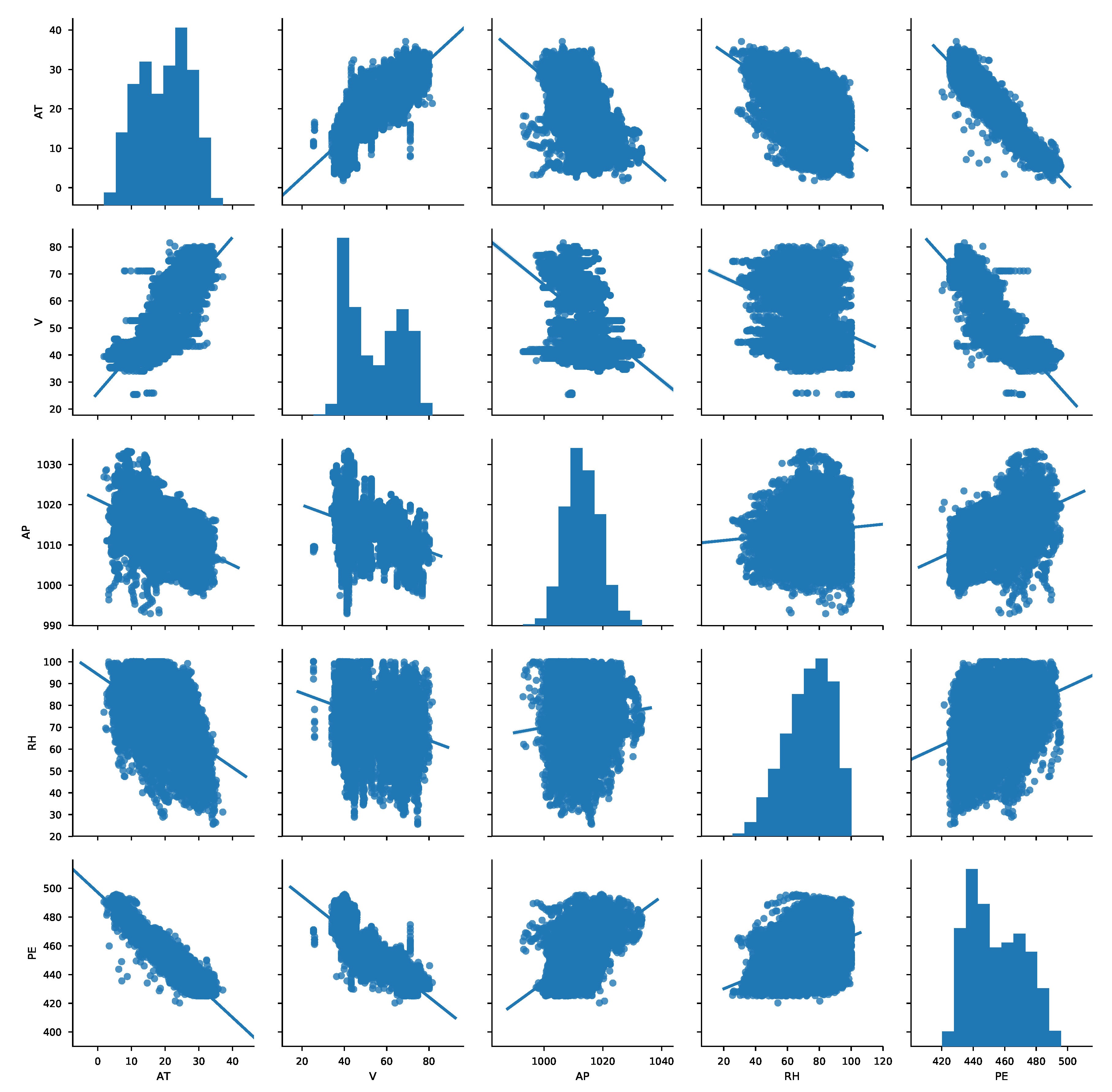
The dataset contains 9568 data points collected from a CCPP over 6 years (2006–2011), when the power plant was set to work with full load over 674 different days. Features described in
Table 1 consist of hourly average ambient temperature, ambient pressure, relative humidity, and exhaust vacuum to predict the net hourly electrical energy production of the plant. Although it is a problem that has already been successfully tackled from a batch processing perspective [
3] due to its manageable number of instances and its data arriving rate, it could be easily transposed to a streaming scenario in which the available data would be huge (instances collected over many years) and in which the data arriving rate would be very constrained (e.g., instances received every second). This more realistic IoT scenario would allow CCPPs to manage a Big Data approach, being able to predict the electrical production every time (e.g., every second) new data is available, and detecting anomalies long before in order to take immediate action.
| Algorithm 1: Experimental benchmark structure. |
![Energies 13 00740 i001 Energies 13 00740 i001]() |
As we can see in
Table 1, our dataset highly varies in magnitudes, units and ranges. Feature scaling can vary our results a lot while using certain algorithms and have a minimal or no effect in others. It is recommendable to scale the features when algorithms compute distances (very often Euclidean distances) or assume normality. In this work we have opted for the min-max scaling method which brings the value between 0 and 1.
4.2. Streaming Evaluation Methodology
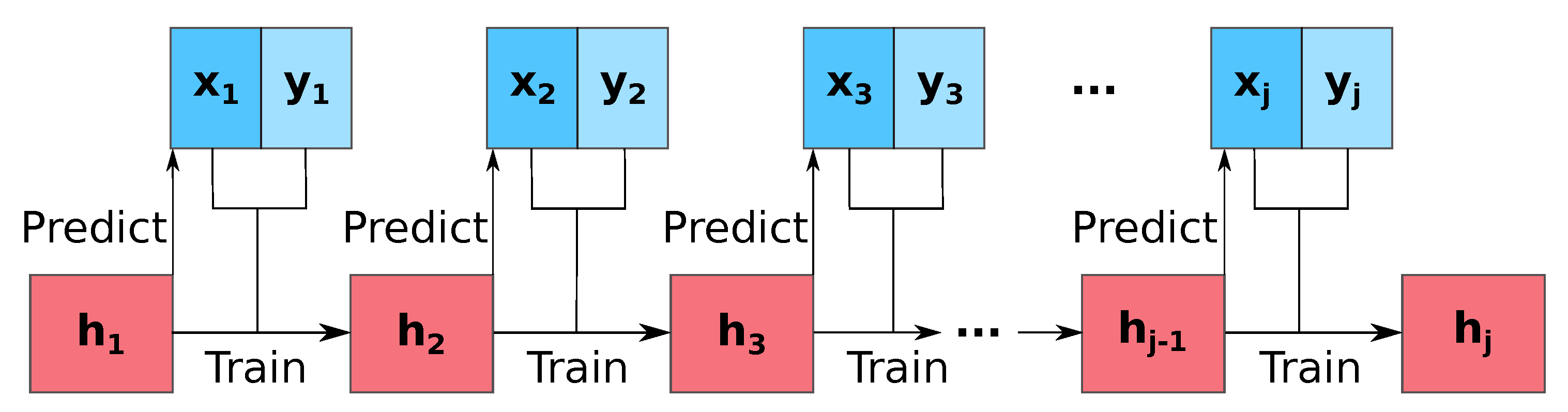
Evaluation is a fundamental task to know when an approach is outperforming another method only by chance, or when there is a statistical significance to that claim. In the case of SL, the methodology is very specific to consider the fact that not all data can be stored in memory (e.g., in online learning only one instance is processed at each time). Data stream regression is usually evaluated in the on-line setting, which is depicted in
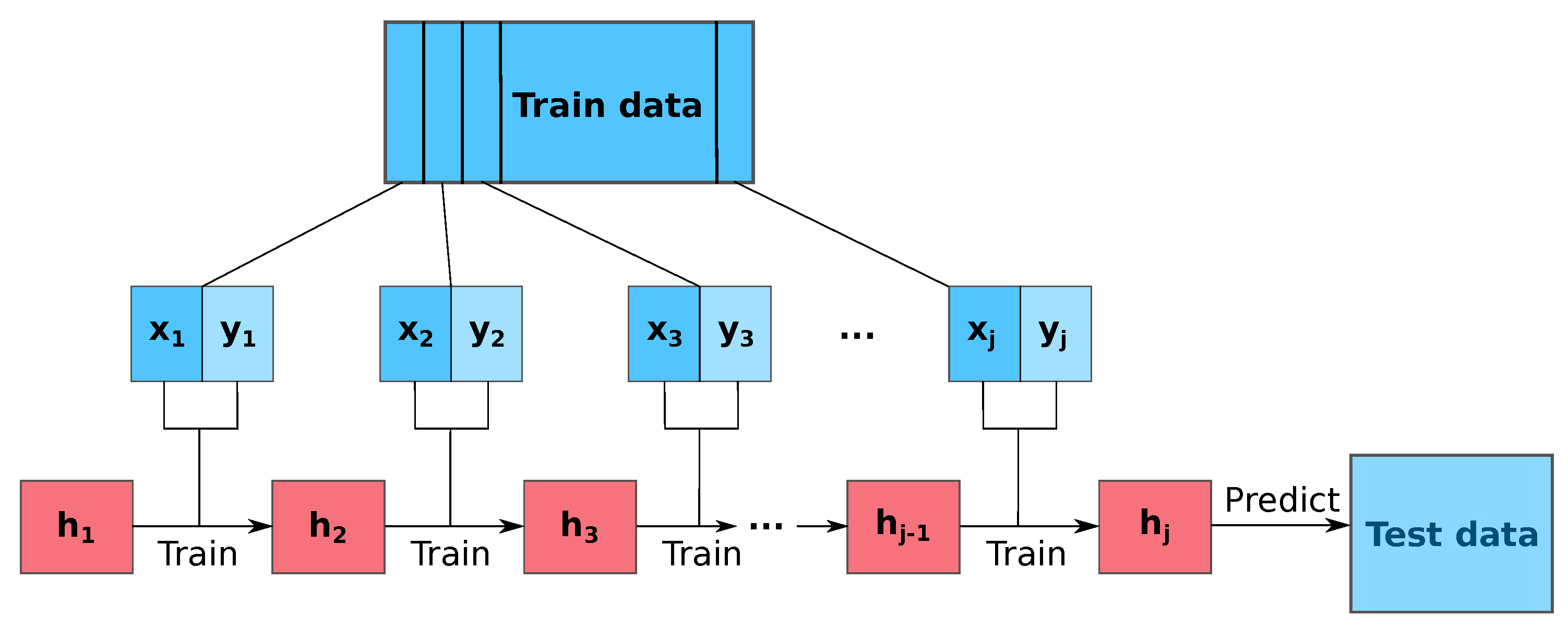
Figure 3, and where data is not split into training and testing set. Instead, each model predicts subsequently one instance, which is afterwards used for the construction of the next model. In contrast, in the traditional evaluation for batch processing (see
Figure 4 and
Figure 5 for non-incremental and incremental types respectively) all data used during training is obtained from the training set.
We have followed this evaluation methodology, proposed in [
43,
56,
58], which recommends to follow these guidelines for streaming evaluation:
4.3. Prediction Metrics
The quality of a regression model is how well its predictions match up against actual values (target values), and we use error metrics to judge the quality of this model. They enable us to compare regressions against other regressions with different parameters. In this work we use several error metrics because each one gives us a complementary insight of the algorithms performance:
Mean Absolute Error (
MAE): it is an easily interpretable error metric that does not indicate whether or not the model under or overshoots actual data.
MAE is the average of the absolute difference between the predicted values and observed value. A small
MAE suggests the model is great at prediction, while a large
MAE suggests that the model may have trouble in certain areas. A
MAE of 0 means that the model is a perfect predictor of the outputs.
MAE is defined as:
Root Mean Square Error (
RMSE): it represents the sample standard deviation of the differences between predicted values and observed values (called residuals).
RMSE is defined as:
Root Mean Square Error (
RMSE): it represents the sample standard deviation of the differences between predicted values and observed values (called residuals).
RMSE is defined as:
MAE is easy to understand and interpret because it directly takes the average of offsets, whereas RMSE penalizes the higher difference more than MAE. However, even after being more complex and biased towards higher deviation, RMSE is still the default metric of many models because loss function defined in terms of RMSE is smoothly differentiable and makes it easier to perform mathematical operations. Researchers will often use RMSE to convert the error metric back into similar units, making interpretation easier
Mean Square Error (
MSE): it is just like
MAE, but squares the difference before summing them all instead of using the absolute value. We can see this difference in the equation below:
Because MSE is squaring the difference, will almost always be bigger than the MAE. Large differences between actual and predicted are punished more in MSE than in MAE. In case of outliers presence, the use of MAE is more recommendable since the outlier residuals will not contribute as much to the total error as MSE
R Squared (
): it is often used for explanatory purposes and explains how well the input variables explain the variability in the target variable. Mathematically, it is given by:
6. Discussion
We start the discussion by highlighting the relevance of having a representative set of preparatory instances in a SL process. As it was introduced in
Section 3.2, in streaming scenarios it is not possible to access all historical data, and then it is required to apply some strategy to make assumptions for the incoming data, unless a drift occurs (in which case it would be necessary an adaptation to the new distribution). One of these strategies consists of storing the first instances of the stream (preparatory instances) to carry out a set of preparatory techniques that make the streaming algorithms ready for the streaming process. We have opted for this strategy in our work, and in this section we will explain the impact of these preparatory process on the final performance of the SRs.
Preparatory techniques contribute to improve the performance of the SRs. Theoretically, by selecting a subset of variables/features (variable selection) that contributes most to the prediction variable, we avoid irrelevant or partially relevant features that can negatively impact on the model performance. By selecting the most suitable parameters of algorithms (hyper-parameter tuning), we obtain SRs better adjusted to data. And by training our SRs before the streaming process starts (pre-training), we obtain algorithms ready for the streaming process with better performances. The drawback lies in the fact that as many instances we collect at the beginning of the process, as much time the preparatory techniques will need to be carried out. This is a trade-off that we should have to consider in each scenario, apart from the limits previously mentioned.
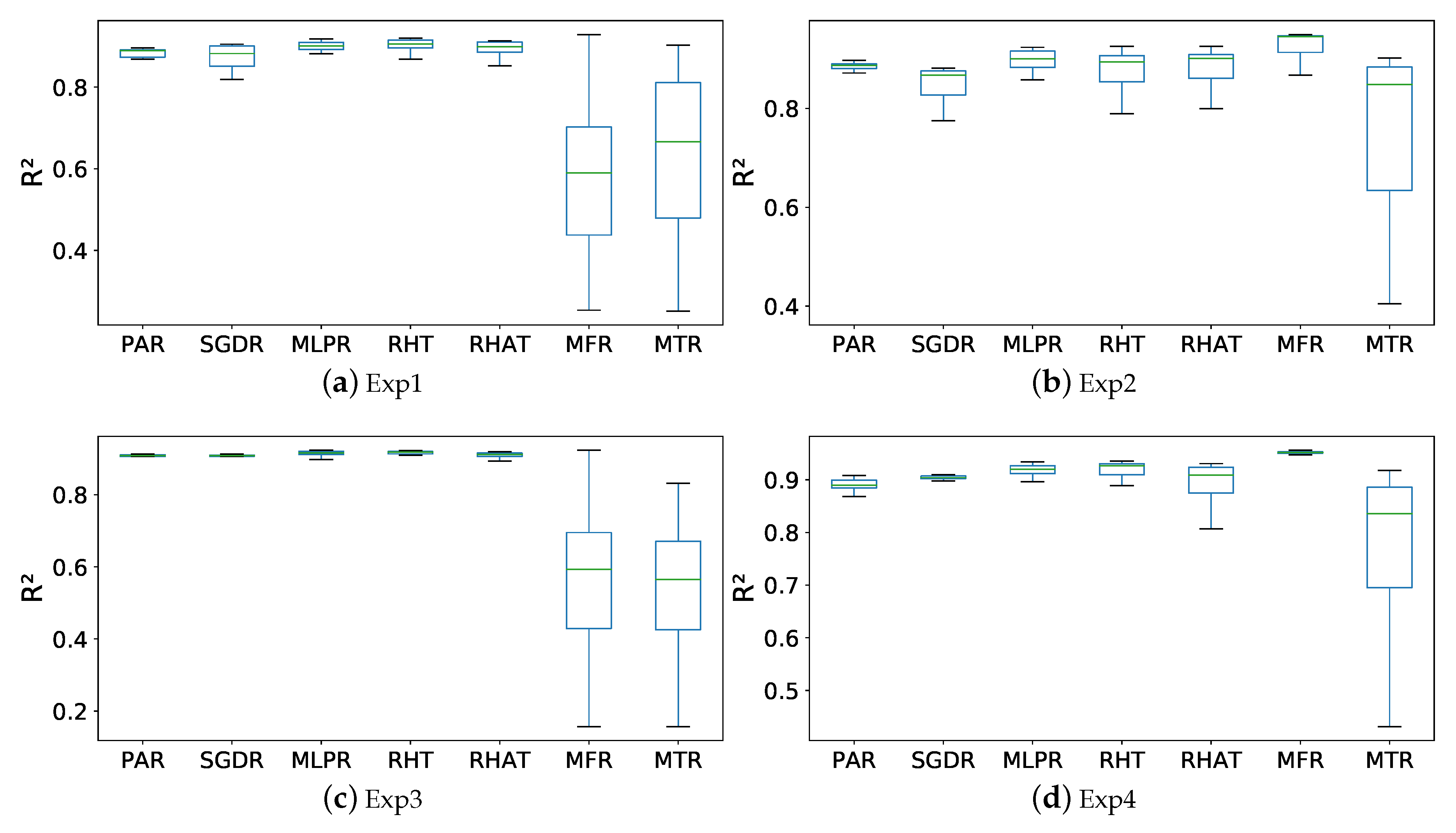
Regarding the number of the preparatory instances, as it often occurs with machine learning techniques, the more instances for training (or other purposes) are available, the better the performance of the SRs can be, because data distribution is better represented with more data and the SRs are more trained and adjusted to the data distribution. But on the other hand, the scenario usually poses limits in terms of memory size, computational capacity, or the moment in which the streaming process has to start, among others. Comparing the experiments 1 and 3 (see
Table 3 and
Table 5 where the selection process was carried out and the preparatory instances were a
and
of the dataset respectively) with the experiments 2 and 4 (see
Table 4 and
Table 6 where the variable selection process was not carried out and the preparatory instances were also a
and
of the dataset respectively), we observe how in almost all cases (except for
MTR and
MFR when variable selection was carried out) the error metrics improve when the number of preparatory instances is larger. Therefore, by setting aside a group of instances for preparatory purposes, we can generally achieve better results for these stream learners.
In the case of the variable selection process, we deduce from the comparison between
Table 3 and
Table 4 that this preparatory technique improves the performance of
RHT and
RHAT, and it also reduces their processing time. For
PAR,
SGDR, and
MLPR, it achieves a similar performance but also reduces their processing time. Thus it is recommendable for all of them, except for
MTR and
MFR, when the preparatory size is
. In the case of the comparison between
Table 5 and
Table 6, this preparatory technique improves the performances of
PAR and
RHAT, and it also reduces o maintains their processing time. For
SGDR,
MLPR and
RHT the performances and the processing times are very similar. Thus it is also recommendable for all of them, except again for
MTR and
MFR, when the preparatory size is
. In what refers to which features have been selected for the streaming process in the experiments 1 and 3, we see in
Table 7 how AT and V have been preferred over the rest by the hyper-parameter tuning method, which has also been confirmed in
Section 5.1 due to their correlation with the target variable (PE).
Regarding the selection of the best SR,
Table 3,
Table 4,
Table 5 and
Table 6 show how
MLP and
RHT show the best error metrics for both preparatory sizes when the variable selection process is carried out. When there is no a variable selection process, then the best error metrics are achieved by
MFR. However, in terms of processing time,
SGDR and
MTR are the fastest stream learners. Due to the fact that we have to find a balance between error metric results and time processing, we recommend
RHT. It is worth mentioning that if we check the performance metrics (
MSE,
RMSE,
MAE, and
),
RHT shows better results than
RHAT, and then we could assume that there are no drift occurrences in the dataset. In case of drifts,
RHAT should exhibit better performance metrics than
RHT because it has been designed for non-stationary environments.
7. Conclusions
This work has presented a comparison of streaming regressors for electrical power production prediction in a combined cycle power plant. This prediction problem had been tackled before with the traditional thermodynamical analysis, which had shown to be computational and time processing expensive. However, some studies have addressed this problem by applying Machine Learning techniques, such as regression algorithms, and managing to reduce the computational and time costs. These new approaches have considered the problem under a batch learning perspective in which data is assumed to be at rest, and where regression models do not continuously integrate new information into already constructed models. Our work presents a new approach for this scenario, in which data are arriving continuously and where regression models have to learn incrementally. This approach is closer to the emerging Big Data and IoT paradigms.
The results obtained show how competitive error metrics and processing times have been achieved when applying a SL approach to this specific scenario. Specifically, this work has identified RHT as the most recommendable technique to achieve the electrical power production prediction in the CCPP. We have also highlighted the relevance of the preparatory techniques to make the streaming algorithms ready for the streaming process, and at the same time, the importance of selecting properly the number of preparatory instances. Regarding the importance of the features, as in previous cases which tackled the same problem from a batch learning perspective, we do recommend to carry out a variable selection process for all SRs (except for MTR and MFR) because it reduces the streaming processing time and at the same time it is worthy due to the performance gain. Finally, as future work, we would like to transfer this SL approach to other processes in combined cycle power plants, and even to other kinds of electrical power plants.