Assessment of a Hydrokinetic Energy Converter Based on Vortex-Induced Angular Oscillations of a Cylinder

Abstract

Vortex-induced oscillations offer a potential means to harness hydrokinetic energy even at low current speeds. In this study, we consider a novel converter where a cylinder undergoes angular oscillations with respect to a pivot point, in contrast to most previous configurations, where the cylinder undergoes flow-induced oscillations transversely to the incident free stream. We formulate a theoretical model to deal with the coupling of the hydrodynamics and the structural dynamics, and we numerically solve the resulting nonlinear equation of cylinder motion in order to assess the performance of the energy converter. The hydrodynamical model utilizes a novel approach where the fluid forces acting on the oscillating cylinder are split into components acting along and normal to the instantaneous relative velocity between the moving cylinder and the free stream. Contour plots illustrate the effects of the main design parameters (in dimensionless form) on the angular response of the cylinder and the energy efficiency of the converter. Peak efficiencies of approximately 20% can be attained by optimal selection of the main design parameters. Guidelines on the sizing of actual converters are discussed.

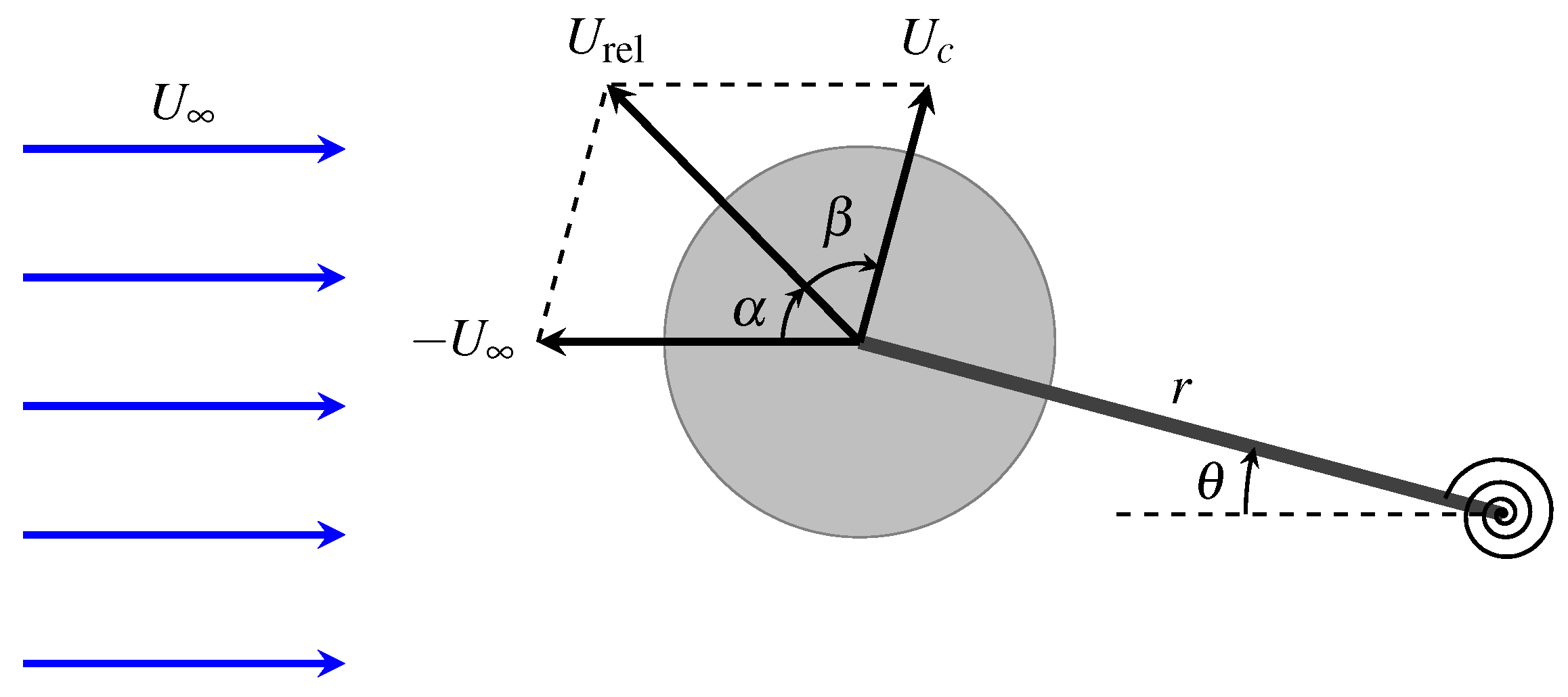
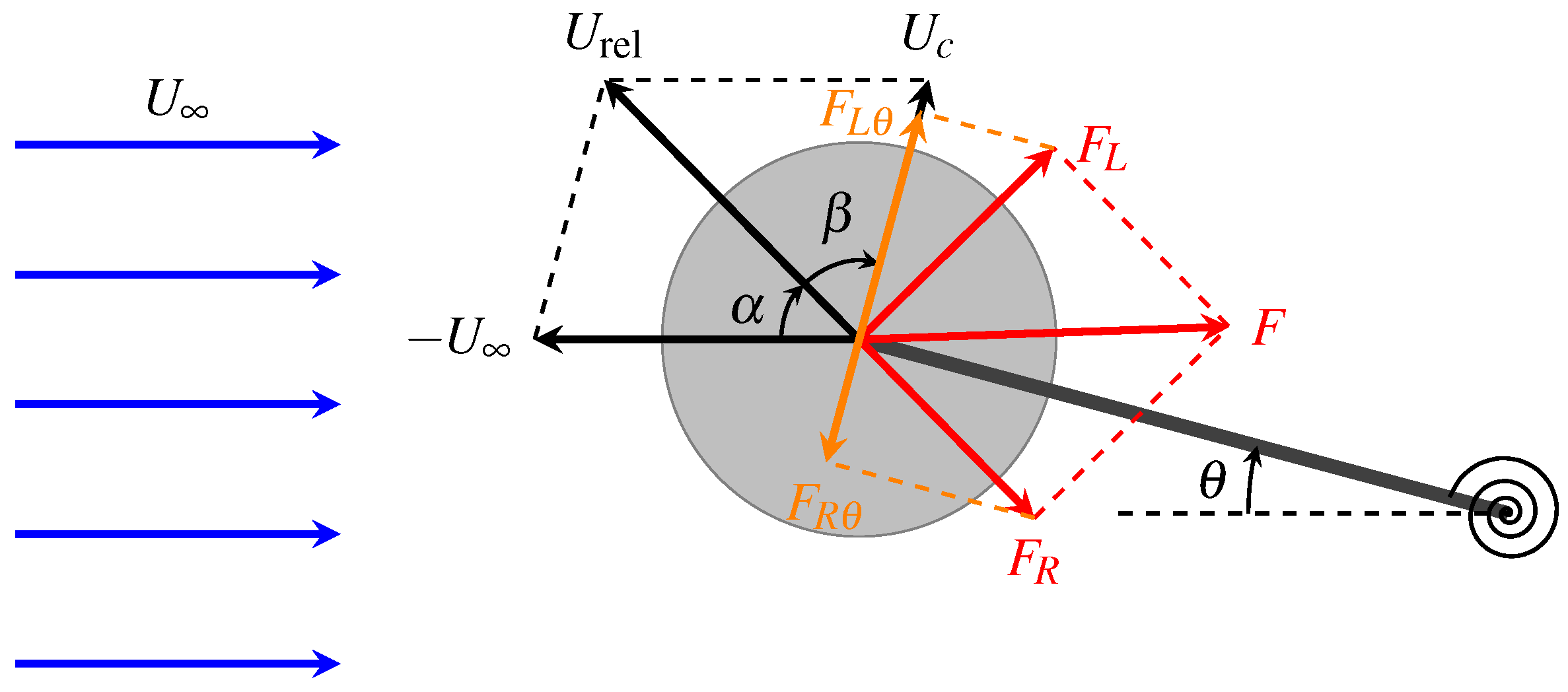
1. Introduction

Driven by the need to increase the percentage of renewable sources in the energy-production mix during the last decade, much research has focused on the development and advancement in science, technology, and engineering of wave, wind, and current energy converters, primarily in offshore installations [1,2,3,4]. Conventional devices harnessing the kinetic energy of water currents are usually based on propeller-like turbines, which require relatively high current speeds of above 1 m/s. Unlike conventional turbines that operate with a single degree of freedom to rotate around a horizontal or vertical axis, a novel concept is to develop hydrokinetic energy converters based on flow-induced oscillatory motions of their power-generating elements. These oscillatory motions have two degrees of freedom, which allows for a more versatile operation; such converters can be designed to exploit high-amplitude and/or high-frequency oscillations to generate significant power, even at currents speeds as low as 0.1 m/s, with minimal disruption of the environment. Thus, novel energy converters based on oscillating structures may, at least in principle, avoid some of the limitations of conventional technologies and expand the availability of resource fields.

The concept of exploiting flow-induced oscillatory motions of bluff bodies for energy harnessing has received considerable attention in recent years. Various aspects and pertinent phenomena have been investigated in several studies with a view to assess the performance and optimize the design of hydrokinetic energy converters [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21]. Probably, the best-known concept is the VIVACE converter, which was developed by the Marine Renewable Energy Laboratory (MRELab) in the University of Michigan [5,6]. Its operation relies on the fundamental phenomenon of vortex-induced vibration; when an elastically-mounted cylinder is placed normal to a cross-flow, it can respond to periodic fluid forcing induced by vortices regularly shed in its after-body wake if the excitation frequency is close to the natural vibration frequency of the structure [22,23,24]. Vortex-induced vibration has been known for a long time and is mostly unwanted, as it compromises the integrity of equipment, such as the heat-exchanger tubes, oil risers, offshore platforms, transmission cables, cable-stayed bridges, tall chimneys, etc. due to fatigue of the structural components. On the other hand, vortex-induced vibration may be purposefully enhanced in hydrokinetic energy converters where electricity can be produced, e.g., by electromagnetic induction through the oscillating components.

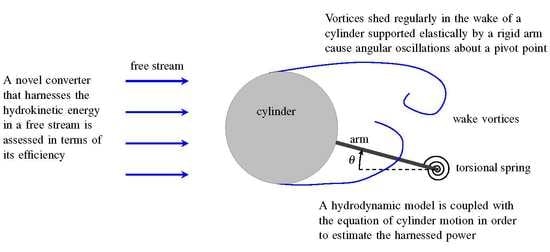
More recently, a hydrokinetic energy converter has been proposed which is essentially a modification of the original configuration of the VIVACE converter; in the new design, the cylinder is attached to a supporting arm so that it can undergo vortex-induced angular oscillations with respect to a pivot point [25]. In this new configuration, the length of the cylinder-supporting arm offers an additional design parameter to control the system’s response and, thereby, the efficiency of hydrokinetic energy conversion. This device has been shown to have potential benefits [25]. However, its performance depends on several design parameters, including the dimensions of the oscillating cylinder and its mass moment of inertia, arm length, damping, stiffness, and current speed, whose influences have not been studied in detail and are thus unknown. The objective of the present study is to make a preliminary assessment of the effects of these design parameters on the performance of the hydrokinetic energy converter through the development of a time-domain model to cope with the flow–structure interaction. Based on this preliminary study, a suitable prototype of the converter can be designed and put to test.

2. Physical and Mathematical Models

2.1. Physical System

Figure 1 depicts a three-dimensional schematic of the hydrokinetic energy converter considered in the present study. The system consists of a cylindrical rod, or simply the ‘cylinder’, which is attached from its top to a supporting arm. The supporting arm can rotate about a fixed pivot bar (pivot point) so that the main cylinder can perform one-degree-of-freedom rotational oscillations about the pivot bar while the supporting arm maintains the cylinder in an upright position. The cylindrical rod is placed perpendicular to a fluid stream with a uniform velocity profile, i.e., the cylinder is considered to be sufficiently far from obstructing solid boundaries. Elastic springs are attached to the supporting arm on one end and to a fixed frame on the other end. The springs provide restoring forces that keep the cylinder at a neutral position with the supporting arm parallel to the incident fluid stream. There are two possible configurations where the pivot point can be positioned either downstream or upstream of the main cylinder. For economy of presentation, we consider in this study only the case where the pivot point is located downstream, since this configuration yields higher efficiencies, as shown in previous experiments [25]. Unsteady hydrodynamic forces due to periodic vortex shedding can induce rotational oscillations of the main cylinder about the pivot point. For a long cylinder with no free-end effects, we assume that the flow and the fluid forces are homogeneous along the cylinder axis, so that it suffices to consider a two-dimensional segment for the analysis of the cylinder motion. In the following, pertinent structural dynamics and hydrodynamics models are developed in order to study the hydrokinetic to mechanical energy conversion.

2.2. Kinematics

We start with some equations describing the kinematics of the problem, which are essential in order to formulate the hydrodynamical model, which is based on the relative velocity between the cylinder and the free stream. Figure 2 presents the two-dimensional geometrical model of the problem under consideration. In this configuration, the pivot point is located downstream of the cylinder. The supporting arm has length r and the main cylinder has diameter D. At a random time, the supporting arm forms an angle $\theta$ with respect to the free stream of speed $U_{\infty }$ while the main cylinder moves with linear velocity $U_c$, arbitrarily taken towards the top. The angle is considered positive in the clockwise direction. The linear velocity of the cylinder is $U_c=r\dot{\theta }$, where $\dot{\theta }$ is the angular velocity (the overdot denotes a derivative with respect to time). The relative velocity between the moving cylinder and the free stream is the vector difference ${\overrightarrow{U}}_{\mathrm{rel}}={\overrightarrow{U}}_c-{\overrightarrow{U}}_{\infty }$, where the angle between ${\overrightarrow{U}}_{\infty }$ and ${\overrightarrow{U}}_c$ is $\alpha +\beta =\pi /2+\theta$. Thus, the magnitude of the relative velocity is $U_{\mathrm{rel}}=\sqrt{U_{\infty }^2+U_c^2+2U_{\infty }{U}_{c}cos(\alpha +\beta )}$. Substituting $U_c=r\dot{\theta }$ and $cos(\alpha +\beta )=-sin\theta$ results in

$$U_{\mathrm{rel}}=U_{\infty }\sqrt{1+{\left(\frac{r\dot{\theta }}{U_{\infty }}\right)}^2-2\frac{r\dot{\theta }}{U_{\infty }}sin\theta }.$$

(1)

The angle $\beta$ between ${\overrightarrow{U}}_{\mathrm{rel}}$ and ${\overrightarrow{U}}_c$ will be needed in order to project the resolved hydrodynamic forces acting along and normal to the relative velocity vector into the direction of cylinder motion. Using the definitions of internal and external products between vectors, we can express the cosine and sine of $\beta$ as

$$\begin{array}{c}cos\beta =\frac{{\overrightarrow{U}}_{\mathrm{rel}}·{\overrightarrow{U}}_c}{\parallel {\overrightarrow{U}}_c\parallel \parallel {\overrightarrow{U}}_{\mathrm{rel}}\parallel }=\frac{U_c+U_{\infty }sin\theta }{U_{\mathrm{rel}}},\end{array}$$

(2a)

$$\begin{array}{c}sin\beta =\frac{{\overrightarrow{U}}_{\mathrm{rel}}\times {\overrightarrow{U}}_c}{\parallel {\overrightarrow{U}}_c\parallel \parallel {\overrightarrow{U}}_{\mathrm{rel}}\parallel {\overrightarrow{e}}_z}=\frac{U_{\infty }cos\theta }{U_{\mathrm{rel}}}.\end{array}$$

(2b)

Above, ${\overrightarrow{e}}_z$ is the unit vector along the the axis of the cylinder. Finally, we can express the above equations as functions of the angular displacement $\theta$ and the angular velocity $\dot{\theta }$ as

$$\begin{array}{c}cos\beta =\frac{r\dot{\theta }+U_{\infty }sin\theta }{\sqrt{U_{\infty }^2+2r\dot{\theta }{U}_{\infty }sin\theta +{\left(r\dot{\theta }\right)}^2}},\end{array}$$

(3a)

$$\begin{array}{c}sin\beta =\frac{U_{\infty }cos\theta }{\sqrt{U_{\infty }^2+2r\dot{\theta }{U}_{\infty }sin\theta +{\left(r\dot{\theta }\right)}^2}}.\end{array}$$

(3b)

2.3. Structural Dynamics

The main cylinder is assumed to undergo angular oscillations, $\theta \left(t\right)$, due to the action of periodic hydrodynamic forcing. The two-dimensional motion of the cylinder is governed by the balance of angular momentum about the pivot point,

$$I_r\ddot{\theta }+c\dot{\theta }+k\theta =r{F}_{\theta },$$

(4)

where $I_r$ is the mass moment of inertia about the pivot point, c is the equivalent structural damping factor, k is the stiffness of the torsional spring, r is the length of the supporting arm, and $F_{\theta }\left(t\right)$ is the projection of the total hydrodynamic force in the direction of the instantaneous linear velocity of the cylinder. Note that the linear springs have been replaced by an equivalent torsional spring that provides a restoring force, as shown in Figure 2. It is assumed here that the mechanical restoring force from the springs varies linearly with angular displacement of the supporting arm, and that the structural damping is proportional to the velocity of the arm. By introducing the natural undamped frequency of the system, $f_N=(1/2\pi )\sqrt{k/I_r}$, and the ratio of structural damping to the critical damping, $\zeta =c/2\sqrt{k{I}_r}$, we can rewrite the equation of cylinder motion as

$$I_r\ddot{\theta }+4\pi I_r\zeta f_N\dot{\theta }+4{\pi }^2{I}_r{f}_N^2\theta =r{F}_{\theta }.$$

(5)

The mass moment of inertia of a cylinder rotating about a pivot point can be calculated using the parallel axis theorem, $I_r=I_c+m{r}^2$, where $I_c$ is the mass moment of inertia of the same body rotating about a parallel axis passing through the center of mass and m is the body mass. For a long homogeneous cylinder, $I_c=\frac{1}{8}m{D}^2$ and, therefore, $I_r=m\left(r^2+\frac{1}{8}{D}^2\right)$. The left-hand side of Equation (5) is an ordinary (linear) differential equation of second order. The non-linearity of the problem rests on the right-hand side of Equation (5), which represents the hydrodynamic forcing.

2.4. Hydrodynamics

The hydrodynamic force per unit spanwise length, F, exerted on the cylinder is decomposed into components, denoted $F_R$ and $F_L$, respectively along and normal to the instantaneous relative velocity between the oscillating cylinder and the free stream, as shown in Figure 3. It should be noted that at an arbitrary instant, F generally forms an angle with respect to the free stream. According to this model, the longitudinal component $F_R$ always resists the cylinder motion, whereas the normal component $F_L$ acts as an excitation source due to lift in vortex-induced vibration. This hydrodynamical model has been previously tested for the simpler case of rectilinear oscillations of an elastically-mounted circular cylinder transverse to a free stream, i.e., the classical problem of vortex-induced vibration [26,27]. It has also been experimentally verified that $F_R$ always does negative work on the cylinder, whereas $F_L$ primarily does positive work [28].

The reaction force incorporates fluid damping due to drag and fluid inertia due to added mass, which can be modeled by the well-known Morison’s equation [29], i.e.,

$$F_R\left(t\right)=\frac{1}{4}\rho \pi D^2{C}_A{\dot{U}}_{\mathrm{rel}}+\frac{1}{2}\rho D{C}_D{U}_{\mathrm{rel}}^2,$$

(6)

where $\rho$ is the density of the fluid, and $C_A$ and $C_D$ are the added mass (inertia) and drag coefficients, respectively. The novelty here is that Morison’s equation is used to model the reaction force acting in the direction of the instantaneous relative velocity between the vibrating cylinder and the free stream. A velocity-squared-dependent quasi-steady drag force is applicable for separated flows dominated by the convection of vorticity in the wake [30]. The above reaction force introduces strongly non-linear terms in the total force, as will be seen further below. It should also be noted that $F_R$ depends on the motion of the cylinder; thus, it is time-dependent.

The excitation force is modeled as a periodic function of time

$$F_L\left(t\right)={\displaystyle \frac{1}{2}}\rho U_{\infty }^{2}D{C}_{L}sin(2\pi f_{vs}t),$$

(7)

where $C_L$ is the lift coefficient and $f_{vs}$ is the vortex shedding frequency. That is, vortices that regularly shed in the wake at the shedding frequency induce a periodic force on the cylinder. A major complication in vortex-induced vibration is that the actual vortex shedding frequency depends not only on the Reynolds number as for a fixed cylinder, but also on the frequency of cylinder motion. A large number of studies have been devoted to examining vortex synchronization for cylinders undergoing both forced and free oscillation; e.g., see the review in [23]. Many studies have shown that the frequency of vortex shedding varies between $\frac{1}{2}{f}_{v0}<f_{vs}<f_{v0}$, where $f_{v0}$ is the vortex shedding frequency from a fixed cylinder at the same Reynolds number, often referred to as the Strouhal frequency. In the following, we will assume that the vortex shedding frequency remains within the above range.

2.5. Flow–Structure Interaction

The next step is to introduce the resolved hydrodynamic forces from Equations (6) and (7) into the equation of cylinder motion (5). Note that ${\overrightarrow{F}}_R$ is collinear with ${\overrightarrow{U}}_{\mathrm{rel}}$ while ${\overrightarrow{F}}_L$ is normal to ${\overrightarrow{U}}_{\mathrm{rel}}$. Thus, we project ${\overrightarrow{F}}_R$ and ${\overrightarrow{F}}_L$ into the direction of ${\overrightarrow{U}}_c$ to obtain ${\overrightarrow{F}}_{R\theta }$ and ${\overrightarrow{F}}_{L\theta }$, respectively. From Figure 3, we see that

$$F_{\theta }=F_{L\theta }-F_{R\theta }=F_{L}sin\beta -F_{R}cos\beta ,$$

(8)

where $\beta$ is the angle between ${\overrightarrow{U}}_{\mathrm{rel}}$ and ${\overrightarrow{U}}_c$. Substitution of the cosine and sine of $\beta$ from (3a) and (3b), respectively, and of $F_R$ and $F_L$ from (6) and (7), respectively, into $F_{\theta }$ and of the result into the equation of cylinder motion (5), after some lengthy manipulations, leads to

$$\begin{array}{c}\hfill \left[I_r+\frac{1}{4}\rho \pi D^2{r}^2{C}_A\frac{U_{\infty }^2}{U_{\mathrm{rel}}^2}{\left(\frac{r\dot{\theta }}{U_{\infty }}-sin\theta \right)}^2\right]\ddot{\theta }+\\ \hfill \left[c+\frac{1}{4}\rho \pi D^2{r}^2{C}_A\frac{U_{\infty }^2}{U_{\mathrm{rel}}^2}\left(\dot{\theta }sin\theta -\frac{r{\dot{\theta }}^2}{U_{\infty }}\right)cos\theta +\frac{1}{2}\rho D{r}^2{C}_D{U}_{\mathrm{rel}}\right]\dot{\theta }+\\ \hfill k\theta -\frac{1}{2}\rho Dr{C}_D{U}_{\mathrm{rel}}{U}_{\infty }sin\theta =\\ \hfill \frac{1}{2}\rho U_{\infty }^{2}Dr\frac{U_{\infty }}{U_{\mathrm{rel}}}cos\theta C_{L}sin\left(2\pi f_{vs}t\right).\end{array}$$

(9)

With the aid of the above equation, we can examine the actions of the different terms. The terms inside the square bracket on the first line represent the total inertia of the system. Similarly, the terms on the second line represent the total damping of the system, and the terms on the third line represent the total stiffness of the system. The term on the fourth line, i.e., on the right-hand side of the equation, represents the excitation function. It can be seen that the hydrodynamics modify the properties of the structural system. Terms involving $C_A$ contribute to both the inertia and damping of the system. In fact, fluid inertia introduces strong non-linearity in the equation of motion, as the corresponding terms involve the squared angular velocity. Terms involving $C_D$ contribute to the damping and stiffness of the system. It is interesting to note that the $C_A$ term on the second line of Equation (9) introduces small negative damping on the average (instantaneously takes both positive and negative values). However, the $C_D$ term on the second line of Equation (9) is solely positive and dominates the fluid damping. It should also be noted that for small angles, $sin\theta \approx \theta$ and the term on the third line of Equation (9) can be expressed as $\left(k-\frac{1}{2}\rho DL{C}_D{U}_{\mathrm{rel}}{U}_{\infty }\right)\theta$; thus, fluid damping due to drag lowers the total stiffness of the system.

The equation of cylinder motion (9) can be cast in the following non-dimensional form

$$\begin{array}{c}\hfill \left[m^{*}\left(1+\frac{1}{8L^{*2}}\right)+{\left(\frac{L^{*}{\dot{\theta }}^{*}}{U^{*}}-sin{\theta }^{*}\right)}^2{U}_{\mathrm{rel}}^{*-2}{C}_A\right]{\ddot{\theta }}^{*}+\\ \hfill \left[4\pi m^{*}\zeta \left(1+\frac{1}{8L^{*2}}\right)+\left({\dot{\theta }}^{*}sin{\theta }^{*}-\frac{L^{*}{\dot{\theta }}^{*2}}{U^{*}}\right)cos{\theta }^{*}{U}_{\mathrm{rel}}^{*-2}{C}_A+\frac{2}{\pi }{U}^{*}{U}_{\mathrm{rel}}^{*}{C}_D\right]{\dot{\theta }}^{*}+\\ \hfill 4{\pi }^2{m}^{*}\left(1+\frac{1}{8L^{*2}}\right){\theta }^{*}-\frac{2}{\pi }\frac{U^{*2}}{L^{*}}{U}_{\mathrm{rel}}^{*}{C}_{D}sin{\theta }^{*}=\frac{2}{\pi }\frac{U^{*2}}{L^{*}}\frac{cos{\theta }^{*}}{U_{\mathrm{rel}}^{*}}{C}_{L}sin\left(2\pi S_f{U}^{*}\tau \right),\end{array}$$

(10)

where time is normalized with the undamped natural oscillation period of the system, i.e., $\tau =t/T_N=f_{N}t$, i.e., the dependent variables become ${\theta }^{*}=\theta /(1\mathrm{radian})$, ${\dot{\theta }}^{*}=\dot{\theta }/f_N$, and ${\ddot{\theta }}^{*}=\ddot{\theta }/f_N^2$. The relative velocity is normalized with the free-stream velocity, $U_{\mathrm{rel}}^{*}=U_{\mathrm{rel}}/U_{\infty }$. The resulting equation of motion (10) includes the following dimensionless parameters:

non-dimensional arm length, ${\displaystyle L^{*}=\frac{r}{D}}$,

mass ratio, ${\displaystyle m^{*}=\frac{m}{\frac{1}{4}\pi \rho D^2}}$,

damping ratio, ${\displaystyle \zeta =\frac{c}{2\sqrt{k{I}_r}}}$,

reduced velocity, ${\displaystyle U^{*}=\frac{U_{\infty }}{f_{N}D}}$.

Equation (10) is highly non-linear. Thus, for the purposes of the present study, we numerically solved the equation of cylinder motion using the MATLAB ODE Suite, which provides a powerful yet easy to implement tool for numerical solution of ordinary differential equation initial value problems [31]. The solution of Equation (10) requires as input the hydrodynamic parameters, $C_A$, $C_D$, $C_L$, and $S_f$, where $S_f=f_{vs}D/U_{\infty }$, which is the actual Strouhal frequency of vortex shedding driving the motion of the cylinder.

2.6. Power Extraction Efficiency

The instantaneous power $P\left(t\right)$ delivered to the energy converter can be calculated from the product of the driving force times the velocity of the cylinder, $P\left(t\right)=F_{\theta }\left(t\right)U_c\left(t\right)=F_{\theta }\left(t\right)r\dot{\theta }\left(t\right)$. The term $F_{\theta }r$ can be obtained from the left-hand side of the equation of motion (5) so that

$$P\left(t\right)=\left(\ddot{\theta }+4\pi \zeta f_N\dot{\theta }+4{\pi }^2{f}_N^2\theta \right)I_r\dot{\theta }.$$

(11)

The average power over many cycles of motion is a practical metric to quantify the performance of the energy converter. Assuming that the motion of the cylinder is periodic with period T, the average power can be calculated from the following integral

$$〈P〉=\frac{1}{T}{\int }_{T}P\left(t\right)\mathrm{d}t=\frac{1}{T}{\int }_T\left(\ddot{\theta }\left(t\right)+4\pi \zeta f_N\dot{\theta }\left(t\right)+4{\pi }^2{f}_N^2\theta \left(t\right)\right)I_r\dot{\theta }\left(t\right)\mathrm{d}t.$$

(12)

The first and third term in the integral make a zero net contribution, so that only the second term contributes to the net power. Typically, the average power delivered to the energy converter is normalized by the power of the fluid stream within the frontal area of the cylinder [7], which yields the following efficiency metric:

$$\eta =\frac{〈P〉}{\frac{1}{2}\rho D{U}_{\infty }^3}=\frac{2{\pi }^2{m}^{*}\zeta }{U^{*3}}\left(L^{*2}+\frac{1}{8}\right)\frac{1}{T^{*}}{\int }_{T^{*}}{\dot{\theta }}^{*2}\left(\tau \right)\mathrm{d}\tau .$$

(13)

In order to compute the efficiency of the hydrokinetic energy converter, the time series ${\dot{\theta }}^{*}\left(\tau \right)$ appearing in the integral can be obtained from the numerical solution of Equation (10).

3. Results

In this section, we present results from simulations with the non-linear model developed in the previous section (Equation 10) in order to assess the effect of the basic mechanical parameters of the hydrokinetic energy converter on its efficiency (Equation 13). In particular, we consider variations of the dimensionless arm length $L^{*}$, mass ratio $m^{*}$, damping ratio $\zeta$, and reduced velocity $U^{*}$. A normalized time step of $\delta \tau =5\times {10}^{-4}/U^{*}St$ was employed for the integration of Equation (10) for more than 200 cycles of oscillation, for which the resulting motion typically (but not always) settled to a steady periodic oscillation about the neutral position at zero angle.

The values of the hydrodynamic parameters employed in the present study, which are required as input parameters for the solution of the equation of cylinder motion, Equation (10), are listed in

Table 1. Hydrodynamic parameters employed in the present study.

${\mathit{C}}_{\mathit{A}}$	${\mathit{C}}_{\mathit{D}}$	${\mathit{C}}_{\mathit{L}}$	${\mathit{S}}_{\mathit{f}}$
1.00	1.35	1.50	0.155

. These values were selected on the basis of the following considerations. The added mass coefficient takes the theoretical value for inviscid potential flow about a circular cylinder, as discussed in [32]. The drag and lift coefficients are higher than their corresponding values for a non-oscillation cylinder in the same range of Reynolds numbers due to vortex synchronization in the wake of oscillating cylinders [22,23]. The Strouhal number is assumed to have a constant value lower than the corresponding value for a non-oscillation cylinder, as discussed earlier; the selected value is typical around peak amplitude for cylinders undergoing vortex-induced vibration transversely to a free stream [23]. The above choices of the hydrodynamical parameters should be considered appropriate for smooth cylinders placed in uniform free streams at Reynolds numbers for which the boundary layer on the cylinder is laminar and transition to turbulence occurs in the shear layers after flow separation, that is, $Re\approx {10}^3-5\times {10}^5$.

Sets of simulations were carried out where the reduced velocity $U^{*}$ is varied at set values of $L^{*}$, $m^{*}$, and $\zeta$. Due to the large size of the test matrix, initially, we present results in the form of contours in the 2D parameter space of $U^{*}$ and each one of $\{L^{*},m^{*},\zeta \}$ for some representative values of the other two parameters from the set. The cylinder response is characterized by the amplitude of angular deflection, denoted ${\theta }_o$, and the amplitude of displacement transversely to the free stream, $A^{*}=L^{*}{\theta }_o$. It should be noted that ${\theta }_0$ is dimensionless, since the equation of motion has been solved for the dimensionless angular displacement ${\theta }^{*}$, which corresponds to angles in radians normalized with 1 radian. The efficiency of hydrokinetic energy conversion is characterized by the efficiency $\eta$.

3.1. Effect of Arm Length

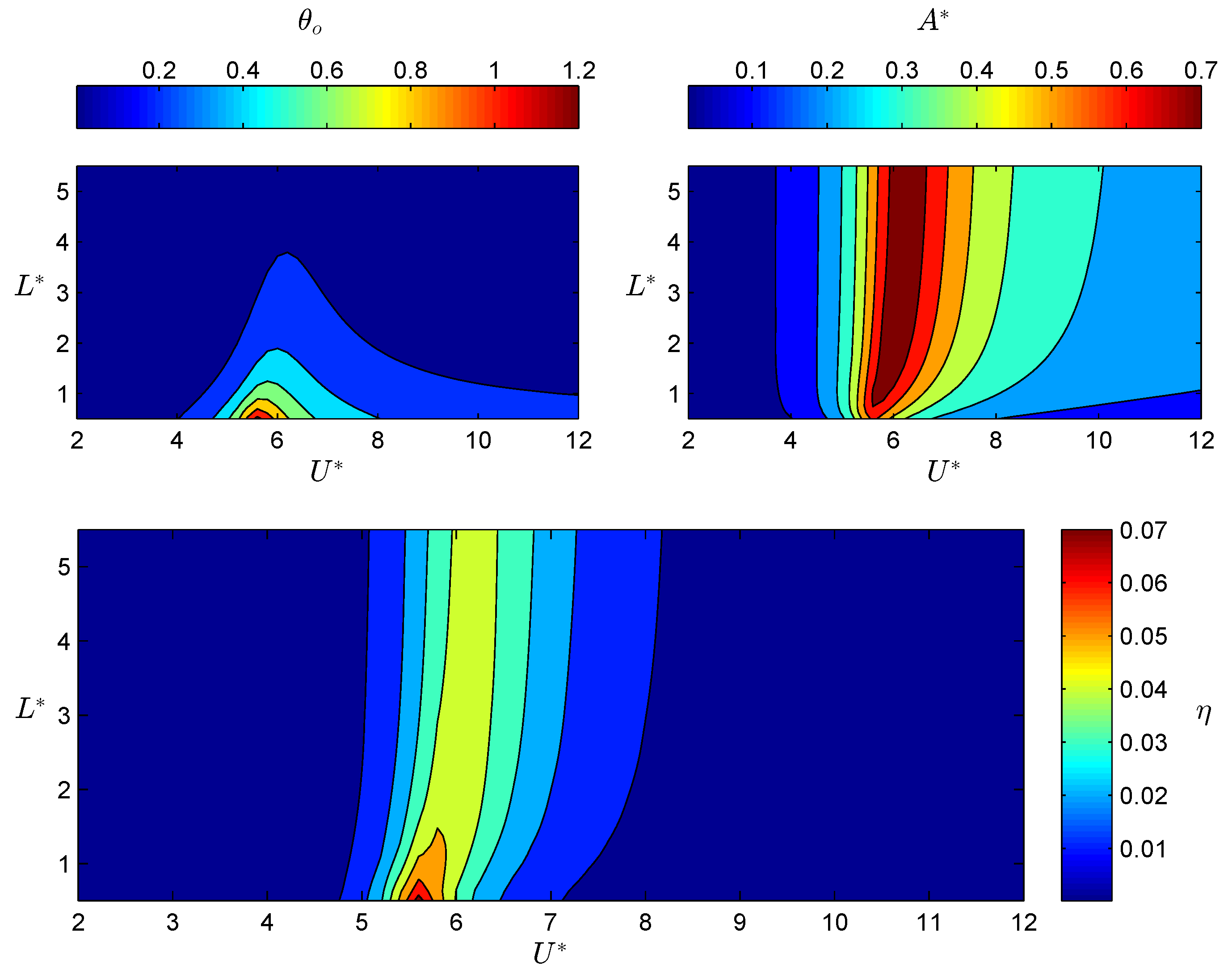
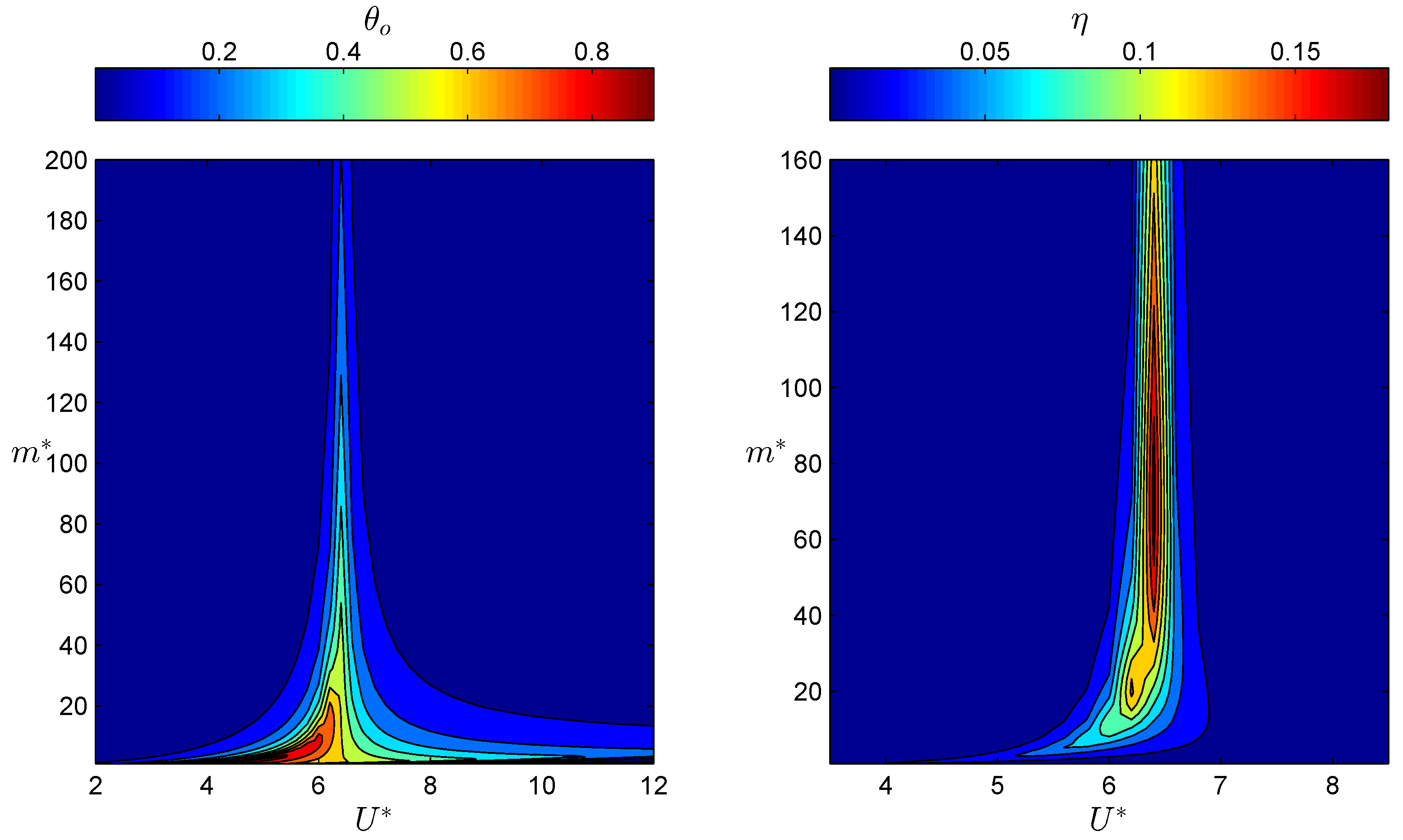
Figure 4 shows contours of ${\theta }_o$, $A^{*}$, and $\eta$ as functions $U^{*}$ and $L^{*}$ at fixed values of $m^{*}=5$ and $\zeta =0.01$. It can be observed that ${\theta }_o$ strongly depends on both $U^{*}$ and $L^{*}$. At a fixed $L^{*}$ value, ${\theta }_o$ attains a peak level that corresponds to $U^{*}\approx S{t}^{-1}$ with the precise value being slightly dependent on $L^{*}$, i.e., $U^{*}$ at peak shifts to slightly higher values with $L^{*}$. This may be attributable to the decrease in the total stiffness of the system due to the drag term $\left(k-\frac{1}{2}\rho DL{C}_D{U}_{\mathrm{rel}}{U}_{\infty }\right)\theta$, which increases in proportion to L. The peak level of ${\theta }_o$ gradually decreases with increasing $L^{*}$, while a global maximum of 1.26 is attained at the lowest $L^{*}$ value. The variation of the transverse amplitude $A^{*}$ as a function of only $U^{*}$ also displays a peak at the same location as ${\theta }_o$ does, but, conversely to the variation of ${\theta }_o$, peak levels of $A^{*}$ increase with $L^{*}$, particularly in the range of low $L^{*}$ values; in the range of high $L^{*}$ values, $A^{*}$ is almost independent of $L^{*}$. The power efficiency $\eta$ attains a global maximum value of 7.5% at $(L^{*},U^{*})=(0.5,5.6)$, where ${\theta }_o$ also displays a global maximum. However, it should be noted that global maxima in ${\theta }_o$ and $\eta$ do not coincide in general.

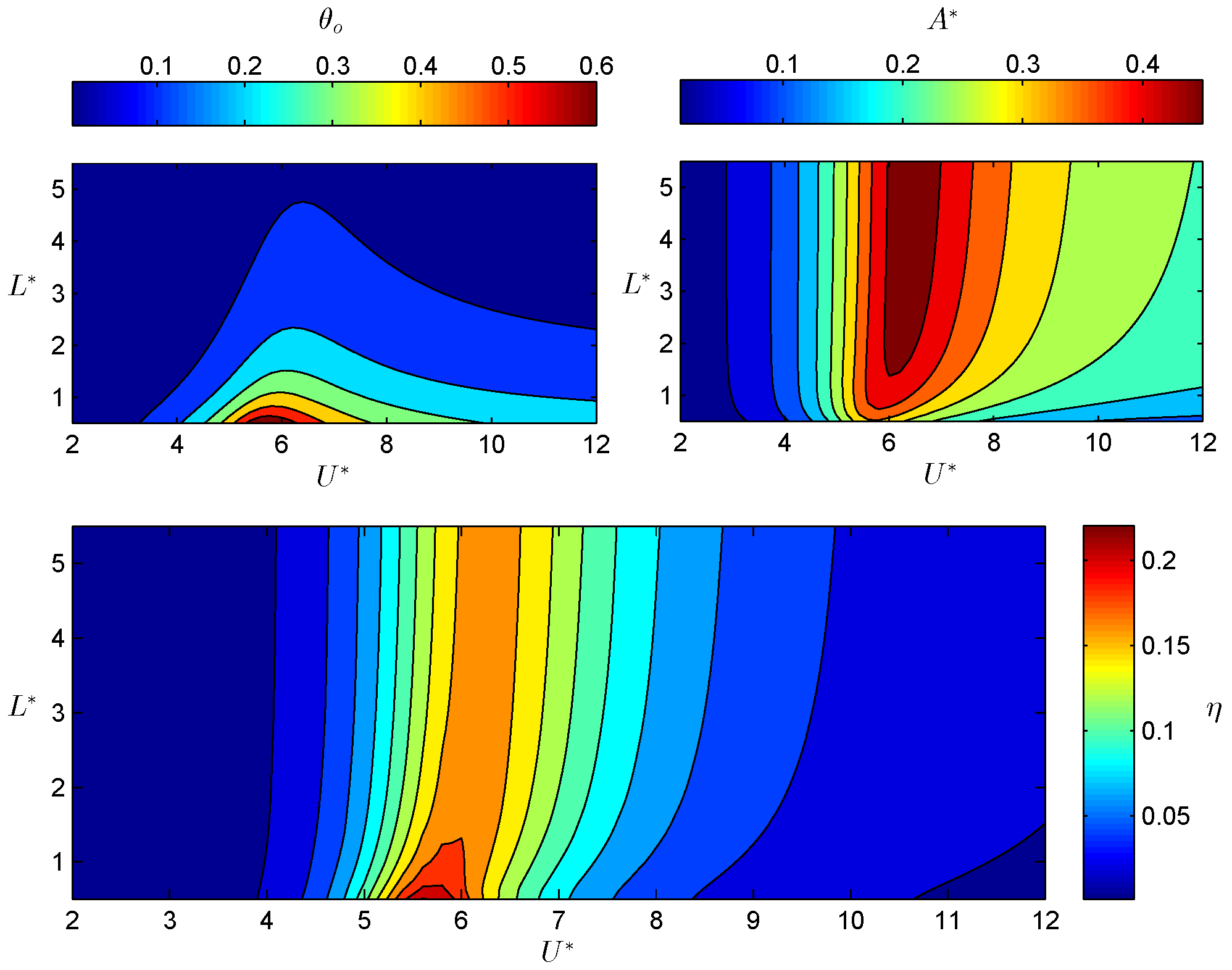
In Figure 5, we present contours of ${\theta }_o$, $A^{*}$, and $\eta$ as functions $U^{*}$ and $L^{*}$ at fixed values of $m^{*}=50$ and $\zeta =0.01$. Both ${\theta }_o$ and $A^{*}$ display similar variations to those in the previous case with $(m^{*},\zeta )=(5,0.01)$, but their peak levels decreased by approximately half (cf. Figure 4). Yet, the conversion efficiency $\eta$ approximately doubled for $(m^{*},\zeta )=(50,0.01)$, reaching a global maximum of 18.1% at $(L^{*},U^{*})=(0.5,6.4)$. In addition, the peak level of $\eta$ as a function of $U^{*}$ at fixed $L^{*}$ does not depend strongly on $L^{*}$ any more, unlike at $m^{*}=5$. However, the range of appreciable response and high efficiency shrunk by approximately half, now limited in the range $5.5<U^{*}<7.5$ at $m^{*}=50$ compared to $4<U^{*}<10$ at $m^{*}=5$.

Figure 6 shows contours of ${\theta }_o$, $A^{*}$, and $\eta$ as functions $U^{*}$ and $L^{*}$ at fixed values of $m^{*}=5$ and $\zeta =0.1$, i.e., damping has now been increased. The contours are quite similar to those for $\zeta =0.01$, but now, peak levels ${\theta }_o$ and $A^{*}$ have decreased, whereas peak levels of $\eta$ have increased, reaching a global maximum of 22.1% at $(L^{*},U^{*})=(0.5,5.6)$. Finally, we can see in Figure 7 that using high values of both mass and damping ratios of $(m^{*},\zeta )=(50,0.1)$ results in a reduction in both the cylinder response and the efficiency of the converter comparatively to all previous cases with lower $m^{*}$ or $\zeta$ values.

3.2. Effect of Mass Ratio

The results presented in the previous section show that the mass ratio $m^{*}$ has a marked effect on the response and efficiency of the energy converter. In order to get a more detailed picture of the influence of variations in $m^{*}$, we carried out series of simulations with varying $m^{*}$ at a constant value of $\zeta$ and $L^{*}$. A value of $L^{*}=0.8$ was employed, as the above simulations have shown that the best efficiencies are obtained at the lowest $L^{*}$ values. 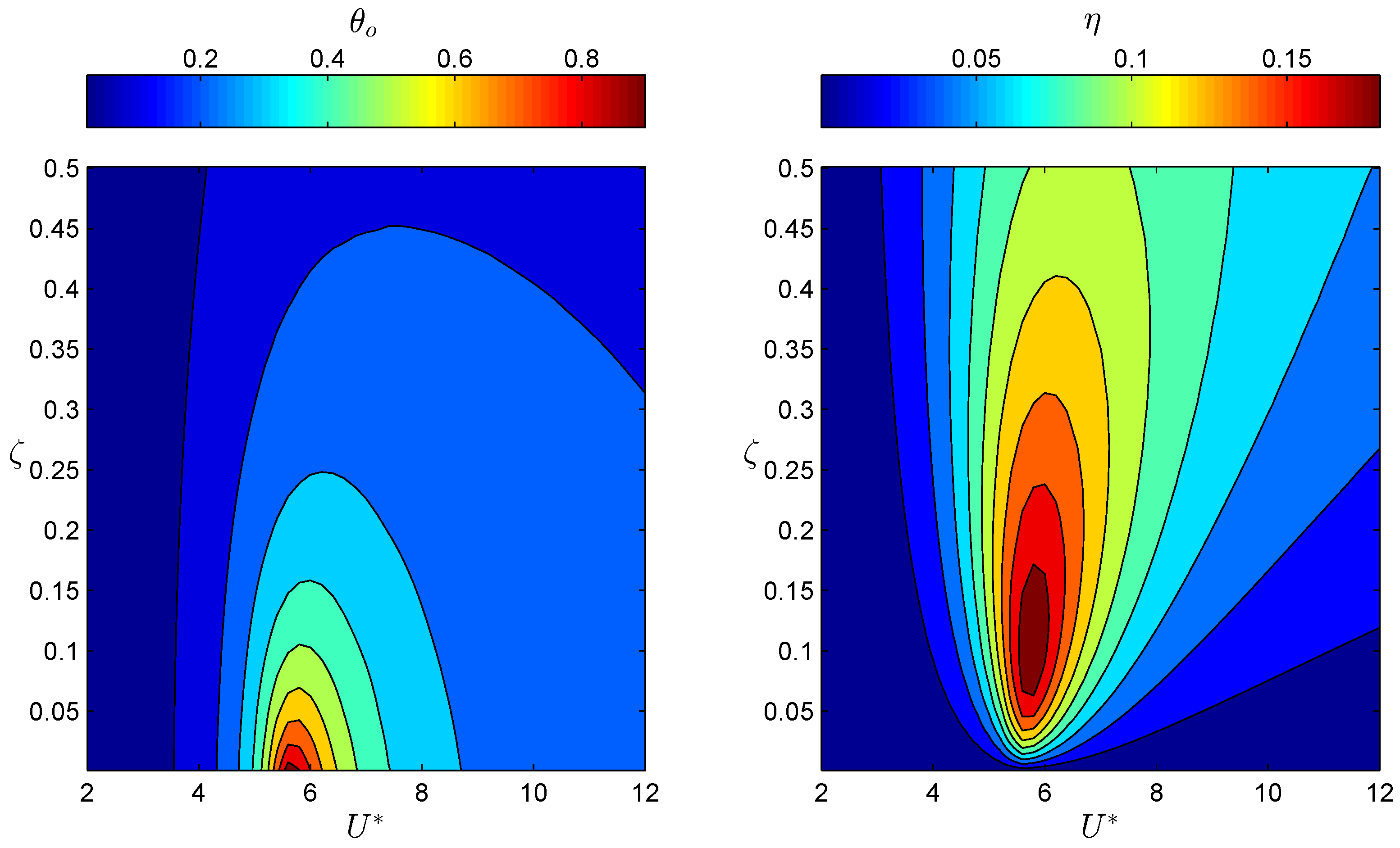Figure 8 shows contours of ${\theta }_o$ and $\eta$ as functions $U^{*}$ and $m^{*}$ at fixed values of $L^{*}=0.8$ and $\zeta =0.01$. It can be seen that ${\theta }_o$ strongly depends on both $U^{*}$ and $L^{*}$. At a fixed $m^{*}$ value, ${\theta }_o$ peaks at a specific $U^{*}$ value that depends on $m^{*}$. In the lower $m^{*}$ range, the location of peak ${\theta }_o$ quickly shifts to higher $U^{*}$ values. Moreover, the $U^{*}$ range of significant ${\theta }_o$ response is wide but shrinks with increasing $m^{*}$. We have observed that irregular oscillations about a non-zero mean deflection angle appear in the higher $U^{*}$ range; for instance, at $m^{*}=1.644$, oscillations about a mean deflection angle appear for $U^{*}>7.2$, which might be related to the shift in the location of peak ${\theta }_o$ at low $m^{*}$ values. The efficiency attains a sharp peak as a function of $U^{*}$ and a global maximum $\eta$ of 18.8% is obtained at $(m^{*},U^{*})=(74,6.4)$. In addition, a local maximum $\eta$ of 14.4% is obtained at $(m^{*},U^{*})=(19.7,6.2)$. Note that axes in the $\eta$ contours have been modified to better depict results in the neighborhood of interest. Figure 9 shows corresponding results for $L^{*}=0.8$ and $\zeta =0.1$. It can be observed that a maximum $\eta$ of 19.5% is now obtained at $(m^{*},U^{*})=(5.24,5.8)$, i.e., the optimum $m^{*}$ in terms of efficiency decreases as $\zeta$ increases while keeping $L^{*}$ and $\zeta$ fixed. This can be attributable to competing indirect and direct effects; a nonlinear decrease in angular response ${\theta }_o$ and a linear increase in power efficiency with $m^{*}$.

3.3. Effect of Damping Ratio

In this section, we focus on the effect of the damping ratio $\zeta$ on the cylinder response and energy conversion efficiency guided by the results of the foregoing sections. For the first series of simulations, we employ a value of $m^{*}=75$, which corresponds to the optimum $m^{*}$ in terms of efficiency at a low value of the damping ratio of $\zeta =0.01$ (see Figure 8). Figure 10 shows contours of ${\theta }_o$ and $\eta$ as functions of $U^{*}$ and $\zeta$ for $(L^{*},m^{*})=(0.8,75)$. It can be seen that ${\theta }_o$ decreases with increasing damping ratio as might be expected. However, $\eta$ attains a global maximum of 19.0% at $(U^{*},\zeta )=(6.4,0.0083)$, which does not correspond to the lowest value of the damping ratio. Nevertheless, the maximum efficiency is attained at a relatively low value of the damping ratio, which is not practical for energy converters where high damping is required in the electromechanical converter (conversion from mechanical to electrical energy). On the other hand, employing a comparatively low value of $m^{*}=5$ yields appreciable response along with high efficiencies over a wide range of reduced velocities, as can be seen in Figure 11. A global maximum of $\eta$ of 19.4% is obtained at $(\zeta ,U^{*})=(0.10,5.8)$ for $(L^{*},m^{*})=(0.8,5)$.

4. Discussion

In this section, the results from simulations regarding the performance of the kinetic-energy harvester based on vortex-induced angular oscillations of a circular cylinder are discussed in a broader context. It should be pointed out that the objective of this preliminary work is to assess the effect of the main design parameters related to the conversion of the kinetic energy of a free stream to mechanical energy of the oscillating cylinder (aerodynamic efficiency). The contours of the efficiency $\eta$ as a function of pairs of the parameters $\{L^{*},m^{*},\zeta ,U^{*}\}$ show that high aerodynamic efficiencies up to 22.1% can be achieved via appropriate selection of the main design parameters. The estimated aerodynamic efficiency is comparable to that of the original VIVACE based on purely transverse vortex-induced oscillations of the cylinder, which can reach 33.2%. However, we expect that the actual efficiency of the new converter will be higher than estimated here, as we have employed a conservative value for the excitation lift coefficient $C_L$. Previous experimental assessment of the novel energy harvester yielded a maximum aerodynamic efficiency $\eta$ of 31.4% [25]. It should be noted that $\eta$ was not directly measured, but estimated from motion results using a theoretical formula for a micro-electric generator. In that experiment, a rigid cylinder made of polypropylene was tested in a water channel, which is estimated to have a mass ratio of the order of 10. However, the actual values of mass and damping ratios were not reported in [25]. Taking into account the working hypotheses and assumptions employed here, our theoretical study yields comparable results and complements the previous experimental work on the effects of mass and damping ratios, thereby providing useful guidance on the best design of the hydrokinetic energy harvester.

The model results clearly indicate that the highest efficiencies are obtained at the smallest $L^{*}$ values. Therefore, the swept frontal area of the proposed converter will be smaller by at least 10% (estimated from $A^{*}$ contours in Figure 6) and the power density of the proposed converter will be increased comparatively to the original VIVACE. The actual performance of the energy harvester might be somewhat different because, for small arm lengths, the motion of the cylinder differs more from a rectilinear oscillation than for large arm lengths. It is known that the frequency of vortex shedding is related to the wake width behind the cylinder, which inevitably depends on the amplitude of transverse oscillation of the cylinder [33]. Although the present hydrodynamic model takes into account only the relative velocity between the moving cylinder and the free stream, it is implicitly assumed—in the selection of the Strouhal number value—that vortex synchronization in the cylinder wake will be similar to that in the case of oscillations of the cylinder purely transverse to the free stream. To our knowledge, this has yet to be studied in the published literature. Nonetheless, we have found that the trends in the contours of the aerodynamic efficiency remain similar for different values of the Strouhal number and, hence, our findings might be expected to hold true in general.

At a given value of the mass ratio $m^{*}$, there is an optimal value of the damping ratio $\zeta$. Conversely, at a given $\zeta$ value, there corresponds an optimal $m^{*}$ value. This might suggest that there exists an optimal value of the combined mass–damping parameter $m^{*}\zeta$ for which the efficiency is maximized. For purely transverse vortex-induced vibrations, the best efficiencies have been obtained at approximately constant $m^{*}\zeta$ values of 0.2 at $Re=3800$ and 0.35 at $Re={10}^4$, according to a parametric study in [19]. For our results presented in Figure 8, Figure 9, Figure 10 and Figure 11, $m^{*}\zeta$ spans a range between a minimum value of 0.005 to a maximum value of 18.75. Over this very wide range, the efficiency attains peak values of approximately 19% at four points listed in

Table 2. Best efficiency points of the novel hydro-kinetic energy converter for $L^{*}=0.8$.

${\mathit{m}}^{*}$	$\mathit{\zeta }$	${\mathit{m}}^{*}\mathit{\zeta }$	$\mathit{\eta }$
74	0.01	0.74	0.188
5.24	0.1	0.524	0.195
75	0.0083	0.6225	0.190
5	0.1	0.5	0.194

. All four points fall within a comparatively narrow range of $m^{*}\zeta$ values with an average value of 0.6. This strongly supports the suggestion of an optimal $m^{*}\zeta$ value. The optimal value of combined mass–damping and the attained best efficiency in the present study are both higher than in reference [19], which might be attributable to the different configurations considered, i.e., angular vs. purely transverse oscillations.

In practice, the mechanical energy captured by the harvester will typically be converted into electrical energy by a generator. For a first approximation, this conversion process can be modeled as added damping in the system [6]. Thus, the total system damping is composed of

$$\zeta ={\zeta }_{\mathrm{struct}}+{\zeta }_{\mathrm{loss}}+{\zeta }_{\mathrm{gen}},$$

(14)

where ${\zeta }_{\mathrm{struct}}$ is the structural damping of the energy converter (kinetic-to-mechanical energy conversion), ${\zeta }_{\mathrm{loss}}$ is the damping associated with power losses in the bearings, belts, etc. of the converter (transmission system), and ${\zeta }_{\mathrm{gen}}$ is the damping associated with the electrical loads (mechanical-to-electrical energy conversion). Only the ${\zeta }_{\mathrm{gen}}$ part of the damping provides harnessed energy. Therefore, a practical system requires relatively high values of ${\zeta }_{\mathrm{gen}}$ combined with minimal values of ${\zeta }_{\mathrm{struct}}$ and ${\zeta }_{\mathrm{loss}}$. It should be noted that the efficiencies reported here are based on the total damping, i.e., in the efficiency computation using Equation (13) $\zeta$ should be replaced by ${\zeta }_{\mathrm{gen}}$. Therefore, actual efficiencies will be slightly lower than reported. However, this is partly compensated by the underestimation of efficiency due to the use of a conservative excitation coefficient.

Given the considerations regarding damping given in the foregoing paragraph, the total damping of the system—including the electrical generator—has to be high, which necessitates the use of relatively low $m^{*}$ values. As an example, taking $m^{*}=5$, a nearly optimized design will have a total damping of $\zeta =0.10$. Interestingly, the latter value is close to the optimal one $(\zeta =0.12)$ of the VIVACE converter at its best efficiency point [6]. At lower mass ratios, e.g., $m^{*}<3$, the operation of the system might be compromised, as we have noted that small amplitude oscillations about a non-zero mean angle can be induced.

In turn, the total damping ratio of the system should correspond to the optimal one for the given mass ratio ($\zeta \approx 0.1$ for low $m^{*}$ values). Since the damping ratio depends on the system damping c (including damping in mounting structure, losses, and electric loads) as well as on the stiffness k of the supporting springs, the actual values of c and k have to be jointly determined, taking into account the fact that peak efficiencies are achieved within a narrow band of reduced velocities $(U^{*}\approx 5.8)$. These requirements result in the following relationship:

$$U^{*}\zeta =\frac{c\pi U_{\infty }}{kD}\Rightarrow k\approx 5.4\frac{U_{\infty }}{D}c.$$

(15)

Pairs of $(c,k)$ values can be selected on the basis of the above relationship, taking into account the practical limits of these mechanical parameters for the intended size of the equipment. This allows for a versatile mechanical design of the converter without directly affecting the aerodynamic efficiency.

At Reynolds numbers lower than assumed here, i.e., $Re<{10}^3$, the aerodynamic efficiency might be expected to be limited by viscous effects. As a consequence, the minimum diameter of the cylinder is determined by the minimum required Reynolds number for a specific fluid (air or water) at a given wind or current speed. In practice, this factor does not pose a substantial constraint even at low speeds. For example, the minimum diameter for a wind speed of 0.5 m/s is 3 cm and that for a water current speed of 0.1 m/s is 1 cm. The weight (mass) of the oscillating structure is determined by the mass ratio requirement discussed in the previous paragraph $(m^{*}\approx 5)$. The requirement for low mass ratios results in very lightweight structures in air, which makes the use of the proposed kinetic-energy converter impractical in this case. Therefore, the use of the converter mostly aims to harness the hydro-kinetic energy of water currents. Based on the above considerations,

Table 3. Estimated power output per unit span of the cylinder generated by the novel hydro-kinetic energy converter.

${\mathit{U}}_{\mathit{\infty }}$ (m/s)	D (cm)	m (kg/m)	P (mW/m)
0.1	1	0.39	1
0.1	5	9.82	5
0.1	25	245.4	25
0.5	1	0.39	125
0.5	5	9.82	625
0.5	25	245.4	3125
1.0	1	0.39	1000
1.0	5	9.82	5000
1.0	25	245.4	25,000

shows calculations of the power generated (per unit length of the cylinder) by the novel hydro-kinetic energy converter at representative current speeds and cylinder diameters.