2.2. Model Description
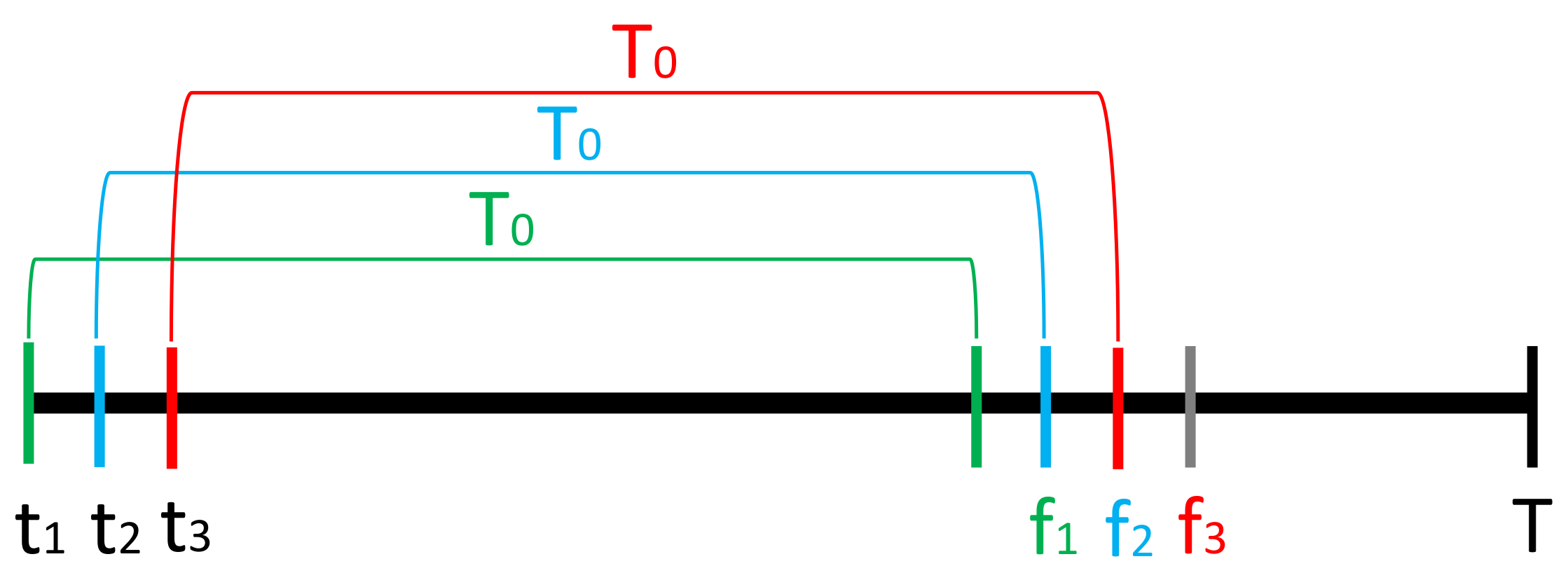
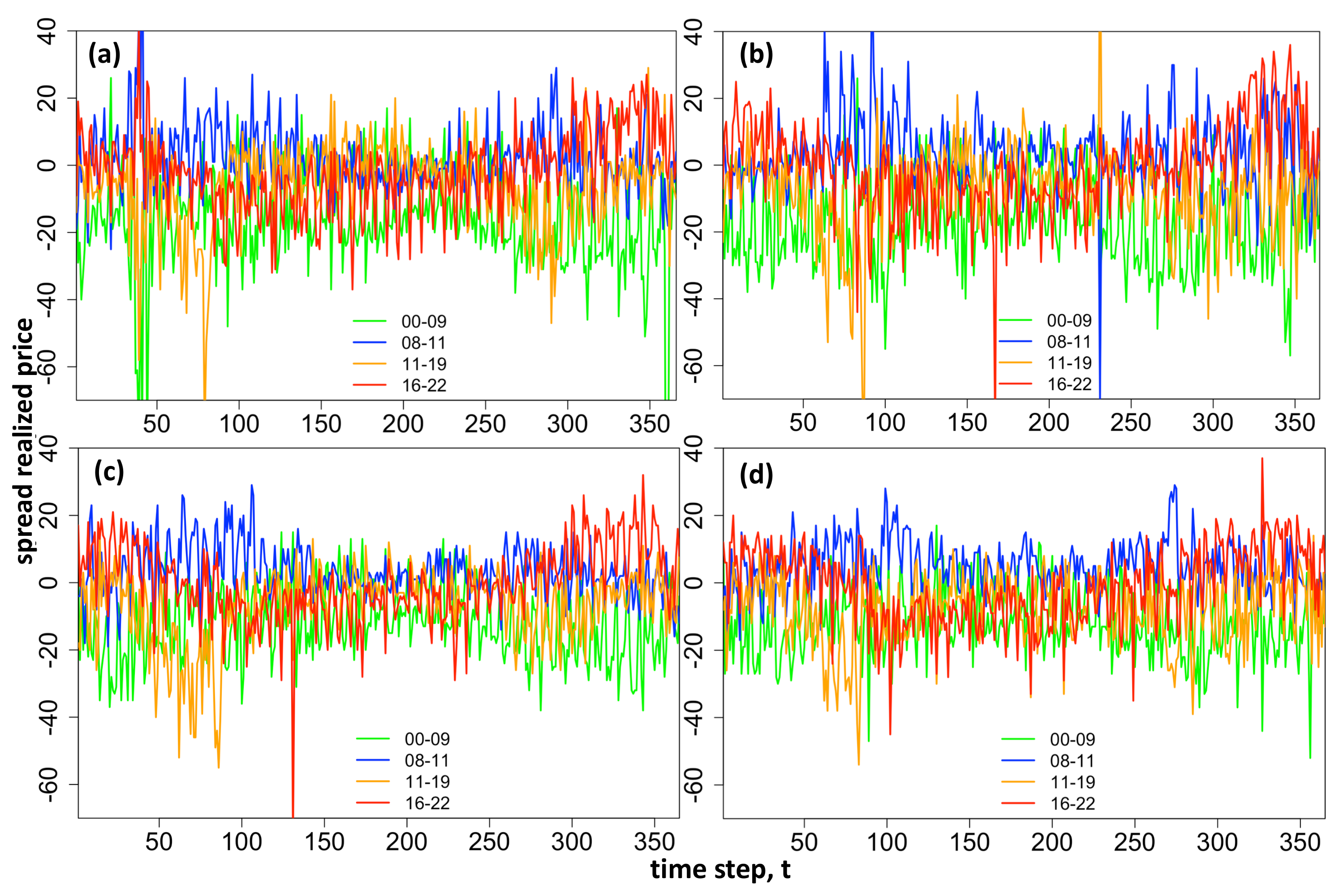
An intraday spread, , between two hours, denoted by spread number s, of the day-ahead electricity spot prices, is calculated by taking away the later hour price information from the earlier one, resulting in a positive spread if later hour is less expensive and negative otherwise. Each day therefore comprises of 276 separate spreads, and with 1917 days in the time series, the full data set is denoted by . Each electricity spread time series is tested for stationarity using the Augmented Dickey–Fuller test (adf.test() with 10 lags and a linear trend) and is confirmed to be stationary at the 1% significance level.
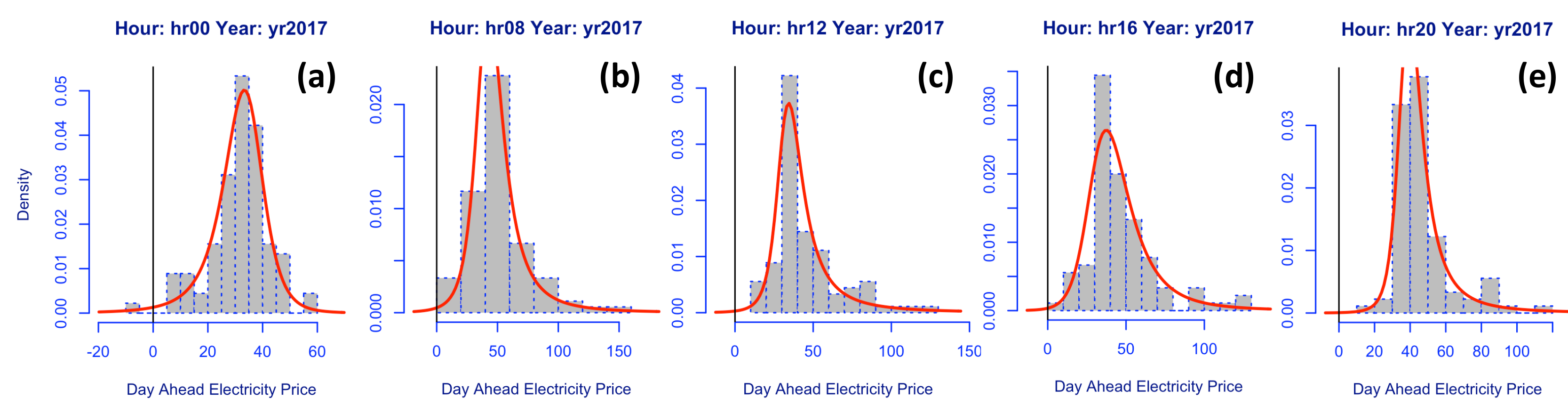
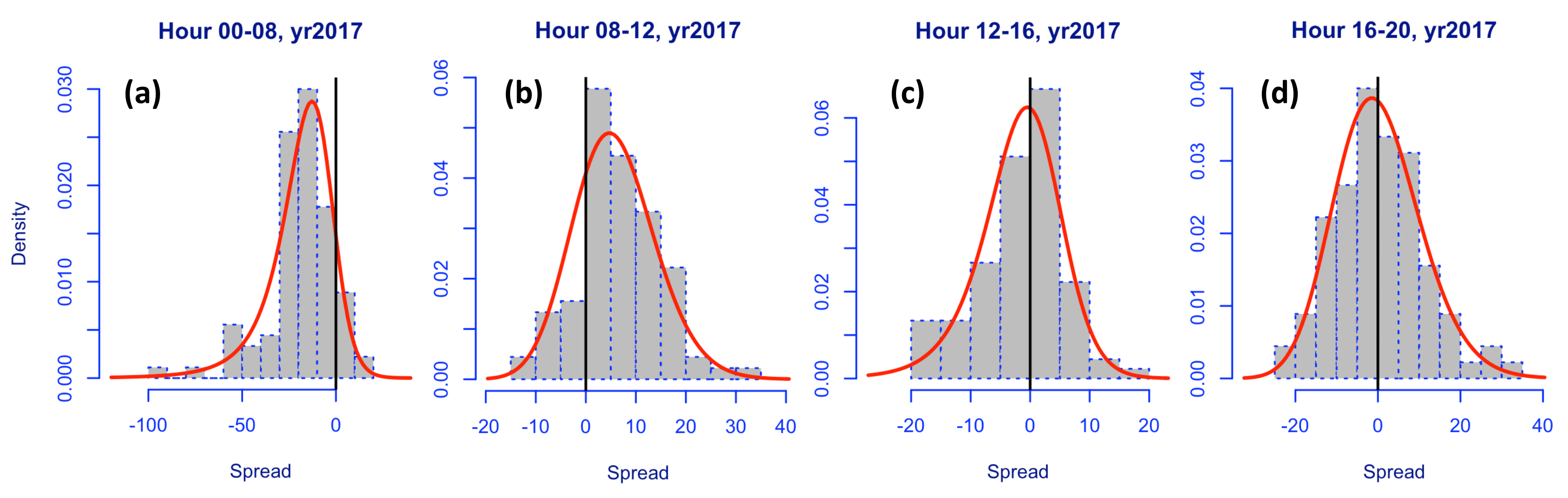
We plot example histograms for intraday spreads obtained between hours 00–08, 08–12, 12–16, 16–20 for the example year 2017.
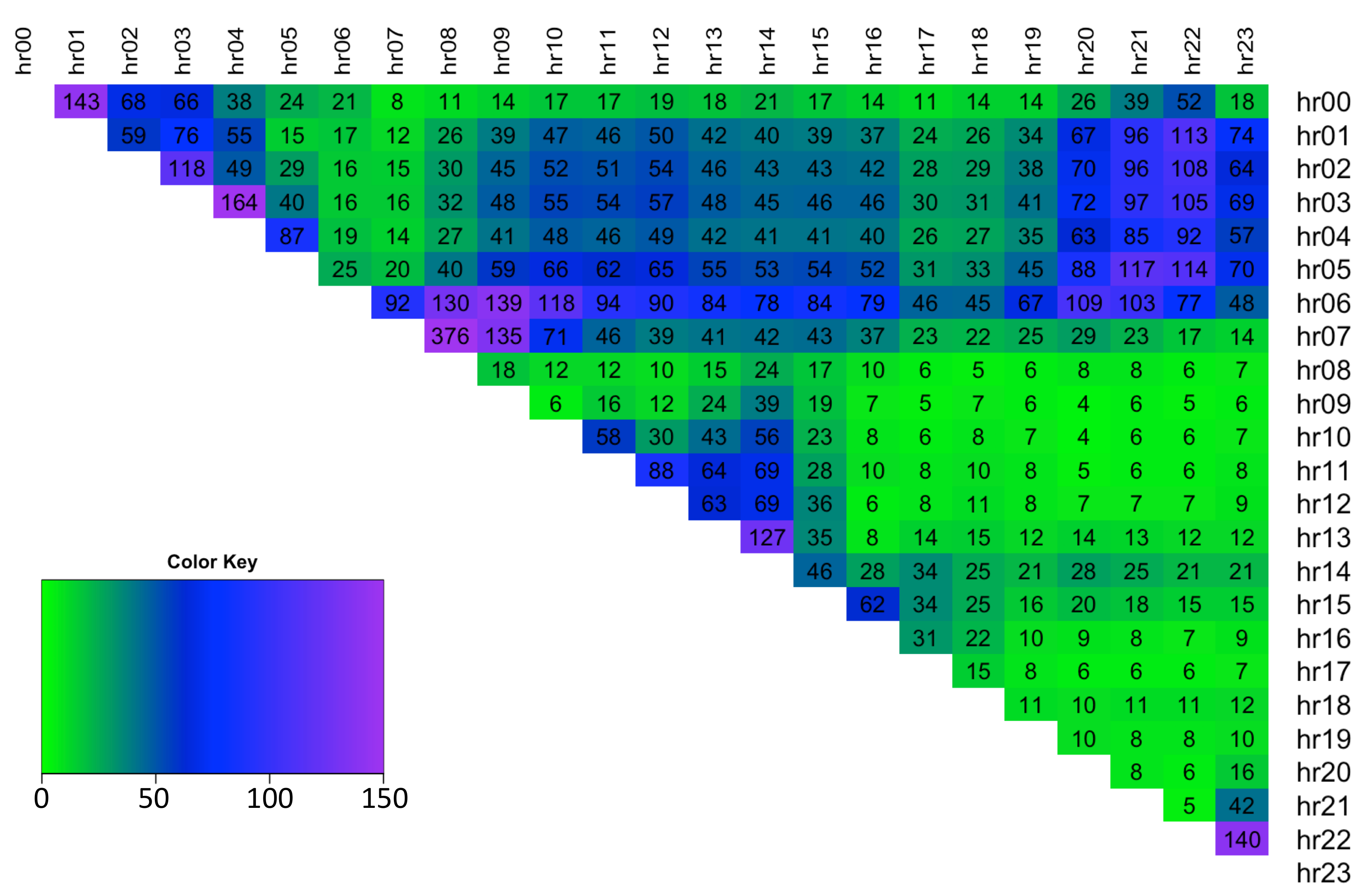
Figure 3 depicts the high skewness and kurtosis of the spreads and shows the variation between spread distribution shapes for different hours of the day. Note data is symmetrical about the diagonal thus only the upper diagonal is plotted.
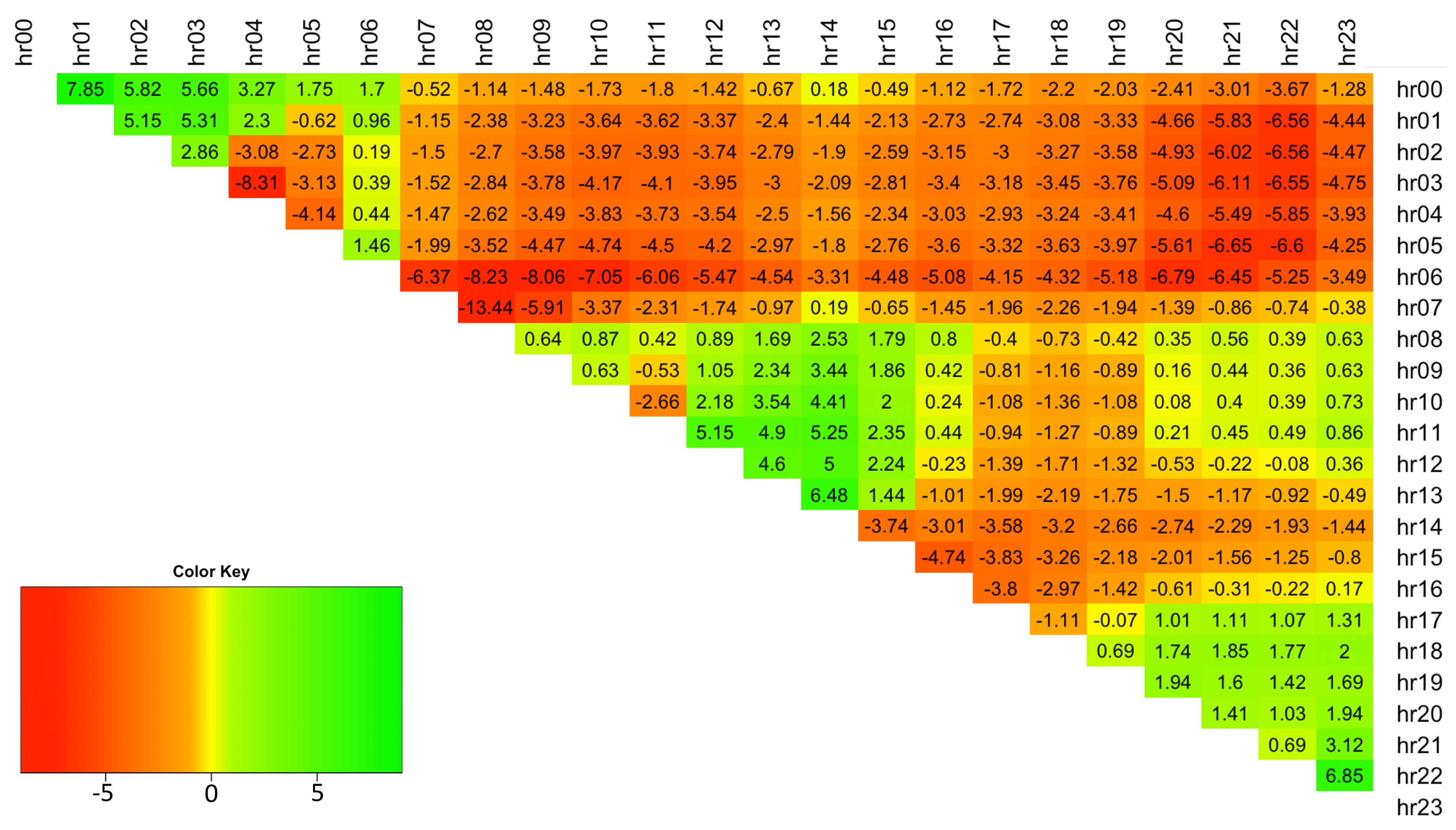
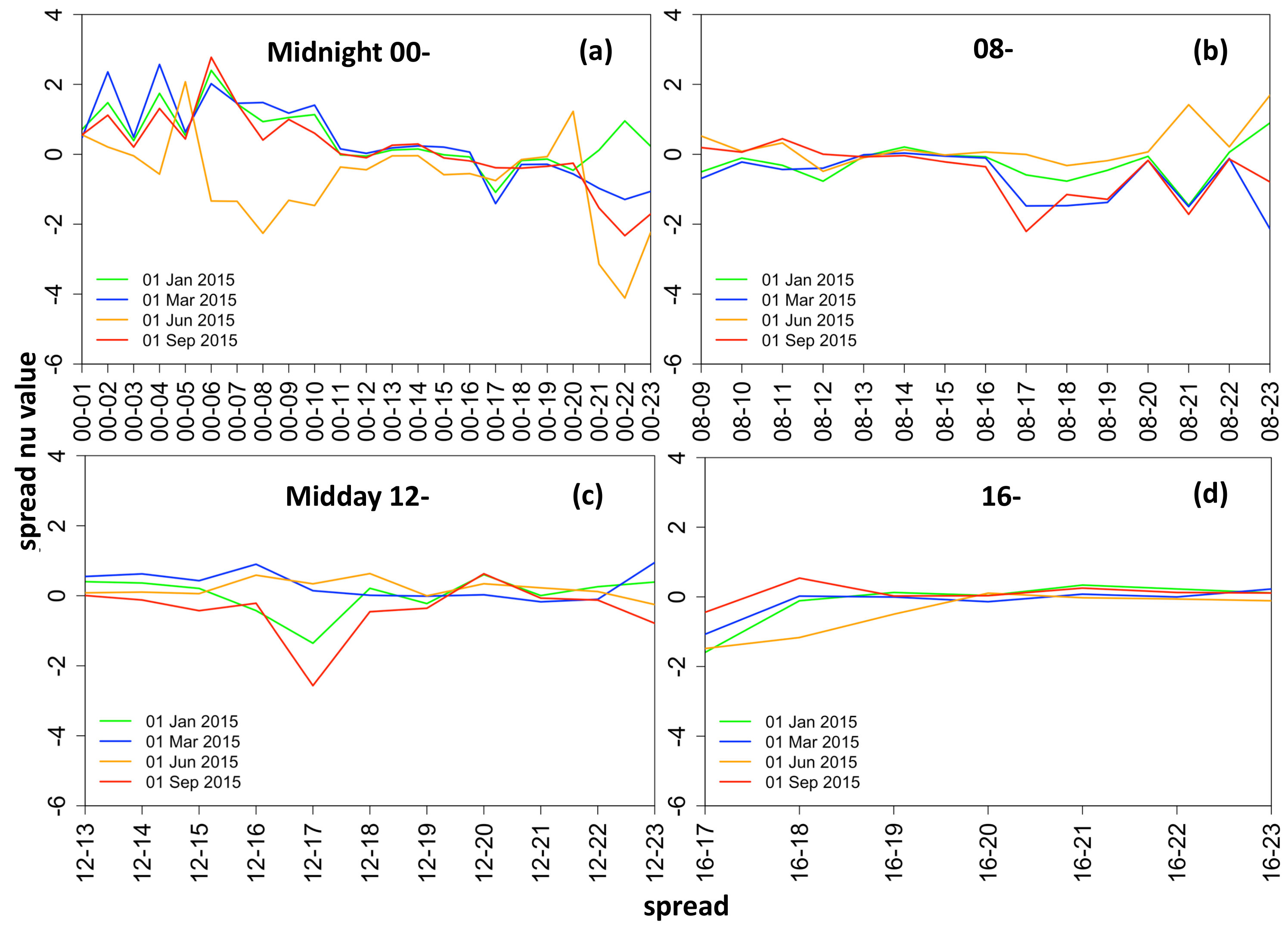
The hourly spread data possesses a high degree of skewness in the range [−8.31, 7.85] (see
Figure 4). The plot shows that typically the spreads are negatively skewed (note spreads are obtained by
).
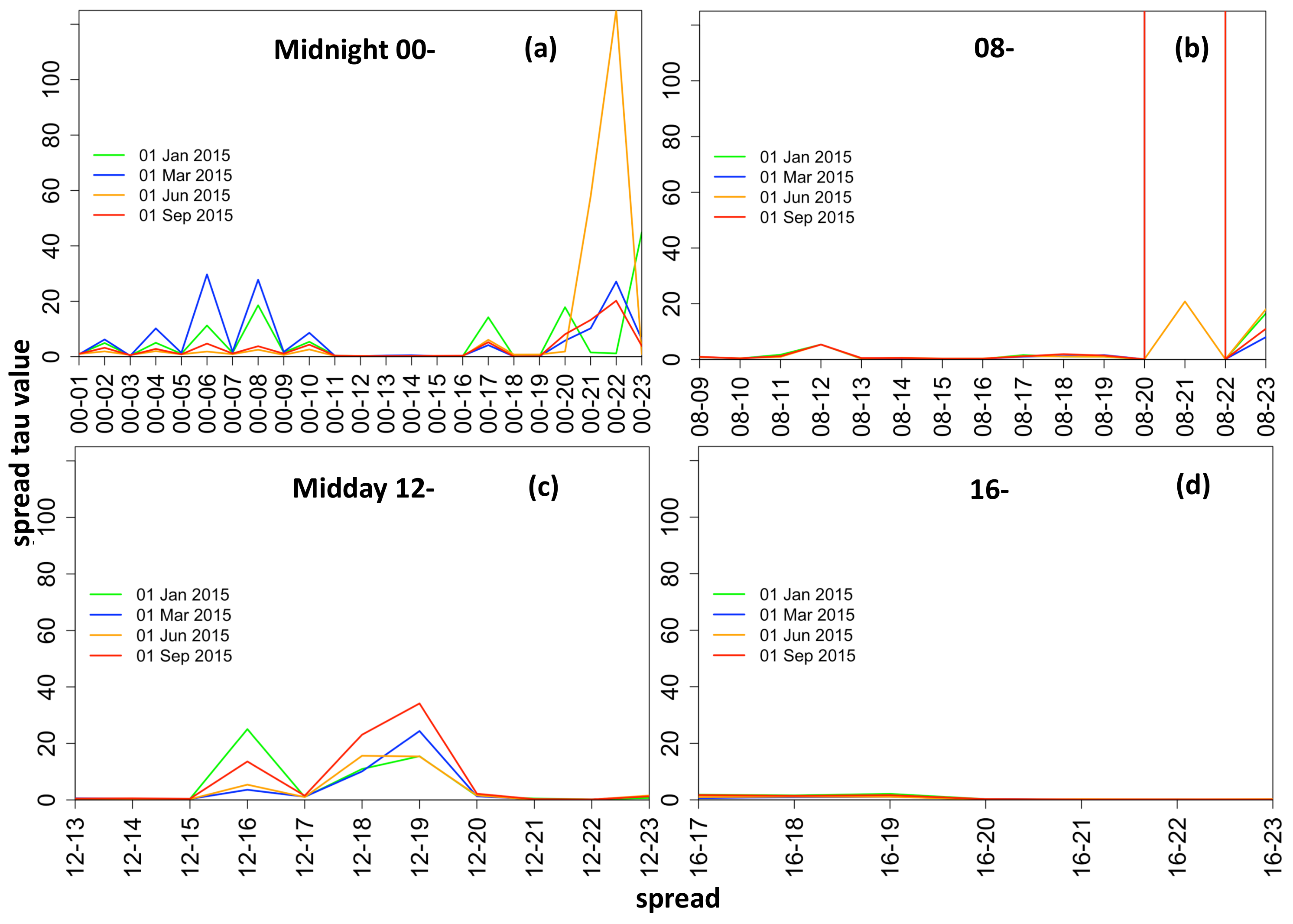
The hourly spread data displays a high degree of positive excess kurtosis and thus indicates that spreads have Leptokurtic distributions in the range of [3.8, 140] (see
Figure 5).
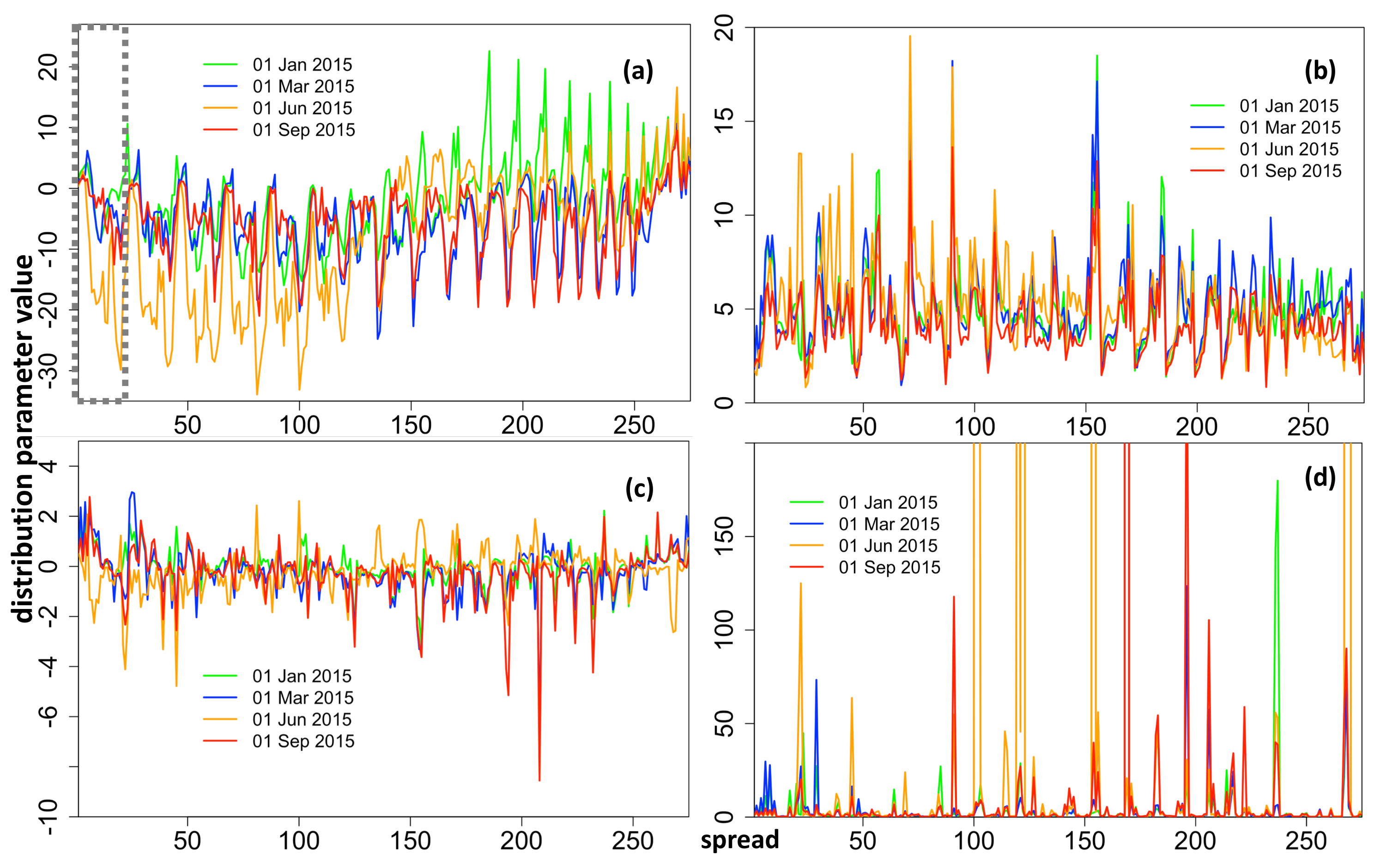
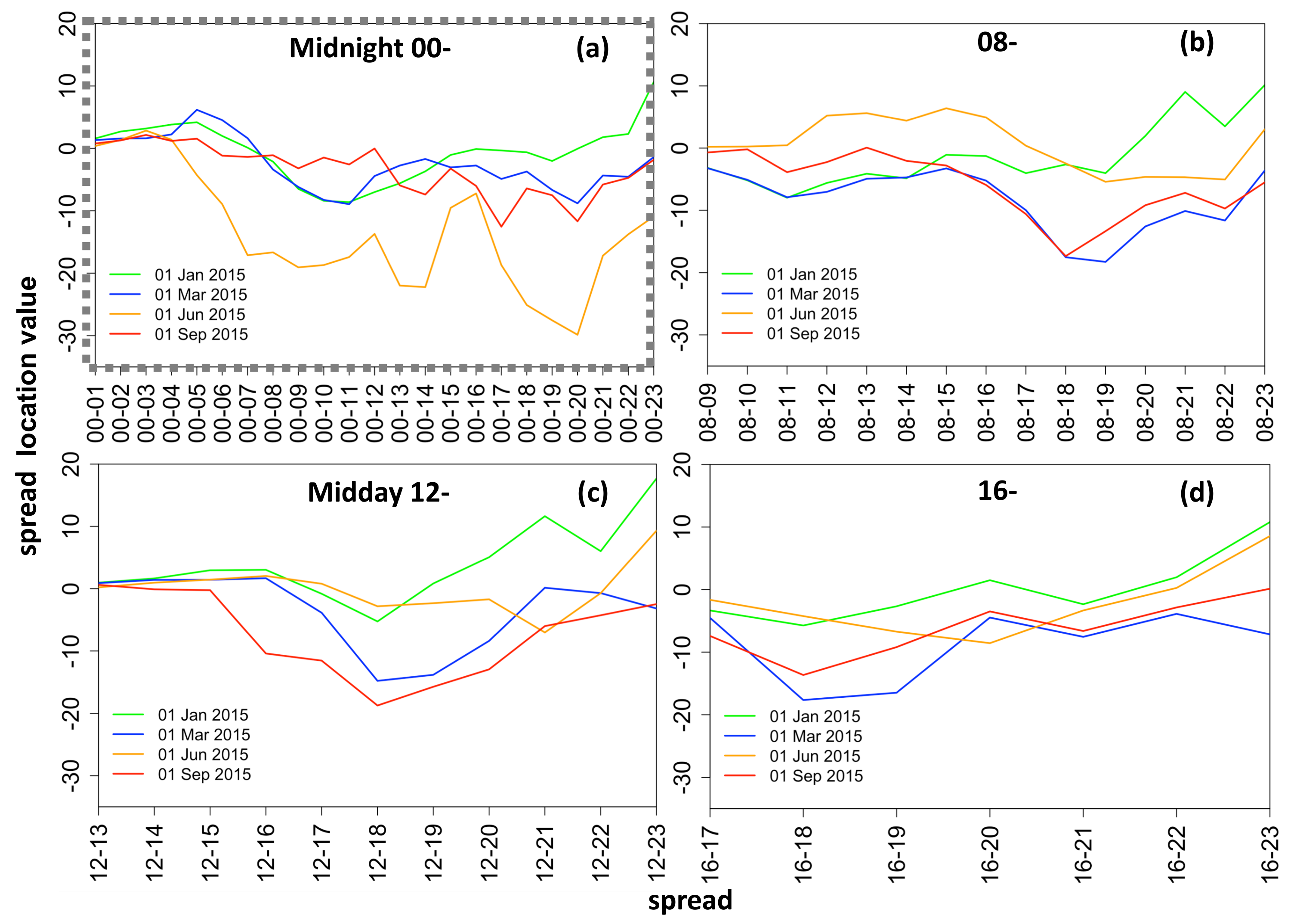
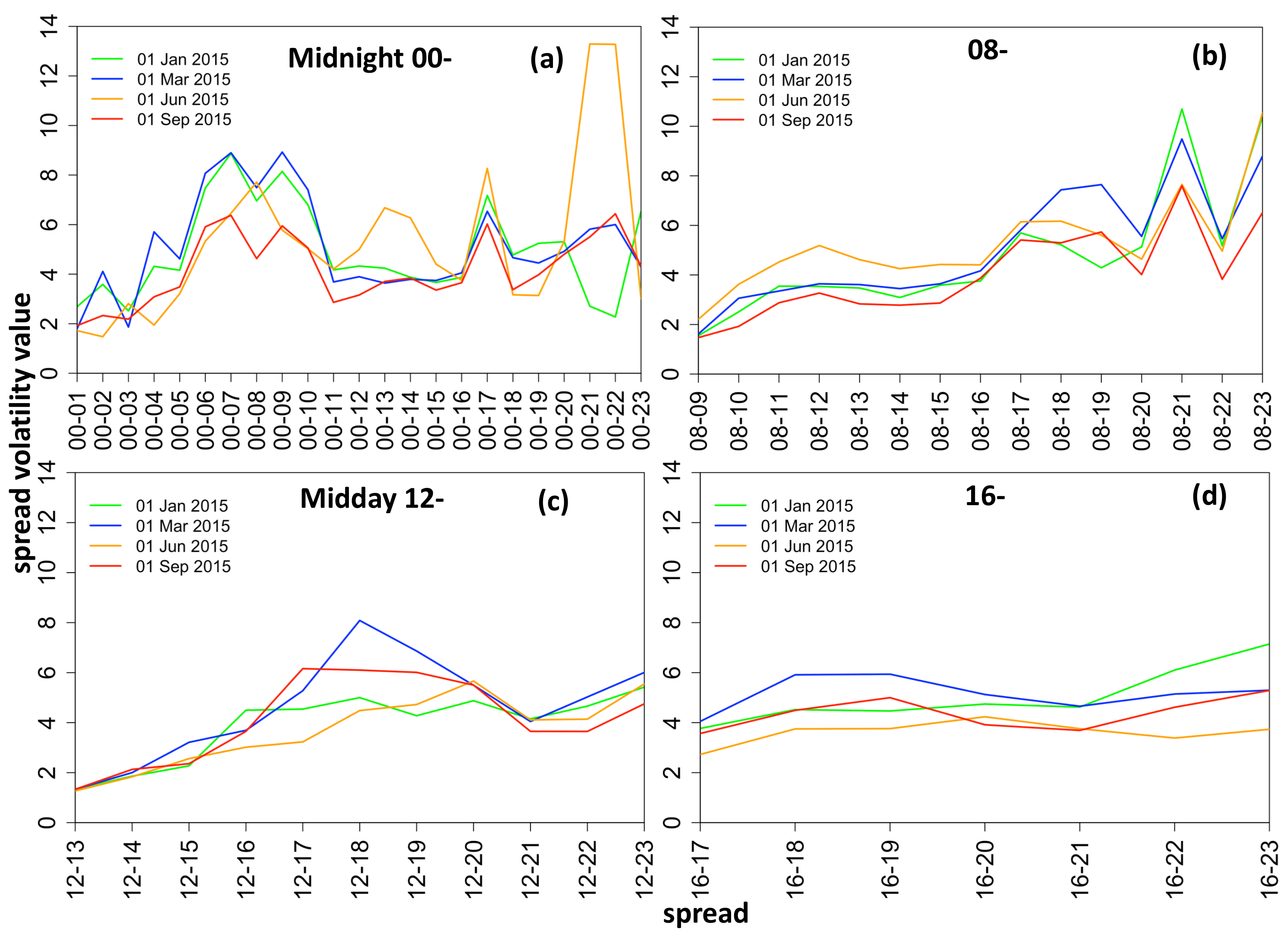
Therefore, given the above analysis, we chose to model the full four-parameter distribution of electricity price spreads at each time step (day), t. The spreads between exogenous variables are likewise formed by taking away the later hour values from the earlier ones in all cases except for the gas forward prices, coal forward prices and the dummy variable, for which only the daily, rather than hourly, values are available. Hence the following exogenous variables are considered for modeling : (1) spread of the lagged intraday electricity price, (2) gas Gaspool forward daily price, (3) coal ARA forward daily price, (4) spread of wind day-ahead forecast, (5) spread of solar day-ahead forecast, (6) dummy variable taking the value of 1 for weekends/holidays, (7) spread of the day-ahead total load forecast, and (8) an interaction load variable, calculated as i.e., an average of the load for the two hours from which the spread is calculated, weighted by the load spread obtained for those hours. This variable provides interaction of in order to account for the rate of change in load. The full exogenous variables spread data is a 3D matrix denoted by , where the first column is a vector of 1s used in the calculation of the off-set.
Estimation using the Generalised Additive Model for Location, Scale and Shape (GAMLSS) framework [
11] facilitates modeling each parameter (
) of the response variable’s distribution as a function of explanatory variables. The range of possible distributions includes both exponential family (as per Generalised Linear Model (GLM)) and general family distributions, which allow for both discrete/continuous and highly skewed/kurtotic distributions (unlike GLM). The probability density function of response variable for
T observations is given by
, where
indicates a number given for each unique spread between two intra-day hours,
is a vector of distribution parameters, and
represents the distribution of spread number
s on day
t. We use parametric linear GAMLSS framework which relates distribution parameters to explanatory variables by
where
specifies the distribution parameter corresponding to
respectively;
is a vector comprised of values for distribution parameter
k over
time steps (i.e.,
,
);
T is the number of observations;
is the monotonic link function of distribution parameter
k;
is the linear predictor vector for distribution parameter
k;
vector of coefficients learnt for parameter
k;
is the number of significant exogenous variables for parameter
k obtained at 5% significance level; and
is the design matrix with each column containing spread data for significant independent variables. Equation (
1) can be re-written for each distribution parameter as:
The choice of the link function influences how the linear predictor (i.e., systematic component
) relates to each parameter. For example, a log link function for the standard deviation
results in the relationship
, hence the distribution parameter itself is obtained through a transformation
. Parameters
are calculated by maximizing the penalized likelihood using an RS algorithm which does not require calculation of the likelihood function’s cross derivatives, but is a generalisation of the algorithm for fitting Mean and Dispersion Additive Models, (MADAM) as in [
11]. The RS algorithm is a simple and fast method for larger data sets which does not require accurate starting values for distribution parameters to ensure convergence (constant default starting values are typically adequate) [
12]. The RS algorithm is more suited for cases where the parameters of population probability density functions are information orthogonal and is reported by authors to be successfully used for the convergence of all the suitable distributions defined within the GAMLSS framework, although it may occasionally be slow.
To model electricity spreads within the GAMLSS approach, the distribution parameters sigma and tau should take positive values only but the mu and nu should be able to take either positive or negative values. Therefore distributions with the following link functions for each parameter are considered (see
Table 1): location (mu):
identity; scale (sigma):
log; shape (nu):
identity; shape (tau):
log.
There are seven candidate distributions which we consider to be sufficiently flexible and which correspond to the necessary link function specifications: Johnson’s SU, Johnson’s original SU (JSU), skew power exponential type 1 (SEP1), skew power exponential type 2 (SEP2), skew t type 1 (ST1), skew t type 2 (ST2), and skew t type 5 (ST5). The Box–Cox power exponential and Box–Cox t distributions are not suitable due to only being defined on the positive interval
, while the electricity spread data is highly skewed and kurtotic (see
Figure 4 and
Figure 5). The skew t type 3 and 4 are also unsuitable since they are only defined for positive skewness yet the spread data is often negatively skewed.
The expected value of a random variable
for each distribution in
Table 1 does not in general equal to the location parameter
. To be precise, it is given by
, where
is the standardized value of
, the expectation of
is not always zero and is specified for each distribution separately (see Appendix Equations (A1)–(A4) for details), and
are the location, scale and shape parameters of the given distribution at time step
t. In the case of Johnson’s SU and skew t type 1 distributions, the expected value does equal the distribution location parameter,
. Large fitted/forecasted tau values are capped at 100 for algorithmic convergence.
2.3. Distribution Selection
This section performs a thorough analysis of candidate distributions, shown in
Table 1, to establish which of the distributions fits each spread hour data the best. This allows us to subsequently perform out-of-sample forecasting analysis using a rolling window estimation technique, presented in
Section 3, where the best-chosen distribution is used to fit a model to each spread number and perform 1-step ahead forecasts on a rolling basis.
For model specifications, we begin by analysing which of the seven-candidate distributions fits each spread hour the best. We also analyse whether using a single distribution for modeling all of the spread data is a viable possibility as this might be useful for applications requiring analytical generality. The analysis is divided into two main steps: (a) simple distribution fit, where each distribution of
Table 1 is fitted to the spreads in the training data set and the Akaike Information Criterion (AIC) is used to assess the goodness of fit; and (b) factor-based distribution fit, where for each spread hour, the candidate distributions resulting from the analysis of step (a) are used to build a model using exogenous factors. The fit of these models is assessed using a validation data set and a number of goodness of fit measures.
Methodology
To perform a thorough analysis when selecting the best distribution for each spread, we use a training data set, comprised of the first 60% of the spread time series. This is used for model fitting, following which a validation data set, comprised of the next 20% of the spread time series, is used for building forecasts and model evaluation. The validation set is used when there is a question of model selection prior to final out-of-sample forecasting in the backtesting set of data [
13]. The validation thus ensures that the predictive power of our trained models is evaluated on the unseen (validation) data set rather than on the fitting in-sample data. This is to avoid over-fitting and ensures that the final backtesting 20% of the data has neither been used for model fitting nor model selection.
The simple distribution fit analysis is performed using the training data,
. Therefore, for each spread number
and each distribution
of
Table 1, we build a model
, resulting in
models. The AIC criteria of models
, obtained for spread number
s, are ranked in ascending order and the distribution corresponding to the model with the lowest AIC criterion is selected as the “distribution of best fit”. Occasionally GAMLSS failed to fit the distribution to the spreads data, in which case that distribution was omitted for that spread. This problem was encountered for spread hours and distributions: 00–01 SEP1, 03–04 SEP2, 12–13 SEP1.
The results show that skew t type 5 distribution is selected most often as the distribution of best fit based on this simple selection criterion (see
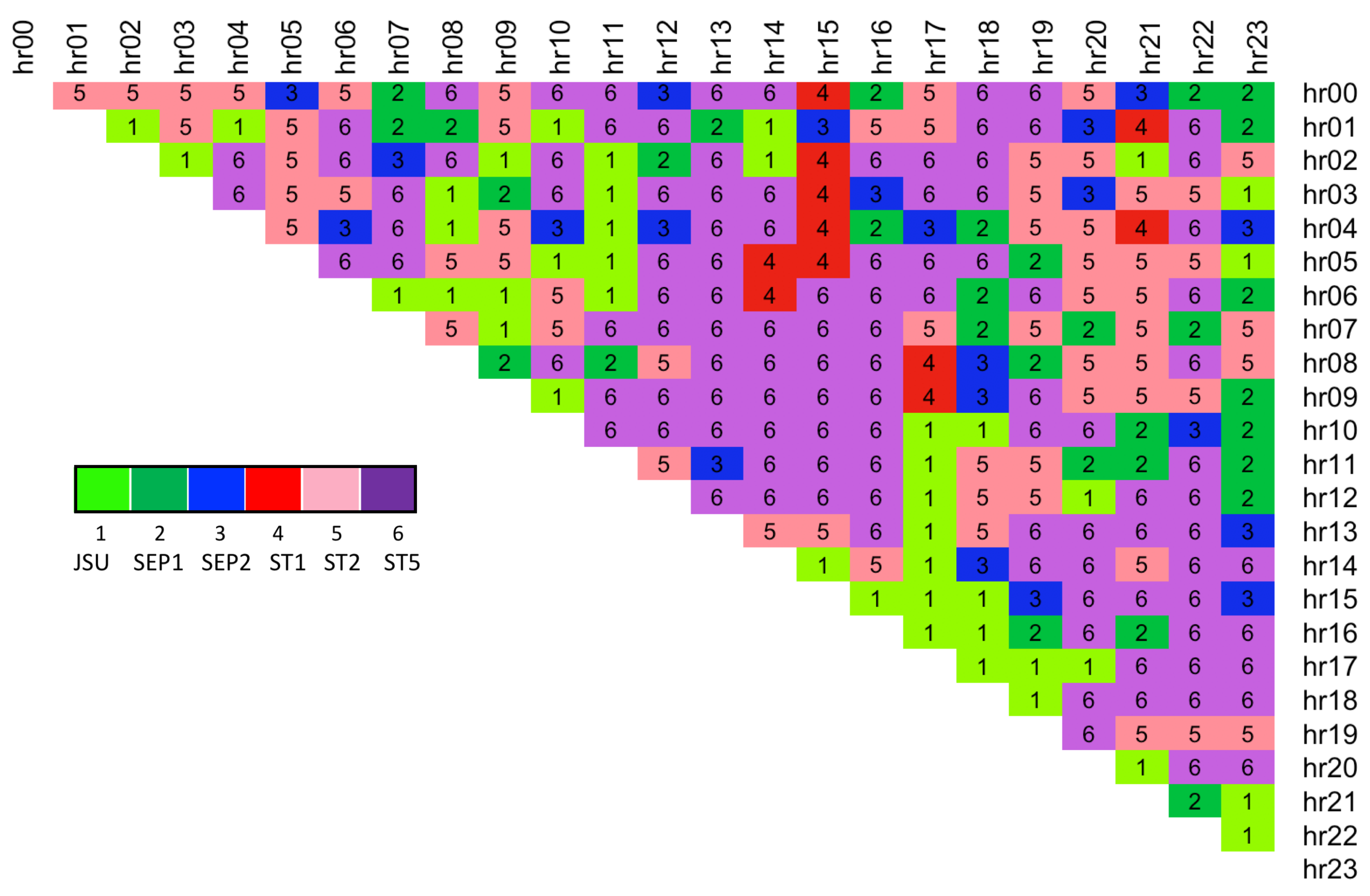
Table 2). It is closely followed by the same family Skew t type 1 distribution. Overall, all of the distributions except JSUo are indicated as potentially of the best fit for the training spread data. A more detailed breakdown of the spread hours for which each distribution was selected is displayed in
Figure 6. We use the result to further analyse the six possible distributions with an factor-based distribution fit method.
The results of simple distribution fit indicated that six out of seven continuous four-parameter distributions could be used for modeling electricity spread data (see
Table 2), which are
—JSU,
—SEP1,
—SEP2,
—ST1,
—ST2, and
—ST5. Hence we proceed with a factor-based analysis by estimating each time-varying parameters of the candidate distributions using exogenous variables within the GAMLSS framework. The training data set is comprised of the dependent
and independent
variables, where for each spread number
s, under distribution
, the initial equations relating each distribution parameter to its linear predictor are:
where
is initial vector of coefficients for distribution parameter
k,
is the initial vector of independent variables where
is the spread of lagged day-ahead electricity price,
is the gas Gaspool forward daily price,
is the coal ARA forward daily price,
is the spread of wind day-ahead forecast,
is the spread of solar day-ahead forecast,
is the dummy variable taking value 1 for weekends/holidays,
is the spread of the day-ahead total load forecast, and
is the interaction load variable.
The models are specified using iterative updating of the equations for each distribution parameter, where the refinement is performed by deleting the most insignificant variable one-by-one and re-estimating the model, until all variables are significant at 5% (see Algorithm 1). This results in
models containing the estimated coefficients. However during the process it became apparent that some distributions were not suitable for modeling certain spreads within the GAMLSS framework. Convergence was not achieved for some distribution parameters, typically
and occasionally
(see
Appendix C.1) and whenever this happened the distribution was omitted from candidacy for that spread.
Evaluation
The models estimated using the factor-based distribution fit are analysed in four ways: (1) producing the expected value fit over the training data, (2) producing the expected value fit over validation data (comprising next 20% of unseen time series, at data points ), (3) analysing the goodness of fit over the validation data using Root Mean Squared Error, and (4) analysing the goodness of fit over validation data using Pinball Loss function measure.
| Algorithm 1 Factor-based distribution fit—model specification and estimation |
- 1:
for each spread number do - 2:
Extract full training data design matrix i.e., time steps - 3:
for each distribution do - 4:
Initialise iteration number - 5:
Initialise model using RS algorithm [ 11] - 6:
while any insignificant at 5% do - 7:
- 8:
Find most insignificant coeff. (except intercept) across all k - 9:
Remove exogenous variable associated with from Equation for k and from - 10:
Re-estimate model using RS algorithm
|
Expected Value Fit Over Training Data
Although the main focus of the methodology is to fit and forecast the density functions, it is a useful specification check to initially look at the calibration of the mean values. Therefore, the fitted distribution parameters
for each distribution
are used to find the fitted expected value
of the training spread price data for
and training data points
using expected value expression relevant to each distribution (see
Appendix B).
Expected Value Fit Over Validation Data
The fitted models
, containing the estimated coefficients for each spread number
under each distribution
, are used to forecast the distribution parameters,
over validation data. We note that the same estimated model
is used to build the forecasts over validation time series, i.e., each vector of estimated coefficients
for distribution parameters
is re-used at each time step
t to make the predictions. Once the distribution parameters are forecasted the expected value of the spread is calculated using
Appendix A Equations (A1)–(A4).
Goodness of Fit Measure—Root Mean Squared Error
The Root Mean Squared Error (RMSE), was additionally used to check the accuracy of the forecasted expected value of the spreads over the validation data set. The RMSE is calculated for each spread
and for each distribution
, using:
The distribution resulting in the lowest RMSE was selected as the best. As the expected value at each time step t is calculated from all of the four forecasted parameters , the RMSE measure provides a goodness of fit based on the forecast for the entire distribution specification.
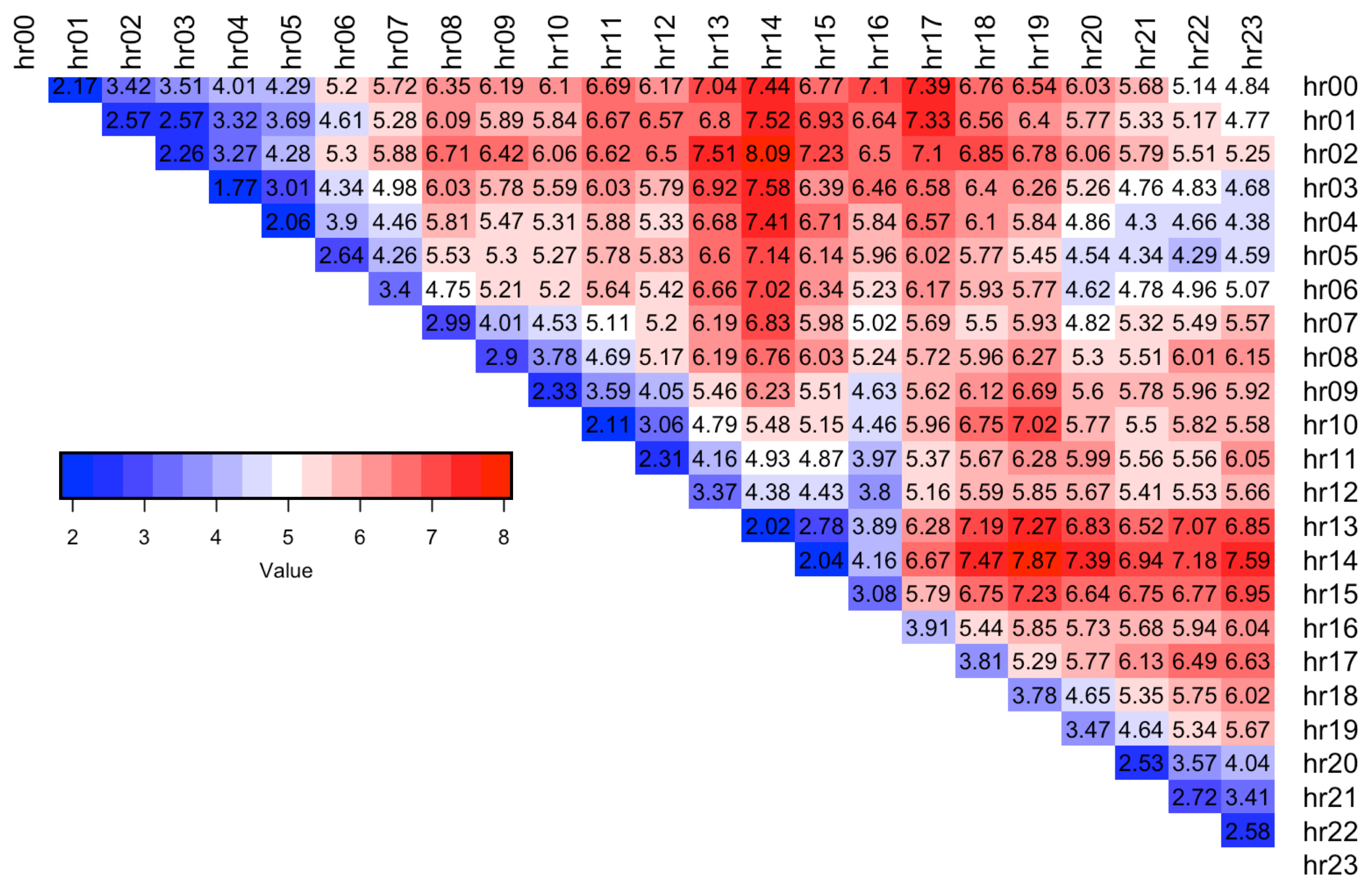
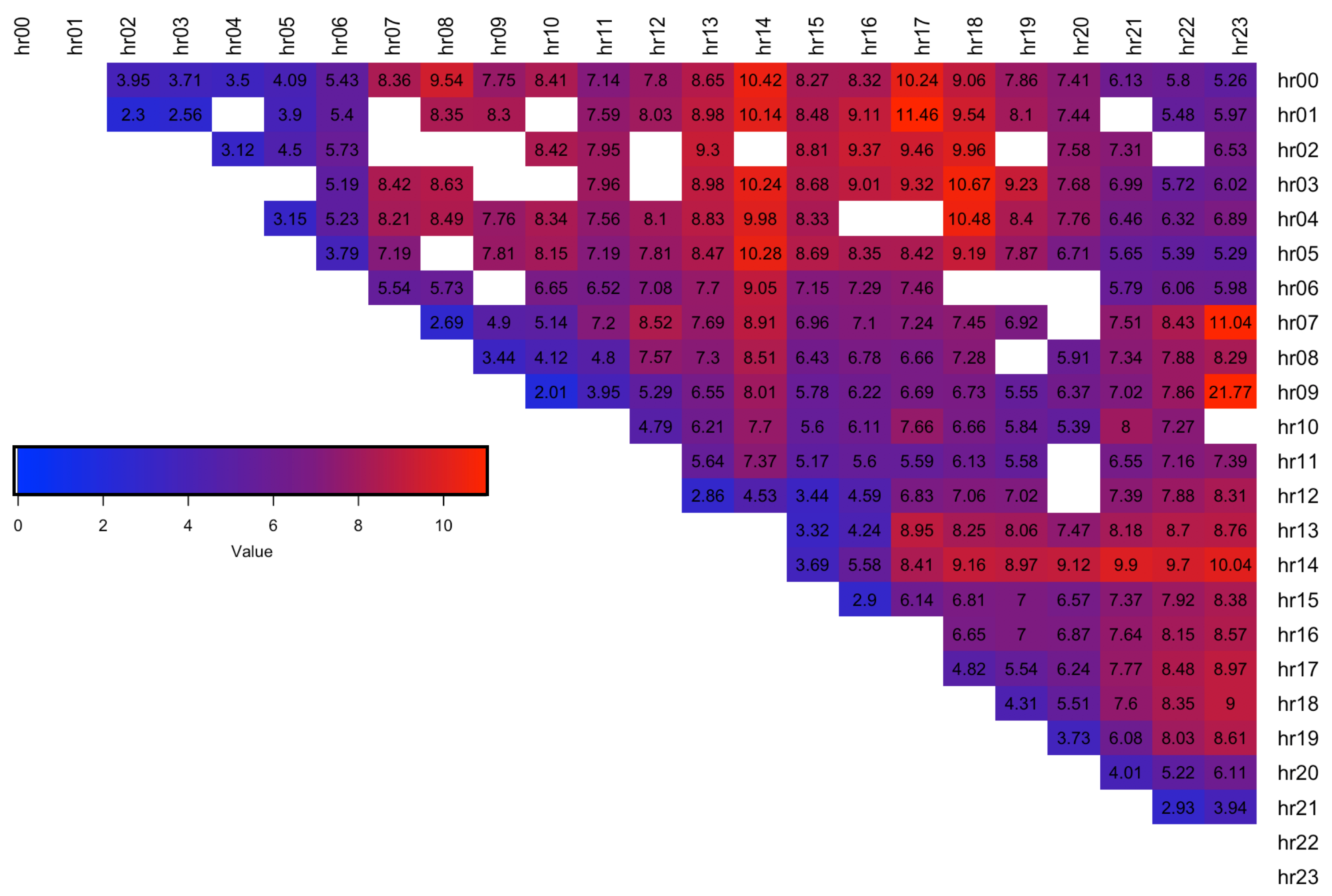
The results are summarised in
Table 3, which shows that ST5 distribution was used to form models corresponding to the lowest error across
of the spreads. This is in line with the finding of the simple distribution fit over the spread training data which indicated that ST5 is chosen as the best distribution most often (see
Table 2). A detailed breakdown of best distribution assignment for each spread hour and the corresponding RMSE values are shown in
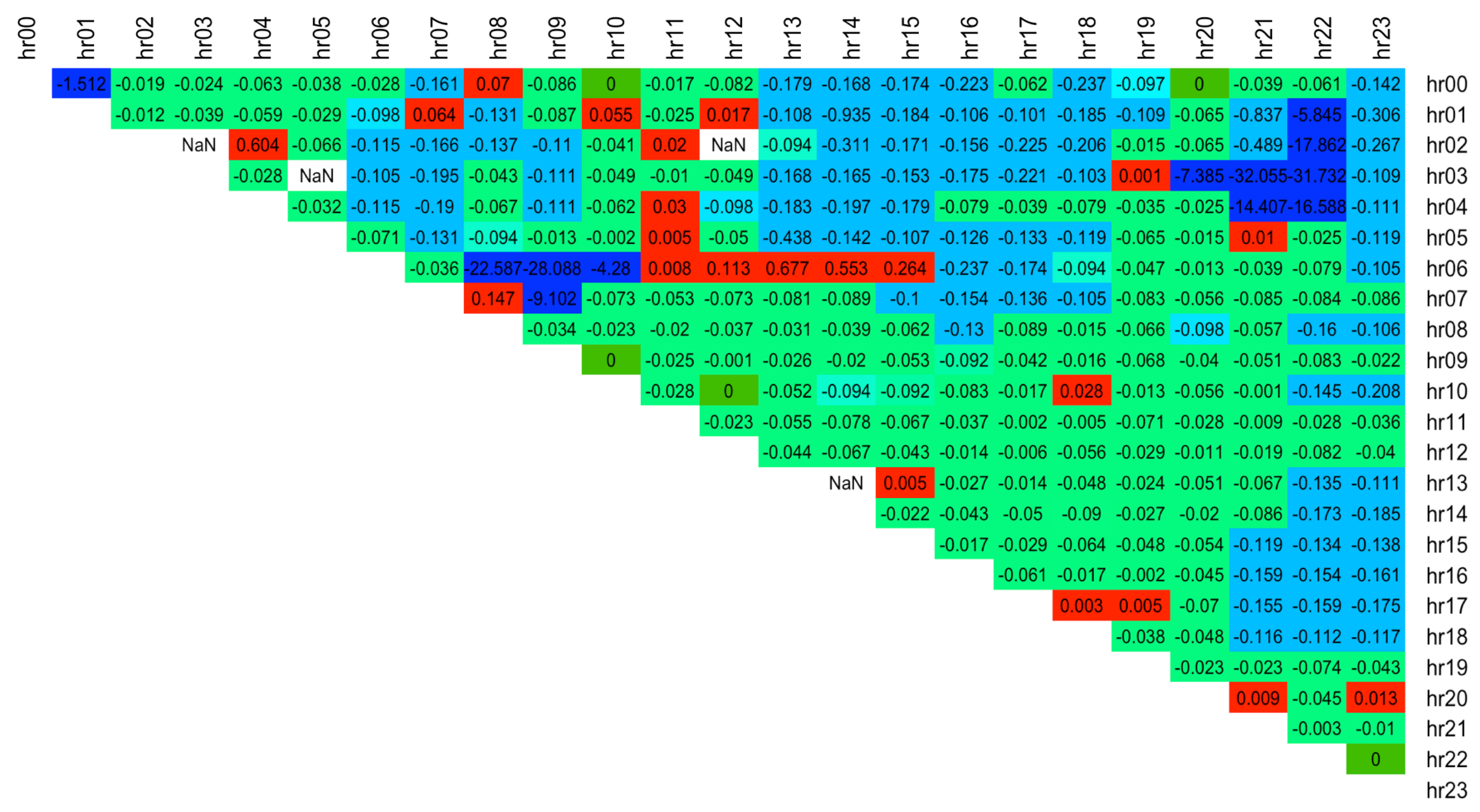
Figure 7 and
Figure 8 respectively, where blue indicates a lower error. The results show that spreads with hours 13.00, 14.00 are the hardest to forecast since they have the highest RMSE error (dark red).
Goodness of Fit Measure—Pinball Loss Score
As our main modeling focus is upon estimating the entire four-parameter distributions fitted to the spread data at each time step, we focus next upon the calibration of the estimated quantiles, using the Pinball Loss (PL) function [
14]. The PL function is always positive, and has a higher value the further away the quantile estimate is away from the target value. The quantiles are deemed to be fitted the best when the Pinball Loss is at its lowest. The quality of quantile fit is important for Value-at-Risk compliance in the context of risk management applications. We adopt this measure as our main performance metric to select the best distribution for each spread. We follow Algorithm 2 when making an assessment of each predictive density power and outline the steps involved in calculating the performance measure below.
Pinball Loss Values. At each time step
t, the target quantiles
are extracted by inverting the cumulative distribution function of distribution
specified with forecasted distribution parameters
and compared to the realisation of true spread price,
, using:
This results in Pinball Loss Values vector,
, where
is the number of quantiles extracted. Certain quantiles failed to converge when calculating the full set of 99 values due to convergence issues around distribution tails. To resolve this we removed the tail quantiles one pair at a time and attempted to extract the quantiles again (i.e., resulting in 97 quantiles:
and if still not convergent 95 quantiles
). If this still did not resolve the issue, we omitted calculating the Pinball Loss value for that time step and recorded the number of such occurrences,
n. Note: JSU and ST5 extracted quantiles 100% of the time, making these two distributions the most stable out of the 6 tested. This is in contrast to ST1 and ST2 distributions which failed to converge often (see
Appendix C Table A1 for the number of times each distribution failed to extract a quantile).
Pinball Loss Scores. At each time step,
t, the average over Pinball Loss Values is obtained resulting in a single Pinball Loss Score,
:
This results in a vector , where and n denotes the number of occurrences when was not available for calculation.
Pinball Loss Performance Measure. The final step in calculating a single value describing the goodness-of-fit measure using the Pinball Loss function is finding the average of the Pinball Loss Scores across the full validation forecast horizon at time steps
(i.e., 383 days):
The distribution corresponding to the model with the lowest Pinball Loss Performance Measure, , is selected as the distribution of best fit for spread number s.
| Algorithm 2 Model selection using Pinball Loss function |
- 1:
for each spread number do - 2:
Extract validation data design matrix i.e., time steps - 3:
for each distribution do - 4:
Forecast parameters of resulting in each - 5:
for time step do - 6:
Obtain vector of quantiles using - 7:
for each quantile do - 8:
Calculate Pinball Loss value using Equation ( 11) - 9:
Calculate Pinball Loss Score using Equation ( 12) - 10:
Calculate Pinball Loss Performance Measure using Equation ( 13) - 11:
Find and select corresponding distribution as best fit for s
|
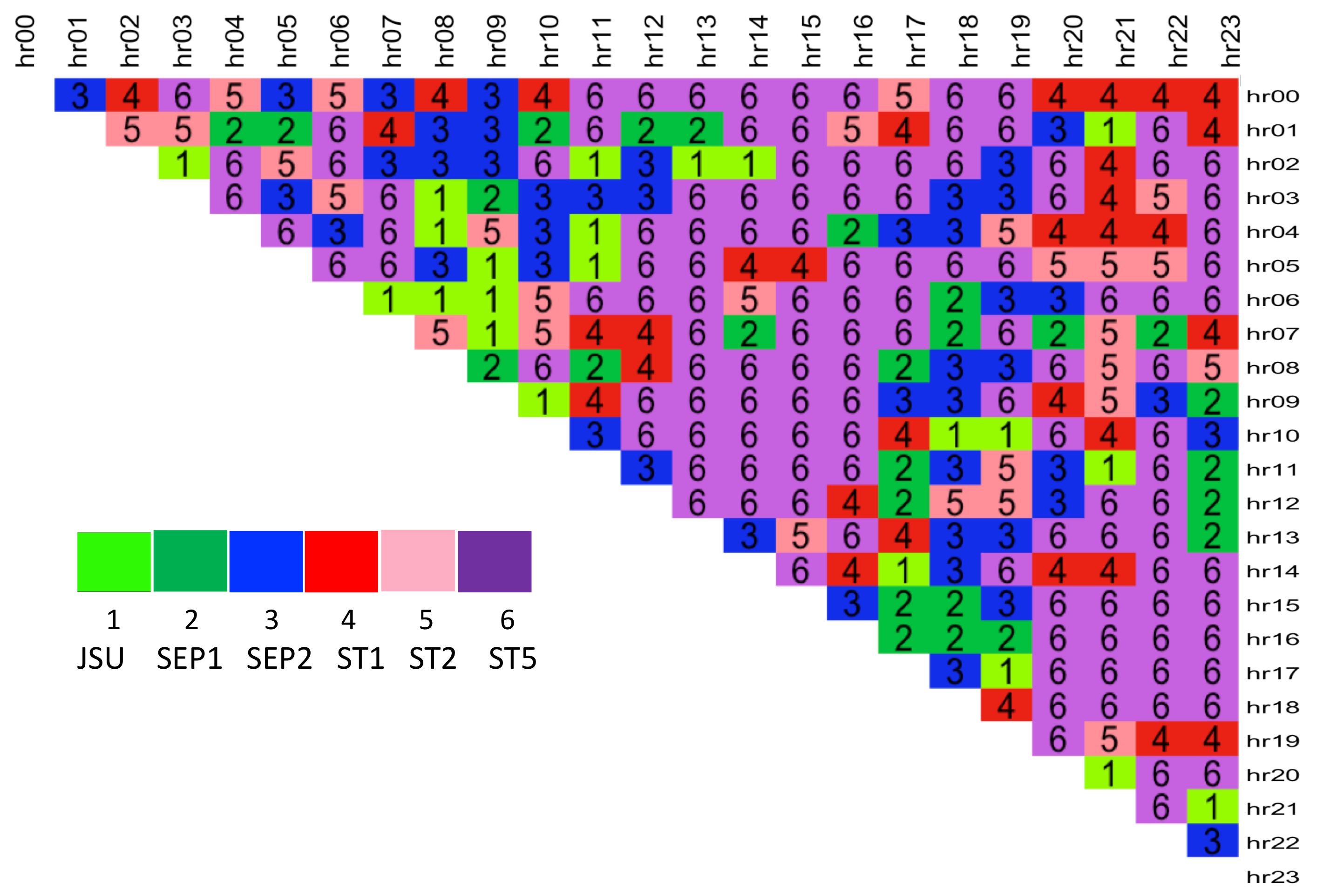
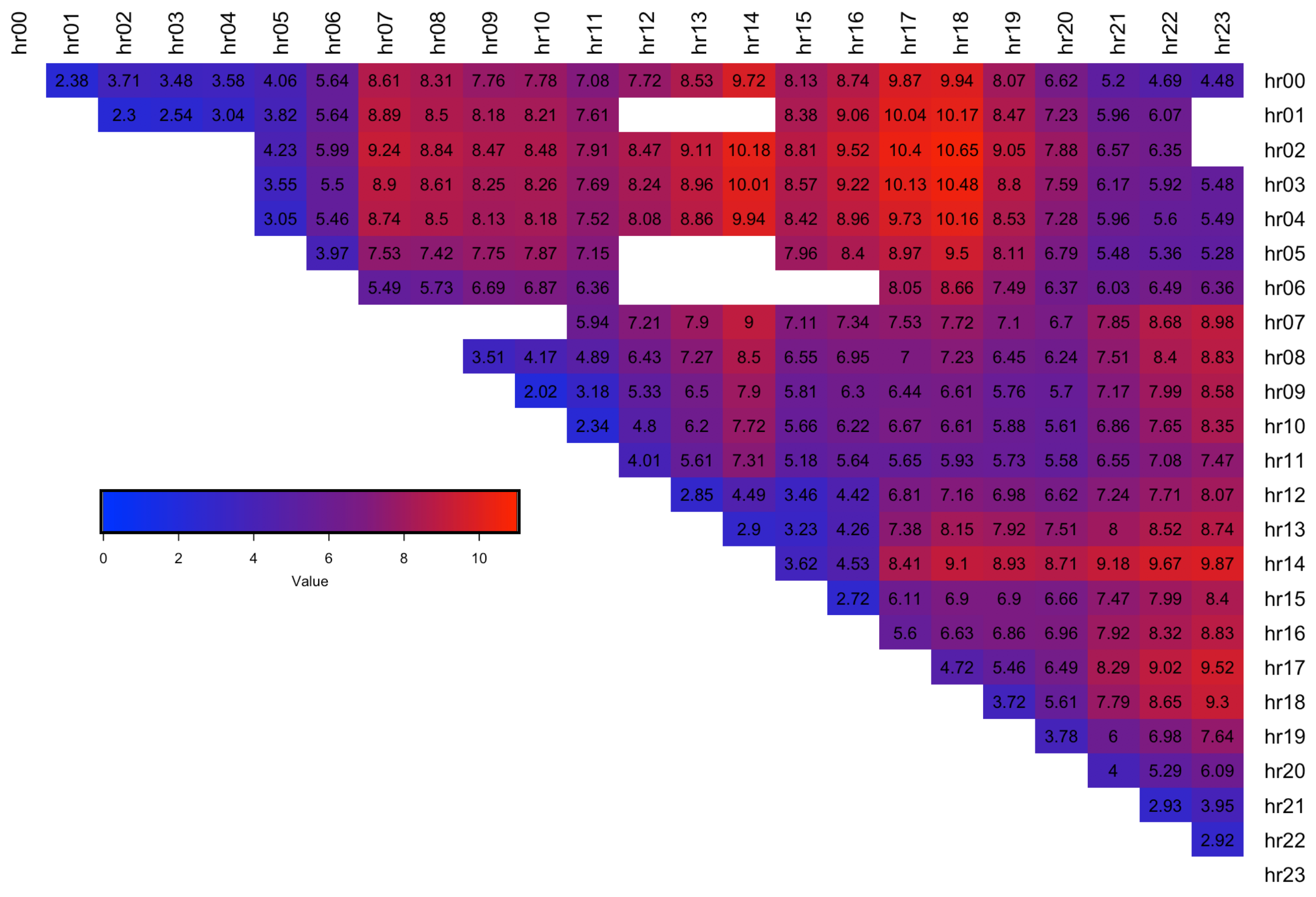
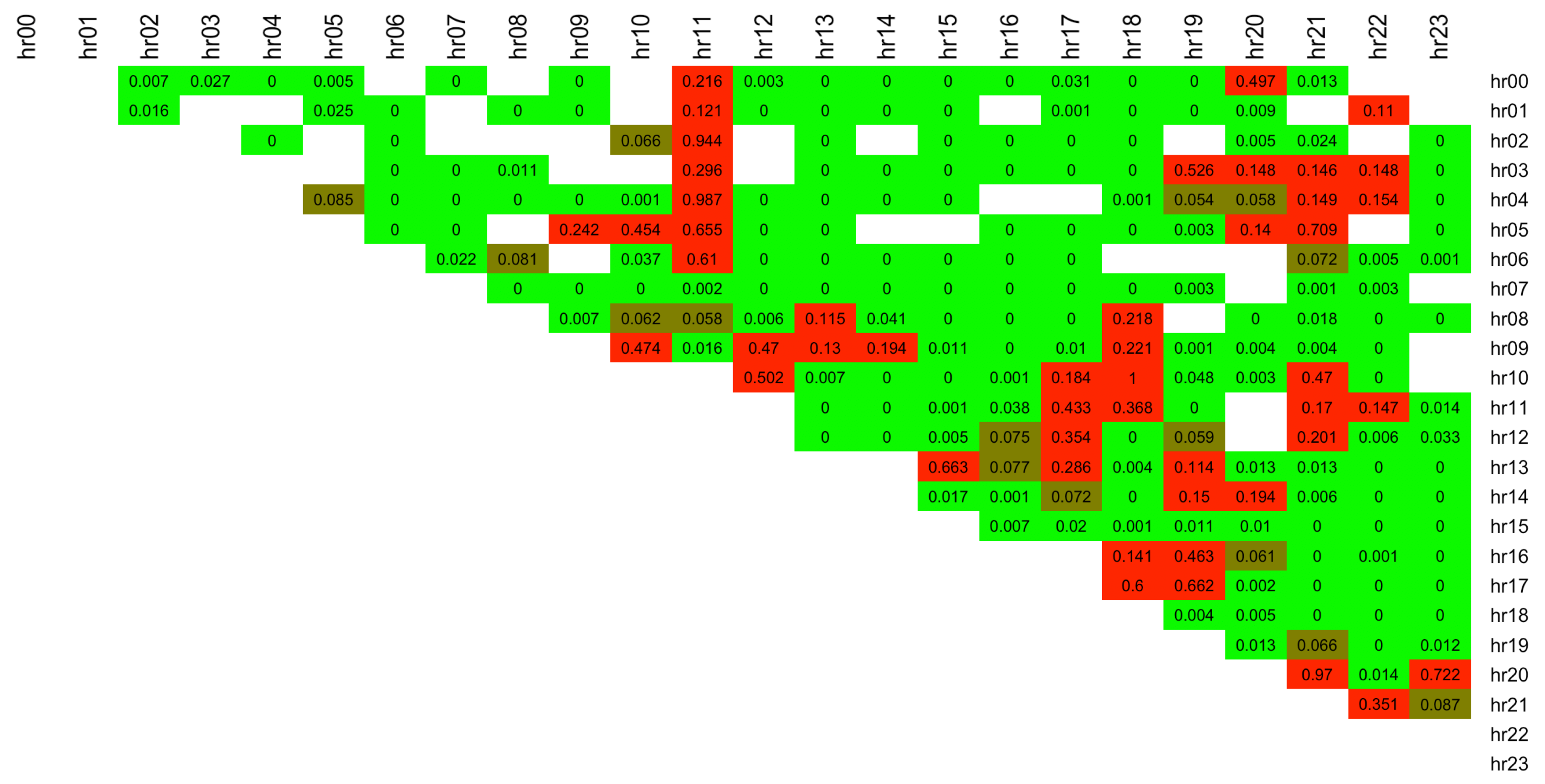
The Pinball Loss Performance Measures are analysed for each spread
s and the results are presented in a
upper diagonal matrix, containing the best distribution number selected for each intraday spread between the hours indicated by the row and column labels (see
Figure 9). The figure shows that the majority of the spreads are fitted best with ST5 distribution (number 6, purple colour). This is in line with the results obtained from the factor-based distribution fit using the RMSE measure (see
Figure 7), and with the simple best distribution fit given by
function (see
Figure 6), which both favoured the ST5 distribution.
Table 4 specifies the number of times each distribution was selected as the best from the 276 possible spreads. While ST5 is selected for almost 50% of the spreads, the other 5 distributions were selected nearly with the same proportion for the remaining half of the spread data.
Further to this, we calculate the % difference of the best distribution PL score vs. that of the next best distribution, , for each spread number s. When ST5 was selected as the best distribution, the average difference of the performance measure is 4.84% compared to, when other distributions were selected as best, the average difference is 1.44% (with approx 1/3 of these cases containing ST5 is the second-best). This makes the case for ST5 to potentially be used as a general best fit distribution across all spreads.