Optimal Phase Arrangement of Distribution Transformers for System Unbalance Improvement and Loss Reduction
Abstract
:1. Introduction
2. The Problem Description
2.1. Transformer Connection Types
2.2. Transformer Equivalent Load
2.3. The Objective Function for Phase Rearrangement of Transformers
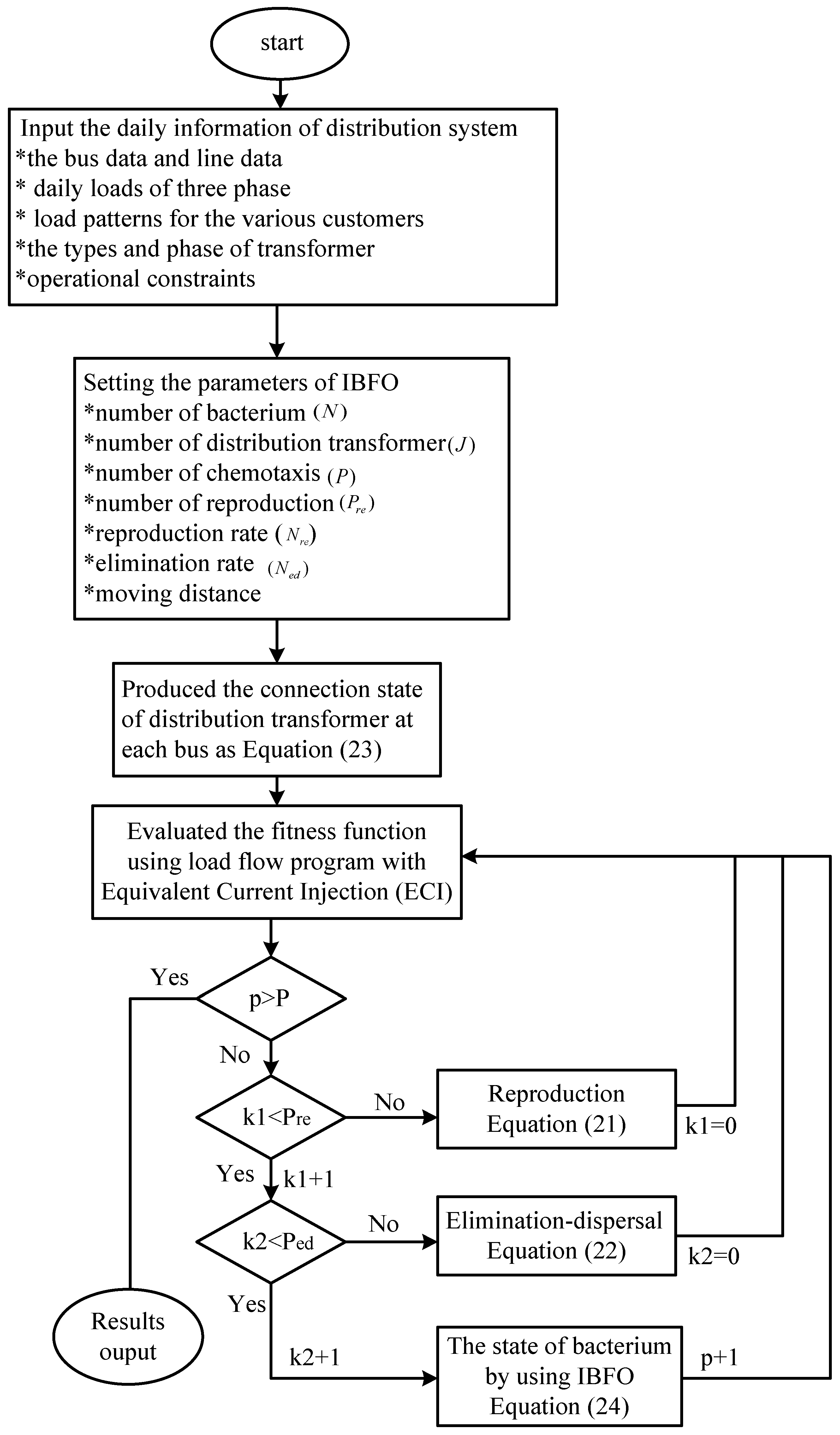
3. Solution Algorithm
3.1. Bacterial Chemotaxis
3.2. Bacterial Reproduction
3.3. Elimination-Dispersal
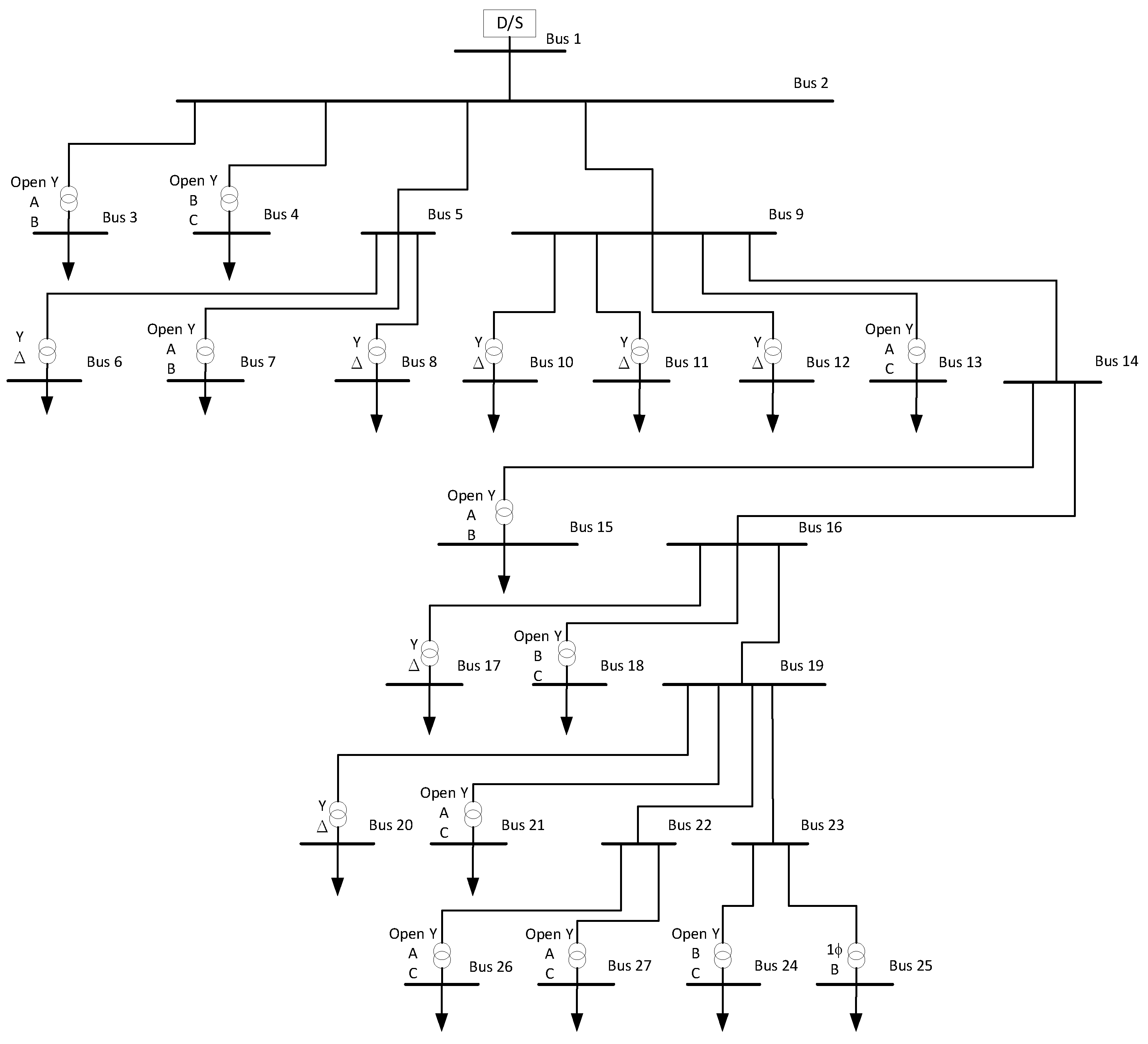
4. Case Study
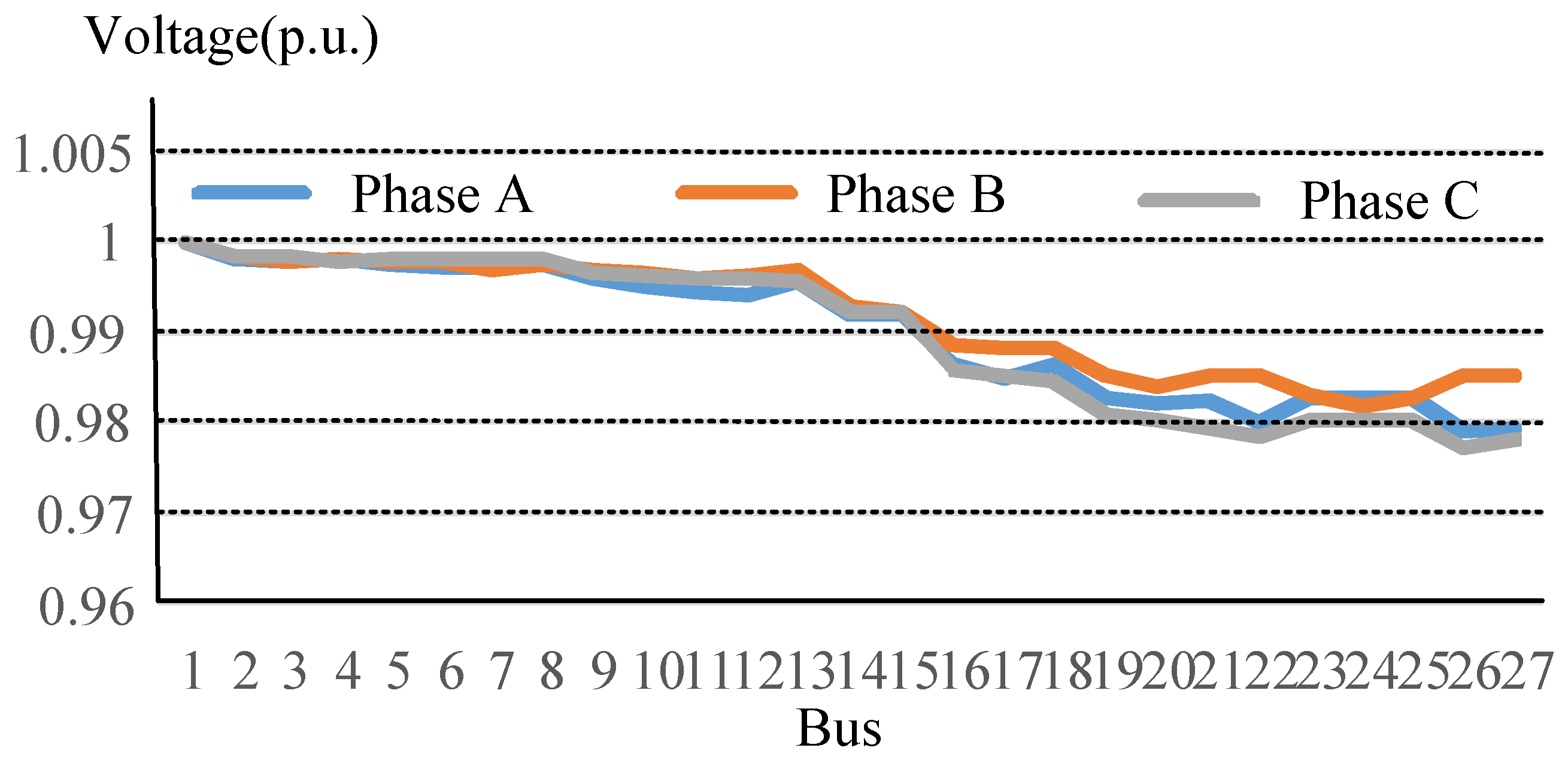
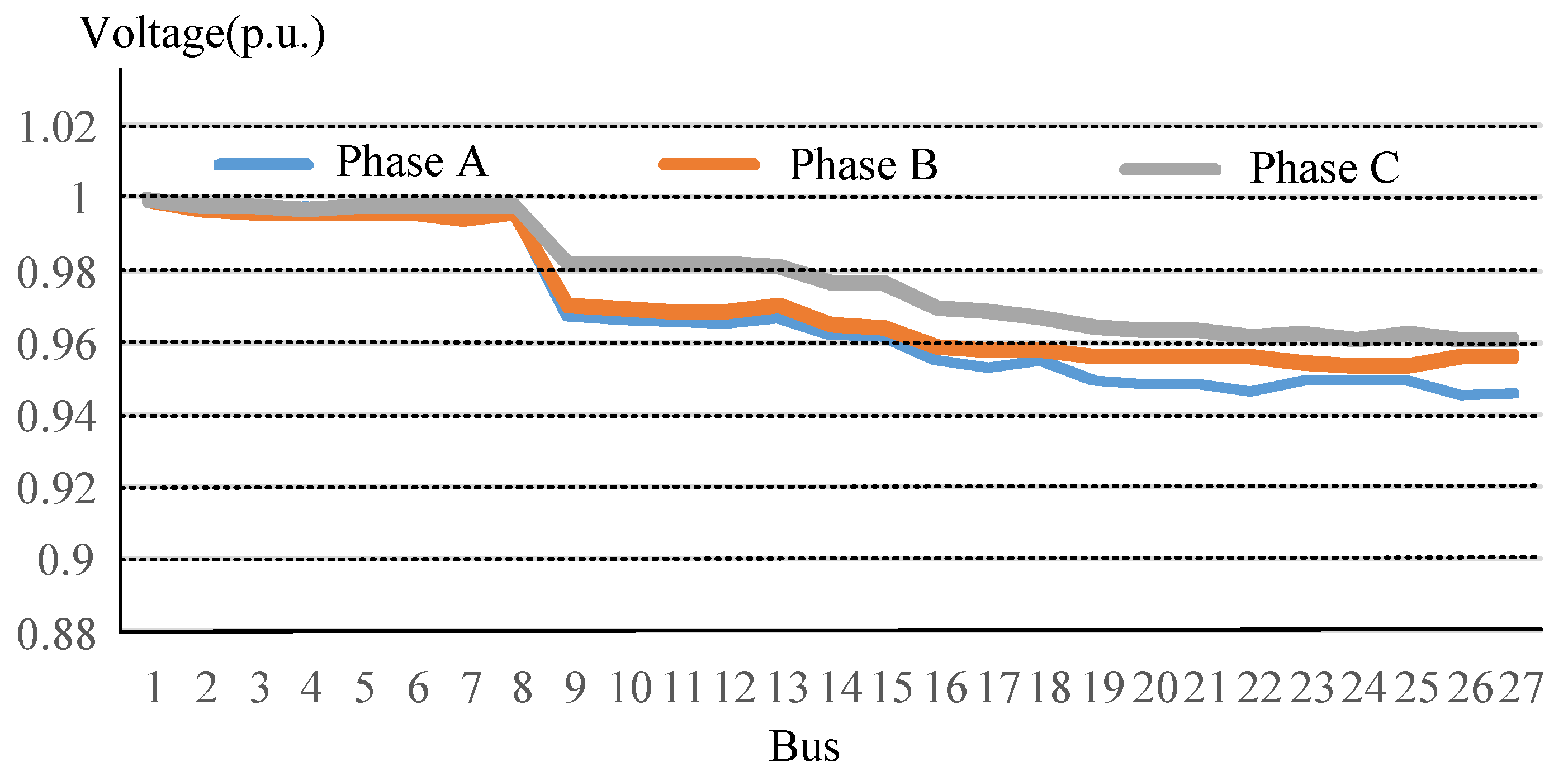
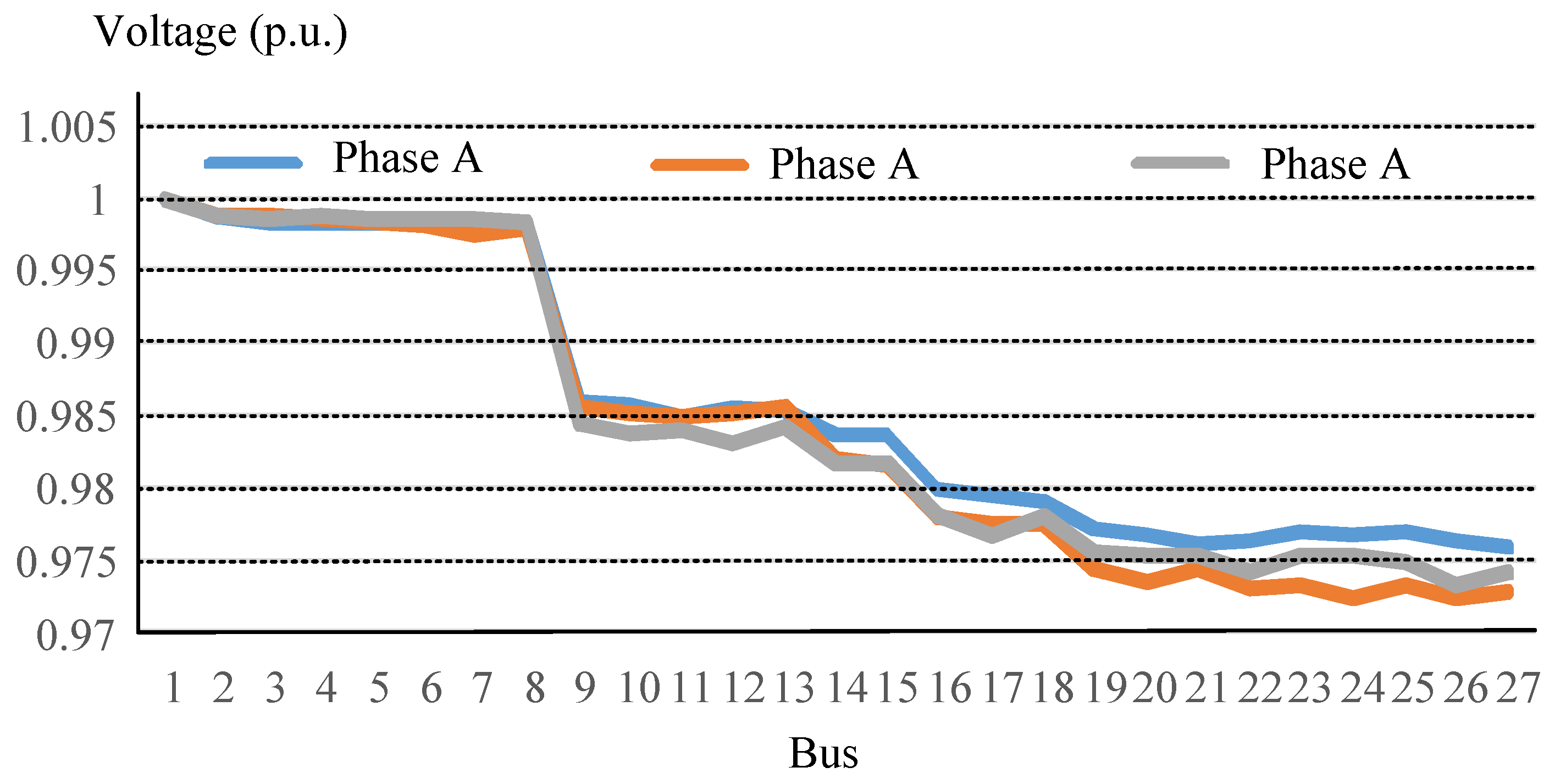
4.1. Voltage Profile Improvement
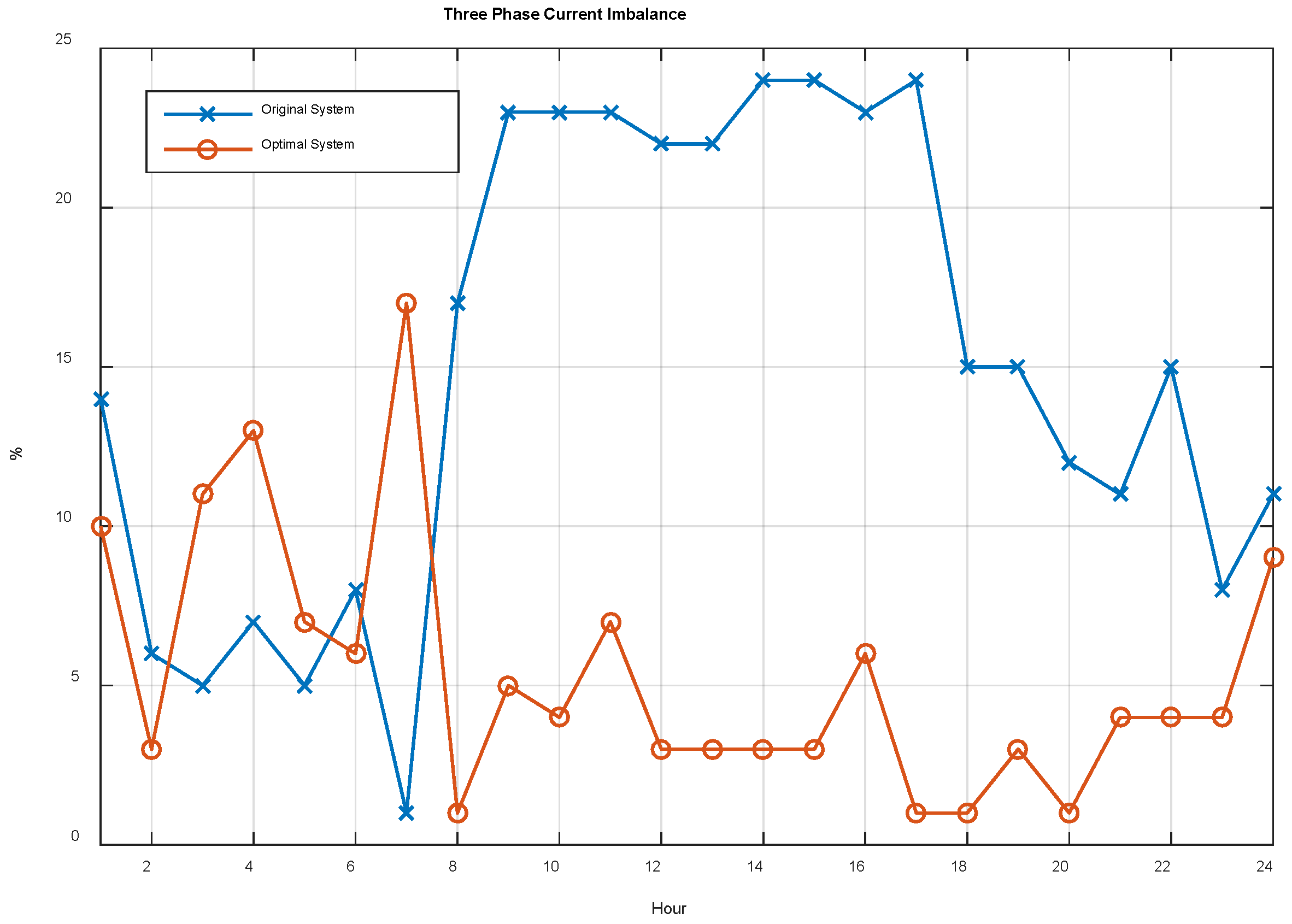
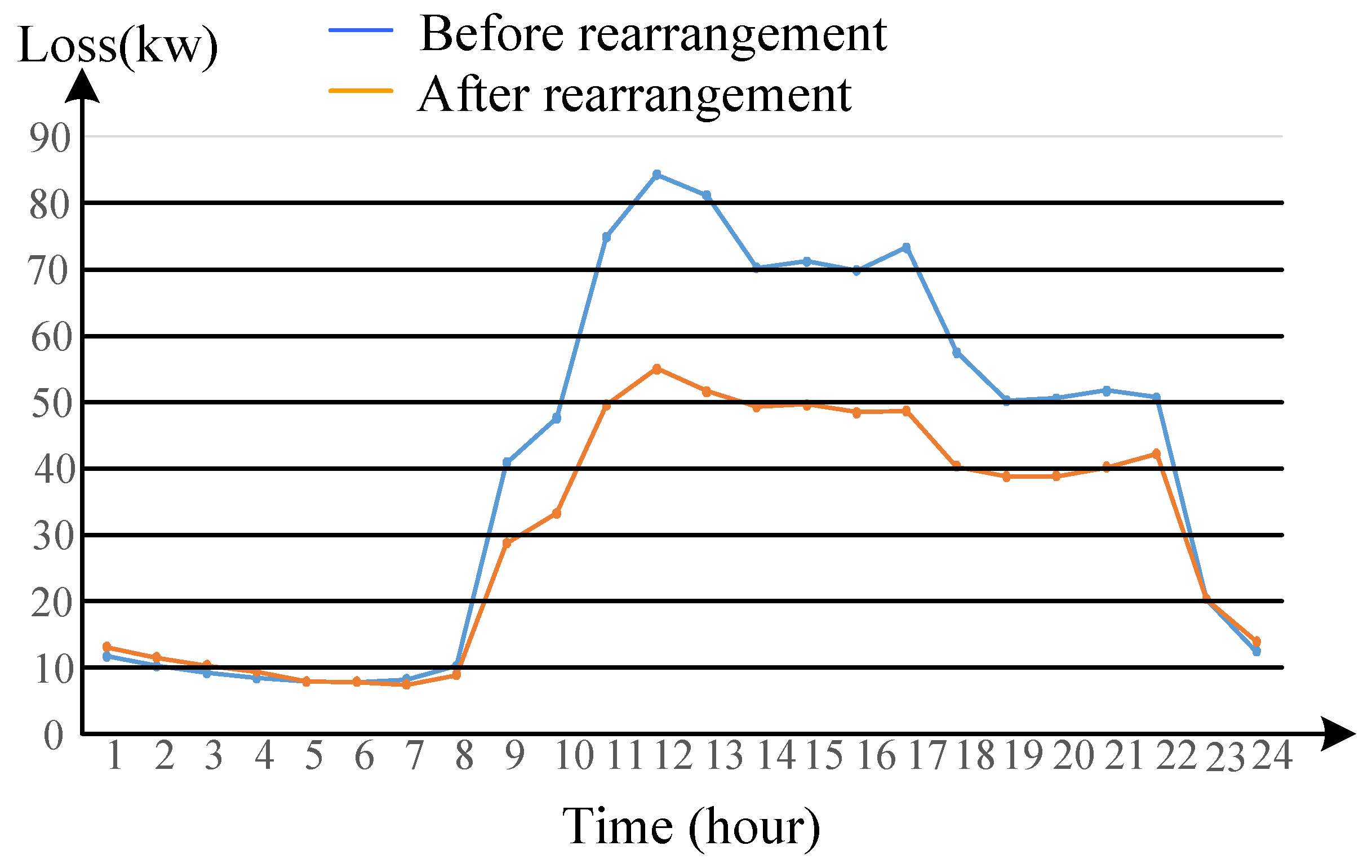
4.2. Unbalance and Loss Improvement
4.3. Convergence Test
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| the equivalent loads for A, B, C phase | |
| the A-phase and B-phase loads connected to the neutral wires | |
| the single-phase loads connected to the two-wire | |
| the three-phase load | |
| per unit load at hour t of load customer i | |
| percentage of hourly energy consumption over a daily period of load customer i | |
| monthly energy consumption of customer i in CIS | |
| the number of monthly days | |
| hourly real power demand of customer i | |
| transformer hourly loading at hour t | |
| the number of customers | |
| the rate of load growth of the customer | |
| the time period of load forecasting | |
| The total line loss of distribution feeders at t-th time | |
| the status of phase arrangement | |
| the total number of branches in the feeder | |
| the voltage of i-th bus | |
| the admittance of branch | |
| the voltage phase angle difference between bus-i and bus-j | |
| upper limit of branch current magnitude | |
| lower/upper limit of bus voltage magnitude () | |
| the neutral line current | |
| the maximal valve of current | |
| the j-th state value of n-th bacterium at the p-th chemotaxis. is the number of bacterial chemotaxis. | |
| the j-th state value of the bacterium, a bacterium combined by J state values into a complete solution | |
| The total number of bacteria | |
| the tumble direction vector of the bacterium | |
| The distance for the bacterium at each step | |
| State value of the n-th bacterium after the p-th chemotaxis | |
| The fitness value of the n-th bacterium at the p-th chemotaxis | |
| The fitness value of the n-th bacterium after the p-th chemotaxis | |
| State value of the n-th bacterium after the (p + 1)-th chemotaxis | |
| The count of the bacterial reproduction | |
| The number of chemotaxis process | |
| The number of bacterial reproduction | |
| The fitness values sorted after the chemotaxis procedure | |
| The count of bacterial elimination | |
| The number of chemotaxis |
References
- Su, Y.S.; Lin, W.M.; Chang, S.C.; Tsay, M.T. Improving the system unbalance and losses of distribution feeders based on transformer rearrangement. In Proceedings of the IEEE Region 10 Conference TENCON, Chiang Mai, Thailand, 24–24 November 2004; Volume 1, pp. 448–451. [Google Scholar]
- Chang, C.Y. Effect of Open-Wye/Open-Delta Transformer and v-v Transformer to the Operation of Distribution System. Master’s Thesis, National Sun Yat-Sen University, Kaohsiung, Taiwan, June 1987. [Google Scholar]
- Chen, T.H.; Chang, J.D. Open wye-open delta and open delta-open delta transformer models for rigorous Distribution system analysis. IET Gener. Transm. Distrib. 1992, 139, 227–234. Available online: https://ieeexplore.ieee.org/document/141497 (accessed on 21 January 2020). [CrossRef]
- Panagiotis, E.; Ekonomou, L. (Eds.) Electricity Distribution, Intelligent Solutions for Electricity Transmission and Distribution Networks; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 978-3-662-49434-9. [Google Scholar] [CrossRef]
- Porumb, R.; Toader, C.; Golovanov, N.; Leonida, T.; Seritan, G. Energy Efficiency Rating of Transformers under Unbalanced Linear Regime. In Proceedings of the Optimization of Electrical & Electronic Equipment—OPTIM, Side, Turkey, 2–4 September 2015; pp. 538–544, ISBN 978-1-4673-7239-8. [Google Scholar]
- Chen, T.H.; Cherng, J.T. Optimal phase arrangement of distribution transformers connected to a primary feeder for system unbalance improvement and loss reduction using a Genetic algorithm. In Proceedings of the 21st International Conference on Power Industry Computer Applications, Connecting Utilities, PICA 99, To the Millennium and Beyond, Santa Clara, CA, USA, 21–21 May 1999. [Google Scholar]
- Singh, D.; Misra, R.K.; Mishra, S. Distribution system feeder re-phasing considering voltage-dependency of loads. Int. J. Electr. Power Energy Syst. 2016, 76, 107–119. [Google Scholar] [CrossRef]
- Abril, I.P. NSGA-II phase balancing of primary distribution circuits by the reconnection of their circuit laterals and distribution transformers. Electr. Power Syst. Res. 2014, 109, 1–7. [Google Scholar] [CrossRef]
- Lin, C.H.; Chen, C.S.; Ku, T.T.; Ho, C.Y. Mitigation of three-phase unbalancing for distribution feeders by rephasing of laterals and distribution transformers. In Proceedings of the IEEE PES T&D Conference, New Orleans, LA, USA, 19–22 April 2010; Volume 1, pp. 1–6. [Google Scholar]
- Huang, S.J.; Tai, T.Y.; Liu, X.Z.; Su, W.F.; Gu, P.H. Application of bird-mating optimization to phase adjustment of open-wye/open-delta transformers in a power grid. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; Volume 1, pp. 1275–1279. [Google Scholar]
- Ali, B.; Siddique, I. Distribution system loss reduction by automatic transformer load balancing. In Proceedings of the International Multi-Topic Conference (INMIC), Lahore, Pakistan, 24–26 November 2017; Volume 1, pp. 1–5. [Google Scholar]
- Tsay, M.T.; Chan, S.Y. The Optimal Loss Reduction of Distribution Feeder Based on Transformer Rearrangement. Int. J. Electr. Power Energy Syst. 2001, 23, 343–348. [Google Scholar] [CrossRef]
- Tsay, M.T.; Chan, S.Y. Improvement in System Unbalance and Loss Reduction of Distribution Feeders Using Transformer Phase Rearrangement and Load Diversity. Int. J. Electr. Power Energy Syst. 2003, 25, 395–401. [Google Scholar] [CrossRef]
- Passion, K.M. Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Syst. 2002, 22, 52–67. [Google Scholar]
- Naveen, S.; Kumar, K.S.; Rajalakshmi, K. Distribution system reconfiguration for loss minimization using modified bacterial foraging optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 69, 90–97. [Google Scholar] [CrossRef]
- Bhushan, B.; Singh, M. Adaptive control of DC motor using bacterial foraging algorithm. Appl. Soft Comput. 2011, 11, 4913–4920. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1568494611002262 (accessed on 21 January 2020). [CrossRef]
- Elattar, E.E. A hybrid genetic algorithm and bacterial foraging approach for dynamic economic dispatch problem. Int. J. Electr. Power Energy Syst. 2015, 69, 18–26. [Google Scholar] [CrossRef]
- Saad, N.H.; El-Sattar, A.A.; Marei, M.E. Improved bacterial foraging optimization for grid connected wind energy conversion system based PMSG with matrix converter. Ain Shams Eng. J. 2018, 9, 2183–2193. [Google Scholar] [CrossRef]
- Fitriyanah, D.N.; Abadi, I. Fuzzy Logic Control Design of Mobile PV Using Bacterial Foraging Optimization. In Proceedings of the 2018 International Seminar on Intelligent Technology and Its Applications (ISITIA), Bali, Indonesia, 30–31 August 2018; Volume 1, pp. 1–5. [Google Scholar]
- Xiong, X.; Wu, W.; Li, N.; Yang, L.; Zhang, J.; Wei, Z. Risk-Based Multi-Objective Optimization of Distributed Generation Based on GPSO-BFA Algorithm. IEEE Access 2019, 7, 30563–30572. [Google Scholar] [CrossRef]
- Chen, H.; Luo, J.; Xu, Y.; Wu, C.; Li, C.; Zhang, Q. Chaos Enhanced Bacterial Foraging Optimization for Global Optimization. IEEE Access 2018, 6, 64905–64919. [Google Scholar]
- Zhao, W.; Wang, L. An effective bacterial foraging optimizer for global optimization. Inf. Sci. 2016, 329, 719–735. [Google Scholar] [CrossRef]
- Zhao, F.; Si, J.; Wang, J. Research on optimal schedule strategy for active distribution network using particle swarm optimization combined with bacterial foraging algorithm. Int. J. Electr. Power Energy Syst. 2016, 78, 637–646. [Google Scholar] [CrossRef]
- Nithya, S.; Jeyanthi, K.M. Genetic algorithm based bacterial foraging optimization with three-pass protocol concept for heterogeneous network security enhancement. J. Comput. Sci. 2017, 21, 275–282. [Google Scholar] [CrossRef]
- Chalermchaiarbha, S.; Ongsakul, W. Stochastic weight trade-off particle swarm optimization for nonconvex economic dispatch. Energy Convers. Manag. 2013, 70, 66–75. [Google Scholar] [CrossRef]
- Lin, W.M.; Teng, J.H. Three-phase distribution network fast-decoupled power flow solutions. Int. J. Electr. Power Energy Syst. 2000, 22, 375–380. [Google Scholar] [CrossRef]
- Chaturvedi, K.T.; Pandit, M.; Srivastava, I. Self-organizing hierarchical particle swarm optimization for nonvex economic dispatch. IEEE Trans. Power Syst. 2008, 23, 1079–1087. [Google Scholar] [CrossRef]
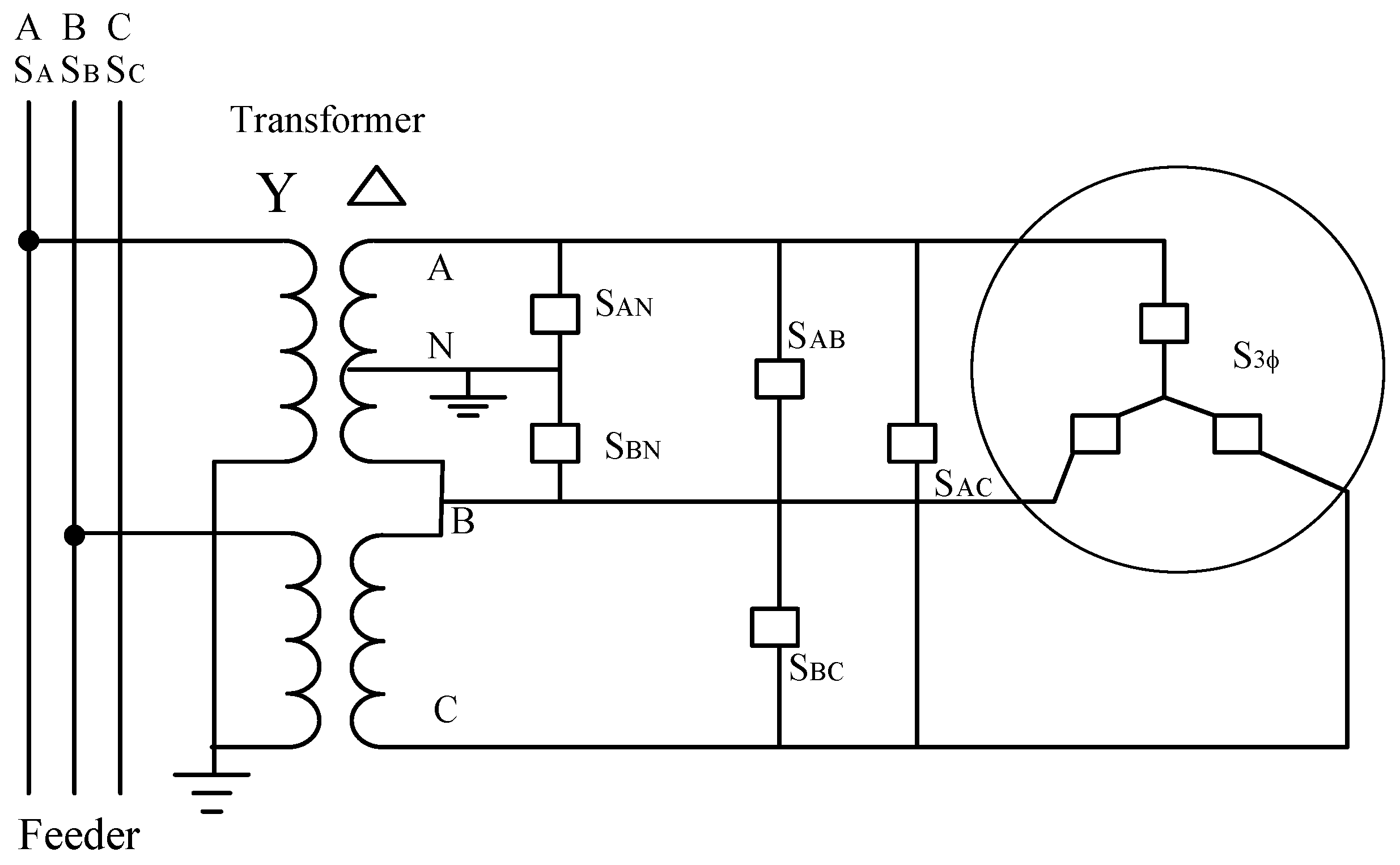


| Type | Open-Wye/Open Delta Transformer | Single-Phase Transformer | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | A | B | C | A | B | × | A | × | × |
| 2 | A | C | B | A | × | C | × | B | × |
| 3 | B | A | C | × | B | C | × | × | C |
| 4 | B | C | A | - | - | - | - | - | - |
| 5 | C | A | B | - | - | - | - | - | - |
| 6 | C | B | A | - | - | - | - | - | - |
| Transformer Type | The No. of Transformer | Total Capacity (KVA) |
|---|---|---|
| Three-phase | 7 | 3500 |
| Open-Y/open- | 10 | 5000 |
| Single-phase | 1 | 100 |
| Total | 18 | 8600 |
| Bus No. | Transformer Type | Original Connected | Phase Rearrangement |
|---|---|---|---|
| 3 | A,B | - | |
| 4 | A,B | B to C, C to A | |
| 6 | A,B,C | - | |
| 7 | A,B | - | |
| 8 | A,B,C | A to C, -, C to A | |
| 10 | A,B,C | A to C, -, C to A | |
| 11 | A,B,C | A to C, -, C to A | |
| 12 | A,B,C | - | |
| 13 | B,C | -, C to A | |
| 15 | A,B | A to C, - | |
| 17 | A,B,C | A to B, B to C, C to A | |
| 18 | B,C | - | |
| 20 | A,B,C | -, B to C | |
| 21 | A,C | A to C, C to B | |
| 24 | B,C | B to A, C to B | |
| 25 | B | - | |
| 26 | A,B | - | |
| 27 | A,B | A to C, - |
| GA | PSO | BFO | IBFO | |
|---|---|---|---|---|
| Maximum converged loss (kW) | 1031.12 | 969.09 | 906.98 | 854.80 |
| Minimal converged loss (kW) | 695.57 | 677.11 | 667.68 | 659.01 |
| Average converged loss (kW) | 869.46 | 826.08 | 761.16 | 730.84 |
| CPU time (sec) | 84.81 | 48.67 | 60.82 | 69.94 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, C.-S.; Tsai, M.-T. Optimal Phase Arrangement of Distribution Transformers for System Unbalance Improvement and Loss Reduction. Energies 2020, 13, 545. https://doi.org/10.3390/en13030545
Tu C-S, Tsai M-T. Optimal Phase Arrangement of Distribution Transformers for System Unbalance Improvement and Loss Reduction. Energies. 2020; 13(3):545. https://doi.org/10.3390/en13030545
Chicago/Turabian StyleTu, Chia-Sheng, and Ming-Tang Tsai. 2020. "Optimal Phase Arrangement of Distribution Transformers for System Unbalance Improvement and Loss Reduction" Energies 13, no. 3: 545. https://doi.org/10.3390/en13030545
APA StyleTu, C.-S., & Tsai, M.-T. (2020). Optimal Phase Arrangement of Distribution Transformers for System Unbalance Improvement and Loss Reduction. Energies, 13(3), 545. https://doi.org/10.3390/en13030545




