A Computational Workflow for Flow and Transport in Fractured Porous Media Based on a Hierarchical Nonlinear Discrete Fracture Modeling Approach
Abstract
1. Introduction
2. Modeling Methods
2.1. Description of the Modeling Workflow
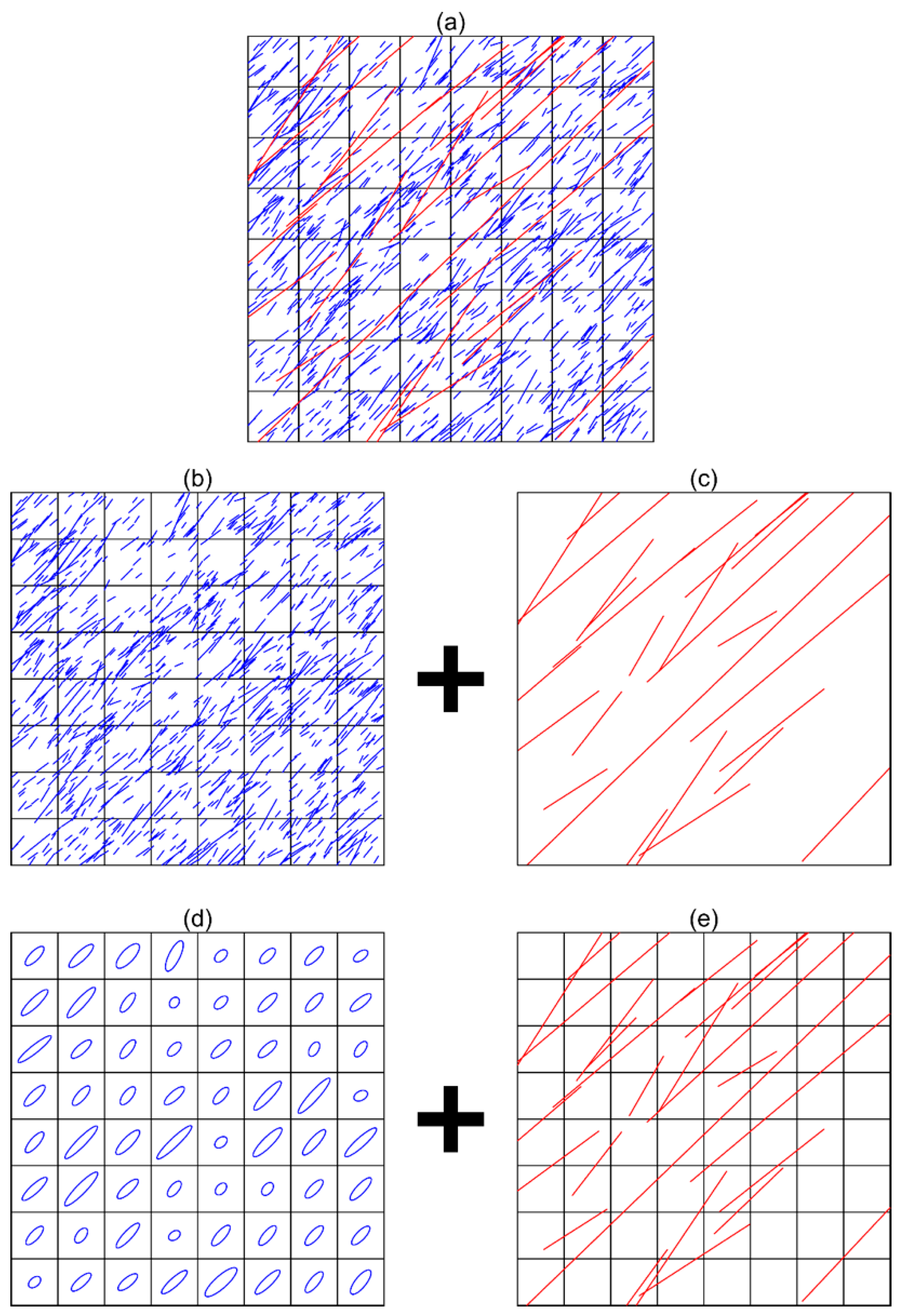
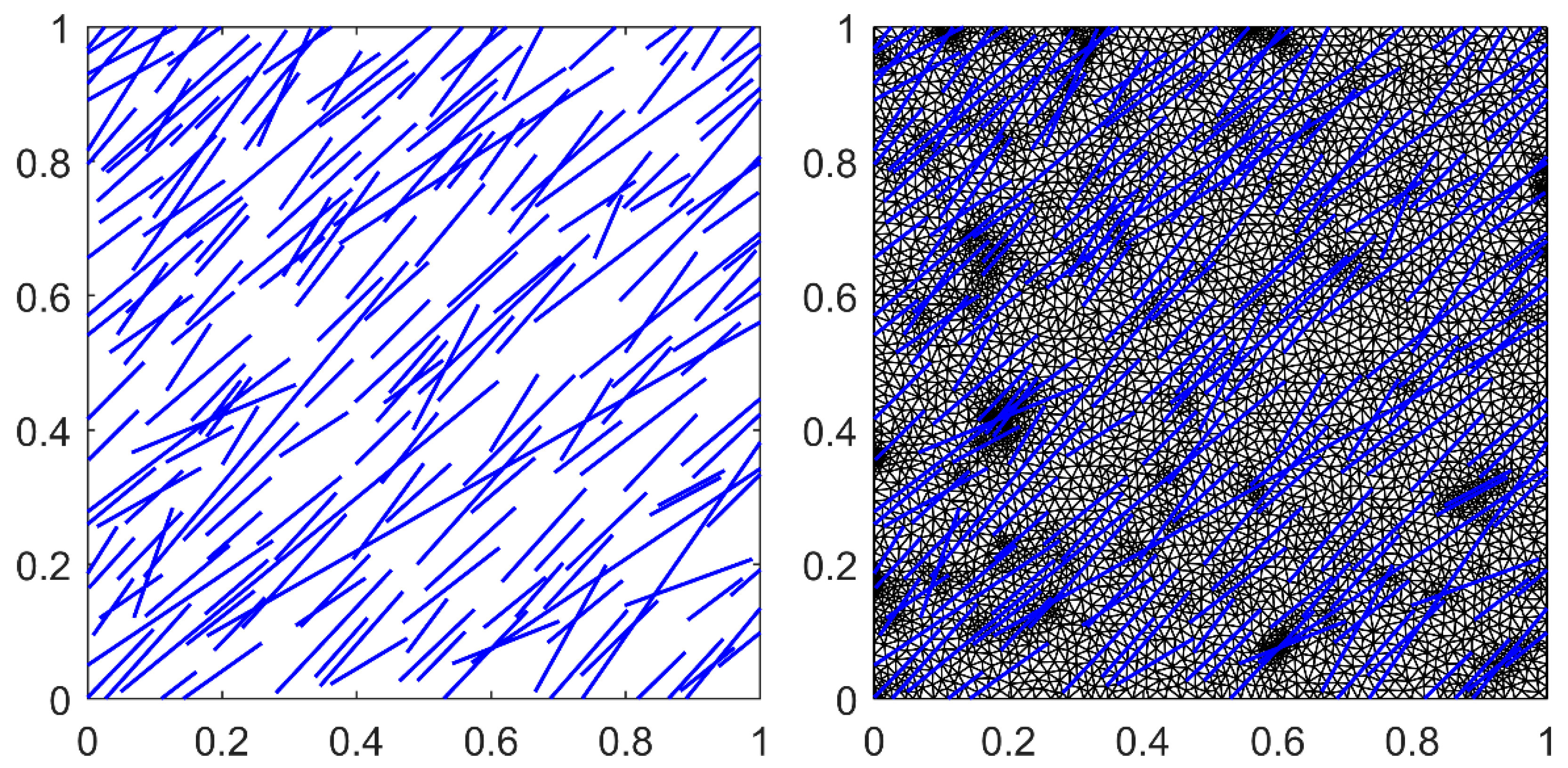
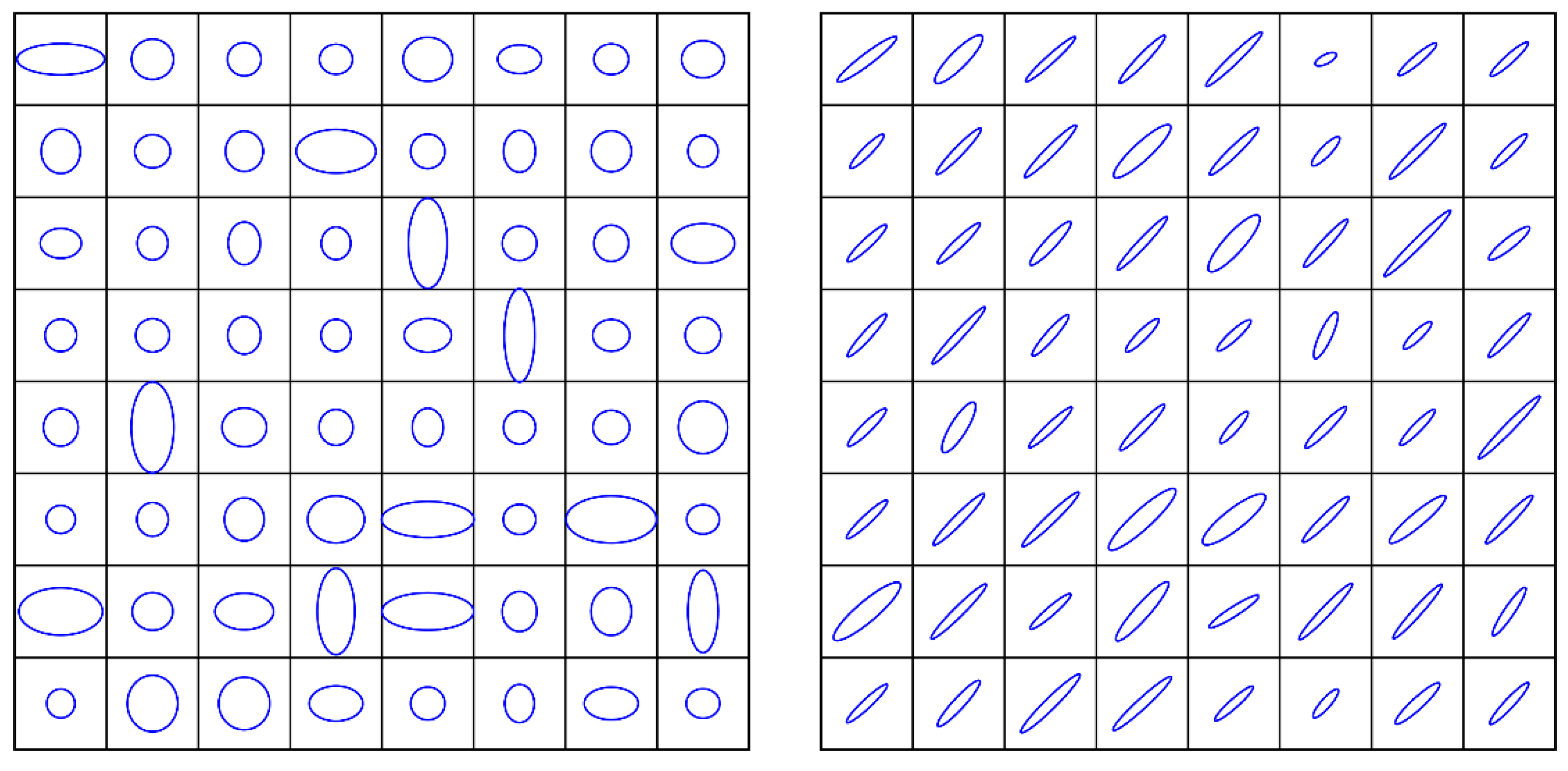
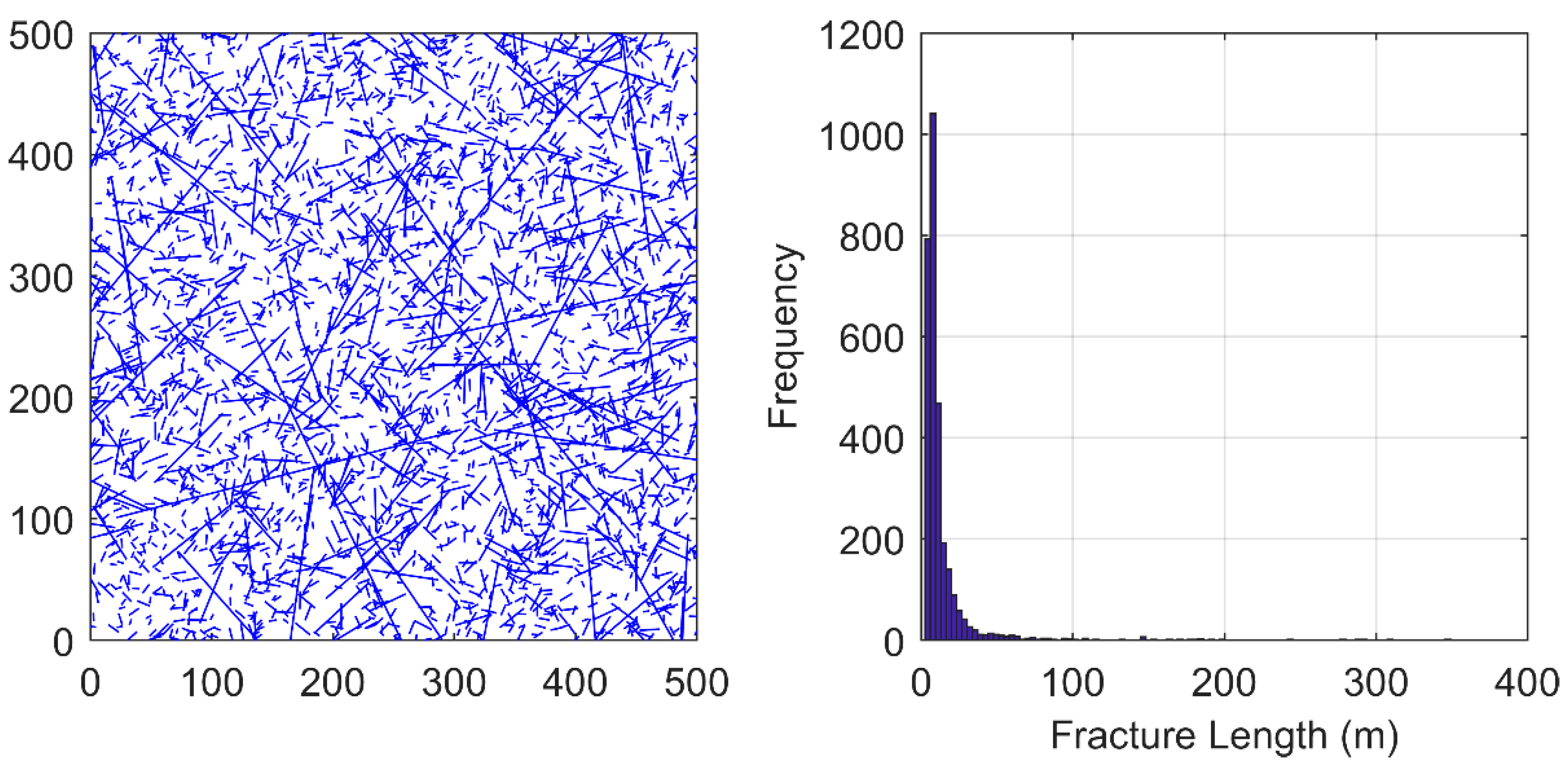
2.2. Discrete Fracture Network (DFN) Generation
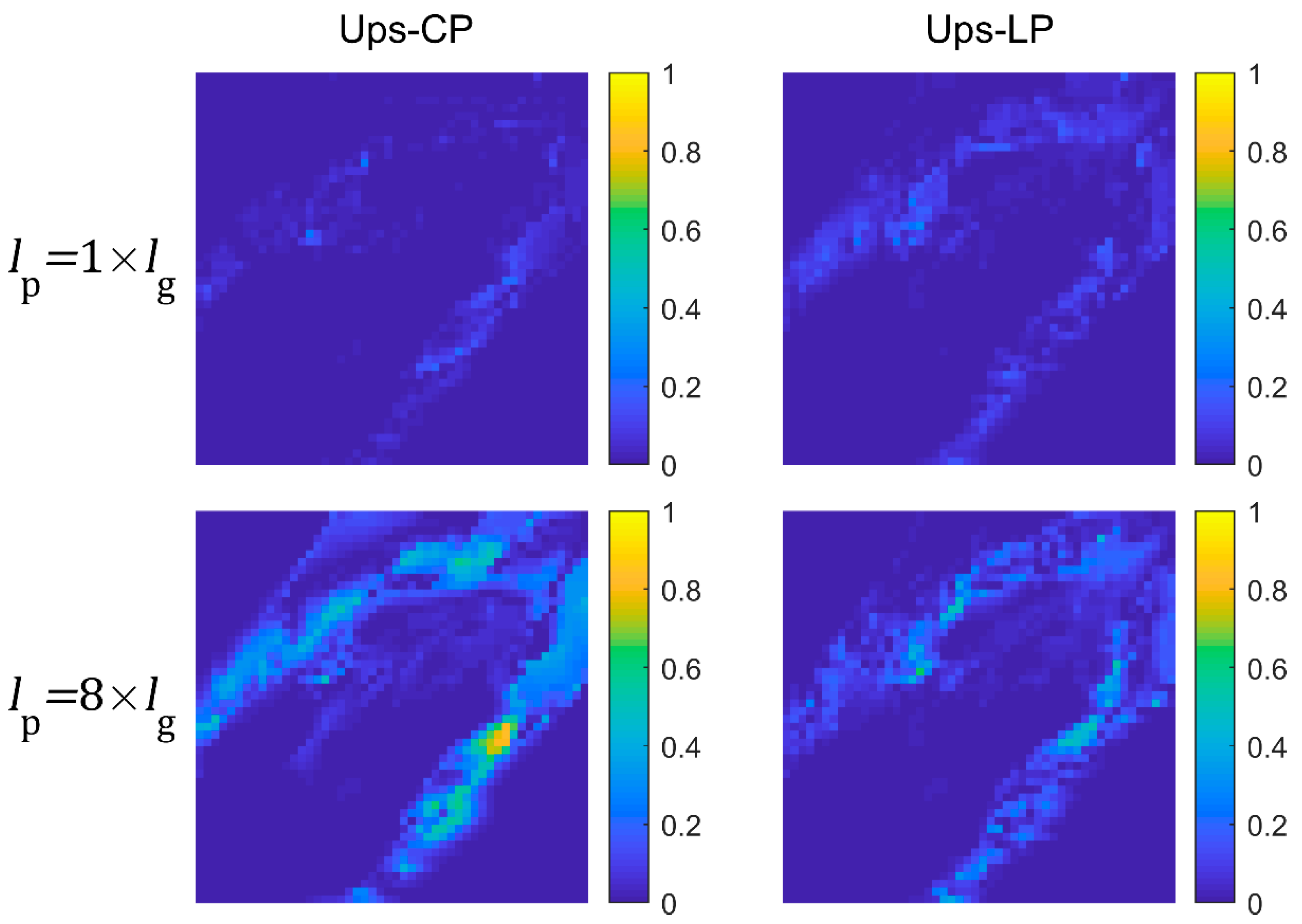
2.3. Numerical Upscaling
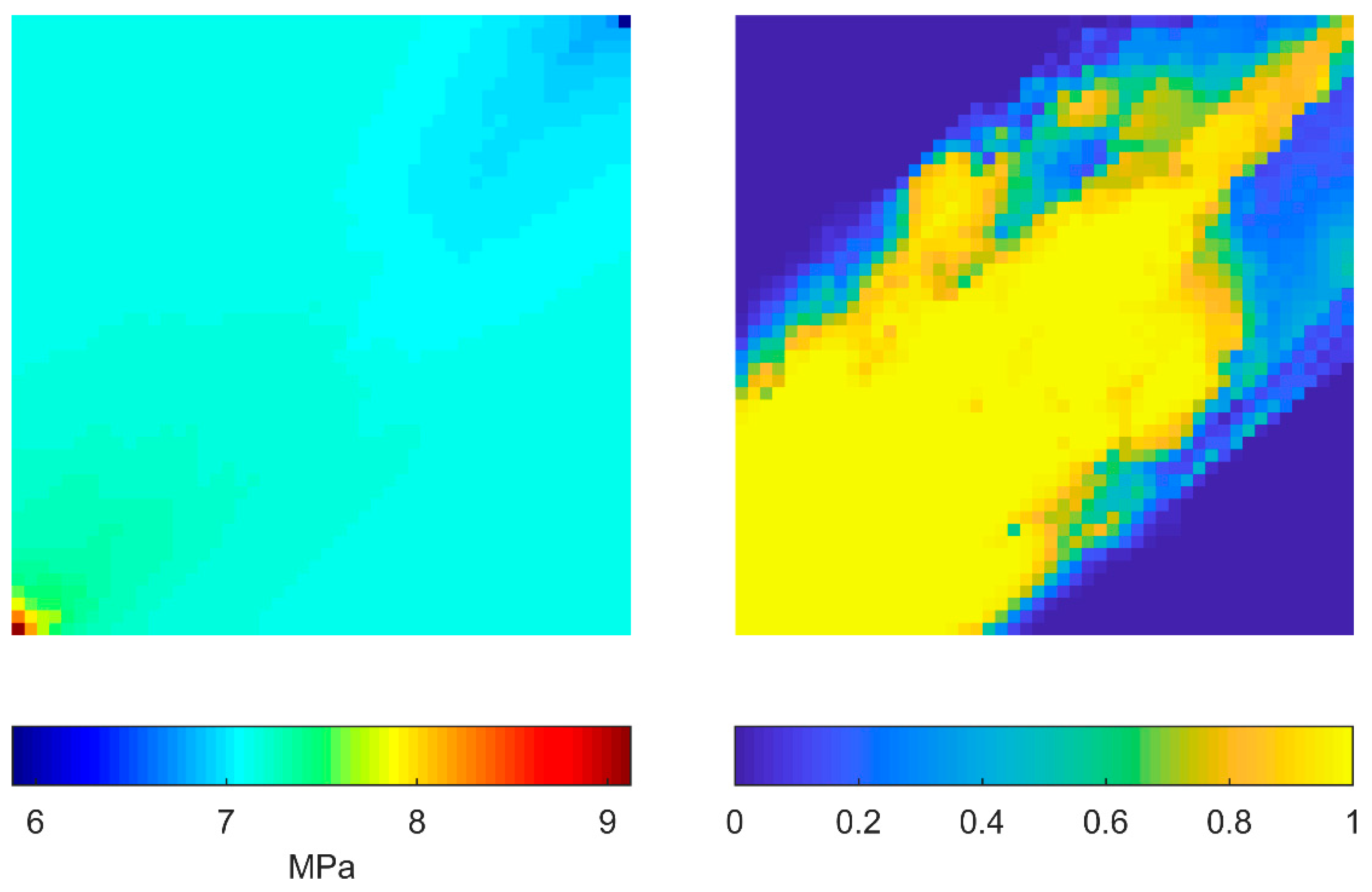
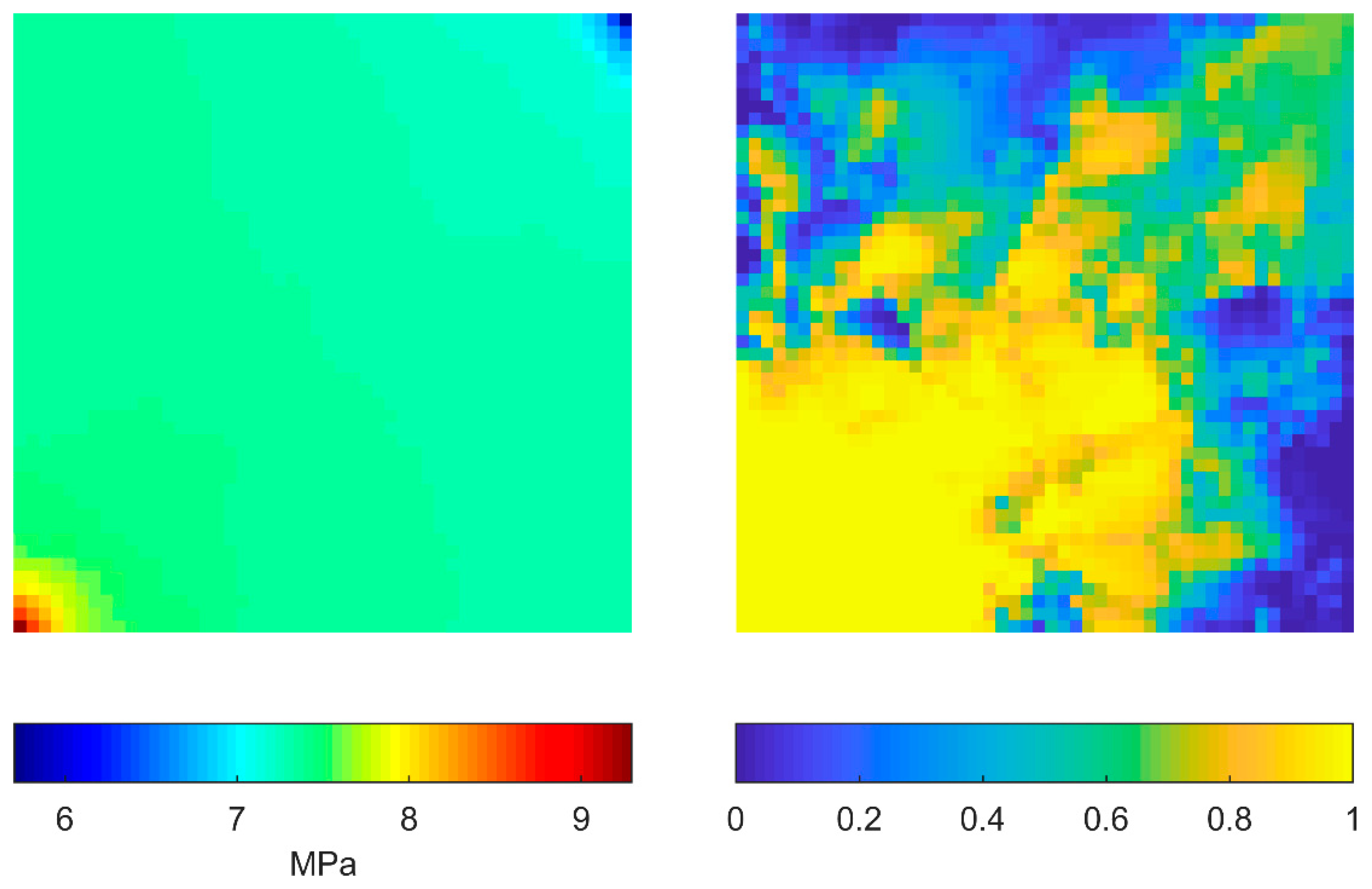
3. Results and Discussion
3.1. Case 1: Effect of Partition Length
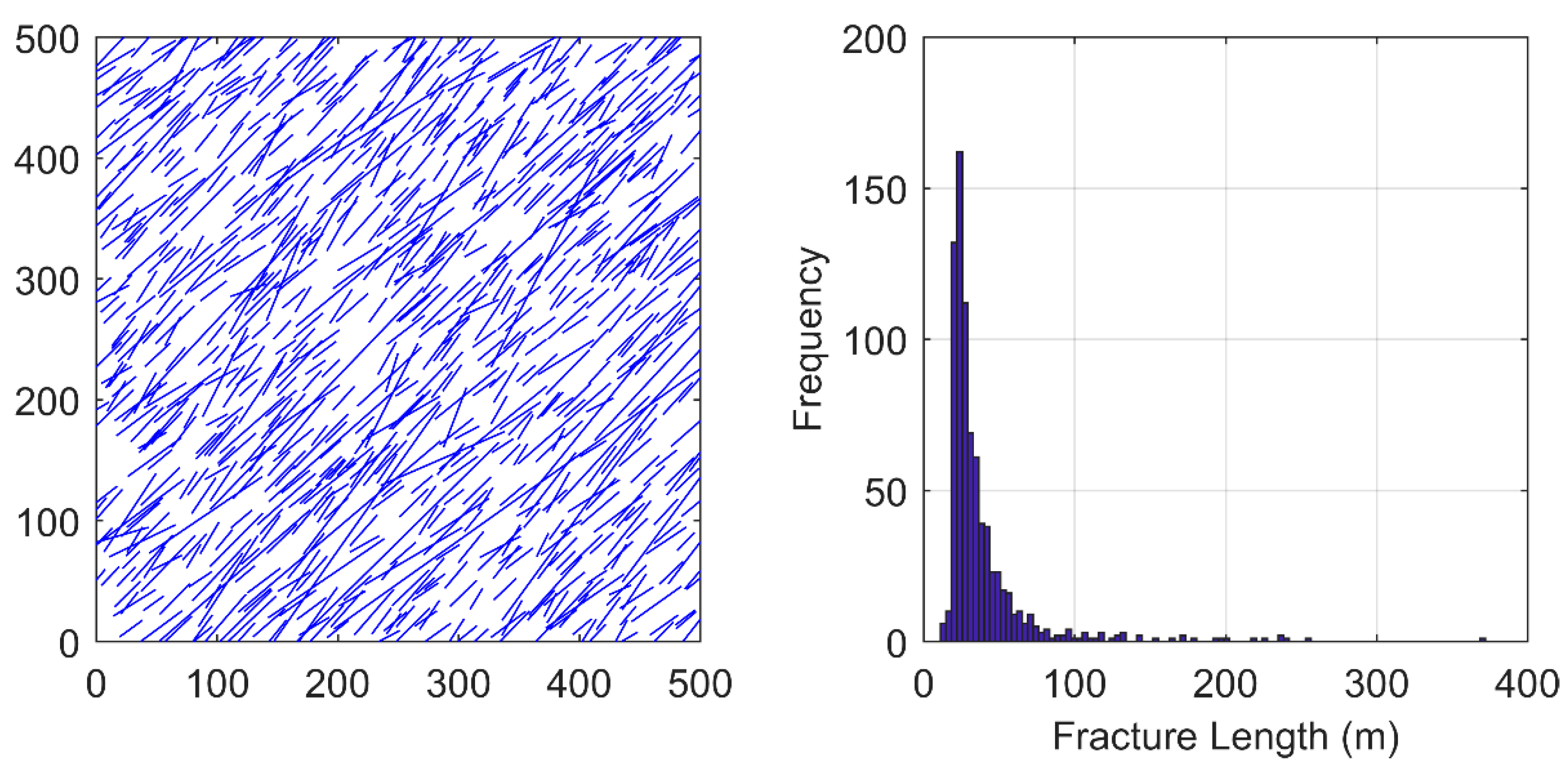
3.2. Case 2: Effect of Fracture Length Distribution
3.3. Case 3: Effect of Fracture Orientation
4. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berre, I.; Doster, F.; Keilegavlen, E. Flow in Fractured Porous Media: A Review of Conceptual Models and Discretization Approaches. Transp. Porous Media 2019, 130, 215–236. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Kazemi, H.; Merrill, L.S., Jr.; Porterfield, K.L.; Zeman, P.R. Numerical Simulation of Water-Oil Flow in Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1976, 16, 317–326. [Google Scholar] [CrossRef]
- Thomas, L.K.; Dixon, T.N.; Pierson, R.G. Fractured Reservoir Simulation. Soc. Pet. Eng. J. 1983, 23, 42–54. [Google Scholar] [CrossRef]
- Dean, R.H.; Lo, L.L. Simulations of Naturally Fractured Reservoirs. SPE Reserv. Eng. 1988, 3, 638–648. [Google Scholar] [CrossRef]
- Kazemi, H.; Gilman, J.R.; Elsharkawy, A.M. Analytical and Numerical Solution of Oil Recovery from Fractured Reservoirs with Empirical Transfer Functions (includes associated papers 25528 and 25818). SPE Reserv. Eng. 1992, 7, 219–227. [Google Scholar] [CrossRef]
- Lim, K.T.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Pet. Sci. Eng. 1995, 13, 169–178. [Google Scholar] [CrossRef]
- Heinemann, Z.E.; Mittermeir, G.M. Rigorous Derivation of the Kazemi-Gilman-Elsharkawy Generalized Dual Porosity Shape Factor. Transp. Porous Media 2006. [Google Scholar] [CrossRef]
- Geiger, S.; Roberts, S.; Matthäi, S.K.; Zoppou, C.; Burri, A. Combining finite element and finite volume methods for efficient multiphase flow simulations in highly heterogeneous and structurally complex geologic media. Geofluids 2004, 4, 284–299. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An Efficient Discrete-Fracture Model Applicable for General-Purpose Reservoir Simulators. SPE J. 2004, 9, 227–236. [Google Scholar] [CrossRef]
- Li, L.; Lee, S.H. Efficient Field-Scale Simulation of Black Oil in a Naturally Fractured Reservoir through Discrete Fracture Networks and Homogenized Media. SPE Reserv. Eval. Eng. 2008, 11, 750–758. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K.; Johns, R.T. Development of an Efficient Embedded Discrete Fracture Model for 3D Compositional Reservoir Simulation in Fractured Reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef]
- Lee, S.H.; Jensen, C.L.; Lough, M.F. Efficient Finite-Difference Model for Flow in a Reservoir With Multiple Length-Scale Fractures. SPE J. 2000, 5, 268–275. [Google Scholar] [CrossRef]
- Lee, S.H.; Lough, M.F.; Jensen, C.L. Hierarchical modeling of flow in naturally fractured formations with multiple length scales. Water Resour. Res. 2001, 37, 443–455. [Google Scholar] [CrossRef]
- Wong, D.L.Y.; Doster, F.; Geiger, S.; Kamp, A. Partitioning Thresholds in Hybrid Implicit-Explicit Representations of Naturally Fractured Reservoirs. Water Resour. Res. 2020, 56, e2019WR025774. [Google Scholar] [CrossRef]
- Zhang, W.; Al Kobaisi, M. Cell-Centered Nonlinear Finite-Volume Methods with Improved Robustness. SPE J. 2020, 25, 288–309. [Google Scholar] [CrossRef]
- Berens, P. CircStat: A MATLAB Toolbox for Circular Statistics. J. Stat. Softw. 2009, 31, 1–21. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Durlofsky, L.J. Upscaling and gridding of fine scale geological models for flow simulation. In Proceedings of the 8th International Forum on Reservoir Simulation Iles Borromees, Stresa, Italy, 20–24 June 2005; pp. 1–59. [Google Scholar]
- Zhang, W.; Al Kobaisi, M. Discrete Fracture-Matrix Simulations Using Cell-Centered Nonlinear Finite Volume Methods. In ECMOR XVII; European Association of Geoscientists & Engineers: Edinburgh, UK, 2020. [Google Scholar]
- Zhang, W.; Al Kobaisi, M. Nonlinear finite volume method for 3D discrete fracture-matrix simulations. SPE J. 2020. [Google Scholar] [CrossRef]












| DFM-NTPFA | 55.0631 | 32.6250 | 27.7312 | 50.1693 |
| EDFM-TPFA | 55.6896 | 33.5183 | 27.9913 | 50.1626 |
| 50 | md | ||
| 2.5 | 0.8 | ||
| 5 m | 10 md | ||
| 500 m | 0.2 |
| % of Fractures Modeled Explicitly | |
|---|---|
| 28.38 | |
| 9.68 | |
| 3.37 | |
| 1.97 | |
| 1.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Diab, W.; Hajibeygi, H.; Al Kobaisi, M. A Computational Workflow for Flow and Transport in Fractured Porous Media Based on a Hierarchical Nonlinear Discrete Fracture Modeling Approach. Energies 2020, 13, 6667. https://doi.org/10.3390/en13246667
Zhang W, Diab W, Hajibeygi H, Al Kobaisi M. A Computational Workflow for Flow and Transport in Fractured Porous Media Based on a Hierarchical Nonlinear Discrete Fracture Modeling Approach. Energies. 2020; 13(24):6667. https://doi.org/10.3390/en13246667
Chicago/Turabian StyleZhang, Wenjuan, Waleed Diab, Hadi Hajibeygi, and Mohammed Al Kobaisi. 2020. "A Computational Workflow for Flow and Transport in Fractured Porous Media Based on a Hierarchical Nonlinear Discrete Fracture Modeling Approach" Energies 13, no. 24: 6667. https://doi.org/10.3390/en13246667
APA StyleZhang, W., Diab, W., Hajibeygi, H., & Al Kobaisi, M. (2020). A Computational Workflow for Flow and Transport in Fractured Porous Media Based on a Hierarchical Nonlinear Discrete Fracture Modeling Approach. Energies, 13(24), 6667. https://doi.org/10.3390/en13246667






