Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes
Abstract
1. Introduction
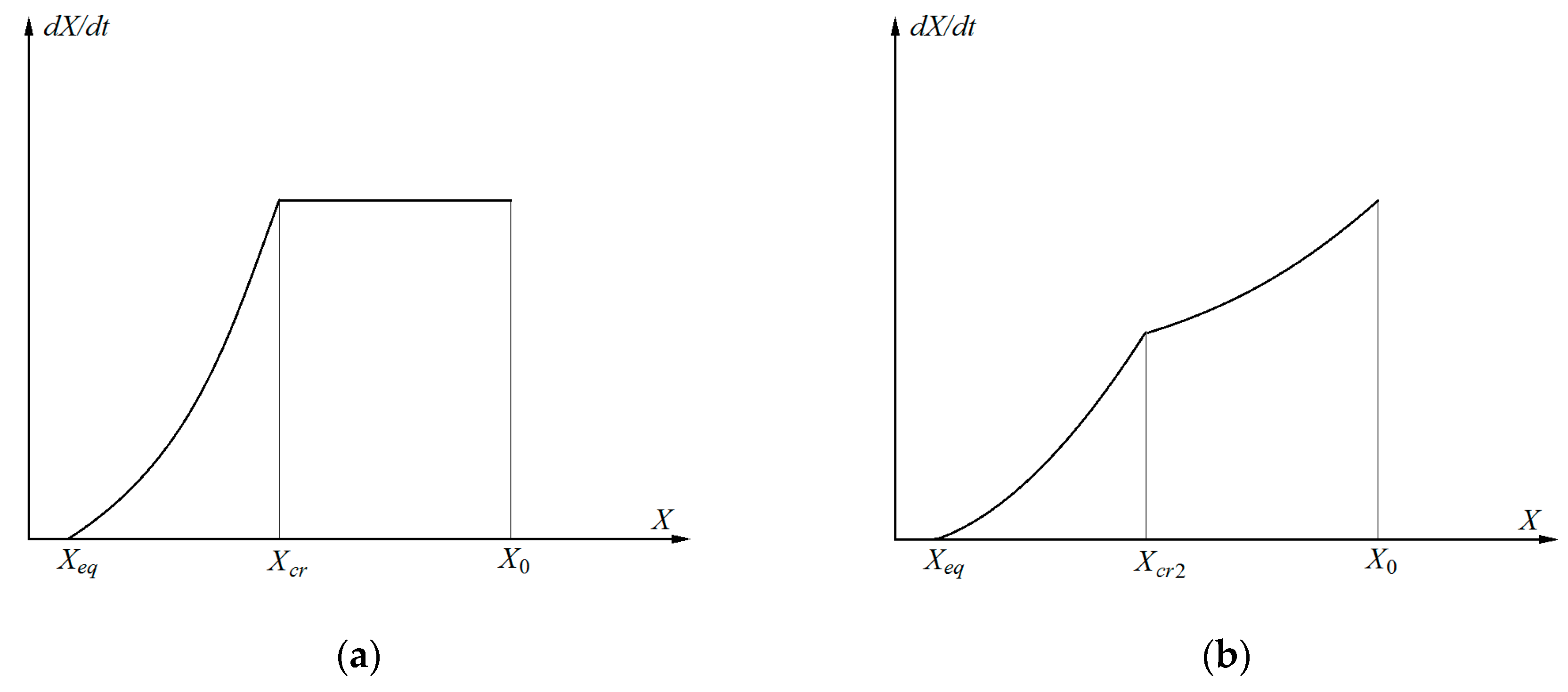
2. Mathematical Model
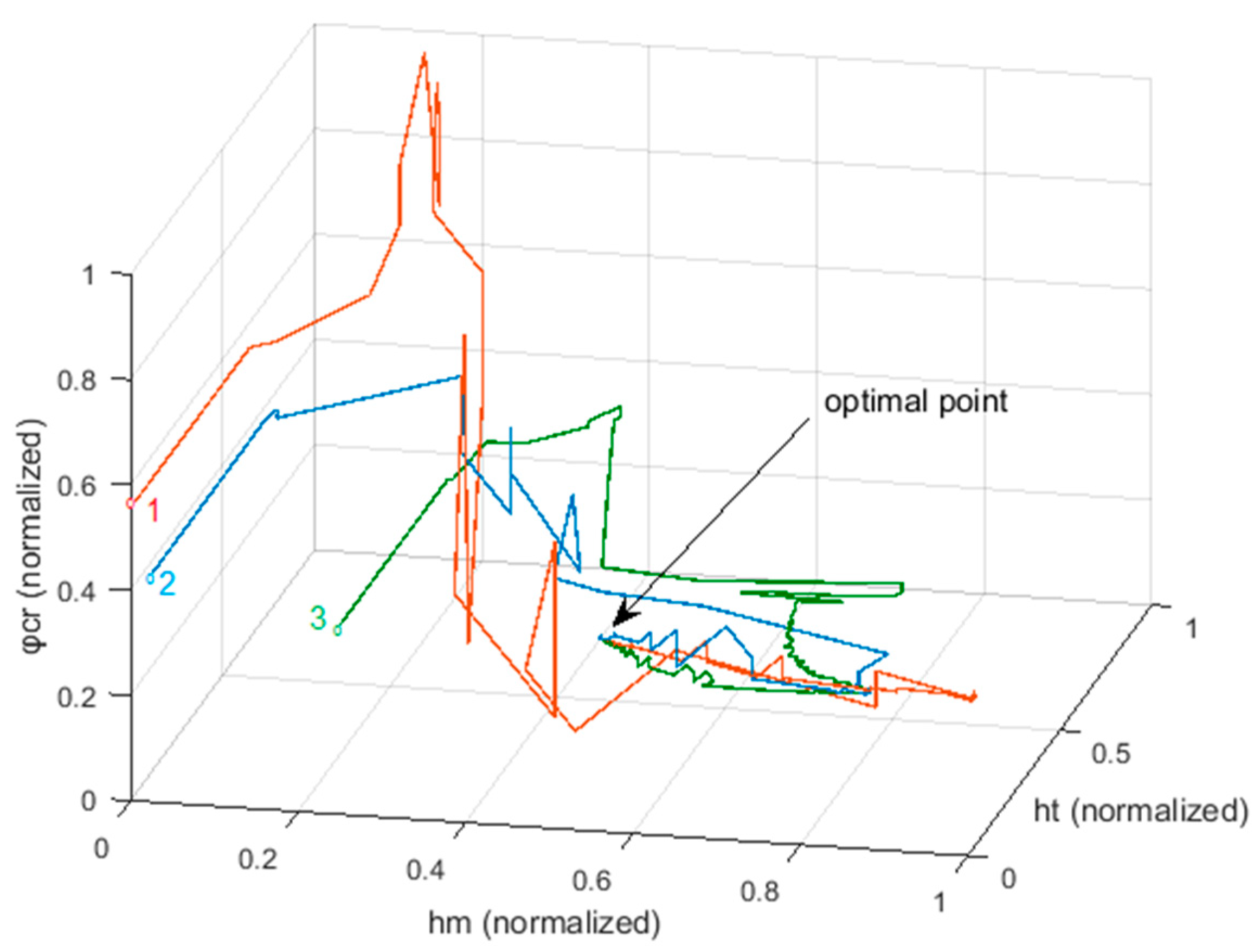
3. Solution Method
4. Model Parameter Determination
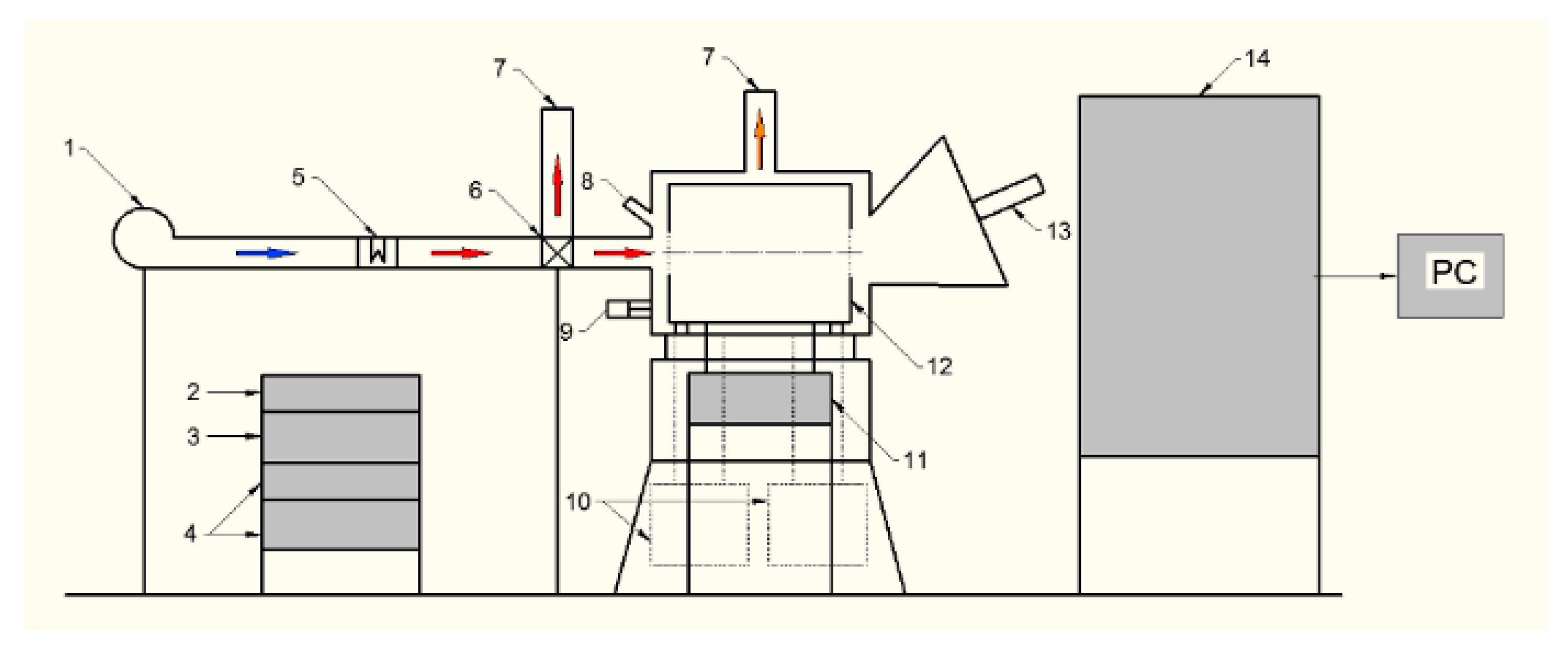
5. Materials and Methods
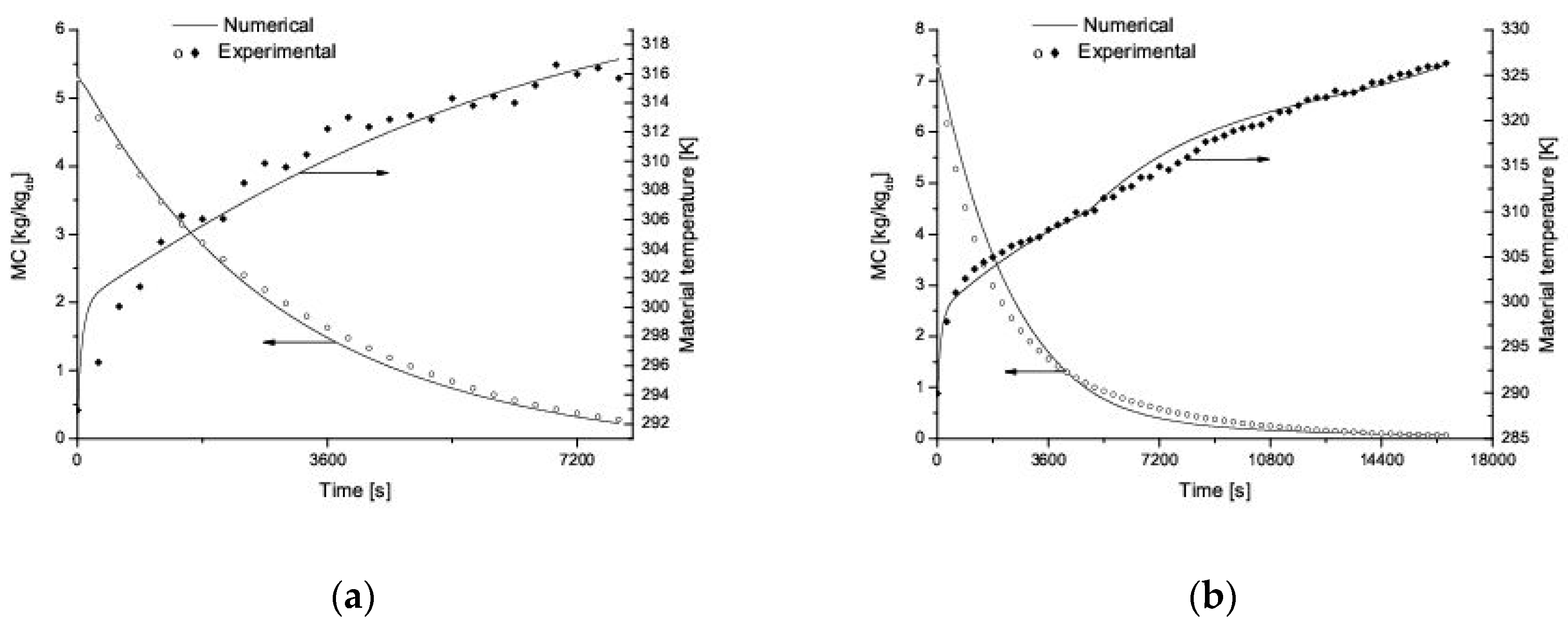
6. Numerical Results
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Designation | Unit |
| specific heat of dry solid | J/kgK | |
| specific heat of moisture (water) | J/kgK | |
| objective function | 1 | |
| mass transfer coefficient | kg/m2s | |
| heat transfer coefficient | J/m2sK | |
| latent heat of evaporation | J/kg | |
| dry mass | kg | |
| saturated vapor pressure | Pa | |
| time | s | |
| surface of sample | m2 | |
| initial surface of sample | m2 | |
| surface of mass exchange | m2 | |
| surface of heat exchange | m2 | |
| MC | moisture content dry basis | kg/kgdb |
| absolute temperature | K | |
| initial temperature | K | |
| ambient air temperature | K | |
| experimental value of temperature | K | |
| maximal value of temperature | K | |
| minimal value of temperature | K | |
| numerical value of temperature | K | |
| volume of sample | m3 | |
| initial volume of sample | m3 | |
| moisture content dry basis | kg/kgdb | |
| initial moisture content dry basis | kg/kgdb | |
| critical moisture content dry basis | kg/kgdb | |
| second critical moisture content dry basis | kg/kgdb | |
| equilibrium moisture content dry basis | kg/kgdb | |
| experimental value of moisture content | kg/kgdb | |
| maximal value of moisture content | kg/kgdb | |
| minimal value of moisture content | kg/kgdb | |
| numerical value of moisture content | kg/kgdb | |
| volumetric shrinkage coefficient | 1 | |
| relative air humidity | 1 | |
| relative air humidity in ambient air | 1 | |
| air humidity close to the dried sample surface | 1 | |
| second critical air relative humidity | 1 | |
| heat due to absorption of ultrasonic waves | W | |
| function—simplifying designation | kg/s | |
| function—simplifying designation | K/s |
References
- Jayaraman, K.S.; Das Gupta, D.K. Drying of Fuits and Vegetables. In Handbook of Industrial Drying, 4th ed.; Mujumdar, A.S., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 611–636. [Google Scholar]
- Chen, G.; Mujumdar, A.S. Drying Herbal Medicines and Tea. In Handbook of Industrial Drying, 4th ed.; Mujumdar, A.S., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 637–646. [Google Scholar]
- Musielak, G.; Mierzwa, D.; Kroehnke, J. Food Drying Enhancement by Ultrasound—A Review. Trends Food Sci. Technol. 2016, 56, 126–141. [Google Scholar] [CrossRef]
- Szadzińska, J.; Pashminehazar, R.; Kharaghani, A.; Tsotsas, E.; Łechtańska, J. Microwave and Ultrasound Assisted Convective Drying of Raspberries: Drying Kinetics and Microstructural Changes. Dry. Technol. 2018, 37, 1–12. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Riera, E.; de la Fuente Blanco, S.; Rodriguez-Corral, G.; Acosta-Aparicio, V.M.; Blanco, A. Application of High-Power Ultrasound for Dehydration of Vegetables: Processes and Devices. Dry Technol. 2007, 25, 1893–1901. [Google Scholar] [CrossRef]
- Cárcel, J.A.; García-Pérez, J.V.; Benedito, J.; Mulet, A. Food Process Innovation through New Technologies. J. Food Eng. 2012, 110, 200–207. [Google Scholar] [CrossRef]
- Bantle, M.; Hanssler, J. Ultrasonic Convective Drying Kinetics of Clipfish during the Initial Drying Period. Dry Technol. 2013, 31, 1307–1316. [Google Scholar] [CrossRef]
- Siucińska, K.; Konopacka, D. Application of Ultrasound to Modify and Improve Dried Fruit and Vegetable Tissue—A Review. Dry Technol. 2014, 32, 1360–1368. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Mierzwa, D. Ultrasound-Assisted Convective Drying of Biological Materials. Dry Technol. 2015, 33, 1601–1613. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Pawłowski, A. Intensification of Apple Drying due to Ultrasound Enhancement. J. Food Eng. 2015, 156, 1–9. [Google Scholar] [CrossRef]
- Gallego-Juárez, J.A.; Rodríguez-Corral, G.; San Emeterio-Prieto, J.L.; Montoya-Vitini, F. Electroacoustic Unit for Generating High Sonic and Ultrasonic Intensities in Gases and Interphases. U.S. Patent No. 5,299,175, 29 March 1994. [Google Scholar]
- Gallego-Juárez, J.A.; Riera, E.; Rodríguez-Corral, G.; Gálvez Moraleda, J.C.; Yang, T.S. A New High-Intensity Ultrasonic Technology for Food Dehydration. Dry Technol. 1999, 17, 597–608. [Google Scholar] [CrossRef]
- García-Pérez, J.V.; Cárcel, J.A.; de la Fuente-Blanco, S.; Riera-Franco de Sarabia, E. Ultrasonic Drying of Foodstuff in a Fluidized Bed: Parametric Study. Ultrasonics 2006, 44, e539–e543. [Google Scholar] [CrossRef]
- Khmelev, V.N.; Shalunov, A.V.; Barsukov, R.V.; Abramenko, D.S.; Lebedev, A.N. Studies of Ultrasonic Dehydration Efficiency. J. Zhejiang Univ. Sci. A 2011, 12, 247–254. [Google Scholar] [CrossRef]
- Kouchakzadeh, A.; Ghobadi, P. Modeling of Ultrasonic-Convective Drying of Pistachios. Agric. Eng. Int. CIGR J. 2012, 14, 144–149. [Google Scholar]
- Konopacka, D.; Parosa, R.; Piecko, J.; Połubok, A.; Siucińska, K. Ultrasound & Microwave Hybrid Drying Device for Colored Fruit Preservation—Product Quality and Energy Efficiency. In Proceedings of the 8th Asia-Pacific Drying Conference (ADC 2015), Kuala Lumpur, Malaysia, 10–12 August 2015; pp. 252–258. [Google Scholar]
- Cárcel, J.A.; García-Pérez, J.V.; Riera, E.; Mulet, A. Influence of Highintensity Ultrasound on Drying Kinetics of Persimmon. Dry Technol. 2007, 25, 185–193. [Google Scholar] [CrossRef]
- García- Pérez, J.V.; Cárcel, J.A.; Benedito, J.; Mulet, A. Power Ultrasound Mass Transfer Enhancement in Food Drying. Food Bioprod. Process. 2007, 85, 247–254. [Google Scholar] [CrossRef]
- Cárcel, J.A.; García-Pérez, J.V.; Riera, E.; Mulet, A. Improvement of Convective Drying of Carrot by Applying Power Ultrasound. Influence of Mass Load Density. Dry Technol. 2011, 29, 174–182. [Google Scholar] [CrossRef]
- Gamboa-Santos, J.; Montilla, A.; Cárcel, J.A.; Villamiel, M.; García-Pérez, J.V. Air-Borne Ultrasound Application in the Convective Drying of Strawberry. J. Food Eng. 2014, 128, 132–139. [Google Scholar] [CrossRef]
- Rodríguez, O.; Santacatalina, J.V.; Simal, S.; García- Pérez, J.V.; Femenia, A.; Rosselló, C. Influence of Power Ultrasound Application on Drying Kinetics of Apple and its Antioxidant and Microstructural Properties. J. Food Eng. 2014, 129, 21–29. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Pawłowski, A. Modeling of Kinetics in Stationary and Intermittent Drying. Dry Technol. 2010, 28, 1023–1031. [Google Scholar] [CrossRef]
- Aversa, M.; Van der Voort, A.-J.; de Heij, W.; Tournois, B.; Curcio, S. An Experimental Analysis of Acoustic Drying of Carrots: Evaluation of Heat Transfer Coefficients in Different Drying Conditions. Dry Technol. 2011, 29, 239–244. [Google Scholar] [CrossRef]
- Raszkowski, T.; Samson, A. Numerical Approaches to the Heat Transfer Problem in Modern Electronic Structures. Comput. Sci. 2017, 18, 71–93. [Google Scholar] [CrossRef]
- Zwarycz-Makkles, K.; Majorkowska-Mech, D. Gear and Runge-Kutta Numerical Discretization Method in Differential Equations of Adsorption in Adsorption Heat Pump. Appl. Sci. 2018, 8, 2437. [Google Scholar] [CrossRef]
- Duc, L.A.; Hyuk, K.D. Mathematical Modeling and Simulation of Rapeseed Drying on Concurrent-Flow Dryer. In Current Drying Processes; Palqa-Rosas, I., Ed.; IntechOpen: Rijeka, Croatia; London, UK, 2020. [Google Scholar] [CrossRef][Green Version]
- Krupowicz, A. Numerical Methods of Initial Value Problems of Ordinary Differential Equations; PWN: Warsaw, Poland, 1986. [Google Scholar]
- Rosenbrock, H.H. An Automatic Method for Finding the Greatest or Least Value of a Function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Mujumdar, A.S. Principles, Classification, and Selection of Dryers. In Handbook of Industrial Drying, 4th ed.; Mujumdar, A.S., Ed.; CRC Press: Boca Raton, FL, USA, 2014; pp. 3–30. [Google Scholar]
- Musielak, G.; Banaszak, J. Non-Linear Heat and Mass Transfer during Convective Drying of Kaolin Cylinder under Non-Steady Conditions. Transp. Porous Media 2007, 66, 121–134. [Google Scholar]
- Strumiłło, C. Foundations of the Drying Theory and Technology, 2nd ed.; WNT: Warsaw, Poland, 1983. [Google Scholar]
- Davis, M. Numerical Methods and Modelling for Chemical Engineers; Wiley: Montreal, QC, Canada, 1984. [Google Scholar]
- Toledo, R.T. Fundamentals of Food Process Engineering; Heldman, D.R., Ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- DTU Food. Available online: http://www.foodcomp.dk/v7/fcdb_details.asp?FoodId=1128 (accessed on 16 April 2016).
- Szadzińska, J.; Kowalski, S.J.; Stasiak, M. Microwave and ultrasound enhancement of convective drying of strawberries: Experimental and modeling efficiency. Int. J. Heat Mass Transf. 2016, 103, 1065–1074. [Google Scholar] [CrossRef]
- Kowalski, S.J.; Pawłowski, A.; Szadzińska, J.; Łechtańska, J.; Stasiak, M. High power airborne ultrasound assist in combined drying of raspberries. Innov. Food Sci. Emerg. Technol. 2016, 34, 225–233. [Google Scholar] [CrossRef]
- Szadzińska, J.; Łechtańska, J.; Kowalski, S.J.; Stasiak, M. The effect of high power airborne ultrasound and microwaves on convective drying effectiveness and quality of green pepper. Ultrason. Sonochem. 2017, 34, 531–539. [Google Scholar] [CrossRef]
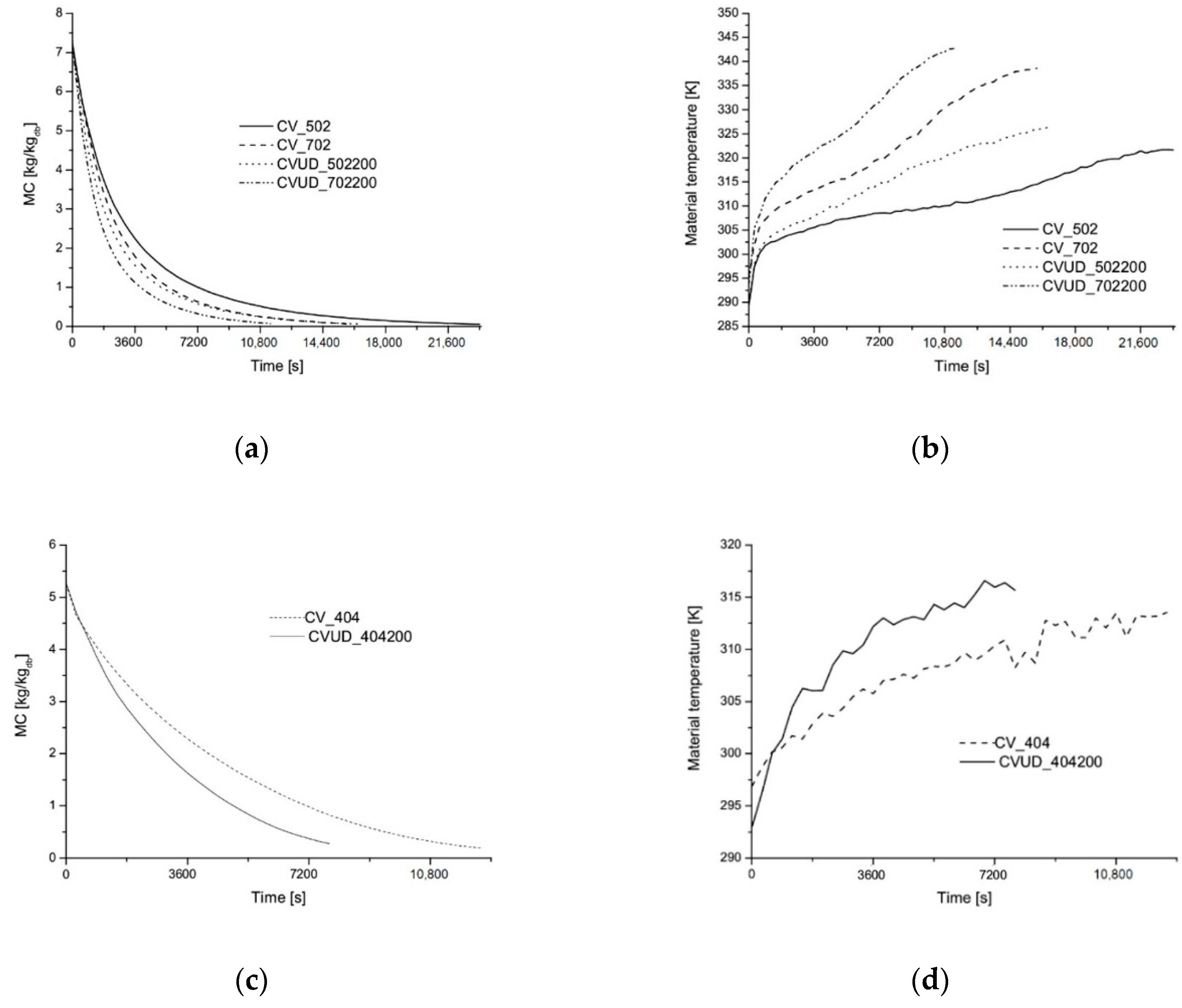
| Scheme No. and Abbreviation | Convective Drying Parameters | Ultrasound Power If Used |
|---|---|---|
| Apples | ||
| 1—CV_404 | 40 °C, air flow 4 m/s (effective 0.8 m/s) | – |
| 2—CVUD_404200 | 40 °C, air flow 4 m/s (effective 0.8 m/s) | 200 W |
| Carrots | ||
| 1—CV_502 | 50 °C, air flow 2 m/s (effective 0.4 m/s) | – |
| 2—CV_702 | 70 °C, air flow 2 m/s (effective 0.4 m/s) | – |
| 3—CVUD_502200 | 50 °C, air flow 2 m/s (effective 0.4 m/s) | 200 W |
| 4—CVUD_702200 | 70 °C, air flow 2 m/s (effective 0.4 m/s) | 200 W |
| Scheme No. and Abbreviation | Calculated Parameters | Assumed Value | Value of the Objective Function | |||
|---|---|---|---|---|---|---|
| hm (kg/m2s) | hT (J/m2sK) | φcr2 (1) | ΔQ (W) | Xcr2 (kg/kg) | ||
| 1—CV_502 | 0.000416 | 24.3 | 0.191 | – | 0.3 | 0.6589 |
| 2—CV_702 | 0.00116 | 20.8 | 0.194 | – | 1.0 | 0.2682 |
| 3—CVUD_502200 | 0.000773 | 44.5 | 0.323 | 0.584 | 0.3 | 0.1048 |
| 4—CVUD_702200 | 0.00140 | 40.5 | 0.275 | 0.887 | 0.8 | 0.1219 |
| Scheme No. and Abbreviation | Calculated Parameters | Value of the Objective Function | ||
|---|---|---|---|---|
| hm (kg/m2s) | hT (J/m2sK) | ΔQ (W) | ||
| 1—CV_404 | 0.000501 | 22.5 | – | 0.1235 |
| 2—CVUD_404200 | 0.000843 | 29.4 | 0.158 | 0.1321 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stasiak, M.; Musielak, G.; Mierzwa, D. Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes. Energies 2020, 13, 6577. https://doi.org/10.3390/en13246577
Stasiak M, Musielak G, Mierzwa D. Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes. Energies. 2020; 13(24):6577. https://doi.org/10.3390/en13246577
Chicago/Turabian StyleStasiak, Marcin, Grzegorz Musielak, and Dominik Mierzwa. 2020. "Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes" Energies 13, no. 24: 6577. https://doi.org/10.3390/en13246577
APA StyleStasiak, M., Musielak, G., & Mierzwa, D. (2020). Optimization Method for the Evaluation of Convective Heat and Mass Transfer Effective Coefficients and Energy Sources in Drying Processes. Energies, 13(24), 6577. https://doi.org/10.3390/en13246577




