Abstract
We present a Buildings-to-Grid (BtG) integration framework with intermittent wind-power generation and demand flexibility management provided by buildings. First, we extend the existing BtG models by introducing uncertain wind-power generation and reformulating the interactions between the Transmission System Operator (TSO), Distribution System Operators (DSO), and buildings. We then develop a unified BtG control framework to deal with forecast errors in the wind power, by considering ancillary services from both reserves and demand-side flexibility. The resulting framework is formulated as a finite-horizon stochastic model predictive control (MPC) problem, which is generally hard to solve due to the unknown distribution of the wind-power generation. To overcome this limitation, we present a tractable robust reformulation, together with probabilistic feasibility guarantees. We demonstrate that the proposed demand flexibility management can substitute the traditional reserve scheduling services in power systems with high levels of uncertain generation. Moreover, we show that this change does not jeopardize the stability of the grid or violate thermal comfort constraints of buildings. We finally provide a large-scale Monte Carlo simulation study to confirm the impact of achievements.
1. Introduction
An essential requirement of power grids with high wind-power penetration is the ancillary reserve power service, which can reduce unwanted power curtailment and enable higher integration of renewable generation. The reserve scheduling task of the Transmission System Operator (TSO) in power grids deals with day-ahead scheduling of the generator reserve power, in order to compensate for mismatches between the forecast and actual wind power [1]. Due to the growing penetration levels of wind-power generation, TSOs need to deal with increasing levels of uncertainty, thus imposing novel challenges and responsibilities for TSOs to avoid blackouts and other contingencies. This trend highlights the necessity for TSOs to introduce new types of ancillary services by enabling end-users (buildings) demand-side flexibility.
Approximately 40% of the global energy is consumed by buildings, with half of this being directly related to Heating, Ventilation, and Air Conditioning (HVAC) [2,3]. Buildings control decisions are typically only optimized locally to minimize energy consumption, but not in the wider scope of optimal control of the electricity grid. Demand-side flexibility of buildings represents the capability to shift production and/or consumption of electricity in time, while still satisfying consumer comfort requirements, and without changing the total production or consumption [4]. Building demand-side flexibility has been identified as an important asset for providing ancillary services being managed by the Distribution System Operators (DSOs) [5,6].
However, TSOs still have a much more prominent role in scheduling ancillary services, and DSOs often miss a majority of the scheduling information [7]. For a resilient, sustainable power system, DSOs need monitoring, simulation and control strategies that allow them to act as an active system operator of the future smart grid. Due to their uncertain and intermittent nature, renewable energy sources, such as wind power, contribute to power imbalance in the grid, making the task of frequency control more difficult [8]. Consequently, DSOs have the inevitable task to engage in providing ancillary services to the grid, in order to secure grid frequency, voltage levels, and the power balance [9].
It is worth noting that flexibility-based services are already available in some countries. For example, in the United Kingdom, National Grid ESO saw significant reductions in the electricity demand as a result of the COVID-19 pandemic [10]. As a response, the system operator introduced a novel Optional Downward Flexibility Management Service, which can curtail energy production from renewables when demand is lower than forecast [11]. Moreover, the European Network Code on Requirements for Generators (RfG) was issued in 2016, to harmonize standards that all power generating units (both conventional and renewable) must respect [12]. To show compliance, all new generators above 50 MW must undergo extensive simulation and testing, before they are allowed to connect to the grid [13]. However, despite these illustrative examples, more fundamental research is required to show the potential and limitations of such flexibility-based services.
The use of consumer appliances to provide dynamical demand response has been studied extensively in recent work, such as [5,6,14]. The potential of using building HVAC control as a source of ancillary services for the grid is shown by [15,16]. In [17,18], the authors develop the so-called Buildings-to-Grid (BtG) integration framework, which couples buildings and grid dynamics explicitly. Similarly, refs. [19,20] study how building demand response programs can be enabled in BtG systems via model predictive control (MPC). However, none of these studies explicitly coupled appliances, e.g., storage systems or building HVAC power load, to the grid dynamics in the presence of uncertain generation, which highlights the potential of developing a unified control framework to handle uncertain renewable energy sources in the BtG setting using building demand-side flexibility.
Research Contributions
In this paper, we propose a unified dynamical BtG framework by modeling the building demand-side flexibility, while also explicitly formulating the hierarchical interactions between the TSO, DSOs, and buildings. Such a demand-side flexibility asset can be considered to be a short-term operating reserve, which may yield an economic benefit in a robust fashion. The main novelty of this paper is that the proposed demand-side flexibility model in the BtG framework with uncertain generation can substitute the traditional reserve scheduling service in power systems with wind farms, without losing stability properties of the power grid and violating the buildings desired thermal comfort. This paper extends our previous work in [21,22], by presenting explicit expressions to quantify the available building demand-side flexibility from specific assets, and by providing more detailed insights in both the theoretical and experimental results.
The remaining part of this paper is organized as follows. In Section 2, we present the BtG model dynamics, and ancillary service deployment via traditional reserves and demand-side flexibility is discussed in Section 3. Using the proposed BtG model dynamics, we provide a stochastic MPC formulation in Section 4, and then a robust tractable reformulation in Section 5 to achieve a desired level of constraints fulfillment with a-priori probabilistic certificates. We simulate an extended version of an IEEE benchmark case study in Section 6, to demonstrate the functionality of our proposed hierarchical integrated energy system model and control technique. Finally, our main conclusions are summarized in Section 7.
2. Buildings-to-Grid System Modeling
Consider a hierarchical electrical energy network consisting of one TSO network together with a wind farm production unit connected to multiple DSO networks, to which individual buildings are connected.
2.1. Wind Integrated TSO Model Dynamics
Consider to be the set of TSO buses (nodes), to be the set of TSO generators, and to be the set of DSOs connected to the TSO network. Define also to be an incidence matrix such that the entries, , relate generators to the TSO buses, respectively. The set of neighboring nodes of TSO bus k is defined by .
The TSO network is modeled using the existing swing equation model, e.g., [21,23], where we extend the active power swing equation for bus k by integrating wind-power production in the following form:
where , and are the voltage angle, angular velocity (frequency), and angular acceleration of bus k, and and are inertia and damping coefficients, respectively. The power flow between buses is considered to be purely reactive, and is characterized by the line susceptance, , and the difference in voltage angle, . The susceptance is the imaginary part of admittance, which is a measure of how easily a circuit will allow a current to flow through a line [24]. denotes the power dispatch of generator m, is the wind farm power injection at bus k, and is the load of any DSO network connected to bus k. Furthermore, and are generator reserve and demand-side flexibility power contributions, respectively, which are defined formally in Section 3, and are used to compensate for errors in the wind-power forecast. Without loss of generality, it is assumed that is a realization of an unknown stochastic process defined on some probability space . It is important to note that we do not require the sample space and the probability measure to be known explicitly, as will be explained later. We only need a finite number of realizations of the uncertain variable , and it is sufficient to consider that they are independent and identically distributed (i.i.d).
The second order differential equation for TSO bus k in Equation (1) can be rewritten as two first-order equations, by defining the angular frequency deviation , where is the absolute frequency of bus k, and is the synchronous frequency. Using this notation, the complete TSO network dynamics are captured in the following state-space model:
with state variable , and appropriate matrices , , and . For the full derivation of the system parameters for a similar model without wind-power integration, the reader is referred to [17,21,25]. The element of vector for bus k is defined as . and represent the power demand and flexibility from all DSO networks connected to the TSO, respectively, and are obtained as follows:
where , represent the load and flexibility of DSO i on each TSO bus, respectively. with entries denotes the active power flow from TSO bus k to bus l of DSO i, and is nonzero only for border buses (i.e., buses that are physically connected via a line). Similarly, represents the flexibility power flow between the TSO and DSO i.
Remark 1.
To determine the power flow across the TSO and DSO networks, we follow a DC power approximation and follow the small-angle approximation to assume that . Using such an approximation and letting be the set of lines in the TSO network, we can define the Laplacian matrix for the TSO network with entries defined by
We can now construct the following augmented matrix which can be used to obtain the power flow in the TSO network lines:
A similar expression can be written for DSO network to obtain for DSO i.
2.2. DSO Model Dynamics
Consider to be the set of buses (nodes) of DSO i. Denote by the neighborhood set of node l of DSO i. Each DSO network is connected to the parent TSO through one or multiple border buses. DSO network dynamics are the same as in Equation (1), but with the additional assumption that no generators are connected to DSO buses, leading to and in the DSO swing equations. Please note that this is not a restrictive assumption, as the model can easily be extended to include generation in the DSO network as well. The dynamics at bus l of DSO i are described as
where the subscript in denotes element l of the respective vector, is the frequency-sensitive portion of the uncontrollable load at bus l, and , denote the total building demand and flexibility at bus l of DSO i. The resulting state-space model for DSO i is given by:
where is the state vector, and and are system matrices. The parameter and its element for bus l are defined as . The total building demand and flexibility at node l can be determined as follows:
where incidence matrix relates the buses of DSO i to the buildings in the network. Each building is assumed to be connected to exactly one DSO bus, and thus, . , , are the power storage, HVAC power demand, and uncontrollable miscellaneous power consumption of all buildings, respectively. Finally, , represent the total storage and the total building HVAC flexibility, respectively.
2.3. Building and Storage Model Dynamics
2.3.1. Building Thermal Comfort Model
The framework developed in this paper explicitly couples building decision variables to the power grid. Traditional resistance and capacitor (RC) networks are widely used to model thermodynamics of building envelopes [15]. Both highly detailed models with variables for many zones, e.g., [26,27,28], and low order models with a single lumped zone, e.g., [17,18], have been proposed in the literature. As the envisioned purpose of the framework is to integrate large clusters of buildings into the grid, a low order thermal building model is most appropriate, considering the resulting computational complexity. Using the 3R-2C circuits model for each building adopted from [17], consider the thermal dynamics:
where and are the wall and zone (interior room) temperatures, respectively, and is the ambient temperature. The resistance of the external walls, internal walls, and windows are given by the resistance parameters , and . The lumped thermal capacities of the building exterior walls and the zone are denoted by and , respectively. Moreover, represents the sum of the solar radiation absorbed on the external walls, and is the total heat gain from internal sources. The room temperature is controlled by the cooling load , which is proportional to the HVAC power consumption via . The thermal dynamics in Equation (5) for an individual building are written as the following state-space model:
where is the state vector and is an uncertain vector. Please note that for the buildings model, we consider to be equivalent to the forecast value of the uncertain parameters. For the explicit derivation of system matrices , , and , we refer the reader to [21]. Since we aim to describe the dynamics of clusters of buildings, let be the total number of buildings, and denote by the full set of buildings connected to the grid. In the absence of communication between buildings, the dynamics of all buildings combined are described by the following state-space model with block diagonal system matrices (full matrix definitions are omitted for brevity):
2.3.2. Electrical Energy Storage Model
Define to be the energy state variable (state of charge, or SoC) and the normal and flexibility power input rate variable, respectively, for a dedicated electrical storage unit j of building . Consider now the discrete-time dynamical model of storage unit j as:
where is the given initial SoC, h is the discretization step size, and and are efficiency coefficients of the storage unit. Although the current equation models energy loss proportionally, higher order equations for losses can be modeled as well. Denote by and the diagonal matrices composed of and for all buildings , respectively.
Remark 2.
The proposed models for the TSO, DSO, and building thermal comfort dynamics in Equations (1), (4), and (6), respectively, are continuous-time. To formulate a discrete optimal control problem in the MPC paradigm, the dynamics are discretized using the first-order backward Euler implicit method proposed in [29]. The discretized dynamics in the three distinct model areas are then denoted by the following functions:
for all time steps such that is the finite-time step of the simulation study.
3. Ancillary Service Deployment
In this section, we first describe common practice in the TSO network to deal with highly fluctuating wind-power integration, the so-called reserve scheduling service, and then present a novel formulation for building demand flexibility to be deployed as an ancillary service to handle uncertain wind power in the energy network.
3.1. Reserve Scheduling Formulation
Wind-power generation suffers from uncertainty and limited predictability [30]. Consider to be the forecast value of the wind power for every wind farm in the set , and denote the error between forecast and actual power by . When , the power balance in the TSO network between production and demand is not satisfied anymore. To restore power balance, the common practice is to deploy so-called reserve power such that by adjusting the generator power output, forecast errors are compensated with altered generation (denoted by ). Increasing the generator output is called up-spinning reserve (), and decreasing the output is down-spinning reserve (). To schedule the reserve power, one can define the reserve power as follows:
and consider to determine and at each time step k. Please note that the new scheduled power should also satisfy the generation limits, i.e., , where and are the minimum and maximum limits of power generation units, respectively.
3.2. Building Flexibility Formulation
Define to be the building flexibility and consider the capability to increase energy consumption as increased-demand flexibility ( and the capability to decrease energy consumption as decreased-demand flexibility (). If instead of generator reserve power, demand flexibility is used to mitigate the wind-power forecast error, one can schedule the flexibility as follows:
and consider to determine and at each time step k.
Consider now the flexibility contribution of individual buildings in the network via two sources: (1) building storage systems, and (2) building HVAC loads, which yields the following bounds on the building flexibility at time step k:
where , , , and represent the increased- and decreased-demand flexibility using the storage unit and HVAC load, respectively. The available storage flexibility of building can be formulated as:
where h is the discretization step size, and , , , and are the SoC limits and storage power limits, respectively. Storage flexibility is defined as the margin between the current storage power and the upper and lower bounds, respectively, constrained by the SoC limits on . As indicated in Figure 1, increased-demand storage flexibility () is the maximum amount of power with which can be increased for one time step width h, such that both the maximum storage power injection constraint (Figure 1a) and the storage energy limit (Figure 1b) are still satisfied.
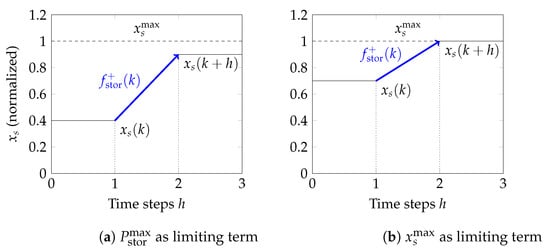
Figure 1.
Visualization of positive storage flexibility.
A similar expression is derived for the available HVAC flexibility of building , such that both HVAC power limits and building comfort levels are still satisfied:
where , are the minimum and maximum limits of HVAC power usage, respectively. and are the minimum and maximum HVAC power such that the comfort level constraints are still satisfied:
where and represent the thermal comfort level limits at time k. Positive HVAC flexibility is visualized in Figure 2, showing that the limiting term is either the HVAC power (Figure 2a) or the thermal comfort level (Figure 2b).
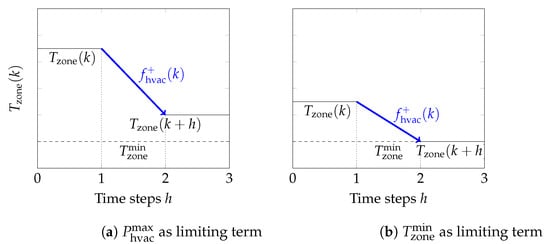
Figure 2.
Visualization of positive HVAC flexibility.
3.3. Reserve Scheduling Together with Building Flexibility
Including both reserve and flexibility in the grid power balance yields
where the sum of reserve and flexibility mitigates the total wind-power forecast error:
Based on Equation (12), the following constraint encodes that the scheduled reserve and flexibility is always sufficient to compensate the wind-power error:
4. Stochastic MPC Formulation
Model predictive control (MPC) is a flexible paradigm that defines receding-horizon-based optimization problems, enabling the specification of time-domain objectives together with the ability to explicitly enforce constraints on system dynamics. Two extensions to MPC exist when the system dynamics and/or constraints are subject to uncertainties, namely robust and stochastic MPC. Robust MPC is able to handle the uncertainties using the so-called worst-case approach while still ensuring that the state constraints are met. Alternatively, stochastic MPC has attractive features, due to its ability to handle uncertain systems in a less conservative way. Stochastic MPC considers the stochastic characteristics of the uncertainties and treats system constraints in a probabilistic manner, i.e., using chance constraints. In this section, we formulate a receding horizon stochastic optimization problem to compute an optimal decisions sequence that minimizes a given objective function, subject to the uncertain BtG model dynamics and chance constraints.
Given the set of prediction time steps such that is the length of the prediction horizon, consider the concatenated vector of control decision variables to be
The objective function consists of two parts. The first part penalizes TSO and DSO grid frequency deviations, while part two accounts for the operating costs, e.g., power generation, etc. The initial grid state variables are given by , the vector of uncertainty is , and , , , and are diagonal cost matrices associated with the TSO and DSO states, generation, and HVAC power usage respectively. Finally, , , , and are the cost vectors related to increased- and decreased-demand, up- and down-spinning reserves, respectively. Using these definitions, the cost function can be formulated as follows:
The cost function in Equation (18) is a random variable, since it depends on the uncertain TSO and DSO state variables. Therefore, we consider to obtain a deterministic cost function, which can be approximated empirically following the approach in [31] by averaging the value of its argument for some number of different realizations of the uncertain variable, which plays a tuning parameter role, i.e., .
The discretized dynamics in Equation (9) are non-deterministic, due to the uncertainty in the wind, reserve, and flexibility power. To obtain a set of deterministic dynamics, consider now the special case when , and denote the corresponding TSO, DSO, building, and storage dynamics by , , , . In this case, , which means that the optimal reserve and flexibility contributions as determined in Equation (16) are both zero. Using this notation, we are in a position to formulate a finite-horizon stochastic control problem for each sampling time k using the following optimization program:
- TSO deterministic frequency model dynamics:
- TSO generation, ramping, line, and balance constraints:where and are ramping limits of power generation units, is defined in Remark 1, and and are the TSO power flow limits.
- DSO deterministic frequency dynamics, :
- DSO power line and balance constraints, :where is defined in Remark 1, and and are the DSO power flow limits.
- Buildings deterministic thermal comfort dynamics:
- Buildings thermal comfort, power balance, and HVAC usage constraints:where and are the minimum and maximum bounds for the desired thermal comfort of buildings.
- Buildings electrical storage unit dynamics:
- Buildings storage capacity and power usage constraints:
- Probabilistic constraint:where and are given by Equation (9), is the level of admissible constraint violation, , , and , such that the formulation for , , , and are given in Section 3.2.
The constraint Equation (19i) is a chance constraint, which ensures that the feasibility probability for the constraint is above the specified level. Using the proposed chance constraint Equation (19i), stochastic MPC offers an alternative approach to robust MPC. Since stochastic MPC directly incorporates the trade-off between constraint feasibility and control performance, the corresponding solutions are generally less conservative.
Please note that Equations (19a)–(19h) are all based on the deterministic BtG dynamics for the special case when no ancillary services are required, i.e., , R, , , , and are all zero. On the contrary, the probabilistic constraint Equation (19i) depends on the non-deterministic dynamics. Hence, the optimization problem in Equation (19) is a finite-horizon, chance-constrained quadratic program, whose stages are coupled by the dynamics of the TSO, DSO, buildings thermal comfort, and storage systems at each sampling time k. We note that the proposed optimization program in Equation (19) is in general a non-convex problem which is hard to solve. The feasible set of Equation (19) is non-convex and hard to determine explicitly in the presence of chance constraints Equation (19i). In the following section, we will develop a tractable framework to obtain a probabilistically feasible solution.
5. Tractable Robust MPC Reformulation
Using a more compact notation, the chance constraints Equation (19i) can be written as
To this end, we approximate the proposed probabilistic constraints in Equation (20) using the following robust reformulation:
where is a bounded uncertainty set compared to which is an unbounded and unknown uncertainty set in Equation (20). In the perspective of power systems, the proposed tractable reformulation Equation (21) translates the unbounded set of wind-power scenarios to a bounded set which contains the more probable scenarios of wind power with a high level of confidence. Please note that the proposed constraint Equation (21) is a robust constraint, since it should be satisfied for all . Obviously, for any feasible solution for Equation (21), implies . Therefore, by choosing that covers at least a content of , i.e., satisfies , any feasible solution for Equation (21) must satisfy , implying that it is also feasible for Equation (20) (see [32] for more detailed descriptions). In other words,
Lemma 1.
Any feasible solution for Equation (21) using a -content set is a feasible solution for the probabilistic constraint in Equation (20) with probability .
Proof.
The proof is straightforward, and we omit it for the sake of brevity. □
Let us now introduce as a bounded set. We assume for simplicity that is an axis-aligned hyper-rectangular set. Please note that this is not a restrictive assumption and any convex set, e.g., ellipsoids and polytopes, could have been chosen instead as described in [31]. We can define as an interval, where the vector defines the hyper-rectangle bounds.
Consider now the following optimization problem that aims to determine the set with minimal volume:
where S is a finite number of i.i.d samples needed to be available from either a known distribution or through historical observations. If we denote by the optimal solution of Equation (22), then the following proposition provides an explicit relation between the number of required samples S and the -content set .
Proposition 1.
Fix , , determine , and solve Equation (22) to obtain its optimal solution . Then, with probability of at least ,
Proof.
The proof is based on the results in [33] by noting that the proposed optimization problem Equation (22) is a convex program with the number of decision variables equivalent to the number of uncertain variables . We therefore omit the proof for the sake of brevity. □
Using the proposed robust reformulation in Equation (21), one can obtain a tractable formulation similar to (Proposition 1, [34]). The obtained solution of the optimization program in Equation (19), where Equation (19i) is replaced with Equation (21), is the optimal input sequence . Following the MPC paradigm, only the first element of the optimal control input is implemented at time k, and we proceed based on the receding horizon principle. This means that at every time step k, the robust reformulation of Equation (19) is solved using the current measurement of the state variables .
6. Numerical Case Study
To demonstrate the grid regulative capacity of (a) reserve scheduling and (b) building HVAC and storage flexibility on the BtG system under wind-power penetration, we consider the following three cases in the simulation study: (1) BtG system with only reserve power enabled, (2) BtG system with only flexibility power enabled, (3) BtG system with both reserve and flexibility power enabled. Please note that we consider the same cost coefficients for both reserve and flexibility deployments in the cost function Equation (18). Throughout the simulation horizon, the wind-power penetration is around 10–15% of the total electricity generation in all cases.
6.1. Simulation Setup
Consider a network of 1 TSO with 3 generators (GRs), 2 DSOs, 13 buildings, and 1 wind farm (WF), as visualized in Figure 3. The case studies are simulated for h with the prediction horizon of an hour and time resolution min. Thus, the length of the prediction horizon is steps. To generate the number of required scenarios of wind power, we use the Markov chain model in [30]. Following Proposition 1, we choose , , and , and then solve Equation (22) to obtain the bounded set at each sampling time k. The associated cost parameters are , power generation and consumption are valued at , and reserve and flexibility scheduling at Please note that to have a fair comparison, we assumed the same cost coefficients for both reserve and flexibility. Since our simulation study considers large-scale buildings, the limits for each storage unit are set equivalent to four Tesla Model S batteries [35], i.e., , , , and . Simulations were implemented in MATLAB, with Yalmip as interface [36] and Gurobi as solver [37]. Building parameters and miscellaneous (uncontrollable) load profiles for the large-scale, commercial buildings were adopted from [17]. Grid parameters (line length, cable type, line susceptance, etc.) were obtained from the MatPower IEEE 5-bus power system [38], with some parameters (e.g., power line limits) scaled appropriately for the current simulation studies. For further details on the building and grid parameters, we refer the reader to the sources above. We also carried out Monte Carlo simulations with the system under optimal control input simulated for 10,000 different wind-power scenarios. We obtain a-posteriori the violation probability (empirical violation level), by means of counting the number of trajectories that violate any of the constraints, to check if the theoretical maximum violation level is indeed satisfied.
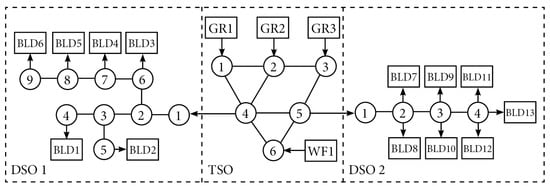
Figure 3.
Network topology of the MPC problem, indicating the grid structure, generators (GR) buildings (BLD) and wind farm (WF).
6.2. Simulation Results
The power balance in the TSO network for all cases is presented in Figure 4, showing a reduced production for Case 2 and 3, compared to Case 1. In particular, Case 2 yields a total reduction in conventional generation of 2.7% compared to Case 1, whereas for Case 3, this reduction is 12.8%. The solid black line shows the forecast wind power, and the dark green bars show the actual wind power. As shown in both Figure 4 and Figure 6, between 3:00–11:00 and 15:00–17:00, the wind-power error is negative, , and from 12:00–14:00 and 18:00–24:00, the error is positive, . To restore the power balance, when , Case 2 employs the decreased-demand flexibility and on the contrary, Case 1 uses the up-spinning reserve power to reduce output power dispatch. Similarly, when , Case 2 employs the increased-demand flexibility and on the contrary, Case 1 uses the down-spinning reserve power to reduce output power dispatch.
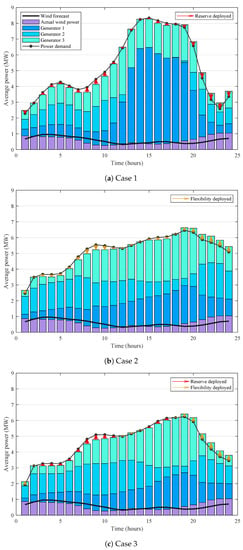
Figure 4.
Power balance in the TSO network, showing the wind-power forecast (lower solid line), actual wind power (purple bars), and reserve and flexibility deployment in bright red and yellow, respectively. Other colored bars represent production by conventional generators.
Figure 5 depicts the frequency deviations in the TSO and DSO networks for Case 3. Frequency deviations for all the cases are kept well below allowable limits. Enabling building-side flexibility results in a reduction of 5.3% in cumulative squared frequency deviation for the total network, and a reduction of 32.5% in the DSO network only.
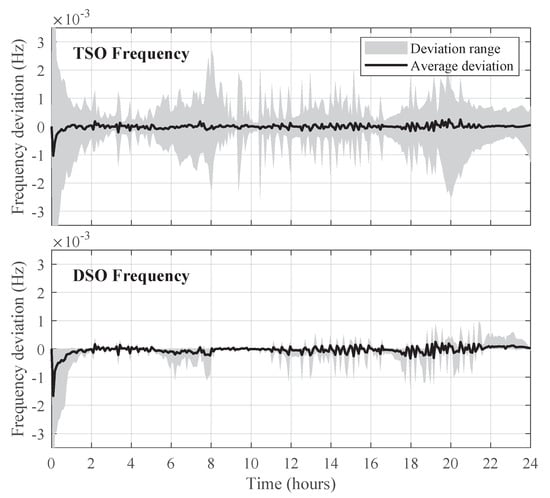
Figure 5.
Case 3—Frequency deviations in the TSO and DSO networks.
The wind-power error together with the reserve and flexibility dispatch for Case 3 is presented in Figure 6. As reserve and flexibility are valued at the same cost in the objective function, the distribution between the two indicates that both mechanisms are cooperating well to meet the power balance. The total flexibility dispatch accounts for 44.37% of the total compensation for the wind-power error over the 24h simulation time. It is shown that in the case of a positive wind-power error, flexibility dispatch is promoted over reserve, while for a negative wind-power error, the opposite is observed. Finally, Figure 6 also shows that the wind-power error is perfectly compensated throughout the full day, by the sum of flexibility and reserve deployment.
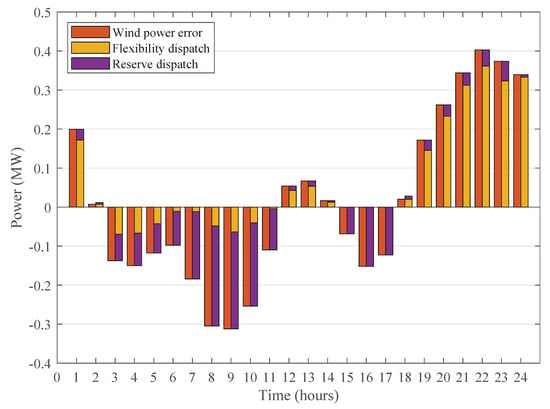
Figure 6.
Wind-power error for Case 3, and distribution of reserve and flexibility dispatch. Flexibility dispatch comprises 44.37% of all wind-power error compensation.
The reserve and flexibility scheduling is compared to the actual dispatch in more detail in Figure 7. In line with Figure 6, up-spinning reserve is promoted over decreased-demand flexibility, while increased-demand is favored over down-spinning reserve. Although total power demand differs by less than 10% between all cases, this motivates why the power dispatch of the cases is of different shape, as observed in Figure 4. As shown in Figure 6, it is important to note that the reserve and flexibility scheduling capacity is always significantly higher than the actual reserve or flexibility dispatch (i.e., the portion of the capacity that is deployed in the operational decision-making). This suggests that the current reserve and flexibility scheduling capacity is also sufficient for dealing with higher wind-power penetration levels than the current 10%.
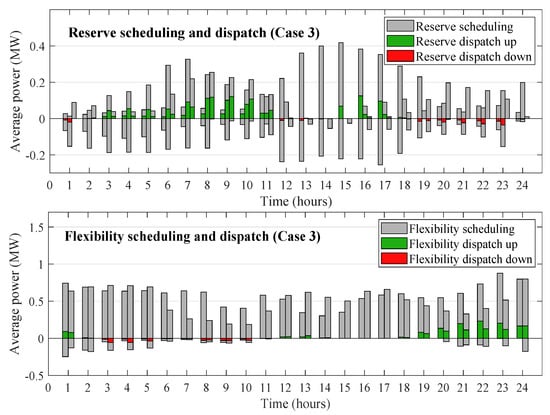
Figure 7.
Case 3—Actual reserve (per generator) and flexibility (per building cluster connected to the same DSO) dispatch per hour compared to the reserve and flexibility scheduled.
The results of our Monte Carlo simulation to determine the empirical constraint violation level are presented in Figure 8 for all 3 cases along with a case in which no reserve or flexibility is used. As the majority of violations are observed during peak load hours, only this portion of the simulation horizon is presented. For the case with no reserve or flexibility, empirical violation levels are extremely high, as any deviation of the wind power from the forecast trajectory almost exclusively results in violation of the power line limits. For Case 1 and 3, maximum empirical violation levels are around 0.1%, whereas for Case 2, no violations were observed in any of the 10,000 iterations. In all three cases, the empirical violation level is well below the theoretical limit of .
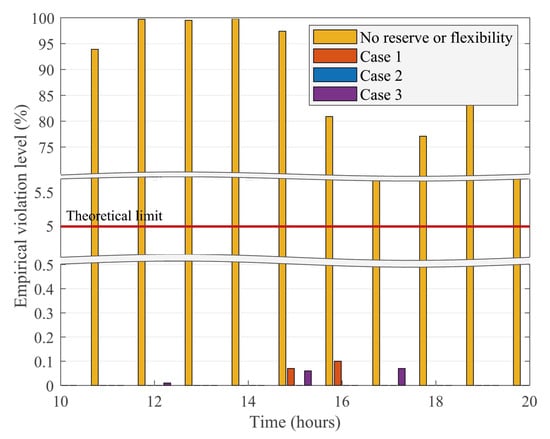
Figure 8.
Monte Carlo empirical violation levels (note the double break in the Y-axis and the limited time span of the plot).
7. Conclusions
In this paper, we have presented two new developments for the BtG integration framework. First, we extended the existing models by introducing uncertain wind-power generation and by explicitly formulating the interactions between TSO, DSOs, and buildings. Second, we developed a unified BtG framework to handle uncertain generation, by integrating demand-side flexibility provided by individual buildings into the traditional process of reserve scheduling. We provided explicit expressions to determine the available amount of building demand-side flexibility from HVAC and electrical storage units. Using the unified BtG model, we formulated a finite-horizon stochastic control problem and provided a tractable robust reformulation with probabilistic feasibility guarantees. As the main outcome of our proposed BtG framework, we conclude that the demand-side flexibility can substitute the traditional reserve scheduling services in power systems in the presence of wind-power generation, without losing stability properties of the power grid and violating the buildings thermal comfort of occupants.
At the same time, the proposed framework is still rather idealistic, and relies on multiple major assumptions. As a final note, we discuss some of these assumptions, and provide possible directions for future research:
- First of all, we did not consider the impact of imperfect communication between the TSO, DSOs, and buildings, and other sources of uncertainty than the wind power, such as demand uncertainty, were left out of scope. Hence, in a more sophisticated BtG integration framework, multiple sources of uncertainty should be incorporated.
- Second, the BtG framework in the current work is formulated as a centralized MPC framework. Although the current centralized implementation runs in reasonable time for hundreds of buildings, we believe that it is worth exploring decentralized control frameworks, e.g., [39], in order to reduce the computational complexity of the problem.
- Finally, part of our current work focuses on integrating the psychological impact of end-users for participating in the ancillary service market, by providing demand-side flexibility to the grid. We are interested in constructing models to simulate the willingness of end-users to participate in the ancillary service market, in order to study how different stimuli can influence the psychological behavior of consumers.
Author Contributions
Formal analysis, V.R.; Funding acquisition, J.M.A.S.; Investigation, V.R.; Methodology, V.R.; Software, T.S.B.; Supervision, J.M.A.S.; Validation, V.R.; Visualization, T.S.B.; Writing, original draft, V.R. and T.S.B.; Writing, review and editing, V.R. and T.S.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the incentives and algorithms for efficient, reliable, sustainable and socially acceptable energy system integration (ERSAS) research program funded by the Dutch organization for scientific research (NWO) with grant number 647-002-005.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rostampour, V.; Ter Haar, O.; Keviczky, T. Distributed Stochastic Reserve Scheduling in AC Power Systems With Uncertain Generation. IEEE Trans. Power Syst. 2018, 34, 1005–1020. [Google Scholar] [CrossRef]
- Lawrence, T.M.; Boudreau, M.C.; Helsen, L.; Henze, G.; Mohammadpour, J.; Noonan, D.; Patteeuw, D.; Pless, S.; Watson, R.T. Ten questions concerning integrating smart buildings into the smart grid. Build. Environ. 2016, 108, 273–283. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Buildings Energy Data Book: Buildings Technologies Program, Energy Efficiency and Renewable Energy; US Department of Energy: Washington, DC, USA, 2011.
- Roossien, B. Mathematical Quantification of Near Real-Time Flexibility for Smart Grids; Energy Research Centre (NL): Sint Maartensvlotbrug, The Netherlands, 2011; pp. 1–34. Available online: http://www.flexines.org/publicaties/eindrapport/BIJLAGE14a.pdf (accessed on 9 December 2020).
- Pavlak, G.S.; Henze, G.P.; Cushing, V.J. Optimizing commercial building participation in energy and ancillary service markets. Energy Build. 2014, 81, 115–126. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, N.; Wang, W.; Guan, X.; Xu, Z.; Dong, B.; Liu, T. Coordinating the operations of smart buildings in smart grids. Appl. Energy 2018, 228, 2510–2525. [Google Scholar] [CrossRef]
- Eurelectric. Active Distribution System Management a Key Tool for the Smooth Integration—Findings and Recommendations. Technical Report. 2013. Available online: https://www.eurelectric.org/media/1781/asm_full_report_discussion_paper_final-2013-030-0117-01-e.pdf (accessed on 9 December 2020).
- Andersson, G. Modelling and Analysis of Electric Power Systems; EEH—Power Systems Laboratory, ETH Zurich: Zürich, Switzerland, 2008; pp. 1–183. Available online: https://www.yumpu.com/en/document/read/4227429/modelling-and-analysis-of-electric-power-systems-eeh-eth-zurich (accessed on 9 December 2020).
- ENTSO-E. Towards Smarter Grids: Developing TSO and DSO Roles and Interactions for the Benefit of Consumers. 2015, pp. 1–8. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/Publications/Position%20papers%20and%20reports/150303_ENTSO-E_Position_Paper_TSO-DSO_interaction.pdf (accessed on 9 December 2020).
- Bahmanyar, A.; Estebsari, A.; Ernst, D. The impact of different COVID-19 containment measures on electricity consumption in Europe. Energy Res. Soc. Sci. 2020, 68, 101683. [Google Scholar] [CrossRef] [PubMed]
- NG ESO. Optional Downward Flexibility Management (ODFM) Service Documents; National Grid ESO: Warwick, UK, 2020; Available online: https://www.lexology.com/library/detail.aspx?g=cc311166-d06d-43e2-8ac8-474a8f8b5278 (accessed on 9 December 2020).
- Commission Regulation (EU). Establishing a Network Code on Requirements for Grid Connection of Generators. Off. J. Eur. Union 2016. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=OJ%3AJOL_2016_112_R_0001 (accessed on 9 December 2020).
- Bruendlinger, R. Review and Assessment of Latest Grid Code Developments in Europe and Selected International Markets with Respect to High Penetration PV. In Proceedings of the 6th Solar Integration Workshop, Vienna, Austria, 14–17 November 2016. [Google Scholar]
- Short, J.; Infield, D.; Freris, L. Stabilization of Grid Frequency Through Dynamic Demand Control. IEEE Trans. Power Syst. 2007, 22, 1284–1293. [Google Scholar] [CrossRef]
- Blum, D.H. Improving the Use of Commercial Building HVAC Systems for Electric Grid Ancillary Services. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2016. [Google Scholar]
- Lin, Y.; Barooah, P.; Mathieu, J.L. Ancillary Services Through Demand Scheduling and Control of Commercial Buildings. IEEE Trans. Power Syst. 2017, 32, 186–197. [Google Scholar] [CrossRef]
- Taha, A.F.; Gatsis, N.; Dong, B.; Pipri, A.; Li, Z. Buildings-to-Grid Integration Framework. IEEE Trans. Smart Grid 2017, 10, 1237–1249. [Google Scholar] [CrossRef]
- Dong, B.; Taha, A.F.; Gatsis, N.; Li, Z.; Pipri, A. Impact of Occupancy-Based Buildings-to-Grid Integration on Frequency Regulation in Smart Grids. Proc. Am. Control Conf. 2018, 5399–5405. [Google Scholar] [CrossRef]
- Anwar, M.B.; Cabrera, C.A.; Neu, O.; O’Malley, M.; Burke, D.J. An integrated Building-to-Grid model for evaluation of energy arbitrage value of Thermal Storage. In Proceedings of the 2016 International Conference for Students on Applied Engineering, ICSAE 2016, Newcastle Upon Tyne, UK, 20–21 October 2016; pp. 64–69. [Google Scholar]
- Razmara, M.; Bharati, G.R.; Hanover, D.; Shahbakhti, M.; Paudyal, S.; Robinett, R.D. Enabling Demand Response programs via Predictive Control of Building-to-Grid systems integrated with PV Panels and Energy Storage Systems. Proc. Am. Control Conf. 2017, 56–61. [Google Scholar] [CrossRef]
- Badings, T.S.; Rostampour, V.; Scherpen, J.M. Distributed Building Energy Storage Units for Frequency Control Service in Power Systems. IFAC Control Smart Grid Renew. Energy Syst. (CSGRES) 2019, 52, 228–233. [Google Scholar] [CrossRef]
- Rostampour, V.; Badings, T.S.; Scherpen, J.M.A. Buildings-to-Grid Integration with High Wind Power Penetration. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019. [Google Scholar] [CrossRef]
- Trip, S.; Burger, M.; De Persis, C. An internal model approach to frequency regulation in inverter-based microgrids with time-varying voltages. In Proceedings of the IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 223–228. [Google Scholar]
- Conejo, A.J.; Baringo, L. Power System Operations; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Badings, T.S. Buildings-to-Grid Integration for Demand-Side Flexibility in Power Systems with Uncertain Generation. Master’s Thesis, University of Groningen, Groningen, The Netherlands, 2019. [Google Scholar]
- Dong, B. Integrated Building Heating, Cooling and Ventilation Control. Tesis 2010, 1–174. [Google Scholar] [CrossRef]
- Razmara, M.; Bharati, G.R.; Shahbakhti, M.; Paudyal, S.; Robinett, R.D. Bilevel optimization framework for smart building-to-grid systems. IEEE Trans. Smart Grid 2018, 9, 582–593. [Google Scholar] [CrossRef]
- Danza, L.; Belussi, L.; Meroni, I.; Salamone, F.; Floreani, F.; Piccinini, A.; Dabusti, A. A Simplified Thermal Model to Control the Energy Fluxes and to Improve the Performance of Buildings. Energy Procedia 2016, 101, 97–104. [Google Scholar] [CrossRef]
- Sincovec, R.F.; Erisman, A.M.; Yip, E.L.; Epton, M.A. Analysis of Descriptor Systems Using Numerical Algorithms. IEEE Trans. Autom. Control 1981, 26, 139–147. [Google Scholar] [CrossRef]
- Papaefthymiou, G.; Klockl, B. MCMC for wind power simulation. IEEE Trans. Energy Convers. 2008, 23, 234–240. [Google Scholar] [CrossRef]
- Rostampour, V.; Keviczky, T. Probabilistic Energy Management for Building Climate Comfort in Smart Thermal Grids with Seasonal Storage Systems. IEEE Trans. Smart Grid 2018, 10, 3687–3697. [Google Scholar] [CrossRef]
- Hong, L.J.; Huang, Z.; Lam, H. Learning-based Robust Optimization: Procedures and Statistical Guarantees. arXiv 2017, arXiv:1704.04342. [Google Scholar]
- Calafiore, G.C.; Campi, M.C. The scenario approach to robust control design. IEEE Trans. Autom. Control 2006, 51, 742–753. [Google Scholar] [CrossRef]
- Rostampour, V.; Keviczky, T. Robust randomized model predictive control for energy balance in smart thermal grids. In Proceedings of the European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 1201–1208. [Google Scholar]
- Tesla. Website Support—Tesla Model S Specifications. 2018. Available online: https://www.tesla.com/models (accessed on 9 December 2020).
- Löfberg, J. YALMIP: A toolbox for modeling and optimization in MATLAB. In Proceedings of the International Symposium on Computer Aided Control Systems Design, Taipei, Taiwan, 2–4 September 2004; pp. 284–289. [Google Scholar]
- Gurobi Optimization. Gurobi Optimizer Reference Manual. 2019. Available online: https://www.gurobi.com/wp-content/plugins/hd_documentations/documentation/9.0/refman.pdf (accessed on 9 December 2020).
- Zimmerman, R.D.; Murillo-Sánchez, C.E.; Thomas, R.J. MATPOWER: Steady-state operations, planning, and analysis tools for power systems research and education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- Patel, N.R.; Risbeck, M.J.; Rawlings, J.B.; Wenzel, M.J.; Turney, R.D. Distributed economic model predictive control for large-scale building temperature regulation. Proc. Am. Control Conf. 2016, 895–900. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).