Effect of Rheological Properties of Aqueous Solution of Na-CMC on Spray Angle for Conical Pressure-Swirl Atomizers
Abstract
1. Introduction
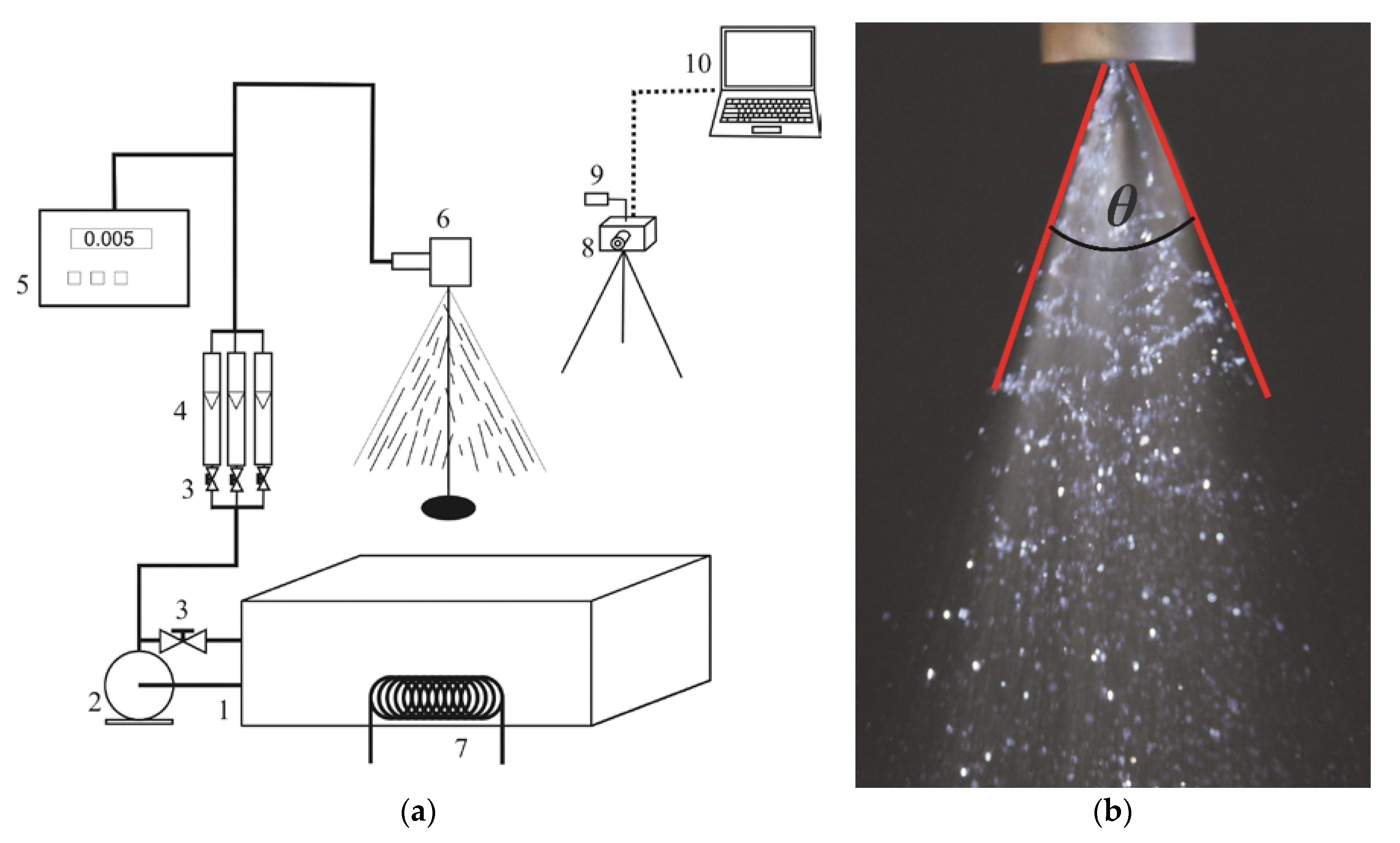
2. Materials and Methods
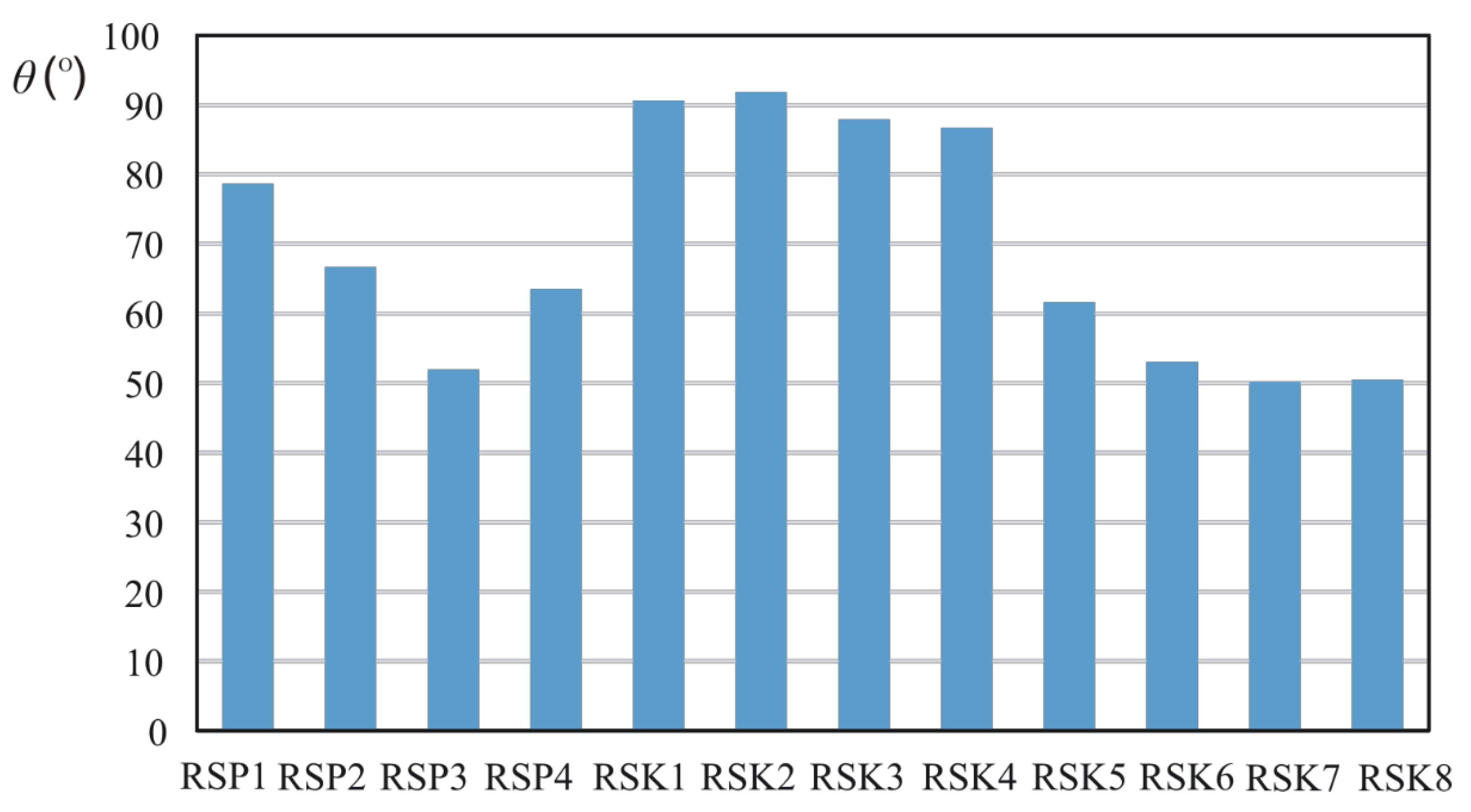
- Atomizers with a conical swirl chamber with different height-to-diameter ratios, with an inlet port located perpendicular to the atomizer axis and cylindrical orifices (RSP1, RSP2, RSP3, and RSP4);
- Atomizers with a conical swirl chamber with different height-to-diameter ratios, with an inlet port located at an angle of 60° in relation to the atomizer axis and cylindrical orifices (RSK1, RSK2, RSK3, RSK4, RSK5, RSK6, RSK7, and RSK8).
3. Results
3.1. Rheological Properties of Tested Liquids
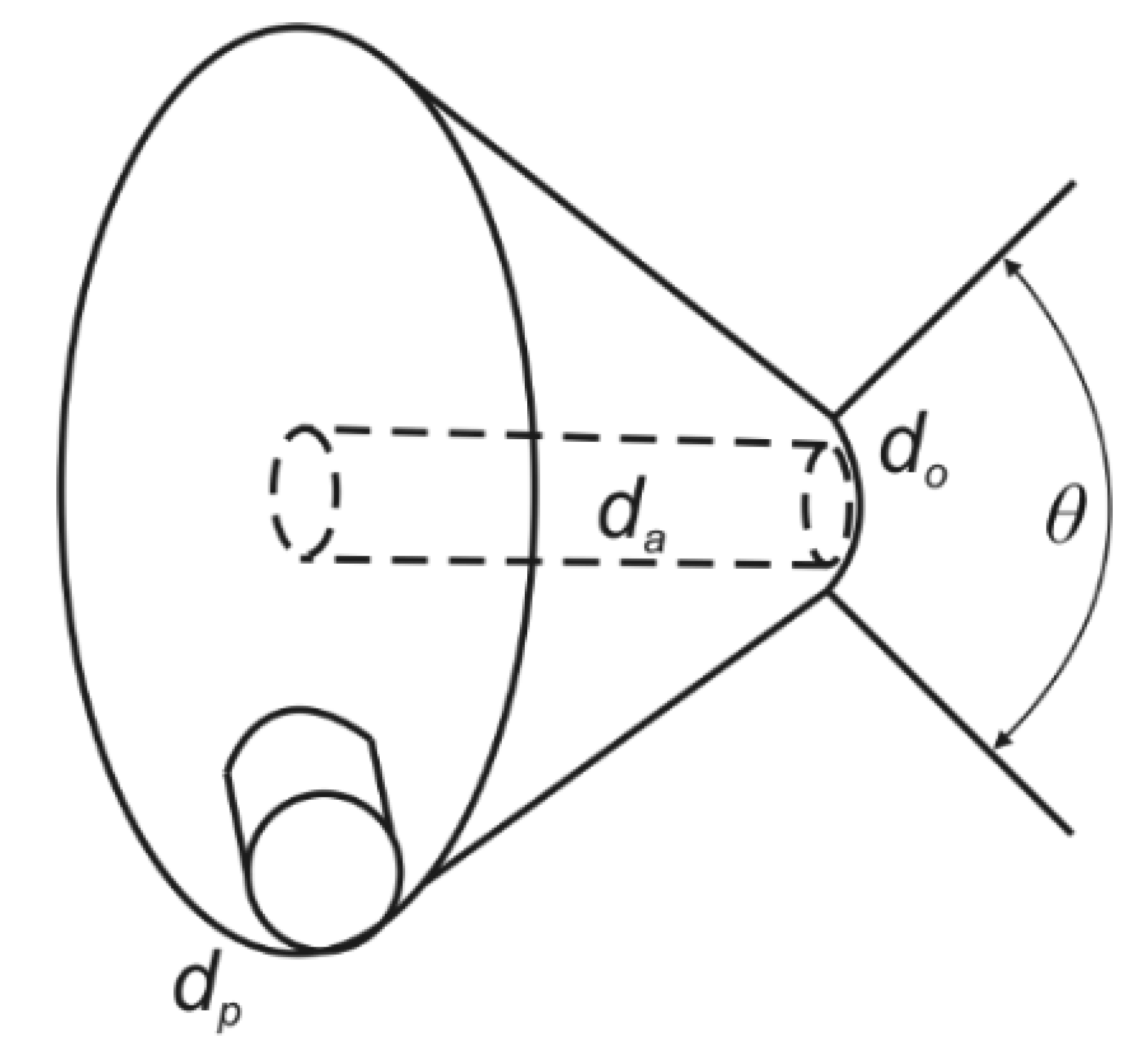
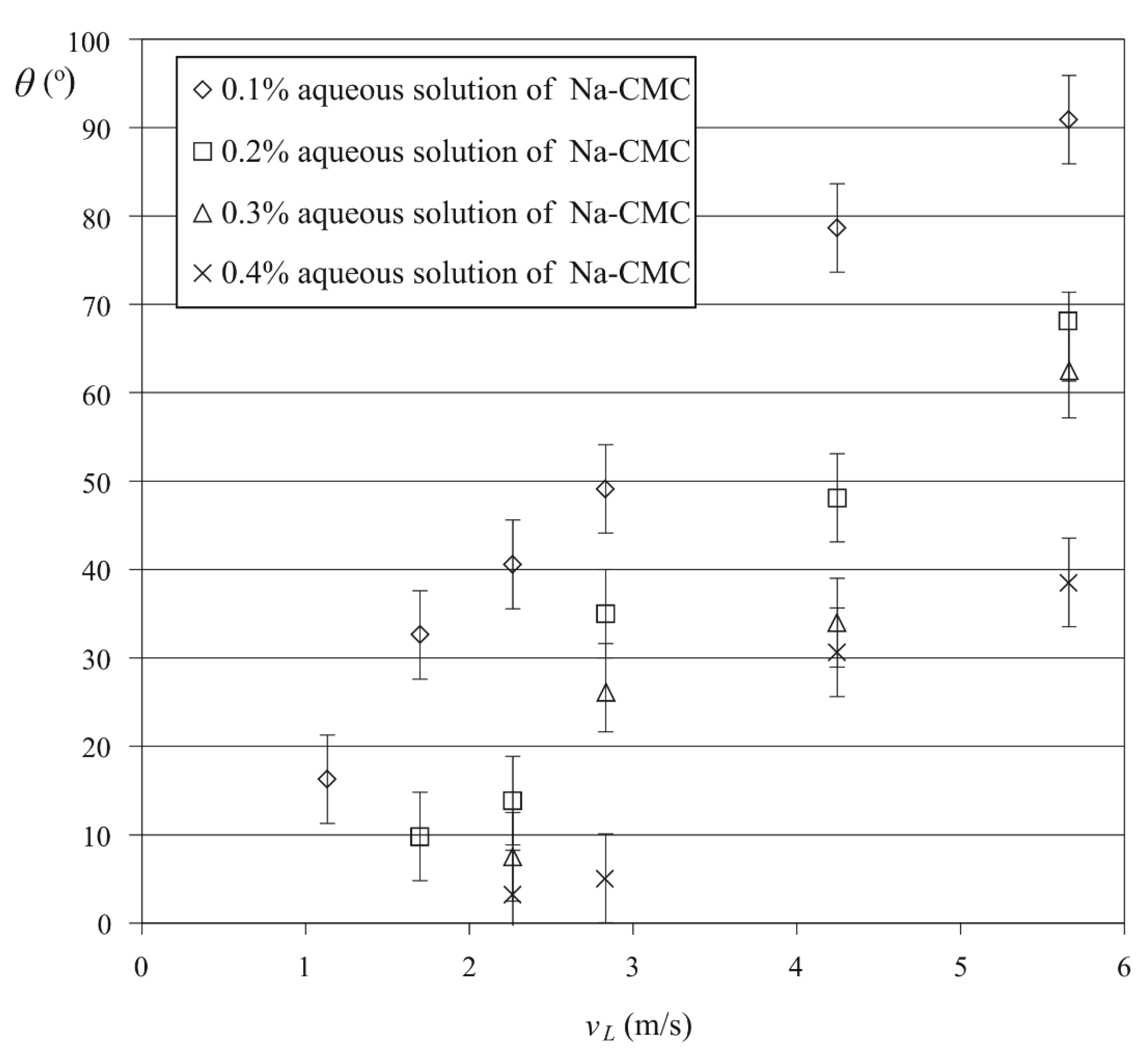
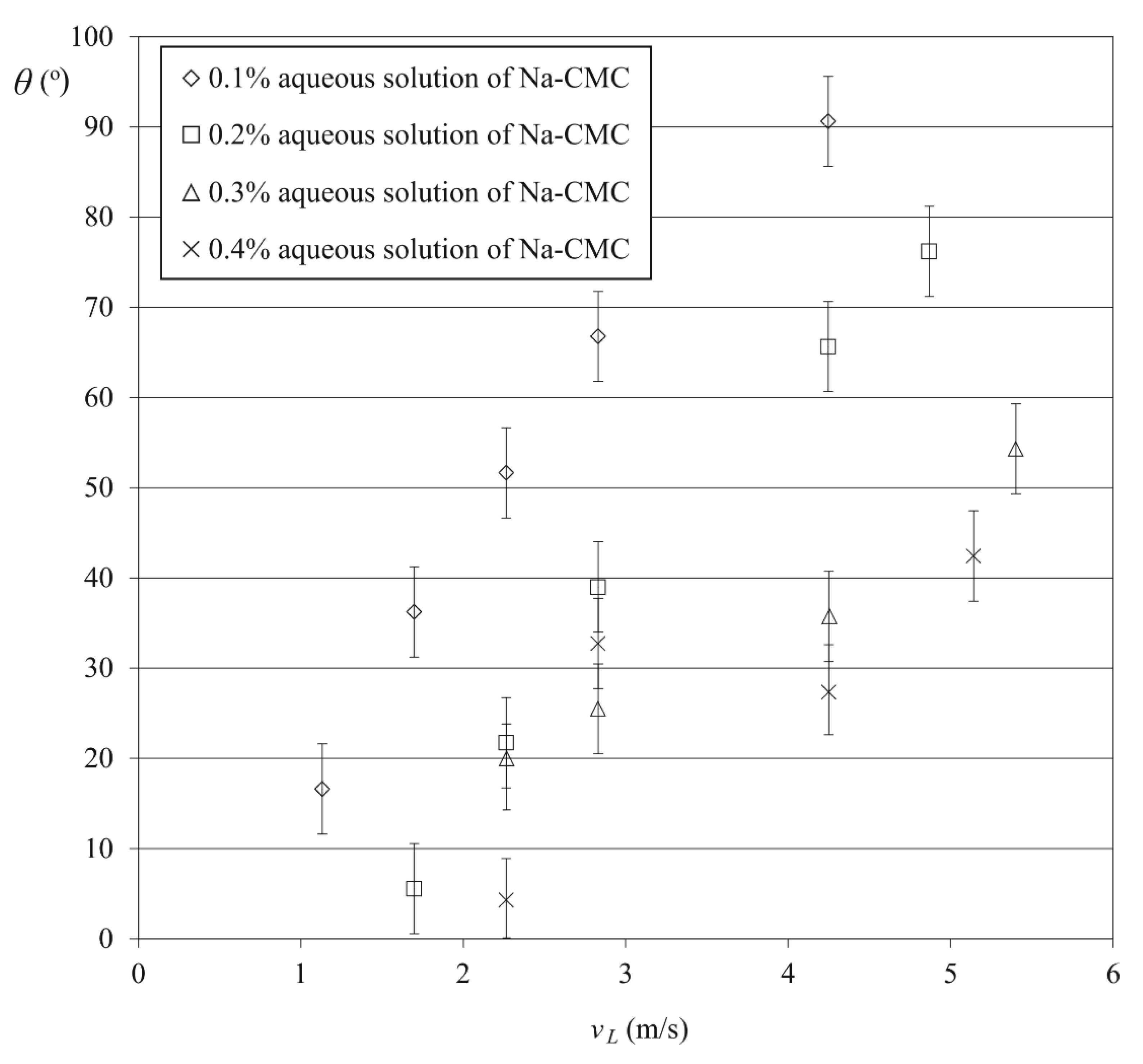
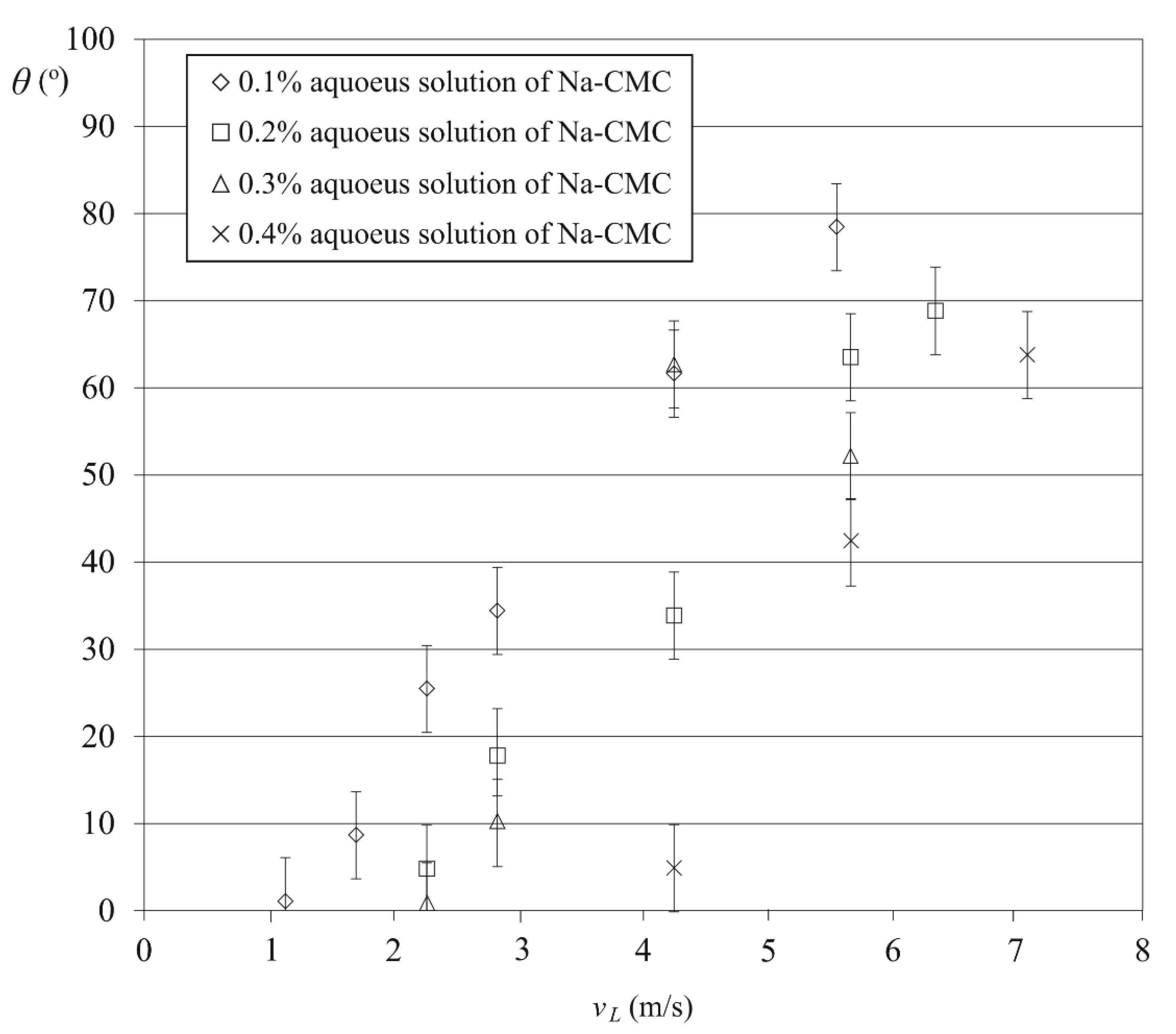
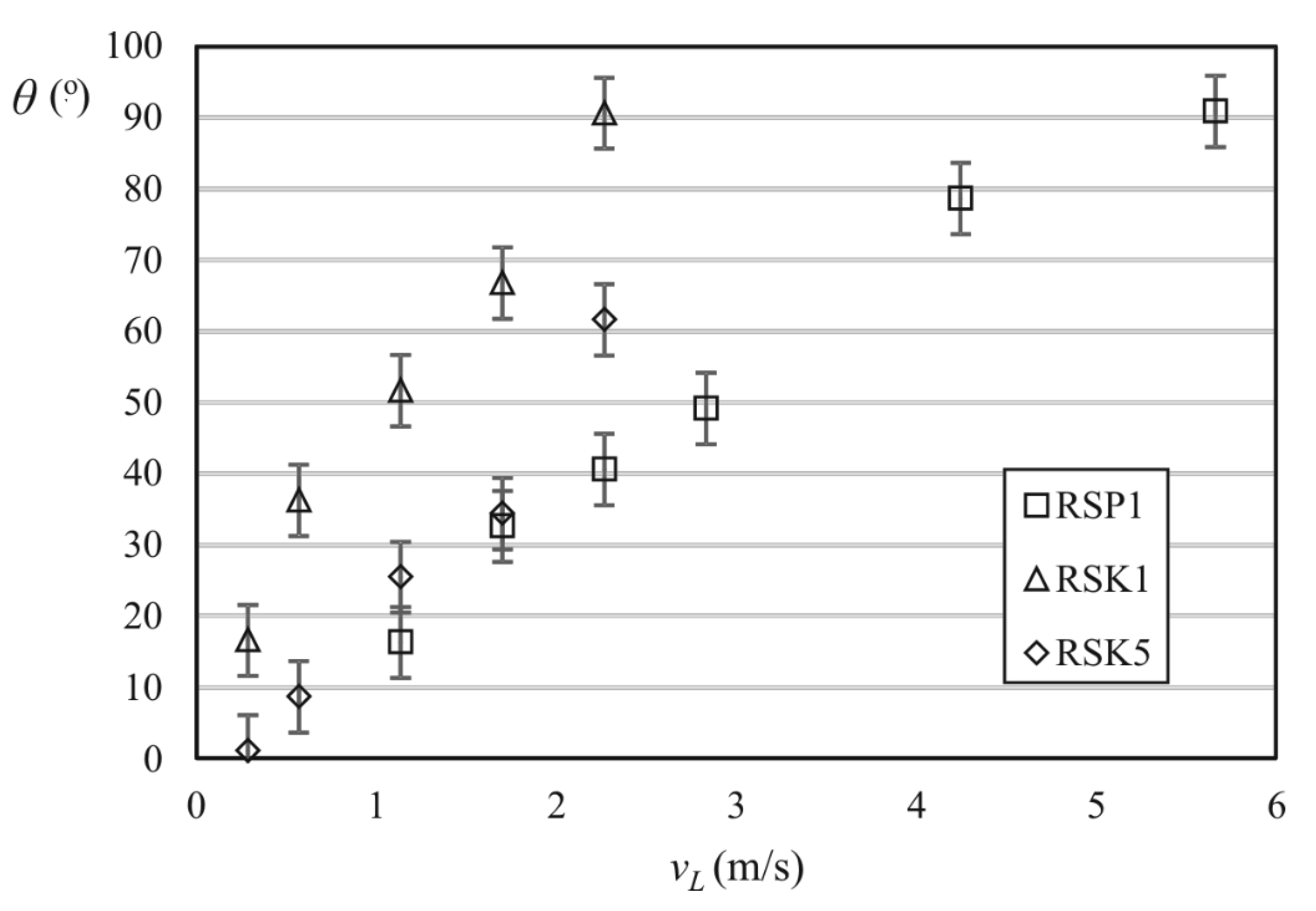
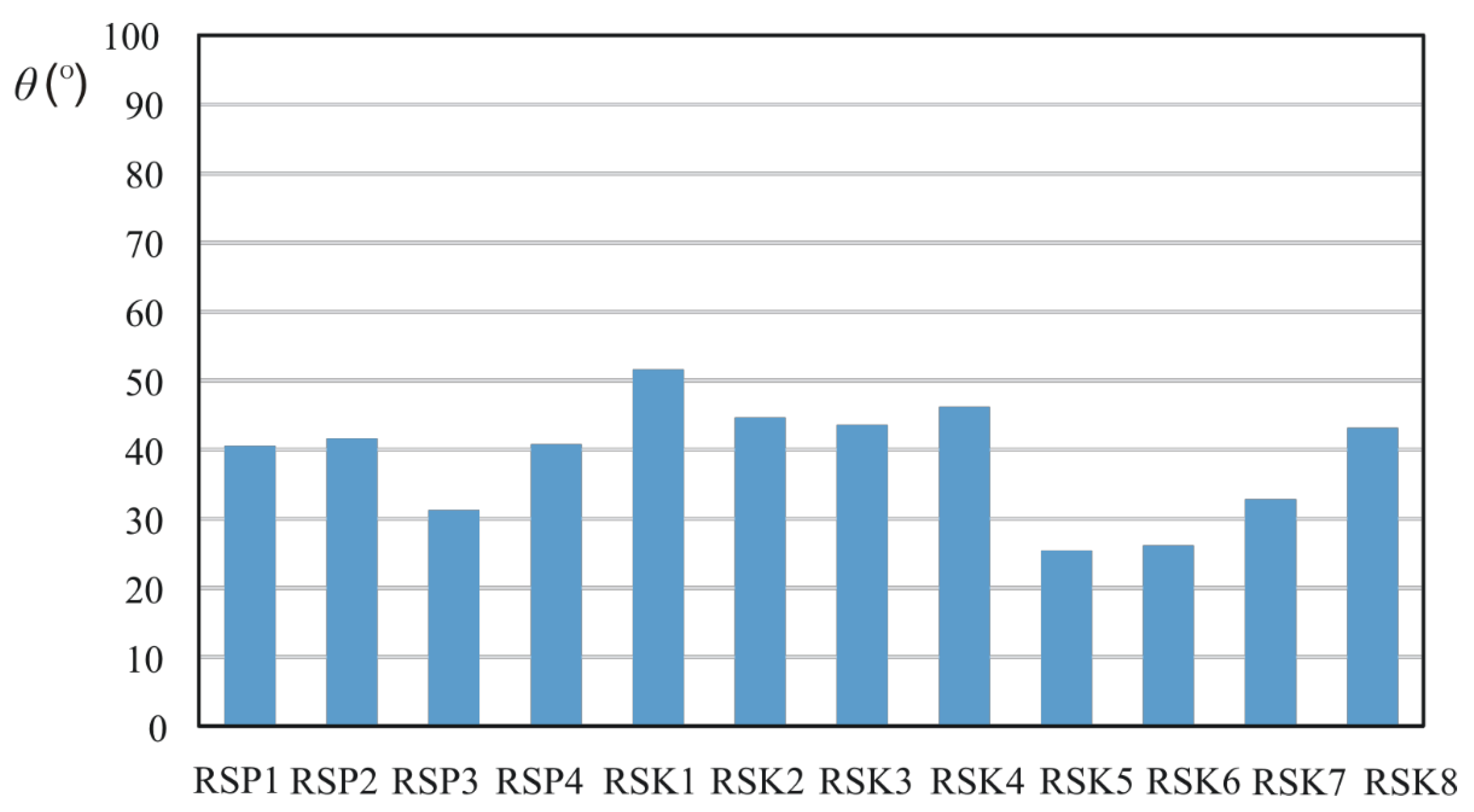
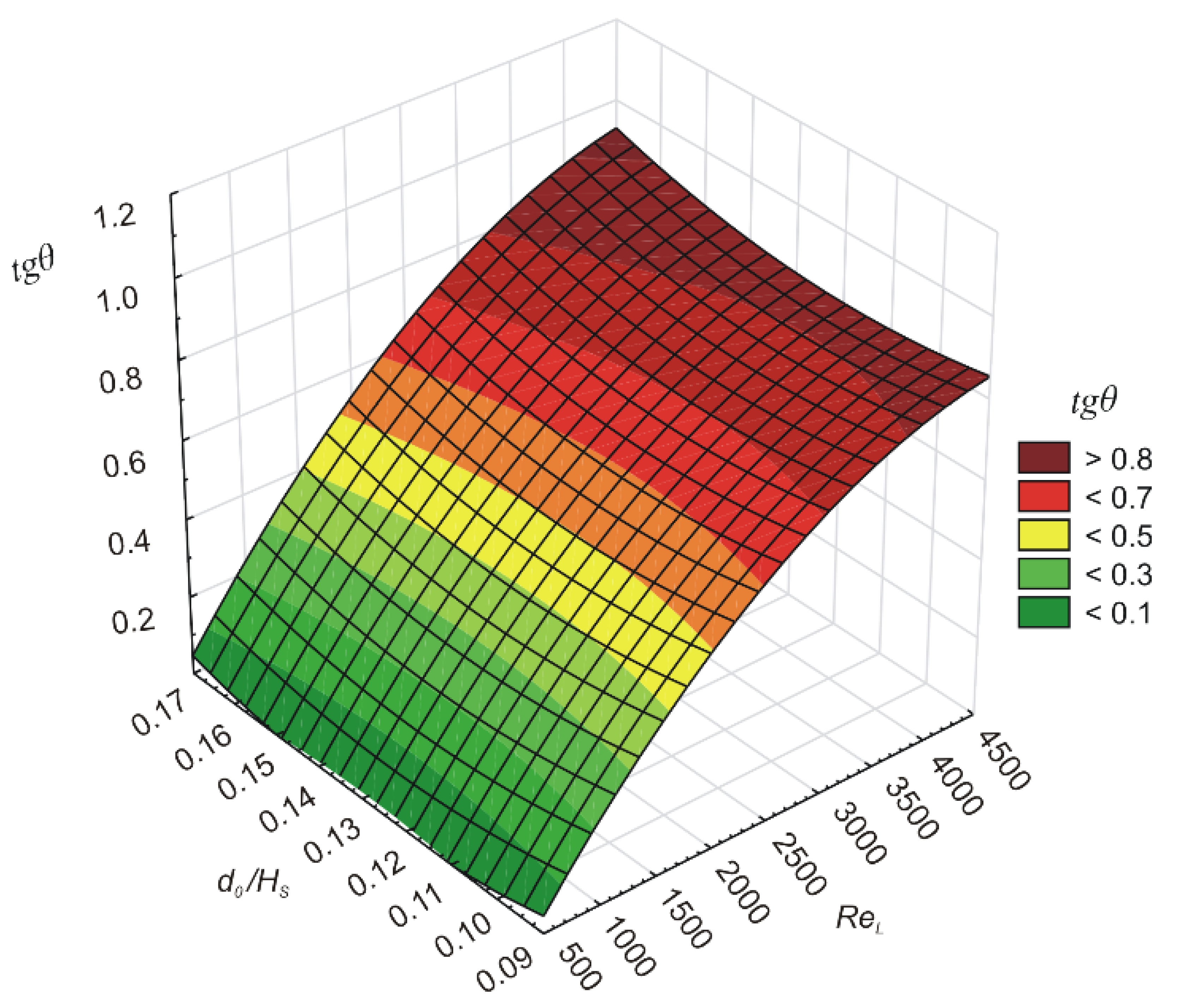
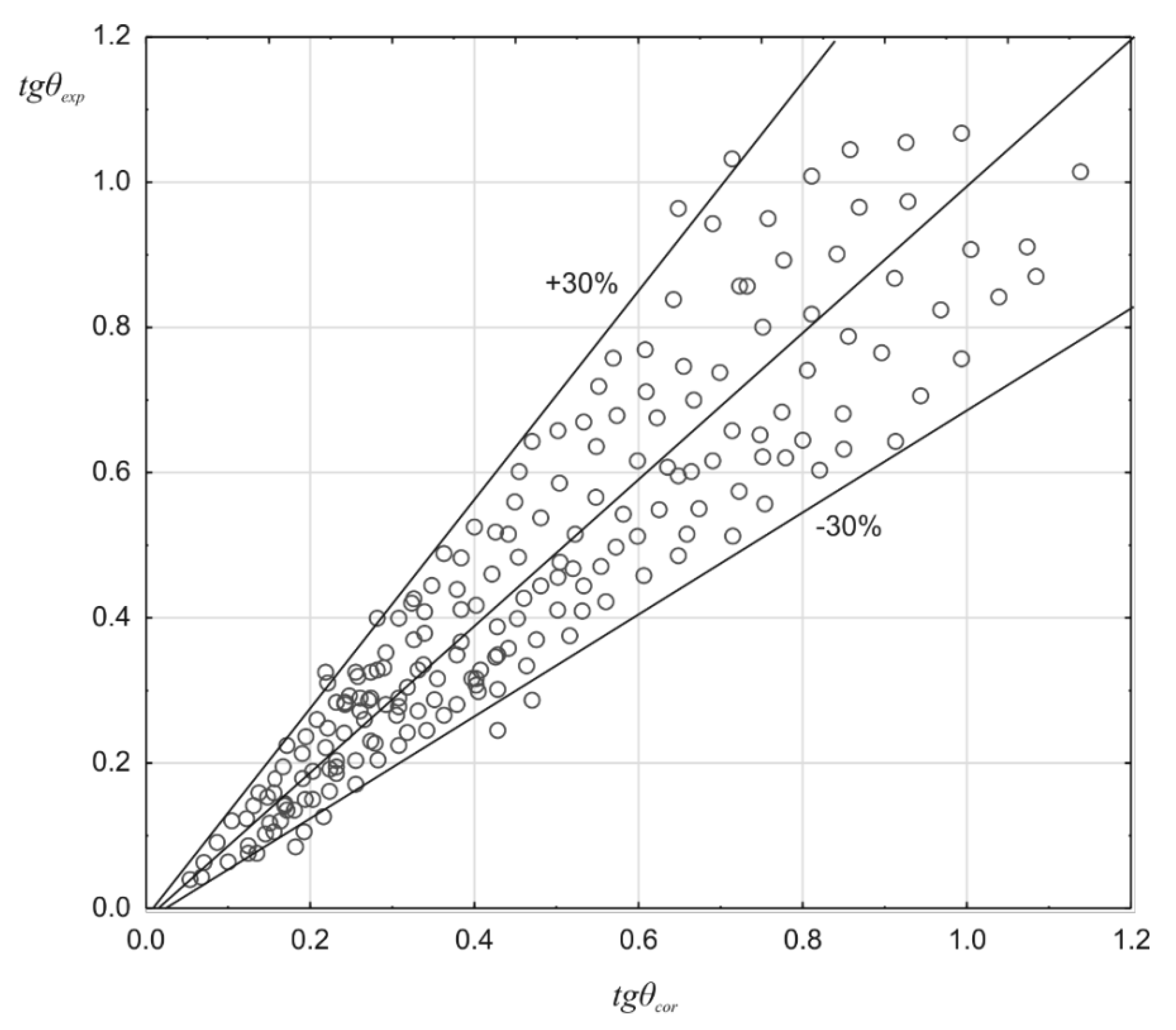
3.2. Spray Angle
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sobiech, Ł.; Grzanka, M.; Skrzypczak, G.; Idziak, R.; Włodarczak, S.; Ochowiak, M. Effect of adjuvants and pH adjuster on the efficacy of sulcotrione herbicide. Agronomy 2020, 10, 539. [Google Scholar] [CrossRef]
- Ochowiak, M.; Broniarz-Press, L. Analysis of the breakup of aqueous polymer solution jet. Chem. Eng. Equip. 2007, 4–5, 91–93. [Google Scholar]
- Som, S.K.; Mukherjee, S.G. Theoretical and experimental on the coefficient of discharge and spray cone angle of swirl spray atomizing nozzle. Acta Mech. 1980, 32, 79–102. [Google Scholar] [CrossRef]
- Lee, E.J.; Oh, S.Y.; Kim, H.Y.; James, S.C.; Yoon, S.S. Measuring air core characteristics of a pressure-swirl atomizer via a transparent acrylic nozzle at various Reynolds numbers. Exp. Therm. Fluid Sci. 2010, 34, 1475–1483. [Google Scholar] [CrossRef]
- Ochowiak, M.; Krupińska, A.; Włodarczak, S.; Matuszak, M.; Markowska, M.; Janczarek, M.; Szulc, T. The two-phase conical swirl atomizers: Spray characteristics. Energies 2020, 13, 3416. [Google Scholar] [CrossRef]
- Lee, M.-Y.; Lee, G.-S.; Kim, C.-J.; Seo, J.-H.; Kim, K.-H. Macroscopic and microscopic spray characteristics of diesel and gasoline in a constant volume chamber. Energies 2018, 11, 2056. [Google Scholar] [CrossRef]
- Fan, X.; Liu, C.; Mu, Y.; Wang, K.; Wang, Y.; Gang Xu, G. Experimental investigations of flow field and atomization field characteristics of pre-filming air-blast atomizers. Energies 2019, 12, 2800. [Google Scholar] [CrossRef]
- Kim, K.; Lim, O. Investigation of the spray development process of gasoline-biodiesel blended fuel sprays in a constant volume chamber. Energies 2020, 13, 4819. [Google Scholar] [CrossRef]
- Wang, X.; Huang, Z.; Kuti, O.A.; Zhang, W.; Nishida, K. Experimental and analytical study of biodiesel and diesel spray characteristics under ultra-high injection pressure. Int. J. Heat Fluid Flow 2010, 4, 659–666. [Google Scholar] [CrossRef]
- Basak, A.; Patra, J.; Ganguly, R.; Datta, A. Effect of transesterification of vegetable oil on liquid flow number and spray cone angle for pressure and twin fluid atomizers. Fuel 2013, 112, 347–354. [Google Scholar] [CrossRef]
- Yao, S.; Zhang, J.; Fang, T. Effect of viscosities on structure and instability of sprays from a swirl atomizer. Exp. Therm. Fluid Sci. 2012, 39, 158–166. [Google Scholar] [CrossRef]
- Lee, S.; Park, S. Experimental study on spray break-up and atomization processes from GDI injector using high injection pressure up to 30 MPa. Int. J. Heat Fluid Flow 2014, 45, 14–22. [Google Scholar] [CrossRef]
- Ochowiak, M.; Broniarz-Press, L.; Różańska, S.; Matuszak, M.; Włodarczak, S. Characteristics of spray angle for effervescent-swirl atomizers. Chem. Eng. Process. Process Intensif. 2015, 98, 52–59. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Atomization and Sprays; Hemisphere Publishing Corporation: New York, NY, USA, 1989. [Google Scholar]
- Ballester, J.; Dopazo, C. Discharge coefficient and spray angle measurements for small pressure-swirl nozzles. At. Sprays 1994, 4, 351–367. [Google Scholar]
- Zhang, T.; Dong, B.; Chen, X.; Qiu, Z.; Jiang, R.; Li, W. Spray characteristics of pressure-swirl nozzles at different nozzle. Appl. Therm. Eng. 2017, 121, 984–991. [Google Scholar] [CrossRef]
- Rashad, M.; Yong, H.; Zekun, Z. Effect of geometric parameters on spray characteristics of pressure swirl atomizers. Int. J. Hydrogen Energy 2016, 41, 15790–15799. [Google Scholar] [CrossRef]
- Durdina, L.; Jedelsky, J.; Jicha, M. Investigation and comparison of spray characteristics of pressure-swirl atomizers for a small-sized aircraft turbine engine. Int. J. Heat Mass Transf. 2014, 78, 892–900. [Google Scholar] [CrossRef]
- Halder, M.R.; Dash, S.K.; Som, S.K. A numerical and experimental investigation on the coefficients of discharge and the spray cone angle of a solid cone swirl nozzle. Exp. Therm. Fluid Sci. 2004, 28, 297–305. [Google Scholar] [CrossRef]
- Mun, R.P.; Byars, J.A.; Boger, D.V. Atomisation of dilute polymer solutions in agricultural spray nozzles. J. Non-Newton. Fluid Mech. 1999, 83, 163–178. [Google Scholar] [CrossRef]
- Wójtowicz, P.; Kotowski, A. Badania modelowe stożkowych regulatorów hydrodynamicznych. Ochrona Środowiska 2008, 3, 37–44. (In Polish) [Google Scholar]
- Ghannam, M.; Esmail, N. Flow behavior of enhanced oil recovery Alcoflood polymers. J. Appl. Polym. Sci. 2002, 85, 2896–2904. [Google Scholar] [CrossRef]
- Zhang, L. Study on the Degradation and Stability for Flooding Polymers. Master’s Thesis, University of Shandong, Shandong, China, 2011. [Google Scholar]
- Chen, Y.Z.; Zhang, Z.; Chen, M.H.; Zhang, X.H.; Tian, Q.S.; Xing, L.M.; Ma, T. Analysis of the main factors affecting the viscosity of the solution of polymer. Liaoning Chem. Ind. 2004, 33, 258–260. [Google Scholar]
- Durdina, L.; Jedelsky, J.; Jicha, M. Spray structure of a pressure-swirl atomizer for combustion applications. In EPJ Web of Conferences; EFM11—Experimental Fluid Mechanics 2011; EDP Sciences: Les Ulis, France, 2012; Volume 25, pp. 1–10. [Google Scholar]
- Dafsari, R.A.; Vashahi, F.; Lee, J. Effect of swirl chamber length on the atomization characteristics of a pressure-swirl nozzle. At. Sprays 2017, 27, 859–874. [Google Scholar] [CrossRef]
- Wimmer, E.; Brenn, G. Viscous flow through the swirl chamber of a pressure-swirl atomizer. Int. J. Multiph. Flow 2013, 53, 100–113. [Google Scholar] [CrossRef]
- Mat Rashid, M.S.F.; Hamid, A.H.A.; Sheng, O.C.; Ghaffar, Z.A. Effect of Inlet Slot Number on the Spray Cone Angle and Discharge Coefficient of Swirl Atomizer. Procedia Eng. 2012, 41, 1781–1786. [Google Scholar] [CrossRef][Green Version]
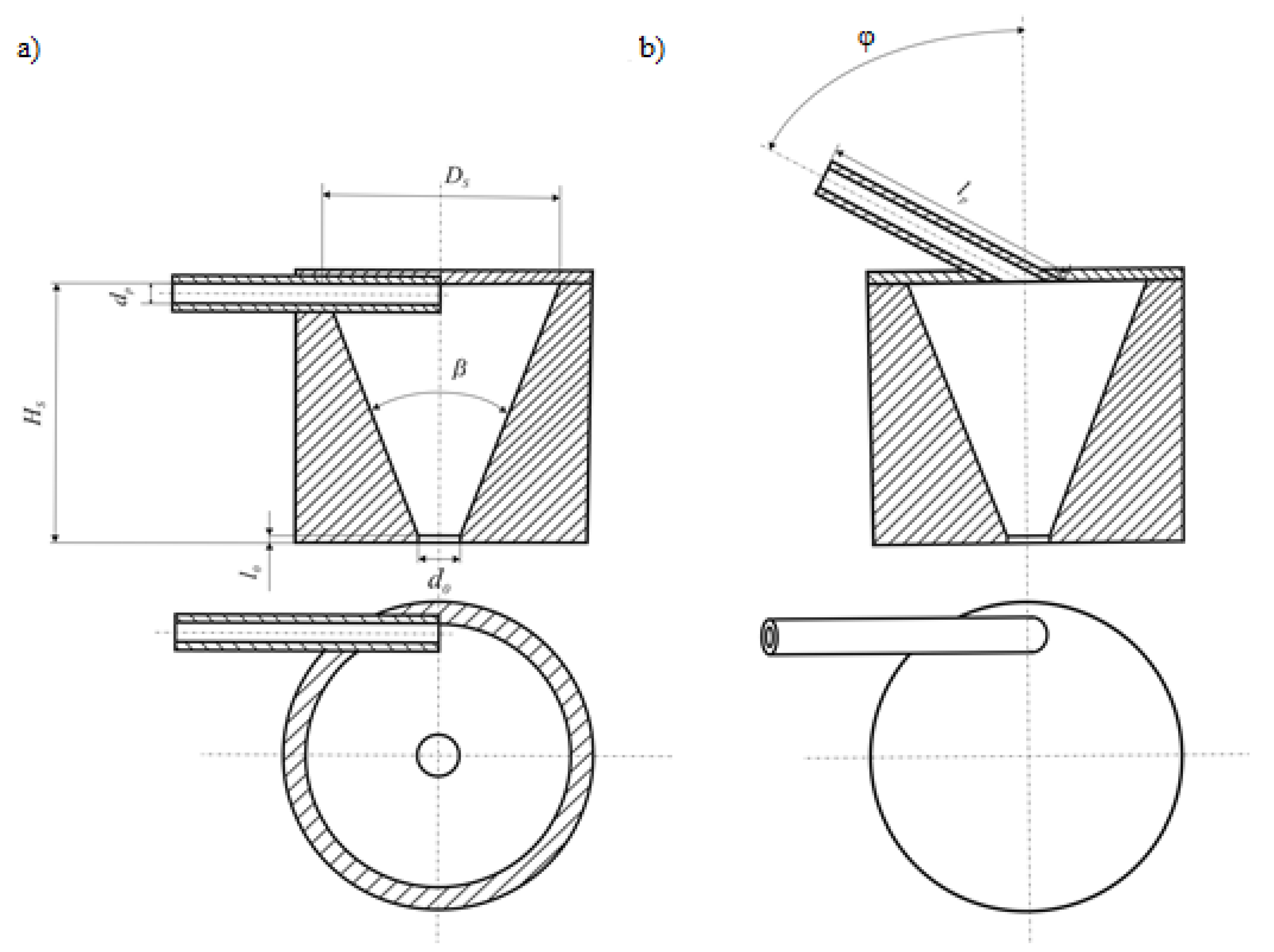


| Atomizer | DS (m) | HS (m) | d0 (m) | l0 (m) | l0/d0 |
|---|---|---|---|---|---|
| RSP1 | 0.020 | 0.015 | 0.0025 | 0.00125 | 0.5 |
| RSP2 | 0.020 | 0.020 | 0.0025 | 0.00125 | 0.5 |
| RSP3 | 0.020 | 0.025 | 0.0025 | 0.00125 | 0.5 |
| RSP4 | 0.020 | 0.020 | 0.0025 | 0.00250 | 1.0 |
| RSK1 | 0.020 | 0.015 | 0.0025 | 0.00125 | 0.5 |
| RSK2 | 0.020 | 0.020 | 0.0025 | 0.00125 | 0.5 |
| RSK3 | 0.020 | 0.025 | 0.0025 | 0.00125 | 0.5 |
| RSK4 | 0.020 | 0.020 | 0.0025 | 0.00250 | 1.0 |
| RSK5 | 0.040 | 0.015 | 0.0025 | 0.00125 | 0.5 |
| RSK6 | 0.040 | 0.020 | 0.0025 | 0.00125 | 0.5 |
| RSK7 | 0.040 | 0.025 | 0.0025 | 0.00125 | 0.5 |
| RSK8 | 0.040 | 0.020 | 0.0025 | 0.00250 | 1.0 |
| Test Solution | Density ρL (kg/m3) | Surface Tension σ (mN/m) | Characteristic Flow Index n (-) | Coefficient of Consistency k (Pa·sn) |
|---|---|---|---|---|
| 0.1% aqueous Na-CMC solution | 999.6 | 71.5 | 0.93 | 0.007 |
| 0.2% aqueous Na-CMC solution | 999.8 | 70.9 | 0.94 | 0.010 |
| 0.3% aqueous Na-CMC solution | 999.8 | 70.6 | 0.89 | 0.023 |
| 0.4% aqueous Na-CMC solution | 999.8 | 69.9 | 0.82 | 0.053 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, K.; Ochowiak, M.; Włodarczak, S. Effect of Rheological Properties of Aqueous Solution of Na-CMC on Spray Angle for Conical Pressure-Swirl Atomizers. Energies 2020, 13, 6309. https://doi.org/10.3390/en13236309
Czernek K, Ochowiak M, Włodarczak S. Effect of Rheological Properties of Aqueous Solution of Na-CMC on Spray Angle for Conical Pressure-Swirl Atomizers. Energies. 2020; 13(23):6309. https://doi.org/10.3390/en13236309
Chicago/Turabian StyleCzernek, Krystian, Marek Ochowiak, and Sylwia Włodarczak. 2020. "Effect of Rheological Properties of Aqueous Solution of Na-CMC on Spray Angle for Conical Pressure-Swirl Atomizers" Energies 13, no. 23: 6309. https://doi.org/10.3390/en13236309
APA StyleCzernek, K., Ochowiak, M., & Włodarczak, S. (2020). Effect of Rheological Properties of Aqueous Solution of Na-CMC on Spray Angle for Conical Pressure-Swirl Atomizers. Energies, 13(23), 6309. https://doi.org/10.3390/en13236309







