Deep Learning Based Successive Interference Cancellation Scheme in Nonorthogonal Multiple Access Downlink Network
Abstract
1. Introduction
- We design a CNN-based SIC scheme for downlink NOMA communication systems. The proposed scheme can be used instead of implementing a conventional SIC scheme.
- We apply CNN as a scheme to solve the imperfections of SIC that are not considered in the conventional NOMA communication system. The proposed SIC scheme can mitigate the losses caused by imperfect SIC and then improve the sum rate of the decoded signal.
- We provide simulation results with various key deep learning parameters. These parameters include the number of users, number of epochs, power allocation, modulation type, learning rate and batch size. The proposed scheme performed better than the conventional SIC scheme in various simulations.
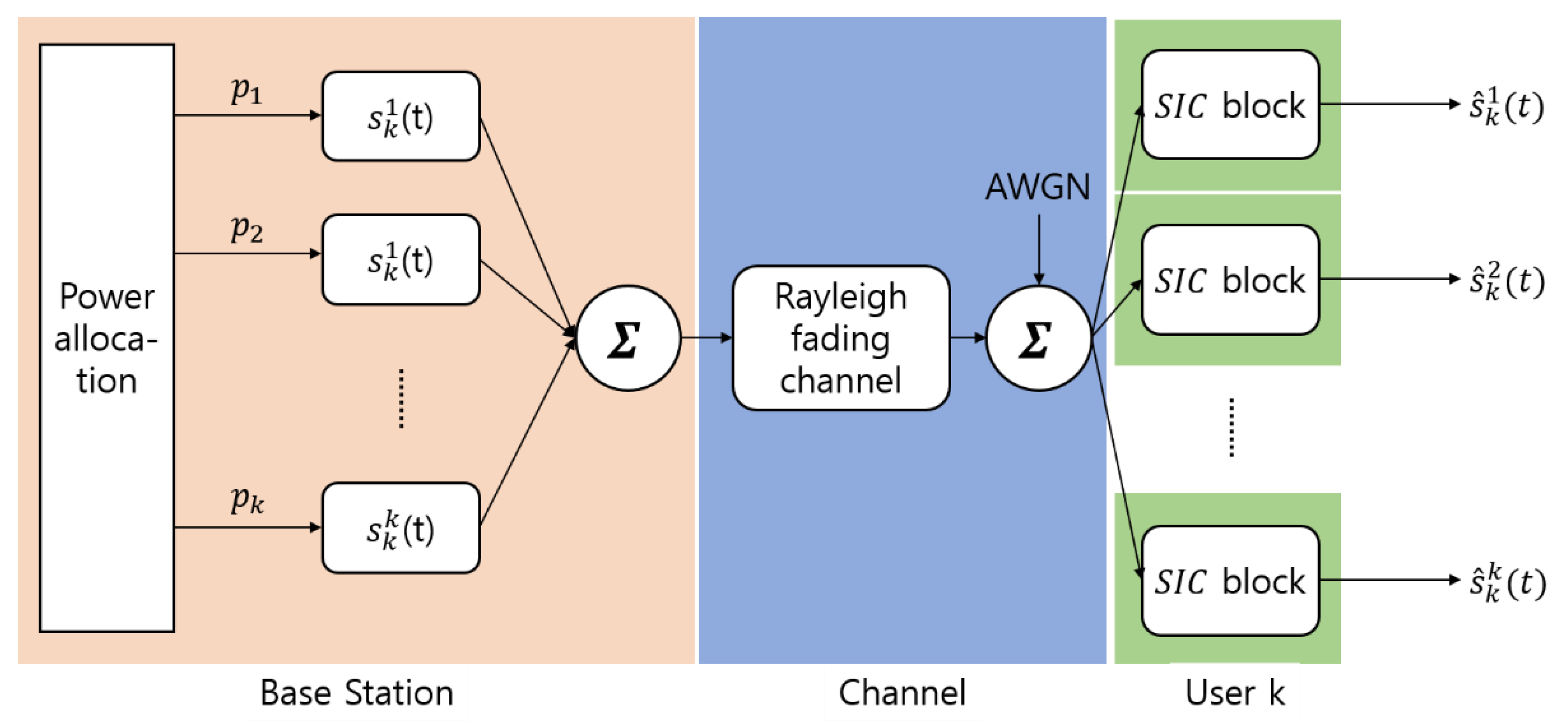
2. System Model
3. Performance of Deep Learning-Based Nonorthogonal Multiple Access (NOMA) Scheme
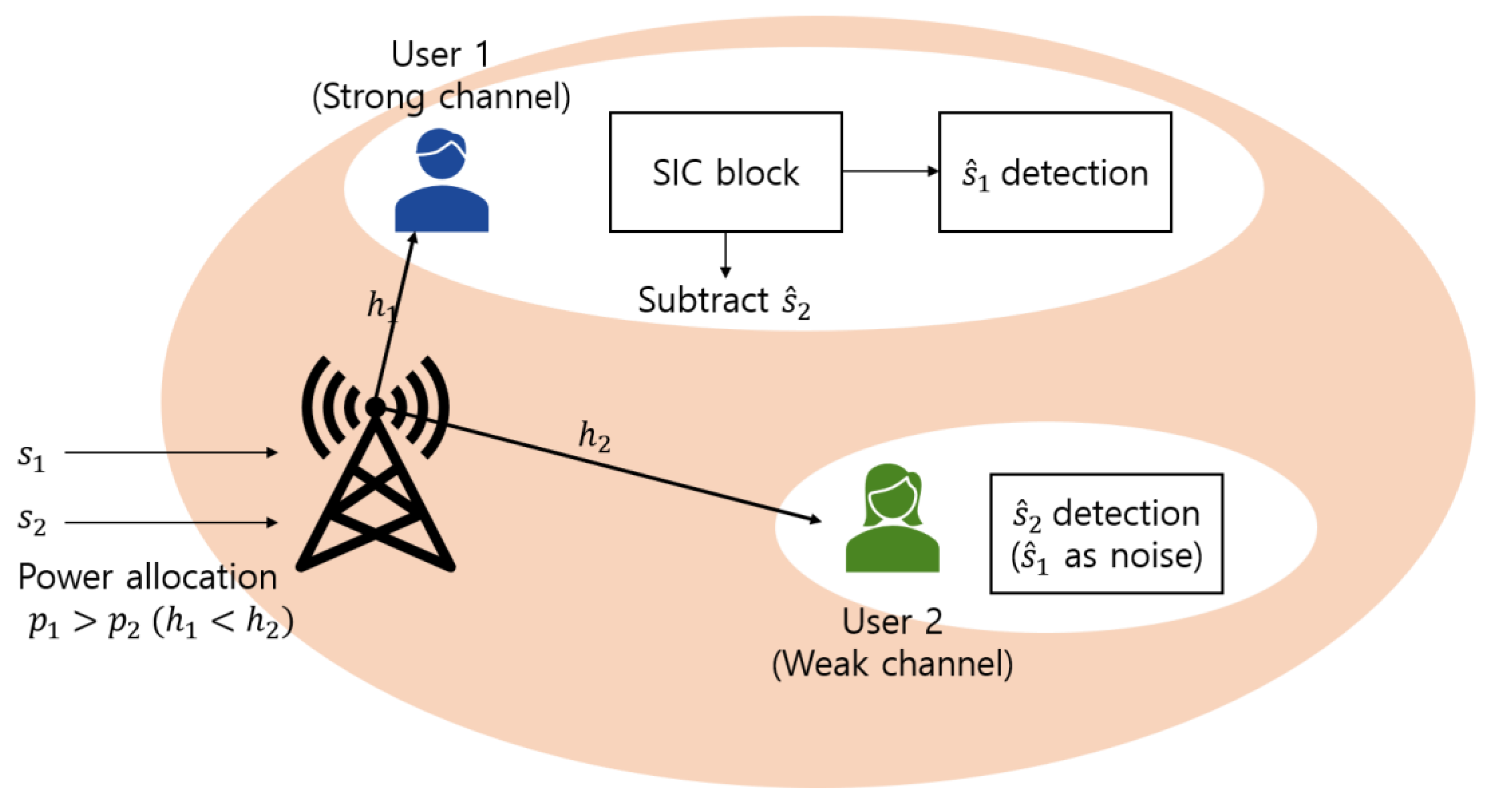
3.1. Conventional NOMA and Successive Interference Cancellation (SIC) Scheme
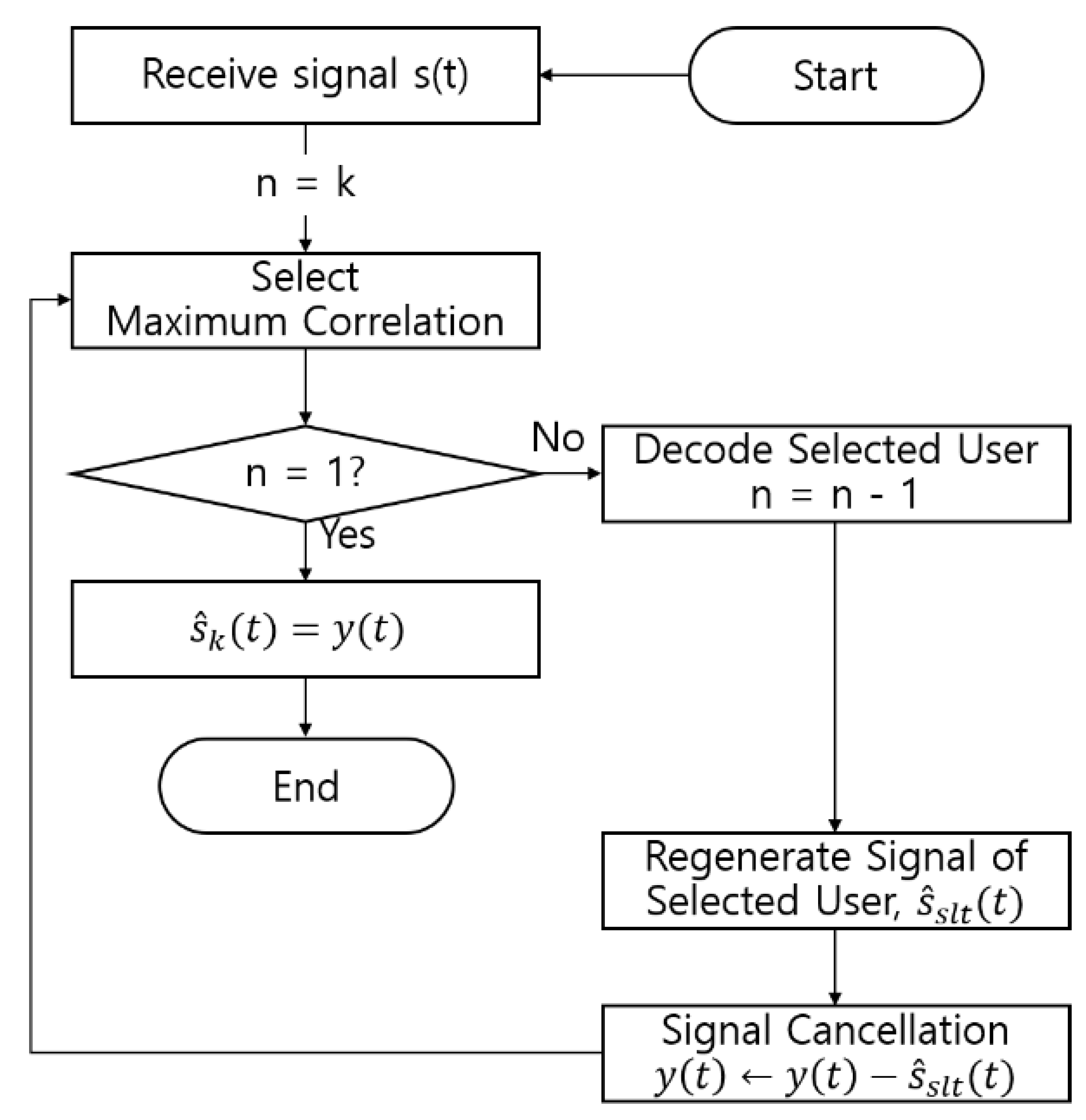
3.2. Imperfections of Conventional SIC
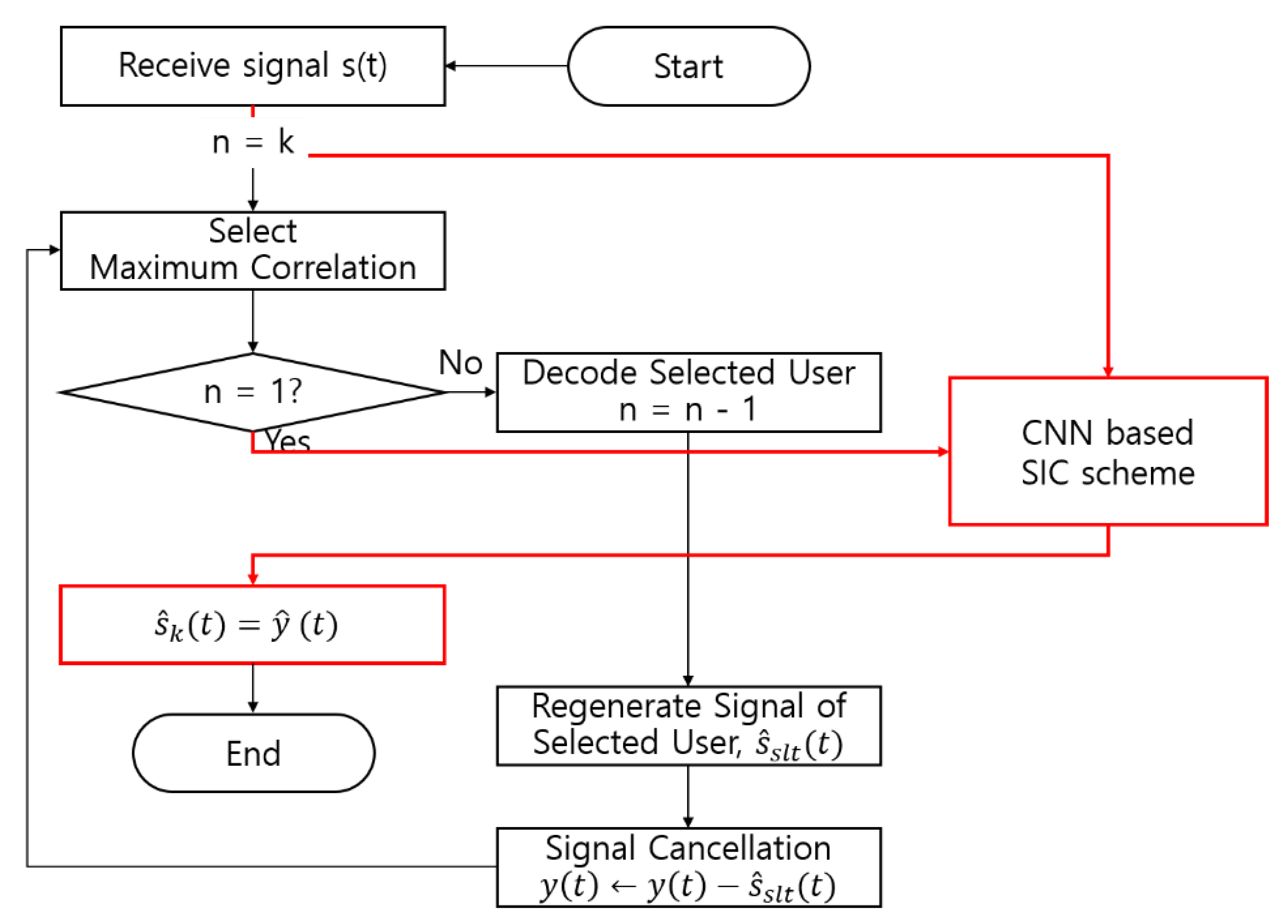
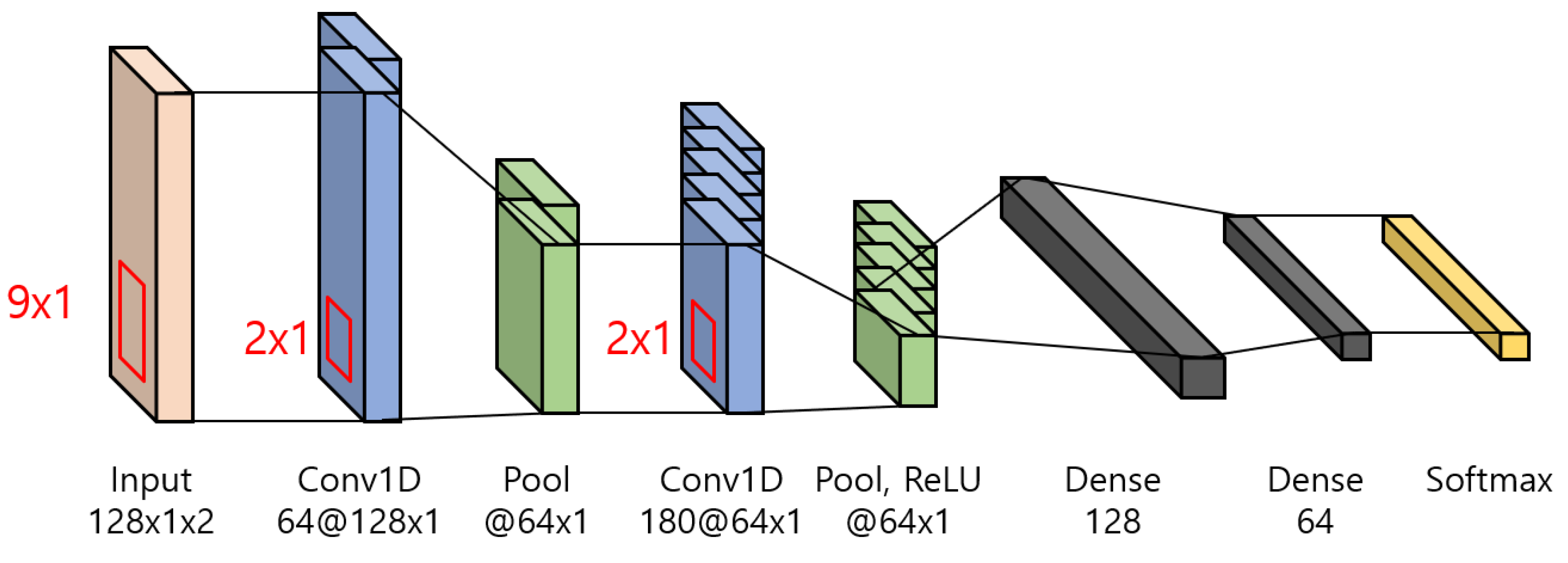
3.3. Convolutional Neural Network (CNN)-Based SIC Scheme
| Algorithm 1. CNN-Based SIC Training Process Algorithm |
| 1: Initialize the CNN model. The initial input = conventional SIC scheme, the weight w = 0, 2: the error threshold = 0.1 and the dropout probability = 0.5. 3: Generate a set of data streams from the conventional NOMA communication data. 4: Sample a batch size, learning rate and modulation, respectively. 5: while iteration < epochs 6: Simulate an imperfect SIC scheme with the proposed fading and noise channel. 7: Train the CNN network with the aid of the proposed scheme. 8: Update the estimation signals of other users. 9: Minimize the mean square error between the received signal and deep-learned signal. 10: return CNN network. |
| Algorithm 2. CNN-Based SIC Testing Process Algorithm |
| 1: Load the CNN network from the training process. 2: Initialize the channel with the proposed fading and noise channel. 3: Process the CNN network. 4: Calculate the loss function as shown in Equation (10). 5: Return . |
3.4. Activation Functions for CNN-Based SIC Scheme
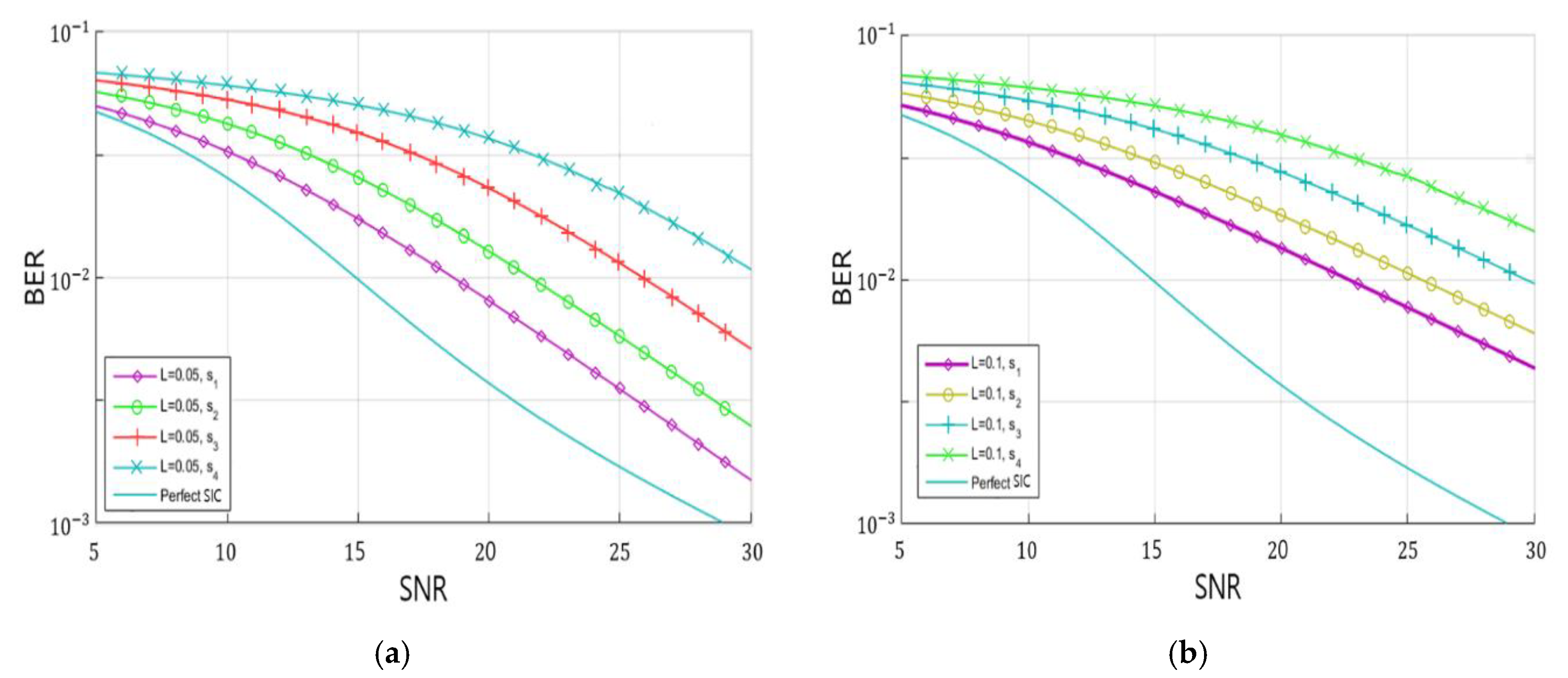
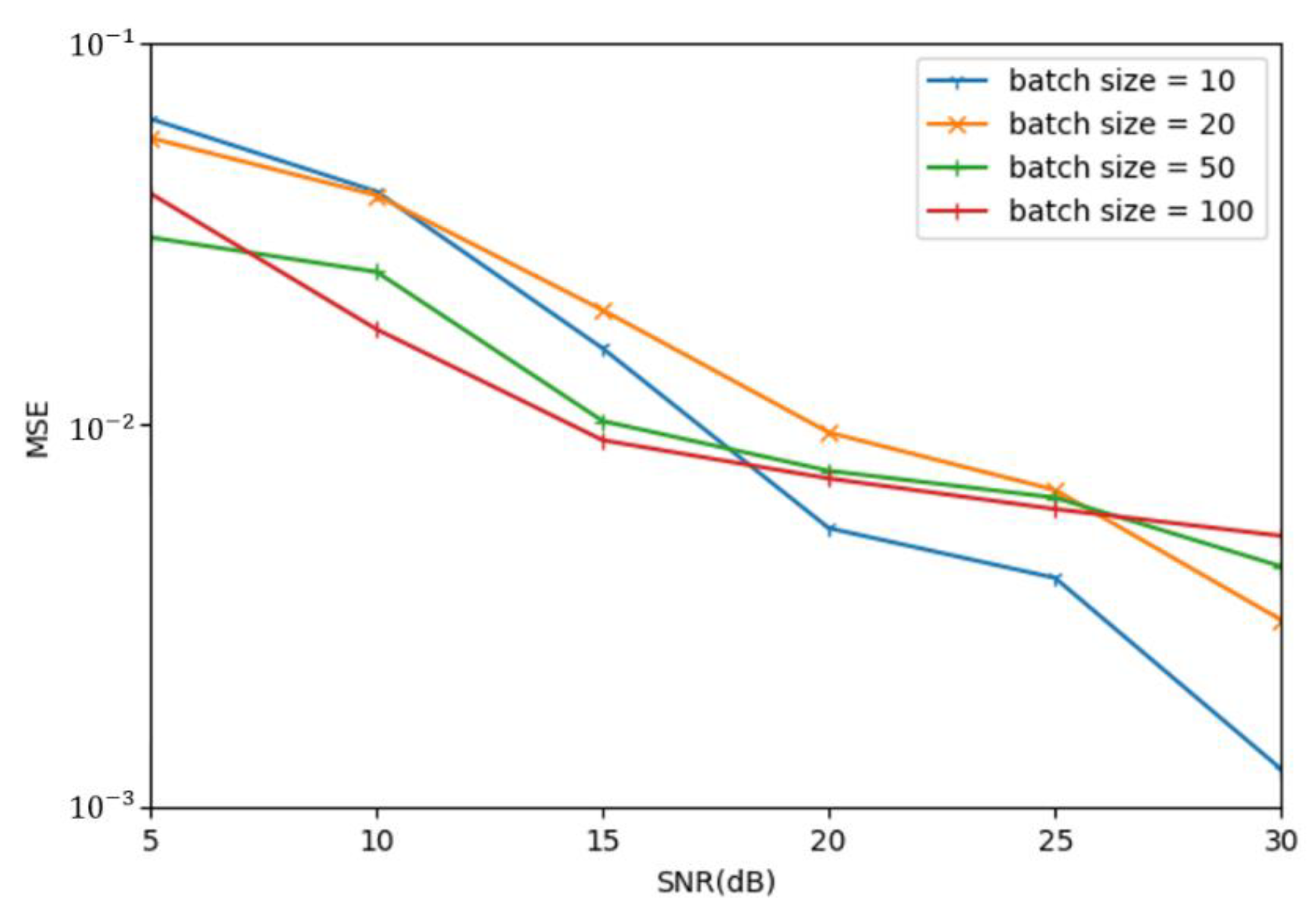
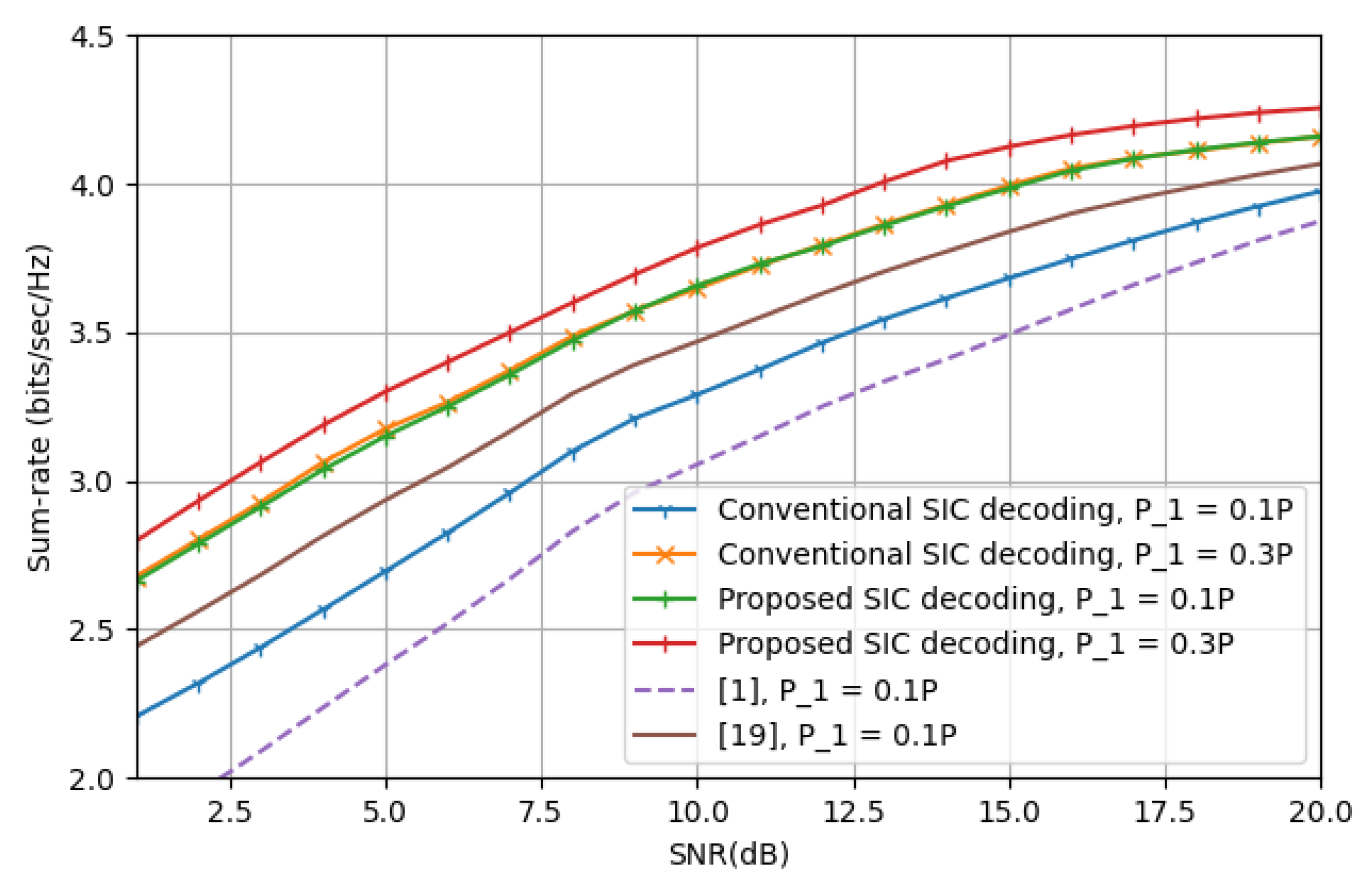
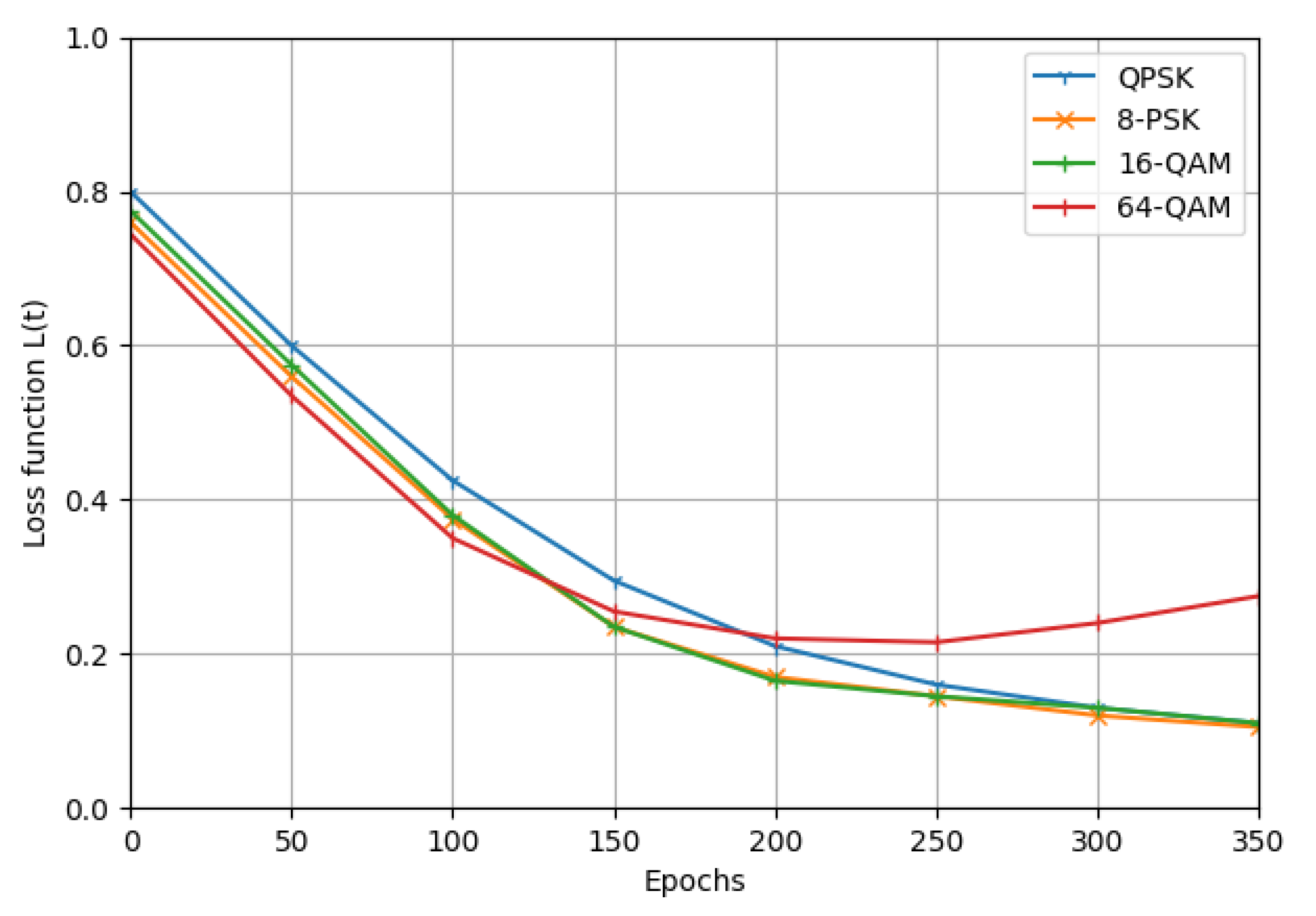
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ding, Z.G.; Adachi, F.; Poor, H.V. The application of MIMO to non-orthogonal multiple access. IEEE Trans. Wirel. Commun. 2015, 15, 537–552. [Google Scholar] [CrossRef]
- Higuchi, K.; Benjebbour, A. Non-orthogonal multiple access (NOMA) with successive interference cancellation for future radio access. IEICE Trans. Commun. 2015, 98, 403–414. [Google Scholar] [CrossRef]
- Huh, H.; Kim, J.Y. Performance of a multicarrier DS/CDMA system with successive interference cancellation. Eur. Trans. Telecommun. 2002, 13, 237–243. [Google Scholar] [CrossRef]
- Hasan, M.K.; Shahjalal, M.; Islam, M.M.; Alam, M.M.; Ahmed, M.F.; Jang, Y.M. The role of deep learning in NOMA for 5G and beyond communications. In Proceedings of the Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 19–21 February 2020. [Google Scholar] [CrossRef]
- Luo, J.; Tang, J.; So, D.K.; Chen, G.; Cumanan, K.; Chambers, J.A. A deep learning-based approach to power minimization in multi-carrier NOMA with SWIPT. IEEE Access 2019, 7, 17450–17460. [Google Scholar] [CrossRef]
- Liu, M.; Song, T.; Gui, G. Deep cognitive perspective: Resource allocation for NOMA-Based heterogeneous IoT with imperfect SIC. IEEE Internet Things J. 2019, 6, 2885–2894. [Google Scholar] [CrossRef]
- Gui, G.; Huang, H.; Song, Y.; Sari, H. Deep learning for an effective nonorthogonal multiple access scheme. IEEE Trans. Vehi. Technol. 2018, 67, 8440–8450. [Google Scholar] [CrossRef]
- Ye, N.; Li, X.; Yu, H.; Wang, A.; Liu, W.; Hou, X. Deep learning aided grant-free NOMA toward reliable low-latency access in tactile internet of things. IEEE Trans. Indus. Inform. 2019, 15, 2995–3005. [Google Scholar] [CrossRef]
- Mahady, I.A.; Bedeer, E.; Ikki, S.; Yanikomeroglu, H. Sum-rate maximization of NOMA systems under imperfect successive interference cancellation. IEEE Commun. Lett. 2019, 23, 474–477. [Google Scholar] [CrossRef]
- Tuan, H.D.; Nasir, A.A.; Nguyen, H.H.; Duong, T.Q.; Poor, H.V. Nonorthogonal multiple access with improper Gaussian signaling. IEEE J. Sel. Top. Signal Process. 2019, 13, 496–507. [Google Scholar] [CrossRef]
- Chen, X.; Jia, R.; Ng, D.W.K. On the design of massive non-orthogonal multiple access with imperfect successive interference cancellation. IEEE Trans. Commun. 2019, 67, 2539–2551. [Google Scholar] [CrossRef]
- Li, S.; Derakhshani, M.; Lambotharan, S. Outage-constrained robust power allocation for downlink MC-NOMA with imperfect SIC. In Proceedings of the IEEE International Conference on Communications (ICC), Kansas, MO, USA, 20–24 May 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Ali, S.; Hossain, E.; Kim, D.I. Non-orthogonal multiple access (NOMA) for downlink multiuser MIMO systems: User clustering, beamforming, and power allocation. IEEE Access 2016, 5, 565–577. [Google Scholar] [CrossRef]
- Cai, Y.; Qin, Z.; Cui, F.; Li, G.Y.; McCann, J.A. Modulation and multiple access for 5G networks. IEEE Commun. Surv. Tutor. 2018, 20, 629–646. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Avazov, N.; Dobre, O.A.; Kwak, K. Power-domain non-orthogonal multiple access (NOMA) in 5G systems: Potentials and challenges. IEEE Commun. Surv. Tutor. 2015, 19, 721–742. [Google Scholar] [CrossRef]
- Selim, B.; Muhaidat, S.; Sofotasios, P.C.; Al-Dweik, A.; Sharif, B.S.; Stouraitis, T. Radio frequency frontend impairments in non-orthogonal multiple access systems. IEEE Vehic. Technol. 2019, 14, 89–97. [Google Scholar] [CrossRef]
- Benjebbour, A.; Saito, Y.; Kishiyama, Y.; Li, A.; Harada, A.; Nakamura, T. Concept and practical considerations of nonorthogonal multiple access (NOMA) for future radio access. In Proceedings of the 2013 International Symposium on Intelligent Signal Processing and Communication Systems, Naha, Japan, 12–15 November 2013; pp. 770–774. [Google Scholar] [CrossRef]
- You, W.; Shen, C.; Wang, D.; Chen, L.; Jiang, X.; Zhu, Z. An intelligent deep feature learning method with improved activation functions for machine fault diagnosis. IEEE Access 2020, 8, 1975–1985. [Google Scholar] [CrossRef]
- Kang, J.M.; Kim, I.M.; Chun, C.J. Deep Learning-Based MIMO-NOMA with Imperfect SIC Decoding. IEEE Sys. J. 2020, 14, 3414–3417. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Operating system | Ubuntu 19.10 (Canonical Ltd, London, UK) |
| Framework | TensorFlow 1.15.2 (Google Co., Mountain View, CA, USA) |
| Programming language | Python 3.7.7 (Python Software Foundation, Wilmington, DE, USA) |
| Batch size | 10, 20, 50, 100 |
| Number of users | 2, 4 |
| Modulation | Phase shift keying (PSK), Quadrature amplitude modulation (QAM) |
| Number of training samples | 819,200 |
| Power allocation factor of | 0.1, 0.3 |
| Activation function | ReLU, sigmoid, tanh, LReLU, ELU |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sim, I.; Sun, Y.G.; Lee, D.; Kim, S.H.; Lee, J.; Kim, J.-H.; Shin, Y.; Kim, J.Y. Deep Learning Based Successive Interference Cancellation Scheme in Nonorthogonal Multiple Access Downlink Network. Energies 2020, 13, 6237. https://doi.org/10.3390/en13236237
Sim I, Sun YG, Lee D, Kim SH, Lee J, Kim J-H, Shin Y, Kim JY. Deep Learning Based Successive Interference Cancellation Scheme in Nonorthogonal Multiple Access Downlink Network. Energies. 2020; 13(23):6237. https://doi.org/10.3390/en13236237
Chicago/Turabian StyleSim, Isaac, Young Ghyu Sun, Donggu Lee, Soo Hyun Kim, Jiyoung Lee, Jae-Hyun Kim, Yoan Shin, and Jin Young Kim. 2020. "Deep Learning Based Successive Interference Cancellation Scheme in Nonorthogonal Multiple Access Downlink Network" Energies 13, no. 23: 6237. https://doi.org/10.3390/en13236237
APA StyleSim, I., Sun, Y. G., Lee, D., Kim, S. H., Lee, J., Kim, J.-H., Shin, Y., & Kim, J. Y. (2020). Deep Learning Based Successive Interference Cancellation Scheme in Nonorthogonal Multiple Access Downlink Network. Energies, 13(23), 6237. https://doi.org/10.3390/en13236237






