Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm
Abstract
1. Introduction
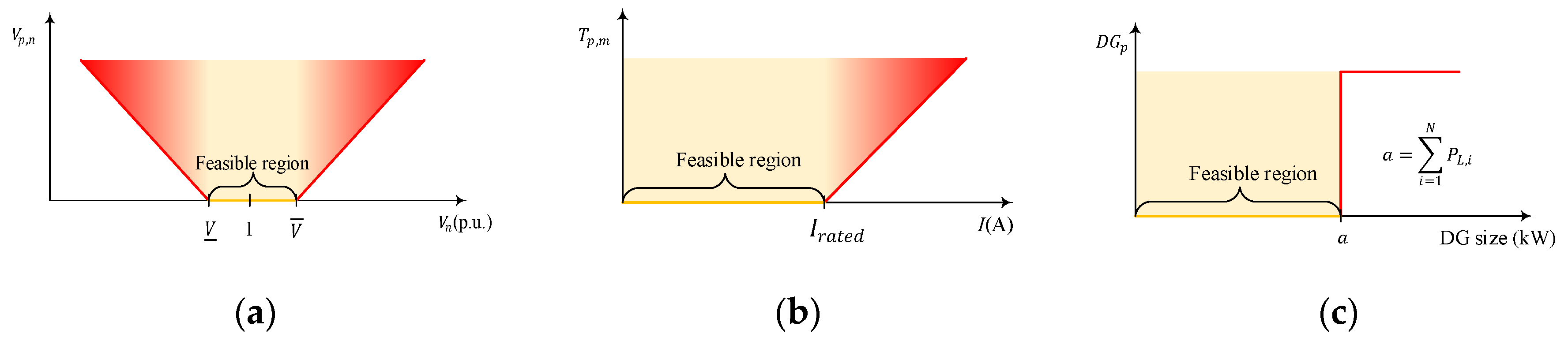
2. Problem Formulation
- Voltage constraint
- 2.
- Thermal constraint
- 3.
- DG capacity constraint
- 4.
- Nodal power balance constraint
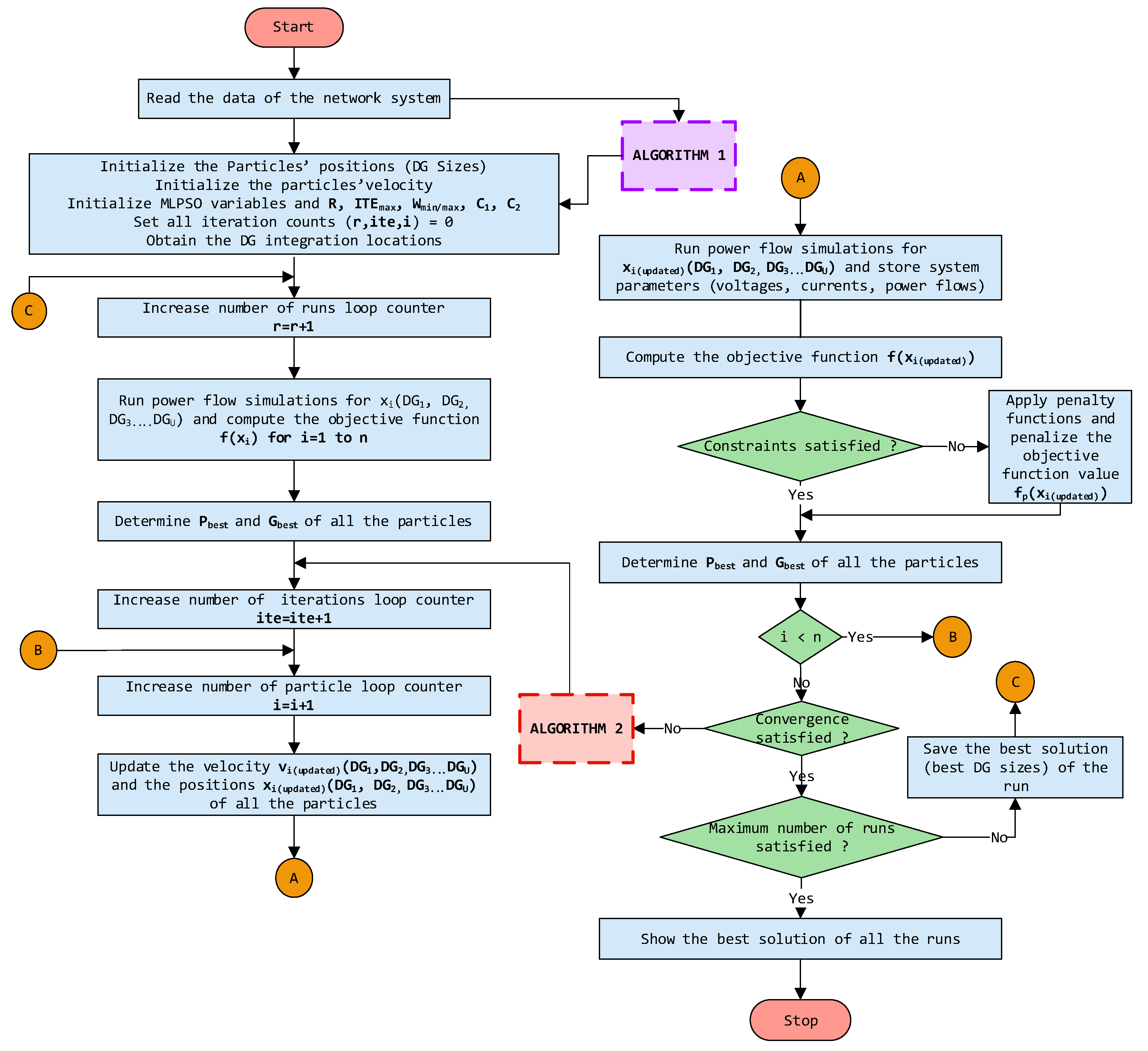
3. Optimization Framework
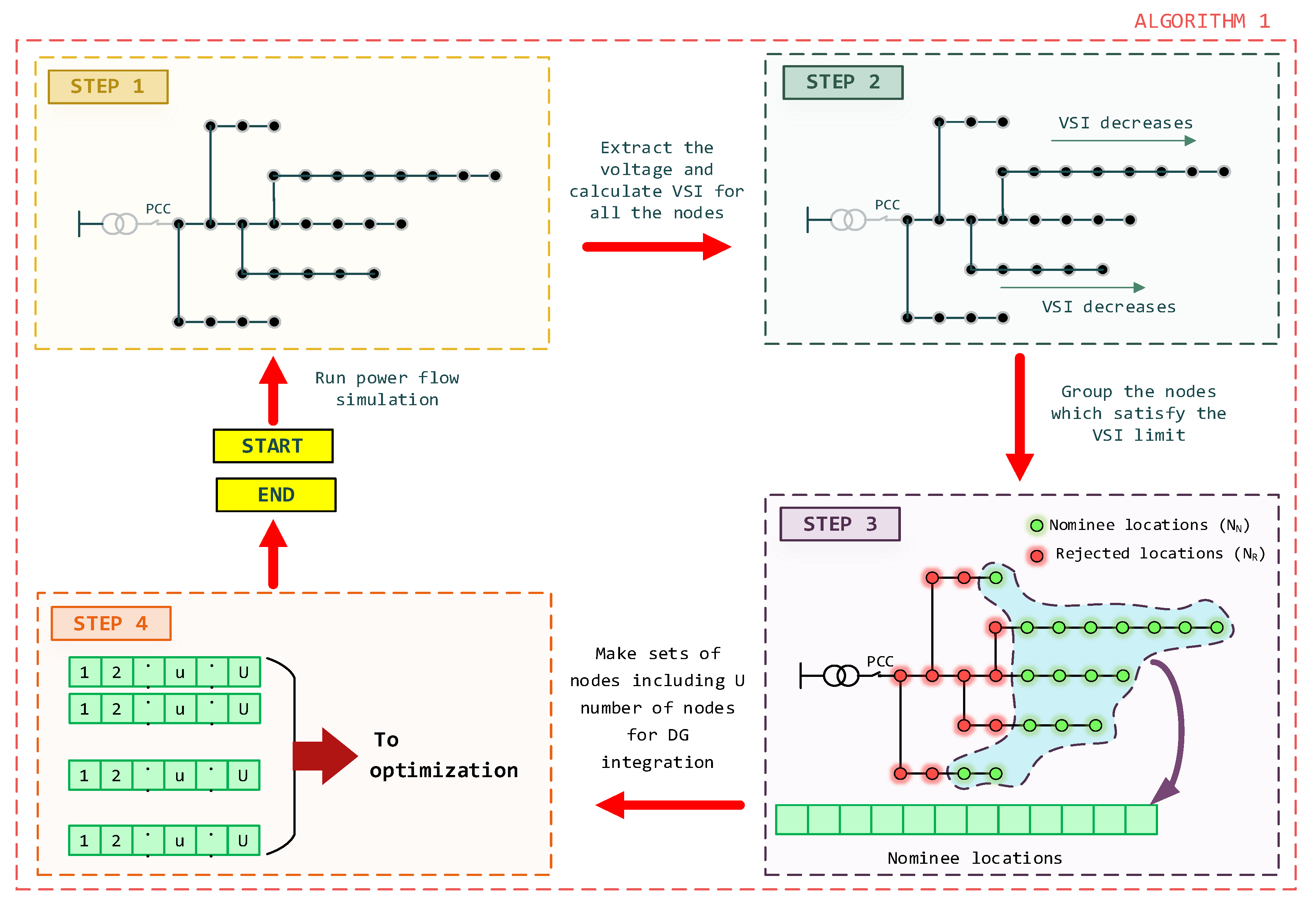
3.1. Optimal Placement of Generators
| Algorithm 1. Identification of nominee locations for DG integration. | |
| Input: | Network data of the considered network system. |
| Step 1: | Read the data of the network system and perform the load flow analysis. |
| Step 2: | Extract the voltages of all the nodes and calculate VSI using Equation (12). |
| Step 3: | Group the nodes which satisfy the VSI limit (). |
| Step 4: | Make sets of nodes including number of nodes (i.e., 1 × vectors) for DG integration from the grouped nodes ( is the number of DGs connecting to the system). |
| Output: | DG integration location sets. |
3.2. Optimal Sizing of Generators
3.2.1. Concept and Flight Equations of MLPSO
3.2.2. Leader Assignment Process
3.2.3. Self-Learning Process
- Gaussian mutation;
- Opposition based mutation;
- DE based mutation;where , , , , , , , are the best leader’s position value in dimension after the Gaussian mutation, the leader’s position value in dimension after the opposition based mutation, the leader’s position value in dimension after the DE based mutation, the maximum position value of all the leaders in dimension, the minimum position value of all the leaders in dimension, best leader’s position in dimension, leader’s position in dimension, and scale factor, respectively. and are two randomly generated numbers. (). The algorithm of the self-learning process is given in Algorithm 2.
| Algorithm 2. Leaders’ self-learning procedure | |
| Input: | Number of leaders, initial standard deviation of Gaussian distribution, the updated swarm of particles. |
| Step 1: | Calculate the standard deviation for the iteration. |
| Step 2: | Sort all the particles in the swarm in ascending order considering the objective function value of the particles (). |
| Step 3: | Choose the number of leaders from the sorted list of particles. |
| Step 4: | Select the best leader and apply Gaussian mutation for all the dimensions of the position vector and evaluate the objective function value (). |
| Step 5: | If the objective function value obtained from the mutated values is better than the current objective function value, replace the values of all dimensions of the position vector with the mutated values. |
| Step 6: | Else keep the current values of the position vector. |
| Step 7: | Apply DE-based mutation upon whole leader set and evaluate the objective function values (). |
| Step 8: | If the objective function value obtained from the mutated values is better than the current objective function value, replace the values of all dimensions of the position vector with the mutated values. |
| Step 9: | Else keep the current values of the position vector. |
| Step 10: | Apply opposition-based mutation upon whole leader set and evaluate the objective function values (). |
| Step 11: | If the objective function value obtained from the mutated values is better than the current objective function value, replace the values of all dimensions of the position vector with the mutated values. |
| Step 12: | Else keep the current values of the position vector. |
| Output: | Improved leaders. |
3.2.4. Mapping of the Terms of the Optimization Process
3.2.5. Implementation of MLPSO Algorithm
4. Results
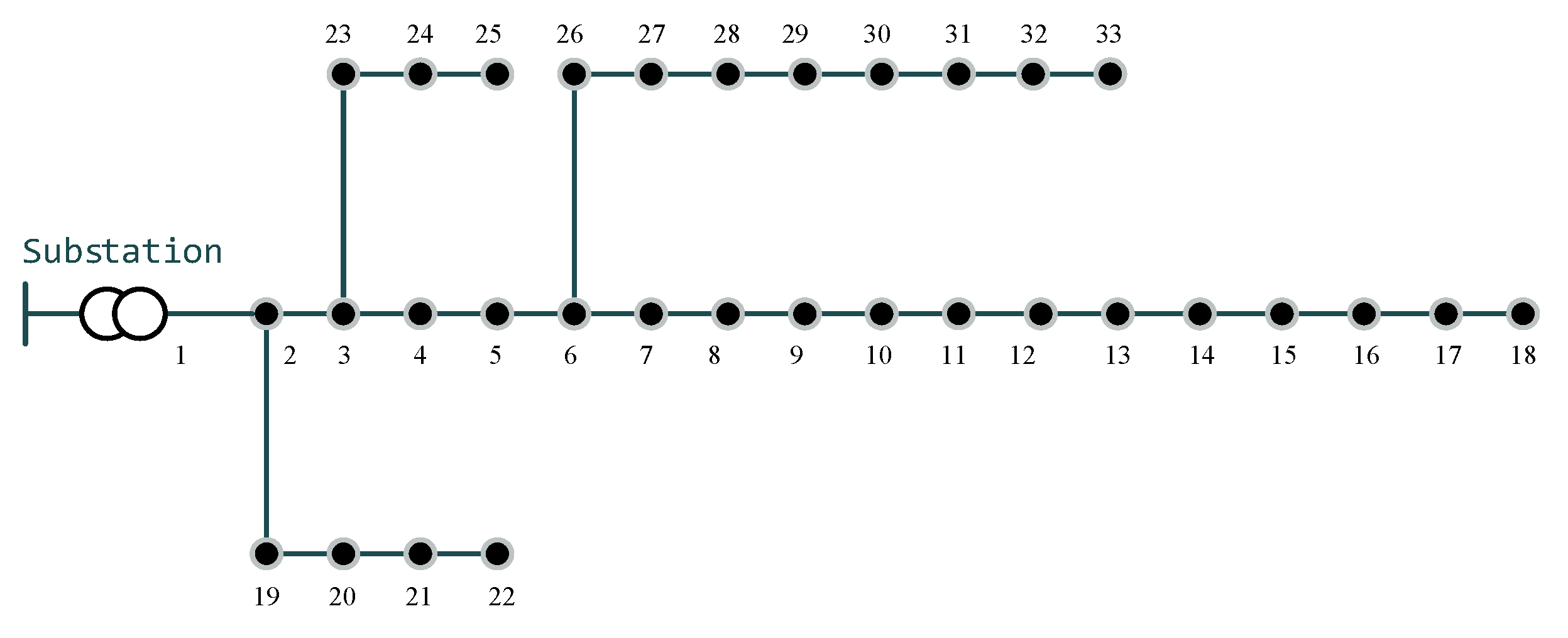
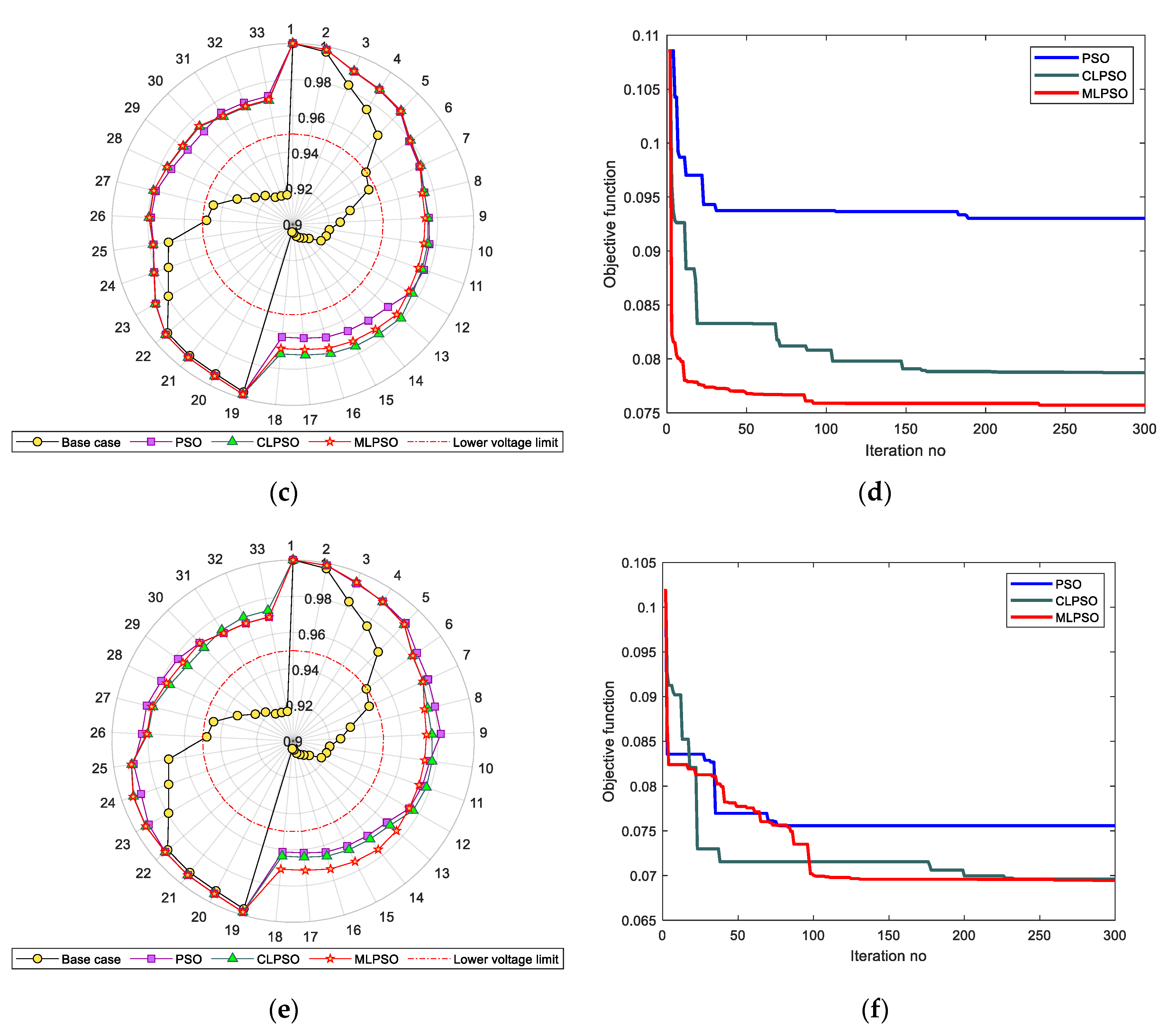
4.1. Standard IEEE 33 Bus System
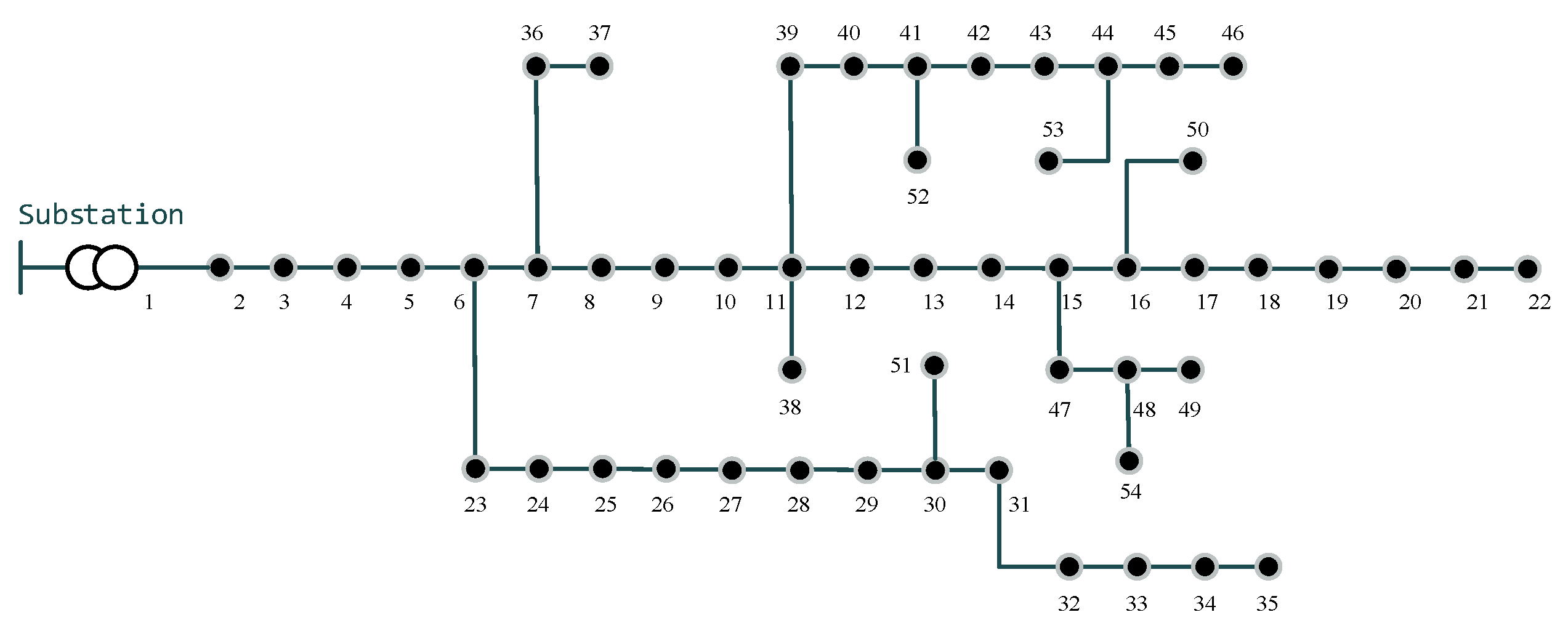
4.2. Malaysian Bus System
5. Discussion
5.1. Standard IEEE 33 Bus System
5.2. Malaysian 54 Bus System
5.3. Comparison of the Results for the Standard IEEE 33 Bus System with Other Optimization Algorithms
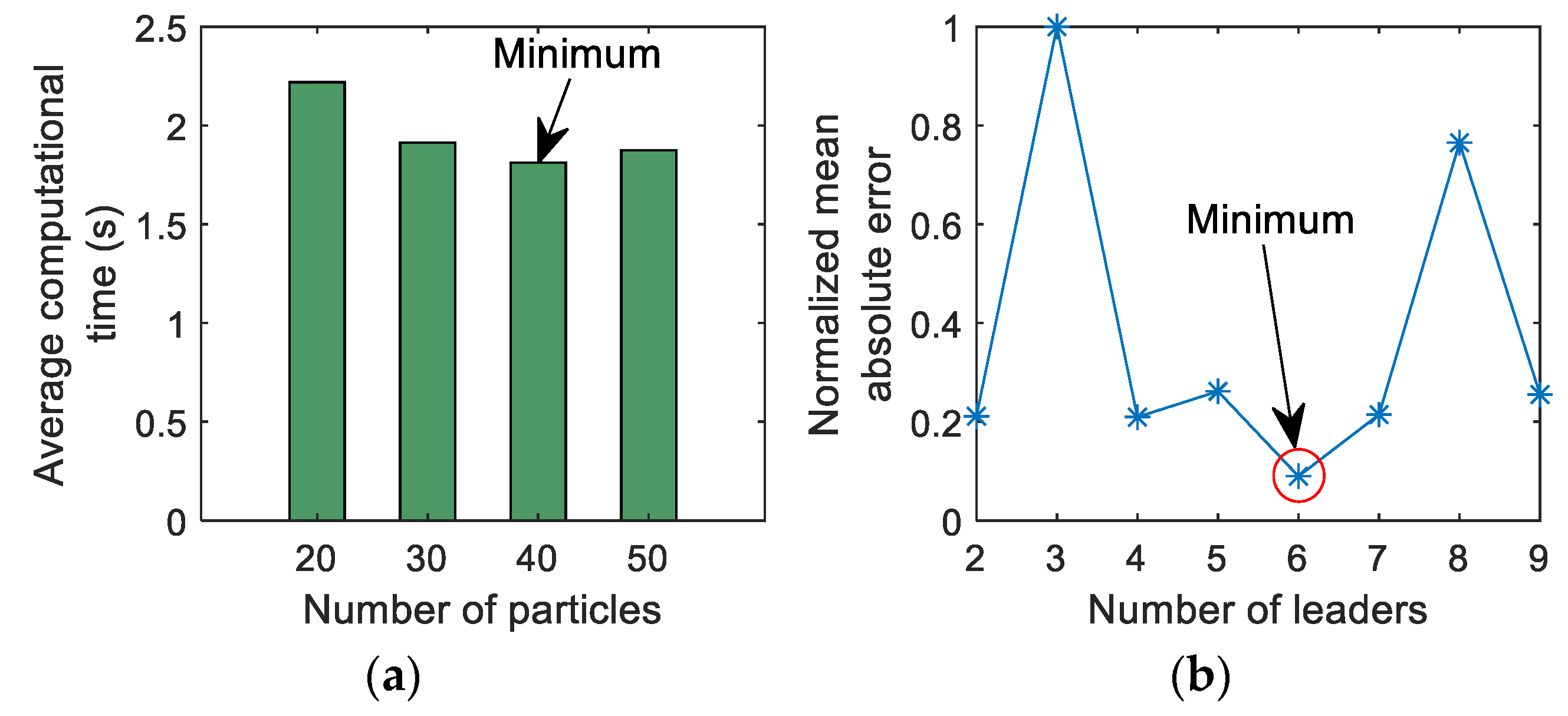
5.4. Effect of the Selected Optimization Parameters
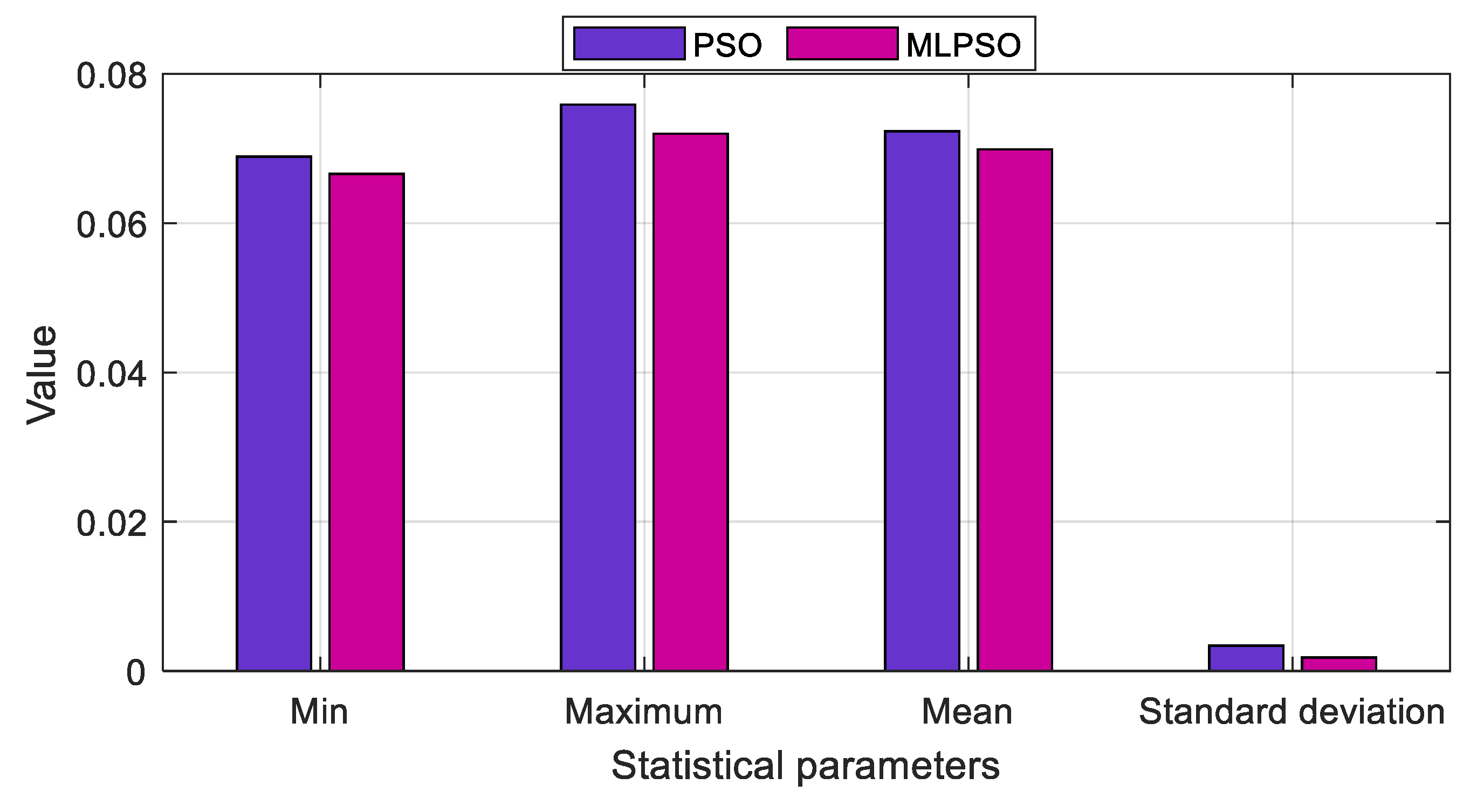
5.5. Effect of the Initialization of Particles in the Swarm
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Artificial Bee Colony | KHA | Khrill Herd Algorithm |
| ACO | Ant Colony Optimization | kV | KiloVolts |
| ASFLA | Adaptive Shuffled Frogs Leaping Algorithm | kW | KiloWatts |
| BA | Bat Algorithm | LHS | Left Hand Side |
| BBO | Biography Based Optimization | LSF | Loss Sensitivity Factor |
| BFOA | Bacterial Foraging Optimization Algorithm | MILP | Mixed Integer Linear Programing |
| BSOA | Backtracking Search Optimization Algorithm | MINLP | Mixed Integer Nonlinear Programing |
| CLPSO | Comprehensive Learning Particle Swarm Optimization | MLPSO | Multileader Particle Swarm Optimization |
| CSA | Cuckoo Search Algorithm | MOTA | Multiobjective Taguchi Approach |
| CSCA | Chaotic Sine Cosine Algorithm | Mvar | Mega Var |
| DE | Differential Evolution | MW | MegaWatts |
| DG | Distributed Generation | NA | Not Applicable |
| ELF | Exhaustive Load Flow | p.u. | Per Unit |
| EMA | Exchange Market Algorithm | PSO | Particle Swarm Optimization |
| FWA | Fireworks Algorithm | QOCSOS | Quasi-Oppositional Chaotic Symbiotic Organisms Search |
| GA | Genetic Algorithm | RHS | Right Hand Side |
| GAMS | General Algebraic Modeling System | SA | Simulated Annealing |
| GSA | Gravitational Search Algorithm | SFLA | Shuffled Frogs Leaping Algorithm |
| HGWO | Hybrid Grey Wolf Optimization | SKHA | Stud Khrill Herd Algorithm |
| HPSO | Hybrid Particle Swarm Optimization | SSA | Slap Swarm Algorithm |
| HSA | Harmony Search Algorithm | TM | Taguchi Method |
| IA | Improved Analytical | TS | Tabu Search |
| IEEE | Institute of Electrical and Electronics Engineers | VSI | Voltage Stability Index |
| IWD | Intelligent Water Drop | WCA | Water Cycle Algorithm |
| IWO | Invasive Weed Optimization |
Appendix A
References
- Gupta, A.R.; Kumar, A. Optimal placement of D-STATCOM using sensitivity approaches in mesh distribution system with time variant load models under load growth. Ain Shams Eng. J. 2018, 9, 783–799. [Google Scholar] [CrossRef]
- Dovì, V.G.; Battaglini, A. Energy Policy and Climate Change: A Multidisciplinary Approach to a Global Problem. Energies 2015, 8, 13473–13480. [Google Scholar] [CrossRef]
- CIGRE. Impact of Increasing Contribution of Dispersed Generation on The Power System: Final Report; CIGRE: Paris, France, 1998. [Google Scholar]
- Akorede, M.F.; Hizam, H.; Pouresmaeil, E. Distributed energy resources and benefits to the environment. Renew. Sustain. Energy Rev. 2010, 14, 724–734. [Google Scholar] [CrossRef]
- Khan, Z.W.; Khan, S. Analyzing the impacts of Distributed Generation on power losses and voltage profile. In Proceedings of the 2015 International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 19–20 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–4. [Google Scholar]
- Pepermans, G.; Driesen, J.; Haeseldonckx, D.; Belmans, R.; D’Haeseleer, W. Distributed generation: Definition, benefits and issues. Energy Policy 2005, 33, 787–798. [Google Scholar] [CrossRef]
- Guan, F.; Zhao, D.; Zhang, X.; Shan, B.; Liu, Z. Research on distributed generation technologies and its impacts on power system. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Liu, W.; Luo, F.; Liu, Y.; Ding, W. Optimal Siting and Sizing of Distributed Generation Based on Improved Nondominated Sorting Genetic Algorithm II. Processes 2019, 7, 955. [Google Scholar] [CrossRef]
- Nguyen, T.D.T.; Ruan, J.; Nguyen, Q.N.; Le, N.G.; Tan, D.; Hu, L. Study of Economical-Technical Impacts of Distributed Generation on Medium-Voltage Grid. TELKOMNIKA Indones. J. Electr. Eng. 2014, 12, 1177–1187. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.; Mokhlis, H.; Bakar, A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Jordehi, A.R. Allocation of distributed generation units in electric power systems: A review. Renew. Sustain. Energy Rev. 2016, 56, 893–905. [Google Scholar] [CrossRef]
- Haji Abbas, M.P.; Huy, P.D.; Ramachandaramurthy, V.K. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy Rev. 2017, 75, 293–312. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical strategies for renewable distributed generation integration considering energy loss minimization. Appl. Energy 2013, 105, 75–85. [Google Scholar] [CrossRef]
- Gözel, T.; Hocaoglu, M.H. An analytical method for the sizing and siting of distributed generators in radial systems. Electr. Power Syst. Res. 2009, 79, 912–918. [Google Scholar] [CrossRef]
- Sa’Ed, J.A.; Amer, M.; Bodair, A.; Baransi, A.; Favuzza, S.; Zizzo, G. A Simplified Analytical Approach for Optimal Planning of Distributed Generation in Electrical Distribution Networks. Appl. Sci. 2019, 9, 5446. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Rueda-Medina, A.C.; Franco, J.F.; Rider, M.J.; Padilha-Feltrin, A.; Romero, R. A mixed-integer linear programming approach for optimal type, size and allocation of distributed generation in radial distribution systems. Electr. Power Syst. Res. 2013, 97, 133–143. [Google Scholar] [CrossRef]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Vita, V.; Alimardan, T.; Ekonomou, L. The Impact of Distributed Generation in the Distribution Networks’ Voltage Profile and Energy Losses. In Proceedings of the 2015 IEEE European Modelling Symposium (EMS), Madrid, Spain, 6–8 October 2015; IEEE: Piscataway, NJ, USA, 2016; pp. 260–265. [Google Scholar]
- Vita, V. Development of a Decision-Making Algorithm for the Optimum Size and Placement of Distributed Generation Units in Distribution Networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Singh, D.; Singh, D.; Verma, K. GA based energy loss minimization approach for optimal sizing & placement of distributed generation. Int. J. Knowl. Based Intell. Eng. Syst. 2008, 12, 147–156. [Google Scholar] [CrossRef]
- Biswas, S.; Goswami, S.K.; Chatterjee, A. Optimum distributed generation placement with voltage sag effect minimization. Energy Convers. Manag. 2012, 53, 163–174. [Google Scholar] [CrossRef]
- Hadavi, S.; Zaker, B.; Karami, H.; Arani, A.A.K.; Gharehpetian, G.B. Optimal placement and sizing of DGs considering static voltage stability. In Proceedings of the 2017 Conference on Electrical Power Distribution Networks Conference (EPDC), Semnan, Iran, 19–20 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 12–16. [Google Scholar]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. DG allocation for benefit maximization in distribution networks. IEEE Trans. Power Syst. 2012, 28, 639–649. [Google Scholar] [CrossRef]
- Rugthaicharoencheep, N.; Lantharthong, T.; Ratreepruk, A.; Ratchatha, J.; Rugthaichareoncheep, N. Application of Tabu Search for Optimal Placement and Sizing of Distributed Generation for Loss Reduction. Adv. Mater. Res. 2012, 433, 7190–7194. [Google Scholar] [CrossRef]
- Prabha, D.R.; Jayabarathi, T.; Umamageswari, R.; Saranya, S. Optimal location and sizing of distributed generation unit using intelligent water drop algorithm. Sustain. Energy Technol. Assess. 2015, 11, 106–113. [Google Scholar] [CrossRef]
- Sudabattula, S.K.; Kowsalya, M. Optimal allocation of solar based distributed generators in distribution system using Bat algorithm. Perspect. Sci. 2016, 8, 270–272. [Google Scholar] [CrossRef]
- Candelo-Becerra, J.E.; Riaño, H.E.H. Distributed Generation Placement in Radial Distribution Networks using a Bat-inspired Algorithm. DYNA 2015, 82, 60–67. [Google Scholar] [CrossRef]
- Onlam, A.; Yodphet, D.; Chatthaworn, R.; Surawanitkun, C.; Siritaratiwat, A.; Khunkitti, P. Power Loss Minimization and Voltage Stability Improvement in Electrical Distribution System via Network Reconfiguration and Distributed Generation Placement Using Novel Adaptive Shuffled Frogs Leaping Algorithm. Energies 2019, 12, 553. [Google Scholar] [CrossRef]
- Devi, S.; Geethanjali, M. Application of Modified Bacterial Foraging Optimization algorithm for optimal placement and sizing of Distributed Generation. Expert Syst. Appl. 2014, 41, 2772–2781. [Google Scholar] [CrossRef]
- Kowsalya, M. Optimal size and siting of multiple distributed generators in distribution system using bacterial foraging optimization. Swarm Evol. Comput. 2014, 15, 58–65. [Google Scholar] [CrossRef]
- Ravindran, S.; Victoire, A.A. A bio-geography-based algorithm for optimal siting and sizing of distributed generators with an effective power factor model. Comput. Electr. Eng. 2018, 72, 482–501. [Google Scholar] [CrossRef]
- Zaid, N.M.; Mokhtar, M.K.; Musirin, I.; Rahmat, N.A. Multi-Objective Optimization for Sizing of Distributed Generation Using Cuckoo Search Algorithm. Appl. Mech. Mater. 2015, 785, 34–37. [Google Scholar] [CrossRef]
- Kumari, R.V.S.L.; Kumar, G.V.N.; Nagaraju, S.S.; Jain, M.B. Optimal sizing of distributed generation using particle swarm optimization. In Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), Kannur, India, 6–7 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 499–505. [Google Scholar]
- Tolba, M.A.; Tulsky, V.N.; Diab, A.A.Z. Optimal allocation and sizing of multiple distributed generators in distribution networks using a novel hybrid particle swarm optimization algorithm. In Proceedings of the 2017 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), St. Petersburg, Russia, 1–3 February 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1606–1612. [Google Scholar]
- Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. Comprehensive learning particle swarm optimization for sizing and placement of distributed generation for network loss reduction. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 16–23. [Google Scholar] [CrossRef]
- Kennedy, J. Small worlds and mega-minds: Effects of neighborhood topology on particle swarm performance. In Proceedings of the 1999 Congress on Evolutionary Computation—CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; IEEE: Piscataway, NJ, USA, 2003; Volume 3, p. 1931. [Google Scholar]
- Kennedy, J.; Mendes, R. Population structure and particle swarm performance. In Proceedings of the 2002 Congress on Evolutionary Computation. CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; IEEE: Piscataway, NJ, USA, 2003; Volume 2, pp. 1671–1676. [Google Scholar]
- Long, H.X.; Xu, W.B.; Wang, X.G.; Sun, J. Using selection to improve quantum-behaved particle swarm optimization. Kongzhi yu Juece/Control Decis. 2010, 25, 1499–1506. [Google Scholar]
- Jordehi, A.R. Enhanced leader PSO (ELPSO): A new PSO variant for solving global optimisation problems. Appl. Soft Comput. 2015, 26, 401–417. [Google Scholar] [CrossRef]
- Akbari, R.; Ziarati, K. A cooperative approach to bee swarm optimization. J. Inf. Sci. Eng. 2011, 27, 799–818. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. 47-Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 11, pp. 111–117. [Google Scholar]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A comprehensive review of the voltage stability indices. Renew. Sustain. Energy Rev. 2016, 63, 1–12. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Efficient optimization technique for multiple DG allocation in distribution networks. Appl. Soft Comput. 2020, 86, 105938. [Google Scholar] [CrossRef]
- Murty, V.V.V.S.N.; Kumar, A. Optimal DG integration and network reconfiguration in microgrid system with realistic time varying load model using hybrid optimisation. IET Smart Grid 2019, 2, 192–202. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Baharudin, Z.; Vo, D.N. A Quasi-Oppositional-Chaotic Symbiotic Organisms Search algorithm for global optimization problems. Appl. Soft Comput. 2019, 77, 567–583. [Google Scholar] [CrossRef]
- Sambaiah, K.S.; Jayabarathi, T. Optimal allocation of renewable distributed generation and capacitor banks in distribution systems using salp swarm algorithm. Int. J. Renew. Energy Res. 2019, 9, 96–107. [Google Scholar]
- El-Ela, A.A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal Placement and Sizing of Distributed Generation and Capacitor Banks in Distribution Systems Using Water Cycle Algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Daneshvar, M.; Babaei, E. Exchange Market Algorithm for Multiple DG Placement and Sizing in a Radial Distribution System. J. Energy Manag. Technol. 2018, 2, 54–65. [Google Scholar]
- Meena, N.K.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Multi-objective Taguchi approach for optimal DG integration in distribution systems. IET Gener. Transm. Distrib. 2017, 11, 2418–2428. [Google Scholar] [CrossRef]
- Sanjay, R.; Jayabarathi, T.; Raghunathan, T.; Ramesh, V.; Mithulananthan, N. Optimal Allocation of Distributed Generation Using Hybrid Grey Wolf Optimizer. IEEE Access 2017, 5, 14807–14818. [Google Scholar] [CrossRef]
- ChithraDevi, S.; Lakshminarasimman, L.; Balamurugan, R. Stud Krill herd Algorithm for multiple DG placement and sizing in a radial distribution system. Eng. Sci. Technol. Int. J. 2017, 20, 748–759. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Hybrid approach for optimal placement of multiple DGs of multiple types in distribution networks. Int. J. Electr. Power Energy Syst. 2016, 75, 226–235. [Google Scholar] [CrossRef]
- Elfergany, A.A. Optimal allocation of multi-type distributed generators using backtracking search optimization algorithm. Int. J. Electr. Power Energy Syst. 2015, 64, 1197–1205. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Injeti, S.K.; Kumar, N.P. A novel approach to identify optimal access point and capacity of multiple DGs in a small, medium and large scale radial distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 142–151. [Google Scholar] [CrossRef]
- Rao, R.S.; Ravindra, K.; Satish, K.; Narasimham, S.V.L. Power Loss Minimization in Distribution System Using Network Reconfiguration in the Presence of Distributed Generation. IEEE Trans. Power Syst. 2013, 28, 317–325. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N. Multiple Distributed Generator Placement in Primary Distribution Networks for Loss Reduction. IEEE Trans. Ind. Electron. 2011, 60, 1700–1708. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Suganthan, P. Particle swarm optimiser with neighbourhood operator. In Proceedings of the 1999 Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; CEC 1999: Washington, DC, USA, 1999; Volume 3, pp. 1958–1962. [Google Scholar]







| Variable | Definition in Optimal Sizing | Definition in MLPSO Algorithm |
|---|---|---|
| Possible solutions of DG sizes | Number of particles in the swarm | |
| Number of DGs | Number of dimensions of the particle | |
| Minimum DG capacity | The lower bound of the search space | |
| Maximum DG capacity | The upper bound of the search space | |
| Number of DG optimization simulations | Maximum number of optimization runs | |
| Maximum number of iterations of an optimization simulation | Maximum number of iterations per optimization run | |
| Incremental counter (index) for the number of runs | Index of the optimization run | |
| Incremental counter (index) for the number of iterations | Index of the iteration of an optimization run | |
| The total power loss of the system with the integration of DGs | The objective function value of the optimization problem | |
| The penalized total power loss of the system with the integration of DGs | The objective function value of the optimization problem with penalties |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of particles in the swarm () | 40 | Number of leaders (L) | 6 |
| Maximum number of runs () | 10 | Cognitive coefficient () | 2 |
| Maximum number of iterations () | 103 | Social coefficient () | 2 |
| Upper bound of the inertia weight () | 0.9 | Maximum allowable voltage () | 1.05 p.u. |
| Lower bound of the inertia weight () | 0.4 | Maximum allowable voltage () | 0.95 p.u. |
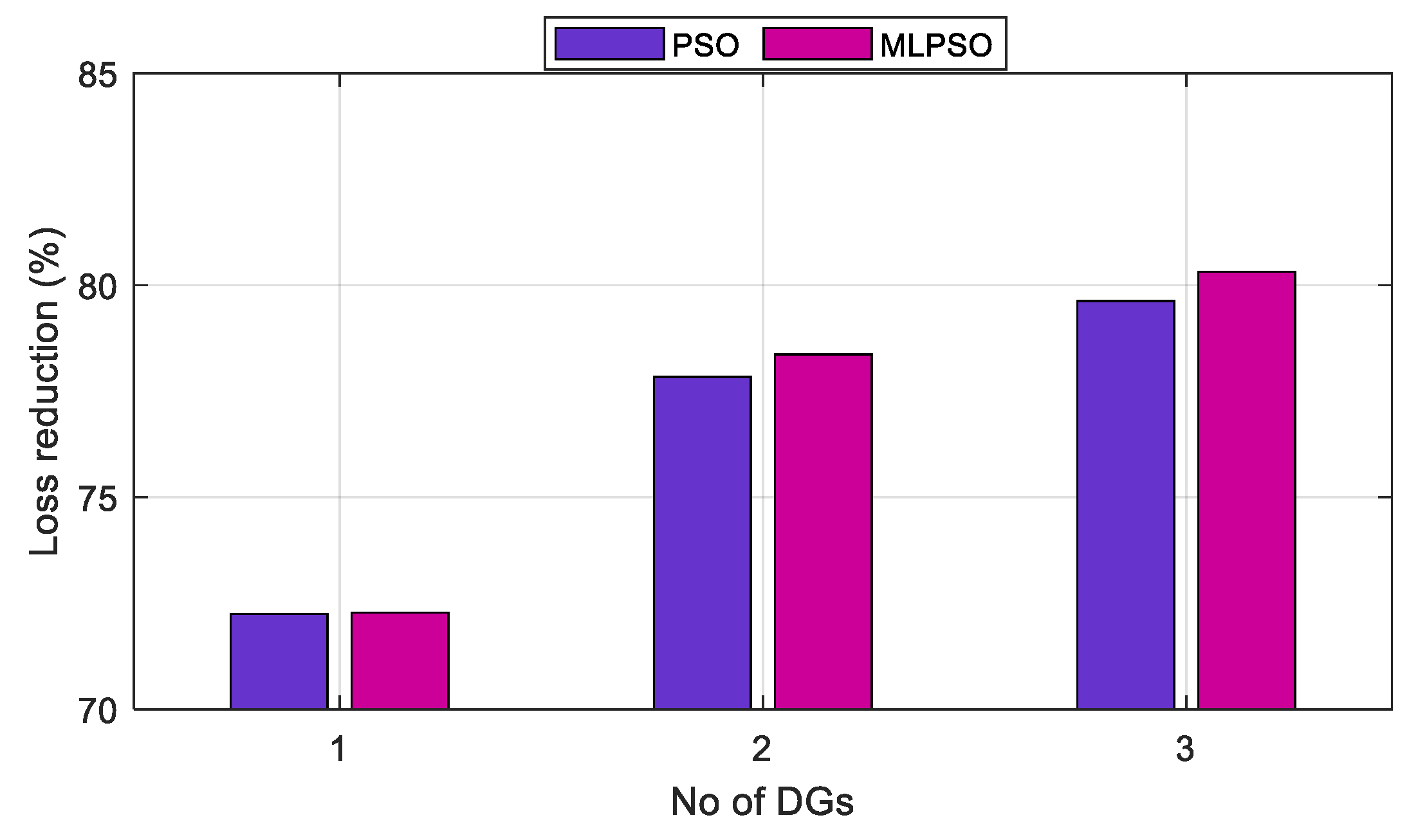
| Algorithm | L1 | S1 (MW) | L2 | S2 (MW) | L3 | S2 (MW) | Active Power Loss (kW) | Loss Reduction (%) |
|---|---|---|---|---|---|---|---|---|
| Base | - | - | - | - | - | - | 210.070 | - |
| PSO | 6 | 2.42 | - | - | - | - | 102.330 | 51.27 |
| 11 | 0.96 | 31 | 0.95 | - | - | 82.995 | 60.49 | |
| 29 | 1.08 | 25 | 0.85 | 9 | 1.04 | 73.630 | 64.94 | |
| CLPSO | 6 | 2.43 | - | - | - | - | 102.125 | 51.40 |
| 30 | 1.10 | 13 | 0.89 | - | - | 81.720 | 61.10 | |
| 11 | 0.93 | 32 | 0.85 | 24 | 1.05 | 70.300 | 66.54 | |
| MLPSO | 6 | 2.42 | - | - | - | - | 102.120 | 51.40 |
| 30 | 1.15 | 13 | 0.82 | - | - | 81.620 | 61.15 | |
| 14 | 0.76 | 30 | 1.03 | 24 | 1.07 | 68.460 | 67.40 |
| Algorithm | Minimum Voltage (p.u.) and Node | Maximum Voltage (p.u.) and Node | Mean Voltage (p.u.) |
|---|---|---|---|
| PSO | 0.9613 at node 18 | 1 at node 1 | 0.9815 |
| CLPSO | 0.9637 at node 18 | 1 at node 1 | 0.9816 |
| MLPSO | 0.9699 at node 33 | 1 at node 1 | 0.9824 |
| Algorithm | L1 | S1 (MW) | L2 | S2 (MW) | L3 | S2 (MW) | Active Power Loss (kW) | Loss Reduction (%) |
|---|---|---|---|---|---|---|---|---|
| Base | - | - | - | - | - | - | 338.46 | - |
| PSO | 14 | 4.075 | - | - | - | - | 93.886 | 72.25 |
| 17 | 2.138 | 43 | 1.885 | - | - | 75.000 | 77.84 | |
| 15 | 2.330 | 25 | 1.010 | 43 | 1.329 | 68.922 | 79.63 | |
| MLPSO | 14 | 4.074 | - | - | - | - | 93.792 | 72.28 |
| 16 | 2.324 | 43 | 1.487 | - | - | 73.191 | 78.37 | |
| 16 | 2.182 | 31 | 0.562 | 44 | 1.342 | 66.599 | 80.32 |
| Algorithm | Minimum Voltage (p.u.) and Node | Maximum Voltage (p.u.) and Node | Mean Voltage (p.u.) |
|---|---|---|---|
| PSO | 0.9677 at node 22 | 1 at node 1 | 0.9814 |
| MLPSO | 0.9707 at node 22 | 1 at node 1 | 0.9828 |
| Algorithm | Ref | Year | DG Sizes (kW) | DG Locations | Reduction of Power Loss (%) | Minimum Voltage (p.u.) |
|---|---|---|---|---|---|---|
| The proposed algorithm | 760, 1030, 1070 | 14, 30, 24 | 67.40 | 0.9699 | ||
| CSCA | [45] | 2020 | 871, 1091.47, 954.08 | 13, 24, 30 | 64.50 | 0.9690 |
| CLPSO | [37] | 2020 | 930, 850, 1050 | 11, 32, 24 | 66.54 | 0.9816 |
| GSA-GAMS | [46] | 2019 | 801.22, 1091.31, 1053.59 | 13, 24, 30 | 65.64 | 0.9686 |
| ASFLA | [30] | 2019 | 545.7, 993.6, 1209.4 | 24, 29, 12 | 67.00 | 0.9781 |
| SFLA | [30] | 2019 | 563.9, 318.2, 514.4 | 28, 30, 14 | 58.86 | 0.9770 |
| FWA | [30] | 2019 | 589.7, 189.5, 1014.6 | 14, 18, 32 | 56.24 | 0.9680 |
| QOCSOS | [47] | 2019 | 801.7, 1091.3, 1053.6 | 13, 24, 30 | 65.50 | NA |
| SSA | [48] | 2019 | 753.6, 1100.4, 1070.6 | 13, 23, 29 | 65.97 | 0.9686 |
| WCA | [49] | 2018 | 854.6, 1101.7, 1181 | 14, 24, 29 | 66.17 | 0.9730 |
| EMA | [50] | 2018 | 976.6, 1169.09, 943.54 | 30, 24, 12 | 64.32 | 0.9684 |
| TM | [51] | 2017 | 719.9, 719.9, 1439.7 | 15, 26, 33 | 49.52 | 0.9960 |
| MOTA | [51] | 2017 | 980, 960, 1340 | 7, 14, 30 | 52.40 | 0.9986 |
| HPSO | [36] | 2017 | 560, 560, 790 | 8, 13, 31 | 60.26 | 0.9660 |
| HGWO | [52] | 2017 | 802, 1090, 1054 | 13, 24, 30 | 65.34 | NA |
| KHA | [53] | 2017 | 814.9, 750.1, 1142.40 | 24, 14, 30 | 65.26 | 0.9701 |
| SKHA | [53] | 2017 | 801.81, 1091.3, 1053.6 | 13, 24, 30 | 65.50 | 0.9687 |
| PSO-Analytical | [54] | 2016 | 790, 1070, 1010 | 13, 24, 30 | 65.45 | NA |
| BA | [28] | 2016 | 816.3, 952.35, 952.35 | 15, 25, 30 | 64.42 | 0.9800 |
| IWO | [27] | 2016 | 624.7, 104.9, 1056 | 14, 18, 32 | 57.47 | 0.9716 |
| BSOA | [55] | 2015 | 632, 487, 550 | 13, 28, 31 | 57.59 | 0.9554 |
| ACO-ABC | [56] | 2015 | 754.7, 1099.9, 1071.4 | 14, 24, 30 | 66.00 | NA |
| BFOA | [32] | 2014 | 652.1, 198.4, 1067.2 | 14, 18, 32 | 57.38 | 0.9705 |
| SA | [57] | 2013 | 1112.4, 487.4, 867.9 | 6, 18, 30 | 61.12 | 0.9676 |
| HSA | [58] | 2013 | 572.4, 1070, 1046.2 | 17, 18, 33 | 52.26 | 0.9670 |
| LSF | [59] | 2013 | 720, 810, 900 | 18, 33, 25 | 59.72 | NA |
| IA | [59] | 2013 | 900, 900, 720 | 6, 12, 31 | 61.62 | NA |
| ELF | [59] | 2013 | 900, 900, 900 | 13, 30, 24 | 64.83 | NA |
| GA-PSO | [60] | 2012 | 925, 863, 1200 | 11, 16, 32 | 49.20 | 0.9670 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karunarathne, E.; Pasupuleti, J.; Ekanayake, J.; Almeida, D. Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm. Energies 2020, 13, 6185. https://doi.org/10.3390/en13236185
Karunarathne E, Pasupuleti J, Ekanayake J, Almeida D. Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm. Energies. 2020; 13(23):6185. https://doi.org/10.3390/en13236185
Chicago/Turabian StyleKarunarathne, Eshan, Jagadeesh Pasupuleti, Janaka Ekanayake, and Dilini Almeida. 2020. "Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm" Energies 13, no. 23: 6185. https://doi.org/10.3390/en13236185
APA StyleKarunarathne, E., Pasupuleti, J., Ekanayake, J., & Almeida, D. (2020). Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm. Energies, 13(23), 6185. https://doi.org/10.3390/en13236185





