1. Introduction
The state of the world’s environment is widely acknowledged to be declining [
1], with rising temperatures driving global climate change and various planetary boundaries being breached or at risk of being breached [
2,
3]. These trends are due to a combination of growing population and increasing levels of resource consumption and waste generation. Against such well understood problems, it is becoming increasingly recognised that we require a tangible, quantitative vision of what a future sustainable and desirable world might look like [
4].
The concept of the “ecological footprint” (
EF) was first described by Rees [
5] and later Wackernagel and Rees [
6] and Rees [
7] and is used to relate human consumption to carrying capacity via a common, and easily understood, unit of land area. Since its inception the
EF has been used in many studies at global, national and sub-national levels. A database of national
EF accounts covering most countries in the world is maintained and updated by the Global Footprint Network (
www.footprintnetwork.org).
The original EF was conceived as a tool to compare human demand for biocapacity (productive ecosystems) with available supply, either within a study country or globally. A population’s EF is based on consumption directly linked to the productivity of land and sea ecosystems, relating to food (crops and animal products, as well as fish), fibre and timber. Each type of consumption could be represented, via a global average yield factor, by an equivalent land area (the ‘footprint’, in average units known as ‘global hectares’) that would be required to produce the food, fibre or timber. Importantly, the footprint accounting includes an assessment of the ‘biocapacity’, i.e., the land area (in global hectares) available for crops, livestock grazing and so on. The EF accounting method remains an effective means for broadly assessing and communicating concepts relating to the carrying capacity of humans, based on consumption patterns at the national and global level.
Significantly, the
EF presented by Wackernagel and Rees [
6] included an energy footprint by equating energy consumption to land area. For renewable sources of energy (solar, wind, biomass) the yield and the spatial footprint could be estimated as for other forms of land use. However, the vast majority of energy consumed globally is derived from fossil fuels, the extraction of which carries a negligible physical land footprint; hence in the energy footprint, the consumption is not directly linked to the yield of energy with a known land area requirement. Two main options have been presented for the calculation of an areal energy footprint from fossil fuels: (i) the hypothetical substitution of fossil fuel energy with an equivalent amount of biomass energy (area calculated based on biomass energy yields), and (ii) the area of forest that would be required to assimilate the carbon emissions from burning fossil fuel (area calculated from average carbon uptake rates). The latter has been adopted the most widely in
EF studies and is the form used today in the national accounts maintained by the Global Footprint Network.
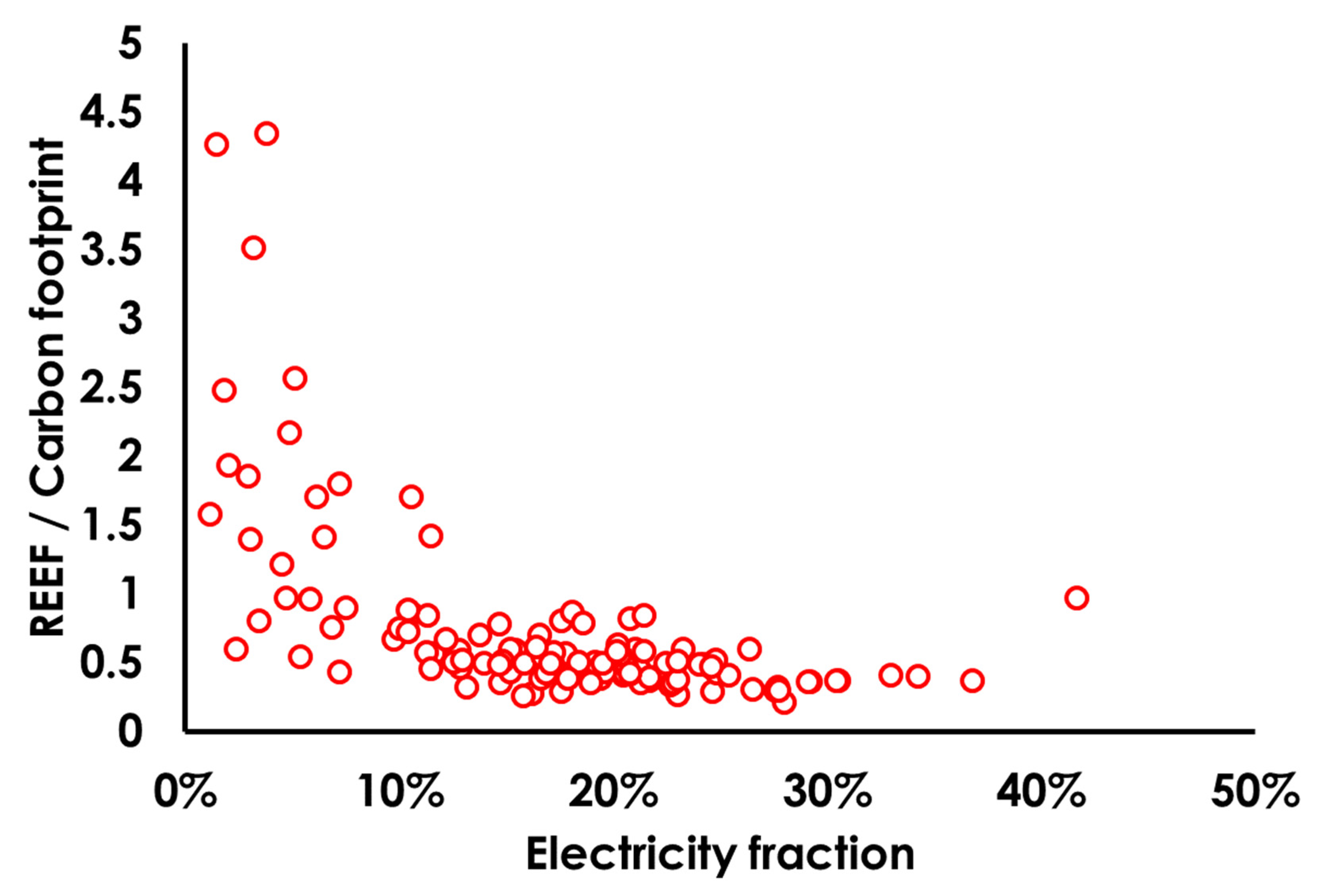
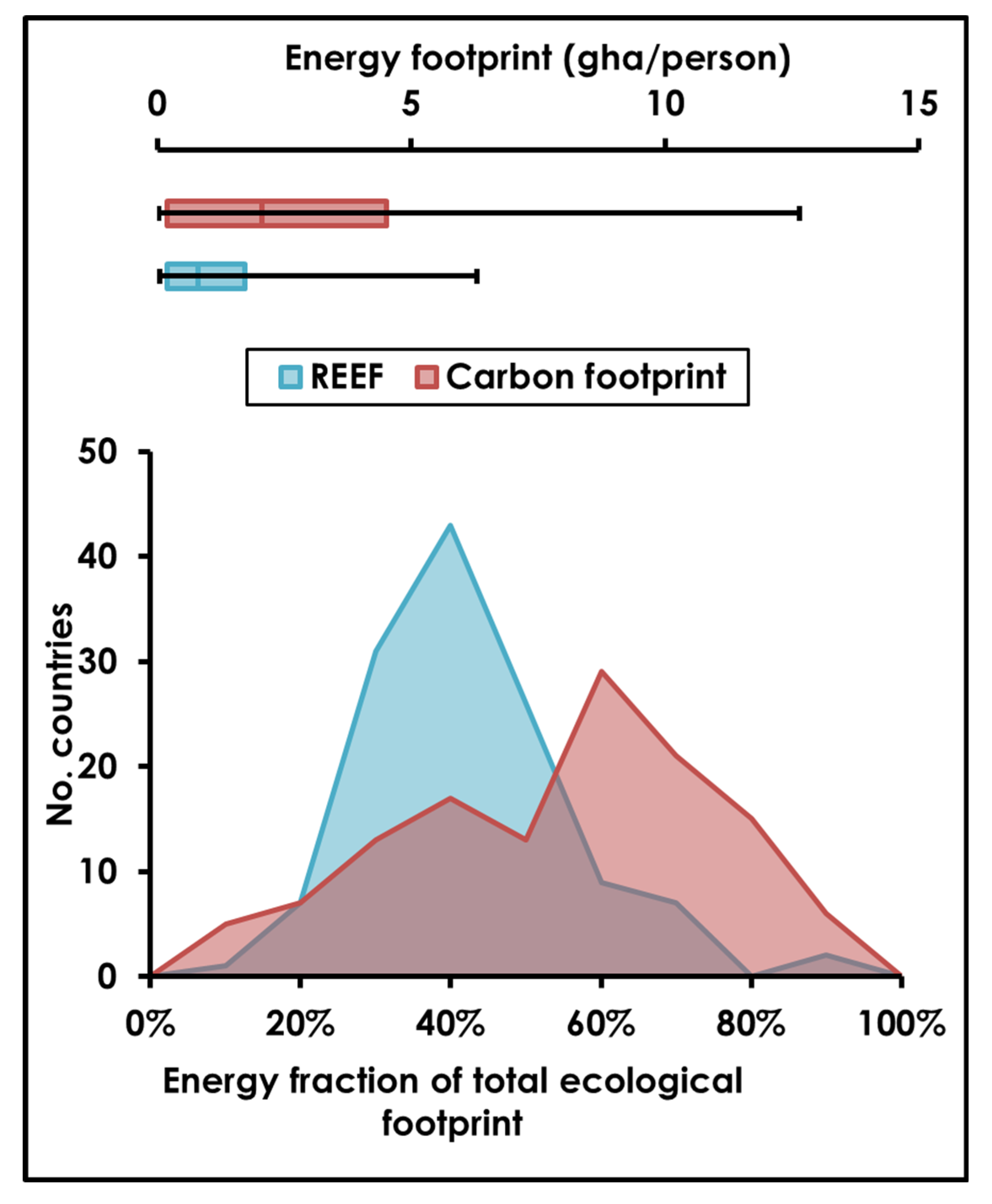
As currently calculated based on carbon uptake equivalence, the global carbon footprint (
CF) is 1.69 global hectares per person, making up some 59% of the total
EF. At the global level, the
CF is the only component of the
EF that can be assessed as beyond the per-capita biocapacity (see
Table 1), as the carbon entering the atmosphere exceeds the uptake capacity and this difference is measurable. Other categories of land use may well be in overshoot especially at the local scale, e.g., due to soil degradation, overfishing, etc., but this is not specifically measurable via the
EF spatial accounting method. Therefore, if the
EF is to be used to demonstrate the human population’s overall environmental footprint relative to Earth’s carrying capacity, it can be said that the energy footprint makes up a substantial fraction of the calculated overshoot.
The use of carbon uptake rates to derive an equivalent land area provides a method for estimating the sustainability—or lack thereof—of carbon emissions from burning fossil fuels. However, several problems may arise if the CF assessment is taken as the principal measure of the sustainability of our energy supply. These problems are articulated briefly below. It must be noted that these are not criticisms of the EF accounting method, but rather point to the need to assess energy sustainability more broadly than carbon uptake alone.
Firstly, present-day energy use is unsustainable for two reasons: (i) excessive carbon emissions and (ii) depletion of non-renewable resources. The carbon-based method of footprint estimation addresses the former but not the latter. Mohr et al. [
8] comprehensively modelled plausible future pathways for fossil fuel production globally, under low and high resource scenarios, and concluded that a supply constraint-driven peak and decline in fossil energy is inevitable by—at the latest—the middle of the 21st century. This means that even if we were able to bring carbon emissions to within biocapacity (say, by widely adopting some future carbon capture and sequestration technology), our energy supply would not be sustainable. A future sustainable energy scenario must be one in which (i) net carbon emissions are reduced to a sustainable level—perhaps zero—and (ii) non-renewable fossil fuels are replaced by renewable energy resources.
Secondly, by reducing all energy to a common unit of carbon emissions, the
CF method does not interrogate the different quality (i.e., usefulness to the economy) of different sources of energy. For example, in Australia, grid-supplied electricity has an average emissions factor of 253 kgCO
2-e/GJ while petrol/gasoline carries an emissions factor of 67.4 kgCO
2-e/GJ [
9]. This means that for the same amount of land to assimilate carbon emissions, 1 GJ of electricity would be equivalent 3.75 GJ of petrol or gasoline. Moreover, these types of energy perform very different functions; notably, certain modes of transport (especially aviation and long-distance freight) are not currently, nor foreseeably likely to become, amenable to electric propulsion.
Thirdly, when only the
CF is counted towards the ‘Energy’ category of the
EF, any land footprint associated with physical energy infrastructure would typically be counted via the ‘Built up land’ category. The spatial footprint associated with expanding renewable energy infrastructure—to reduce the
CF—is relevant to policymakers, and to anyone concerned about whether future energy scenarios could physically fit within the carrying capacity of our planet. Indeed, as Scheidel and Sorman [
10] point out, the low power density of renewable energy sources is likely to result in vast amounts of land being required to generate power. Irrespective of the
EF category to which such a footprint is ultimately added (energy vs. built up land), if we wish to envisage a hypothetical future scenario powered by 100% renewable energy, then a calculation procedure is required to determine the associated land requirements beyond carbon uptake from emissions.
The purpose of this paper is to demonstrate an approach to calculating a hypothetical energy footprint that is based on equivalent renewable energy, for which we propose the term “Renewable Energy Equivalent Footprint” (REEF). Rather than depicting the footprint of the current energy paradigm based on land uptake from unsustainable carbon emissions, the REEF calculates the hypothetical footprint of a future paradigm in which the electricity and fuel demands of today are met entirely by renewable energy. The REEF is an attempt to deliver a transparent, straightforward alternative to the CF, enabling the potential sustainability of energy consumption to be directly evaluated alongside other measures of EF in the context of human carrying capacity.
In this paper, an approach is presented that is deliberately parsimonious, and is intended to be simple, transparent and repeatable rather than computationally complex and heavily data dependent. Importantly, our analysis considers electricity and fuel-based energy separately. This is significant as the net energy yield, as well as the input energy profile, can be very different for electricity and fuel-based renewable energy. Considering different types of energy allows a fuller picture of the relationship between overall energy and the land footprint.
The REEF is intended to be used either in place of, or—perhaps more likely—in conjunction with, the conventional CF for global, national and local EF accounting. The method as described in this paper can also be applied to determine an equivalent land area that would be required to (renewably) support individual energy-consuming activities, to contextualise and communicate the impact of behaviour and consumption patterns in ways that relate more directly to carrying capacity.
2. Materials and Methods
In order to link energy consumption with land area demand, we adopt a simplified energy supply model, dividing energy consumption into two types: electricity and non-electricity (i.e., broadly “fuels”). It is important to differentiate between electricity and fuels, because there are very different physical production systems involved with very different power density (the average rate of energy produced over time per unit area), and different behaviour in terms of input energy that must be invested in the renewable energy production system.
Although it is easy to conceive of a far more complex energy model (e.g., one considering solid, liquid and gaseous renewable fuels, as well as different sources of renewable electricity such as solar, wind, hydro, geothermal etc.), for the purposes of demonstrating an easily replicable model and drawing broad conclusions related to carrying capacity, we contend it is not necessary to segregate further than electricity and non-electricity. Moreover, as we are simulating a hypothetical, long-term future scenario of 100% renewable energy, it would be inappropriate and potentially misleading to assume too much detail about the make-up of the future energy system.
All renewable energy systems—with the exception of geothermal—can be considered to be solar energy, with different technologies capable of harvesting and converting different proportions of overall incoming solar power into forms useful for humans (electricity or biomass). Scheidel and Sorman [
10] reviewed the yields of numerous renewable power systems in the context of a possible future “land grab” in the shift to renewable energy, and showed a tenfold (or more) difference in power density between the lowest (biomass: 0–0.6 with average 0.5 W/m
2) and highest (concentrating solar thermal: 4–10 W/m
2).
Following the conventional
EF calculation procedure [
12], the gross energy production (
Egross for electricity and
Fgross for fuel) is related to an approximate (global average) production area by dividing by the average yield:
where
Yelec and
Yfuel are the global average yields for electricity and biofuel, respectively (units are energy per unit area per time, e.g., GJ/ha/y). The term
EQF is an ‘equivalence factor’, representing the productivity of the biocapacity category relative to average biological productivity [
12]. For simplicity, in this study we will assume
EQF = 1.28, corresponding to the value used for both carbon footprint and forest biocapacity in current
EF assessments [
11], enabling the calculated energy production areas to be compared with forest biocapacity. It is possible to imagine energy production taking place in other land categories (e.g., grazing land), in which case the analysis could be repeated using a different value of
EQF.
The renewable energy equivalent footprint (
REEF) is simply the sum of the two energy production areas, plus the non-energy component of the original carbon footprint:
where
Cenergy and
Ctotal are the energy-related and total carbon emissions used in the original carbon footprint calculation, respectively, and
CF is the area of the original carbon footprint. This formulation allows the
REEF to account for carbon emissions from non-energy activities such as agriculture and cement production.
In addition to the areal power density, we must consider the fact that renewable energy technologies—as with all energy supplies—require input energy (beyond the solar radiation they are harvesting). To be of use to human activity, energy supplies must yield a net or surplus above the energy invested in their generation. This is termed the “energy return on energy invested”, or
EROI. Various energy supply technologies—both non-renewable and renewable—have been reviewed in the literature [
13,
14,
15].
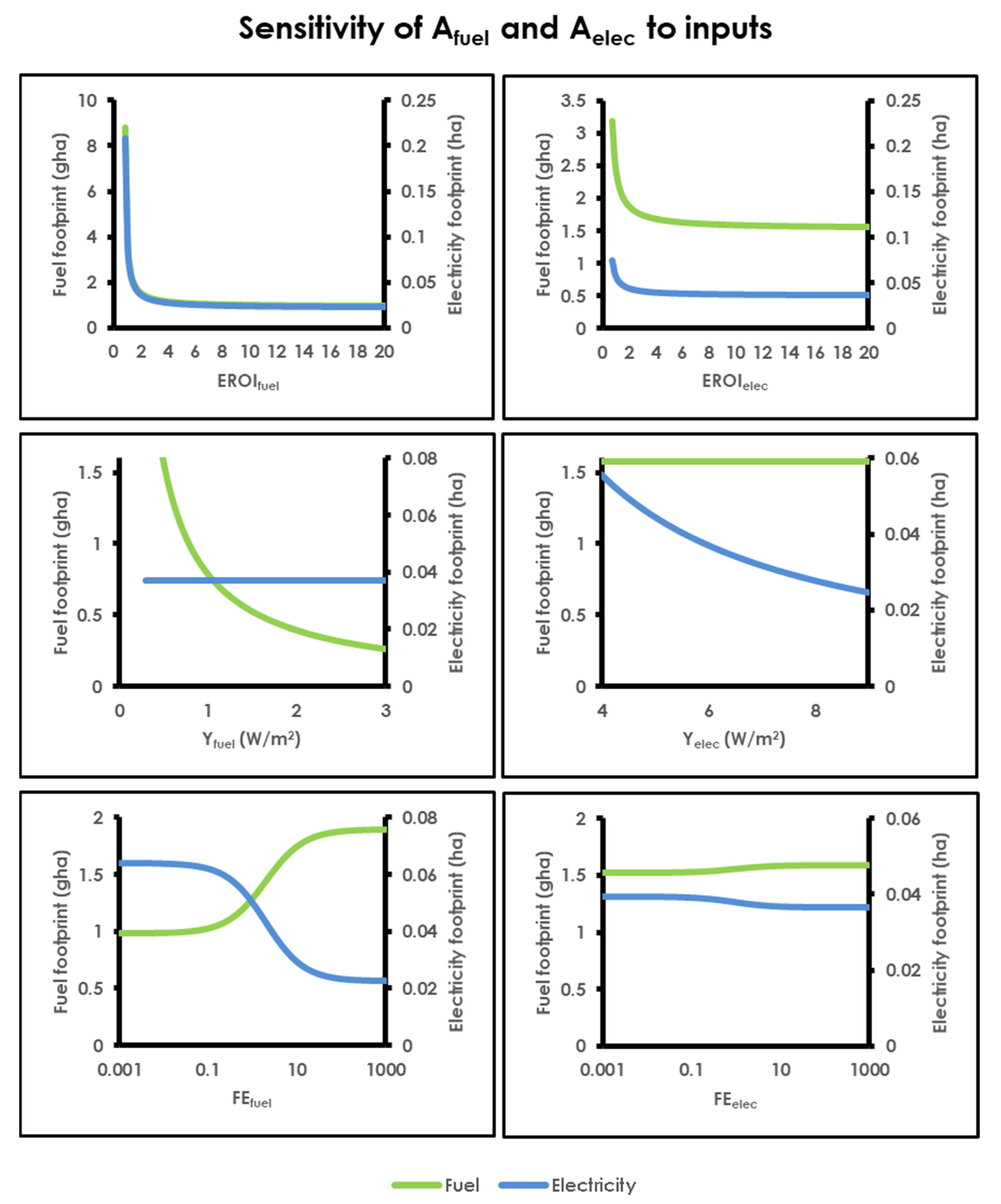
EROI values reported in the literature are highly variable, as different calculation methods yield different net energy depending on the placement of the boundary for inputs versus outputs. However, the consensus is that as the overall
EROI decreases (e.g., if energy becomes harder to obtain), the energy source becomes less useful, and an energy supply with
EROI at or below 1 tends to be viewed as useless as there is no net energy available to use; Hall et al. [
15] proposed a minimum
EROI of 3 for energy to be useful to society. Moriarty and Honnery [
16] claim that the low
EROI of renewable energy technologies relative to fossil fuels imposes a significant limit to their usefulness. However, we contend that when multiple energy types are included in the supply model (even as few as two, as in ours), it is possible to envisage a scenario of cross-subsidisation where high-
EROI forms of energy can provide input for low-
EROI forms of energy. In such a system, the production of highly energy-dense, but low-
EROI, liquid fuels derived from biomass may plausibly be subsidised by more efficient (high-
EROI) solar electricity. As long as the system obtains a satisfactory net energy yield overall, and a sufficient fraction of the energy re-invested in the low-
EROI production component can be met using high-
EROI energy, it may be possible to envisage a basically functional energy supply.
In our simplified energy supply model, both types of renewable energy are assumed to receive inputs from both types of energy, i.e., electricity is invested in both electricity and biomass production, and likewise biomass energy is invested in both biomass and electricity production, in relatively predictable proportions.
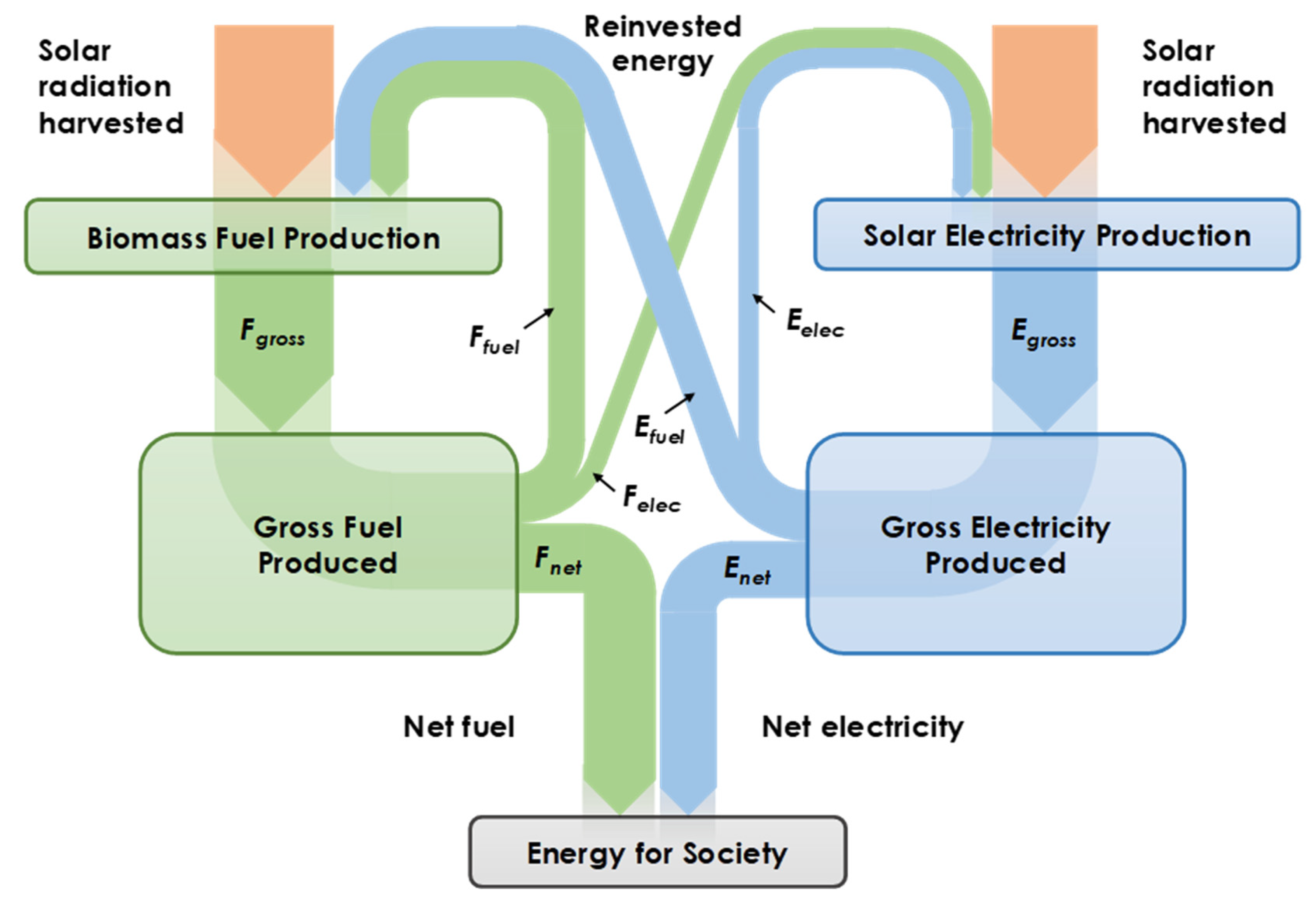
Figure 1 shows the simplified energy supply model with cross-subsidisation of energy sources and net energy flows to society.
The calculation procedure begins with the assumption that net electricity (
Enet) and fuel (
Fnet) demands are known, or can be reliably estimated. These could be the per capita energy demands at a national level, or the demand from a specific activity. Assuming conservation of energy, for electricity we then have:
where
Eelec is the electrical energy reinvested in the electricity production system, and
Efuel is the electrical energy reinvested in the biofuel production system. Units for all terms in Equation (4) are energy per time (e.g., PJ/y).
Likewise, for fuel, we have:
where
F denotes fuel energy and subscripts are as per Equation (4).
The model must account for reinvestment of energy in the energy supply, so we can relate the gross output of energy to the input energy via the energy return on energy invested (
EROI, dimensionless) for each fuel type:
Finally, we define a fuel-electricity input ratio (
FE, dimensionless) for the energy invested:
It is assumed that the following parameters are known, or can be reliably estimated: net energy requirements (
Enet and
Fnet) for a given nation or process under consideration; energy return on energy invested for each energy production system (
EROIelec and
EROIfuel); and the fuel-electricity input ratio for each energy production system (
FEfuel and
FEelec). This leaves six unknown variables (
Egross,
Eelec,
Efuel,
Fgross,
Felec and
Ffuel) which can be solved using the six simultaneous equations (Equations (4)–(9)). A solution procedure is given in
Appendix A.
The REEF can be calculated for a given energy-consuming activity, or for the overall energy needs of a community, a nation or the world.
To calculate the REEF required to support a specific energy-consuming activity, we first require the energy consumption rate (Fnet and Enet). Then the EROI and FE terms must be obtained for both energy production processes. Note that even if evaluating the REEF for a single type of energy (e.g., transport fuel demand where Enet = 0), the remaining terms are still required for both types of energy to evaluate the whole input to the energy production system. For example, demand for renewable transport fuel for a specific transport activity will require land for the biofuel production, plus the land for extra fuel to be reinvested in the production process, as well as additional land for solar electricity to supply the electrical demands of the biofuel production process, even if no electricity is consumed in the final activity.
To calculate the
REEF at the community, national or global level, we need net energy use separated into fuel and electricity. In the following section we will present the results of the
REEF calculated for 127 countries. We assume final energy demand is a satisfactory proxy for net energy (
Enet,
Fnet) used in the
REEF model. For this analysis, data for final energy demand (total, electricity, and later, transport) for 2014 were purchased from the International Energy Agency (
https://www.iea.org/data-and-statistics).
4. Discussion
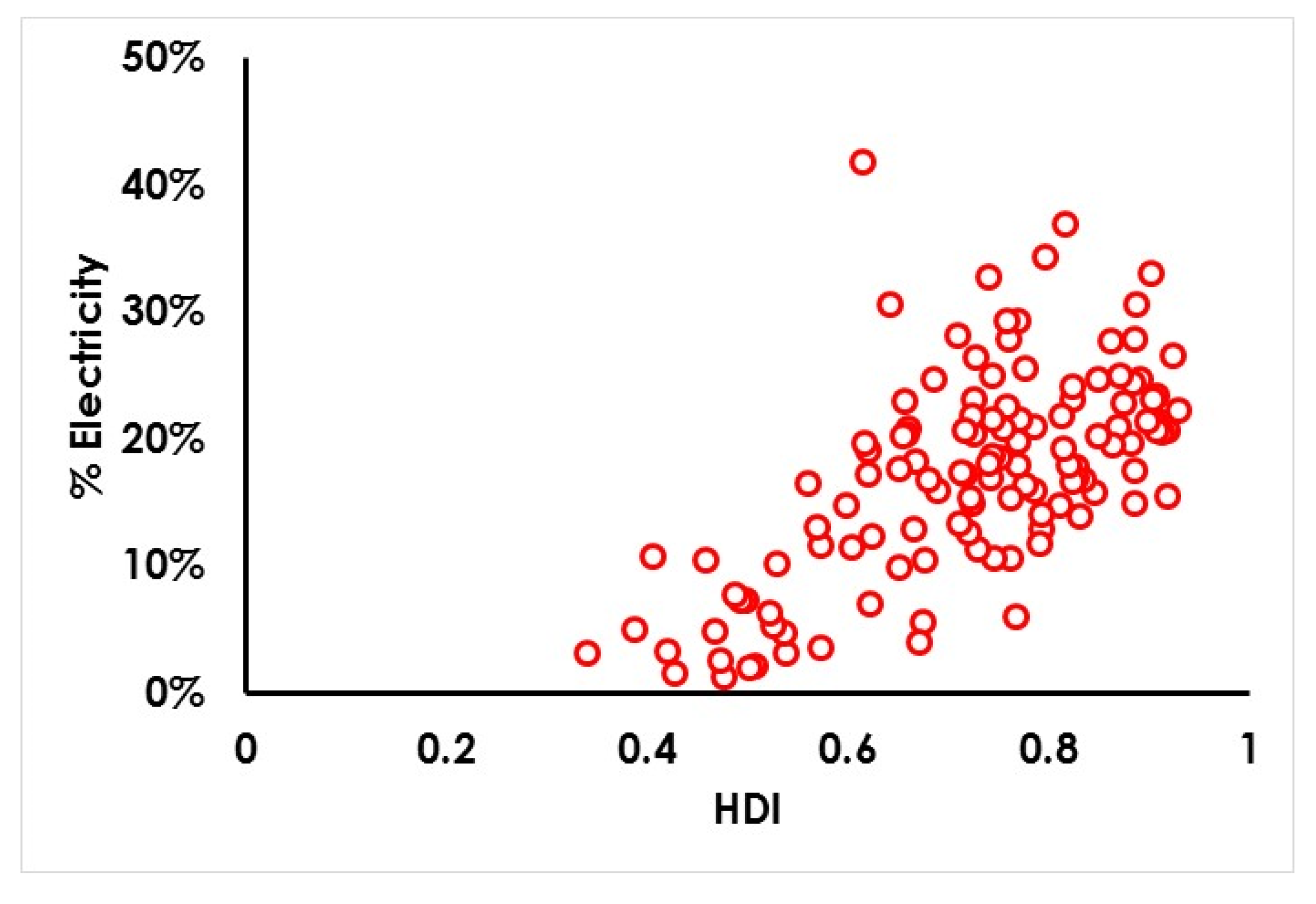
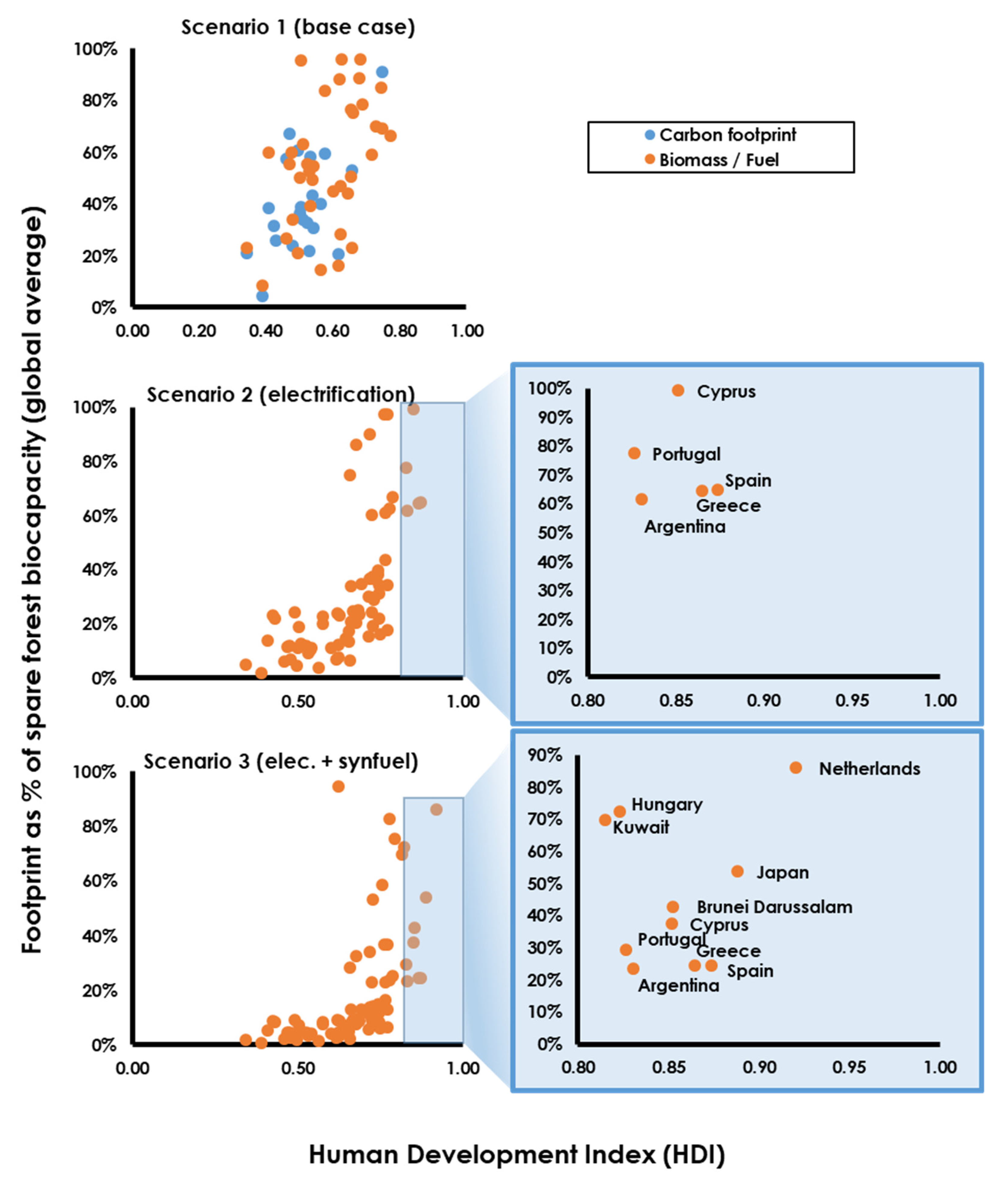
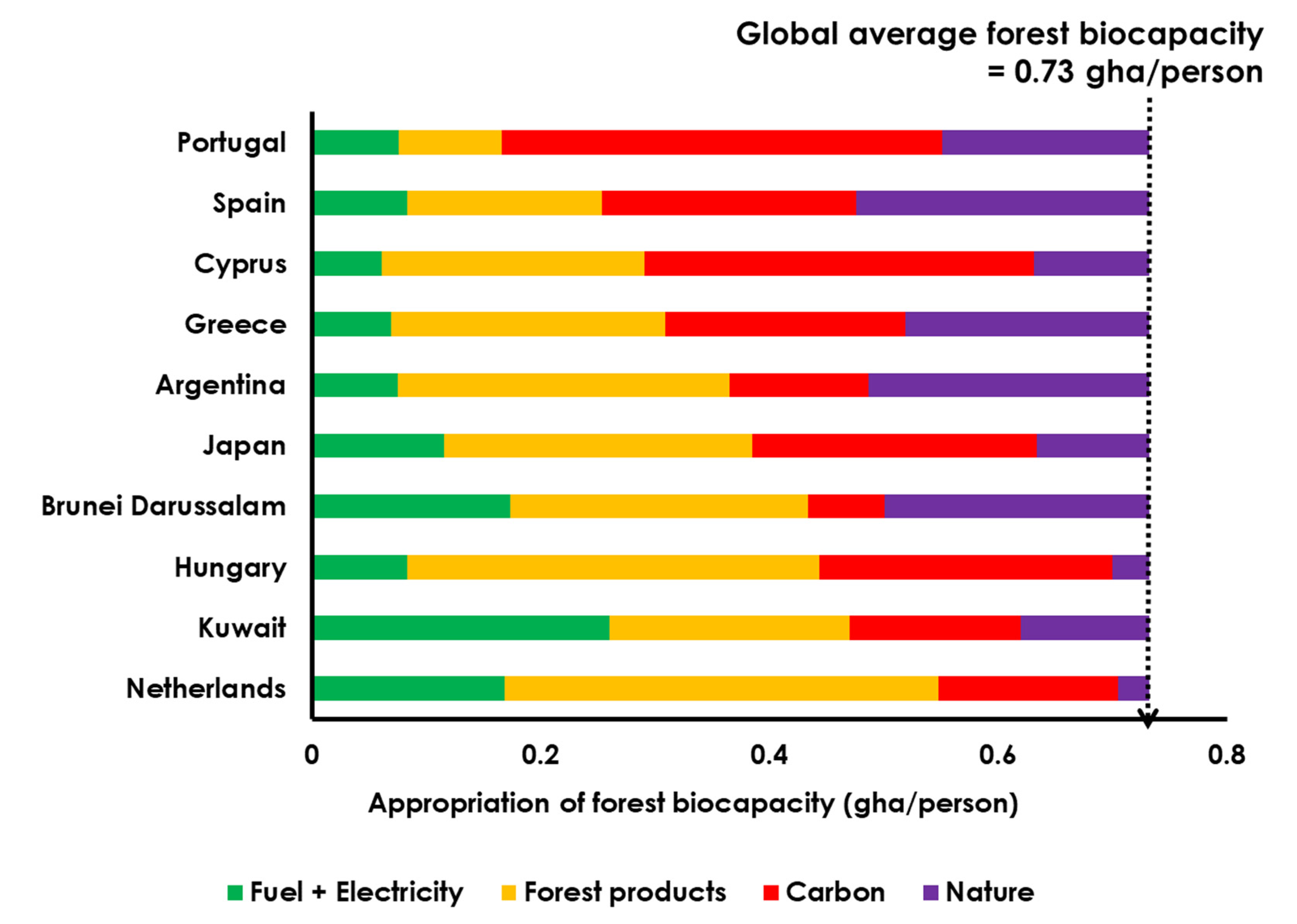
Based on this assessment, five high-HDI countries (Argentina, Cyprus, Greece, Portugal and Spain) have an energy and forest product consumption profile that—if adopted worldwide—could theoretically be met by high-tech renewably derived fuels, while theoretically preserving 50% or more of the world’s forest biocapacity. This finding offers a starting place for discussion of policy and behaviour change, by providing a culturally and economically diverse range of contemporary nations exhibiting consumption patterns that it may be possible to emulate globally in a sustainable way.
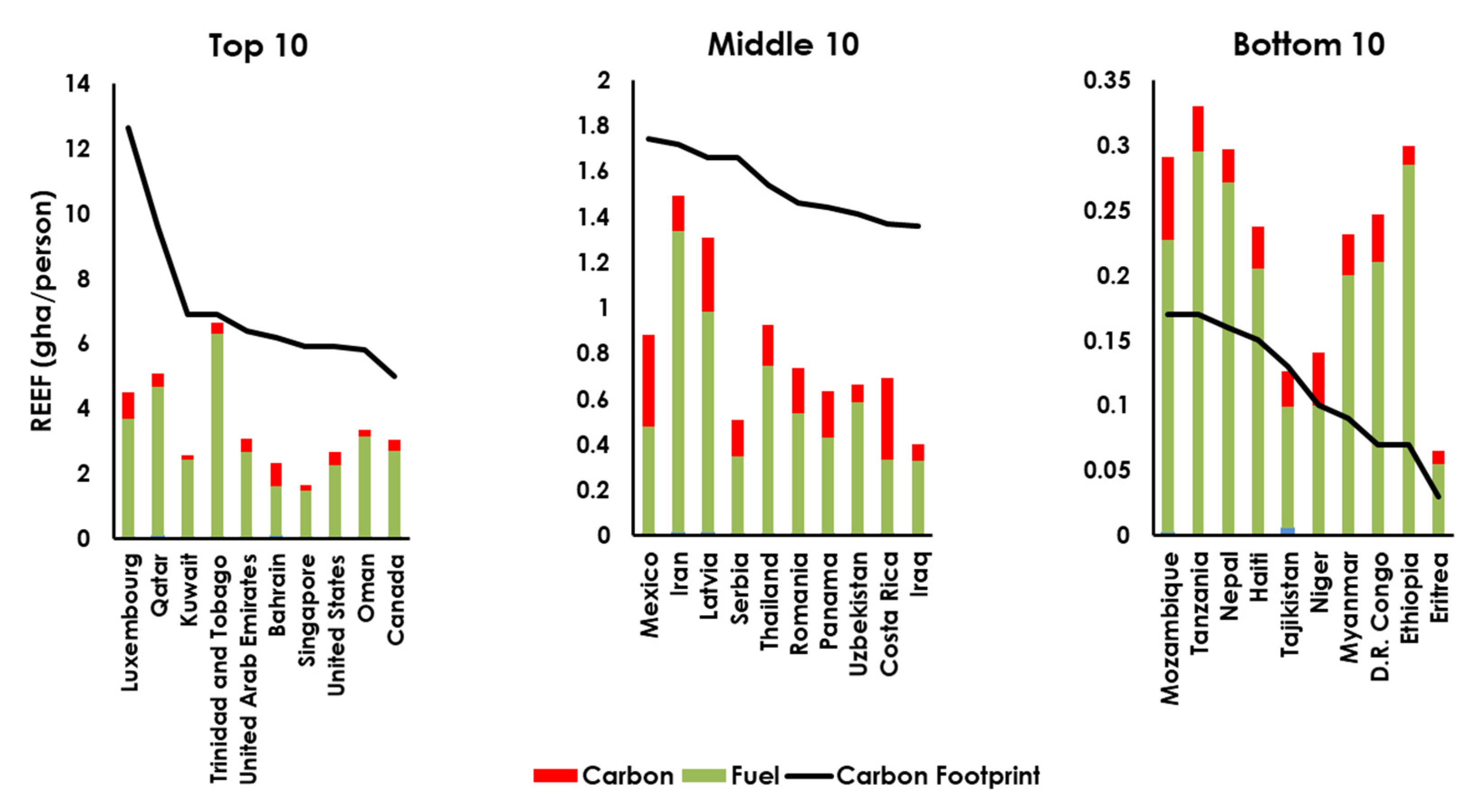
Table 5 provides some characteristic information about the energy demand profiles in these exemplar countries, as well as the demand profiles from the highest and lowest HDI nations (Australia and Niger respectively). For context, as currently assessed, Australia’s forest product footprint alone (0.89 gha/person) exceeds the global average forest biocapacity, leaving no room to equitably accommodate even its non-energy carbon footprint (0.34 gha/person), let alone the additional renewable energy footprint (0.17 gha/person in the most optimistic case). Thus, Australia does not currently offer a consumption profile that can be sustainably emulated worldwide.
The five best exemplars from
Figure 9 are characterised by a relatively consistent level of total energy consumption (50–70 GJ/capita/y). Interestingly, Smil [
18] quoted this exact range as being optimal for achieving the twin objectives of a fair share of energy worldwide and a satisfactory quality of life.
The remaining exemplar countries show different consumption profiles. The Netherlands has total energy consumption at 142 GJ/capita/y, akin to Australia’s energy consumption and more than double the average of the other six countries. Coupled with a large forest footprint, the Netherlands represents a consumption profile that—if adopted globally—would demand a large fraction of the world’s forests. Brunei Darussalam and Kuwait also present high energy consumption cases; however, modest forest product footprint and non-energy carbon footprints mean that these nations are technically able to be accommodated within biocapacity, albeit still demanding more than 50% of forest capacity. Japan and Hungary, meanwhile, have energy demands similar to the five exemplar countries, but their larger non-energy carbon and forest product footprints mean that the overall consumption profile for these two countries exceeds 50% of forest biocapacity.
In order to provide full context, Niger has been included as the lowest-HDI country out of the 127 considered in this analysis. The energy demand per capita in Niger is around one-tenth of the five main exemplar countries, and can be taken as an undesirable lower limit to energy demand.
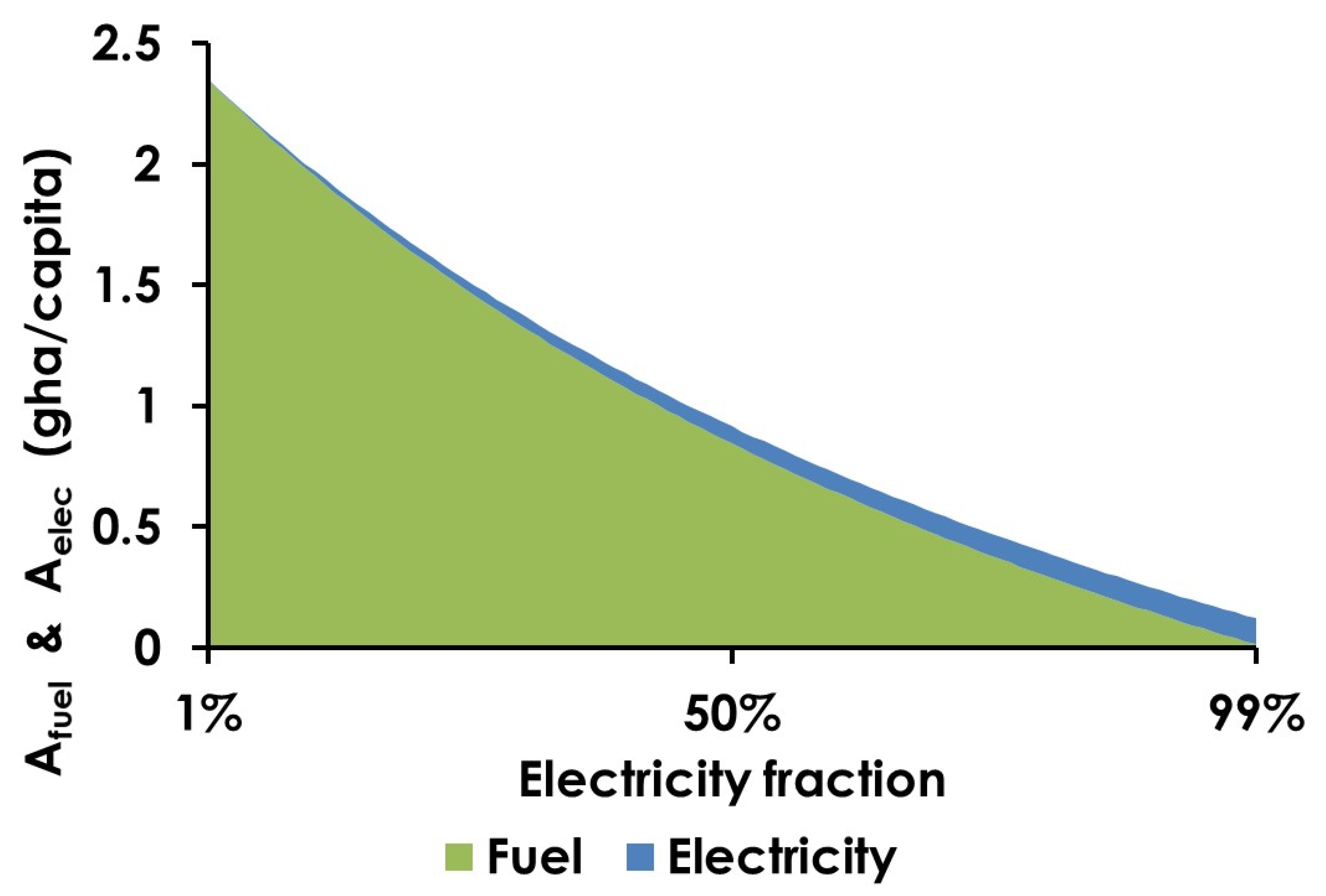
Of the five exemplars, the four European countries (Cyprus, Greece, Portugal and Spain) already have a high degree of electrification by present-day global standards, in the range of 24–28% of final energy demand. It is noteworthy, therefore, that the assumption made for Scenarios 2 and 3 would require approximately a trebling of electrification to get to the assumed level of 75% of final energy demand. Such an increase in electricity as a fraction of the overall energy mix is required to bring even these exemplar countries up to a globally transferrable consumption profile that could theoretically be met by renewable energy, while leaving some room for nature. The technical challenges posed by such a transition should not be underestimated. It should also be noted that an energy system so significantly dominated by renewable electricity would require very large amounts of energy storage, which would potentially reduce the EROI to below the values assumed in this analysis. The impact of electrification on storage needs and net energy yields is beyond the scope of this preliminary study, but warrants further investigation.
5. Conclusions
The conventional carbon footprint (CF) is a useful tool for quantifying the extent to which the carbon emissions from—predominantly—fossil fuel energy consumption have placed humanity beyond the carrying capacity of global ecosystems. In essence the CF can be viewed as a means to quantify the unsustainability of the present condition. In this paper we have presented a complementary tool, the renewable energy equivalent footprint (REEF), which can be used to quantify the footprint of an alternative energy supply, based on estimates of net yields from renewable energy sources, and accounting for cross-subsidisation of different energy types within the supply system.
By considering two different renewable energy sources (electricity and biofuel), the REEF method allows potential land area requirements to be calculated separately. This is important, for while it is plausible to consider renewable electricity production taking place somewhat passively with minimal competition with other productive land uses (e.g., offshore wind, onshore wind sharing land with grazing and cropping or natural ecosystems, rooftop solar, and desert solar farms), biofuel production requires suitable growing conditions that place it in likely competition with other bio-productive land. Assuming that grazing and cropping area will be non-negotiable in the future, we have presented the hypothetical biofuel area in relation to its most likely source of biocapacity: forest land.
Based on mid-range estimates of renewable energy yield and the present-day fraction of electricity to total energy demand, no high-HDI nation could have its future fuel demands met with a globally equitable share of forest biocapacity. It is only by invoking hypothetical alternative technology scenarios that a globally sustainable energy future can be envisaged. Even in the most optimistic scenario (coupling radical electrification of the energy system with use of high-yielding synthetic fuels), there is a very limited number of exemplar countries (five) with present-day energy consumption patterns that may be replicated across the globe in an approximately sustainable way. These five countries (Argentina, Cyprus, Greece, Portugal and Spain) exhibit a satisfactorily high HDI and a sufficiently small renewable energy footprint that it may spare more than 50% of the planet’s forest biocapacity after considering the extraction of forest products, which also places a demand on these ecosystems. While it is not guaranteed that these exemplar countries currently have (or will have) a sustainable consumption pattern, nor whether the optimistic technological projections will prove possible in the future, at present they offer a useful starting place when attempting to envision the changes that may be required to create a sustainable and desirable future world, powered entirely by renewable energy.
The REEF method complements the conventional CF approach in several important ways. Firstly, the CF can only conclude that there are currently no countries that exhibit both a satisfactory level of HDI (>0.8) and a carbon assimilation area that can be met within a globally equitable share of forest land. Secondly, even in countries with a sufficiently low CF (almost all of which have HDI < 0.6), the low carbon emissions do not constitute a sustainable energy system as long as these countries remain dependent on non-renewable fossil fuels. Finally, the CF does not capture the required land footprint to replace non-renewable, carbon-intensive fossil fuels with carbon-neutral, renewable energy sources. The REEF method allows us to uncover—albeit only with optimistic assumptions about technology—at least a small handful of high-HDI nations whose energy consumption profile may be replicable worldwide without fossil fuels, while also quantifying the additional land footprint of the renewable energy infrastructure.
By considering both electricity and fuel energy in a simplified renewable energy mix, the REEF demonstrates that there is no possibility of a sustainable energy supply with today’s low-yielding biofuels coupled with our modest degree of electrification; to achieve a sustainable and equitable energy future we must (a) treble the fraction of electricity in our supply mix, and (b) develop synthetic fuel sources to cover the remainder.
In summary, the REEF analysis demonstrates that a sustainable and desirable future powered by renewable energy: (i) may be possible, depending on the worldwide adoption of consumption patterns typical of several key exemplar countries; (ii) is highly dependent on major future technological development, such as radical electrification of the energy supply and the development of synthetic fuels; and (iii) is still likely to require appropriation of a substantial, but hopefully sustainable, fraction of the world’s forest area or potentially an equivalent area of land of lower bio-productivity. This analysis has been conducted based on recent population numbers; further population growth will inevitably increase the burden on the world’s forests and make a renewable energy future proportionally more difficult to attain and sustain.