Load Frequency Control of Photovoltaic Generation-Integrated Multi-Area Interconnected Power Systems Based on Double Equivalent-Input-Disturbance Controllers
Abstract
1. Introduction
2. System Description and Modeling
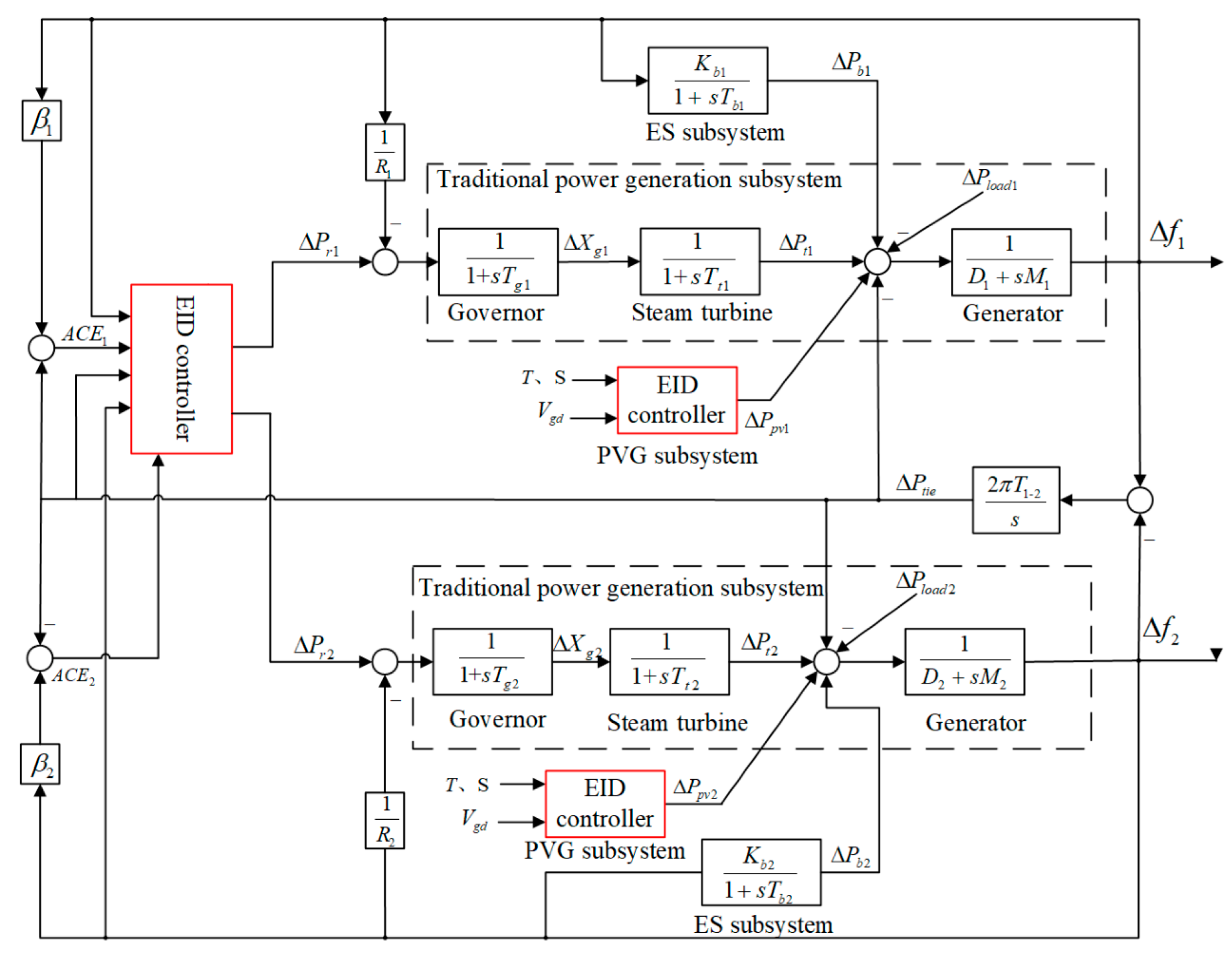
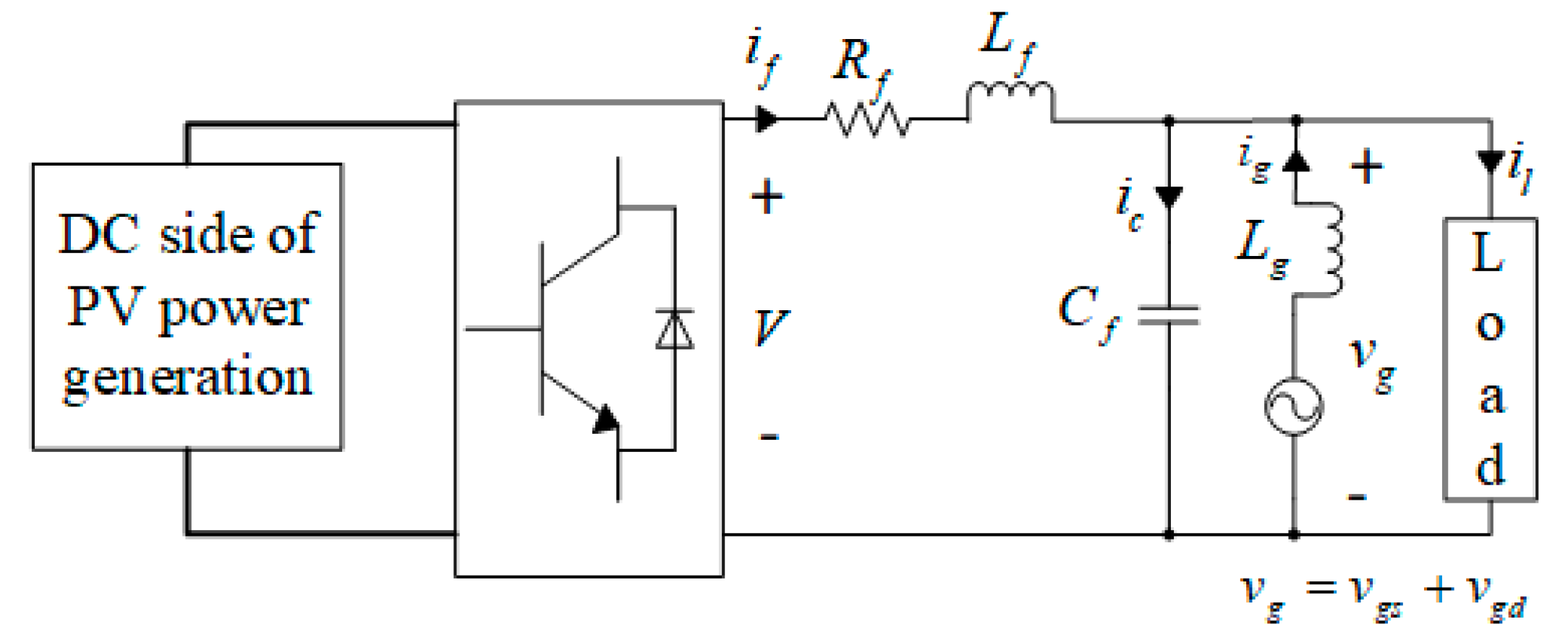
2.1. Description of PVG Integrated Multi-Area Interconnected Power System
2.2. Modeling of PVG Integrated Multi-Area Interconnected Power System
3. Design of Double EID Controllers
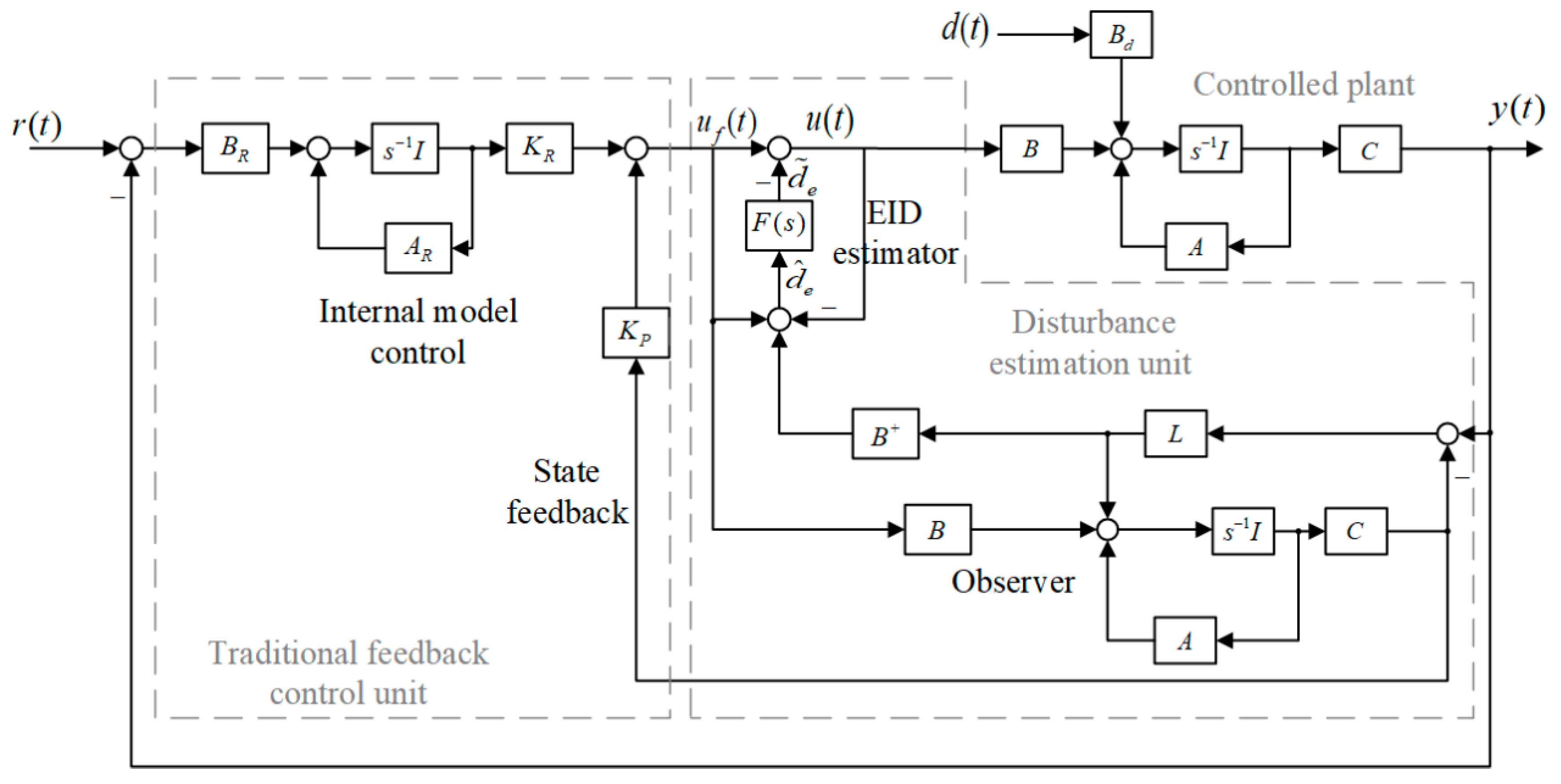
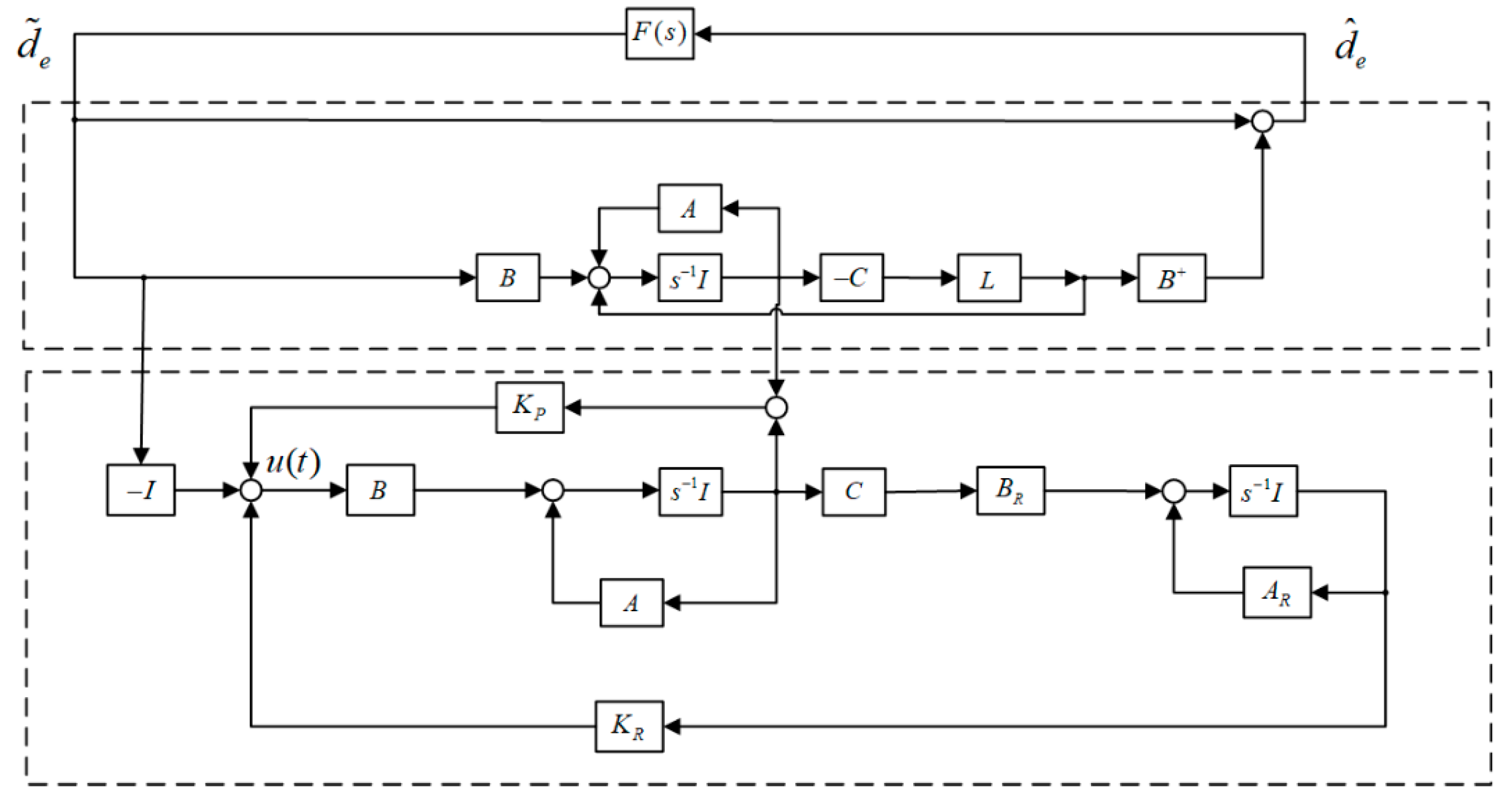
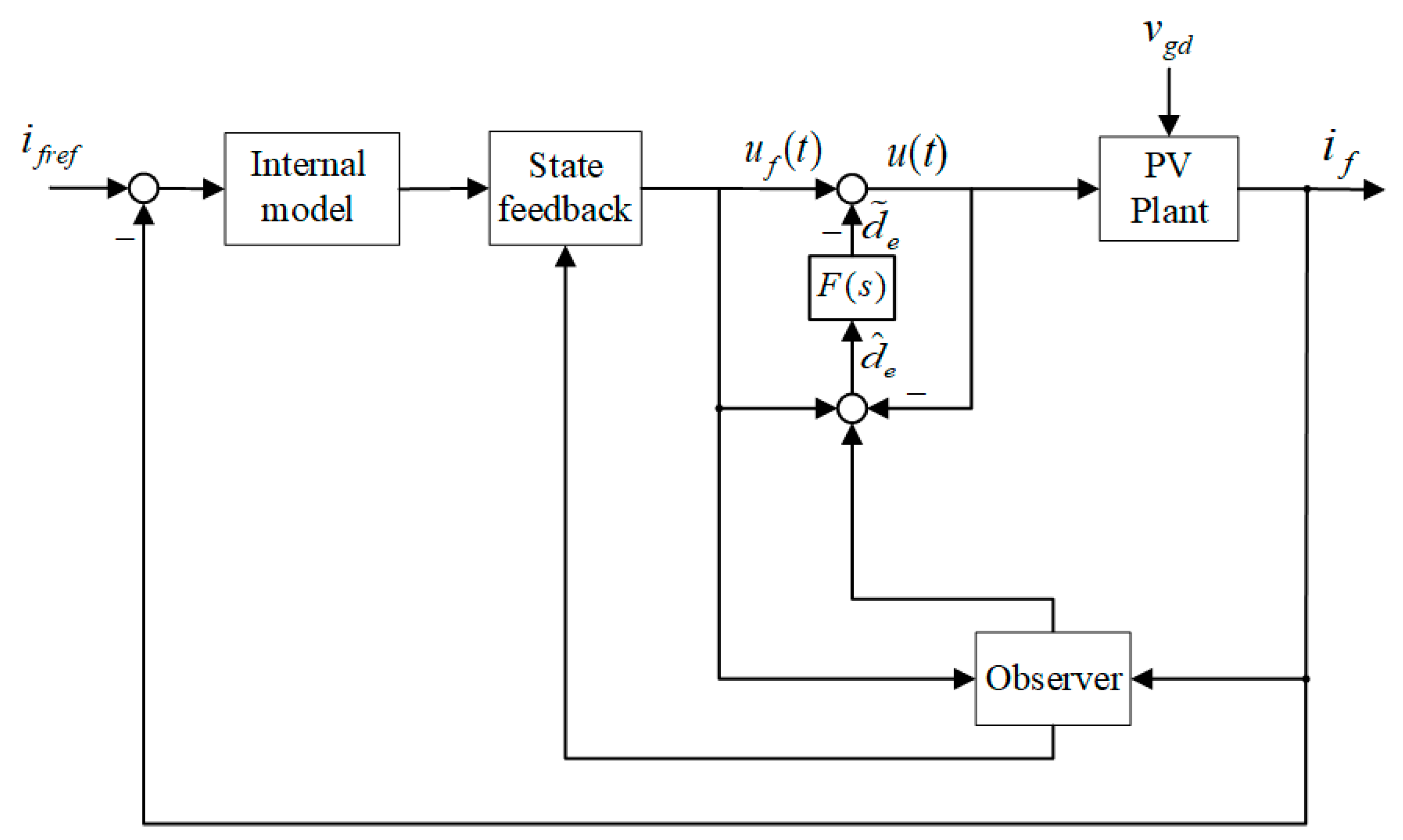
3.1. EID Method
3.2. System Stability
3.3. Double EID Control Strategy
4. Results and Discussion
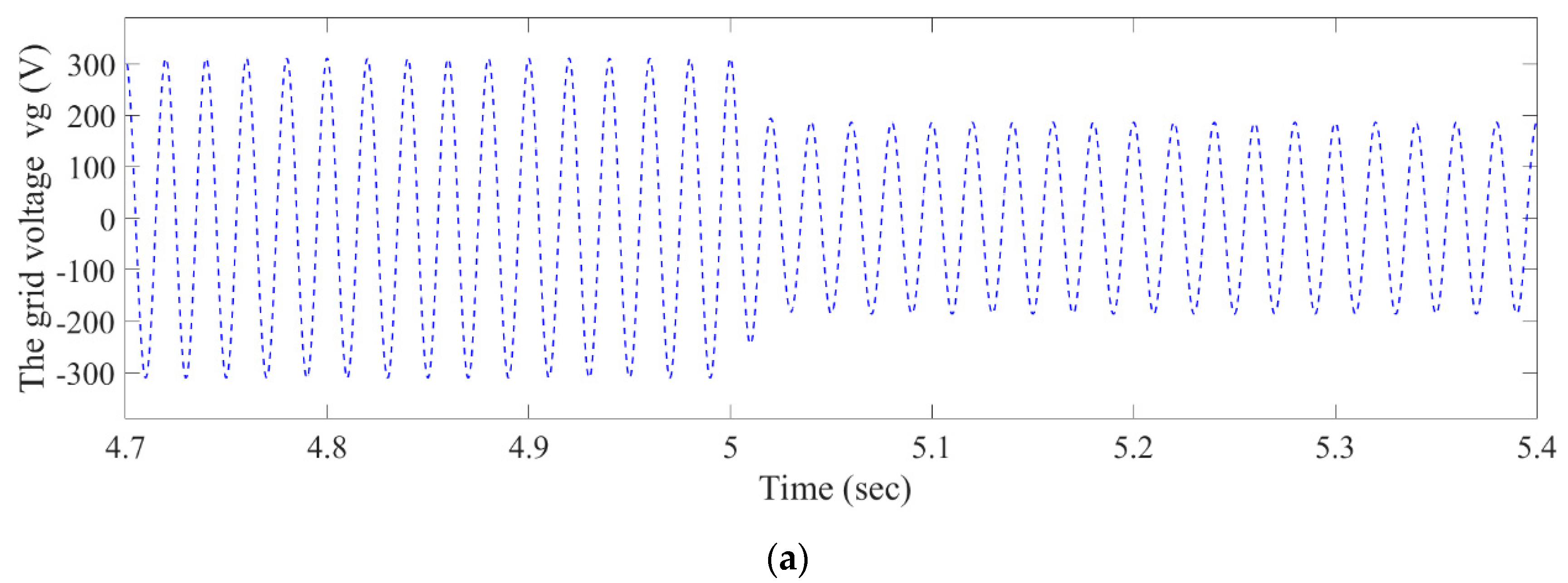
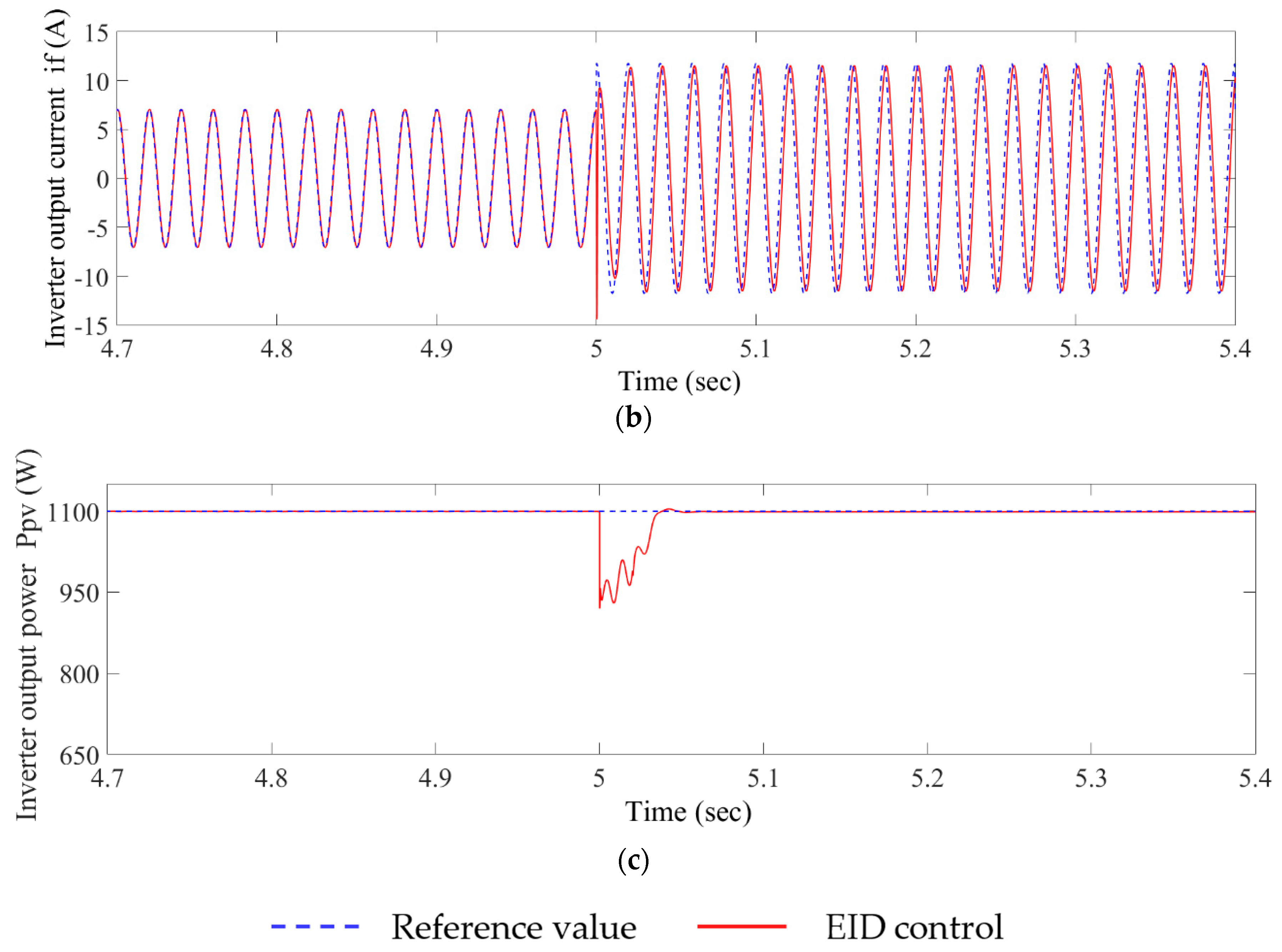
4.1. Output Power Response of PVG Subsystem with Grid Voltage Sag
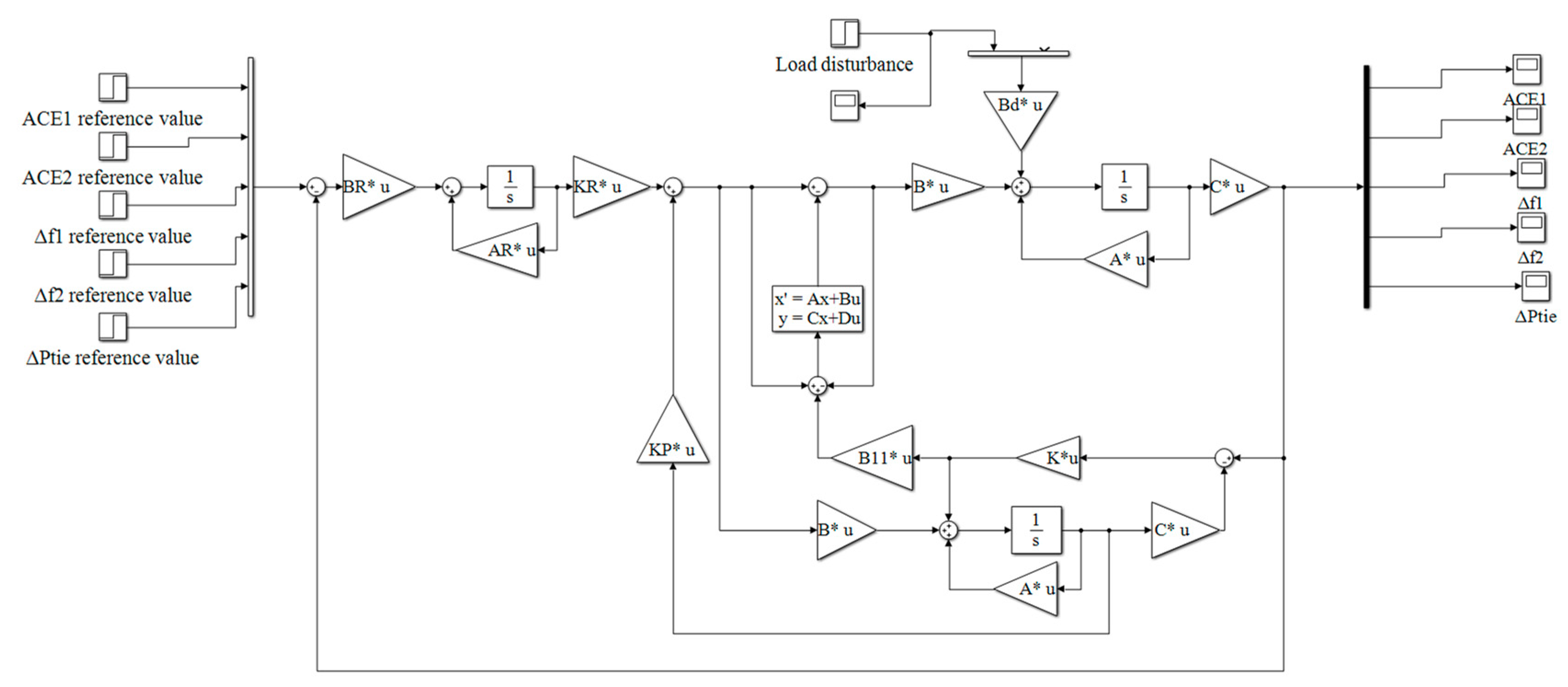
4.2. Load Frequency Response of Step Load Disturbances
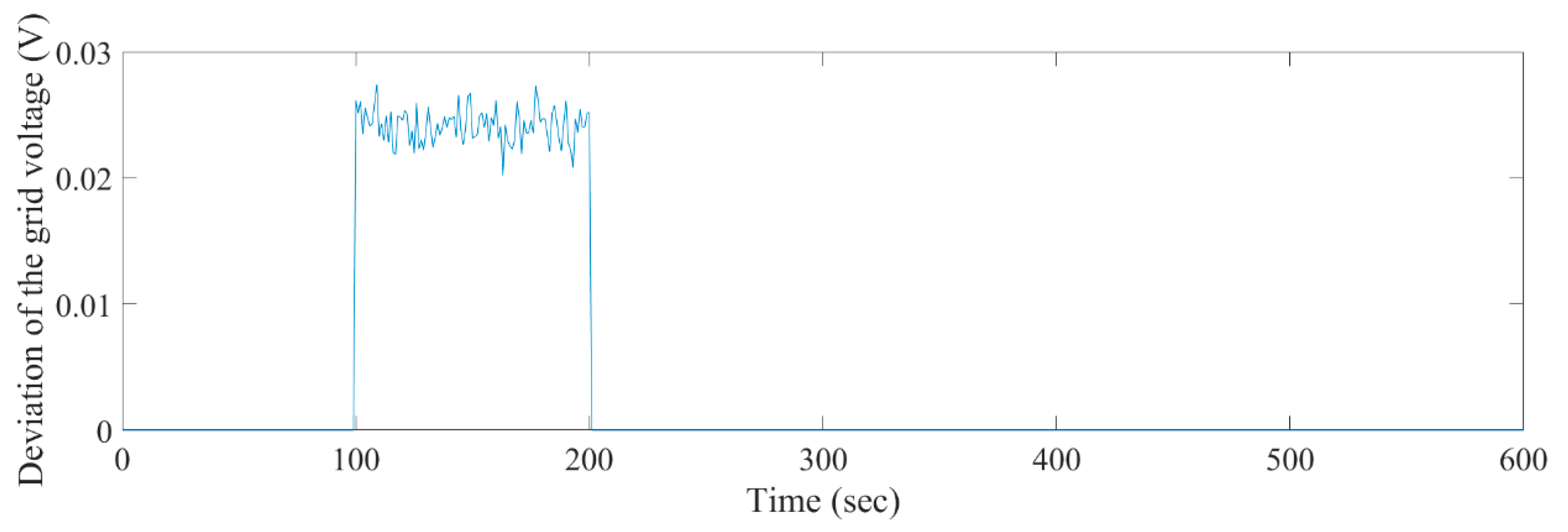
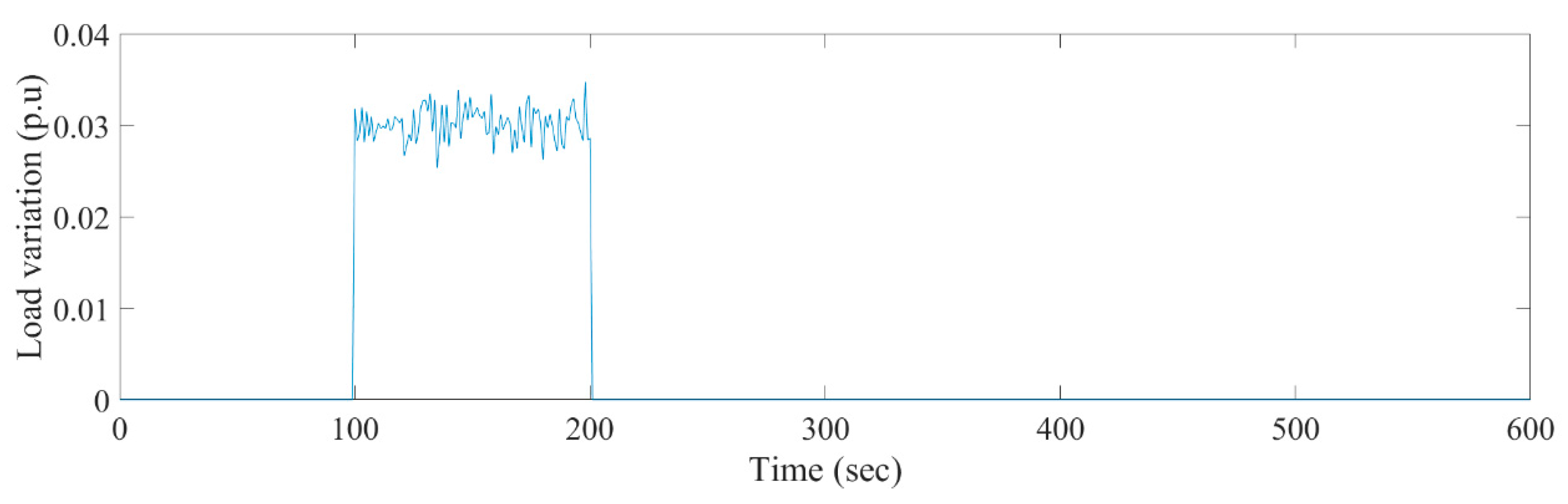
4.3. Load Frequency Response for Random Loads
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ∆Pri | Regulating power of AGC | p.u.MW |
| ∆Xgi | Governor position increment | p.u |
| ∆Pti | Output power deviation of traditional generator | p.u.MW |
| ∆Pbi | Output power deviation of ES subsystem | p.u.MW |
| ∆Ppvi | Output power fluctuation of PVG | p.u.MW |
| ∆Ploadi | Load disturbance | p.u.MW |
| ∆fi | Frequency deviation | Hz |
| ACEi | Area control error | p.u.MW |
| ∆Ptie | Power change of tie line | p.u.MW |
| Tgi | Time constant of governor | s |
| Tti | Time constant of traditional generator | s |
| Tbi | Time constant of ES subsystem | s |
| Kbi | The gain of ES subsystem | dB |
| Di | Load damping coefficient | p.u.MW/Hz |
| Mi | moment of inertia | s.p.u.MW/Hz |
| Ri | adjustment coefficient | Hz/p.u.MW |
Appendix A
| Parameter | Unit | Value |
|---|---|---|
| Tg1 | s | 0.3 |
| Tt1 | s | 0.1 |
| Tb1 | s | 0.12 |
| Kb1 | dB | 6 |
| D1 | s/Hz | 2.75 |
| M1 | s/Hz | 10.5 |
| R1 | Hz/p.u | 0.425 |
| β1 | p.u/Hz | 0.425 |
| Rf | Ω | 0.02 |
| Lf | H | 0.001 |
| Lg | H | 0.003 |
| Tg2 | s | 0.3 |
| Tt2 | s | 0.08 |
| Tb2 | s | 0.2 |
| Kb | dB | 5 |
| D2 | s/Hz | 12 |
| M2 | s/Hz | 2 |
| R2 | Hz/p.u | 0.6 |
| β2 | p.u/Hz | 0.6 |
| Ttie1-2 | s | 0.25 |
References
- Ma, M.; Liu, X.; Zhang, C. LFC for multi-area interconnected power system concerning wind turbines based on DMPC. IET Gener. Transm. Distrib. 2017, 11, 2689–2696. [Google Scholar] [CrossRef]
- You, S.; Kou, G.; Liu, Y. Impact of high PV penetration on the inter-area oscillations in the U.S. eastern interconnection. IEEE Access 2017, 5, 4361–4369. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, X.; Xue, F. Impacts of large scale and high voltage level photovoltaic penetration on the security and stability of power system. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 28–31 March 2010. [Google Scholar]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Impact of increased penetration of photovoltaic generation on power systems. IEEE Trans. Power Syst. 2013, 28, 893–901. [Google Scholar] [CrossRef]
- Tamimi, B.; Canizares, C.; Bhattacharya, K. System stability impact of large-scale and distributed solar photovoltaic generation: The case of Ontario, Canada. IEEE Trans. Sustain. Energy 2013, 4, 680–688. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, L.; Zhan, L.; Gracia, J.R.; King, T.J. Active power control of solar PV generation for large interconnection frequency regulation and oscillation damping. Int. J. Energy Res. 2016, 40, 353–361. [Google Scholar] [CrossRef]
- Eftekharnejad, S.; Vittal, V.; Heydt, G.T.; Keel, B.; Loehr, J. Small signal stability assessment of power systems with increased penetration of photovoltaic generation: A case study. IEEE Trans. Sustain. Energy 2013, 4, 960–967. [Google Scholar] [CrossRef]
- Quintero, J.; Vittal, V.; Heydt, G.T.; Zhang, H. The impact of increased penetration of converter control-based generators on power system modes of oscillation. IEEE Trans. Power Syst. 2014, 29, 2248–2256. [Google Scholar] [CrossRef]
- Abd-Elazim, S.M.; Ali, E.S. Load frequency controller design of a two-area system composing of PV grid and thermal generator via firefly algorithm. Neural Comput. Appl. 2018, 30, 607–616. [Google Scholar] [CrossRef]
- Sa-ngawong, N.; Ngamroo, I. Intelligent photovoltaic farms for robust frequency stabilization in multi-area interconnected power system based on PSO-based optimal Sugeno fuzzy logic control. Renew. Energy 2015, 74, 555–567. [Google Scholar] [CrossRef]
- Mi, Y.; Yang, F.; Li, D.; Wang, C.; Loh, P.C.; Wang, P. The sliding mode load frequency control for hybrid power system based on disturbance observer. Int. J. Electr. Power Energy Syst. 2016, 74, 446–452. [Google Scholar] [CrossRef]
- Zeng, G.; Xie, X.; Chen, M. An adaptive model predictive load frequency control method for multi-area interconnected power systems with photovoltaic generations. Energies 2017, 10, 1840. [Google Scholar] [CrossRef]
- Saxena, S.; Hote, Y.V. Decentralized PID load frequency control for perturbed multi-area power systems. Int. J. Electr. Power Energy Syst. 2016, 81, 405–415. [Google Scholar] [CrossRef]
- Ray, P.K.; Mohanty, S.R.; Kishor, N. Proportional–integral controller based small-signal analysis of hybrid distributed generation systems. Energy Conv. Manag. 2011, 52, 1943–1954. [Google Scholar] [CrossRef]
- Singh, V.P.; Kishor, N.; Samuel, P. Improved load frequency control of power system using LMI based PID approach. J. Frankl. Inst. Eng. Appl. Math. 2017, 354, 6805–6830. [Google Scholar] [CrossRef]
- Pandi, V.R.; Al-Hinai, A.; Feliachi, A. Coordinated control of distributed energy resources to support load frequency control. Energy Conv. Manag. 2015, 105, 918–928. [Google Scholar] [CrossRef]
- Ali, E.S.; Abd-Elazim, S.M. BFOA based design of PID controller for two area Load Frequency Control with nonlinearities. Int. J. Electr. Power Energy Syst. 2013, 51, 224–231. [Google Scholar] [CrossRef]
- Bendjedia, M.; Tehrani, K.A.; Azzouz, Y. Design of RST and fractional order PID controllers for an induction motor drive for electric vehicle application. In Proceedings of the 7th IET International Conference on Power Electronics, Machines and Drives, Manchester, UK, 8–10 April 2014. [Google Scholar]
- Kouba, N.E.; Menaa, M.; Hasni, M.; Tehrani, K.; Boudour, M. A novel optimized fuzzy-PID controller in two-area power system with HVDC link connection. In Proceedings of the International Conference on Control, Decision and Information Technologies (CoDIT), St. Paul’s Bay, Malta, 6–8 April 2016; pp. 204–209. [Google Scholar]
- Aziz, S.; Wang, H.; Liu, Y.; Peng, J.; Jiang, H. Variable universe fuzzy logic-based hybrid LFC control with real-time implementation. IEEE Access 2019, 7, 25535–25546. [Google Scholar] [CrossRef]
- Sudha, K.R.; Santhi, R.V. Load frequency control of an interconnected reheat thermal system using type-2 fuzzy system including SMES units. Int. J. Electr. Power Energy Syst. 2012, 43, 1383–1392. [Google Scholar] [CrossRef]
- Ghafouri, A.; Milimonfared, J.; Gharehpetian, G.B. Fuzzy-adaptive frequency control of power system including microgrids, wind farms, and conventional power plants. IEEE Syst. J. 2018, 12, 2772–2781. [Google Scholar] [CrossRef]
- Yousef, H.A.; AL-Kharusi, K.; Albadi, M.H.; Hosseinzadeh, N. Adaptive fuzzy logic load frequency control of multi-area power system. Int. J. Electr. Power Energy Syst. 2015, 68, 384–395. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T. Fuzzy control of distributed PV inverters/energy storage systems/electric vehicles for frequency regulation in a large power system. IEEE Trans. Smart Grid 2013, 4, 479–488. [Google Scholar] [CrossRef]
- Prasad, S.; Purwar, S.; Kishor, N. Load frequency regulation using observer based non-linear sliding mode control. Int. J. Electr. Power Energy Syst. 2019, 104, 178–193. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Decentralized sliding mode control of WG/PV/FC microgrids under unbalanced and nonlinear load conditions for on-and off-grid modes. IEEE Syst. J. 2018, 12, 3108–3119. [Google Scholar] [CrossRef]
- Kalla, U.K.; Singh, B.; Murthy, S.S.; Jain, C.; Kant, K. Adaptive sliding mode control of standalone single-phase microgrid using hydro, wind, and solar PV array-based generation. IEEE Trans. Smart Grid 2018, 9, 6806–6814. [Google Scholar] [CrossRef]
- Dhar, S.; Dash, P.K. A new backstepping finite time sliding mode control of grid connected PV system using multivariable dynamic VSC model. Int. J. Electr. Power Energy Syst. 2016, 82, 314–330. [Google Scholar] [CrossRef]
- Mi, Y.; He, X.; Hao, X.; Li, Z. Frequency control strategy of multi-area hybrid power system based on frequency division and sliding mode algorithm. IET Gener. Transm. Distrib. 2019, 13, 1145–1152. [Google Scholar] [CrossRef]
- Wang, C.; Mi, Y.; Fu, Y.; Wang, P. Frequency control of an isolated micro-grid using double sliding mode controllers and disturbance observer. IEEE Trans. Smart Grid 2016, 9, 923–930. [Google Scholar] [CrossRef]
- Ma, M.; Chen, H.; Liu, X. Distributed model predictive load frequency control of multi-area interconnected power system. Int. J. Electr. Power Energy Syst. 2014, 62, 289–298. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Bevrani, H.; Hassan, A.A.; Hiyama, T. Decentralized model predictive based load frequency control in an interconnected power system. Energy Convers. Manag. 2011, 52, 1208–1214. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Lee, K.Y. Coordinated distributed MPC for load frequency control of power system with wind farms. IEEE Trans. Ind. Electron. 2017, 64, 5140–5150. [Google Scholar] [CrossRef]
- Ersdal, A.M.; Imsland, L.; Uhlen, K. Model predictive load-frequency control. IEEE Trans. Power Syst. 2016, 31, 777–785. [Google Scholar] [CrossRef]
- Sun, X.; Liao, K.; Yang, J.; He, Z. Model predictive control based load frequency control for power systems with wind turbine generators. In Proceedings of the IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 18 November 2019; pp. 1387–1392. [Google Scholar]
- Banis, F.; Guericke, D.; Madsen, H.; Poulsen, N.K. Load frequency control in microgrids using target-adjusted MPC. IET Renew. Power Gener. 2020, 14, 118–124. [Google Scholar] [CrossRef]
- She, J.; Xin, X.; Ohyama, Y. Estimation of equivalent input disturbance improves vehicular steering control. IEEE Trans. Veh. Technol. 2007, 56, 3722–3731. [Google Scholar] [CrossRef]
- Liu, F.; Ma, J. Equivalent input disturbance-based robust LFC strategy for power system with wind farms. IET Gener. Transm. Distrib. 2018, 12, 4582–4588. [Google Scholar] [CrossRef]
- Sun, Y.; Ulsoy, A.G.; Nelson, P.W. Design of observer-based feedback control for time-delay systems with application to automotive powertrain control. J. Frankl. Inst. 2010, 347, 358–376. [Google Scholar]
- She, J.; Fang, M.; Ohyama, Y.; Hashimoto, H.; Wu, M. Improving disturbance-rejection performance based on an equivalent-input- disturbance approach. IEEE Trans. Ind. Electron. 2008, 55, 380–389. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.P.; El Saddik, A. Load frequency control for wide area monitoring and control system (WAMC) in power system with open communication links. In Proceedings of the Power Engineering and Automation Conference (PEAM), Wuhan, China, 18–20 September 2012. [Google Scholar]
- Vafamand, N.; Khooban, M.H.; Dragičević, T.; Boudjadar, J.; Asemani, M.H. Time-delayed stabilizing secondary load frequency control of shipboard microgrids. IEEE Syst. J. 2019, 13, 3233–3241. [Google Scholar] [CrossRef]
- Ahmadi, A.; Aldeen, M. An LMI approach to the design of robust delay-dependent overlapping load frequency control of uncertain power systems. Int. J. Electr. Power Energy Syst. 2016, 81, 48–63. [Google Scholar] [CrossRef]

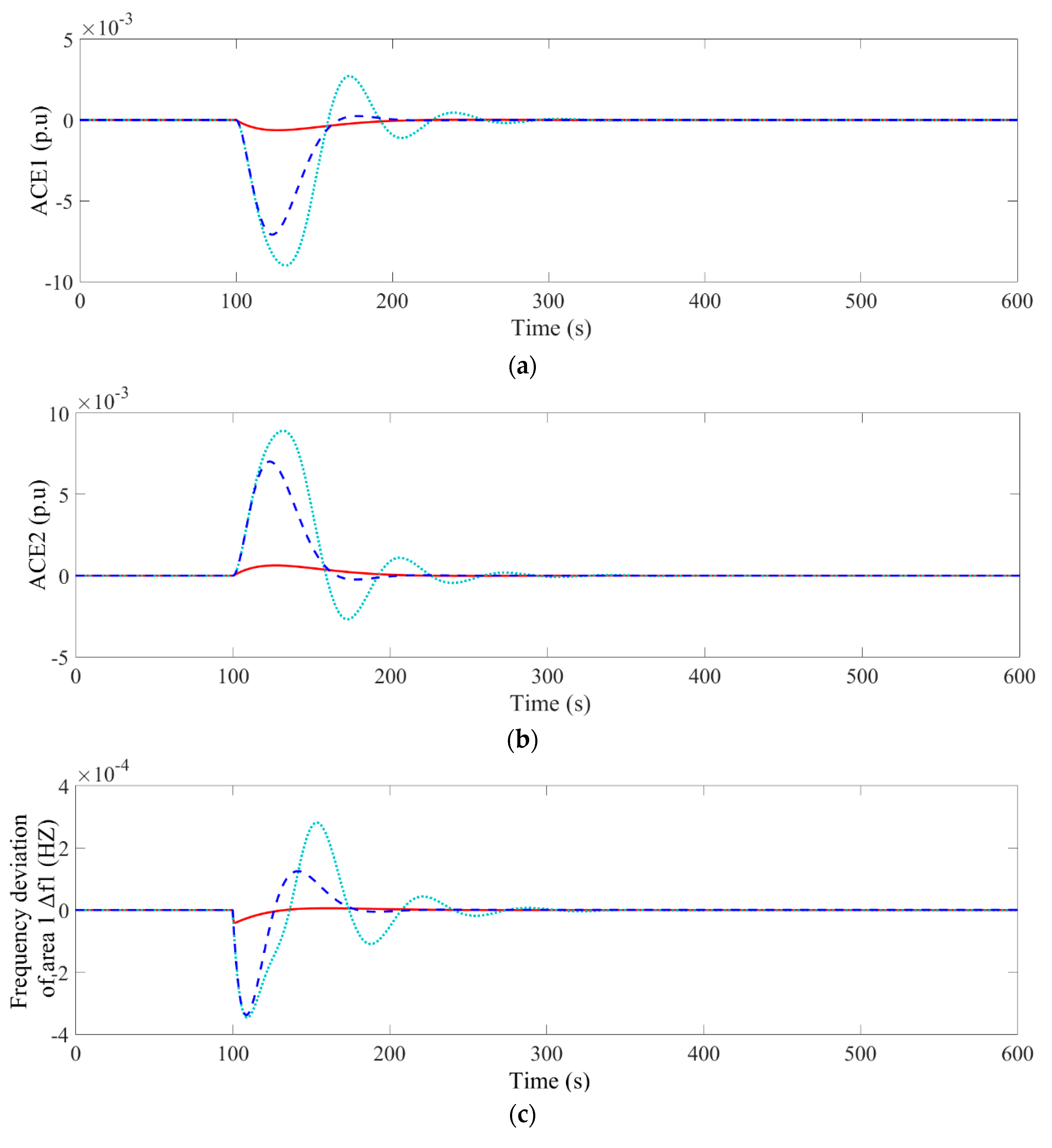
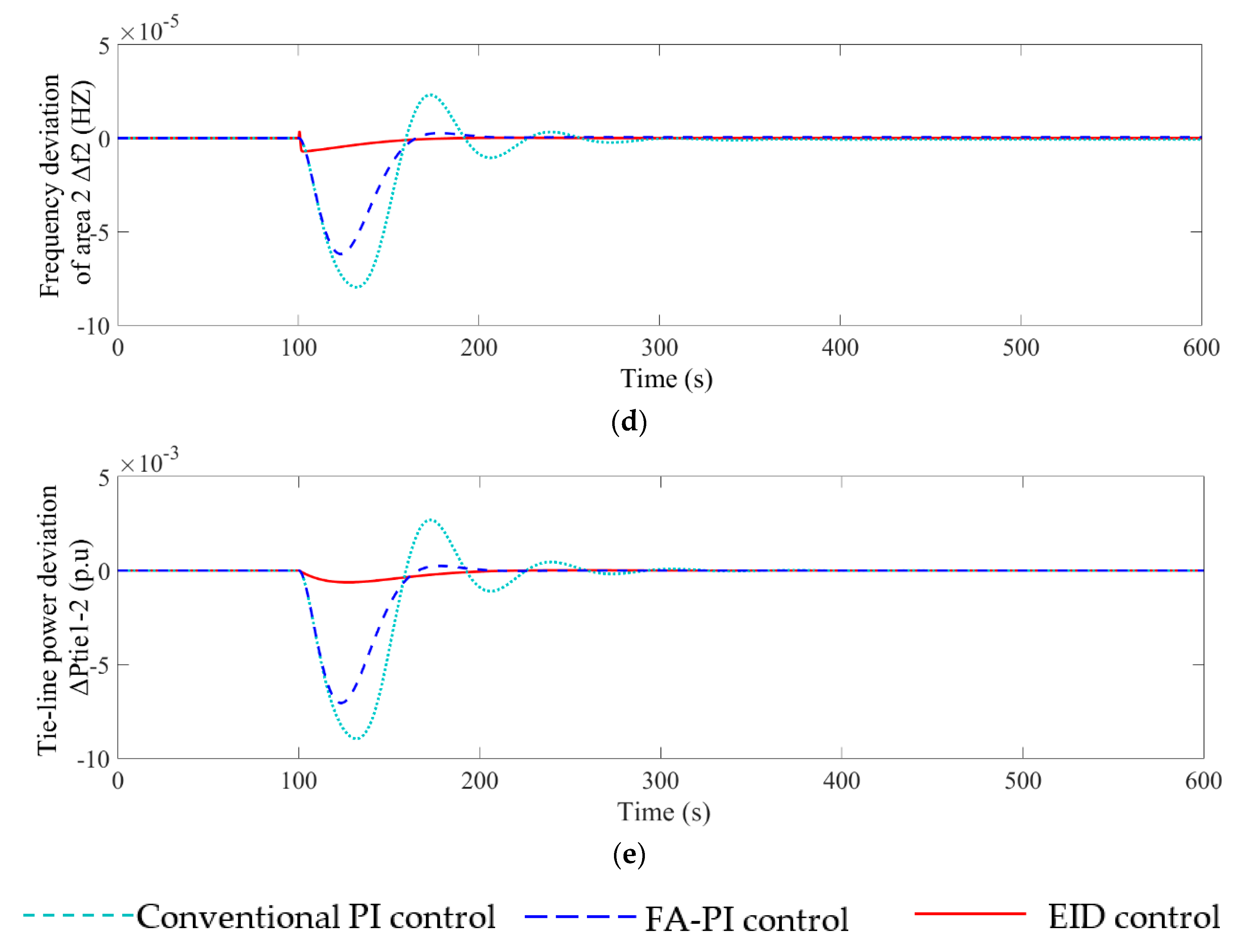
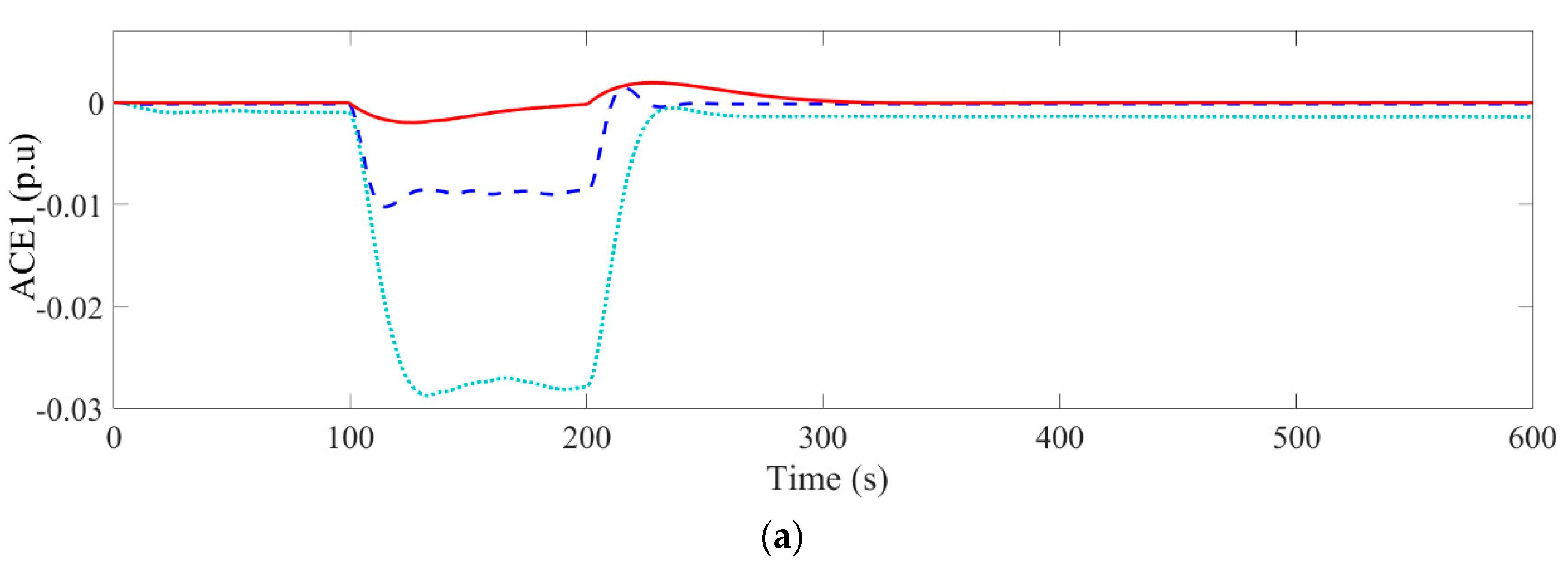
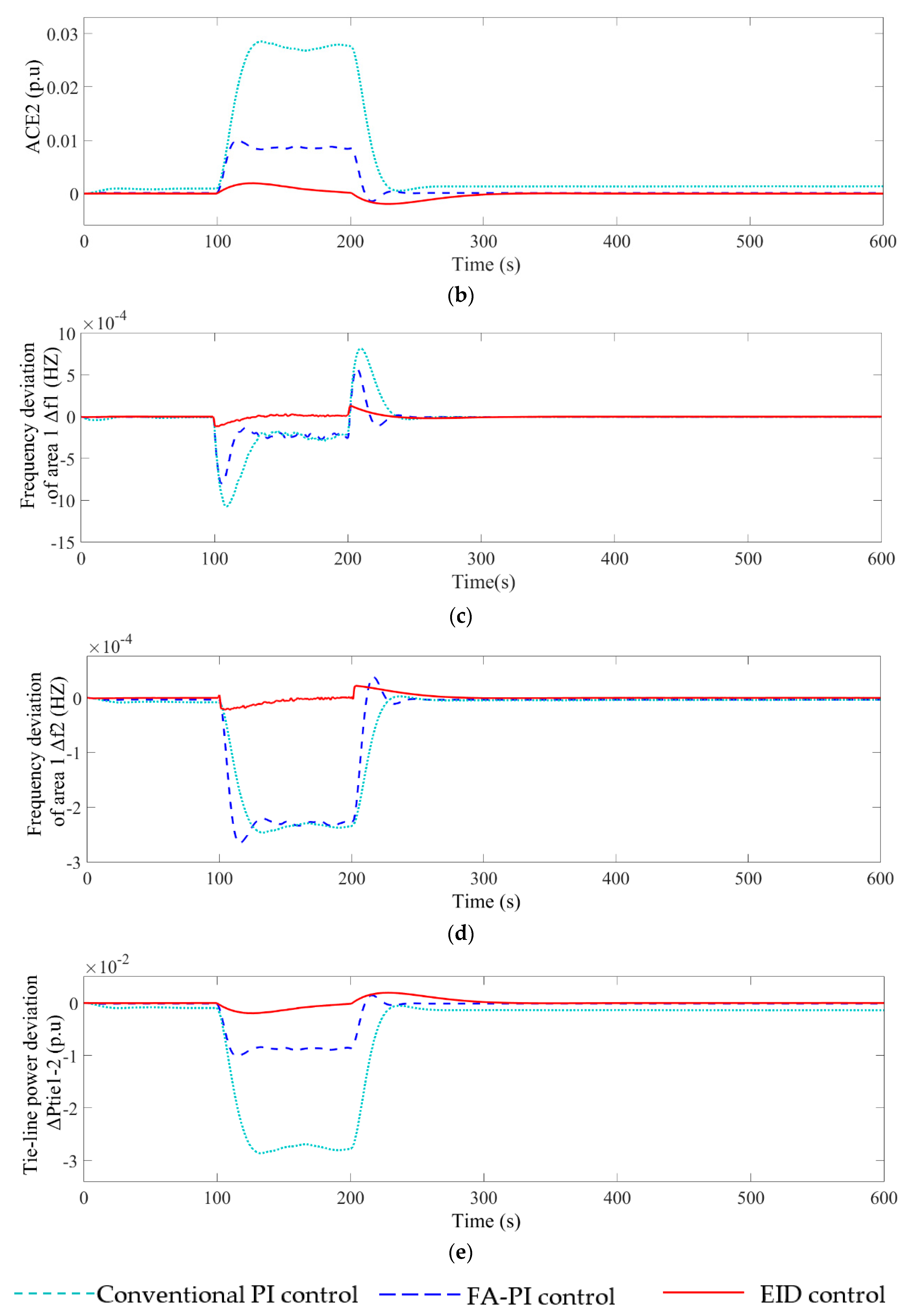
| Method | IAE | ITAE | ISE | ITSE |
|---|---|---|---|---|
| Conventional PI | 0.4433 | 64.73 | 0.002471 | 0.3299 |
| FA-PI [9] | 0.2517 | 32.64 | 0.001225 | 0.1543 |
| Double EID | 0.03876 | 5.556 | 1.699·10−5 | 0.002297 |
| Method | IAE | ITAE | ISE | ITSE |
|---|---|---|---|---|
| Conventional PI | 3.102 | 564.6 | 0.06907 | 11.23 |
| FA-PI [9] | 1.017 | 168 | 0.007695 | 1.189 |
| EID | 0.3011 | 53.1 | 0.0006325 | 0.1019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, M.; Wang, C.; Hu, Y.; Liu, Z.; Yan, C.; He, S. Load Frequency Control of Photovoltaic Generation-Integrated Multi-Area Interconnected Power Systems Based on Double Equivalent-Input-Disturbance Controllers. Energies 2020, 13, 6103. https://doi.org/10.3390/en13226103
Yang M, Wang C, Hu Y, Liu Z, Yan C, He S. Load Frequency Control of Photovoltaic Generation-Integrated Multi-Area Interconnected Power Systems Based on Double Equivalent-Input-Disturbance Controllers. Energies. 2020; 13(22):6103. https://doi.org/10.3390/en13226103
Chicago/Turabian StyleYang, Minghui, Chunsheng Wang, Yukun Hu, Zijian Liu, Caixin Yan, and Shuhang He. 2020. "Load Frequency Control of Photovoltaic Generation-Integrated Multi-Area Interconnected Power Systems Based on Double Equivalent-Input-Disturbance Controllers" Energies 13, no. 22: 6103. https://doi.org/10.3390/en13226103
APA StyleYang, M., Wang, C., Hu, Y., Liu, Z., Yan, C., & He, S. (2020). Load Frequency Control of Photovoltaic Generation-Integrated Multi-Area Interconnected Power Systems Based on Double Equivalent-Input-Disturbance Controllers. Energies, 13(22), 6103. https://doi.org/10.3390/en13226103






