An Operational Approach to Multi-Objective Optimization for Volt-VAr Control
Abstract
1. Introduction
- A general framework for formulating multi-objective Volt-VAr Optimization problems is proposed. Such a model has not been proposed before. The manner in which previous work on VVC–MOO can be expressed in terms of this framework is shown.
- More importantly, the application of simple techniques for MOO on VVC problems is investigated, and the operational interpretation of each of these techniques is discussed. This discussion of operational interpretation is novel to this field and is missing from previous work on VVC–MOO. This discussion, especially when the operational interpretation is intuitive, may lead to the faster adoption of these techniques.
2. Materials and Methods
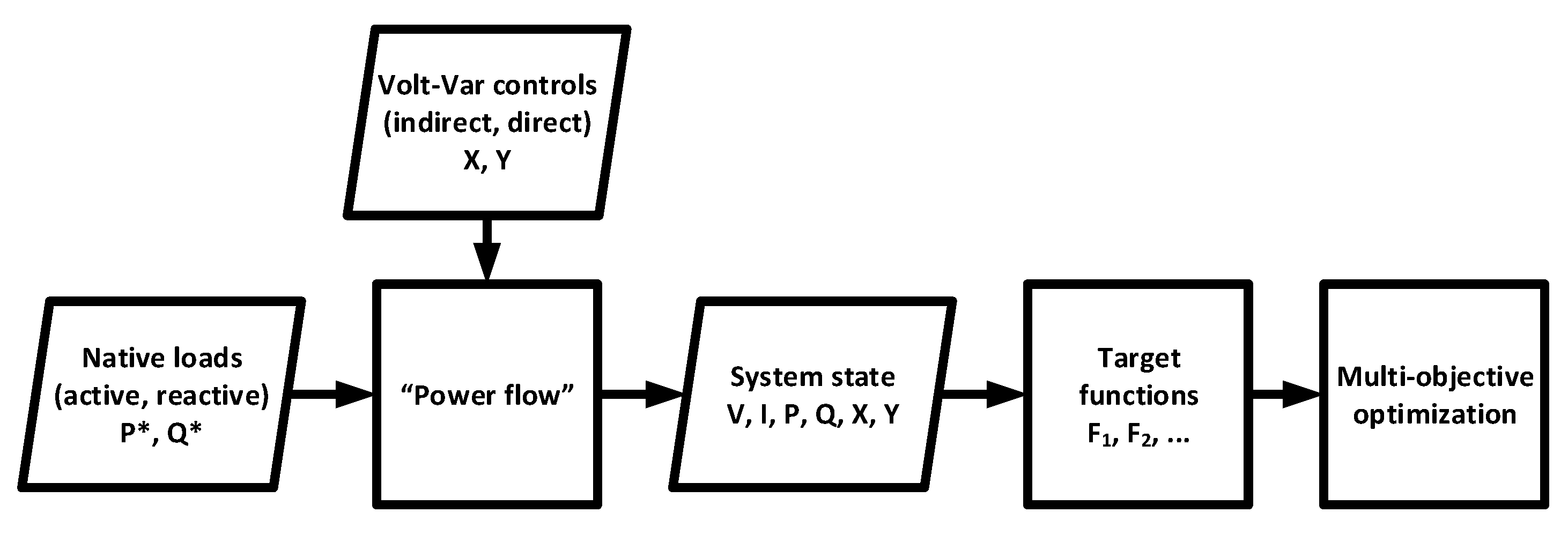
2.1. General Multi-Objective Volt-VAr Optimization
2.1.1. The General VVO Problem
2.1.2. Example Target Functions
- Target voltage and Conservation Voltage Reduction (CVR): For nominal voltages , the deviation function is the sum of differences, under some norm function :Specifically, for CVR , where is a regulatory set minimum voltage.
- Feeder voltage deviation: This can be seen as a variant of target voltage. To express this function, a re-indexing is used, such that is the voltage at element n of feeder m. The index is used to represent the feeder head. The voltage deviation is defined as . Typically (see e.g., [30]), the maximum deviation in each feeder is maximized:
- Root power factor: Typically, the power factor is important at the root of the network; that is, the point where the network is fed. Using the index 1 for that node, the power factor at the root of the network can be written as
- Root active power: The root active power is the total power the network consumes. It is simple to express it as
- Root reactive power: In a similar way, the root reactive power is
- Cost of controls: In the most generic way, the cost of control can be expressed aswhere h is a generic function deriving the cost of controls from the control vectors , . As a simple example, we can consider photo-voltaic generation curtailment. In that case, is the amount of generation curtailed by the installation a, and a simple target function may be used to minimize the total curtailment:
2.1.3. Time and Scenario Based Optimization
2.1.4. The Multi-Objective VVO Problem
2.2. Techniques for Multi-Objective Optimization
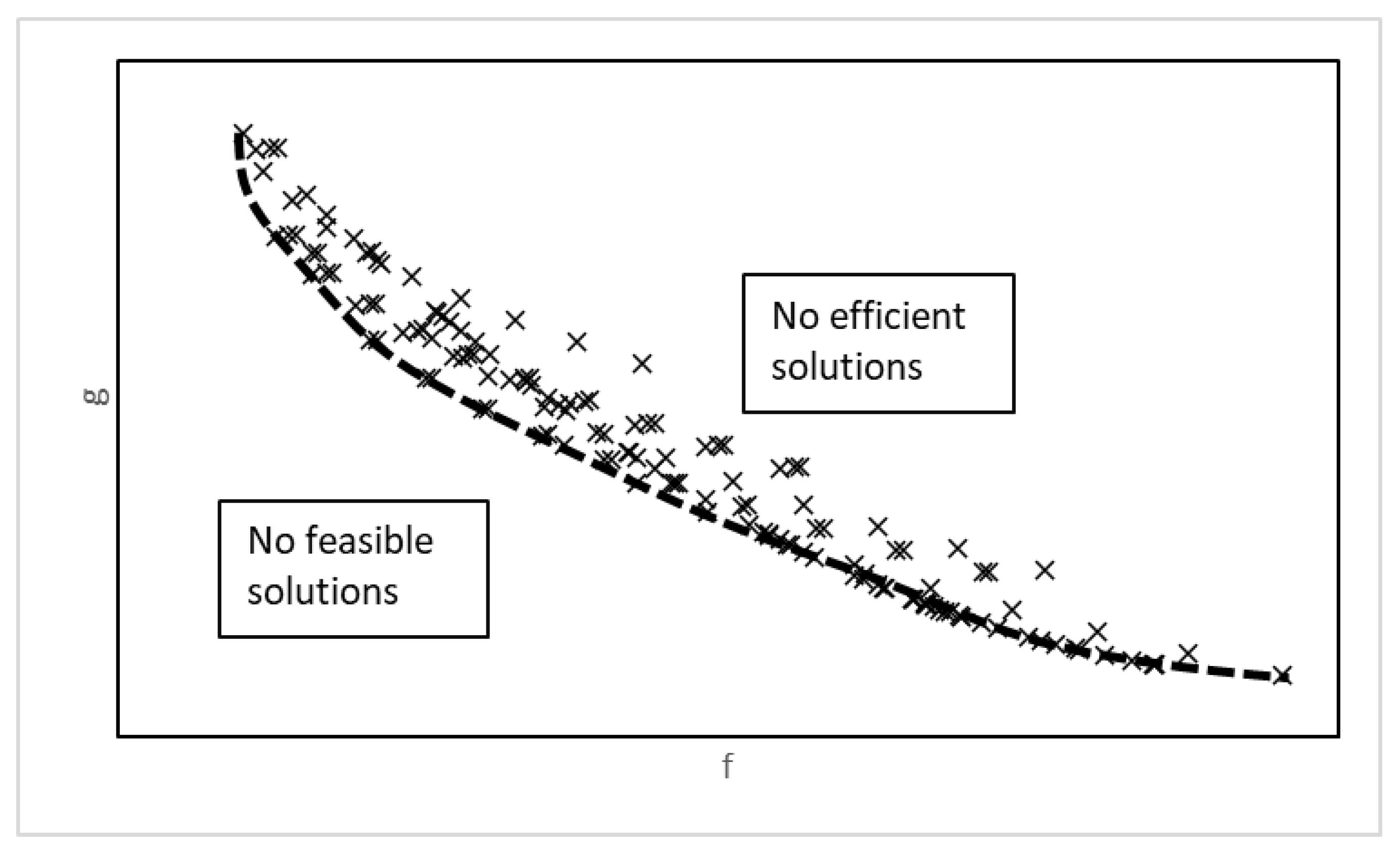
2.2.1. The Weighted-Sum Technique and the Efficient Curve
2.2.2. The E-Constraint Technique
3. Simulation Results
3.1. The Test Feeder
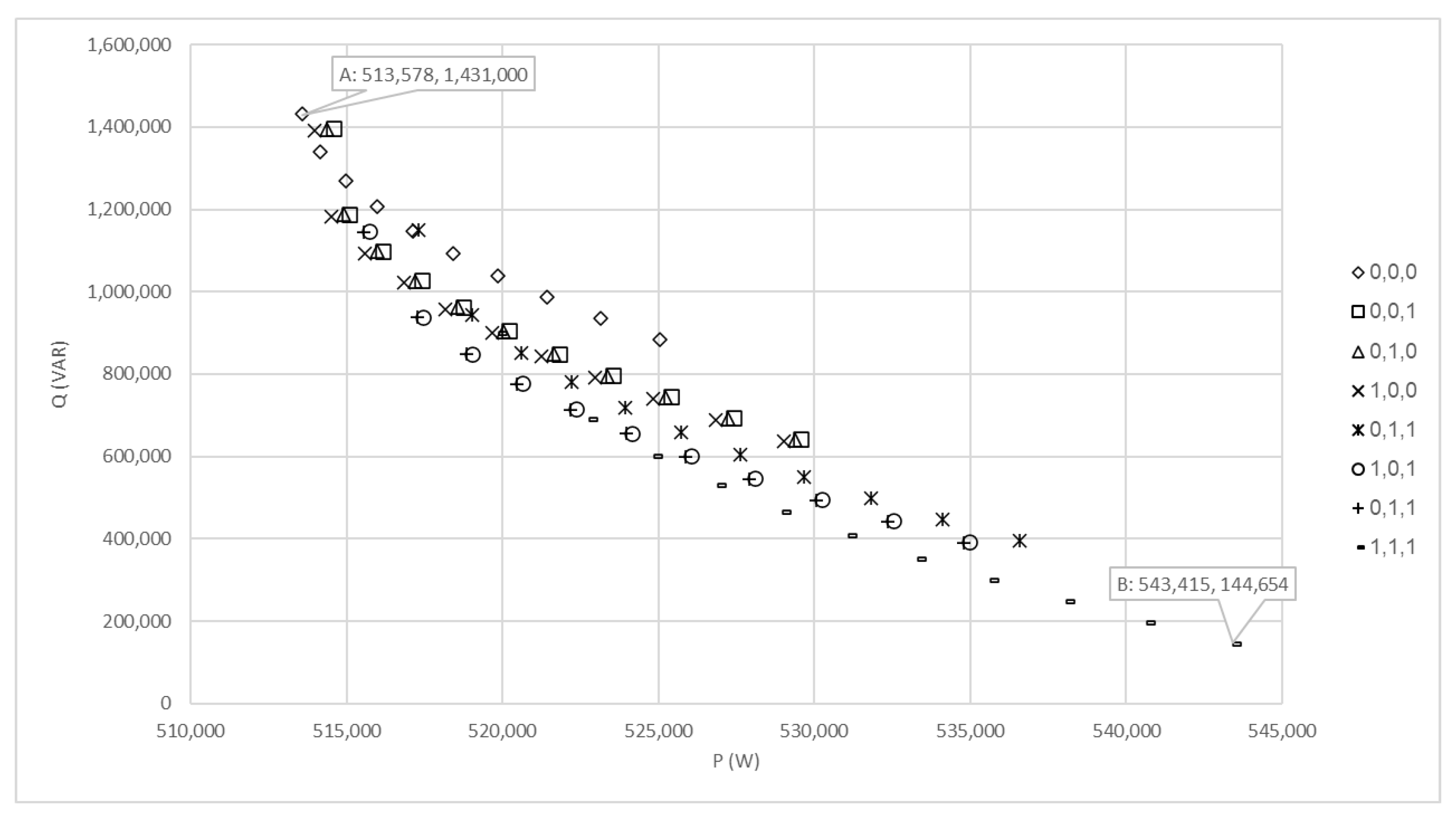
3.2. Applying the Weighted-Sum Technique for Active and Reactive Power Optimization
3.3. Applying the E-Constraint Technique for Active and Reactive Power Optimization
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Masetti, C. Revision of European Standard EN 50160 on power quality: Reasons and solutions. In Proceedings of the 14th International Conference on Harmonics and Quality of Power—ICHQP 2010, Bergamo, Italy, 26–29 September 2010; pp. 1–7. [Google Scholar]
- Yang, Y.; Enjeti, P.; Blaabjerg, F.; Wang, H. Wide-Scale Adoption of Photovoltaic Energy: Grid Code Modifications Are Explored in the Distribution Grid. IEEE Ind. Appl. Mag. 2015, 21, 21–31. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.; Lauby, M. Power System Stability and Control; EPRI Power System Engineering Series; McGraw-Hill Education: New York, NY, USA, 1994. [Google Scholar]
- Hashim, T.T.; Mohamed, A.; Shareef, H. A review on voltage control methods for active distribution networks. Prz. Elektrotechniczny (Electr. Rev.) 2012, 88, 304–312. [Google Scholar]
- Carvallo, A.; Cooper, J. The Advanced Smart Grid: Edge Power Driving Sustainability; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Borozan, V.; Baran, M.E.; Novosel, D. Integrated Volt/VAr control in distribution systems. In Proceedings of the 2001 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No.01CH37194). Columbus, OH, USA, 28 January–1 February 2001; Volume 3, pp. 1485–1490. [Google Scholar]
- Liu, Y.; Zhang, P.; Qiu, X. Optimal volt/var control in distribution systems. Int. J. Electr. Power Energy Syst. 2002, 24, 271–276. [Google Scholar] [CrossRef]
- Niknam, T.; Nayeripour, M.; Olamaei, J.; Arefi, A. An efficient hybrid evolutionary optimization algorithm for daily Volt/Var control at distribution system including DGs. Int. Rev. Electr. Eng. 2008, 3, 513–524. [Google Scholar]
- Tomin, N.; Kurbatsky, V.; Panasetsky, D.; Sidorov, D.; Zhukov, A. Voltage/VAR Control and Optimization: AI approach. IFAC-PapersOnLine 2018, 51, 103–108. [Google Scholar] [CrossRef]
- Ma, H.M.; Man, K.F.; Hill, D.J. Control strategy for multi-objective coordinate voltage control using hierarchical genetic algorithms. In Proceedings of the 2005 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 158–163. [Google Scholar]
- Lemos, F.A.; Feijó, W.L., Jr.; Werberich, L.C.; Rosa, M. Assessment of a sub-transmission and distribution system under coordinated secondary voltage control. In Proceedings of the 14th PSCC-Power System Computational Conference, Seville, Spain, 24–28 June 2002. [Google Scholar]
- Kim, G.W.; Lee, K.Y. Coordination control of ULTC transformer and STATCOM based on an artificial neural network. IEEE Trans. Power Syst. 2005, 20, 580–586. [Google Scholar] [CrossRef]
- Le, A.D.; Muttaqi, K.M.; Negnevitsky, M.; Ledwich, G. Response coordination of distributed generation and tap changers for voltage support. In Proceedings of the 2007 Australasian Universities Power Engineering Conference, Perth, WA, Australia, 9–12 December 2007; pp. 1–7. [Google Scholar]
- Arshad, A.; Lehtonen, M. Multi-agent system based distributed voltage control in medium voltage distribution systems. In Proceedings of the 2016 17th International Scientific Conference on Electric Power Engineering (EPE), Prague, Czech Republic, 16–18 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Raz, D.; Daliot, A. Generalized approach for Volt-VAr-Control through integration of DERs with traditional methods. Grid Future Symp. 2018, 2018, article 55. [Google Scholar]
- Geoffrion, A.M. Solving bicriterion mathematical programs. Oper. Res. 1967, 15, 39–54. [Google Scholar] [CrossRef]
- Gandibleux, X. Multiple Criteria Optimization: State of the Art Annotated Bibliographic Surveys; International Series in Operations Research & Management Science; Springer Science & Business Media: Boston, MA, USA, 2006; Volume 52. [Google Scholar]
- Deb, K. Multi-objective optimization. In Search Methodologies; Springer: Boston, MA, USA, 2014; pp. 403–449. [Google Scholar]
- Jones, D.; Mirrazavi, S.; Tamiz, M. Multi-objective meta-heuristics: An overview of the current state-of-the-art. Eur. J. Oper. Res. 2002, 137, 1–9. [Google Scholar] [CrossRef]
- Coello Coello, C.A. Evolutionary multi-objective optimization: A historical view of the field. IEEE Comput. Intell. Mag. 2006, 1, 28–36. [Google Scholar] [CrossRef]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Miguel Antonio, L.; Coello Coello, C.A. Coevolutionary Multiobjective Evolutionary Algorithms: Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2018, 22, 851–865. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Liu, H.; Guo, Z. Multi-objective metaheuristics for discrete optimization problems: A review of the state-of-the-art. Appl. Soft Comput. 2020, 93, 106382. [Google Scholar] [CrossRef]
- Zeleny, M. Linear Multiobjective Programming; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/Heidelberg, Germany, 1974; Volume 95. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Chichester, NY, USA, 2001; Volume 16. [Google Scholar]
- Antunes, C.H.; Alves, M.J.; Climaco, J. Multiobjective Linear and Integer Programming; Springer: Boston, MA, USA, 2016. [Google Scholar]
- Alarcon-Rodriguez, A.; Ault, G.; Galloway, S. Multi-objective planning of distributed energy resources: A review of the state-of-the-art. Renew. Sustain. Energy Rev. 2010, 14, 1353–1366. [Google Scholar] [CrossRef]
- Fadaee, M.; Radzi, M. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: A review. Renew. Sustain. Energy Rev. 2012, 16, 3364–3369. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for Control of Reactive Power by Distributed Photovoltaic Generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Chen, B.; Begovic, M.M.; He, Y. MPC-Based Voltage/Var Optimization for Distribution Circuits With Distributed Generators and Exponential Load Models. IEEE Trans. Smart Grid 2014, 5, 2412–2420. [Google Scholar] [CrossRef]
- Niknam, T.; Zare, M.; Aghaei, J. Scenario-Based Multiobjective Volt/Var Control in Distribution Networks Including Renewable Energy Sources. IEEE Trans. Power Deliv. 2012, 27, 2004–2019. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, Z.; Xu, Y. Multi-Objective Robust Voltage/VAR Control for Active Distribution Networks. In Proceedings of the 2019 IEEE Power Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; pp. 1–5. [Google Scholar]
- Hou, J.; Xu, Y.; Liu, J.; Xin, L.; Wei, W. A multi-objective volt-var control strategy for distribution networks with high PV penetration. In Proceedings of the 10th International Conference on Advances in Power System Control, Operation Management (APSCOM 2015), Hong Kong, China, 8–12 November 2015; pp. 1–6. [Google Scholar]
- Auchariyamet, S.; Sirisumrannukul, S. Volt/VAr control in distribution systems by fuzzy multiobjective and particle swarm. In Proceedings of the 2009 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Pattaya, Chonburi, Thailand, 6–9 May 2009; Volume 1, pp. 234–237. [Google Scholar] [CrossRef]
- Castro, J.R.; Saad, M.; Lefebvre, S.; Asber, D.; Lenoir, L. Coordinated voltage control in distribution network with the presence of DGs and variable loads using pareto and fuzzy logic. Energies 2016, 9, 107. [Google Scholar] [CrossRef]
- Saravanakathir, B.; Sasiraja, R. Optimal Coordinated Voltage Control Method for Distribution Network in Presence of Distributed Generators. Int. J. Eng. Sci 2017, 7, 12117–12122. [Google Scholar]
- Zare, M.; Niknam, T.; Azizipanah-Abarghooee, R.; Amiri, B. Multi-objective probabilistic reactive power and voltage control with wind site correlations. Energy 2014, 66, 810–822. [Google Scholar] [CrossRef]
- Wang, P.; Deng, X.; Zhou, H.; Yu, S. Estimates of the social cost of carbon: A review based on meta-analysis. J. Clean. Prod. 2019, 209, 1494–1507. [Google Scholar] [CrossRef]
- Blasco, X.; Herrero, J.M.; Sanchis, J.; Martínez, M. A new graphical visualization of n-dimensional Pareto front for decision-making in multiobjective optimization. Inf. Sci. 2008, 178, 3908–3924. [Google Scholar] [CrossRef]
- Cela, R.; Bollaín, M. New cluster mapping tools for the graphical assessment of non-dominated solutions in multi-objective optimization. Chemom. Intell. Lab. Syst. 2012, 114, 72–86. [Google Scholar] [CrossRef]
- de Freitas, A.R.; Fleming, P.J.; Guimarães, F.G. Aggregation trees for visualization and dimension reduction in many-objective optimization. Inf. Sci. 2015, 298, 288–314. [Google Scholar] [CrossRef]
- Tušar, T.; Filipič, B. Visualization of Pareto front approximations in evolutionary multiobjective optimization: A critical review and the prosection method. IEEE Trans. Evol. Comput. 2014, 19, 225–245. [Google Scholar] [CrossRef]
- Reynoso-Meza, G.; Blasco, X.; Sanchis, J.; Herrero, J.M. Comparison of design concepts in multi-criteria decision-making using level diagrams. Inf. Sci. 2013, 221, 124–141. [Google Scholar] [CrossRef]
- Das, D.; Kothari, D.; Kalam, A. Simple and efficient method for load flow solution of radial distribution networks. Int. J. Electr. Power Energy Syst. 1995, 17, 335–346. [Google Scholar] [CrossRef]
- Chassin, D.P.; Schneider, K.; Gerkensmeyer, C. GridLAB-D: An open-source power systems modeling and simulation environment. In Proceedings of the 2008 IEEE/PES Transmission and Distribution Conference and Exposition, Bogota, CO, USA, 13–15 August 2008; pp. 1–5. [Google Scholar]



| Impedance of Line Ending at Bus | |||
|---|---|---|---|
| Bus # | Load | R () | X () |
| 1 | Slack bus, | ||
| 2 | 1.35309 | 1.32349 | |
| 3 | 1.17024 | 1.14464 | |
| 4 | 0.84111 | 0.82271 | |
| 5 | 1.52348 | 1.02760 | |
| 6 | 2.55727 | 1.72490 | |
| 7 | 1.08820 | 0.73400 | |
| 8 | 1.25143 | 0.84410 | |
| 9 | 2.01317 | 1.35790 | |
| 10 | 1.68671 | 1.13770 | |
| 11 | 1.79553 | 1.21110 | |
| 12 | 2.44845 | 1.65150 | |
| 13 | 2.01317 | 1.35790 | |
| 14 | 2.23081 | 1.50470 | |
| 15 | 1.19702 | 0.80740 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raz, D.; Beck, Y. An Operational Approach to Multi-Objective Optimization for Volt-VAr Control. Energies 2020, 13, 5871. https://doi.org/10.3390/en13225871
Raz D, Beck Y. An Operational Approach to Multi-Objective Optimization for Volt-VAr Control. Energies. 2020; 13(22):5871. https://doi.org/10.3390/en13225871
Chicago/Turabian StyleRaz, David, and Yuval Beck. 2020. "An Operational Approach to Multi-Objective Optimization for Volt-VAr Control" Energies 13, no. 22: 5871. https://doi.org/10.3390/en13225871
APA StyleRaz, D., & Beck, Y. (2020). An Operational Approach to Multi-Objective Optimization for Volt-VAr Control. Energies, 13(22), 5871. https://doi.org/10.3390/en13225871






