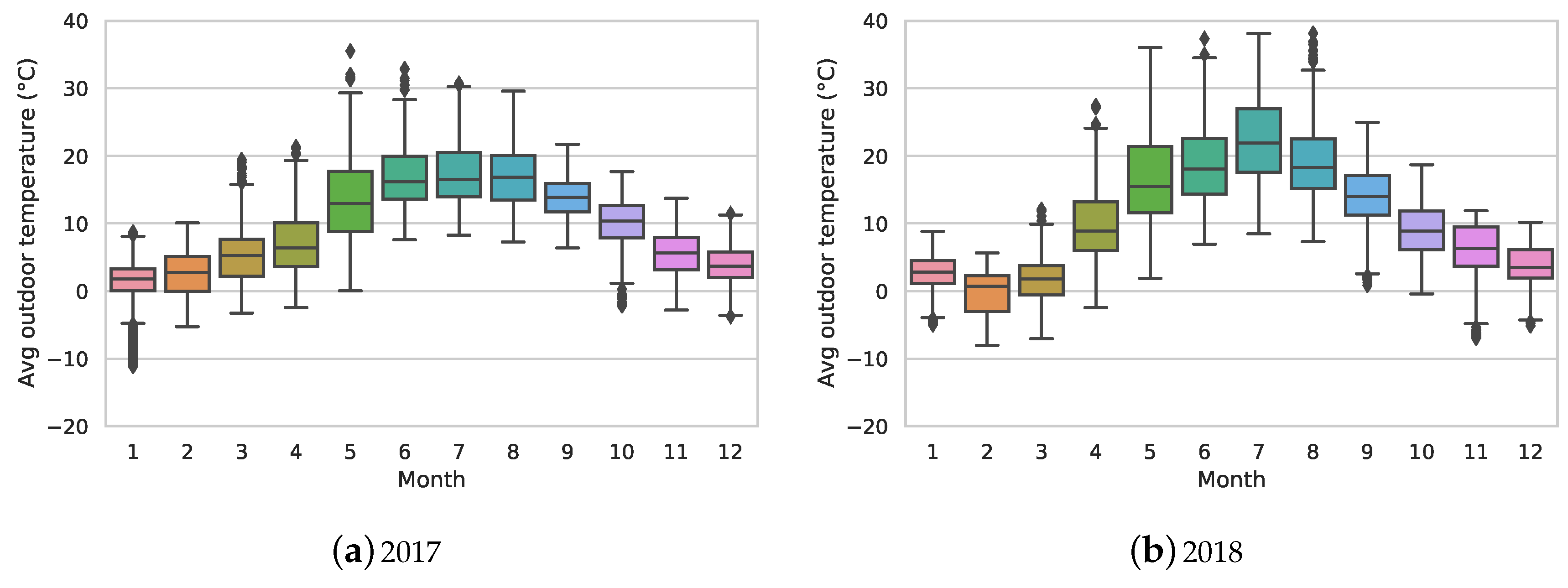
We have studied the operational behaviour of the substations of 47 buildings during a period of two years (2017 and 2018). For each building, we first modelled the substation’s weekly operational behaviour; this was performed by grouping the extracted frequent patterns into clusters of similar patterns. In order to monitor the substations’ performance, we analysed and assessed the similarity between substation’s behaviours for every two consecutive weeks. When the bi-weekly comparison showed more than 25% (a user-specified threshold) difference and if the average temperature was less than or equal to 10 °C, further analysis was conducted by integrating the produced clustering solutions into a consensus clustering. The obtained consensus clustering solution was used to build an MST, where the exemplars were tree nodes and the distances between them represented the tree edges. In order to identify unusual behaviours, the longest edge of the MST was removed. The smallest sub-trees created by the cut were interpreted as faults or deviations.
7.1. Substations Bi-Weekly Performance Signature
As mentioned above in
Section 4.3, the assessed similarities of a substation’s operational behaviour can be used to build the substation performance signature profile for the entire studied period. Additionally, such profiles can be used to compare substations belonging to the same heat load category. We studied four types of buildings: C, R, R-C, and S (see
Table 2 for more information).
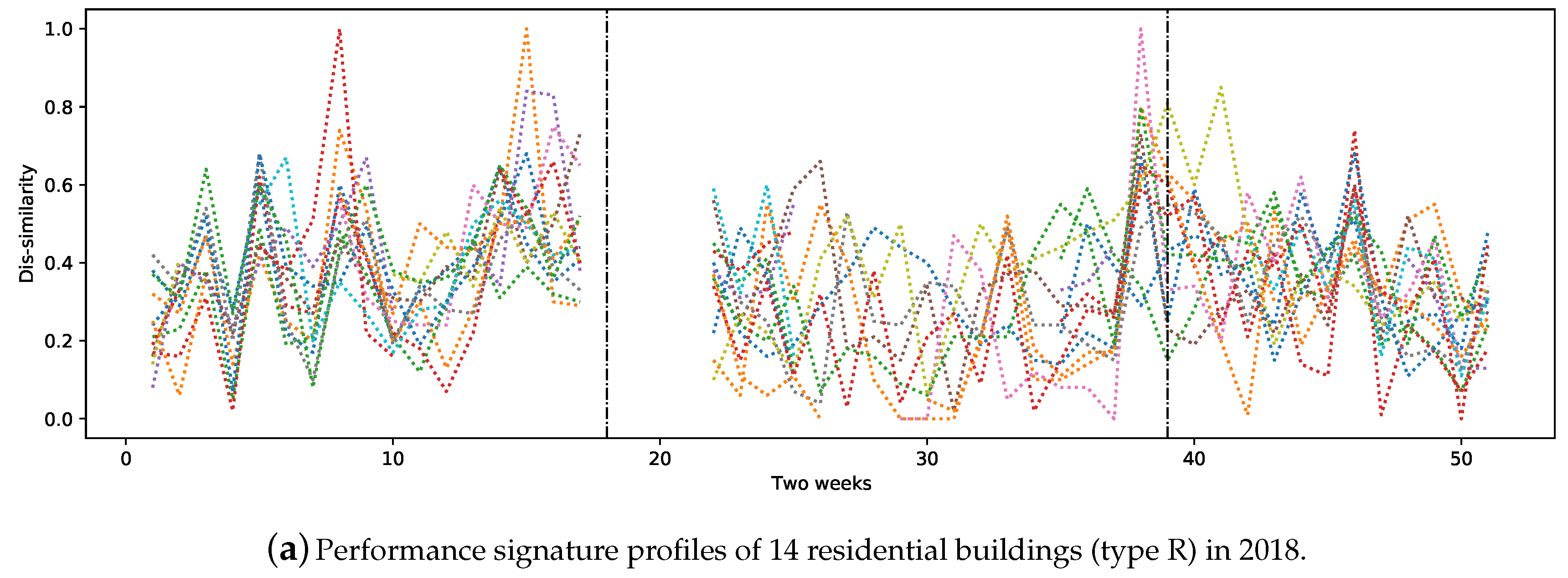
Figure 2a shows the signature profiles of 14 residential buildings in 2018. The area between the two vertical dashed lines represents the non-heating season in all figures.
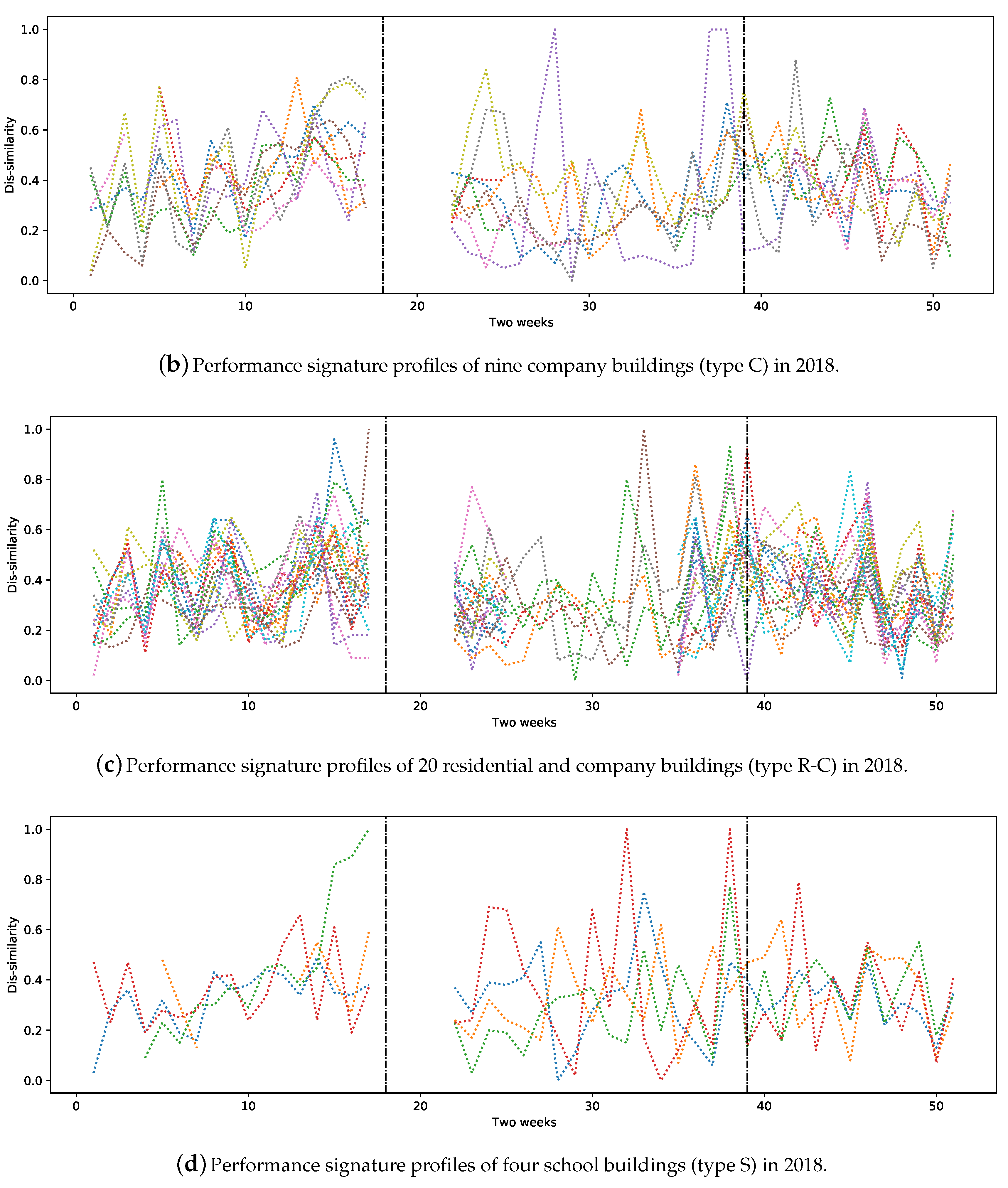
Figure 2b depicts the performance signature profiles of the substations of nine company buildings for the same year.
Figure 2c contains the largest number of buildings belonging to the R-C category; i.e., 20 in total.
Figure 2d represents the signature profiles of four schools. All the studied buildings are located in the same city. As one can see,
Figure 2a–d contains signatures that are quite similar in the period of week 1 until week 18 (1 January–6 May 2018) and week 45 to week 46 (5–18 November 2018).
Although the expectation was to observe similar performance signatures from buildings in the same category, some substations showed quite different behaviours. The main reasons for this can be related to the difference between the average outdoor temperature within two weeks in different areas of the city. Our further analysis showed that buildings of the same type and that are close together tend to have similar performance signature profiles during heating seasons. In addition, the social behaviour of people, special holidays and/or faulty substations and equipment have a high impact on substations’ performance. It is also the case that buildings of same category behave differently, mostly due to installation issues, unsuitable configurations or different brands of equipment. Nevertheless, this requires further analysis by domain experts.
7.2. Modelling Substations’ Operational Behaviour
The weekly operational behaviour of a substation can be modelled by clustering the extracted patterns based on their similarities into groups. Using the AP algorithm, each cluster can be recognized by its exemplar—a representative pattern of the whole group. Each cluster models the substation’s operational behaviour for some hours up to a couple of days based on its frequency. The number of clusters in each clustering solution can be interpreted as different operational modes of the substation for the studied week. High number of clusters may due to the same reasons as those discussed in the section above, such as the difference between outdoor temperatures during the days and nights. The extracted patterns contain five features. Each feature can belong to one of five available categories: low, low_medium, medium, medium_high and high.
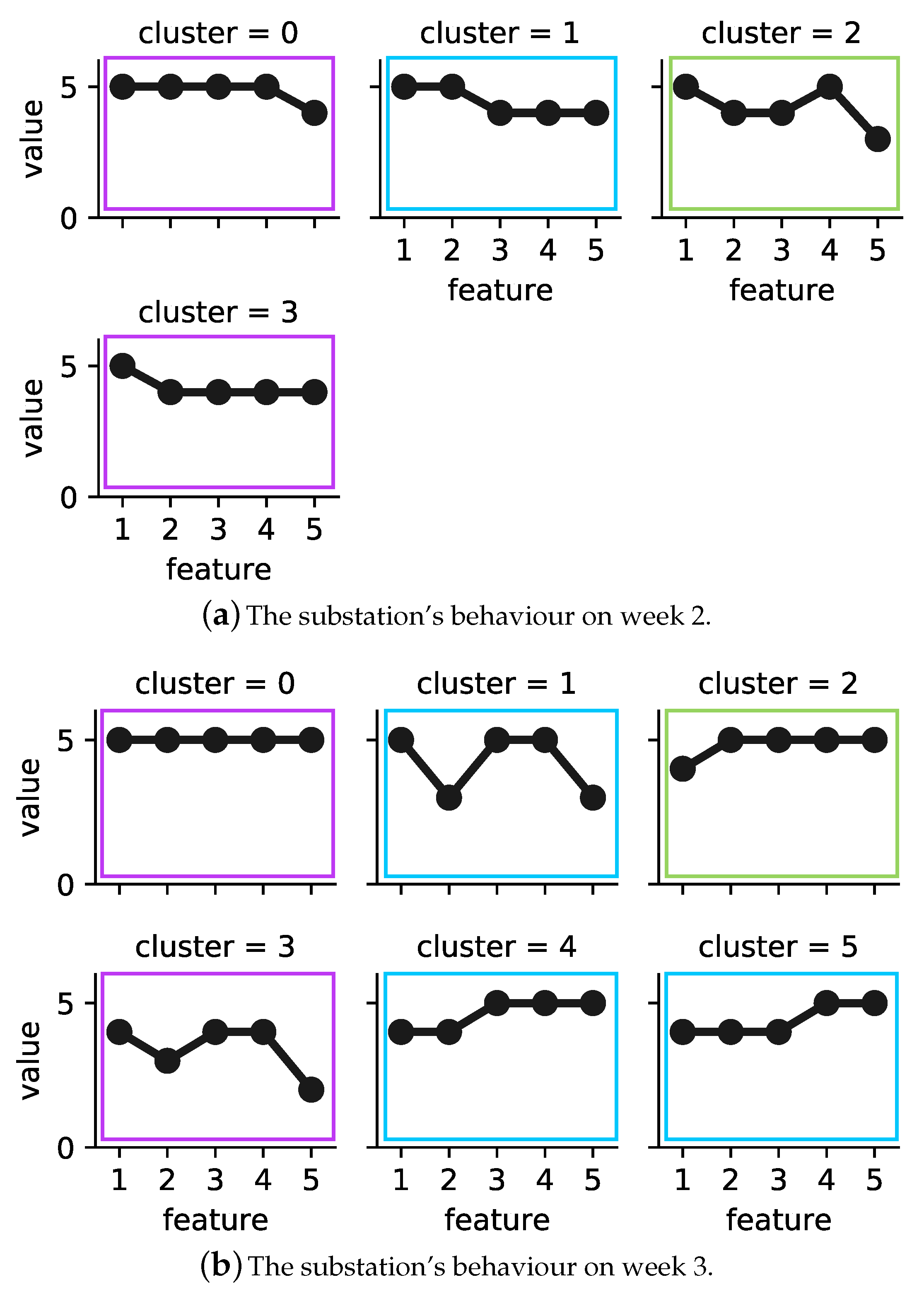
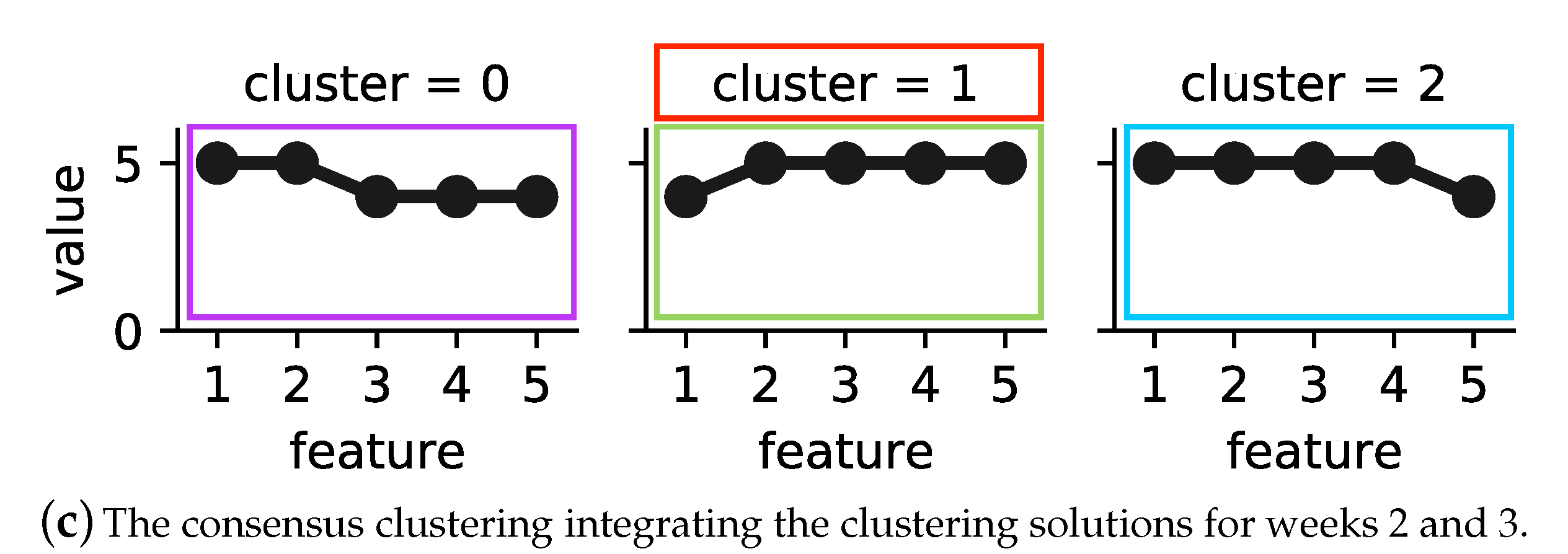
Figure 3 shows the operational behaviour of building B_3’s substation during weeks 2 and 3 in 2017, where low is represented by one and high by five, respectively. Note that each category is the result of differencing to adjust yearly seasonality for each feature.
Figure 3a represents four operational behaviour modes of building B_3’s substation during the second week of 2017. Cluster 2 covers 57 h, the largest number of hours among the sample, while cluster 1 covers only 26 h, which is the lowest number of hours. In week 3 (see
Figure 3b), six operational behaviour modes were detected. Cluster 3 in this week, similar to cluster 2 in week 2, covers 57 h. Cluster 4, with the lowest number of hours, covers only 11 h.
We further analysed the operational behaviour models of weeks 2 and 3 by calculating the similarity between the exemplars of the corresponding clustering solutions. The calculated dissimilarity was above 25%, and the average weekly outdoor temperature was below 10 °C. Therefore, the proposed method integrated the clustering solutions into consensus clustering.
Figure 3c represents the operational behaviour model of the substations for the studied two weeks. The model contained three clusters. In order to detect deviating behaviour, as explained previously in
Section 4.3, first an MST was built on top of the consensus clustering solution. Next, the longest edge of the tree was removed, and sub-trees with the smallest size and that were far from majority of data could be marked as deviating behaviour. In
Figure 3c, cluster 1 (framed in red) is detected as an outlier.
Table 4 and
Table 5 show the distribution of each weekly cluster together with the number of days and hours that they cover across the consensus clustering solution, respectively. As one can see, in
Table 4, the detected operational behaviours in week 2 are divided into four groups, while week 3 contains six categories of different operational behaviours. In week 2, the majority of the behaviours appear across the whole week, except cluster 1, which covers only 6 days. In week 3, on the other hand, clusters 1 and 2 contain operational behaviours observed within 4 days. Clusters 4 and 5 cover 5 days and the last two remaining clusters cover 6 days. Considering the consensus clustering solution, cluster 1 contains the least number of days, at 11, while clusters 0 and 2 include 12 and 14 days, respectively. Note that weekly clustering solutions can have a daily overlap; however, they cover different hours.
Table 5 shows the number of hours covered by each weekly cluster and the total hours for each bi-weekly cluster (consensus cluster). As one can see, consensus cluster 2 contains the most number of hours, at 168. Cluster 0 and 1 cover 88 and 80 h, respectively, within weeks 2 and 3. As mentioned above, by cutting the longest edge of the built MST on top of the consensus clustering solution, the smallest and most distant cluster can be considered as deviating behaviour; i.e., consensus cluster 1. This cluster appears in 11 days (
Table 3, consensus cluster CC1) and in total 80 times (
Table 4, consensus cluster CC1) out of 336 (24 h × 14 days). The data collected for these particular days could be further analysed by domain experts to obtain a better insight and understanding of the identified deviating behaviour.
In general, an increase or decrease in the number of observed clusters in one week in comparison to its neighbouring week can be interpreted as an indication of deviating behaviours. This can occur for different reasons such as a sudden drop in outdoor temperature. Therefore, in order not to take into account every single change as deviating behaviour, we considered the use of a performance measure called overflow. The measure expresses a substation’s performance in terms of the volume flow per unit of energy flow. In the DH domain, the overflow of a well-performing substation is expected to be 20 . Therefore, by computing a substation’s weekly overflow, any bi-weekly detected deviations in conjunction with weekly overflow above 20 could be flagged as real changes in the substation.
Table 6 represents substations with bi-weekly deviating behaviours on an hourly basis and an overflow of more than 20 in 2017 and 2018. In general, substations that belong to the residential category had the highest number of deviating behaviours in both years; i.e., four substations had 95 and three substations had a total of 86 detected deviating behaviours in 2017 and 2018, respectively. In the residential–company category, there was only one substation which in both years contained a considerable number of deviating behaviours; i.e., 88 and 64. The company category contained four substations with 47 and five substations with 38 exhibited deviating behaviours in 2017 and 2018, respectively. For the school category, all four substations contained in total 11 detected deviating behaviours in 2017, while in 2018, only one of these substations contained one deviating behaviour. In
Table 6, those substations that appear in both years are shown in bold.
Figure 4 summarizes the statistics of
Table 6 on a daily basis for the four categories in 2017 and 2018. The plot can help domain experts in identifying categories with the largest number of daily deviating behaviours for a specific time period. For example, substations belonging to company and residential categories had the largest number of deviating behaviours during weeks 42 to 45 in 2017.
7.3. Patterns Representative of Deviating Behaviours
Extracted patterns can provide meaningful information for domain experts; i.e., each pattern represents the status of the five selected features at a specific time period. Note that each category shows the status of a feature at time
t in comparison to its value in time
. As mentioned in
Section 6.2, the yearly seasonality of the data is adjusted by the differencing method.
Table 7 shows the top 10 weekly patterns detected as deviating behaviours in 2017 and 2018. These patterns are exemplars (representative) of the bi-weekly consensus clustering solutions. As one can see in all patterns except pattern number 7, features 3 and 4 (shown in bold in the table)—the primary heat and primary mass flow rate, respectively—hold similar values.
Table 8 shows the top weekly patterns based on the four categories of buildings. The majority of patterns only occurred for specific types of substations, except the pattern “medium, medium, medium, medium, medium_high”, which was observed for the types R-C and S in 2017 (row 6 and 8) and R in 2018 (row 2). Patterns belonging to residential–company and residential categories were the most frequent in number overall. In addition, some of these patterns re-occurred in both 2017 and 2018 for the same categories of substations, as shown in bold in the table.
7.4. Substation Performance
The substation efficiency,
, can be used as an indicator to assess a substation’s operational behaviour throughout the entire year.
Figure 5 depicts the detected deviations for two substations belonging to the residential category, using their average efficiency and overflow for year 2017.
Figure 5a, represents a well-performing substation. Notice that the substation’s efficiency on average is around 98%. In addition, the weekly substation’s overflows for the whole heating season (January–May and November–December) are below 20.
Figure 5b, on the other hand, shows a substation with sub-optimal performance during 2017. As one can see, the substation’s efficiency on average is around 80% during the heating season. Moreover, the weekly overflows for the whole year are above 20. In addition, the proposed approach identified deviating behaviours in 10 weeks, which are marked with red.
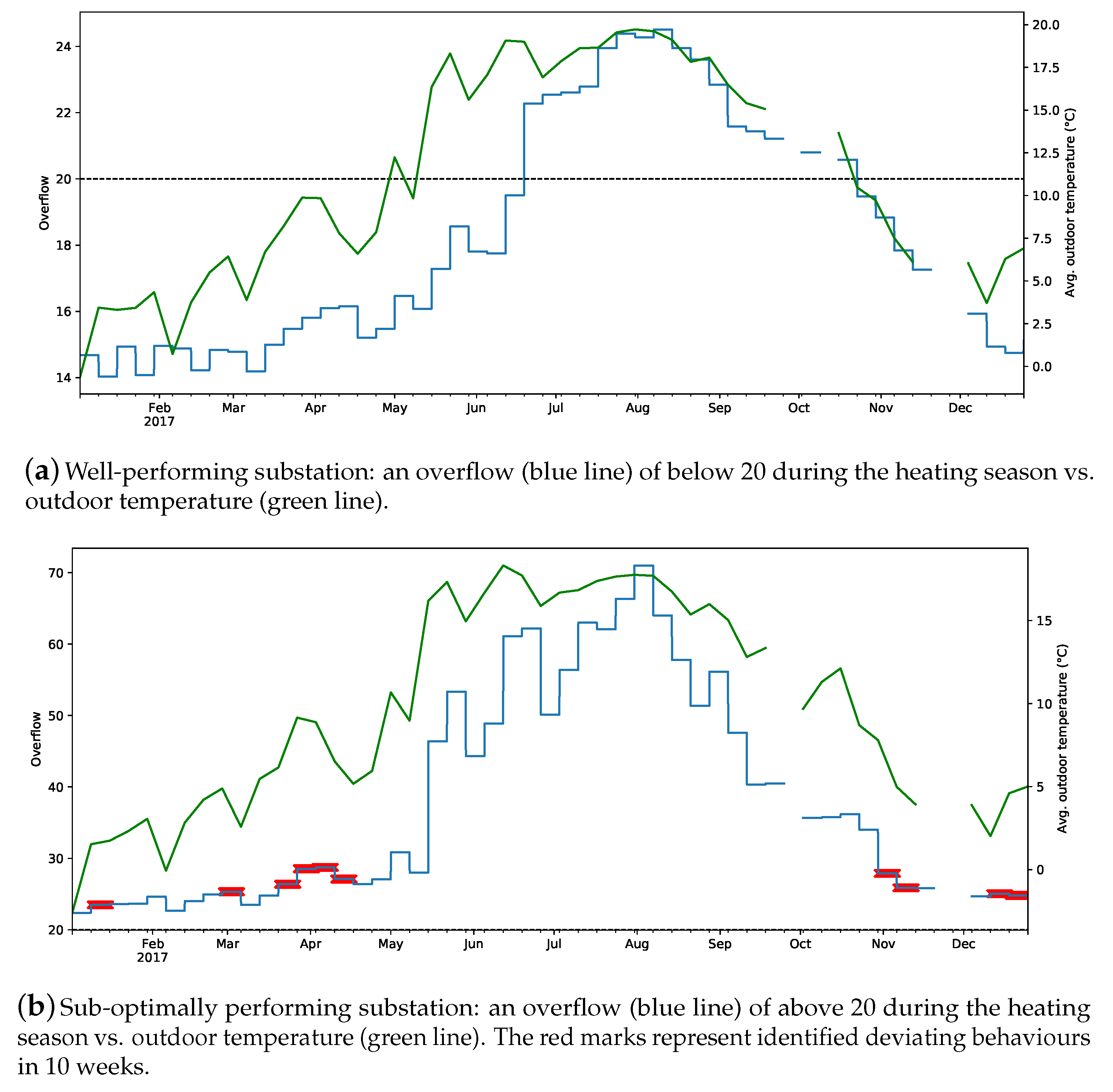
Figure 6 represents the performance of the same substations based on their weekly overflow and outdoor temperature. It is noticeable in
Figure 6b that whenever the outdoor temperature exhibits a sudden change, the proposed approach observes that as deviating behaviour.
Notice that in this study we only consider the smallest sub-trees after cutting the longest edge of an MST as outliers. Nevertheless, one can consider sorting the sub-trees based on their size from smallest to the largest for further analysis. Alternatively, by defining a domain-specific threshold, any edges with a distance greater than the threshold can be removed, and further analysis can be performed on smaller sub-trees.