Reliability Predictors for Solar Irradiance Satellite-Based Forecast
Abstract
:1. Introduction
- helping dispatch operators to propose the cheapest and safest electric mix according to user’s consumption and energy availability.
- limiting financial risks for electricity distributor buying (respectively, producer selling) PV power on the electricity market.
- designing optimal rules for the management of micro-grids including at least a PV system and a battery storage.
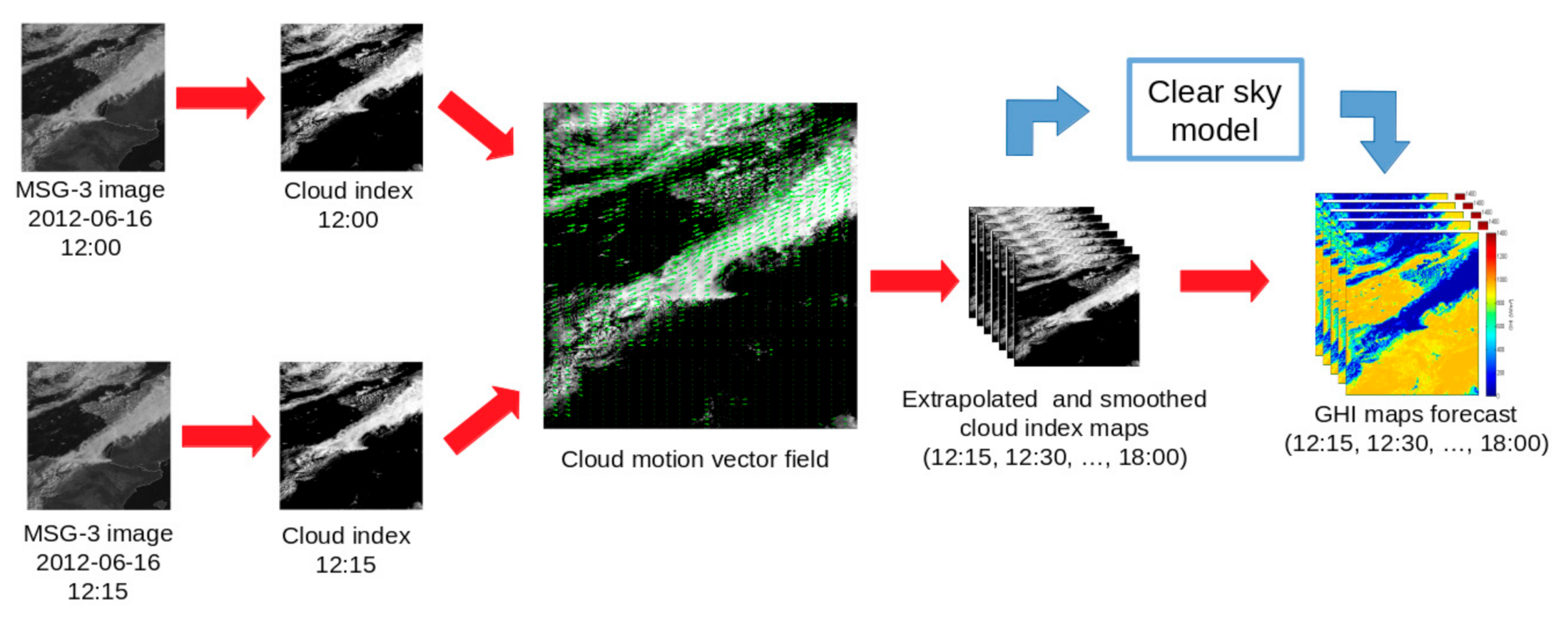
2. Forecasting Using Geostationary Satellite Images
2.1. Preliminaries: Using Satellite Data to Assess GHI
2.2. Overview of Satellite-Based Intraday Forecast Methods
2.3. Material and Methods
2.3.1. Validation Data
2.3.2. Satellite Data
2.3.3. ARPEGE Outputs
2.3.4. Cloud Index Computation
2.3.5. Cloud Motion Vector Field Computation
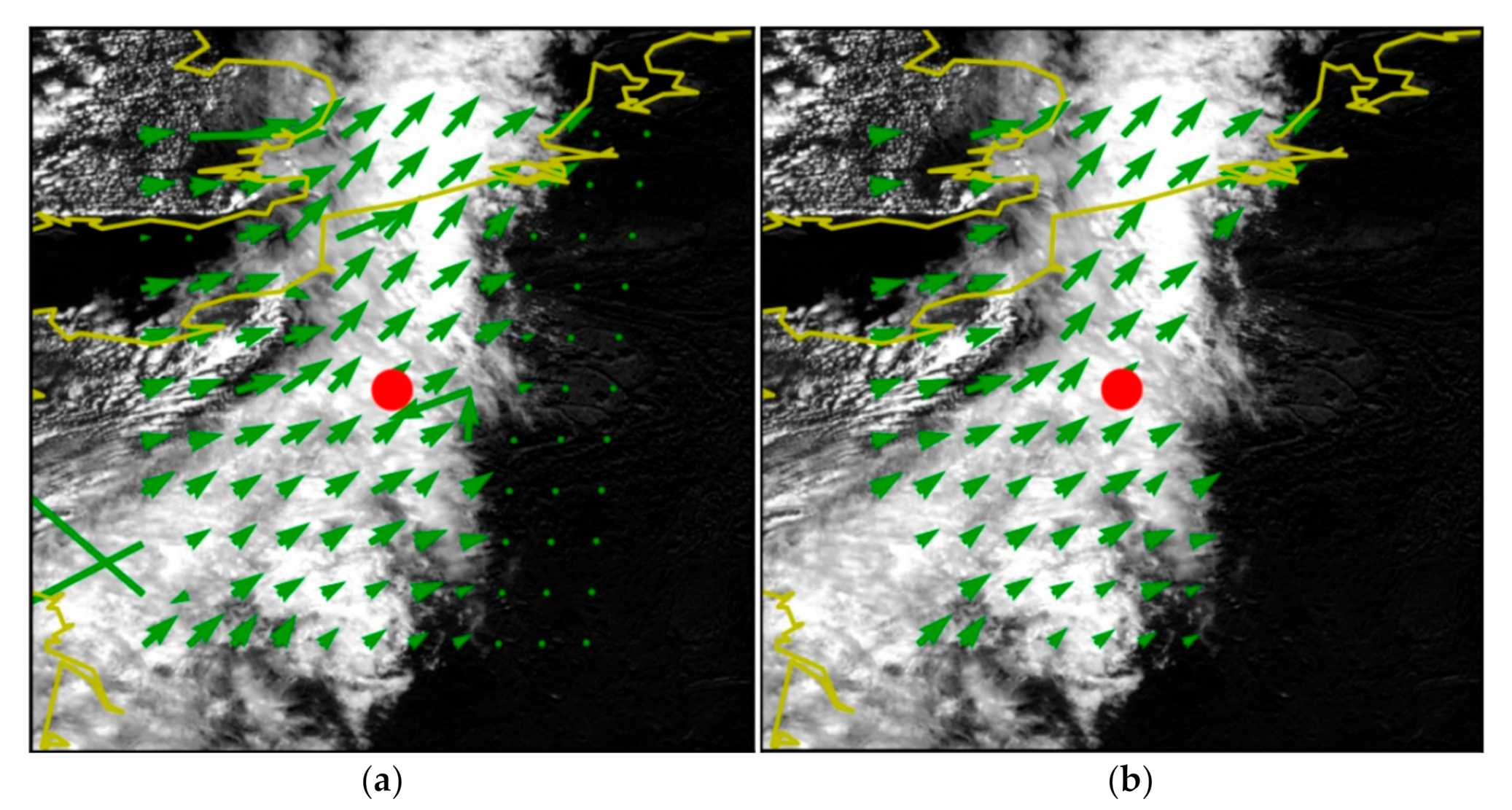
- In the first step, a CMV field is produced with a block-matching method based on the minimization of the sum of squared differences (SSD, or Euclidean distance) of pixel values (radiances). For each vector, if the forecast is initiated at time T0, a square of 36 × 36 pixels—called target window—is selected on the image acquired at T0-15 min (image 1). A square of 96× 96 pixels—the search window—is then selected in the image acquired at T0 (image 2) with the same center as the target window of image 1. The target window of image 1 is displaced pixel-by-pixel in all directions, over all possible positions allowed inside the search window of image 2. The relative position of the two windows presenting the minimal SSD is marked as the motion vector tip, and thus defines the CMV. In practice this process is applied to all the predefined positions of a regular grid and produces a CMV vector field between T0-15 min and T0. In this study we do not take into account the height (or level) of the tracked clouds. The resulting CMV fields may be composed of vectors at different levels. When clouds are present in different, overlapping layers, the satellite generally “sees” the clouds of the uppermost layer in the visible channel.
- A second CMV field has to be calculated over the same grid with the previously described procedure between the image acquired at T0-30 min (image 0) and the image acquired at T0-15 min (image 1), in order to detect unrealistic temporal evolution of the tracked cloud or structure during the half-hour period before T0, the forecast time, by comparing both vector fields. In practice, this second CMV field is extracted before the one derived between T0-15 min and T0).
- Suppression of null vectors (corresponding often to cloud free areas).
- Suppression of vectors with a norm exceeding a realistic wind speed.
- Temporal consistency test: each vector calculated between T0-15 min and T0 is compared to its predecessor computed at the same location in the images acquired at T0-30 min and T0-15 min. If the difference in vector direction or the ratio of magnitude (proportional to the wind speed) of both vectors, exceed fixed thresholds, the vector is suppressed.
- Spatial consistency test: each vector is compared with its nearest neighbors. Similarly, if the difference in direction or the magnitude ratio exceeds fixed thresholds, the vector is suppressed.
- When clouds appear or dissipate (inside the area covered by the target window), they are only present on one image of a pair.
- Sometimes two clouds or cloud groups (or more) can be present at different levels inside a target window and can move at a different speeds or in different directions. The derived CMV may correspond to the motion of one of the clouds (generally the largest one, or in some cases the thickest cloud when semi-transparent clouds (cirrus) are also present. Or the CMV may correspond to some “mixture” of the motion of both clouds.
2.3.6. Cloud Index Image Extrapolation and Post-Processing
2.3.7. Forecast GHI Computation
3. Forecast Predictors
- The deterministic variability only dependent on the course of the Sun, directly and entirely quantified by the solar zenith angle θ.
- The stochastic variability of cloud cover, depending on the weather situation at multiple spatio-temporal scales. Thus, its quantification can be made through various parameters influencing cloudiness at the intra-day scale.
3.1. Predictor Solar Zenith Angle
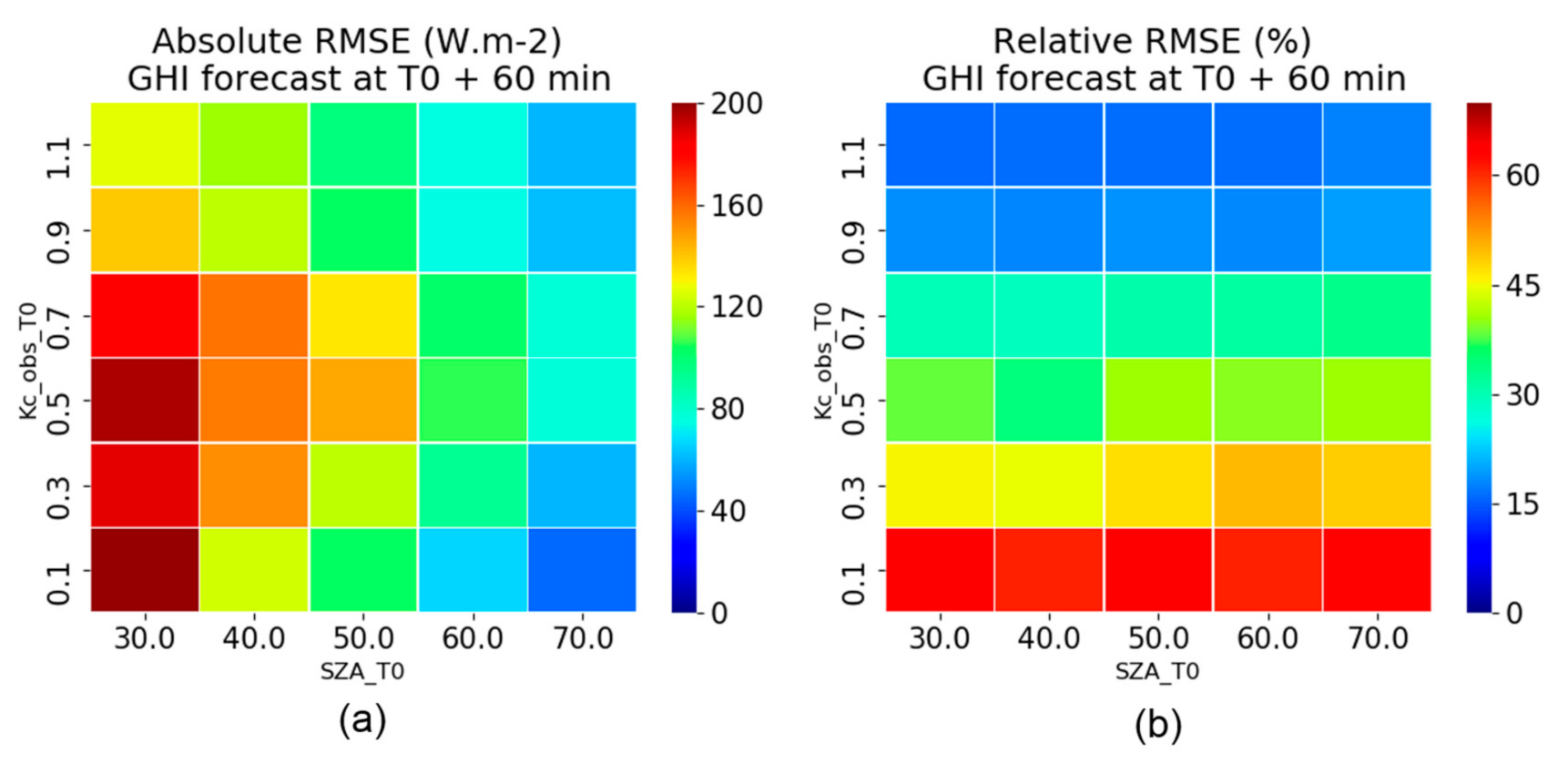
3.2. “Observed” Clear-Sky Index
3.3. Spatial Pattern of Surrounding Clear-Sky Indices Assessed from Satellite
3.4. Weather Regimes of North Atlantic-Europe Domain
- An anticyclone over northern Canada and Greenland and a zonal circulation towards Europe: this regime corresponds to the negative value of the Northern Atlantic Oscillation (NAO) and it is therefore called NAO−.
- An anticyclone in the middle of the Atlantic. This regime is called the Atlantic Ridge.
- An anticyclone over the North Sea: Scandinavian Blocking.
- A depression over Iceland in winter and a pronounced zonal circulation toward Europe in summer. This regime corresponds to the positive phase of the NAO (or NAO+). It is called the Atlantic Low in winter and Zonal in summer.
4. Results
4.1. Evaluation Protocol
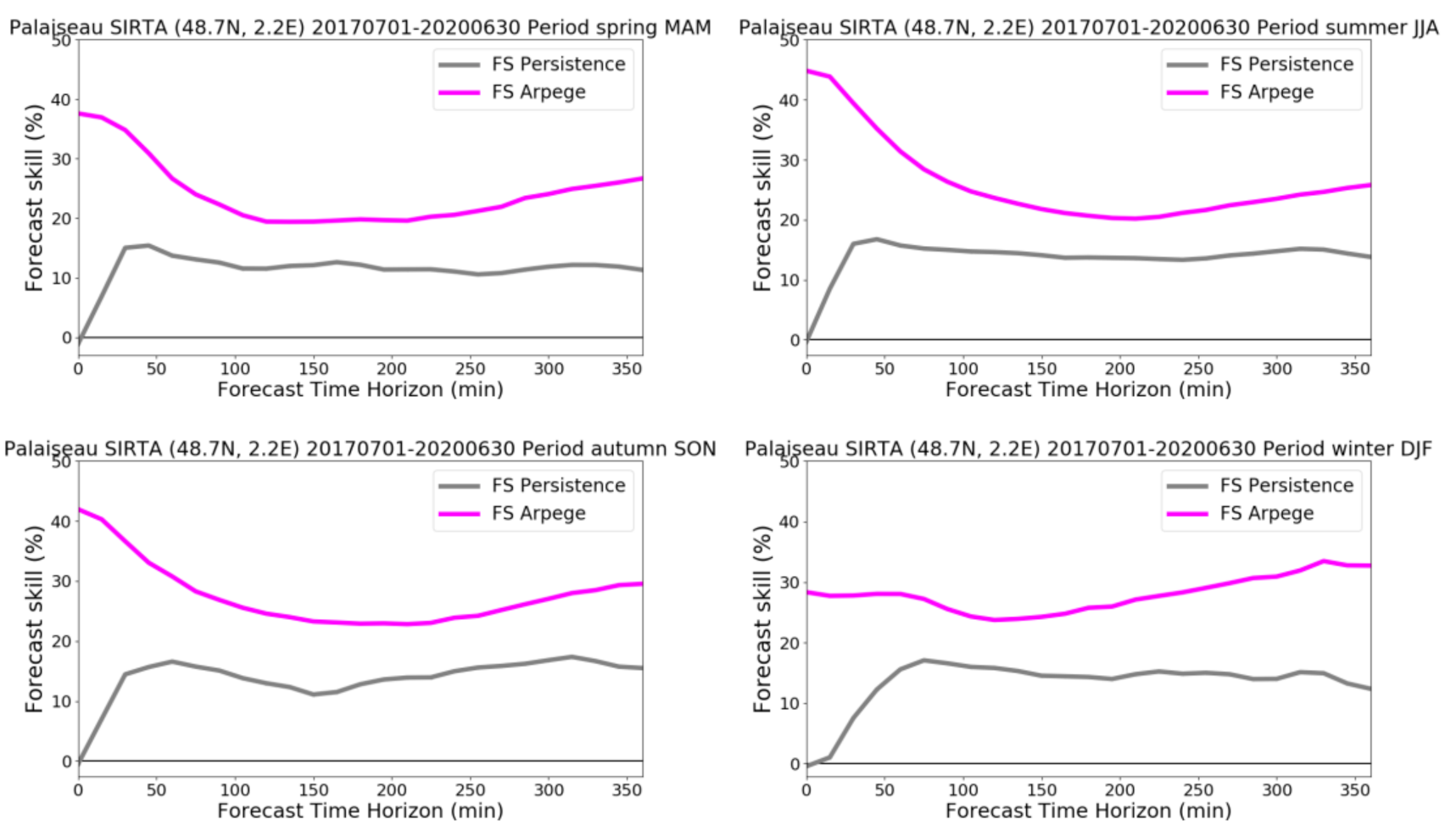
4.2. General Results
4.3. Results against Punctual Predictors
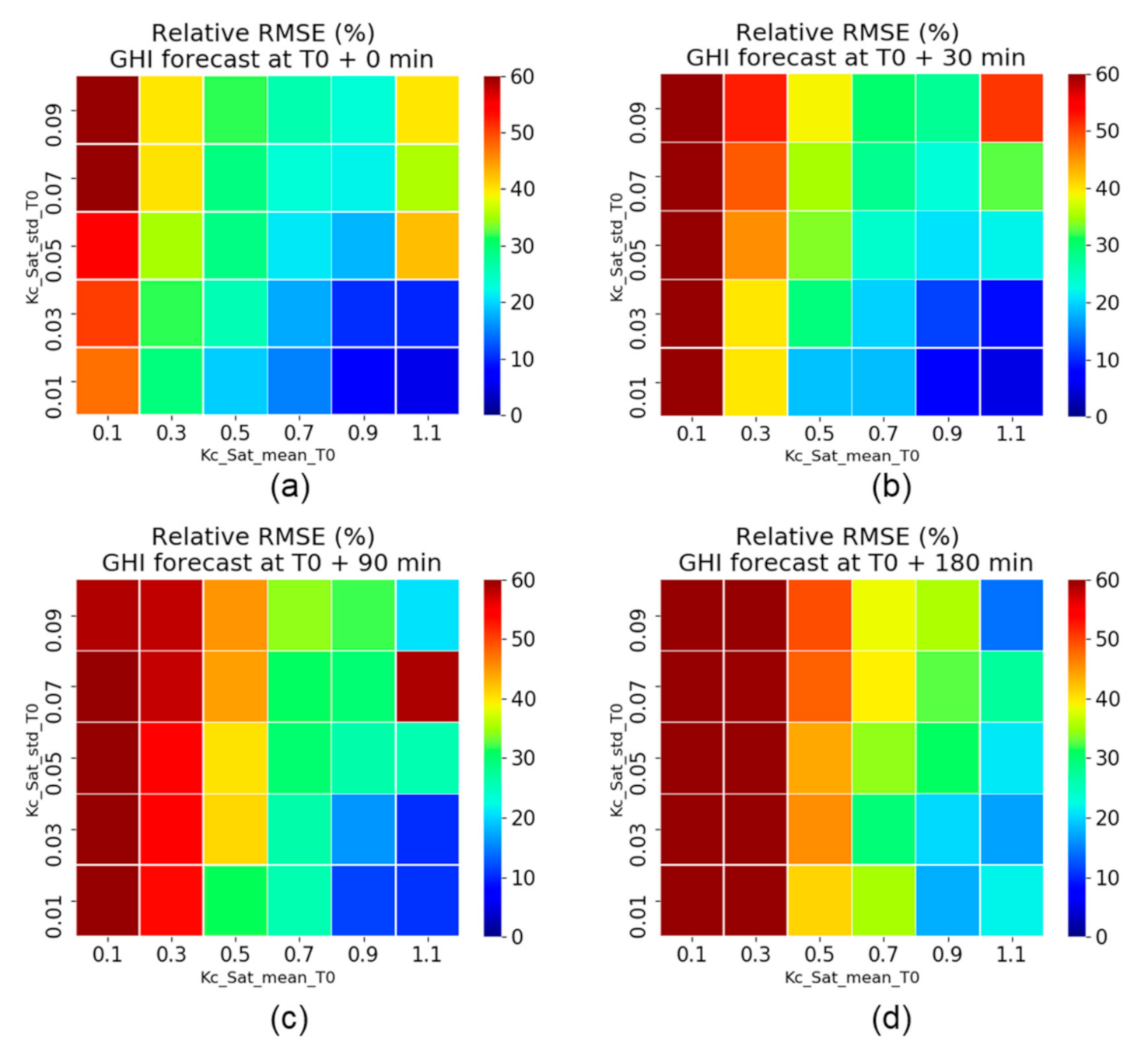
4.4. Results against Neighboring Clear-Sky Index Pattern Observed by Satellite
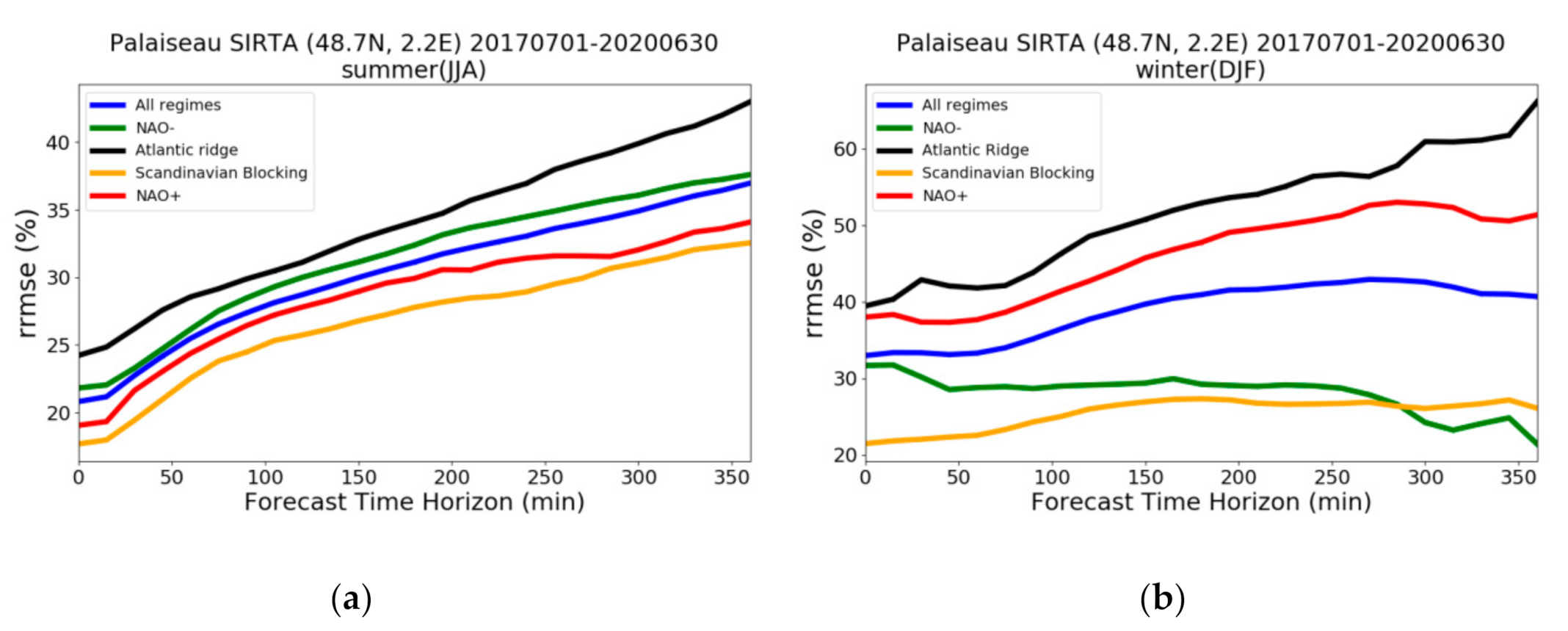
4.5. Results against Synoptic Weather Regimes
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Morjaria, M.; Anichkov, D.; Chadliev, V.; Soni, S. A Grid-Friendly Plant: The Role of Utility-Scale Photovoltaic Plants in Grid Stability and Reliability. IEEE Power Energy Mag. 2014, 12, 87–95. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Renewable Capacity Statistics; International Renewable Energy Agency: Abu Dhabi, UAE, 2020. [Google Scholar]
- Golestaneh, F.; Pinson, P.; Gooi, H.B. Very Short-Term Nonparametric Probabilistic Forecasting of Renewable Energy Generation—With Application to Solar Energy. IEEE Trans. Power Syst. 2016, 31, 3850–3863. [Google Scholar] [CrossRef] [Green Version]
- Calderon-Olbadia, F. Photovoltaic Power Generation Uncertainty Forecast for Microgrid Energy Management Efficiency Enhancement. Ph.D. Thesis, Université Paris-Sud, Paris, France, 2020. [Google Scholar]
- Perez, M.; Perez, R.; Rábago, K.R.; Putnam, M. Overbuilding & curtailment: The cost-effective enablers of firm PV generation. Sol. Energy 2019, 180, 412–422. [Google Scholar]
- Ocker, F.; Jaenisch, V. The way towards European electricity intraday auctions—Status quo and future developments. Energy Policy 2020, 145, 111731. [Google Scholar] [CrossRef]
- Helbig, N. Application of the Radiosity Approach to the Radiation Balance in Complex Terrain. Dr. Thesis, University of Zurich, Zurich, Switzerland, 2009. [Google Scholar]
- Dobos, A.P. PV Watts Version 5 Manual (No. NREL/TP-6A20-62641); National Renewable Energy Lab: Golden, CO, USA, 2014. [Google Scholar]
- Diagne, H.M.; David, M.; Lauret, P.; Boland, J.; Schmutz, N. Review of solar irradiance forecasting methods and a proposition for small-scale insular grids. Renew. Sustain. Energy Rev. 2013, 27, 65–76. [Google Scholar] [CrossRef] [Green Version]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-De-Pison, F.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef] [Green Version]
- Sobri, S.; Koohi-Kamali, S.; Rahim, N.A. Solar photovoltaic generation forecasting methods: A review. Energy Convers. Manag. 2018, 156, 459–497. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Jang, H.S.; Bae, K.Y.; Park, H.-S.; Sung, D.K. Solar Power Prediction Based on Satellite Images and Support Vector Machine. IEEE Trans. Sustain. Energy 2016, 7, 1255–1263. [Google Scholar] [CrossRef]
- Vandeventer, W.; Jamei, E.; Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Soon, T.K.; Horan, B.; Mekhilef, S.; Stojcevski, A. Short-term PV power forecasting using hybrid GASVM technique. Renew. Energy 2019, 140, 367–379. [Google Scholar] [CrossRef]
- Urbich, I.; Bendix, J.; Müller, R. A Novel Approach for the Short-Term Forecast of the Effective Cloud Albedo. Remote. Sens. 2018, 10, 955. [Google Scholar] [CrossRef] [Green Version]
- Kurzrock, F.; Cros, S.; Ming, F.C.; Otkin, J.A.; Hutt, A.; Linguet, L.; Lajoie, G.; Potthast, R. A Review of the Use of Geostationary Satellite Observations in Regional-Scale Models for Short-term Cloud Forecasting. Meteorol. Z. 2018, 27, 277–298. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K.; Renné, D.; Hoff, T.E. Validation of short and medium term operational solar radiation forecasts in the USA. Sol. Energy 2010, 84, 2161–2172. [Google Scholar] [CrossRef]
- Lorenz, E.; Kühnert, J.; Heinemann, D.; Nielsen, K.P.; Remund, J.; Müller, S.C.; Cros, S. Comparison of irradiance forecasts based on numerical weather prediction models with different spatio-temporal resolutions. In Proceedings of the 31st European PV Solar Energy Conference, Hamburg, Germany, 14–18 September 2015. [Google Scholar]
- Wang, P.; van Westrhenen, R.; Meirink, J.F.; van der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Yang, D.; Killinger, S.; Lingfors, D.; Engerer, N. Improved satellite-derived PV power nowcasting using real-time power data from reference PV systems. Sol. Energy 2018, 168, 118–139. [Google Scholar]
- Cros, S.; Turpin, M.; Lallemand, C.; Souchard de Lavoreille, H.; Kurzrock, F. Satellite-Based Cloud Cover Detection and Tracking for Solar Irradiance Forecasting, European Geosciences Union General Assembly; Geophysical Research Abstracts: Vienna, Austria, 2019; Volume 21, p. 14784. [Google Scholar]
- Blanc, P.; Remund, J.; Vallance, L. Short-term solar power forecasting based on satellite images. In Renewable Energy Forecasting; Woodhead Publishing: Sawston, UK, 2017; pp. 179–198. [Google Scholar]
- Sengupta, M.; Habte, A.; Kurtz, S.; Dobos, A.; Wilbert, S.; Lorenz, E.; Stoffel, T.; Renné, D.; Myers, D.; Wilcox, S.; et al. Best Practices Handbook for the Collection and use of Solar Resource Data for Solar Energy Applications; Technical report; NREL: Golden, CO, USA, 2015. [Google Scholar]
- Driemel, A.; Augustine, J.; Behrens, K.; Colle, S.; Cox, C.; Cuevas, E.; Denn, F.M.; Duprat, T.; Fukuda, M.; Grobe, H.; et al. Baseline Surface Radiation Network (BSRN): structure and data description (1992–2017). Earth Syst. Sci. Data 2018, 10, 1491–1501. [Google Scholar] [CrossRef] [Green Version]
- Haeffelin, M.; Barthes, L.; Bock, O.; Boitel, C.; Bony, S.; Bouniol, D.; Chepfer, H.; Chiriaco, M.; Cuesta, J.; Delanoe, J.; et al. SIRTA, a ground-based atmospheric observatory for cloud and aerosol research. Ann. Geophys. 2005, 23, 253–275. [Google Scholar] [CrossRef] [Green Version]
- Ringard, J.; Chiriaco, M.; Bastin, S.; Habets, F. Recent trends in climate variability at the local scale using 40 years of observations: The case of the Paris region of France. Atmospheric Chem. Phys. Discuss. 2019, 19, 13129–13155. [Google Scholar] [CrossRef] [Green Version]
- Tarpley, J.D. Estimating Incident Solar Radiation at the Surface from Geostationary Satellite Data. J. Appl. Meteorol. 1979, 18, 1172–1181. [Google Scholar] [CrossRef] [Green Version]
- Cano, D.; Monget, J.; Albuisson, M.; Guillard, H.; Regas, N.; Wald, L. A method for the determination of the global solar radiation from meteorological satellite data. Sol. Energy 1986, 37, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Cros, S. Création d’une Climatologie du Rayonnement Solaire Incident en Ondes Courtes à L’aide D’images Satellitales. In PhD Thesis; Energie électrique. École Nationale Supérieure des Mines de Paris: Sophia-Antipolis, France, 2004. [Google Scholar]
- Hammer, A.; Heinemann, D.; Hoyer, C.; Kuhlemann, R.; Lorenz, E.; Müller, R.; Beyer, H.G. Solar energy assessment using remote sensing technologies. Remote. Sens. Environ. 2003, 86, 423–432. [Google Scholar] [CrossRef]
- Müller, R.; Behrendt, T.; Hammer, A.; Kemper, A. A New Algorithm for the Satellite-Based Retrieval of Solar Surface Irradiance in Spectral Bands. Remote. Sens. 2012, 4, 622–647. [Google Scholar] [CrossRef] [Green Version]
- Hammer, A.; Heinemann, D.; Lorenz, E.; Lückehe, B. Short-term forecasting of solar radiation: A statistical approach using satellite data. Sol. Energy 1999, 67, 139–150. [Google Scholar] [CrossRef]
- Lorenz, E.; Hammer, A.; Heinemann, D. Short term forecasting of solar radiation based on satellite data. In Proceedings of the EUROSUN 2004, ISES Europe Solar Congress, Freiburg, Germany, 23 June 2004; pp. 841–848. [Google Scholar]
- Wolf, D.E.; Hall, D.J.; Endlich, R.M. Experiments in Automatic Cloud Tracking Using SMS-GOES Data. J. Appl. Meteorol. 1977, 16, 1219–1230. [Google Scholar] [CrossRef] [Green Version]
- Cros, S.; Turpin, M.; Le Guillou, F. Providing intraday solar irradiance forecasts before the sunrise: Satellite-based night cloud index retrieval and forecast, EMS Annual meeting. In Proceedings of the European Conference for Applied Meteorology and Climatology, Dublin, Ireland, 4–8 September 2017. [Google Scholar]
- Cros, S.; Turpin, M.; Lallemand, C.; Verspieren, Q.; Schmutz, N. Soleksat: A flexible solar irradiance forecasting tool using satellite images and geographic web-services. In Proceedings of the 3rd International Conference for Energy & Meteorology, Boulder, CO, USA, 23–26 June 2015. [Google Scholar]
- Gallucci, D.; Romano, F.; Cersosimo, A.; Cimini, D.; Di Paola, F.; Gentile, S.; Geraldi, E.; LaRosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Nowcasting Surface Solar Irradiance with AMESIS via Motion Vector Fields of MSG-SEVIRI Data. Remote. Sens. 2018, 10, 845. [Google Scholar] [CrossRef] [Green Version]
- Nonnenmacher, L.; Coimbra, C.F. Streamline-based method for intra-day solar forecasting through remote sensing. Sol. Energy 2014, 108, 447–459. [Google Scholar] [CrossRef]
- Sirch, T.; Bugliaro, L.; Zinner, T.; Möhrlein, M.; Vázquez-Navarro, M. Cloud and DNI nowcasting with MSG/SEVIRI for the optimized operation of concentrating solar power plants. Atmos. Meas. Tech. 2017, 10, 409–429. [Google Scholar] [CrossRef] [Green Version]
- Urbich, I.; Bendix, J.; Müller, R. The Seamless Solar Radiation (SESORA) Forecast for Solar Surface Irradiance—Method and Validation. Remote. Sens. 2019, 11, 2576. [Google Scholar] [CrossRef] [Green Version]
- Arbizu-Barrena, C.; Ruiz-Arias, J.A.; Rodríguez-Benítez, F.J.; Pozo-Vázquez, D.; Tovar-Pescador, J. Short-term solar radiation forecasting by advecting and diffusing MSG cloud index. Sol. Energy 2017, 155, 1092–1103. [Google Scholar] [CrossRef]
- Mueller, S.C.; Remund, J. Validation of the Meteonorm satellite irradiation dataset. In Proceedings of the 35th European Photovoltaic Solar Energy Conference and Exhibition, Brussels, Belgium, 24–27 September 2018; pp. 1760–1762. [Google Scholar]
- Dong, Z.; Yang, D.; Reindl, T.; Walsh, W.M. Satellite image analysis and a hybrid ESSS/ANN model to forecast solar irradiance in the tropics. Energy Convers. Manag. 2014, 79, 66–73. [Google Scholar] [CrossRef]
- Peng, Z.; Yoo, S.; Yu, D.; Huang, D. Solar irradiance forecast system based on geostationary satellite. In Proceedings of the 2013 IEEE International Conference on Smart Grid Communications, Vancouver, BC, Canada, 21–24 October 2013; pp. 708–713. [Google Scholar]
- Courtier, P.; Freydier, C.; Geleyn, J.; Rabier, F.; Rochas, M. In Proceedings of the Arpege Project at Météo-France, Ecmwf Workshop, European Center for Medium-Range Weather Forecast, Reading, UK, 9–13 September 1991.
- Szantai, A.; Sèze, G. Improved extraction of low-level atmospheric motion vectors over West-Africa from MSG images. In Proceedings of the 9th International Winds Workshop, Annapolis, MA, USA, 14–18 April 2008; pp. 14–18. [Google Scholar]
- Müller, R.; Dagestad, K.; Ineichen, P.; Schroedter-Homscheidt, M.; Cros, S.; Dumortier, D.; Kuhlemann, R.; Olseth, J.; Piernavieja, G.; Reise, C.; et al. Rethinking satellite-based solar irradiance modelling: The SOLIS clear-sky module. Remote. Sens. Environ. 2004, 91, 160–174. [Google Scholar] [CrossRef]
- Ineichen, P. A broadband simplified version of the Solis clear sky model. Sol. Energy 2008, 82, 758–762. [Google Scholar] [CrossRef] [Green Version]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef] [Green Version]
- Cros, S.; Liandrat, O.; Sébastien, N.; Schmutz, N.; Voyant, C. Clear Sky Models Assessment for an Operational PV Production Forecasting Solution. In Proceedings of the 28th European Photovoltaic Solar Energy Conference and Exhibition, Villepinte, France, 30 September–4 October 2013; pp. 4055–4059. [Google Scholar]
- Reda, I.; Andreas, A. Solar position algorithm for solar radiation applications. Sol. Energy 2004, 76, 577–589. [Google Scholar] [CrossRef]
- Legras, B.; Ghil, M. Persistent anomalies, blocking and variations in atmospheric predictability. J. Atmos. Sci. 1985, 42, 433–471. [Google Scholar] [CrossRef] [Green Version]
- Vautard, R. Multiple weather regimes over the North Atlantic: Analysis of precursors and successors. Mon. Wea. Rev. 1990, 118, 2056–2081. [Google Scholar] [CrossRef]
- Van Der Wiel, K.; Bloomfield, H.C.; Lee, R.W.; Stoop, L.; Blackport, R.; Screen, J.A.; Selten, F.M. The influence of weather regimes on European renewable energy production and demand. Environ. Res. Lett. 2019, 14, 094010. [Google Scholar] [CrossRef]
- Cassou, C. Intraseasonal interaction between the Madden–Julian Oscillation and the North Atlantic Oscillation. Nat. Cell Biol. 2008, 455, 523–527. [Google Scholar] [CrossRef]
- Yiou, P.; Goubanova, K.; Li, Z.X.; Nogaj, M. Weather regime dependence of extreme value statistics for summer temperature and precipitation. Nonlinear Process. Geophys. 2008, 15, 365–378. [Google Scholar] [CrossRef] [Green Version]
- Thomas, C.; Wey, E.; Blanc, P.; Wald, L.; Lefèvre, M. Validation of HelioClim-3 Version 4, HelioClim-3 Version 5 and MACC-RAD Using 14 BSRN Stations. Energy Procedia 2016, 91, 1059–1069. [Google Scholar] [CrossRef]
- Agüera-Pérez, A.; Palomares-Salas, J.C.; De La Rosa, J.J.G.; Florencias-Oliveros, O. Weather forecasts for microgrid energy management: Review, discussion and recommendations. Appl. Energy 2018, 228, 265–278. [Google Scholar] [CrossRef]




| Season | Weather Regime | GHI Mean (Wm−2) | Number of Observations |
|---|---|---|---|
| Summer | All regimes | 455 | 12,837 |
| NAO− | 454 | 3139 | |
| Atlantic Ridge | 421 | 3642 | |
| Scandinavian Blocking | 490 | 2985 | |
| Zonal (NAO+) | 467 | 3071 | |
| Winter | All regimes | 176 | 5988 |
| NAO− | 183 | 455 | |
| Atlantic Ridge | 135 | 1635 | |
| Scandinavian Blocking | 215 | 1555 | |
| Atlantic low (NAO+) | 178 | 2343 |
| Forecast Horizon (min) | Observation Mean Wm−2 | Mean Bias Error W.m−2 (%) | Mean Absolute Error Wm−2 (%) | Root Mean Square Error Wm−2 (%) | Correlation Coefficient | Observation Number |
|---|---|---|---|---|---|---|
| 0 | 364 | −17 (−5) | 57 (16) | 85 (23) | 0.94 | 36,541 |
| 15 | 364 | −16 (−4) | 58 (16) | 86 (24) | 0.94 | 36,327 |
| 60 | 382 | −16 (−4) | 70 (18) | 105 (27) | 0.91 | 33,473 |
| 120 | 408 | −18 (−4) | 87 (21) | 126 (31) | 0.87 | 29,131 |
| 180 | 425 | −18 (−4) | 99 (23) | 141 (33) | 0.84 | 25,043 |
| 240 | 431 | −17 (−4) | 107 (25) | 152 (35) | 0.83 | 25,043 |
| 360 | 420 | −11 (−2) | 115 (27) | 163 (39) | 0.78 | 14,067 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cros, S.; Badosa, J.; Szantaï, A.; Haeffelin, M. Reliability Predictors for Solar Irradiance Satellite-Based Forecast. Energies 2020, 13, 5566. https://doi.org/10.3390/en13215566
Cros S, Badosa J, Szantaï A, Haeffelin M. Reliability Predictors for Solar Irradiance Satellite-Based Forecast. Energies. 2020; 13(21):5566. https://doi.org/10.3390/en13215566
Chicago/Turabian StyleCros, Sylvain, Jordi Badosa, André Szantaï, and Martial Haeffelin. 2020. "Reliability Predictors for Solar Irradiance Satellite-Based Forecast" Energies 13, no. 21: 5566. https://doi.org/10.3390/en13215566
APA StyleCros, S., Badosa, J., Szantaï, A., & Haeffelin, M. (2020). Reliability Predictors for Solar Irradiance Satellite-Based Forecast. Energies, 13(21), 5566. https://doi.org/10.3390/en13215566





