Time-Scale Economic Dispatch of Electricity-Heat Integrated System Based on Users’ Thermal Comfort
Abstract
1. Introduction
- Based on the outdoor temperature and the user’s thermal comfort, the fuzzy membership function can be used as the user’s thermal comfort index, which can scientifically reflect the relationship between heating power and users’ comfort reasonably, and put forward the concept of the heat demand envelope belt.
- Considering the users’ comfort index and the characteristics of the real-time power balance and total heat energy balance in the dispatch time scale, the thermal balance dispatch cycle model is established to find the balance point between user comfort and system economy. The thermal inertia of the heating network is used to fully excavate the system operation economy and improve the unit operation flexibility.
- Exploiting the available potential of user-side resources, a time-scale economic dispatch model of electricity-heat integrated systems considering thermal comfort is established. According to the relationship between time-sharing electricity price and thermal price, users can take a demand response (DR) action to obtain the optimal energy purchase cost.
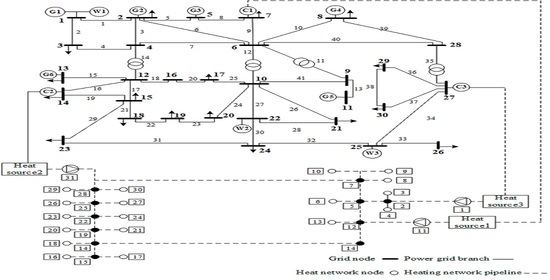
- Taking a typical winter day in a certain area of Liaoning Province of China as an example, considering the specific power network structure, the simulation results are more practical. The simulation results show that the optimization model can determine the optimal heat regulation time of the system, which meets the requirements of user comfort, improve the flexibility of the system, improve the system operation economy, and effectively improve the wind power absorption capacity.
2. Thermal Demand Modeling Method Considering Users’ Thermal Comfort
2.1. Indoor Temperature Model
2.2. Users’ Thermal Comfort Index
2.3. Thermal Demand Envelope Based on Users’ Thermal Comfort
3. Time-Scale Dispatch Model of Electricity-Heat Integrated System
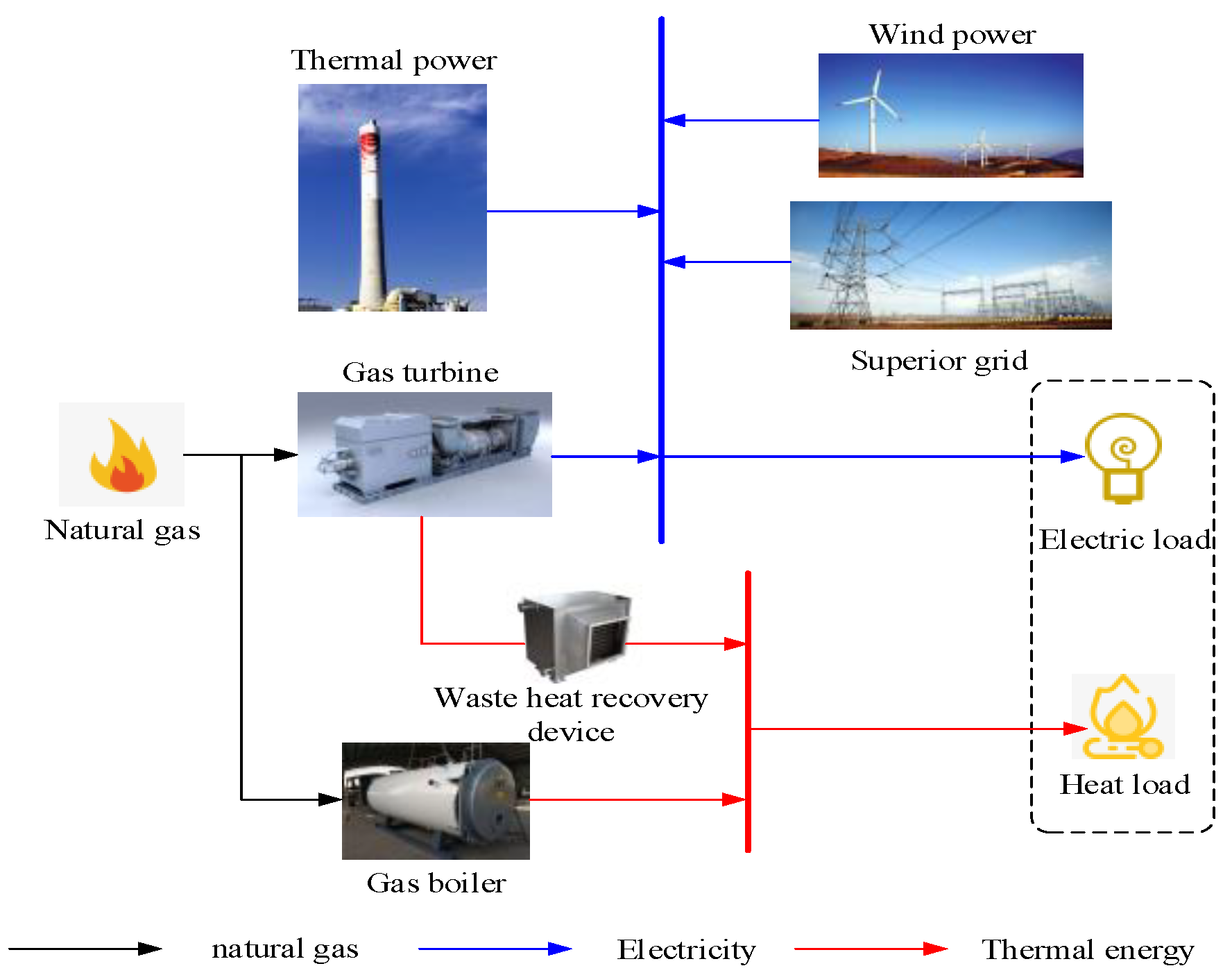
3.1. Electricity-Heat Integrated System Structure
3.2. System Unit Modeling
3.2.1. Gas Turbine
3.2.2. Gas Boiler
3.3. Dispatch Model of Heat Balance Cycle
3.4. Objective Function
3.5. Constraints
4. DR Strategy of the Electric-Heat Interconnection System
4.1. Users’ DR Structure
4.1.1. Power Demand Side Response
4.1.2. Heat Demand Side Response
4.1.3. Energy Management Unit
4.2. Demand-Side Economic Dispatch Model
4.2.1. Objective Function
4.2.2. Restrictions
- User electricity demandwhere represents the pure electricity demand of user j; denotes the electricity demand of user j to convert electricity to heat.
- User thermal demandwhere is the electric conversion efficiency of the air conditioner for user j.
- User hot water pipeline flow restrictionwhere is the rated water flow of user j; is the ratio of the relative water flow of user j; and are the upper and lower limits of the relative water flow ratio, respectively.
4.3. Demand Model Simplification Strategy
5. Bilevel Dispatch Model Optimization Strategy
5.1. Solving the Underlying Model
- Optimal electricity demandwhere and are the upper and lower limits of electricity-to-heat demand, respectively.
- Optimal heat demand
5.2. Bilevel Optimized Operation Strategy
6. Simulation Analysis Discussion
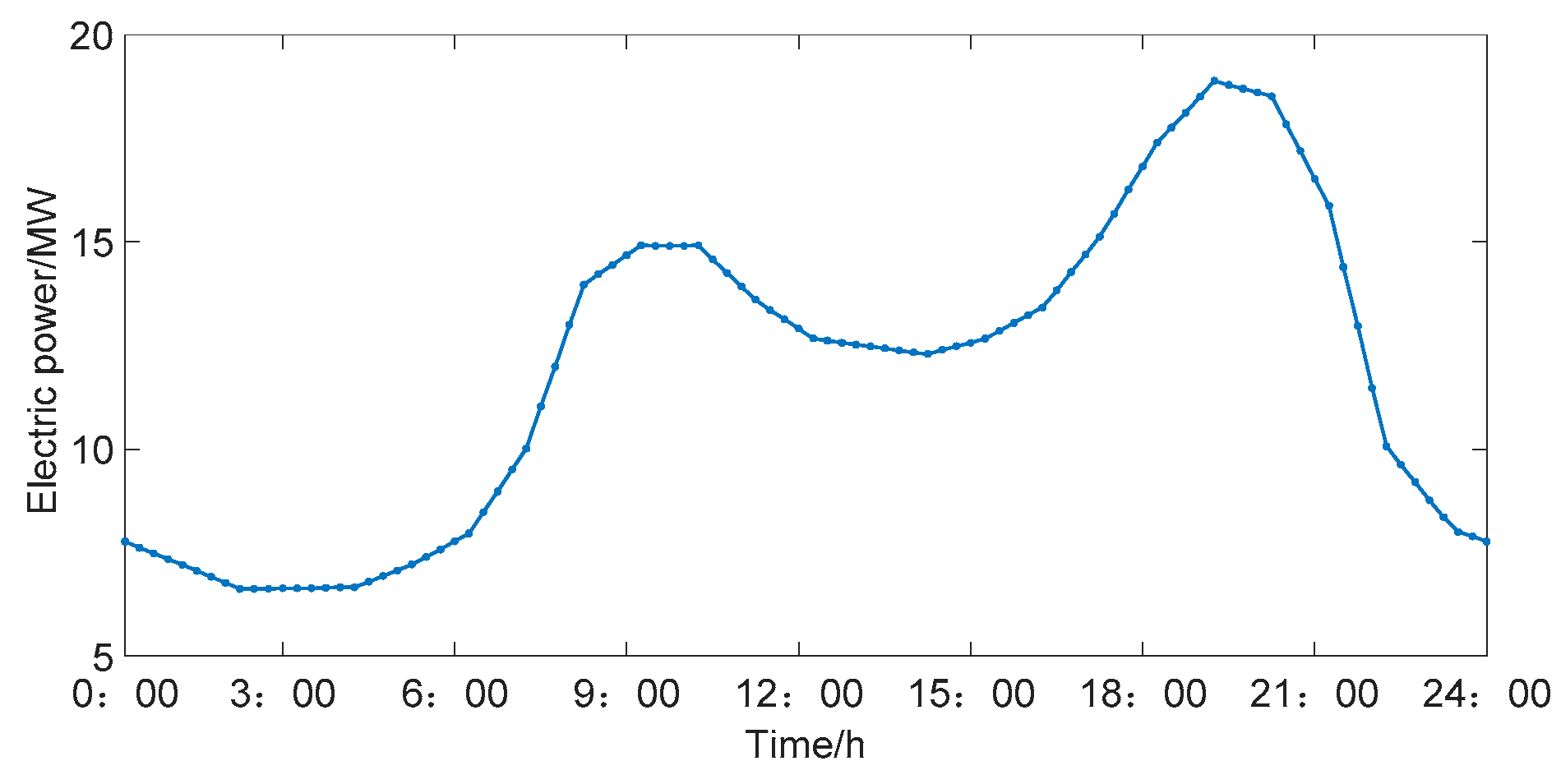
6.1. Example System and Simulation Parameters
6.2. Simulation Analysis without Considering DR
6.2.1. Comparison with Traditional Centralized Algorithms
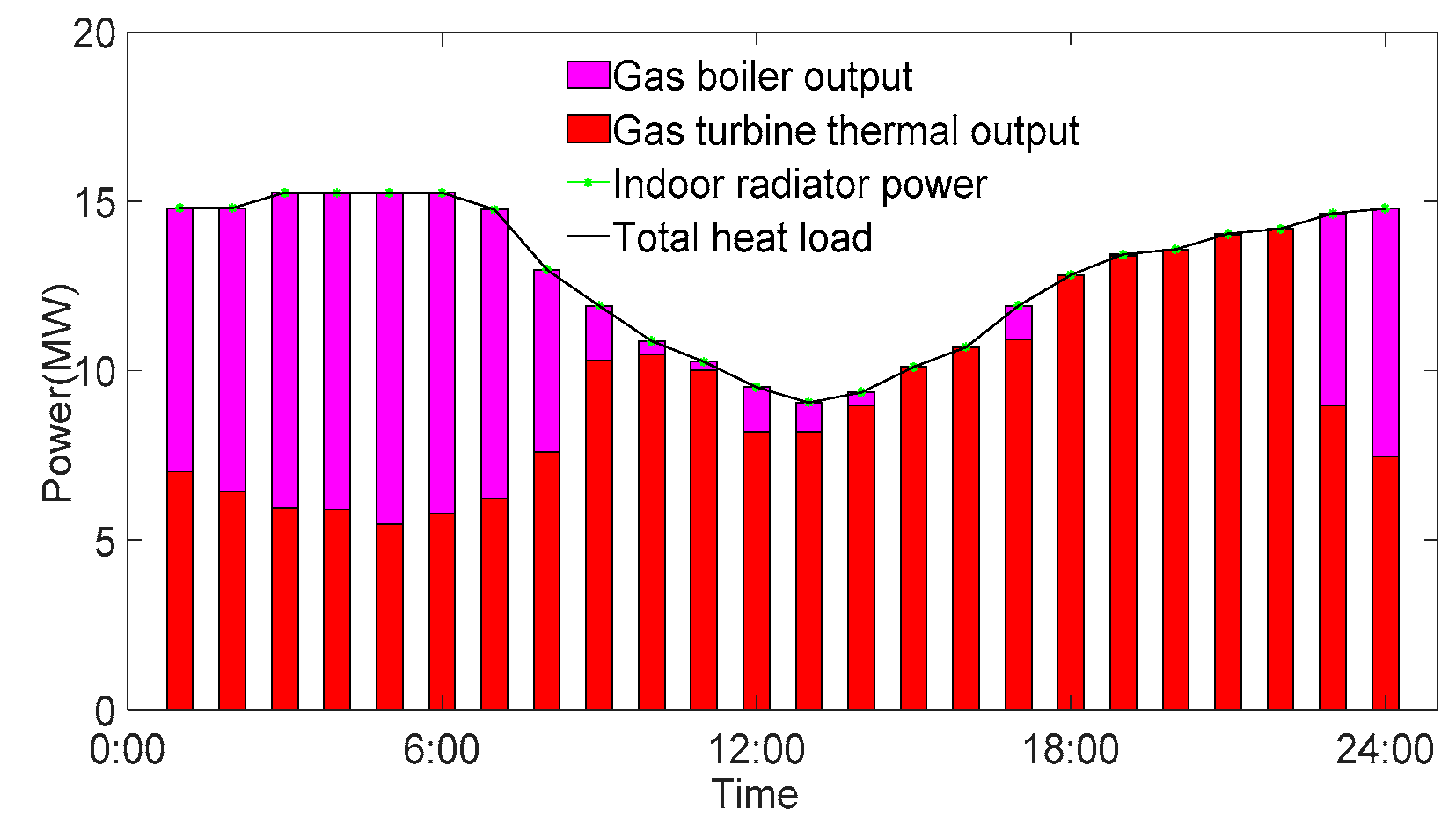
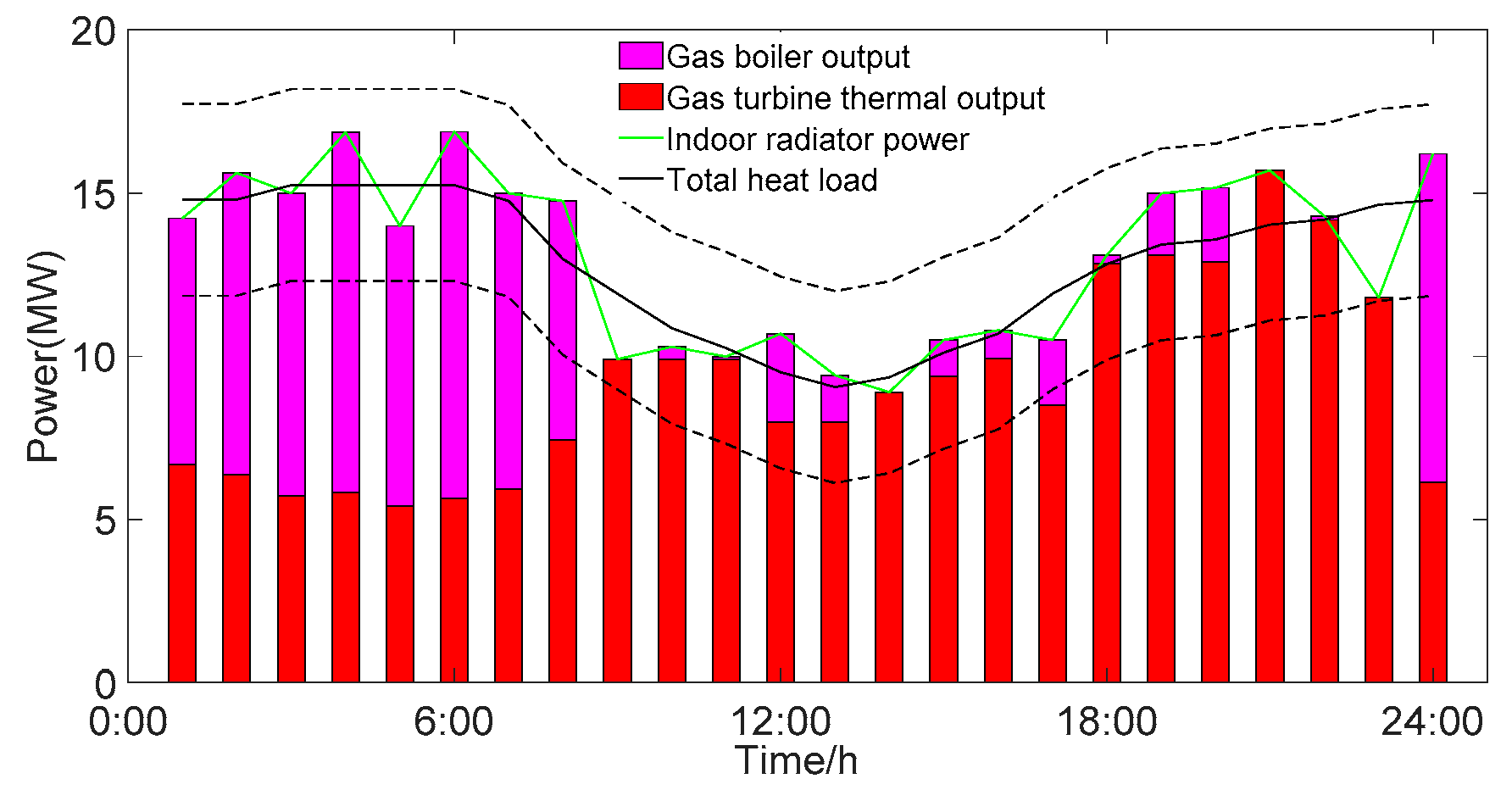
6.2.2. The Influence of the Heat Demand Envelope on Unit Output
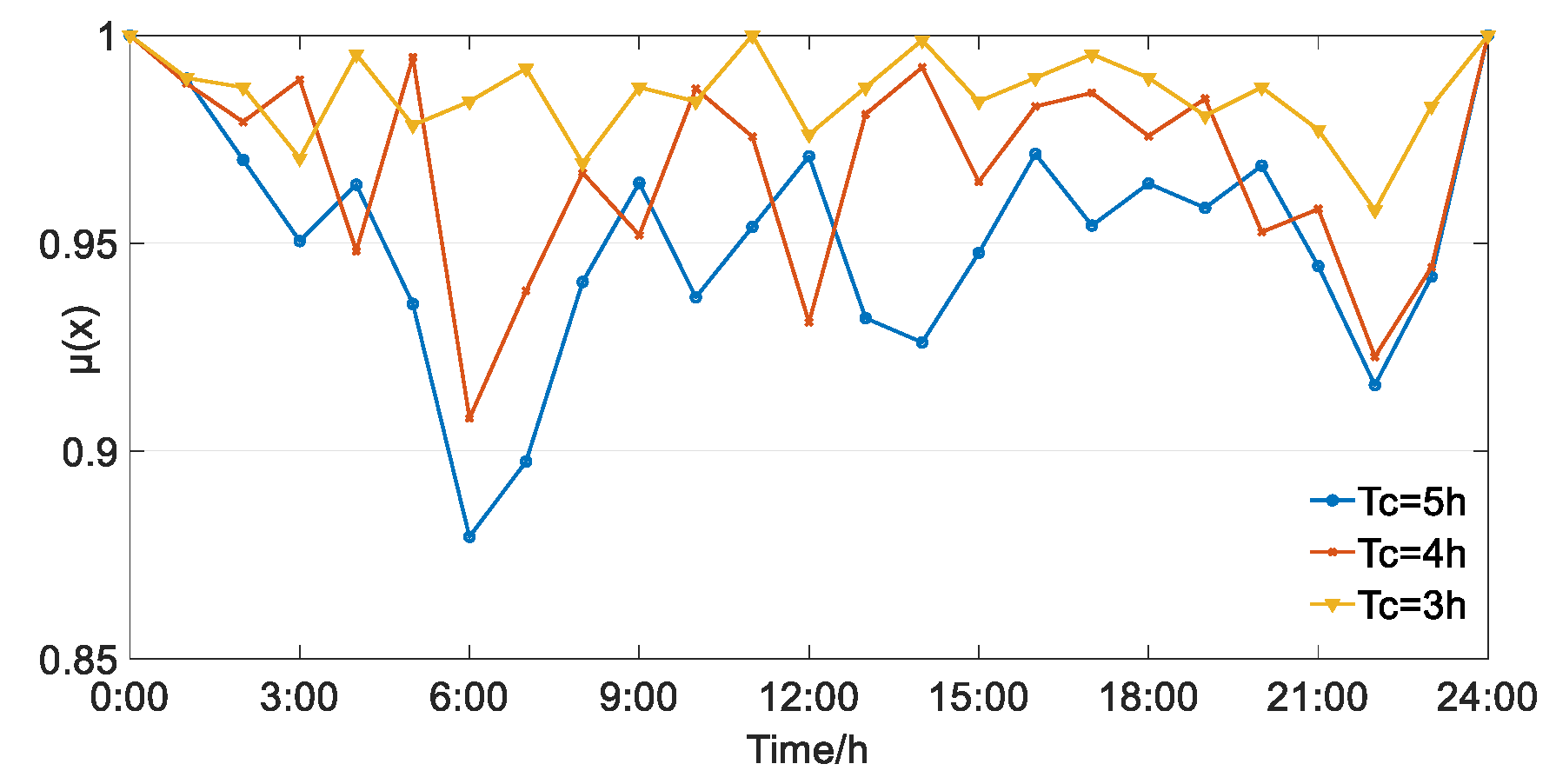
6.2.3. The Influence of Thermal Balance Cycle on Thermal Comfort
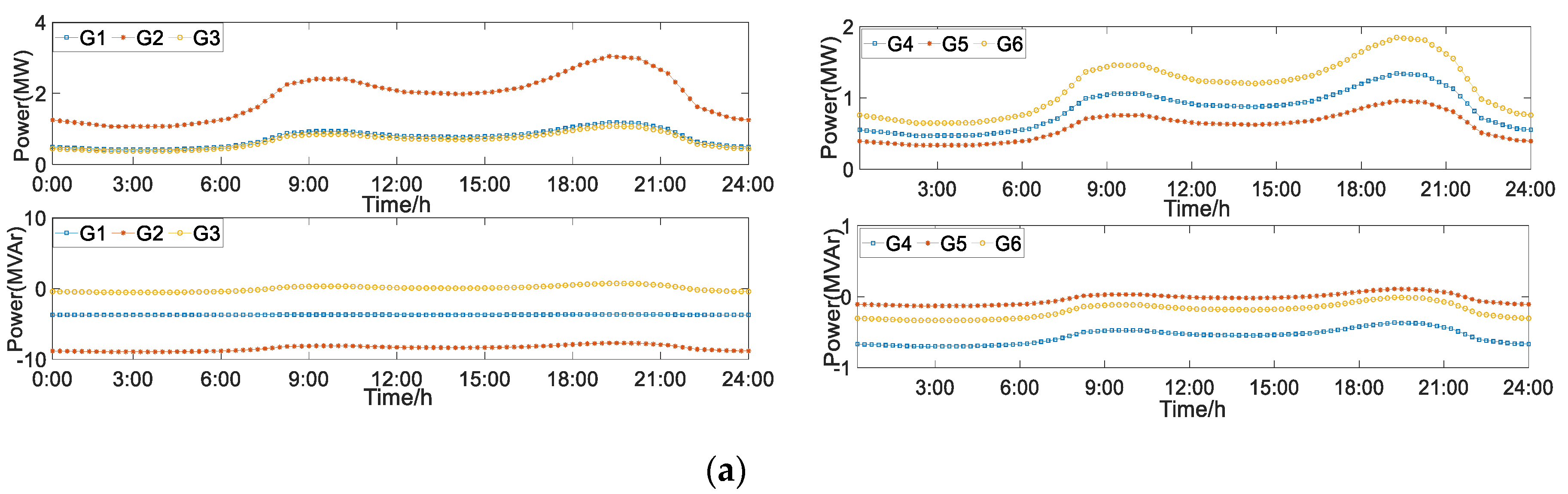
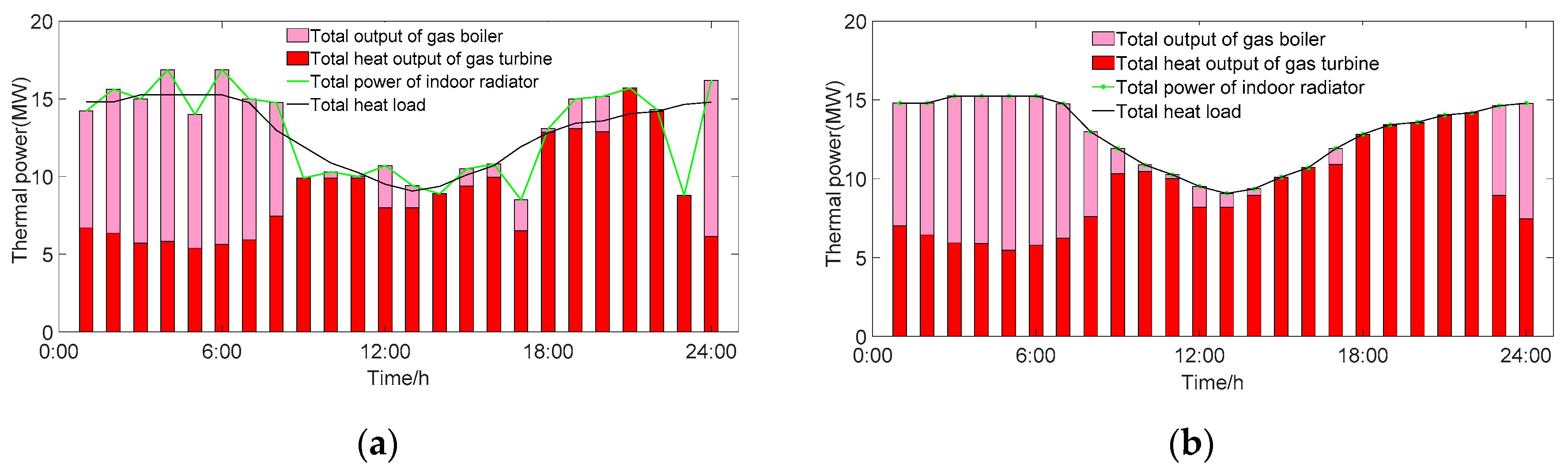
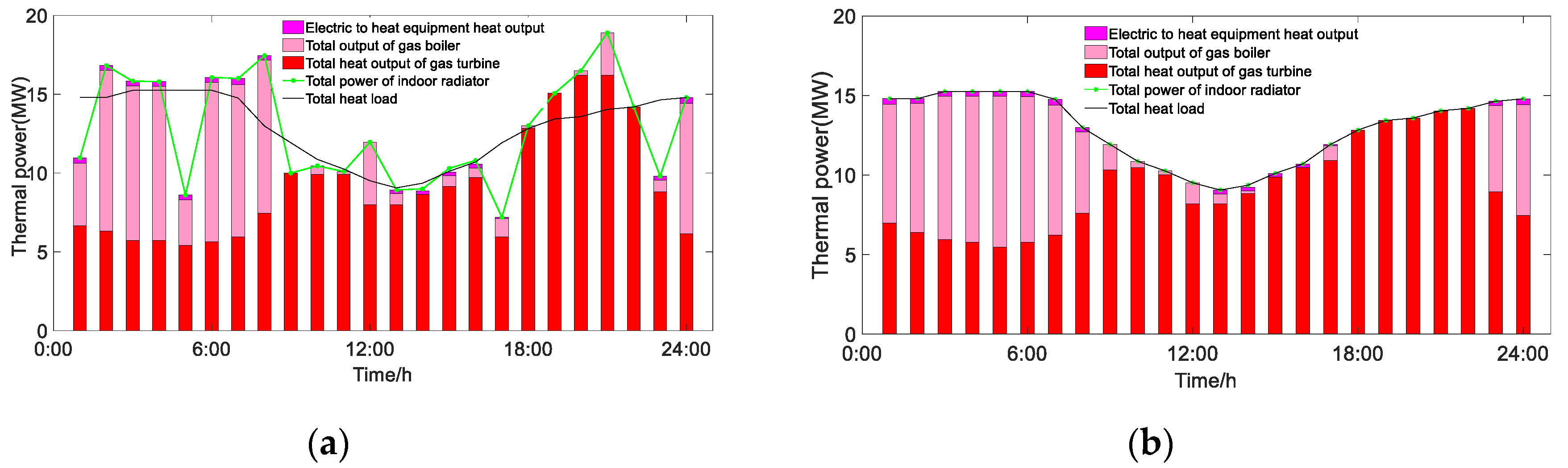
6.2.4. The Influence of the Heat Balance Cycle on Unit Output
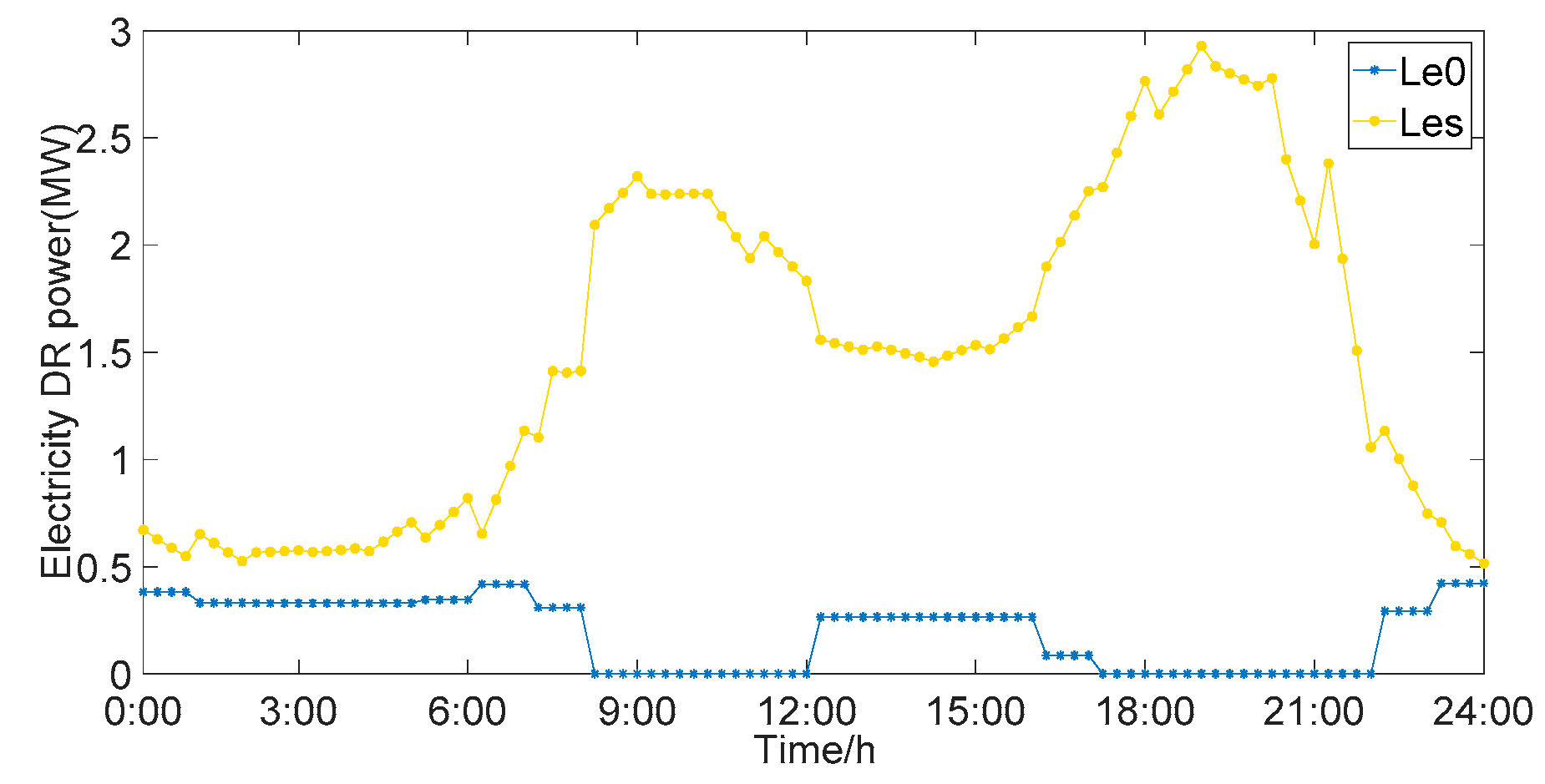
6.3. Considering DR Simulation Analysis
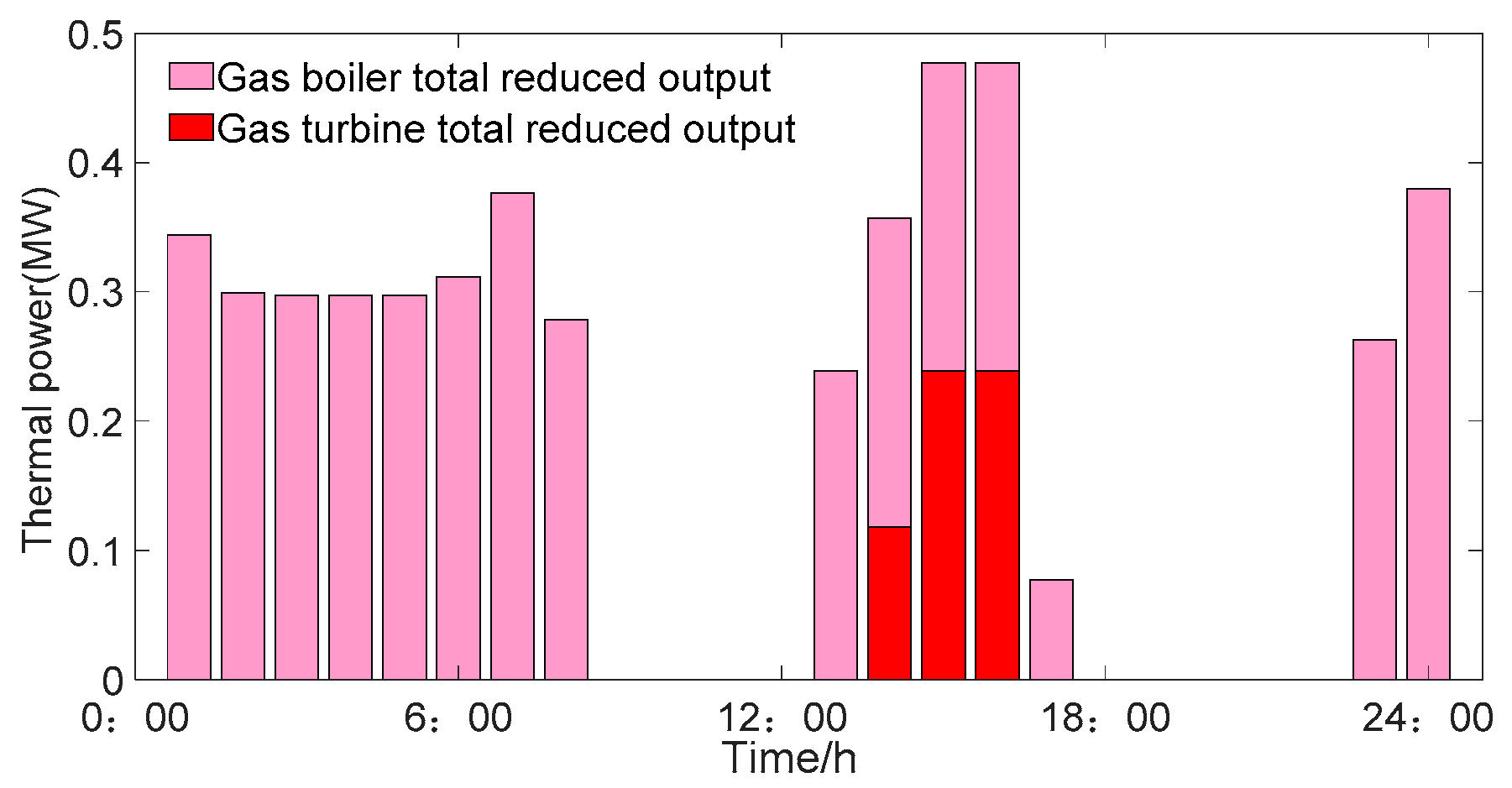
6.3.1. The Influence of DR on the Heat Balance Cycle
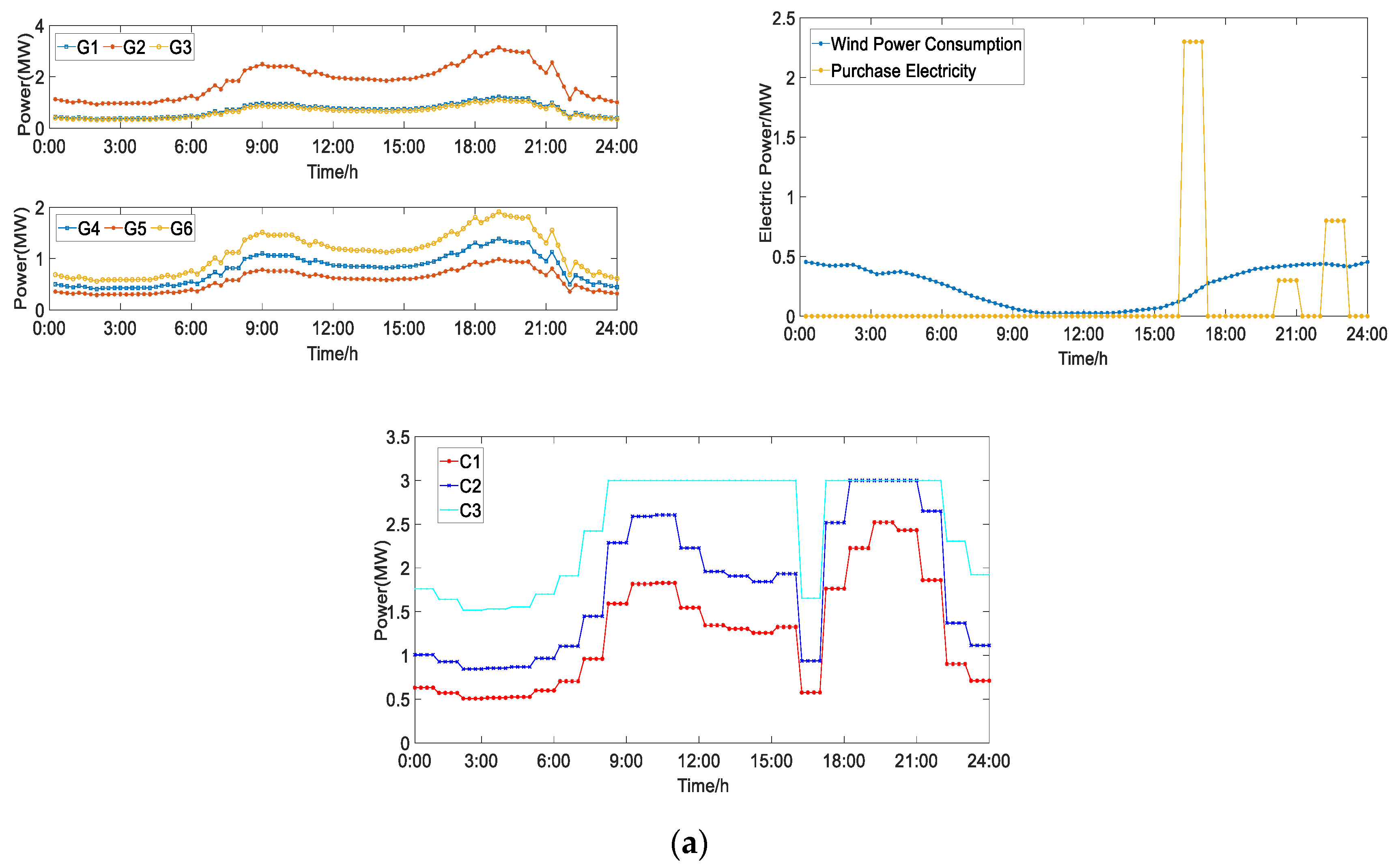
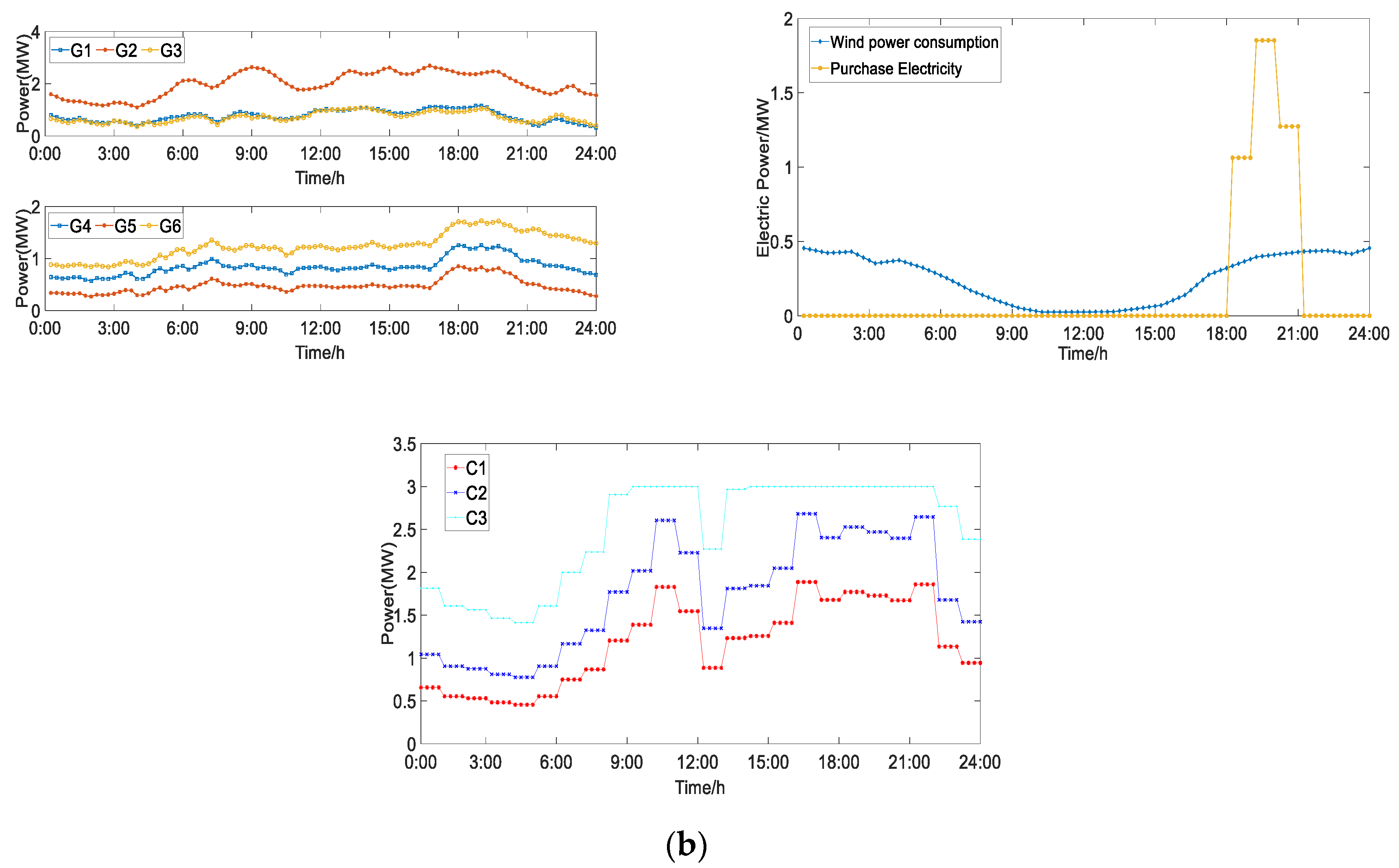
6.3.2. The Influence of DR on Unit Output
6.3.3. The Influence of DR on Wind Power Consumption
6.3.4. The Influence of DR and Optimal Heat Balance Cycle on Economy
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yin, S.R.; Ai, Q.; Zeng, S.Q. Research Challenges and Prospects of Multi-energy Distributed Optimization of Energy Internet. Power Syst. Technol. 2018, 5, 1359–1369. [Google Scholar]
- Zhou, R.J.; Chao, D.X.; Li, X.J. Space Coupled Particle Swarm Optimization Algorithm and IES-CCHP Regional Joint Dispatch under Peak-Valley Electricity Prices. Electr. Power Autom. Equip. 2016, 36, 11–17. [Google Scholar]
- Ameri, M.; Besharati, Z. Optimal Design and Operation of District Heating and Cooling Networks with CCHP Systems in a Residential Complex. Energy Build. 2016, 110, 135–148. [Google Scholar] [CrossRef]
- Gu, W.; Wang, Z.; Wu, Z. An Online Optimal Dispatch Schedule for CCHP Microgrids Based on Model Predictive Control. IEEE Trans. Smart Grid 2016, 99, 1–11. [Google Scholar]
- Chang, C.S.; Fu, W. Stochastic Multi Objective Generation Dispatch of Combined Heat and Power Systems. IEEE Proc. Gener. Transm. Distrib. 2002, 145, 583–591. [Google Scholar] [CrossRef]
- Moradi, H.; Moghaddam, M.P.; Moghaddam, I.G. Opportunities to Improve Energy Efficiency and Reduce Greenhouse Gas Emissions for a Cogeneration Plant. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 785–790. [Google Scholar]
- Dai, Y.H.; Chen, L.; Min, Y. Optimal Dispatch of Combined Operation of Wind Farm and Cogeneration with Heat Storage. Proc. Chin. Soc. Electr. Eng. 2017, 37, 3470–3479. [Google Scholar]
- Chen, X. Increasing the Flexibility of Combined Heat and Power for Wind Power Integration in China: Modeling and Implications. IEEE Trans. Power Syst. 2015, 30, 1848–1857. [Google Scholar] [CrossRef]
- Fragaki, A.; Andersen, A.N. Conditions for Aggregation of CHP Plants in the UK Electricity Market and Exploration of Plant Size. Appl. Energy 2011, 88, 3930–3940. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.; Wang, J.; Zhang, B.; Zheng, T. Transmission-Constrained Unit Commitment Considering Combined Electricity and District Heating Networks. IEEE Trans. Sustain. Energy 2016, 7, 480–492. [Google Scholar] [CrossRef]
- Olaia, E. Energy, Environmental and Economic Analysis of Air-to-Air Heat Pumps as an Alternative to Heating Electrification in Europe. Energies 2020, 13, 3939. [Google Scholar]
- Pei, W.; Deng, W.; Shen, Z.Q. Energy Coordination and Optimization of Hybrid Microgrid with Renewable Energy and Combined Heat and Power. Autom. Electr. Power Syst. 2014, 38, 9–15. [Google Scholar]
- Yu, D.Y.; Liang, J.; Han, X.S.; Zhao, J.G. Profiling the Regional Wind Power Fluctuation in China. Energy Policy 2011, 39, 299–306. [Google Scholar] [CrossRef]
- Anwar, M.B.; Qazi, H.W.; Burke, D.J.; Malley, M.J.O. Harnessing the Flexibility of Demand-Side Resources. IEEE Trans. Smart Grid 2019, 10, 4151–4163. [Google Scholar] [CrossRef]
- Tang, W.; Gao, F. Optimal Operation of Household Micro-Grid Day-Ahead Energy Considering User Satisfaction. High Volt. Eng. 2017, 43, 140–148. [Google Scholar]
- Dou, C.; Meng, C.; Yue, W.; Zhang, B. Double-Deck Optimal Schedule of Micro-Grid Based on Demand-Side Response. IET Renew. Power Gener. 2019, 13, 847–855. [Google Scholar] [CrossRef]
- Michał, T.; Robert, S. Buildings and a district heating network as thermal energy storages in the district heating system. Energy Build. 2018, 179, 49–56. [Google Scholar]
- Semikashev, V.V. Heat comfort of the population of Russia. Stud. Russ. Econ. Dev. 2010, 21, 393–402. [Google Scholar] [CrossRef]
- Zhu, C.Z.; Lu, S.; Zhou, J.H. Day-Ahead Economic Dispatch of Integrated Energy System Based on Electricity-Heat Time Scale Balance. Electr. Power Autom. Equip. 2018, 6, 138–143. [Google Scholar]
- Ge, W.C.; Li, P.; Sun, S.L.; Liu, A.M.; Li, J.J. Pre-Day Coordinated Optimal Control of Large-Scale Electro-thermal Internet Based on the Response of Heating Temperature Demand of Thermal Users. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3567–3572. [Google Scholar]
- Stamminger, R.; Broil, G.; Pakula, C.; Jungbecker, H.; Braun, M.; Rüdenauer, I.; Wendker, C. Synergy potential of smart appliances. Rep. Smart A Proj. 2008, D2.3, 1949–3053. [Google Scholar]
- Wang, J. Planning and Optimized Operation of Regional Integrated Energy System; Southeast University: Nanjing, China, 2017. [Google Scholar]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Najafi, H.R. Stochastic Security and Risk-Constrained Scheduling for an Autonomous Micro-Grid with Demand Response and Renewable Energy Resources. IET Renew. Power Gener. 2017, 11, 1812–1821. [Google Scholar] [CrossRef]
- Chen, J.S. Research on Demand Response Technology for Smart Power Consumption and Household Power Consumption Strategy; Chongqing University: Chongqing, China, 2014. [Google Scholar]
- Xu, B.; Liu, H.X. Optimal Dispatch of Regional Microgrid Based on Demand Response. J. Electr. Power Sci. Technol. 2018, 33, 132–140. [Google Scholar]
- Aalami, H.A.; Moghaddam, M.P.; Yousefi, G.R. Modeling and Prioritizing Demand Response Programs in Power Markets. Electr. Power Syst. Res. 2010, 80, 426–435. [Google Scholar] [CrossRef]
- Mognaddam, M.P.; Abdollahi, A.; Rashidinejad, M. Flexible Demand Response Programs Modeling in Competitive Electricity Markets. Appl. Energy 2011, 88, 3257–3269. [Google Scholar] [CrossRef]
- Lynch, M.; Nolan, S.; Devine, M.T. The Impacts of Demand Response Participation in Capacity Markets. Appl. Energy 2019, 250, 444–451. [Google Scholar] [CrossRef]
- Logenthiran, T.; Srinivasan, D.; Shun, T.Z. Demand Side Management in Smart Grid Using Heuristic Optimization. IEEE Trans. Smart Grid 2012, 3, 1244–1252. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; He, H.; Ren, S.; Weng, G. Real-Time Demand Side Management for a Microgrid Considering Uncertainties. IEEE Trans. Smart Grid 2019, 10, 3401–3414. [Google Scholar] [CrossRef]
- Wang, J.H.; Bloyd, C.N.; Zhao, G.H. Demand Response in China. Energy 2010, 35, 1592–1597. [Google Scholar] [CrossRef]
- Xue, Y.T.; Chen, Y.C.; Li, X.W. A Joint Peak-Valley Time-Of-Use Electricity Price Model Based on Customer Satisfaction and Ramsey Pricing Theory. Power Syst. Prot. Control 2018, 46, 122–128. [Google Scholar]
- Zou, Y.Y.; Yang, L.; Feng, L. Microgrid Heat and Power Coordinated Dispatch Considering Two-Dimensional Controllability of Heat Load. Autom. Electr. Power Syst. 2017, 41, 13–19. [Google Scholar]
- Duquette, J.; Rowe, A.; Wild, P.; Yan, J. Thermal Performance of a Steady State Physical Pipe Model for Simulating District Heating Grids with Variable Flow. Appl. Energy 2016, 178, 383–393. [Google Scholar] [CrossRef]
- Zhang, X.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Optimal Expansion Planning of Energy Hub with Multiple Energy Infrastructures. IEEE Trans. Smart Grid 2015, 6, 2302–2311. [Google Scholar] [CrossRef]
- Moeini-Aghtaie, M.; Dehghanian, P.; Fotuhi-Firuzabad, M.; Abbaspour, A. Multi-Gent Genetic Algorithm: An Online Probabilistic View on Economic Dispatch of Energy Hubs Constrained by Wind Availability. IEEE Trans. Sustain. Energy 2014, 5, 699–708. [Google Scholar] [CrossRef]
- Stephen, B.; Lieven, V. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nocedal, J.; Stephen, J.W. Numerical Optimization, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Yildirim, E.A.; Wright, S.J. Warm-Start Strategies in Interior-Point Methods for Linear Programming. SIAM J. Optim. 2002, 12, 782–810. [Google Scholar] [CrossRef]
- Mousavi, O.A.; Cherkaoui, R. Investigation of P–V and V–Q Based Optimization Methods for Voltage and Reactive Power Analysis. Int. J. Electr. Power Energy Syst. 2014, 63, 769–778. [Google Scholar] [CrossRef]
- Ma, X.S.; Li, Y.L.; Yan, L. Comparison of Traditional Multi-Objective Optimization Methods and Multi-Objective Genetic Algorithms. Electr. Drive Autom. 2010, 32, 48–50. [Google Scholar]








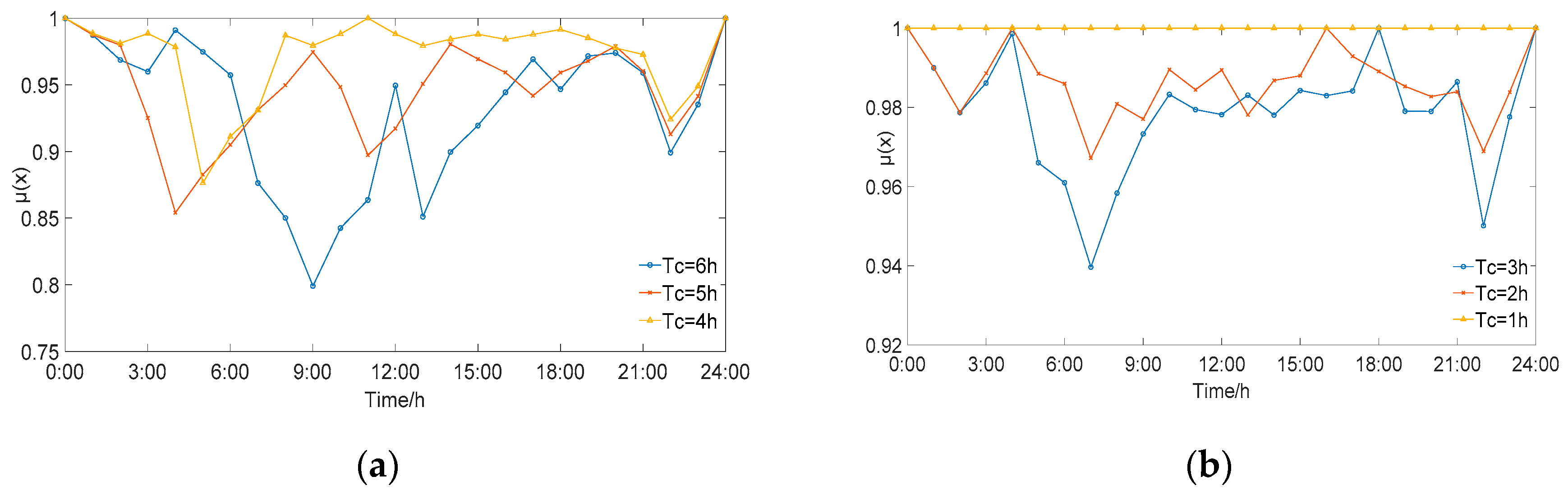


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 4200 | 0.3 | ||
| 200 | 0.75 | ||
| h | 0.25 | 0.95 |
| Unit | Parameter | Value |
|---|---|---|
| G1, G4 | 0.097/50/0 | |
| 3 | ||
| G2, G5 | 0.096/47/0 | |
| 3 | ||
| G3, G6 | 0.094/45/0 | |
| 3 | ||
| C1 | 0.02/100/0 | |
| 0.02/100/0 | ||
| / | 3/6 | |
| C2 | 0.015/95/0 | |
| 0.015/95/0 | ||
| / | 3/6 | |
| C3 | 0.01/90/0 | |
| 0.01/90/0 | ||
| / | 3/6 | |
| W1, W2, W3 | // | 0.5/0.5/0.5 |
| Case | State | = 0.5 MW | = 1 MW | |||
|---|---|---|---|---|---|---|
| Wind Power Consumption (MW·h) | Power Purchase Cost (Ten Thousand Yuan) | Total Cost (Ten Thousand Yuan) | Wind Power Consumption (MW·h) | Total Cost (Ten Thousand Yuan) | ||
| DR | × | 6.026 | 0.312 | 21.1486 | 9.232 | 21.052 |
| 1 h | ||||||
| DR | × | 6.052 | 0.181 | 21.0271 | 9.261 | 21.931 |
| 3 h | ||||||
| DR | √ | 6.136 | 0.307 | 21.126 | 12.087 | 20.947 |
| 1 h | ||||||
| DR | √ | 6.182 | 0.177 | 21.0201 | 12.134 | 20.842 |
| 4 h | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.-R.; Sun, S.-L.; Sun, Q.-Y.; Zhong, W.-Y. Time-Scale Economic Dispatch of Electricity-Heat Integrated System Based on Users’ Thermal Comfort. Energies 2020, 13, 5505. https://doi.org/10.3390/en13205505
Liu X-R, Sun S-L, Sun Q-Y, Zhong W-Y. Time-Scale Economic Dispatch of Electricity-Heat Integrated System Based on Users’ Thermal Comfort. Energies. 2020; 13(20):5505. https://doi.org/10.3390/en13205505
Chicago/Turabian StyleLiu, Xin-Rui, Si-Luo Sun, Qiu-Ye Sun, and Wei-Yang Zhong. 2020. "Time-Scale Economic Dispatch of Electricity-Heat Integrated System Based on Users’ Thermal Comfort" Energies 13, no. 20: 5505. https://doi.org/10.3390/en13205505
APA StyleLiu, X.-R., Sun, S.-L., Sun, Q.-Y., & Zhong, W.-Y. (2020). Time-Scale Economic Dispatch of Electricity-Heat Integrated System Based on Users’ Thermal Comfort. Energies, 13(20), 5505. https://doi.org/10.3390/en13205505