Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter
Abstract
:1. Introduction
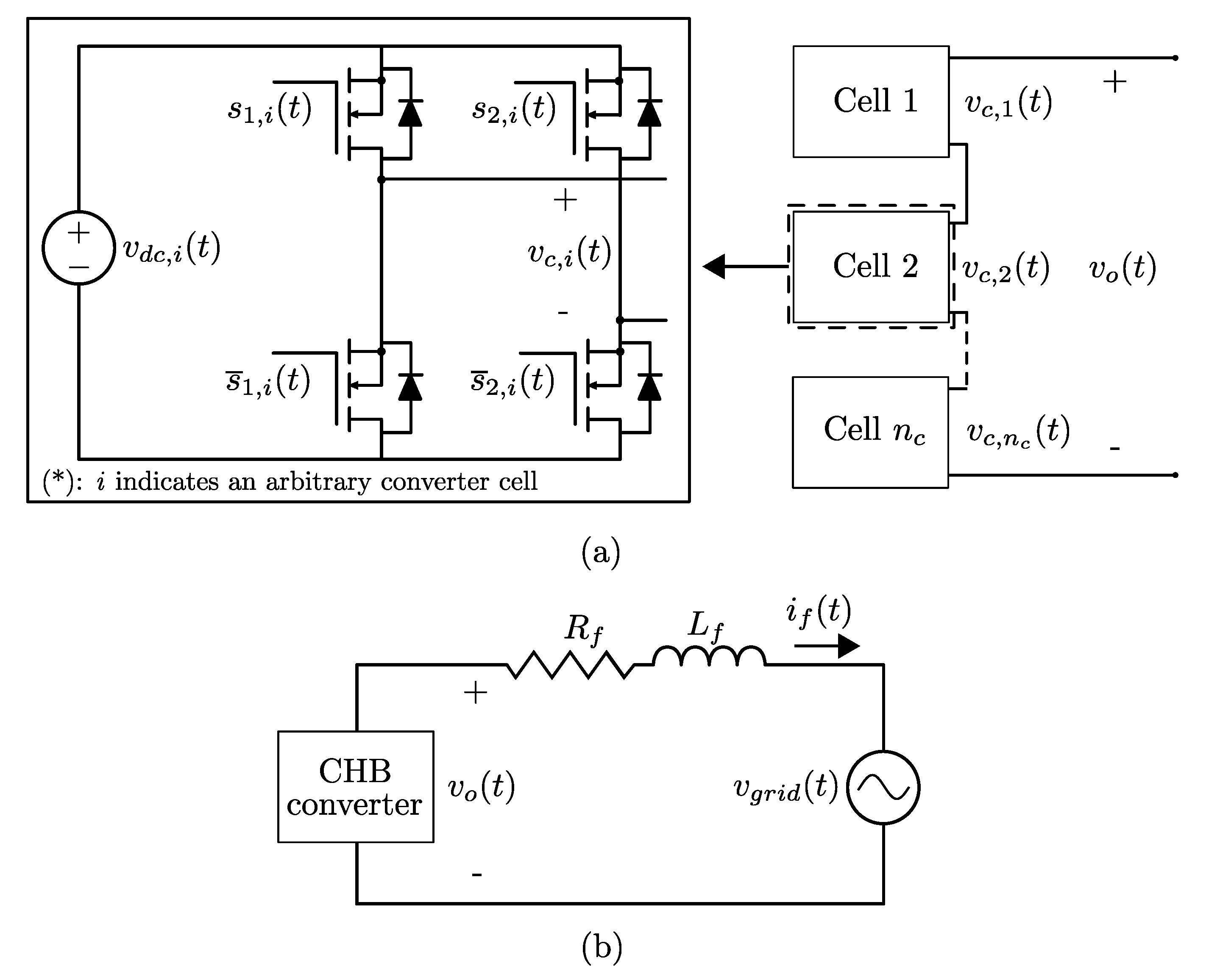
2. Cascaded H-Bridge Converter
3. Proposed Predictive Control
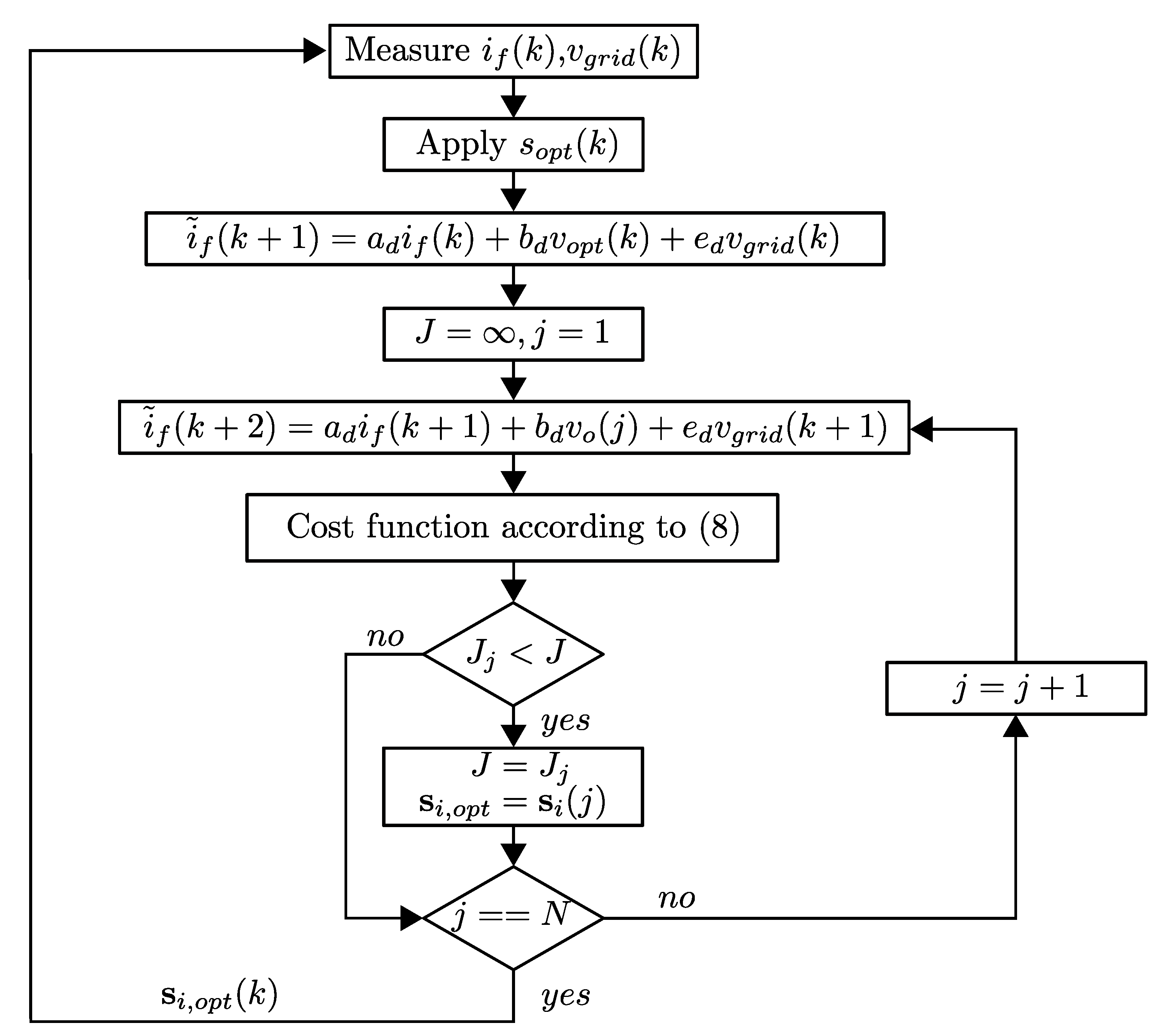
3.1. Conventional FCS-MPC
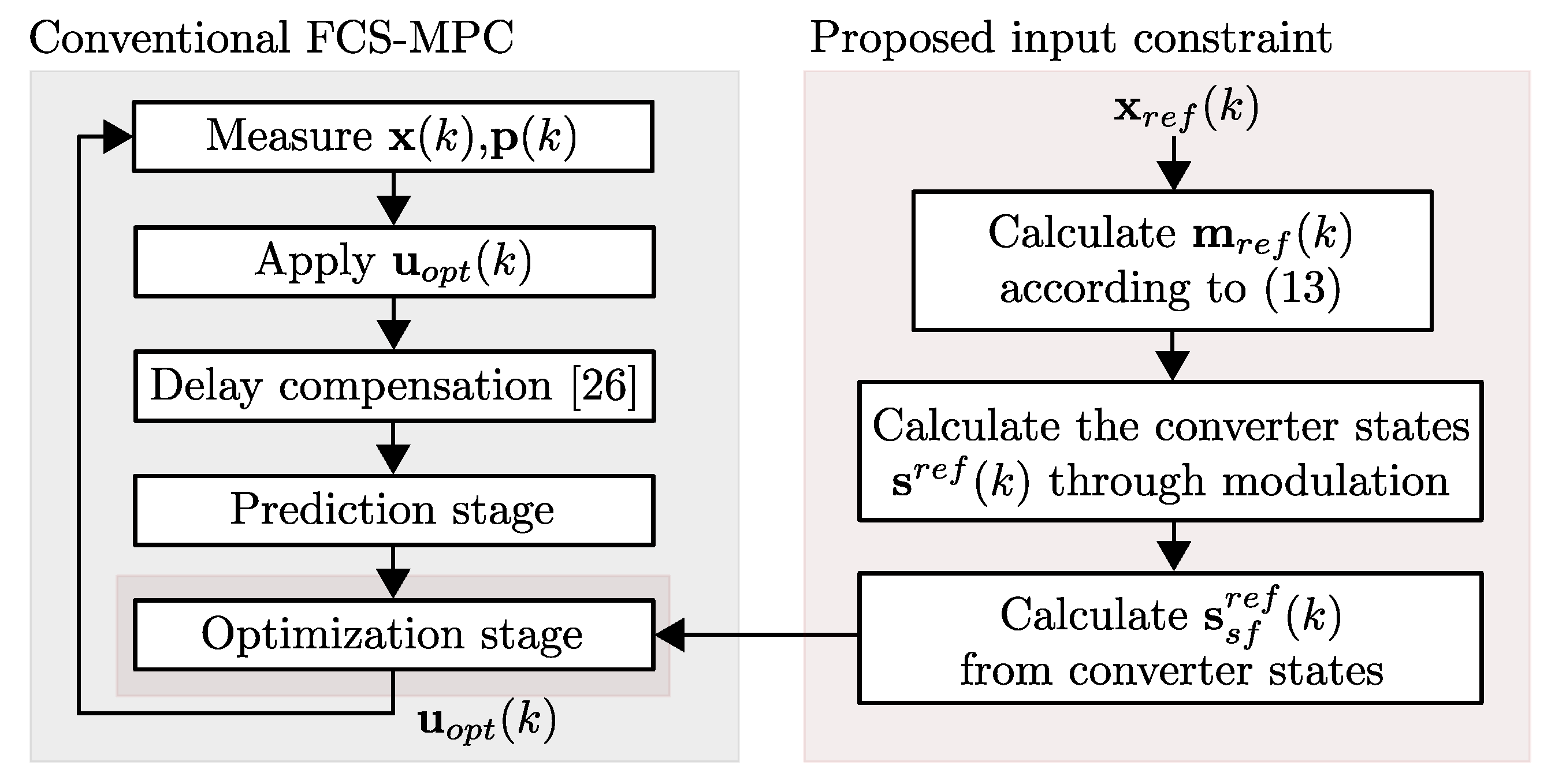
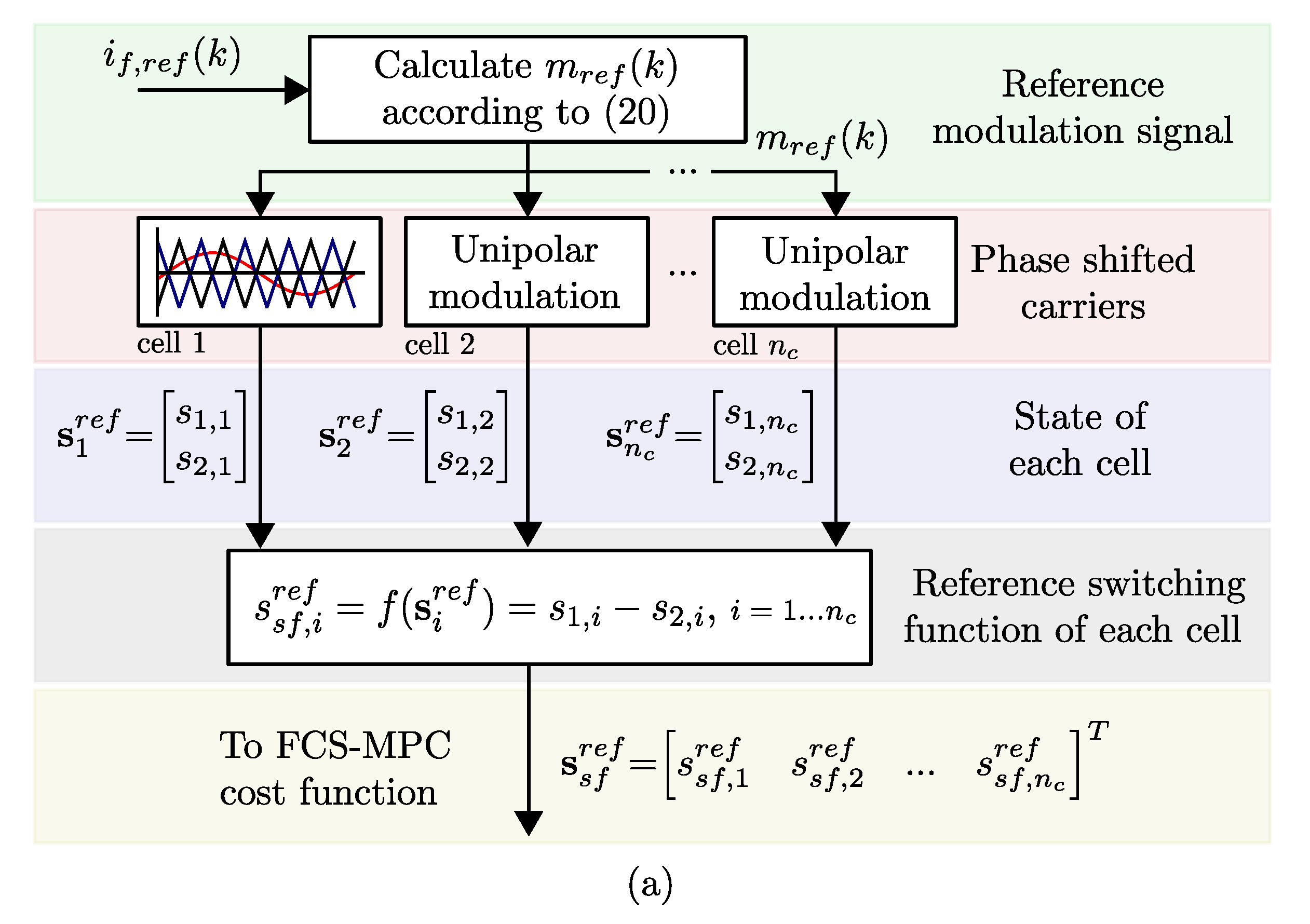
3.2. Proposed FCS-MPC
- Step 1:
- Step 2:
- Step 3:
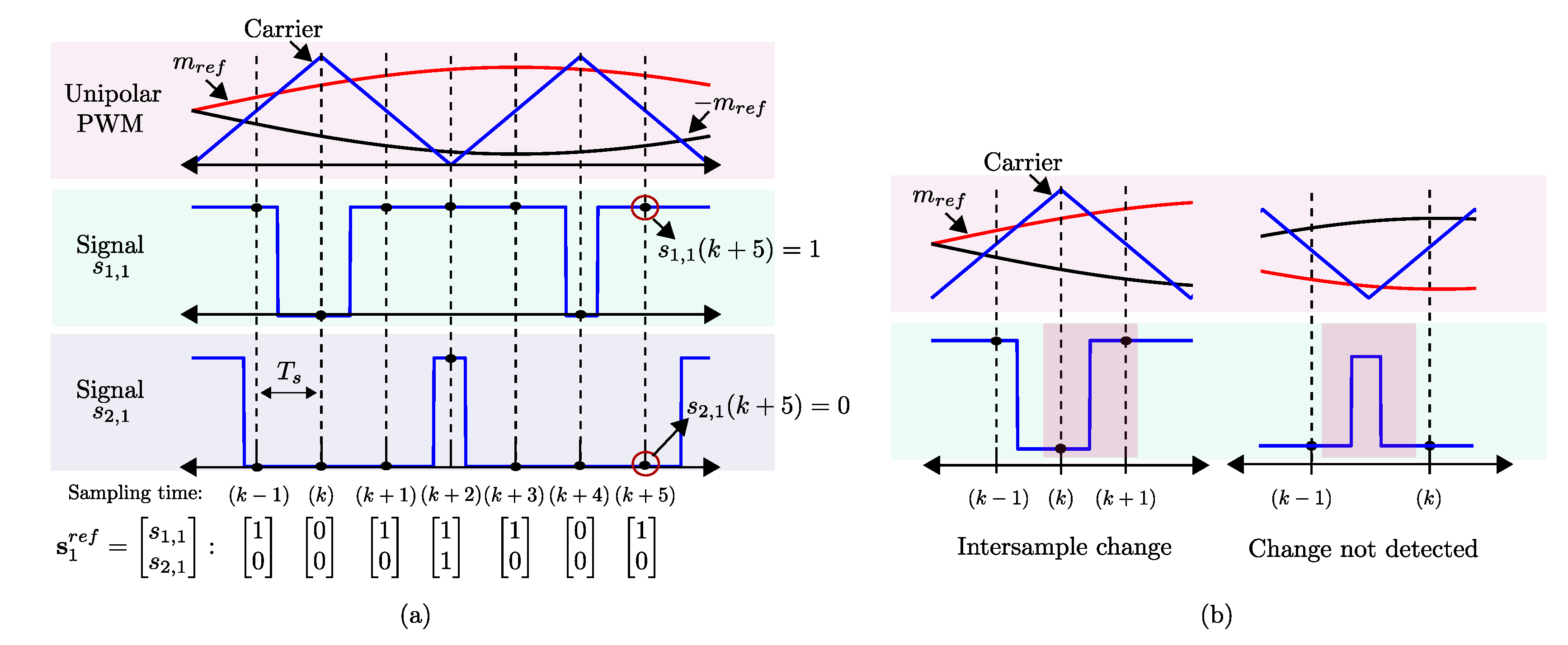
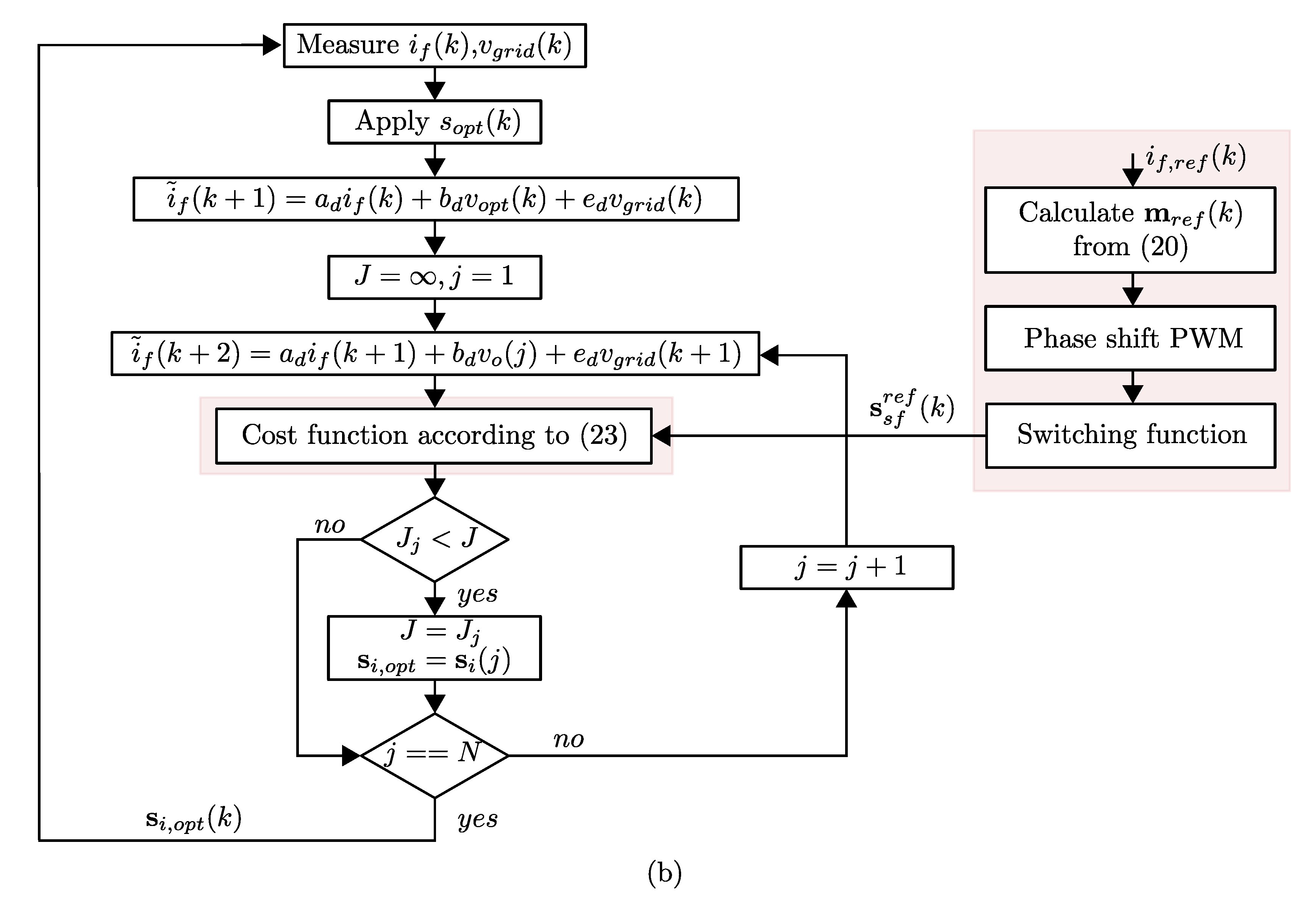
3.3. Proposed Scheme Applied to Single Phase CHB Converter
- Step 1:
- Step 2:
- Step 3:
4. Experimental Results
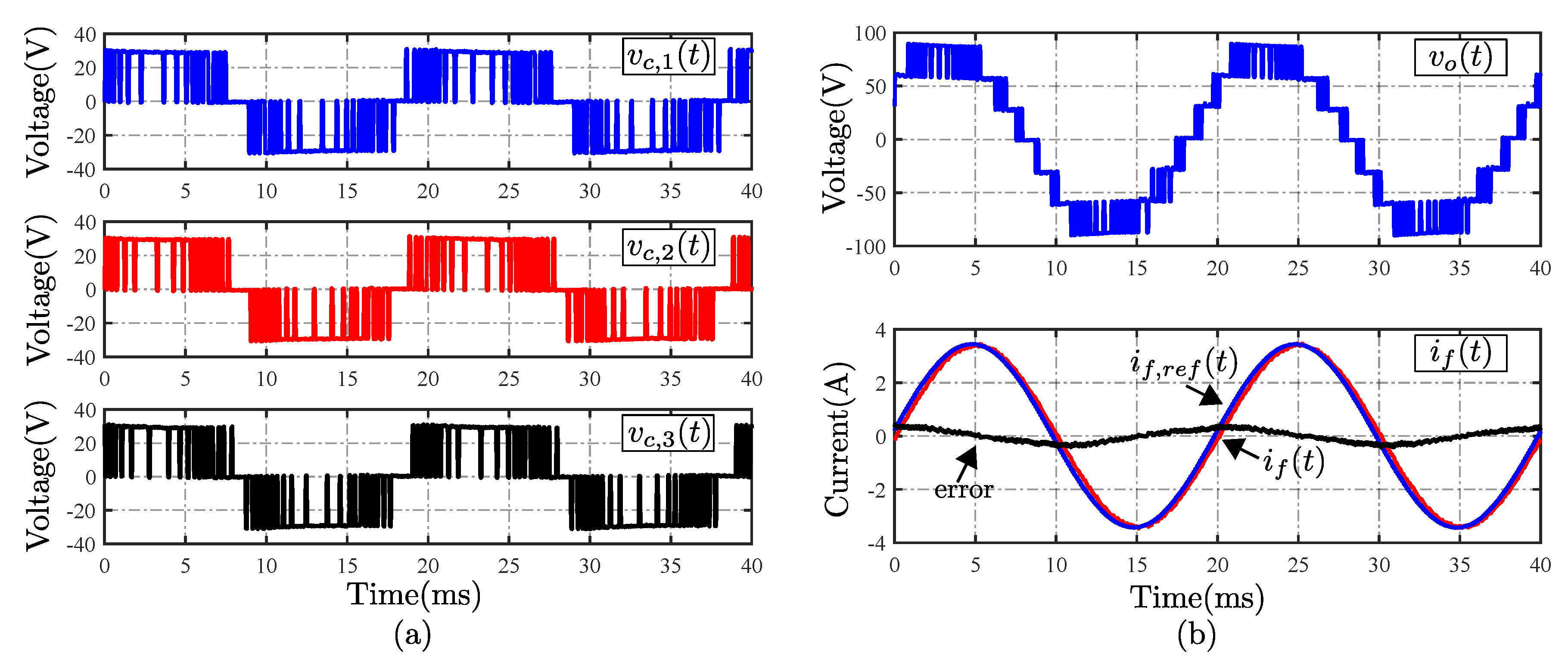
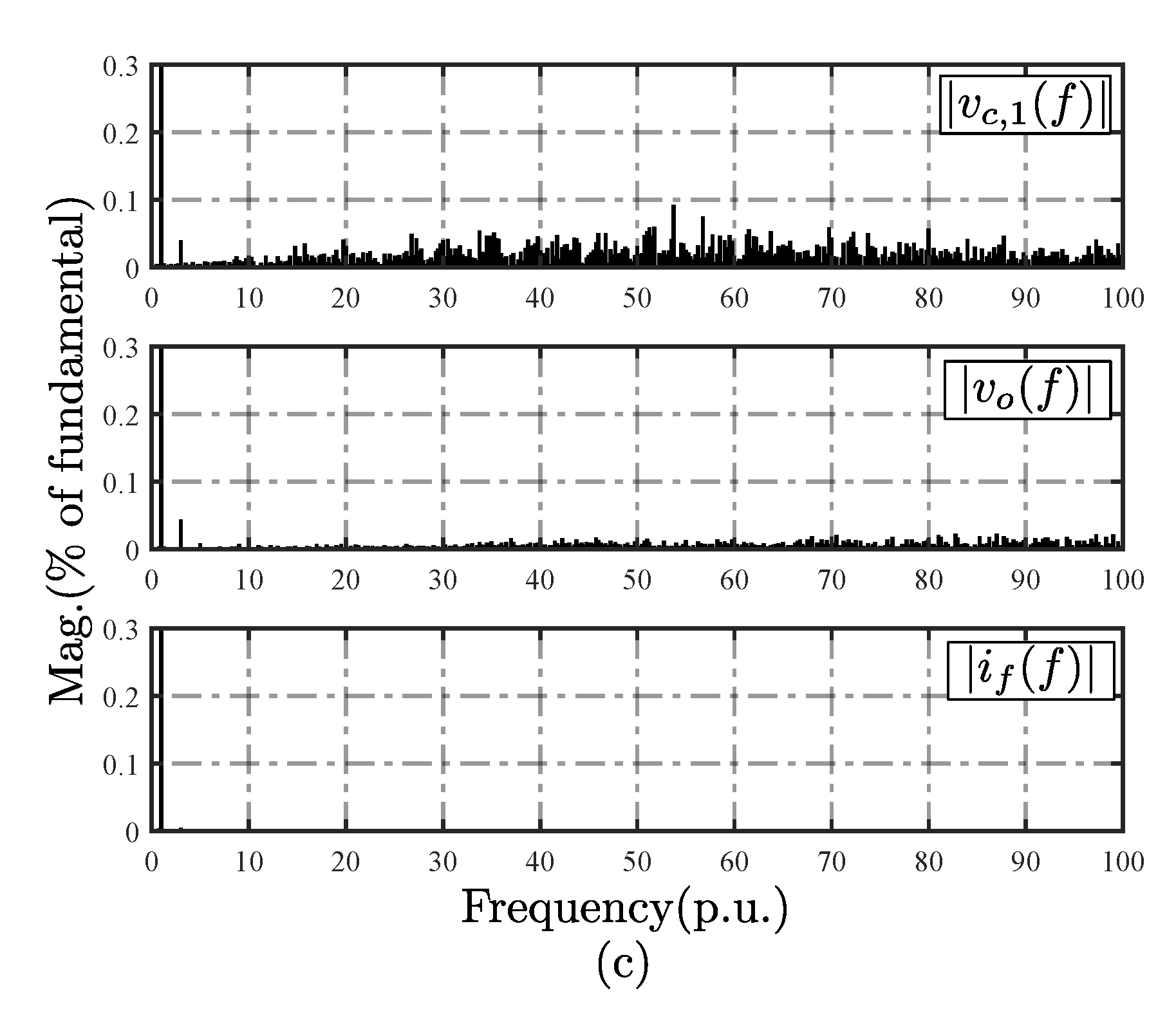
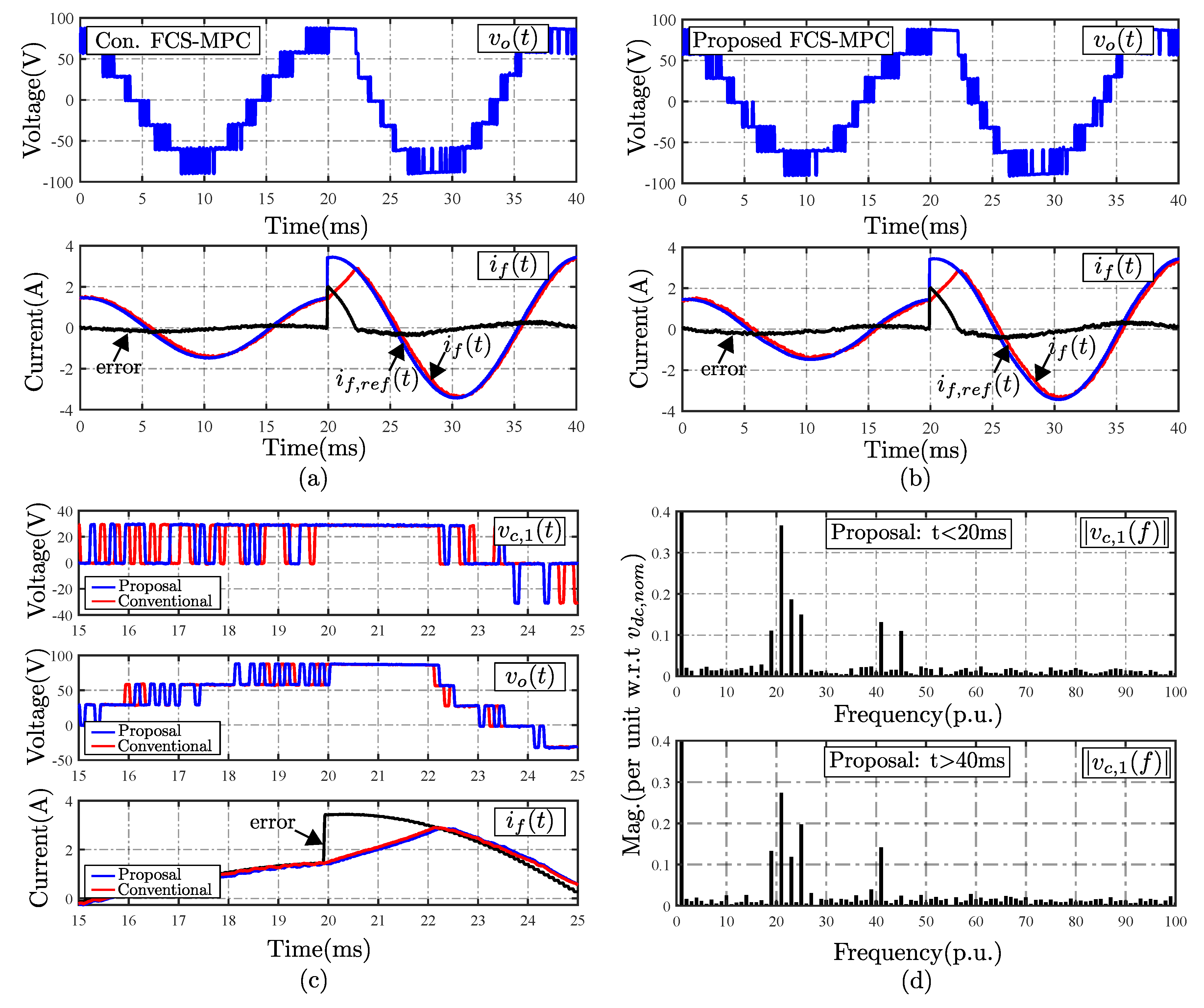
4.1. Steady-State Performance
4.2. Dynamic Performance
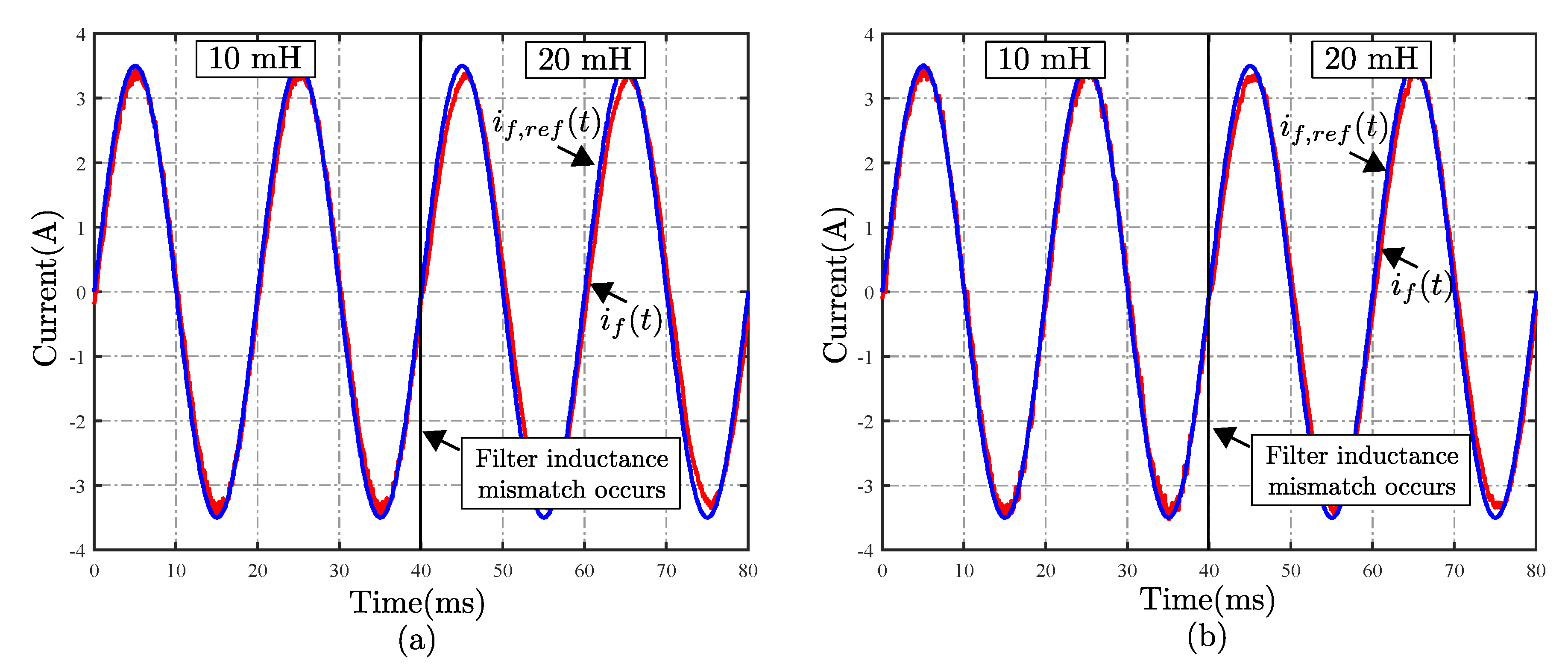
4.3. Parameter Sensitivity
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cortes, P.; Kazmierkowski, M.P.; Kennel, R.M.; Quevedo, D.E.; Rodriguez, J. Predictive control in power electronics and drives. IEEE Trans. Ind. Electron. 2008, 55, 4312–4324. [Google Scholar] [CrossRef]
- Roberts, P.D. A brief overview of model predictive control. In Proceedings of the IEEE Seminar on Practical Experiences with Predictive Control, Middlesbrough, UK, 16 February 2000; Volume 55, pp. 1–3. [Google Scholar]
- Lee, J.H. Model predictive control: Review of the three decades of development. Int. J. Control Autom. Syst. 2011, 9, 415–424. [Google Scholar] [CrossRef]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R.; Zancheta, P.; Abu-Rub, H.; Young, H.A.; Rojas, C.A. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inf. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Huang, J.; Yang, B.; Guo, F.; Wang, Z.; Tong, X.; Zhang, A.; Xiao, J. Priority sorting approach for modular multilevel converter based on simplified model predictive control. IEEE Trans. Ind. Electron. 2018, 65, 4819–4830. [Google Scholar] [CrossRef]
- Aguilera, R.; Lezana, P.; Quevedo, D. Switched model predictive control for improved transient and steady-state performance. IEEE Trans. Ind. Inf. 2015, 11, 968–977. [Google Scholar] [CrossRef]
- Kouro, S.; Cortes, P.; Vargas, R.; Ammann, U.; Rodriguez, J. Model predictive control -A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2009, 56, 1826–1838. [Google Scholar] [CrossRef]
- Sandre-Hernandez, O.; Rangel-Magdaleno, J.; Morales-Caporal, R. A comparison on finite-set model predictive torque control schemes for PMSMs. IEEE Trans. Ind. Electron. 2018, 33, 8838–8847. [Google Scholar] [CrossRef]
- Patsakis, G.; Karamanakos, P.; Stolze, P.; Manias, S.; Kennel, R.; Mouton, T. Variable switching point predictive torque control for the four-switch three-phase inverter. In Proceedings of the IEEE International Symposium on Sensorless Control for Electrical Drives and Predictive Control of Electrical Drives and Power Electronics, Munich, Germany, 17–19 October 2013; Volme 33, pp. 1–8. [Google Scholar]
- Acuna, P.; Aguilera, R.; Ghias, A.; Rivera, M.; Baier, C.; Agelidis, V. Cascade-Free Model Predictive Control for Single-Phase Grid-Connected Power Converters. IEEE Trans. Ind. Electron. 2017, 64, 285–294. [Google Scholar] [CrossRef]
- Ramírez, R.; Espinoza, J.; Baier, C.; Rivera, M.; Villarroel, F.; Guzman, J.; Melín, P. Finite-State Model Predictive Control with Integral Action Applied to a Single-Phase Z-Source Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 228–239. [Google Scholar] [CrossRef]
- Ge, H.; Zhen, Y.; Wang, Y.; Wang, D. Research on LCL filter active damping strategy in active power filter system. In Proceedings of the International Conference on Modelling, Identification and Control, Kunming, China, 10–12 July 2017; pp. 476–481. [Google Scholar]
- Fang, J.; Xiao, G.; Yang, X.; Tang, Y. Parameter design of a novel series-parallel-resonant LCL filter for single-phase half-bridge active power filters. IEEE Trans. Power Electron. 2017, 32, 200–217. [Google Scholar] [CrossRef]
- Ferreira, S.; Gonzatti, R.; Pereira, R.; da Silva, C.; da Silva, L.; Lambert-Torres, G. Finite control set model predictive control for dynamic reactive power compensation with hybrid active power filters. IEEE Trans. Power Electron. 2018, 65, 2608–2617. [Google Scholar] [CrossRef]
- Geldenhuys, J.; du Toit Mouton, H.; Rix, A.; Geyer, T. Model predictive current control of a grid connected converter with LCL-filter. In Proceedings of the IEEE Workshop on Control and Modeling for Power Electronics (COMPEL), Trondheim, Norway, 27–30 June 2016; pp. 1–6. [Google Scholar]
- Yaramasu, V.; Rivera, M.; Wu, B.; Rodriguez, J. Model predictive current control of two-level four-leg inverters—Part I: Concept, algorithm, and simulation analysis. IEEE Trans. Power Electron. 2013, 28, 3459–3468. [Google Scholar] [CrossRef]
- Aguirre, M.; Kouro, S.; Rojas, C.; Rodriguez, J.; Leon, J. Switching frequency regulation for FCS-MPC based on a period control approach. IEEE Trans. Power Electron. 2018, 65, 5764–5773. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.; Degano, M.; Bifaretti, S. Modulated Model Predictive Control for a Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2015, 51, 1610–1620. [Google Scholar] [CrossRef]
- Donoso, F.; Mora, A.; Cardenas, R.; Angulo, A.; Sáez, D.; Rivera, M. Finite-Set Model-Predictive Control Strategies for a 3L-NPC Inverter Operating With Fixed Switching Frequency. IEEE Trans. Ind. Electron. 2018, 65, 3954–3965. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D.; Peng, Z. Cascade-Free Fuzzy Finite-Control-Set Model Predictive Control for Nested Neutral Point-Clamped Converters With Low Switching Frequency. IEEE Trans. Control Syst. Technol. 2019, 27, 2237–2244. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Yang, H.; Fan, S. New Insights into Model Predictive Control for Three-Phase Power Converters. IEEE Trans. Ind. Appl. 2019, 55, 1973–1982. [Google Scholar] [CrossRef]
- Gong, Z.; Wu, X.; Dai, P.; Zhu, R. Modulated Model Predictive Control for MMC-Based Active Front-End Rectifiers Under Unbalanced Grid Conditions. IEEE Trans Ind. Electron. 2019, 66, 2398–2409. [Google Scholar] [CrossRef]
- Malinowski, M.; Gopakumar, K.; Xu, D.; Rodriguez, J.; Pérez, M.A. A Survey on Cascaded Multilevel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2197–2206. [Google Scholar] [CrossRef]
- Wilson, A.; Cortés, P.; Kouro, S.; Rodriguez, J.; Abu-Rub, H. Model predictive control for cascaded h-bridge multilevel inverters with even power distribution. In Proceedings of the IEEE International Conference on Industrial Technology, Vina del Mar, Chile, 14–17 March 2010; Volume 57, pp. 1271–1276. [Google Scholar]
- Cortés, P.; Wilson, A.; Kouro, S.; Rodriguez, J.; Abu-Rub, H. Model Predictive Control of Multilevel Cascaded H-Bridge Inverters. IEEE Trans. Ind. Electron. 2010, 57, 2691–2699. [Google Scholar] [CrossRef]
- Karamanakos, P.; Geyer, T. Guidelines for the Design of Finite Control Set Model Predictive Controllers. IEEE Trans. Ind. Electron. 2020, 7, 7434–7450. [Google Scholar] [CrossRef]
- Cortés, P.; Kouro, S.; La Rocca, B.; Vargas, R.; Rodríguez, J.; León, J.I.; Vazquez, S.; Franquelo, L.G. Guidelines for weighting factors design in Model Predictive Control of power converters and drives. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Gippsland, Australia, 10–13 February 2009; pp. 1–7. [Google Scholar]
- Cortes, P.; Rodriguez, J.; Quevedo, D.; Silva, C. Predictive Current Control Strategy With Imposed Load Current Spectrum. IEEE Trans. Ind. Electron. 2007, 23, 612–618. [Google Scholar]


| 1 | 0 | + |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
| 0 | 1 | − |
| Features | Description | Value |
|---|---|---|
| Cells DC voltage | 30 V | |
| Grid voltage | 120 V | |
| Filter resistance | 0.6 | |
| Filter inductance | 20 mH | |
| Grid frequency | 50 Hz | |
| Sampling frequency | 10 kHz | |
| Carrier frequency | 550 Hz |
| Voltage | Conventional FCS-MPC [24] | Proposed FCS-MPC |
|---|---|---|
| 0.929 | 0.959 | |
| 0.931 | 0.935 | |
| 0.937 | 0.935 | |
| 2.797 | 2.829 |
| Signal | Conventional FCS-MPC [24] | Proposed FCS-MPC |
|---|---|---|
| 32.32 | 49.22 | |
| 33.16 | 47.78 | |
| 30.90 | 47.19 | |
| 9.92 | 10.34 | |
| 1.04 | 1.32 |
| Feature | Conventional FCS-MPC | Proposed FCS-MPC | Period Control [17] | M2PC [18] | Notch Filter [28] |
|---|---|---|---|---|---|
| Switching frequency depends of | Sampling frequency | Carrier ✓ frequency | Weighting factor tuning | SVM frequency | Filter tuning |
| Dynamic response | Fast ✓ | Fast ✓ | Fast ✓ | Fast ✓ | Medium |
| Spread spectrum | High | Low ✓ | Medium | Medium | Low ✓ |
| Implementation | Simple ✓ | Simple ✓ | Medium | Medium | Medium |
| Even power distribution (CHB case) | No | Yes ✓ | No | Yes ✓ | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez, R.O.; Baier, C.R.; Espinoza, J.; Villarroel, F. Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies 2020, 13, 5475. https://doi.org/10.3390/en13205475
Ramírez RO, Baier CR, Espinoza J, Villarroel F. Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies. 2020; 13(20):5475. https://doi.org/10.3390/en13205475
Chicago/Turabian StyleRamírez, Roberto O., Carlos R. Baier, José Espinoza, and Felipe Villarroel. 2020. "Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter" Energies 13, no. 20: 5475. https://doi.org/10.3390/en13205475
APA StyleRamírez, R. O., Baier, C. R., Espinoza, J., & Villarroel, F. (2020). Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies, 13(20), 5475. https://doi.org/10.3390/en13205475







