1. Introduction
The political guidelines for the new European Commission (2019–2024) propose a European Green Deal, that puts Europe at the forefront, to become the world’s first climate neutral continent [
1]. The role of electricity is expected to increase in the coming decade and by 2050 all scenarios contain high end-use electrification, which would mean 53% by 2050, from 20% in 2018 of electricity in final energy consumption share [
2]. Following the agreements achieved internationally in the Paris 2015 summit [
3], the European targets regarding climate and energy, are further set in 2019 for clean energy, under the context of the Clean Energy Package (CEP) [
4]. In order for such targets to be achieved, the continuous developments of electricity markets move towards a homogeneous system, aiming at a full integration. With energy storage, Demand Response (DR), energy communities and aggregators now a reality there are new opportunities for market participation and to generate profits. Market forecasting in order to optimize resources and revenues, is now in the forefront of research and discussions for power generators, power purchasing parties/consumers and regulators alike. Besides the dynamic and highly complex traded value of electricity as a commodity, which is subject to multiple intrinsic and extrinsic variables, trying to predict the market with a high degree of confidence has many benefits for all market participants. Such benefits arise from setting up their respective risk-adjusted bidding strategies and ensuring cost-optimal generation activities, to formulating evidence and insights on the economic development of a country’s power sector, as well as ensuring the reliable security and safe operation of the whole electricity system [
5,
6]. In order to maximize profits, market participants employ forecasting tools with different time horizons based on the different markets they are operating in. These typically vary from half-hourly or hourly settlement periods (real-time, balancing markets, imbalance exposure) to months ahead in the wholesale markets (intraday, day-ahead, spot, derivative markets) similar to those of a commodity. Market participants are faced with a number of risks, including the constant requirement of maintaining the supply-demand equilibrium, the short-term inelastic demand, the generation and load side uncertainties in the system, as well as other quantifiable and non-quantifiable factors, such as fuel prices, cost of unit operation, the markets’ design and requirements and also the impact of weather conditions, just to mention a few. Other uncertainties regarding the complex process of forecasting the electricity price include extreme volatility, high frequency and price spiking behavior, non-constant mean and variance as well as multiple seasonality [
7,
8].
In this context a plethora of studies has been developed over the years, in order to address the compound implications of electricity price forecasting. Aggarwal et al. (2009) [
7] published a comprehensive first of its kind market forecasting review of 47 articles. It focused on the quantitative methodological approaches undertaken, and distinguished them based on the type of the models and their architectures, the input and output variables used, the prediction horizon of the forecasts, as well as the preprocessing and the exploratory analysis of the data and the results. According to the authors, the employed techniques were found to be similar to load forecasting models and were broken down into (a) game theory models including stochastic and parsimonious models, (b) time-series models, which incorporated artificial intelligence and neural-network based algorithms, and finally (c) simulation techniques which accounted for regression or other causal models. The input factors which could have an impact on the electricity prices were grouped into (a) market characteristics (historical generation, supply, load etc.), (b) nonstrategic uncertainties such as forecast load and reserves or weather parameters, (c) other stochastic uncertainties such us generation outages and transmission congestions/contingencies, (d) behavior indices which referred to historical price data, demand elasticity and market participants’ bidding strategies, and (e) temporal effect such as settlement period, day, month, public holidays, seasons etc. The study’s in-depth analysis, found that the time of the day variable and the more complex to model bidding strategies factor were the most significant, suggesting a mathematical equation, which would also incorporate an additive residual term. This term intends to reflect the load and supply deviation from normally and randomly correlated short-term effects in the market. Despite their very systematic approach, they concluded that there was no systematic evidence of one model outperforming another on a consistent basis mainly due to the illiquidity and general paucity of historical electricity market data. The study also reported that some methods, i.e., multivariate dynamic regression, transfer loss models and nonlinear neural-network models, performed qualitatively better compared to univariate Autoregressive Integrated Moving Average (ARIMA) ones. However, the latter in combination with fuzzy logic or a wavelet transformation approach could hold promise in future developments. An even more comprehensive review of hundreds of relevant articles, proceedings and journals in the literature by [
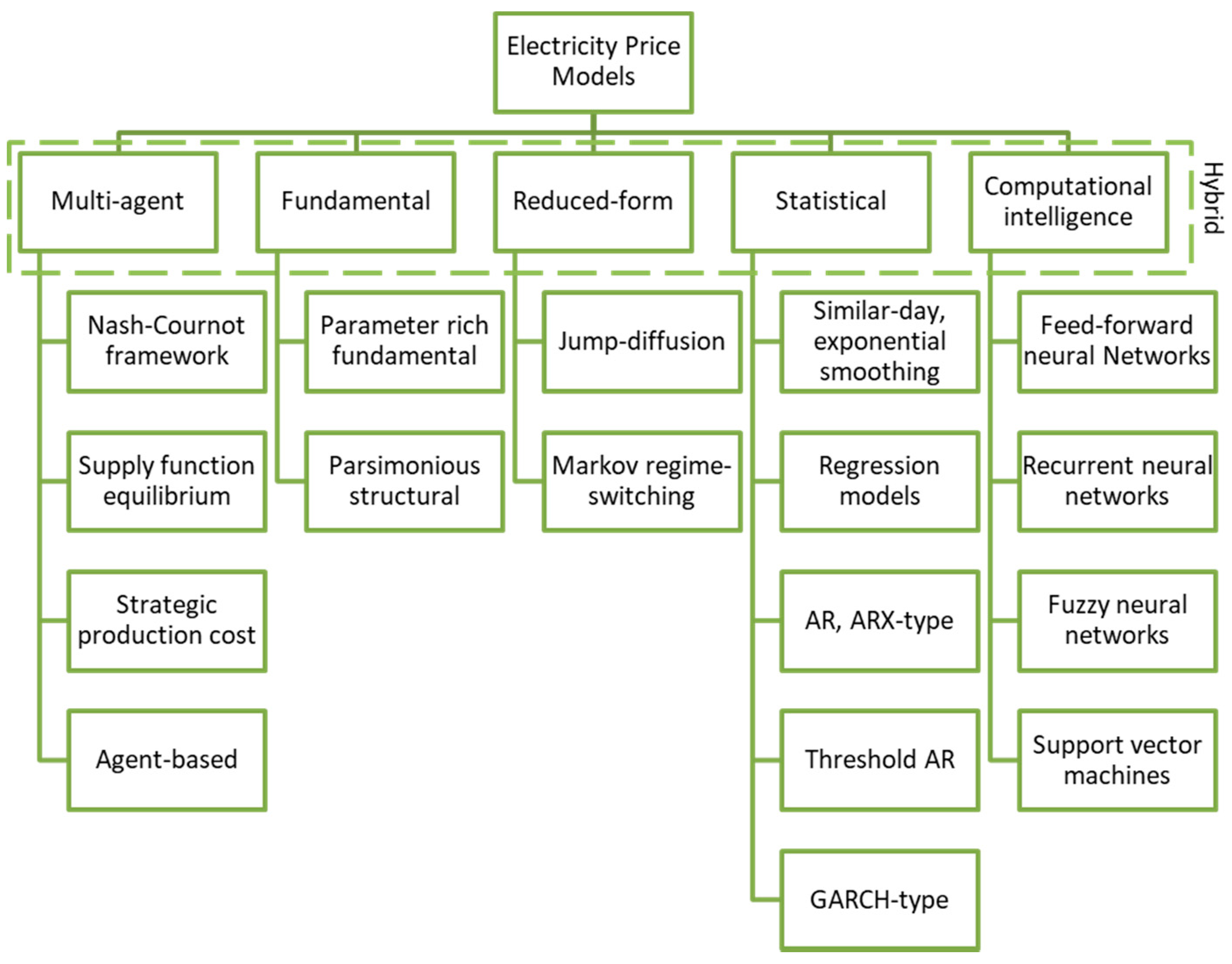
9], suggested the categorization of models into similar categories shown in
Figure 1. The main difference is the addition of the structural or fundamental models, which derive from the modelling of significant economic and physical factors in the power systems as well as hybrid solutions of the following techniques in the sub-branches.
The author highlights in great detail the flexibility of multi-agent models [
10,
11,
12,
13,
14,
15,
16] with regards to the analysis and incorporation of the multi-dimensional strategic behaviors of the market participants as variables and agents. At the same time however, this is one of the main caveats of this family of models since the underlying assumptions used in the model simulations introduce a lot of risk and uncertainty (i.e., a power generator can either be a buyer, or a seller depending on his position or strategy). Evidence in the literature, also shows that another constraint of agent-based models is the prediction accuracy of the electricity price as an output variable, since the outcomes of such models have more qualitative implications (i.e., whether prices will be above marginal costs or not) rather than quantitative [
9]. With regards to fundamental models, they are considered to be more suitable for medium-term forecasts and not so much for short-term predictions, due to data quality, resolution and availability. Due to the nature of the fundamental data used on plant and transmission capacities and costs, they tend to overlook the hourly or half-hourly resolution, of the data needed in the case of short-term price forecasting, hence, they seem to be a better fit for describing market fundamentals. On a similar note, another challenge they face is their sensitivity to violations on significant assumptions made on the economical and physical relationships of the power entities of the market, therefore their optimization and calibration tend to be rather complex when incorporating stochastic fluctuations of fundamental factors. Similarly, purely reduced-form models, such as mean-reverting jump-diffusions and Markov regime-switching models [
17,
18,
19,
20,
21,
22,
23] are expected to perform better on a daily horizon level and less well on a half-hourly or hourly short-term basis, as evidence proves their poor performance [
24,
25]. A hybrid model combining both a Markov-regime switching technique and vector auto regressions in a more macroeconomic context however, as suggested by some authors [
26] might turn out to be more effective. When reviewing the statistical methods employed in the literature, Weron (2014) [
9] refers to the importance of the quality and efficiency of the methods used, highlighting the ability to incorporate filtered, and well-tested fundamental historical data (i.e., during normal days without unusual price movements or spikes). Many discussions have been promoted around the ability of statistical models to capture price volatility and sudden spikes and whether data should be filtered with a more comprehensive exploratory analysis of outlier detection prior to the application and comparison of the different methods. The majority of the literature however, tends to agree that they perform rather poorly to this extent making clear the substantial impact that extreme observations might have on the outcomes of a study and that an adequate stochastic model is essentially more suitable for detecting those price spikes. Many different methods have been suggested in the literature for addressing the issue of capturing those sudden price movements. These include variable price thresholds, regime-switching classification approaches, wavelet filtering and transformation techniques, recursive filters, and fixed price change thresholds. These seem to be the worst-performing method discussed, due to its inability to capture large time spans or seasonal behavior of the market prices [
17,
18,
25,
27,
28,
29,
30,
31]. Additional literature suggests the replacement of those spiky instances with various methods. These include finding instances in the historical data with similar patterns, taking the average/median of periods with matching temporal attributes such as the hour, the day, the month; replace spiking values with a chosen threshold; or simply deriving the mean of neighboring settlement periods and essentially prices [
19,
25,
32,
33]. With regards to artificial intelligence-based, non-parameter/linear techniques employed in the literature, there is a vast pool of them with both strengths and weaknesses. On one hand, they are found to be very flexible, powerful tools able to capture non-linear parameters, and potentially evolution and fuzziness making them more adaptable to complex dynamic systems and constraints. On the other hand, there is no systematic evidence they clearly outperform the previous families of models [
9]. Their rich and complex architecture makes them hard to compare thoroughly, and the calibration of each one of them is so unique that it makes it very challenging to establish a common basis for comparison. However the combination of multilayer perceptron architectures into hybrid models with multiple types of neural networks such as long short-term memory, convolutional neural networks, or recurrent neural networks, or other types of algorithms such as clustering, trigonometric seasonal box-cox transformation, ARIMA, residuals trend and seasonal components approaches, show potential for useful and robust forecasting tools [
5,
6,
34,
35,
36] primarily for day-ahead and spot markets. Less attention has been paid to the forecasting of real-time, balancing prices employing hybrid approaches again such as ARIMA and exponential smoothing approaches, and other combinations of multi-layer perceptron with interfering deterministic and probabilistic techniques [
37,
38,
39,
40].
Across all of the literature, a key point for predicting electricity prices is the selection of the dependent variables, the predictors. Apart from seasonal attributes, which are easily derived from the temporal nature of the output variable (price), there is strong evidence for the fundamental factors that drive the price. These include system loads (demand, consumption and generation), climatic and weather variables, fuel costs, reserve margin variables such us surplus or deficit of generation, and most recently the data around planned maintenance or forced outages of plant trips [
9,
20,
41,
42]. The aforementioned data however, is not always available or found to be significant, as shown in an indicative report for the United Kingdom (UK) market by Maciejowska [
43], who used structural vector autoregressive models, in order to capture speculative electricity shocks. The study highlighted that expected major drivers such as wind generation and supply and demand, were not the ones explaining the extreme volatility of prices in earlier years. Even though the majority of the literature selects a combination of the main fundamental drivers of prices [
44], there is not an optimal, fit-for-all, set of variables that can be established for all power markets. This is because the model category described in the previous paragraphs, the calibration and availability of the data as well as the objective of the research questions, need to be further explored in order to extract the most effective, minimum set of input variables that will not lead to under or over-fitting issues [
9].
The literature review indicates that, price forecasting research has gained a renewed focus, given the growing trend of aggregation activities and the market opening to demand response service providers. The main motivation remains the maximisation of revenues, taking advantage of the Day-Ahead (DA) and the balance markets’ most favourable moments. Aggregators manage portfolios of flexible assets, which given their finite available power, need to be assigned to the most advantageous settlement period (SP) and market, hence the need to predict the price.
This study presents the development of a multi-regression model, testing three machine learning algorithms, Gradient Boosting (GB), Random Forest (RF) and Extreme Gradient Boosting (XGBoost), presenting a combined approach of several categories according to Aggarwal et al. 2009 [
7] classification. Market historical data is used for generation, supply, load, temporal effect such as settlement period, day, month, holiday, season and nonstrategic uncertainties, such as forecast load and probability of reserves plus generation to meet demand. For this latter variable, the Loss of Load Probability (LOLP) is used with different time horizons to capture this uncertainty. The model is a tool for short term forecasting, which can be used from 12 h ahead up to 1 h before the gate closure. With resource adequacy methodologies being implemented and several metrics becoming available for the security of supply, value of loss load, loss of load expected and LOLP, new analysis are possible. In order to conduct the analysis, the ELEXON Balancing Energy Market in the UK is considered. To the best of our knowledge such approach has not been taken before, since the first full year with LOLP data included in this model, has only just become available for the year 2019.
2. Background and Data Analysis Context
2.1. Balancing Market Functioning
In Europe, electricity markets in different zones or member states (MS) may still differ in their rules, terms and operation, but may also be typically found as sequences of year-ahead, month-ahead, day-ahead, intra-day markets and at the very end the energy balancing market (also called Imbalance Market). Yet, the functioning of the balancing market is more sophisticated, as it acts as a bridge between the financial transactions (electricity market) and the physical transactions (the power system). It is the last opportunity for all parties to state a position (load/generation decrease or increase needs/availability), for each settlement period. After this stage only the Balancing Mechanism is left to balance the grid close to real time. In order to focus on a specific framework, in this study the UK Energy Balancing Market is address, which is managed by ELEXON [
45]. ELEXON has the function to oversee the Balancing and Settlement Code (BSC) and ensure its implementation by providing and procuring the services required. Essentially, ELEXON compares how much electricity suppliers and generators state they will consume or produce, with actual observed volumes and enables the imbalance settlement by managing the Balancing Market. ELEXON serves around 470 market participants and settled around 44 TWh in balancing actions and partys’ imbalance volumes in the reported years of 2018/2019 [
46].
The balancing of the Transmission System is under the responsibility of the National Electricity Transmission System Operator (NETSO). NETSO acts as the System Operator (SO) and provides instructions to a party (in accordance with agreed rules), to either decrease or increase generation, or decrease or increase demand (balancing actions).
In practice, every party is required to submit details of their contracts to the BSC Systems, i.e., how much they will consume or generate. After the end of the settlement period, the BSC Systems, compare a party’s contracted (traded) volume (as they initially stated), with its metered volume (at the point of delivery) in order to determine its imbalance (difference between both information). If there is a difference that means a party is in “imbalance” situation of its contracted volume. In this case it will be subject to imbalance charges. After the energy balance and system balance actions (for system management reasons) are taken, adjustments for transmission losses are balanced, a volume-weighted average is taken to calculate the energy imbalance price or charge. Approximately one month after the Settlement Day, where the imbalance took place, parties are billed for imbalance charges. A process of reconciliation (Reconciliation Runs), which can take up to 13 months, run by the BSC Systems, updates the imbalance charges by considering actual metered data instead of the initial estimated one. There are several reasons for imbalances; these include inability of suppliers to not always accurately predict their demand, or generators not always being able to tightly control their generation, as the case of intermittent generation. In addition to this, there is always the possibility that problems with transmission lines may arise. The market trades in half hour Settlement Periods and the BSC does not require parties to meet their contracts. Nevertheless, the Transmission System must balance at every instant. After the Balance Market closes the Balancing Mechanism starts. The minimum capacity position is 1 MW. The capacity position is stated in power and minutes and a 1 min is given for ramping up and down the asset.
2.2. Characterization and Predictors for the UK Market
For the current analysis, the study focusses on the time window between, 1 January 2019 and 31 December 2019, capturing 17,520 observations, corresponding to 30 min time intervals. All the variables collected are also provided with 30 min time intervals, except for the day-ahead price given every hour, and so it was duplicated in each SP. The model uses 19 variables: LOLP with five ahead-of-time values, five corresponding De-rated Margins (DRM), Settlement Periods (SP), Production, Wind and Solar Generation, NIV or Net Imbalance Volume (NetImbVol), Weekdays, Months, Day-ahead Price (Price DA) and the Initial Transmission System Demand (Itsd), or simply system load.
The innovative part of the study is the focus on the LOLP variable. A LOLP value is a measure of scarcity in available surplus generation capacity that the NETSO will calculate for each SP. That is, for a given level of Capacity Requirement (CR) (measured in MW) on the Transmission System, the associated loss of load probability indicates the chance that there will be a lack of Total Generation Capacity (Z) (measured in MW) to meet the CR. There are two types of LOLP values—indicative and final. For a given settlement period, the NETSO produces indicative LOLP values from the available data at defined lead times (at midday the day before and at 8, 4 and 2 h ahead of gate closure for the SP). BSC parties use Indicative LOLP values as an indication of the level of scarcity anticipated ahead of gate closure for a SP. For the same SP, the NETSO produces final LOLP values from data available to it, at gate closure. The final LOLP is the best indication of expected scarcity during the SP. The Commission Interim Report of the Sector Inquiry on Capacity Mechanisms [
47] refers to a calculation of a LOLP, as a more sophisticated method to measure generation adequacy.
Pursuant to the said document [
47], LOLP quantifies the probability of a given level of unmet demand over a certain period of time. The Dynamic LOLP Function Method, is the one used by the NETSO to produce Indicative LOLP values from 1 May 2018, and final LOLP values from 1 November 2018. For a given settlement period, the dynamic model uses a direct relationship between the available generation (Z) and the Capacity Requirement (CR) as shown in Equation (1) [
48]. The term Zj is the Combined Generation Forecast developed in in Equation (2), where Xj is the Conventional Generation Forecast shown in Equation (3).
In Equation (3), the GCAPji variable is the Generation Capacity of a conventional generator and AVi is an Availability Factor. The variable Wj in Equation (2) is the Total Wind Generation Forecast and CR in Equation (1) is the Capacity Requirement. The LOLP is then presented with different time ahead values, these are 1 h, 2 h, 4 h, 8 h, and at noon (12 h) of the previous day. Due to its contribution to the model, the closer it gets to the gate closure the better the prediction of the target variable will be, because it is including all predictors. In other words, the predictions with higher certainty will the ones made 1 h before gate closure.
A crucial variable for any forecasting model is the Net Imbalance Volume. It refers to the resulting volume of positions, which were negotiated in the market for each SP. This volume is different from the one assigned to each party. A party’s imbalance position is simply its metered volumes compared to its contracted volumes. The contracted volumes are adjusted for any accepted bids and offers or delivery of Balancing Services. Energy imbalance volume = Energy − (Balancing Services + contracts). This results in a positive or negative volume of imbalance. A negative imbalance volume means that a party has under-contracted and is therefore short of energy. A positive imbalance volume means that a party has over-contracted and is therefore long on energy. The BSC Systems calculate the imbalance volumes for all parties for every settlement period. The NetImbVol is normally one of the variables used in most models. However, it cannot be a direct input to the model, as it cannot be foreseen ahead of time with sufficient accuracy. Another variable used in the model is the Initial Transmission System Demand variable (given in MW), which is the system load and refers to an average energy in each of the 48 SP of a day. The dataset used in the study is a time series, which was decomposed so as to provide information on weekdays and months. The production is kept separated as base generation (Production), distinct from Wind and Solar generation, with all values provided in MW.
3. Methodology
A multi variable regression was performed using each of the described predictors in
Section 2.2. The dataset initially had 17,520 observations. The mean value of the target variable (Price) in the dataset is £41.99 with a minimum and maximum of −88 and +375 £/MWh respectively. Due to its disproportional value, such observations would introduce high variance in the model if not removed. For this reason, they were considered as outliers and removed by applying a >99.75% and <0.25% quantile exclusion, resulting in 17,428 observations in the dataset. A summary of the main variables is presented in
Table 1.
The model is designed to read the real data for the next day and provide a forecast for each SP. For this to occur, the model reads the forecasted predictors directly from the ELEXON website. This was possible for all variables except the NIV of each SP, which due to the uncertainty of maintenance, shortages of different sorts, failures, and unscheduled interventions is not provided by ELEXON. A strategy to estimate the value of this variable was developed, identifying patterns in the historical dataset and performing a regression to the quantile decomposition.
3.1. Quantile Regression for Net Imbalance Volume
Since the NetImbVol cannot be accurately forecasted, and given the importance provided in the feature importance method contributing as the most important variable, this predictor deserves special attention. ELEXON has identified that the volume has increased over the last years steadily, however just exactly contributes to that, is difficult to predict. Therefore, a range is set on the known predictors that are to be tested, and a query will determine the NetImbVol values for those particular observations already in the dataset. In practice the python code resembles a few simple conditional selections. A pseudo-code is provided below for clarity:
Define function: which can provide a standard error of a mean (m) given a:
List (sample)
confidence level (conf) |
| Return: confidence interval based on: (m, m + conf, m − conf) |
Define: tolerance levels to search historical dataset variables:
searchMin, searchMax = 0.3, 1.7 |
Call variables: Tolerance levels are multiplied by real readings of:
Demand (itsd (MW))
Production (MW)
Wind (MW)
Solar (MW) |
For: a range of 0 to 48 settlement periods:
Return: all NetImbVol of the historical dataset based on the variables between the tolerances [searchMin, searchMax]
Create: a list (sample) with the returned values |
Call function for:
(sample, 0.95 quantile)
(sample, 0.90 quantile)
(sample, 0.80 quantile)
(sample, 0.05 quantile) |
The above pseudo-code explains how the model looks back at historical data from the training dataset and filters the Net Imbalance Volumes observed, in days and settlement periods under similar market conditions, (production, demand, wind and solar generation). The user is able to set the ‘sensitivity/tolerance’ search limits in the historical data, which will subsequently return a smaller or larger sample/list of historical NIV data for each settlement period. As the dataset increases with more historical data (the reason for training the model), these limits can be adjusted in an iterative process in order to increase the accuracy. The query shown in the code, returns a list of NetImbVol values, to which a decomposition of quantiles (5%, 80%, 90% and 95%) is performed. The resulting sets are then input into the model, one at a time as possible NetImbVol values and different regressions are run, one for each of the quantiles. The goal is to incorporate the uncertainty related to this predictor and reflect it in the target variable prediction (Imbalance Price).
3.2. XGBRegressor
When choosing an algorithm, several factors must be considered depending on the problem to be solved. These factors can be the pre-processing requirements, whether it’s a time series set of data, and accuracy level acceptability. Moreover, the speed of running the model and how fast it is to train, or even its complexity, as well as the number of predictors considered. In the current case, it is a time series with no heavy processing power required. It may take longer to train than to provide a prediction. Since the goal is to understand the dynamics and direction of the price, and not so much precisely forecast the absolute value of each SP price, we will consider an R2 score to be very low and unacceptable if under or 50% but would be very acceptable above 65%. A reasonably high number of predictors is being considered with reasonable complexity. Three algorithms were chosen, Random Forest [
49], Gradient Boosting [
50] and XGBoost [
51]. The first two were tested but did not perform well on variable dependency and accuracy respectively, hence the XGBoost was used. When compared to RF or GB the feature importance provided by the XGBoost presents larger variety of contributions. This is an advantage since the most important variable in the GB and RF algorithms is the NetImbVol which is not predictable. XGBoost is a relatively new algorithm in machine learning. It basically follows the principle of gradient boosting, but contains some differences in modeling details. The difference between both, lies on the use of a more normalized model description in the XGBoost. This is used to control over-fitting and typically results in a better model overall performance. From a vast number of hyperparameters, special interest is typically given to: Number of subtrees to be trained (n_estimators), maximum tree depth each tree can grow (max_depth), learning rate, reg_alpha and reg_lambda which are regularization terms that influence the weight at the leaves and the scattering.
3.3. Data Set Analysis
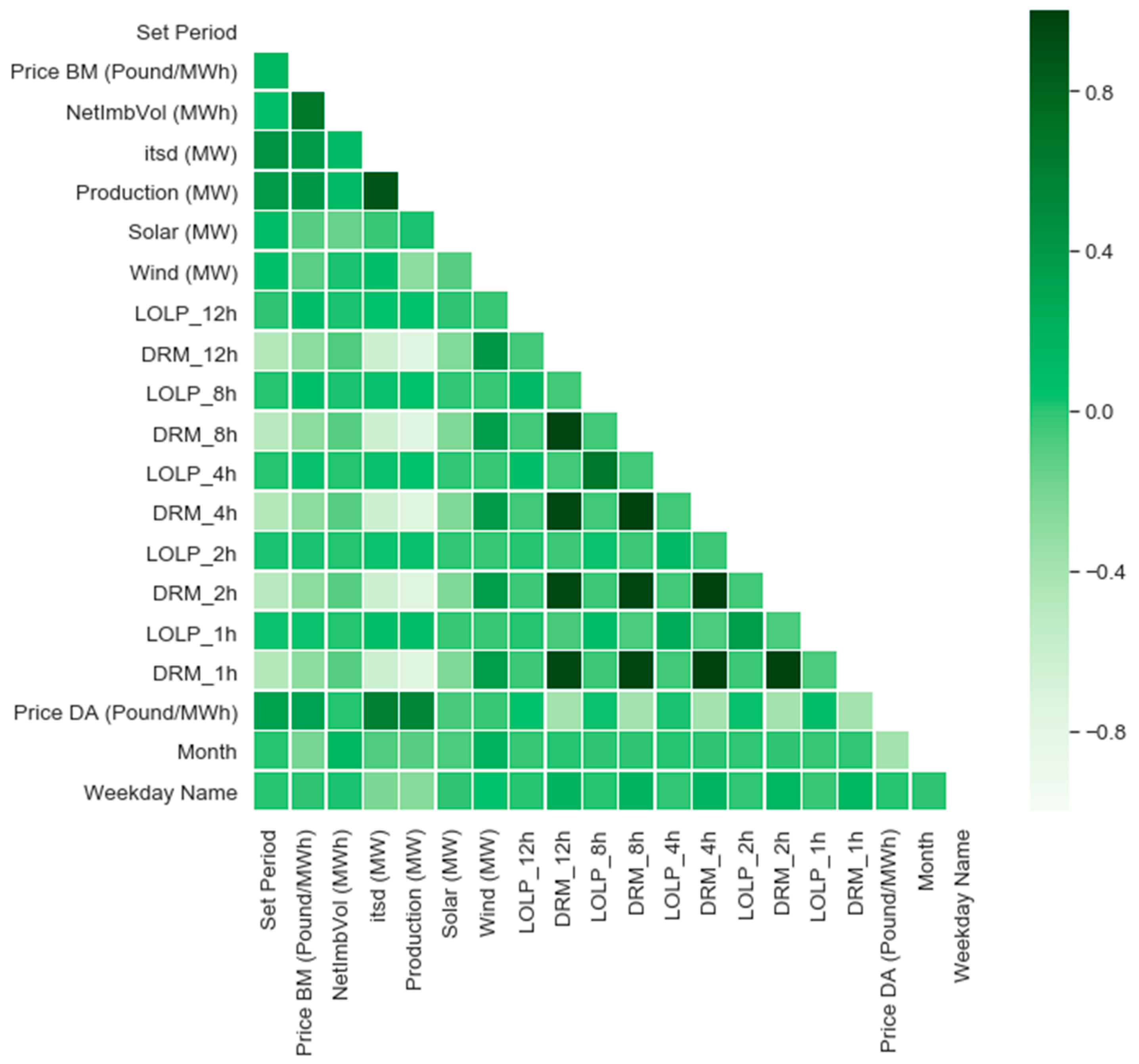
To check for variable independence, a correlation matrix was generated and can be seen in
Figure 2.
It can be observed that there is high correlation between some LOLP variables with different time horizons and also DRM variables as expected. However, since the model is to be run several times until 1 h ahead of the closing gate, in order to provide as accurate estimations as soon as possible, the model will take into account all of these predictors. Additionally, the high correlation between production and demand stands out, which is because one should match the other at all times. The reason for keeping both of the variables is to capture any deviations between the two, which could exist and maybe have an impact on the target variable.
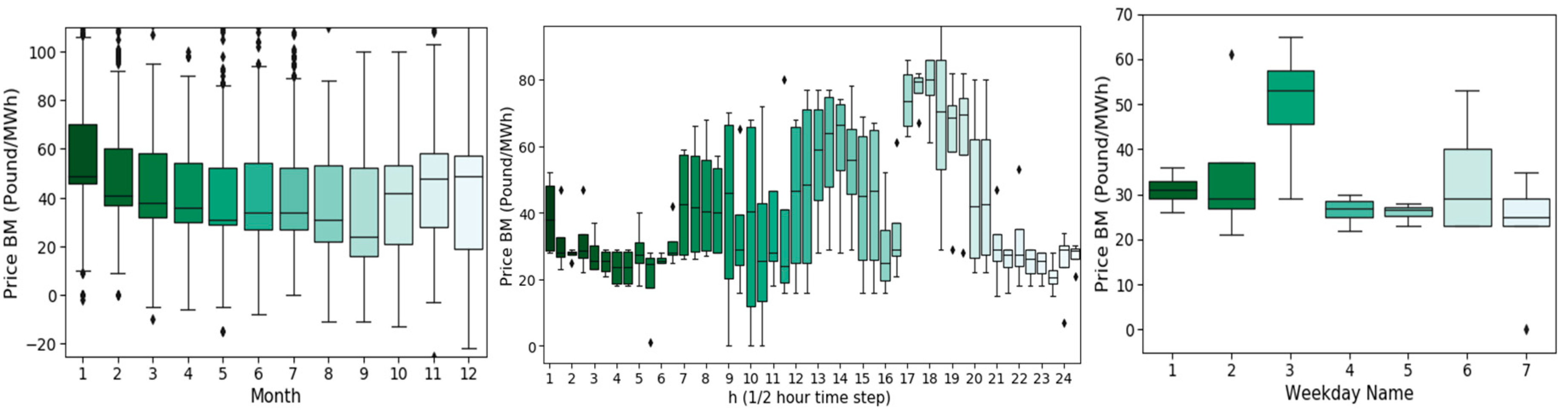
The dataset can be aggregated and observed in a static analysis with pivot tables, where monthly and daily profiles present clear trends. From each box plot a statistical distribution can be derived and the corresponding parameters extracted, if such a statistical analysis approach is desired.
Figure 3 shows the price variation per month of the year 2019, per SP and weekday, with an example of the price variation for the month of June on Tuesdays.
By analyzing each weekday, the corresponding statistical distribution may be extracted.
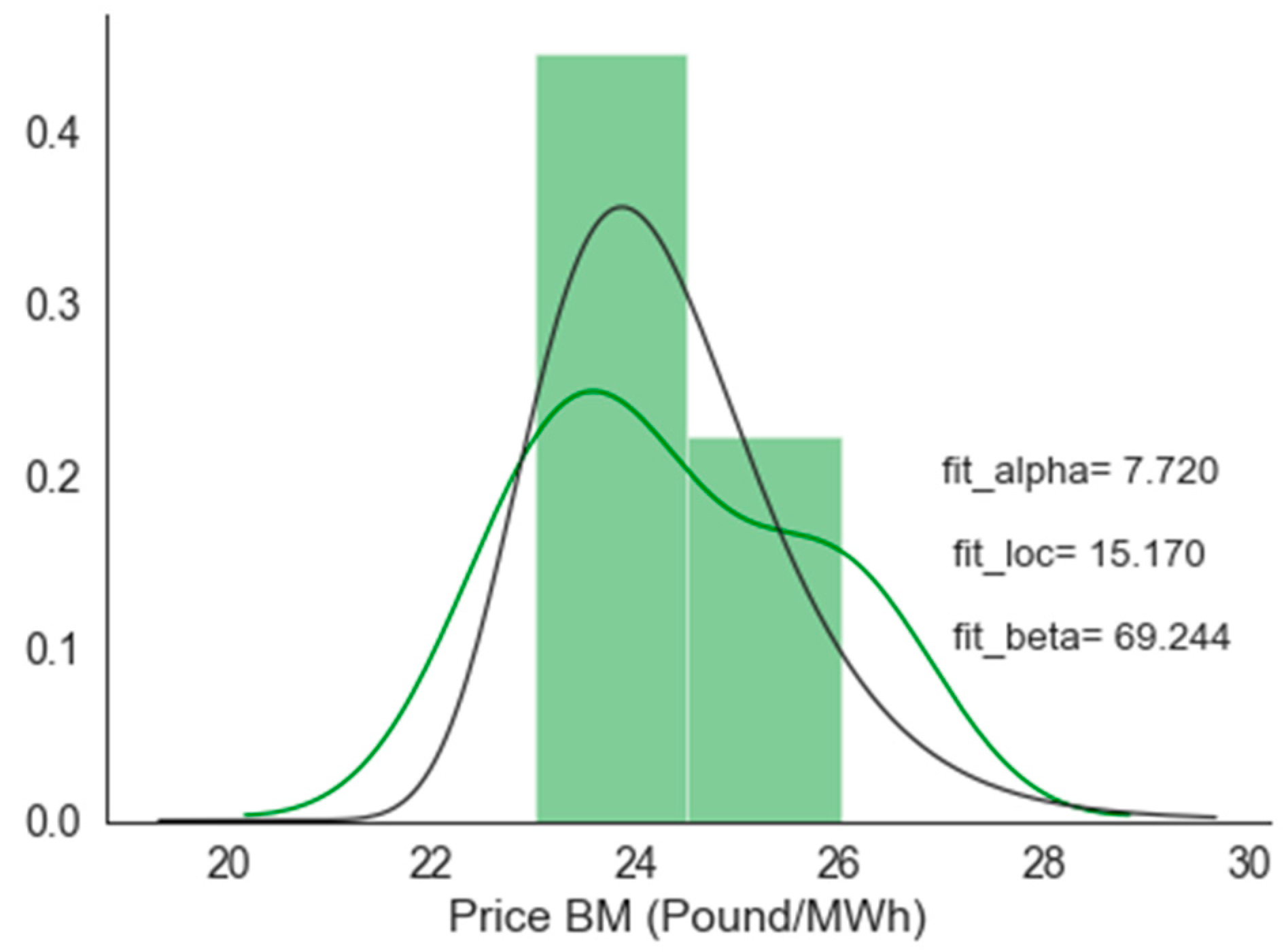
Figure 4 provides the example for a given Sunday, SP 32 and the month of June, fitting an alpha distribution, and showing also the corresponding parameters describing the distribution.
Regarding the regressions used, a 90–10% training and test linear split in time was performed. All three algorithms were analyzed regarding its feature importance and metrics performance. The real time implementation is then developed with the best performing one.
4. Results and Discussion
In this study the Randomized Parameter Optimization was used, which is the randomized search cross validation (CV) method provided by the scikit-learn [
52] library. The hyperparameter tuning is a brute force optimization problem solving, which maximizes the model score. Depending on the steps defined for each variable to be tried, it may take several hours to find the optimal solution. The optimal solutions provided by the optimization of hyperparameters are provided in
Table 2 for each of the algorithms run, so that the results can be replicated.
Table 3 shows the three metrics assessed for each algorithm. The models show medium high R2 scores which is the coefficient of determination, confirmed by the explained variance score. The fact that some outliers were removed might have contributed to a low variance, also visible in the mean absolute error (MAE). However, when the model fails, it fails by a lot, which can be seen in the mean squared error (MSE). When the model is run without the LOLP variables (baseline), it can be seen the decrease in the ability of the model to predict the target variable for example in the R2 score.
It should be mentioned that the accuracies reported in
Table 3, consider the ability to predict the test part of the dataset, having learnt from the training part of the dataset. To have the same accuracy with real time data, would mean that the model could have access to all variables, which is not true because of the NetImbVol value being based on an estimation and quantile decomposition for regression. The feature importance reveals the variables contribution to the target variable estimation.
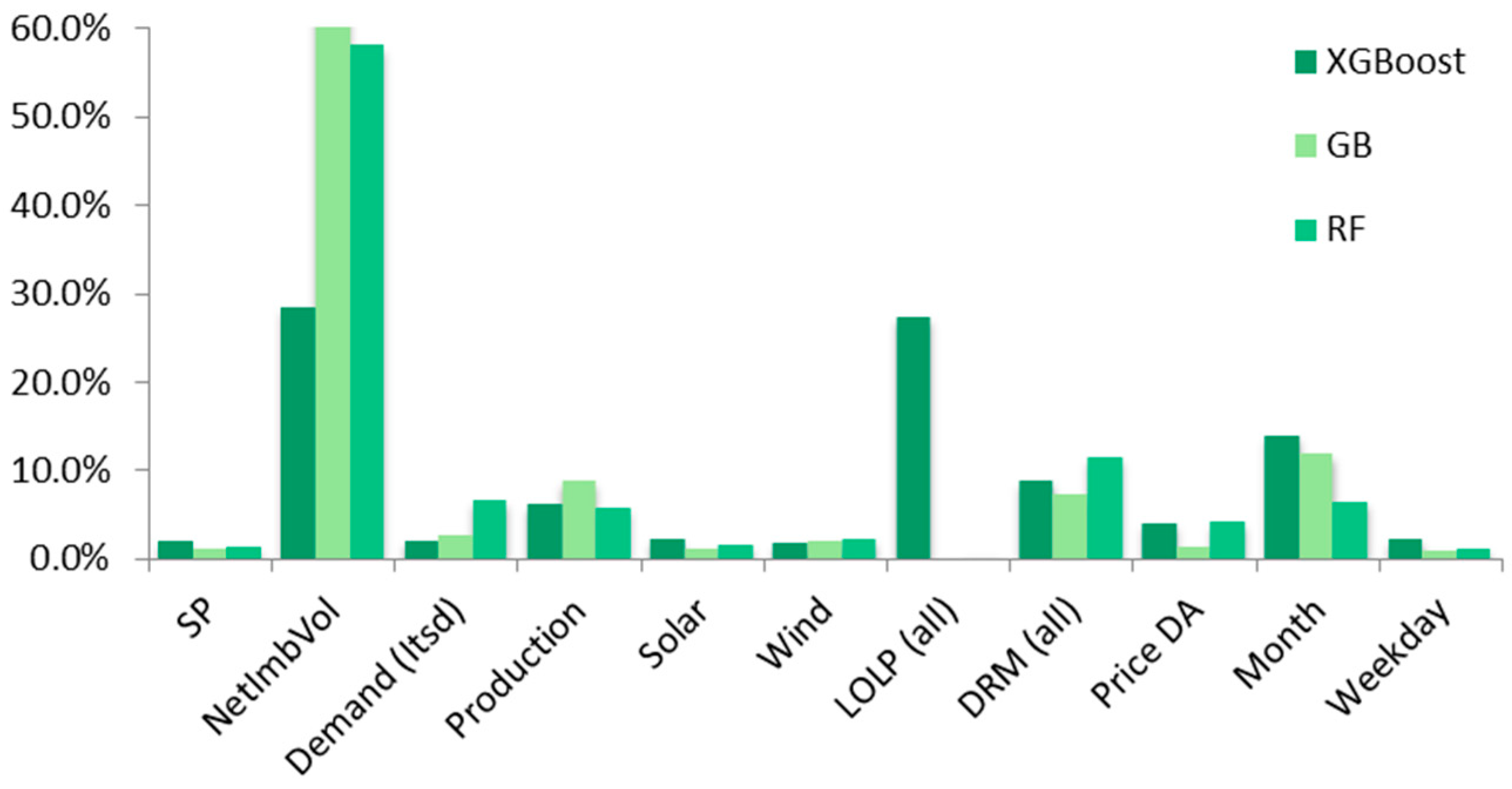
Figure 5 shows all predictors.
It can easily be seen that the impact of the NetImbVol is the greatest. However, the direction in which it contributes to the model cannot be understood. Whether the price is positively or negatively impacted with the increase of the NetImbVol and at what values such change occurs, is not observable. For this reason, the partial dependences can be calculated, where one variable is observed, while maintaining the others at a constant mean value. As an example, the RF is used for the partial dependency’s representation, however the dynamics are similar to the other algorithms, except for the amplitude. This can be seen in
Figure 6, for three predictors.
The partial dependencies show non-linear behavior. Both NetImbVol and Production predictors show increasing steps in price in precise values. Such values should be monitored carefully as they tend to prompt sudden shifts in prices. Analyzing the feature importance, given the high dependence on one variable (NetmbVol), which is the variable that cannot be predicted, the RF and GB algorithms were discarded. The XGBoost appears to be the most appropriate to continue the implementation and hence the real time forecast was performed using this algorithm.
Figure 7 presents the imbalance energy price trends for each of the 48 SP for 23 June 2020. The forecast takes into account real data extracted from the ELEXON website. The only variable, which cannot be forecasted is the Net Imbalance Volume (NetImbVol). To incorporate this uncertainty, the 95%, 90%, 80% and 5% quantiles of the query performed on the historical dataset, were subject to regressions and also shown in the
Figure 7. The result is a variation of the mean prediction, which takes into account a possible fluctuation of the NetImbVol in case its value should be within the quantile range defined.
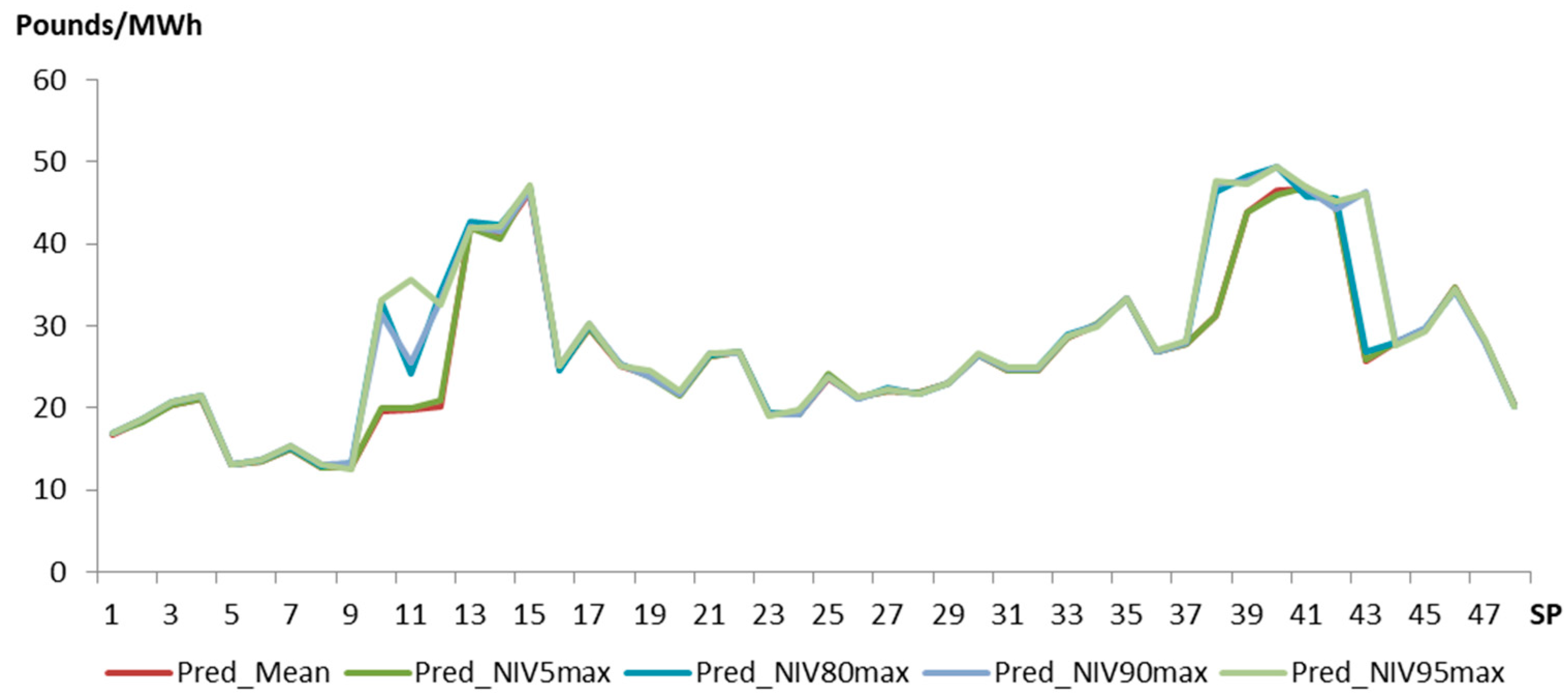
All quantiles were compared with the real observation and checked for correlation. The highest correlation is with the 95% quantile, shown with the mean curve and real observation in
Figure 8.
Comparing the forecast and the real market price, in both plots, one can observe two peaks of the real price, one in the morning period (SP 7 to 18) and one later in the evening (SP 36 to 46), and then a sudden drop at the end of the day also captured by the model. There is a lower high in the middle of the day from SP 23 to SP 30 and a small spike at SP 34, just before the last evening high. In terms of time span and precision of events, the dynamics of the prediction are acceptable in predicting the peaks. Regarding the amplitude, both peaks (morning and evening) are around 50 £/MWh with the second peak being slightly higher than the first, also predicted by the model. The middle peak is not predicted with a value of 23 £/MWh compared to 40.3 £/MWh in the real observation. The evening spike at SP 34, is predicts at SP35 with a 30.5 £/MWh value instead of 35 £/MWh in the real observation.
Regarding the bottom price instances throughout the day, minimum price forecasts predicted the market to clear at 12 £/MWh, while real price observations turned out to be just above 0 £/MWh. Such sudden drops while predicted in some cases, were unable to be followed by the model in terms of amplitude. However, since the interest is to have a fair sensitivity of the trend, the absolute values are less important, hence this behavior is acceptable. The ultimate goal is to know when to allocate the flexibility of the availabe assets. In this regard, the model can be used as a bidding strategy support tool. In the prediction shown in
Figure 8 an aggregator should aim at allocating its DR flexible assets either from SP9 to SP15 or from SP 37 to 45. Moreover, from the statistical analysis on
Figure 3 which refers to the month of June and the test day being a Tuesday (
Figure 8) one can confirm that the evening period from 18 h to 21 h (SP 36 to SP 45) would be the most advantageous period to participate in the market. The accuracy of the model is sufficient for this exercise as well as the MAE. The statistical analysis approach is a useful one, especially when it comes to analysing seasonal patterns. The LOLP variable provided a useful contribution to the model accuracy, while the uncertainty generated by the NetImbVol variable, was well mitigated by the quantile approach and regression.