Exergoeconomic Assessment of a Compact Electricity-Cooling Cogeneration Unit
Abstract
1. Introduction
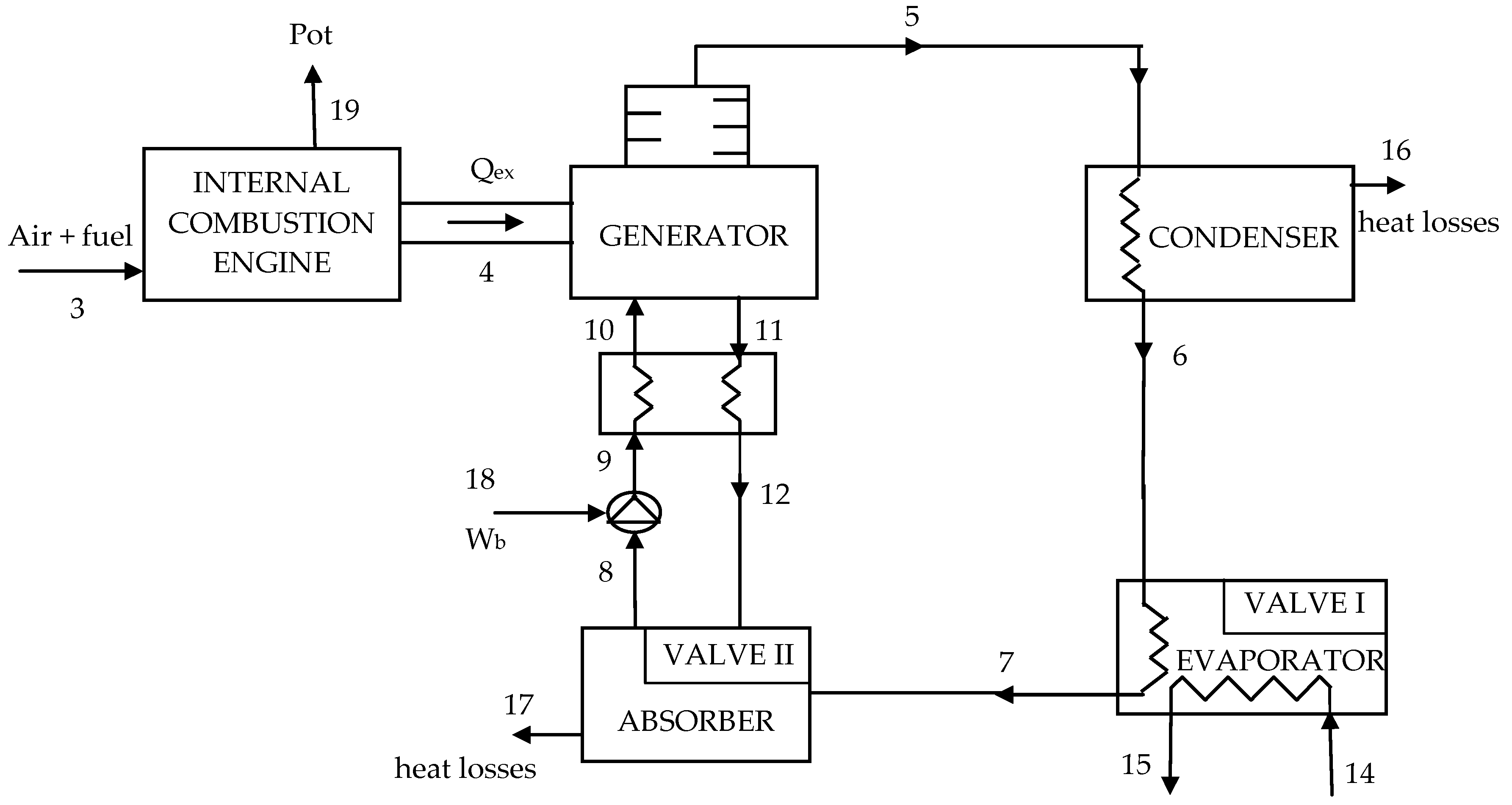
2. Case Study: Description of the Compact Cogeneration Unit
3. Thermodynamic Model
- Steady state,
- Effects of kinetic and potential energy were not considered,
- Isoentalpic expansions were considered for the expansion valves,
- Pressure drops were considered negligible within the overall system,
- Compression and expansion processes were considered adiabatic,
- All processes were internally reversible,
- Combustion air and exhaust gases were considered as ideal gas mixtures,
- Complete combustion was considered for gasoline.
4. Economic Model
5. Exergoeconomics: Application of the SPECO Method
6. Results and Discussion
6.1. Thermodynamic Results
6.2. Exergoeconomic Results
6.3. Finals Remarks
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arrieta, F.R.P.; Sodré, J.R.; Herrera, M.D.M.; Zárante, P.H.B. Exergoeconomic analysis of an absorption refrigeration and natural gas-fueled diesel power generator cogeneration system. J. Nat. Gas Sci. Eng. 2016, 36, 155–164. [Google Scholar] [CrossRef]
- Kanbur, B.B.; Xiang, L.; Dubey, S.; Choo, F.H.; Duan, F. Thermoeconomic assessment of a micro cogeneration system with LNG cold utilization. Energy 2017, 129, 171–184. [Google Scholar] [CrossRef]
- Gholizadeh, T.; Vajdi, M.; Rostamzadeh, H. Energy and exergy evaluation of a new bi-evaporator electricity/ cooling cogeneration system fueled by biogas. J. Clean. Prod. 2019, 233, 1494–1509. [Google Scholar] [CrossRef]
- Pérez, A.A.D.; Palacio, J.C.E.; Venturini, O.J.; Reyes, A.M.M.; Orozco, D.J.R.; Lora, E.E.S.; Olmo, O.A.A. Thermodynamic and economic evaluation of reheat and regeneration alternatives in cogeneration systems of the Brazilian sugarcane and alcohol sector. Energy 2018, 152, 247–262. [Google Scholar] [CrossRef]
- Pina, E.A.; Lozano, M.A.; Ramos, J.C.; Serra, L.M. Tackling thermal integration in the synthesis of polygeneration systems for buildings. Appl. Energy 2020, 269. [Google Scholar] [CrossRef]
- Amar, J.A.; Lahoud, C.; Brouche, M. Decision-making strategy for cogeneration power systems integration in the Lebanese electricity grid. Energy Procedia 2017, 119, 801–805. [Google Scholar] [CrossRef]
- Angrisani, G.; Akisawa, A.; Marrasso, E.; Roselli, C.; Sasso, M. Performance assessment of cogeneration and trigeneration systems for small scale applications. Energy Convers. Manag. 2016, 125, 194–208. [Google Scholar] [CrossRef]
- Pérez-Iribarren, E.; González-Pino, I.; Azkorra-Larrinaga, Z.; Gómez-Arriarán, I. Optimal design and operation of thermal energy storage systems in micro-cogeneration plants. Appl. Energy 2020, 265. [Google Scholar] [CrossRef]
- Freitas, L.A.; Magnani, F.S.; Hornsby, E.M. Robustness of electricity and chilled water supply systems subject to change technical and economic. IEEE Lat. Am. Trans. 2017, 15, 908–915. [Google Scholar] [CrossRef]
- Silva, H.C.N.; Ochoa, A.A.V.; Dutra, J.C.C.; Santos, C.A.C.; Costa, J.A.P. Modeling and simulation of cogeneration systems for buildings on a university campus in Northeast Brazil—A case study. Energy Convers. Manag. 2019, 186, 334–348. [Google Scholar] [CrossRef]
- Uche, J.; Acevedo, L.; Círez, F.; Usón, S.; Martínez-Gracia, A.; Bayod-Rújula, A. Analysis of a domestic trigeneration scheme with hybrid renewable energy sources and desalting techniques. J. Clean. Prod. 2019, 212, 1409–1422. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, G.; Li, D.; Wang, L.; Li, Z. Online energy management and heterogeneous task scheduling for smart communities with residential cogeneration and renewable energy. Energies 2018, 11, 2104. [Google Scholar] [CrossRef]
- Kang, E.; Lee, E.; Ghorab, M.; Yang, L.; Entchev, E.; Lee, K.; Lyu, N. Investigation of energy and environmental potentials of a renewable trigeneration system in a residential application. Energies 2016, 9, 760. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Wang, R.Z. Comparison of absorption refrigeration cycles for efficient air-cooled solar cooling. Sol. Energy 2018, 172, 14–23. [Google Scholar] [CrossRef]
- Dincer, I.; Ratlamwala, T.A.H. Integrated Absorption Refrigeration Systems: Comparative Energy and Exergy Analyses; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Bruckner, S.; Liu, S.; Miró, L.; Radspieler, M.; Cabeza, L.F.; Lavemann, E. Industrial waste heat recovery technologies: An economic analysis of heat transformation technologies. Appl. Energy 2015, 151, 157–167. [Google Scholar] [CrossRef]
- Arora, R.C. Refrigeration and Air Conditioning; PHI Learning Pvt. Ltd.: New Delhi, India, 2012. [Google Scholar]
- Sun, J.; Fu, L.; Zhang, S. A review of working fluids of absorption cycles. Renew. Sustain. Energy Rev. 2012, 16, 1899–1906. [Google Scholar] [CrossRef]
- Li, Y.; Hu, R. Exergy-analysis based comparative study of absorption refrigeration and electric compression refrigeration in CCHP systems. Appl. Therm. Eng. 2016, 93, 1228–1237. [Google Scholar] [CrossRef]
- Abdulrahim, H.K.; Darwish, M.A. Thermal desalination and air conditioning using absorption cycle. Desalin. Water Treat. 2015, 55, 3310–3329. [Google Scholar] [CrossRef]
- Ochoa, A.A.V.; Dutra, J.C.C.; Henríquez, J.R.G.; Santos, C.A.C. Dynamic study of a single effect absorption chiller using the pair LiBr/H2O. Energy Convers. Manag. 2017, 136, 270–282. [Google Scholar] [CrossRef]
- Ochoa, A.A.V.; Dutra, J.C.C.; Henríquez, J.R.G.; Dos Santos, C.A.C.; Rohatgi, J. The influence of the overall heat transfer coefficients in the dynamic behavior of a single effect absorption chiller using the pair LiBr/H2O. Energy Convers. Manag. 2017, 136, 270–282. [Google Scholar] [CrossRef]
- Bouhal, T.; Agrouaz, Y.; El Rhafiki, T.; Kousksou, T.; Zeraouli, Y.; Jamil, A. Technical assessment, economic viability and investment risk analysis of solar heating/cooling systems in residential buildings in Morocco. Sol. Energy 2018, 170, 1043–1062. [Google Scholar] [CrossRef]
- Ochoa, A.A.V.; Dutra, J.C.C.; Henríquez, J.R.G.; Santos, C.A.C.; Costa, J.A.P. Dynamic experimental analysis of a LiBr/H2O single effect absorption chiller with nominal capacity of 35 kW of cooling. Acta Technol. Sci. 2019, 41, 164–173. [Google Scholar] [CrossRef]
- Carvalho, B.C.T.; Melo, C.T.M.C.B.; Romero, A.J.; Khanmohammadi, S.; Carvalho, M. Multicriteria optimization of renewable-based polygeneration system for tertiary sector buildings. Environ. Eng. Manag. J. 2019, 18, 2441–2453. [Google Scholar] [CrossRef]
- Carvalho, M.; Delgado, D.B.M.; Chacartegui, R. Life cycle analysis as a decision criterion for the implementation of solar photovoltaic panels in as Northeast Brazil hospital. In Panagiotis Grammelis. (Org.). Energy, Transportation and Global Warming, 1st ed.; Springer International Publishing: Cham, Switzerland, 2016; Volume 1, pp. 295–314. [Google Scholar] [CrossRef]
- Delgado, D.; Carvalho, M.; Junior, L.M.C.; Abrahão, R.; Chacartegui, R. Photovoltaic solar energy in the economic optimisation of energy supply and conversion. IET Renew. Power Gener. 2018, 12, 1263–1268. [Google Scholar] [CrossRef]
- Kotas, T.J. The Exergy Method of Thermal Plant Analysis; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Carvalho, M.; Silva, J.A. Second law assessment of a Hoffmann kiln for the red ceramics industry. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 525. [Google Scholar] [CrossRef]
- Guerra, J.P.; Cardoso, F.H.; Kulay, A.N.L. Thermodynamic and environmental analysis of scaling up cogeneration units driven by sugarcane biomass to enhance power exports. Energies 2018, 11, 73. [Google Scholar] [CrossRef]
- Silva, J.A.M.; Ávila Filho, S.; Carvalho, M. Assessment of energy and exergy efficiencies in steam generators. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 3217–3226. [Google Scholar] [CrossRef]
- Marques, A.S.; Carvalho, M.; Lourenço, A.B.; Dos Santos, C.A.C. Energy, exergy, and exergoeconomic evaluations of a micro-trigeneration system. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 324. [Google Scholar] [CrossRef]
- Sharifi, M.A.R.; Khalilarya, S. Exergoeconomic evaluation and optimisation of a novel combined power and absorption-ejector refrigeration cycle driven by natural gas. Int. J. Exergy 2016, 19, 232–258. [Google Scholar] [CrossRef]
- Hou, Z.; Wei, X.; Ma, X.; Meng, X. Exergoeconomic evaluation of waste heat power generation project employing organic Rankine cycle. J. Clean. Prod. 2020, 246, 119064. [Google Scholar] [CrossRef]
- Kordlar, M.A.; Mahmoudi, S.M.S. Exergeoconomic analysis and optimization of a novel cogeneration system producing power and refrigeration. Energy Convers. Manag. 2017, 134, 208–220. [Google Scholar] [CrossRef]
- Shu, G.; Wang, X.; Tian, H.; Liang, Y.; Liu, Y.; Liu, P. Analysis of an electricity-cooling cogeneration system for waste heat recovery of gaseous fuel engines. Sci. China Technol. Sci. 2015, 58, 37–46. [Google Scholar] [CrossRef]
- Ochoa, G.V.; Peñaloza, C.A.; Forero, J.D. Thermo-economic assessment of a gas microturbine-absorption chiller trigeneration system under different compressor inlet air temperatures. Energies 2019, 12, 4643. [Google Scholar] [CrossRef]
- Baniasadi, E.; Toghyani, S.; Afshari, E. Exergetic and exergoeconomic evaluation of a trigeneration system based on natural gas-PEM fuel cell. Int. J. Hydrogen Energy 2017, 42, 5327–5339. [Google Scholar] [CrossRef]
- Baghernejad, A.; Yaghoubi, M.; Jafarpur, K. Exergoeconomic comparison of three novel trigeneration systems using SOFC, biomass and solar energies. Appl. Therm. Eng. 2016, 104, 534–555. [Google Scholar] [CrossRef]
- Yang, K.; Zhu, N.; Ding, Y.; Chang, C.; Yuan, T. Thermoeconomic analysis of an integrated combined cooling heating and power system with biomass gasification. Energy Convers. Manag. 2018, 148, 1409–1425. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, Z.; Yang, X.; Zhai, H.; Yang, X. Advanced exergy and exergoeconomic analysis of a novel liquid carbon dioxide energy storage system. Energy Convers. Manag. 2020, 205, 112391. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.; Carvalho, M.; Azevedo, J.L. Exergoenvironmental results of a eucalyptus biomass-fired power plant. Energy 2019, 189, 116188. [Google Scholar] [CrossRef]
- Wang, L.; Yang, Z.; Sharma, S.; Mian, A.; Lin, T.E.; Tsatsaronis, G.; Maréchal, F.; Yang, Y. A review of evaluation, optimization and synthesis of energy systems: Methodology and application to thermal power plants. Energies 2019, 12, 73. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Mazloum, Y.; Sayah, H.; Nemer, M. Exergy analysis and exergoeconomic optimization of a constant-pressure adiabatic compressed air energy storage system. J. Energy Storage 2017, 14, 192–202. [Google Scholar] [CrossRef]
- Kerdan, I.G.; Raslan, R.; Ruyssevelt, P.; Gálvez, D.M. An exergoeconomic-based parametric study to examine the effects of active and passive energy retrofit strategies for buildings. Energy Build. 2016, 133, 155–171. [Google Scholar] [CrossRef]
- Fathia, H.; Tahar, K.; Ali, B.Y.; Ammar, B.B. Exergoeconomic optimization of a double effect desalination unit used in an industrial steam power plant. Desalination 2018, 438, 63–82. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.; Salehi, S.; Yari, M.; Rosen, M.A. Exergoeconomic performance comparison and optimization of single-stage absorption heat transformers. Energies 2017, 10, 532. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, J.; Cao, L.; Wang, Y. Comprehensive analysis and parametric optimization of a CCP (Combined cooling and power) system driven by geothermal source. Energy 2016, 97, 470–487. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Zhao, P.; Dai, Y. Thermodynamic analysis of a new combined cooling and power system using ammonia–water mixture. Energy Convers. Manag. 2016, 117, 335–342. [Google Scholar] [CrossRef]
- Ghaebi, H.; Parikhani, T.; Rostamzadeh, H.; Farhang, B. Thermodynamic and thermoeconomic analysis and optimization of a novel combined cooling and power (CCP) cycle by integrating of ejector refrigeration and Kalina cycles. Energy 2017, 139, 262–276. [Google Scholar] [CrossRef]
- Cao, L.; Wang, J.; Wang, H.; Zhao, P.; Dai, Y. Thermodynamic analysis of a Kalina-based combined cooling and power cycle driven by low-grade heat source. Appl. Therm. Eng. 2017, 111, 8–19. [Google Scholar] [CrossRef]
- Seyfouri, Z.; Ameri, M.; Mehrabian, M.A. Exergo-economic analysis of a low-temperature geothermal-fed combined cooling and power system. Appl. Therm. Eng. 2018, 145, 528–540. [Google Scholar] [CrossRef]
- Parikhani, T.; Ghaebi, H.; Rostamzadeh, H. A novel geothermal combined cooling and power cycle based on the absorption power cycle: Energy, exergy and exergoeconomic analysis. Energy 2018, 153, 265–277. [Google Scholar] [CrossRef]
- Tian, M.W.; Parikhani, T.; Jermsittiparsert, K.; Ashraf, M.A. Exergoeconomic optimization of a new double-flash geothermal-based combined cooling and power (CCP) system at two different cooling temperatures assisted by boosters. J. Clean. Prod. 2020, 120921. [Google Scholar] [CrossRef]
- Ayou, D.S.; Eveloy, V. Energy, exergy and exergoeconomic analysis of an ultra low-grade heat-driven ammonia-water combined absorption power-cooling cycle for district space cooling, sub-zero refrigeration, power and LNG regasification. Energy Convers. Manag. 2020, 213, 112790. [Google Scholar] [CrossRef]
- Xia, J.; Guo, Y.; Li, Y.; Wang, J.; Zhao, P.; Dai, Y. Thermodynamic analysis and comparison study of two novel combined cooling and power systems with separators using CO2-based mixture for low grade heat source recovery. Energy Convers. Manag. 2020, 215, 112918. [Google Scholar] [CrossRef]
- Engineering Equation Solver. Software. 2019. Available online: http://fchartsoftware.com/ees/ (accessed on 2 September 2019).
- Herold, K.E.; Radermarcher, R.; Klein, S.A. Absorption Chillers and Heat Pumps; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Muñoz, M.; Valero, A. Thermoeconomic analysis of a cogeneration plant. In Thermodynamic Analysis and Improvement of Energy Systems; Ruixian, C., Moran, M.J., Eds.; Pergamon Press: Oxford, UK, 1989; pp. 210–219. [Google Scholar]
- Horlock, J.H. Cogeneration-combined heat and power (CHP). In Thermodynamics and Economics; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Petrakopoulou, F.; Tsatsaronis, G.; Morousk, T.; Carassai, A. Advanced exergoeconomic analysis applied to a complex energy conversion system. J. Eng. Gas Turbines Power 2012, 134, 031801. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Advanced exergy-based methods. CRC Handbook of Thermal Engineering; CRC Press LLC: Boca Raton, FL, USA, 2017; p. 107. [Google Scholar]
- Abusoglu, A.; Kanoglu, M. Exergoeconomic analysis and optimization of combined heat and power production: A review. Renew. Sustain. Energy Rev. 2009, 13, 2295–2308. [Google Scholar] [CrossRef]
- Manesh, M.H.K.; Amidpour, M.; Farhadi, A.; Salehi, G.R. Evaluation of coupling desalination with PWR nuclear power plant with pinch, exergy and thermoeconomic analysis. In Proceedings of the 16th International Conference on Nuclear Engineering, Orlando, FL, USA, 11–15 May 2008; American Society of Mechanical Engineers: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Daghigh, R.; Shafieian, A. An investigation of heat recovery of submarine diesel engines for combined cooling, heating and power systems. Energy Convers. Manag. 2016, 108, 50–59. [Google Scholar] [CrossRef]
- Alcântara, S.C.S.; Ochoa, A.A.V.; Costa, J.A.P.; Michima, P.S.A.; Silva, H.C.N. Natural gas based trigeneration system proposal to an ice cream factory: An energetic and economic assessment. Energy Convers. Manag. 2019, 197, 111860. [Google Scholar] [CrossRef]
- Vittorini, D.; Di Battista, D.; Cipollone, R. Engine oil warm-up through heat recovery on exhaust gases–Emissions reduction assessment during homologation cycles. Therm. Sci. Eng. Prog. 2018, 5, 412–421. [Google Scholar] [CrossRef]
- Valencia, G.; Fontalvo, A.; Cárdenas, Y.; Duarte, J.; Isaza, C. Energy and exergy analysis of different exhaust waste heat recovery systems for natural gas engine based on ORC. Energies 2019, 12, 2378. [Google Scholar] [CrossRef]
- Souza, R.J.; Santos, C.A.C.; Ochoa, A.A.V.; Marques, A.S.; Neto, J.L.M.; Michima, P.S.A. Proposal and 3E (energy, exergy, and exergoeconomic) assessment of a cogeneration system using an organic Rankine cycle and an Absorption Refrigeration System in the Northeast Brazil: Thermodynamic investigation of a facility case study. Energy Convers. Manag. 2020, 217, 113002. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Wang, R.Z.; Yang, C. Perspectives for low-temperature waste heat recovery. Energy 2019, 176, 1037–1043. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, N.; Pan, F.; Wang, Q.; Gao, Z.; Chen, G. Comparative study on two low-grade heat driven absorption-compression refrigeration cycles based on energy, exergy, economic and environmental (4E) analyses. Energy Convers. Manag. 2017, 133, 535–547. [Google Scholar] [CrossRef]
- Mohammadi, A.; Ahmadi, M.H.; Bidi, M.; Joda, F.; Valero, A.; Uson, S. Exergy analysis of a Combined Cooling, Heating and Power system integrated with wind turbine and compressed air energy storage system. Energy Convers. Manag. 2017, 131, 69–78. [Google Scholar] [CrossRef]
- Bagheri, B.S.; Shirmohammadi, R.; Mahmoudi, S.M.S.; Rosen, M.A. Optimization and comprehensive exergy-based analyses of a parallel flow double-effect water-lithium bromide absorption refrigeration system. Appl. Therm. Eng. 2019, 152, 643–653. [Google Scholar] [CrossRef]
- Mohtaram, S.; Omidi, M.; Lin, J.; Sun, H.; Chen, W. Exergy analysis of a multi mixture working fluid absorption refrigeration cycle. Case Stud. Therm. Eng. 2019, 15, 100540. [Google Scholar] [CrossRef]
- Schroeder, D.; Hegner, R.; Güngör, A.; Atakan, B. Exergoeconomic analysis of an HCCI engine polygeneration process. Energy Convers. Manag. 2020, 203, 112085. [Google Scholar] [CrossRef]
- Razmara, M.; Bidarvatan, M.; Shahbakhti, M.; Robinett, R.D., III. Optimal exergy-based control of internal combustion engines. Appl. Energy 2016, 183, 1389–1403. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Jia, M.; Kokjohn, S.L.; Chang, Y.; Reitz, R.D. Comprehensive analysis of exergy destruction sources in different engine combustion regimes. Energy 2018, 149, 697–708. [Google Scholar] [CrossRef]
- Song, J.; Song, H.H. Analytical Approach to the Exergy Destruction and the Simple Expansion Work Potential in the Constant Internal Energy and Volume Combustion Process. Energies 2020, 13, 395. [Google Scholar] [CrossRef]
- Shokati, N.; Khanahmadzadeh, S. The effect of different combinations of ammonia-water Rankine and absorption refrigeration cycles on the exergoeconomic performance of the cogeneration cycle. Appl. Therm. Eng. 2018, 141, 1141–1160. [Google Scholar] [CrossRef]
- Shokati, N.; Ranjbar, F.; Yari, M. A comprehensive exergoeconomic analysis of absorption power and cooling cogeneration cycles based on Kalina, part 1: Simulation. Energy Convers. Manag. 2018, 158, 437–459. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.C. Exergoeconomic and exergoenvironmental analyses of an integrated solar combined cycle system. Renew. Sustain. Energy Rev. 2017, 67, 507–519. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.; Souza, G.F.D.; Lima, M.S. Evaluation of cogeneration plant with steam and electricity production based on thermoeconomic and exergoenvironmental analyses. Int. J. Exergy 2018, 25, 203–223. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.S.; Feng, X.J.; Li, J. Energy, exergy and exergoeconomic analyses of a combined supercritical CO2 recompression Brayton/absorption refrigeration cycle. Energy Convers. Manag. 2017, 148, 360–377. [Google Scholar] [CrossRef]
- Rashidi, J.; Yoo, C.K. Exergetic and exergoeconomic studies of two highly efficient power-cooling cogeneration systems based on the Kalina and absorption refrigeration cycles. Appl. Therm. Eng. 2017, 124, 1023–1037. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Mehrpooya, M. A comprehensive exergy-based evaluation on cascade absorption-compression refrigeration system for low temperature applications-exergy, exergoeconomic, and exergoenvironmental assessments. J. Clean. Prod. 2020, 246, 119005. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, T.; Liang, Y.; Sun, H.; Zhu, Y. A novel cooling and power cycle based on the absorption power cycle and booster-assisted ejector refrigeration cycle driven by a low-grade heat source: Energy, exergy and exergoeconomic analysis. Energy Convers. Manag. 2020, 204, 112321. [Google Scholar] [CrossRef]
- Andrzejczyk, R.; Muszynski, T.; Gosz, M. Experimental investigations on heat transfer enhancement in shell coil heat exchanger with variable baffles geometry. Chem. Eng. Process. Process Intensif. 2018, 132, 114–126. [Google Scholar] [CrossRef]
- Yang, D.; Khan, T.S.; Al-Hajri, E.; Ayub, Z.H.; Ayub, A.H. Geometric optimization of shell and tube heat exchanger with interstitial twisted tapes outside the tubes applying CFD techniques. Appl. Therm. Eng. 2019, 152, 559–572. [Google Scholar] [CrossRef]
- Tahery, A.A.; Khalilarya, S.; Jafarmadar, S. Effectively designed NTW shell-tube heat exchangers with segmental baffles using flow hydraulic network method. Appl. Therm. Eng. 2017, 120, 635–644. [Google Scholar] [CrossRef]
- Khan, Z.; Khan, Z.; Tabeshf, K. Parametric investigations to enhance thermal performance of paraffin through a novel geometrical configuration of shell and tube latent thermal storage system. Energy Convers. Manag. 2016, 127, 355–365. [Google Scholar] [CrossRef]
- Riffat, S.; Aydin, D.; Powell, R.; Yuan, Y. Overview of working fluids and sustainable heating, cooling and power generation technologies. Int. J. Low Carbon Technol. 2017, 12, 369–382. [Google Scholar] [CrossRef]
- Mota-Babiloni, A.; Belman-Flores, J.M.; Makhnatch, P.; Navarro-Esbrí, J.; Barroso-Maldonado, J.M. Experimental exergy analysis of R513A to replace R134a in a small capacity refrigeration system. Energy 2018, 162, 99–110. [Google Scholar] [CrossRef]
- Gil, B.; Kasperski, J. Efficiency evaluation of the ejector cooling cycle using a new generation of HFO/HCFO refrigerant as a R134a replacement. Energies 2018, 11, 2136. [Google Scholar] [CrossRef]
- Saengsikhiao, P.; Taweekun, J.; Maliwan, K.; Sae-ung, S.; Theppaya, T. Investigation and Analysis of R463A as an Alternative Refrigerant to R404A with Lower Global Warming Potential. Energies 2020, 13, 1514. [Google Scholar] [CrossRef]
- Życzkowski, P.; Borowski, M.; Łuczak, R.; Kuczera, Z.; Ptaszyński, B. Functional Equations for Calculating the Properties of Low-GWP R1234ze (E) Refrigerant. Energies 2020, 13, 3052. [Google Scholar] [CrossRef]
- Melo, F.M.; Silvestre, A.; Carvalho, M. Carbon footprints associated with electricity generation from biomass syngas and diesel. Environ. Eng. Manag. J. EEMJ 2019, 18, 1391–1397. [Google Scholar]
- Carvalho, M.; Silva, E.S.; Andersen, S.L.; Abrahão, R. Life cycle assessment of the transesterification double step process for biodiesel production from refined soybean oil in Brazil. Environ. Sci. Pollut. Res. 2016, 23, 11025–11033. [Google Scholar] [CrossRef]
- Ochoa, A.A.; Dutra, J.C.C.; Henríquez, J.R.; Santos, C.A.C. Techno-economic and Exergoeconomic Analysis of a micro cogeneration system for a residential use. Acta Sci. Technol. 2016, 38, 327–338. [Google Scholar] [CrossRef][Green Version]
- Cavalcante, A.W.A.; Santos, C.A.C.; Ochoa, A.A.V. Thermodynamic analysis of an energy high performance systems. IEEE Lat. Am. Trans. 2017, 15, 454–461. [Google Scholar] [CrossRef]
- Cavalcanti, E.J.; Carvalho, M.; Silva, D.R. Energy, exergy and exergoenvironmental analyses of a sugarcane bagasse power cogeneration system. Energy Convers. Manag. 2020, 222, 113232. [Google Scholar] [CrossRef] [PubMed]
- Lenzen, M.; Li, M.; Malik, A.; Pomponi, F.; Sun, Y.Y.; Wiedmann, T.; Gómez-Paredes, J. Global socio-economic losses and environmental gains from the Coronavirus pandemic. PLoS ONE 2020, 15, e0235654. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, C.; Delgado, D.B.M.; Lima, K.M.; Cancela, M.C.; Siqueira, C.A.S.; Souza, D.L.B. Effects of the covid-19 pandemic on the Brazilian electricity consumption patterns. Int. J. Energy Res. 2020, e5877. [Google Scholar] [CrossRef]
- Pina, E.A.; Serra, L.M.; Lozano, M.A.; Hernández, A.; Lázaro, A. Comparative analysis and design of a solar-based parabolic trough–orc cogeneration plant for a commercial center. Energies 2020, 13, 4807. [Google Scholar] [CrossRef]
| Subsystem | Factor (%) |
|---|---|
| Generator | 25 |
| Absorber | 25 |
| Evaporator | 20 |
| Condenser | 14 |
| Regenerator | 14 |
| Pump | 2 |
| Equipment | Product | Fuel | Auxiliary Equation |
|---|---|---|---|
| Internal combustion engine | |||
| Steam generator | |||
| Condenser + valve | |||
| Evaporator | |||
| Absorber + valve | ) | ||
| Pump | Not applicable | ||
| Intermediate heat exchanger |
| # | Flows | (kg/s) | T (°C) | P (bar) | H (kJ/kg) | S (kJ/kg.K) |
|---|---|---|---|---|---|---|
| 3 | Fuel | 0.0035 | 25.0 | 1.00 | --- | --- |
| 4 | Exhaust gases | 0.0525 | 680.5 | 3.20 | --- | --- |
| 5 | Refrigerant | 0.0219 | 39.9 | 13.51 | 1297.00 | 4.24 |
| 6 | Refrigerant | 0.0219 | -12.5 | 2.63 | 166.00 | 0.65 |
| 7 | Refrigerant | 0.0219 | 5.0 | 2.63 | 1296.00 | 4.97 |
| 8 | Strong solution | 0.1599 | 42.6 | 2.63 | −30.81 | 0.51 |
| 9 | Strong solution | 0.1599 | 44.9 | 13.51 | −20.27 | 0.54 |
| 10 | Strong solution | 0.1599 | 96.5 | 13.51 | 210.10 | 1.21 |
| 11 | Weak solution | 0.1380 | 124.3 | 13.51 | 369.60 | 1.57 |
| 12 | Weak solution | 0.1380 | 62.8 | 2.63 | 102.70 | 0.85 |
| 14 | Inlet water | 1.1800 | 12.0 | --- | 50.51 | 0.18 |
| 15 | Outlet water | 1.1800 | 7.0 | --- | 29.53 | 0.11 |
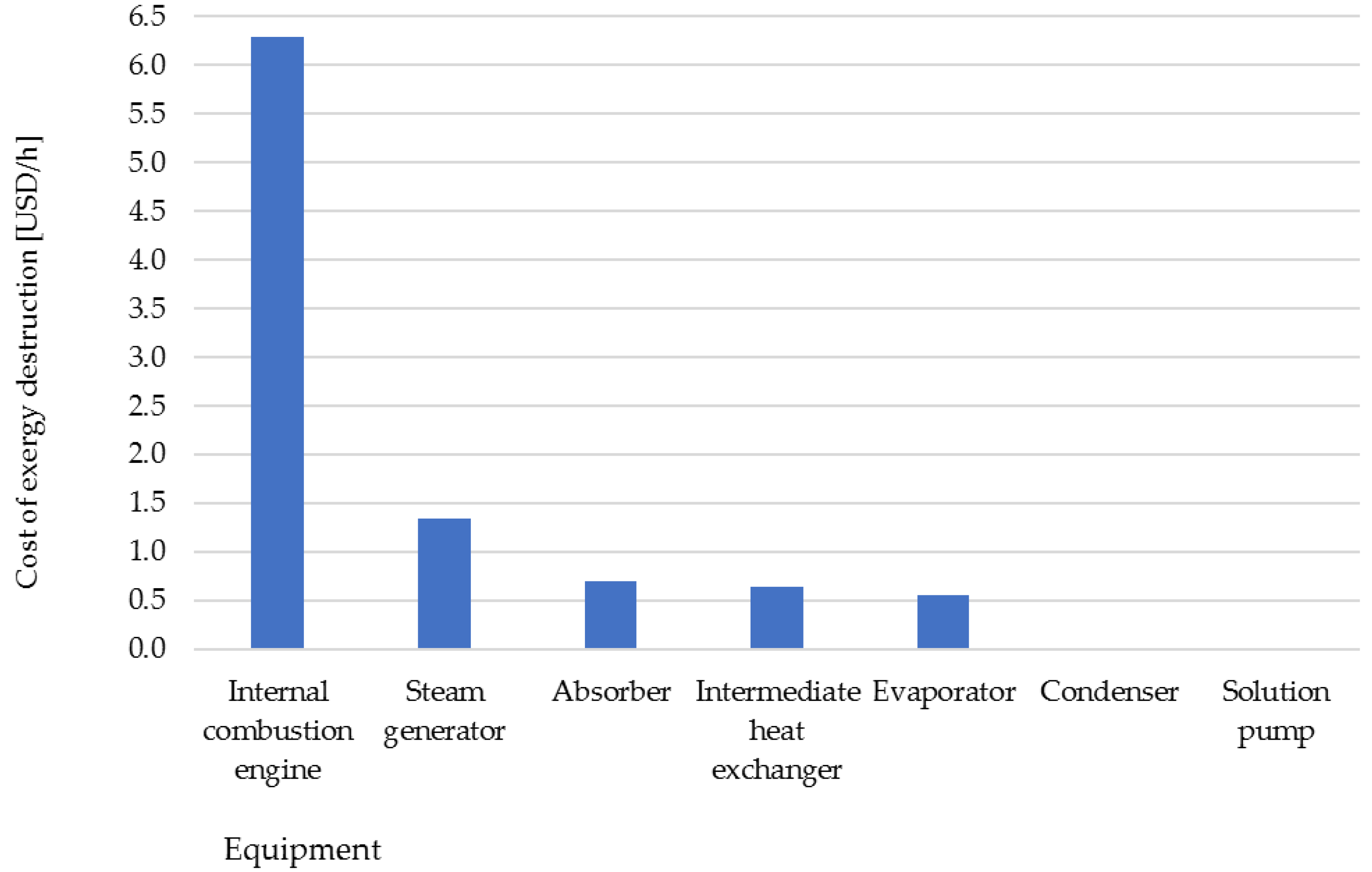
| # | Flows | ex (kJ/kg) | (USD/h) | c (USD/GJ) | |
|---|---|---|---|---|---|
| 3 | Fuel | 39790 | 138.51 | 12.84 | 25.76 |
| 4 | ICE * gases | 7205 | 25.08 | 2.32 | 25.76 |
| 5 | Refrigerant | 354.20 | 7.76 | 1.70 | 60.83 |
| 6 | Refrigerant | 314.00 | 6.88 | 1.51 | 60.83 |
| 7 | Refrigerant | 135.80 | 2.98 | 0.65 | 60.83 |
| 8 | Strong solution | 3.29 | 0.53 | 0.12 | 63.48 |
| 9 | Strong solution | 5.05 | 0.81 | 0.12 | 41.53 |
| 10 | Strong solution | 35.41 | 5.66 | 2.06 | 101.32 |
| 11 | Weak solution | 61.75 | 8.52 | 2.69 | 87.72 |
| 12 | Weak solution | 10.51 | 1.60 | 0.51 | 87.72 |
| 14 | Inlet water | 1.22 | 1.44 | 0.00 | 0.00 |
| 15 | Outlet water | 2.37 | 2.80 | 0.85 | 84.74 |
| 16 | Condenser heat | --- | 0.80 | 0.19 | 66.94 |
| 17 | Absorber heat | --- | 1.81 | 1.28 | 196.32 |
| 18 | Electricity: pump | --- | 1.69 | 0.00 | 0.00 |
| 19 | ICE * power | --- | 45.55 | 10.52 | 64.14 |
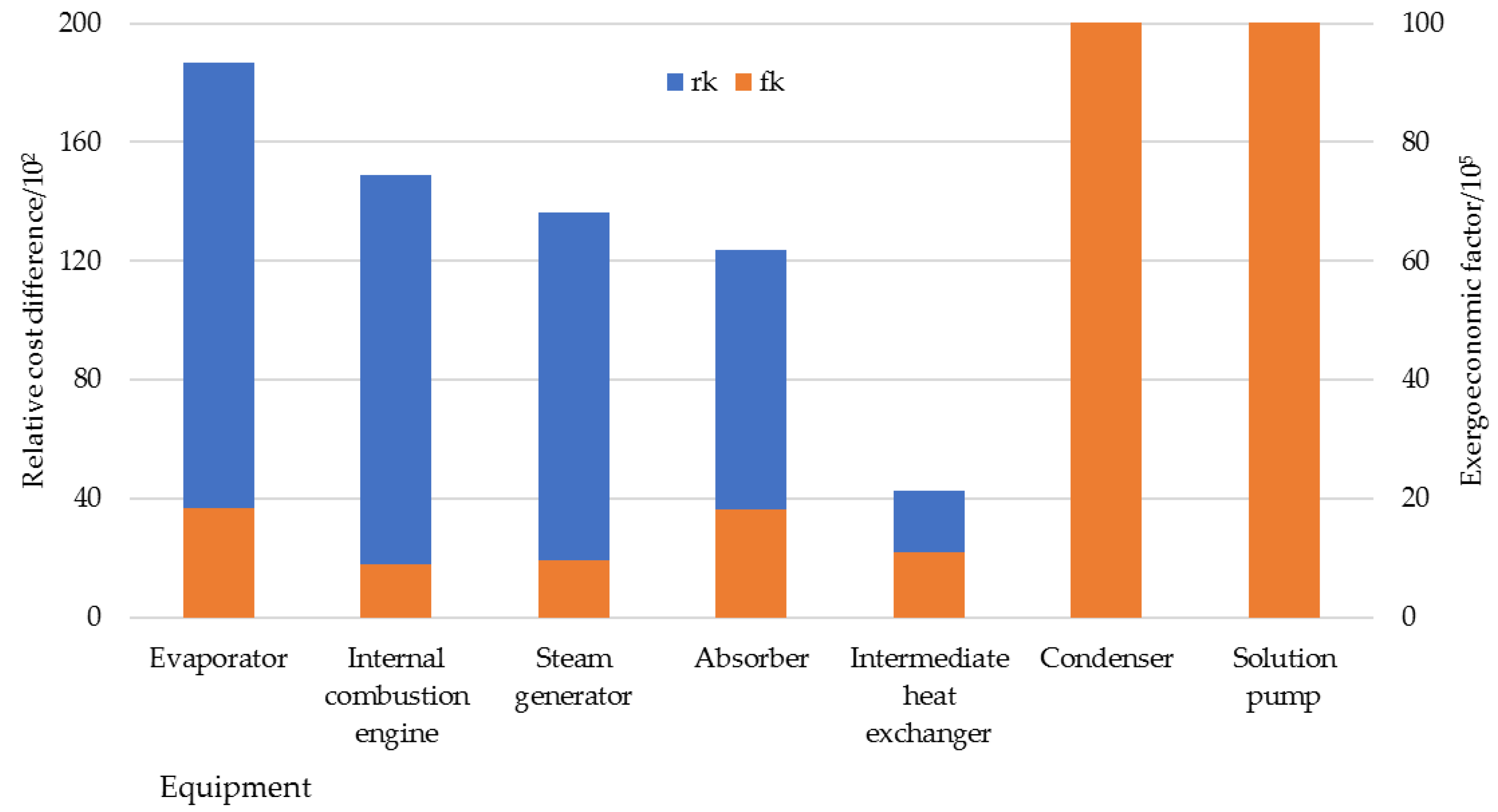
| Equipment | ε (%) | rk (%) | fk (%) | ||
|---|---|---|---|---|---|
| Internal combustion engine | 67.88 | 5.01 | 40.16 | 149.00 | 0.0091 |
| Steam generator | 14.46 | 1.13 | 42.34 | 136.20 | 0.0096 |
| Condenser | 0.08 | 0.63 | 90.91 | 10.04 | 0.4092 |
| Evaporator | 2.54 | 0.90 | 34.87 | 186.80 | 0.0185 |
| Absorber | 2.24 | 1.13 | 44.69 | 123.80 | 0.0182 |
| Pump | 1.41 | 0.09 | 16.57 | 0.00 | 100 |
| Intermediate heat exchanger | 2.07 | 0.63 | 70.09 | 42.69 | 0.0110 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marques, A.d.S.; Carvalho, M.; Ochoa, Á.A.V.; Souza, R.J.; Santos, C.A.C.d. Exergoeconomic Assessment of a Compact Electricity-Cooling Cogeneration Unit. Energies 2020, 13, 5417. https://doi.org/10.3390/en13205417
Marques AdS, Carvalho M, Ochoa ÁAV, Souza RJ, Santos CACd. Exergoeconomic Assessment of a Compact Electricity-Cooling Cogeneration Unit. Energies. 2020; 13(20):5417. https://doi.org/10.3390/en13205417
Chicago/Turabian StyleMarques, Adriano da S., Monica Carvalho, Álvaro A. V. Ochoa, Ronelly J. Souza, and Carlos A. C. dos Santos. 2020. "Exergoeconomic Assessment of a Compact Electricity-Cooling Cogeneration Unit" Energies 13, no. 20: 5417. https://doi.org/10.3390/en13205417
APA StyleMarques, A. d. S., Carvalho, M., Ochoa, Á. A. V., Souza, R. J., & Santos, C. A. C. d. (2020). Exergoeconomic Assessment of a Compact Electricity-Cooling Cogeneration Unit. Energies, 13(20), 5417. https://doi.org/10.3390/en13205417







